下载文档原格式
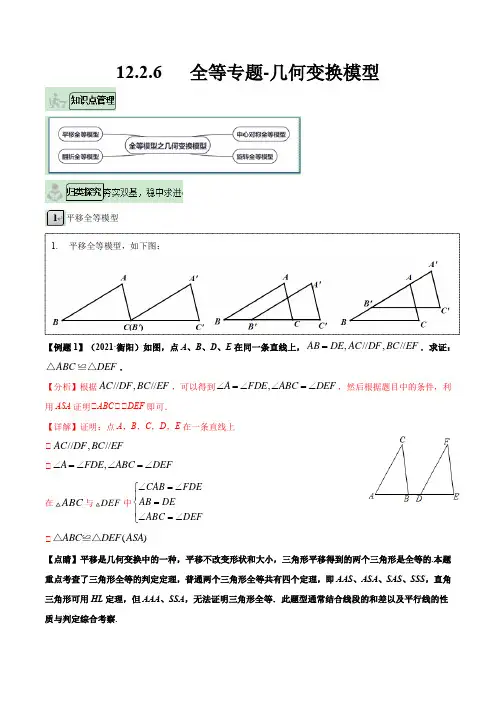
12.2.6 全等专题-几何变换模型平移全等模型【例题1】（2021·衡阳）如图，点A 、B 、D 、E 在同一条直线上，,//,//AB DE AC DF BC EF =．求证：ABC DEF △≌△．【分析】根据//,//AC DF BC EF ，可以得到,A FDE ABC DEF ∠=∠∠=∠，然后根据题目中的条件，利用ASA 证明△ABC △△DEF 即可．【详解】证明：点A ，B ，C ，D ，E 在一条直线上 △//,//AC DF BC EF△,A FDE ABC DEF ∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DEABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩△()ABC DEF ASA △≌△【点睛】平移是几何变换中的一种，平移不改变形状和大小，三角形平移得到的两个三角形是全等的.本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS 、ASA 、SAS 、SSS ，直角三角形可用HL 定理，但AAA 、SSA ，无法证明三角形全等．此题型通常结合线段的和差以及平行线的性质与判定综合考察.1. 平移全等模型，如下图：变式训练【变式1-1】（2021·河南）如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的—个作为结论，写出一个正确的命题，并加以证明． △AB DE =；△AC DF =；△ABC DEF ∠=∠；△BE CF =； 解：我写的真命题是：在ABC 和DEF 中，已知：________________． 求证：________________．（不能只填序号） 【详解】解：将△△△作为题设，△作为结论，可写出一个正确的命题，如下：已知：如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，AB DE =，AC DF =，BE CF =． 求证：ABC DEF ∠=∠． 证明：△BE CF =， △BC EF =．在ABC 和DEF 中，AB DEAC DF BC EF =⎧⎪=⎨⎪=⎩，△()ABC DEF SSS ≌． △ABC DEF ∠=∠；将△△△作为题设，△作为结论，可写出一个正确的命题，如下：已知：如图，在ABC 和DEF 中，B 、E 、C 、F 在同一直线上，AB DE =，ABC DEF ∠=∠，BE CF =． 求证：AC DF =． 证明：△BE CF =， △BC EF =．在ABC 和DEF 中，AB DEABC DEF BC EF =⎧⎪∠=∠⎨⎪=⎩，△()ABC DEF SAS ≌， △AC DF =．【变式1-2】（2021·北京一模）如图，点B ，E ，C ，F 在一条直线上，//,,AB DE AB DE BE CF ==．求证：A D ∠=∠．【分析】根据平行得出B DEF ∠=∠，然后用“边角边”证明ABC DEF △≌△即可． 【详解】证明：△//AB DE ， △B DEF ∠=∠． △BE CF =，△BE EC CF EC +=+． △BC EF =．在ABC 和DEF 中，,,,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩△ABC DEF △≌△． △A D ∠=∠．【变式1-3】（2021·湖北武汉市·九年级三模）已知：如图，点E 、C 在线段BF 上，BE ＝CF ，AB △DE ，AC △DF ．求证：△ABC △△DEF ．【分析】由BE ＝CF ，可推出BC ＝EF ，再由平行线的性质可推出△B ＝△DEF ，△ACB ＝△F ．即可利用“ASA”证明△ABC △△DEF ． 【详解】证明：△BE ＝CF ， △BC ＝EF ，△AB △DE ，AC △DF ， △△B ＝△DEF ，△ACB ＝△F ， 在△ABC 和△DEF 中，B DEFBC EF ACB F ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ， △△ABC △△DEF （ASA ）．翻折全等模型【例2】（2021·全国九年级专题练习）如图，AB ＝AD ，AC ＝AE ，△BAE ＝△DAC ．求证：△C ＝△E ． 【分析】根据△BAE =△DAC ，可推出△BAC =△DAE ，解题已知可证△BAC △△DAE 即可得出答案． 【详解】△△BAE =△DAC ，△△BAE ＋△EAC =△DAC ＋△EAC ， 即：△BAC =△DAE ． 在△BAC 和△DAE 中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩△△BAC △△DAE ． △△C =△E ．【点睛】翻折是几何变换中的一种，翻折不改变形状和大小，其实就是一种抽对称变换.翻折的边，角都对应相等．此题型通常结合公共边、公共角、角的和差以及等量代换综合考察三角形全等. 变式训练【变式2-1】（2021·苏州一模）已知：如图，点D 在AB 上，点E 在AC 上，,AD AE BD CE ==． 求证：B C ∠=∠．【分析】根据全等三角形的判定定理SAS 推出即可． 【详解】证明：△AD ＝AE ，BD ＝CE ， △AB ＝AC ，翻折全等模型，如下图：在△ABE 和△ACD 中AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩， △△ABE △△ACD （SAS ）， △△B =△C ．【变式2-2】（2021·昆明二模）如图，已知AE 平分CAD ∠，AC AD =，求证：CBE DBE ∠=∠． 【分析】根据题意得出CAB DAB ∠=∠，再利用SAS 即可证明ABC ABD △≌△，然后利用全等三角形的性质得出CBA DBA ∠=∠，最后根据等角的补角相等即可证明．【详解】证明：△AE 平分CAD ∠， △CAB DAB ∠=∠． 在ABC 和ABD △中，,,,AC AD CAB DAB AB AB =⎧⎪∠=∠⎨⎪=⎩△ABC ABD △≌△（SAS ）． △CBA DBA ∠=∠． △CBE DBE ∠=∠．【变式2-3】（2021·全国练习）你见过如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB ，CD 于点E ，F ，且AOE DOF =∠∠，你认为OE ，OF 相等吗？请说明理由．【答案】OE OF =，理由见解析【分析】连接BC ，首先证明△ABC △△DCB 可得△A =△D ，然后再证明△ABO △△DCO 可得AO =DO ，最后证明△AEO △△DFO 可得EO =FO ． 【详解】解：OE OF =；理由如下： 连接BC ，如图在ABC ∆和DCB ∆中，AB DC AC BD BC BC =⎧⎪=⎨⎪=⎩， ()ABC DCB SSS ∴∆≅∆，A D ∴∠=∠，在ABO ∆和DCO ∆中，A D AOB DOC AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABO DCO AAS ∴∆≅∆，AO DO ∴=，在AEO ∆和DFO ∆中，A D AO DOAOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()AEO DFO ASA ∴∆≅∆，EO FO ∴=．中心对称全等模型【例题3】（2020·浙江温州市·八年级期末）如图，,,AE BF AD BC DF CE===，求证：//AD CB．【分析】根据AE=BF，得到AF=BE，再利用SSS证明△ADF△△BCE，得到△A=△B，可得AD//B C．【详解】解：△AE=BF，△AE+EF=BF+EF，△AF=BE，又△AD=BC，DF=CE，△△ADF△△BCE（SSS），△△A=△B，△AD//B C．【点睛】中心对称是几何变换中的一种，中心对称不改变形状和大小，其实就是一种特殊的旋转变换（旋转180°）.中心对称的边，角都对应相等．此题型通常结合公共边、公共角、角的和差以及等量代换综合考察三角形全等.变式训练【变式3-1】（2021·辽宁大连市·九年级二模）如图，点A，F，E，D在一条直线上，AF＝DE，CF△BE，AB△CD．求证BE＝CF．中心对称全等模型，如下图：【分析】根据线段的和差关系可得AE ＝DF ，根据平行线的性质可得△D ＝△A ，△CFD ＝△BEA ，利用ASA 可证明△ABE △△DCF ，根据全等三角形的性质即可得结论． 【详解】 △AF ＝DE ，△AF ＋EF ＝DE ＋EF ，即AE ＝DF ， △AB //CD ， △△D ＝△A ， △CF //BE ， △△CFD ＝△BEA ，在△ABE △△DCF 中，A D AE DF BEA CFD ∠=∠⎧⎪=⎨⎪∠=∠⎩，△△ABE △△DCF ， △BE ＝CF ．【点睛】本题考查平行线的性质及全等三角形的判定与性质，熟练掌握相关性质及判定定理是解题关键． 【变式3-2】（2021·广东肇庆市·九年级一模）如图，四边形ABCD 的对角线交于点O ，点E 、F 在AC 上，//DF BE ，且DF BE =，AE CF =．求证：AB CD =，且//AB CD ．【详解】//DF BE BEO DFO ∴∠=∠AEB CFD ∴∠=∠又DF BE =∵，AE CF =ABE CDF ∴△≌△AB CD ∴=，BAE DCF ∠=∠ //AB CD ∴【变式3-3】（2021·山东济南市·七年级期末）如图，已知//AB CD ，AB CD =，BF CE =．求证：AE DF =且//AE DF ．【答案】见解析 【分析】先由平行线的性质得△B =△C ，结合BF EF CE EF +=+，从而利用SAS 判定△ABE △△DCF ；根据全等三角形的性质得AE DF =且//AE DF ． 【详解】 证明：BF CE =，BF EF CE EF ∴+=+，即BE CF =，//AB CD ， B C ∴∠=∠，在ABE △与CDF 中，AB CD B C BE CF =⎧⎪∠=∠⎨⎪=⎩， ()ABE CDF SAS ∴△≌△，AEB DFC ∴∠=∠，AE DF =//AE DF ∴．【点睛】本题考查了全等三角形的判定与性质，属于全等基础知识的考查，难度不大，注意证明过程的规范性．简单旋转全等模型【例题4】（2021·广东广州市·九年级一模）如图，∠B ＝∠E ，∠1＝∠2，BC ＝EC ． 求证：AB ＝DE ．【分析】先证出△ACB =△DCE ，再根据AAS 证明 △ABC △△DEC ，即可得出AB =DE ； 【详解】证明：△△1=△2 ， △△ACB =△DCE ， 在△ABC 和△DCE 中，=B E ACB DCE BC EC ⎧⎪=⎨⎪=⎩∠∠∠∠ △△ABC △△DEC (AAS )， △AB =DE ．变式训练【变式4-1】（2021·陕西中考真题）如图，//BD AC ，BD BC =，点E 在BC 上，且BE AC =．求证：D ABC ∠=∠．【分析】由题意易得EBD C ∠=∠，进而可证EDB ABC ≌△△，然后问题可求证． 【详解】证明：△//BD AC ， △EBD C ∠=∠． △BD BC =，BE AC =， △()EDB ABC SAS ≌． △D ABC ∠=∠．简单旋转全等模型，如下图：【变式4-2】（2021·昆明二模）如图所示，AC BC ⊥，DC EC ⊥，垂足均为点C ，且AC BC =，EC DC =．求证：AE BD =．【分析】根据SAS 证明ACE BCD △≌△即可．【详解】证明：△AC BC ⊥，DC EC ⊥，△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠即ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE BCD ≌△△ △AE BD =【变式4-3】在△ABC 中，AB =AC ，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD =AE ，△DAE =△BAC ，连接CE ．（1）如图1，当点D 在线段BC 上，如果△BAC =90°，则△BCE 为多少？说明理由；（2）设△BAC =α，△BCE =β．△如图2，当点D 在线段BC 上移动，则α，β之间有怎样的数量关系？请说明理由；△当点D 在直线BC 上移动，则α，β之间有怎样的数量关系？请直接写出你的结论，不需证明．【答案】（1）90°；（2）△α＋β＝180°，理由见详解；△点D 在直线BC 上移动，α＋β＝180°或α＝β．【分析】（1）由等腰直角三角形的性质可得△ABC ＝△ACB ＝45°，由“SAS”可证△BAD△△CAE ，可得△ABC ＝△ACE ＝45°，可求△BCE 的度数；（2）△由“SAS”可证△ABD△△ACE 得出△ABD ＝△ACE ，再用三角形的内角和即可得出结论；△分两种情况画出图形，由“SAS”可证△ABD△△ACE 得出△ABD ＝△ACE ，再用三角形的内角和即可得出结论．【详解】解：（1）△AB ＝AC ，△BAC ＝90°，△△ABC ＝△ACB ＝45°，△△DAE ＝△BAC ，△△BAD ＝△CAE ，且AB ＝AC ，AD ＝AE ，△△BAD△△CAE （SAS ）△△ABC ＝△ACE ＝45°，△△BCE ＝△ACB ＋△ACE ＝90°；（2）△α＋β＝180°，理由：△△BAC ＝△DAE ，△△BAC−△DAC ＝△DAE−△DAC ．即△BAD ＝△CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△ACE （SAS ），△△B ＝△ACE ．△△B ＋△ACB ＝△ACE ＋△ACB ．△△ACE ＋△ACB ＝β，△△B ＋△ACB ＝β，△α＋△B ＋△ACB ＝180°，△α＋β＝180°；△如图1：当点D 在射线BC 上时，α＋β＝180°，连接CE ，△△BAC ＝△DAE ，△△BAD ＝△CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△ACE （SAS ），△△ABD ＝△ACE ，在△ABC 中，△BAC ＋△B ＋△ACB ＝180°，△△BAC ＋△ACE ＋△ACB ＝△BAC ＋△BCE ＝180°，即：△BCE ＋△BAC ＝180°，△α＋β＝180°，如图2：当点D 在射线BC 的反向延长线上时，α＝β．连接BE ，△△BAC ＝△DAE ，△△BAD ＝△CAE ，又△AB ＝AC ，AD ＝AE ，△△ABD△△ACE（SAS），△△ABD＝△ACE，△△ABD＝△ACE＝△ACB＋△BCE，△△ABD＋△ABC＝△ACE＋△ABC＝△ACB＋△BCE＋△ABC＝180°，△△BAC＝180°−△ABC−△ACB，△△BAC＝△BCE．△α＝β；综上所述：点D在直线BC上移动，α＋β＝180°或α＝β．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质，三角形的内角和定理，证明△ABD△△ACE是解本题的关键．。
专题12.12 三角形全等作辅助线模型（二）-截长补短（知识讲解）有一类几何题其命题主要证明三条线段长段的“和”或“差”及其比例关系，这一类题目一般可以采取“截长”或“补短”的方法来进行求解。
所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段与已经线段相等，然后证明其中的另一段与已知的另一段的大小关系。
所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等，然后求出延长后的线段与最长的已知线段关系。
有的是采取截长补短后，使之构成某种特定的三角形进行求解。
【典型例题】1、 阅读下面文字并填空：数学习题课上李老师出了这样一道题：“如图1，在ABC V 中，AD 平分BAC Ð，2B C Ð=Ð．求证：AB BD AC +=．李老师给出了如下简要分析：“要证AB BD AC +=就是要证线段的和差问题，所以有两个方法，方法一：‘截长法’如图2，在AC 上截取AE AB =，连接DE ，只要证BD =__________即可，这就将证明线段和差问题__________为证明线段相等问题，只要证出V __________≌△__________，得出B AED Ð=Ð及BD =_________，再证出Ð__________=Ð___________，进而得出ED EC =，则结论成立．此种证法的基础是‘已知AD 平分BAC Ð，将ABD △沿直线AD 对折，使点B 落在AC 边上的点E 处’成为可能．方法二：“补短法”如图3，延长AB 至点F ，使BF BD =．只要证AF AC =即可．此时先证Ð__________C =Ð，再证出V _________≌△_________，则结论成立．”“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法．【答案】方法一：CE ；转化；ABD ；AED ；DE ；EDC ；C ；方法二：F ；AFD ；ACD【分析】方法一：在AC 上截取AE AB =，由SAS 可证ABD AED D @D 可得B AED Ð=Ð，BD=DE ，根据等角对等边得到CE=DE ，即可求证；方法二：延长AB 至点F ，使BF BD =，由AAS 可证AFD ACD D @D ，可得AC=AF ，即可证明：方法一：在AC 上截取AE AB =，连接DE ，如图2∵AD 平分BAC Ð，∴BAD DAC Ð=Ð，在ABD D 和AED D 中AE AB BAD DAC AD AD =ìïÐ=Ðíï=î，∴ABD AED D @D ，∴B AED Ð=Ð，BD=DE ，∵2B C Ð=Ð，∴2AED CÐ=Ð而2AED C EDC C Ð=Ð+Ð=Ð，∴EDC C Ð=Ð，∴DE=CE ，∴AB+BD=AE+CE=AC ，故答案为：CE ；转化；ABD ；AED ；DE ；EDC ；C ；方法二：如图3，延长AB 至点F ，使BF BD =，∴F BDFÐ=Ð∴2ABD F BDF FÐ=Ð+Ð=Ð∴2ABD CÐ=Ð∴F CÐ=Ð在AFD D 和ACD D 中FAD CAD F CAD AD Ð=ÐìïÐ=Ðíï=î，∴AFD ACD D @D ，∴AC=AF ，∴AC=AB+BF=AB+BD ，故答案为：F ；AFD ；ACD ．【点拨】本题考查了全等三角形的判定和性质，属于截长补短类辅助线，核心思想为数学中的转化思想，此类题的关键是要找到最长边和最短边，然后确定截取辅助线的方式．举一反三：【变式】 数学课上，小白遇到这样一个问题：如图1，在等腰Rt ABC D 中，90BAC Ð=°，AB AC =，AD AE =，求证ABE ACD Ð=Ð；在此问题的基础上，老师补充：过点A 作AF BE ⊥于点G 交BC 于点F ，过F 作FP CD ^交BE 于点P ，交CD 于点H ，试探究线段BP ，FP ，AF 之间的数量关系，并说明理由．小白通过研究发现，AFB Ð与HFC Ð有某种数量关系；小明通过研究发现，将三条线段中的两条放到同一条直线上，即“截长补短”，再通过进一步推理，可以得出结论．阅读上面材料，请回答下面问题：（1）求证ABE ACD Ð=Ð；（2）猜想AFB Ð与HFC Ð的数量关系，并证明；（3）探究线段BP ，FP ，AF 之间的数量关系，并证明．【答案】（1）见解析；（2）HFC BFA Ð=Ð，证明见解析；（3）BP AF PF =+，证明见解析【分析】（1）利用SAS 证明ABE ACD @V V 可得结论；（2）设ABE ACD x Ð=Ð=，推出=45BFA x а+，=45HFC x а+，即可证明HFC BFA Ð=Ð；（3）过点C 作CM AC ^交AF 延长线于点M ，延长FP 交AC 于点N ，证明△ABE ≌△CAM ，得出BE AM =和M BEA Ð=Ð，从而证明△NFC ≌△MFC ，得到FM FN =和M FNC Ð=Ð，可得PN=PE ，从而得出BP=AF+PF.（1）证明：∵在△ABE 和△ACD 中，==AB AC A A AE AD ìïÐ=Ðíïî，ABE ACD \D @D （SAS ），ABE ACD \Ð=Ð；（2）设ABE ACD x Ð=Ð=，AF BE ^ ，90BAF x \Ð=°-，()=9045=45BFA x x \а-°-°+，ACD x Ð= ，45HCF x \Ð=°-，FP CD ^ ，()9045=45HFC x x \Ð=°-°-°+，HFC BFA \Ð=Ð；（3）过点C 作CM AC ^交AF 延长线于点M ，延长FP 交AC 于点N ，90BAF FAC Ð+Ð=° ，90BAF ABG Ð+Ð=°，FAC ABG \Ð=Ð，在△ABE 和△CAM 中，===BAE ACM AB AC ABE CAM ÐÐìïíïÐÐî，ABE CAM \D @D （ASA ），BE AM \=，M BEA Ð=Ð，BFA MFC NFC Ð=Ð=Ð ，FC FC =，45ACB BCM Ð=Ð=°，NFC MFC \D @D （ASA ），FM FN \=，M FNC Ð=Ð，FNC BEA \Ð=Ð，PN PE \=，∴BP BE PE AM PE AF FM PE =-=-=+-AF FN PN AF PF =+-=+.【点拨】本题考查了全等三角形的判定和性质、等腰直角三角形的性质以及等角对等边等知识点，解题的关键是根据截长补短法添加适当的辅助线，构造全等三角形证明结论，有一定难度.2、 阅读材料并完成习题：在数学中，我们会用“截长补短”的方法来构造全等三角形解决问题．请看这个例题：如图1，在四边形ABCD 中，∠BAD=∠BCD=90°，AB=AD ，若AC=2cm ，求四边形ABCD 的面积．解：延长线段CB 到E ，使得BE=CD ，连接AE ，我们可以证明△BAE ≌△DAC ，根据全等三角形的性质得AE=AC=2， ∠EAB=∠CAD ，则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°，得S 四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ，这样，四边形ABCD 的面积就转化为等腰直角三角形EAC 面积．（1）根据上面的思路，我们可以求得四边形ABCD 的面积为cm 2．（2）请你用上面学到的方法完成下面的习题．如图2，已知FG=FN=HM=GH+MN=2cm ，∠G=∠N=90°，求五边形FGHMN 的面积．【答案】（1）2；（2）4【分析】（1）根据题意可直接求等腰直角三角形EAC 的面积即可；（2）延长MN 到K ，使NK=GH ，连接FK 、FH 、FM ，由（1）易证FGH FNK V V ≌，则有FK=FH ，因为HM=GH+MN 易证FMK FMH V V ≌，故可求解．【详解】（1）由题意知21=22ABC ADC ABC ABE AEC ABCD AC S S S S S S =+=+==V V V V V 四边形，故答案为2；（2）延长MN 到K ，使NK=GH ，连接FK 、FH 、FM ，如图所示：FG=FN=HM=GH+MN=2cm ，∠G=∠N=90°，\∠FNK=∠FGH=90°，\FGH FNK V V ≌，\FH=FK ，又 FM=FM ，HM=KM=MN+GH=MN+NK ，\FMK FMH V V ≌，\MK=FN=2cm ，\12=242FGH HFM MFN FMK FGHMN S S S S S MK FN =++=´×=V V V V 五边形．【点拨】本题主要考查全等三角形的性质与判定，关键是根据截长补短法及割补法求面积的运用．举一反三：【变式】在△ABC中，∠ACB=2∠B，（1）如图①，当∠C=90°，AD为∠ABC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD．请证明AB=AC+CD；（2）①如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？请直接写出你的结论，不要求证明；②如图③，当∠C≠90°，AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想并证明．【答案】（1）证明见解析；（2）①AB=AC+CD；②AC+AB=CD，证明见解析．【分析】（1）首先得出△AED≌△ACD（SAS），即可得出∠B=∠BDE=45°，求出BE=DE=CD，进而得出答案；（2）①首先得出△AED≌△ACD（SAS），即可得出∠B=∠BDE，求出BE=DE=CD，进而得出答案；②首先得出△AED≌△ACD（SAS），即可得出∠B=∠EDC，求出BE=DE=CD，进而得出答案．（1）证明：∵AD为∠ABC的角平分线，∴∠EAD=∠CAD，在△AED和△ACD中，∵AE=AC，∠EAD=∠CAD，AD=AD，∴△AED≌△ACD（SAS），∴ED=CD，∠C=∠AED=90°，∵∠ACB=2∠B，∠C=90°，∴∠B=45°，∴∠BDE=45°，∴BE=ED=CD，∴AB=AE+BE=AC+CD；①AB=AC+CD．理由如下：在AB上截取AE=AC，连接DE，∵AD为∠ABC的角平分线，∴∠EAD=∠CAD，在△AED和△ACD中，∵AE=AC，∠EAD=∠CAD，AD=AD，∴△AED≌△ACD（SAS），∴ED=CD，∠C=∠AED，∵∠ACB=2∠B，∴∠AED=2∠B，∵∠B+∠BDE=∠AED，∴∠B=∠BDE，∴BE=ED=CD，∴AB=AE+BE=AC+CD；②AC+AB=CD．理由如下：在射线BA上截取AE=AC，连接DE，∵AD为∠EAC的角平分线，∴∠EAD=∠CAD，在△AED和△ACD中，∵AE=AC，∠EAD=∠CAD，AD=AD，∴△AED≌△ACD（SAS），∴ED=CD，∠ACD=∠AED，∵∠ACB=2∠B，∴设∠B=x，则∠ACB=2x，∴∠EAC=3x，∴∠EAD=∠CAD=1.5x，∵∠ADC+∠CAD=∠ACB=2x，∴∠ADC=0.5x，∴∠EDC=x，∴∠B=∠EDC，∴BE=ED=CD，∴AB+AE=BE=AC+AB=CD．【点拨】此题主要考查了全等三角形的判定与性质以及三角形外角的性质等知识，利用已知得出△AED≌△ACD是解题关键．3、（初步探索）截长补短法，是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或旋转等方式使两条短边拼合到一起，从而解决问题．（1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系；（灵活运用）（2）如图2，△ABC为等边三角形，直线a∥AB，D为BC边上一点，∠ADE交直线a 于点E，且∠ADE＝60°．求证：CD＋CE＝CA；（延伸拓展）（3）如图3，在四边形ABCD中，∠ABC＋∠ADC＝180°，AB＝AD．若点E在CB的延长线上，点F在CD的延长线上，满足EF＝BE＋FD，请直接写出∠EAF与∠DAB的数量关系．【答案】（1）DA=DC+DB，证明见详解；（2）见详解；（3）∠EAF=11802DAB°-Ð，证明见详解.【分析】（1）由等边三角形知AB=AC，∠BAC=60°，结合∠BDC=120°知∠ABD+∠ACD=180°，由∠ACE+∠ACD=180°知∠ABD=∠ACE，证△ABD≌△ACE得AD=AE，∠BAD=∠CAE，再证△ADE是等边三角形得DA=DE=DC+CE=DC+DB；（2）首先在AC上截取CM=CD，由△ABC为等边三角形，易得△CDM是等边三角形，继而可证得△ADM≌△EDC，即可得AM=EC，则可证得CD+CE=CA；（3）在DC延长线上取一点G，使得DG=BE，连接AG，先判定△ADG≌△ABE，再判定△AEF≌△AGF，得出∠FAE=∠FAG，最后根据∠FAE+∠FAG+∠GAE=360°，进而推导得到2∠FAE+∠DAB=360°，即可得出结论．解答：DA=DC+DB，理由如下：（1）如图1，延长DC到点E，使CE=BD，连接AE，∵△ABC是等边三角形，∴AB=AC，∠BAC=60°，∵∠BDC=120°，∴∠ABD+∠ACD=180°，又∵∠ACE+∠ACD=180°，∴∠ABD=∠ACE ，∴△ABD ≌△ACE （SAS ），∴AD=AE ，∠BAD=∠CAE ，∵∠BAC=60°，即∠BAD+∠DAC=60°，∴∠DAC+∠CAE═60°，即∠DAE=60°，∴△ADE 是等边三角形，∴DA=DE=DC+CE=DC+DB ，即DA=DC+DB ；（2）证明：在AC 上截取CM=CD ，∵△ABC 是等边三角形，∴∠ACB=60°，∴△CDM 是等边三角形，∴MD=CD=CM ，∠CMD=∠CDM=60°，∴∠AMD=120°，∵∠ADE=60°，∴∠ADE=∠MDC ，∴∠ADM=∠EDC ，∵直线a ∥AB ，∴∠ACE=∠BAC=60°，∴∠DCE=120°=∠AMD ，在△ADM 和△EDC 中，ADM EDC MD CDAMD ECD Ð=Ðìï=íïÐ=Ðî∴△ADM≌△EDC(ASA)，∴AM=EC，∴CA=CM+AM=CD+CE；即CD+CE=CA.（3）∠EAF=11802DAB°-Ð；证明：如图3，在DC延长线上取一点G，使得DG=BE，连接AG，∵∠ABC+∠ADC=180°，∠ABC+∠ABE=180°，∴∠ADC=∠ABE，又∵AB=AD，∴△ADG≌△ABE（SAS），∴AG=AE，∠DAG=∠BAE，∵EF=BE+FD=DG+FD=GF，AF=AF，∴△AEF≌△AGF（SSS），∴∠FAE=∠FAG，∵∠FAE+∠FAG+∠GAE=360°，∴2∠FAE+（∠GAB+∠BAE）=360°，∴2∠FAE+（∠GAB+∠DAG）=360°，即2∠FAE+∠DAB=360°，∴∠EAF=11802DAB°-Ð.【点拨】本题属于三角形综合题，主要考查了全等三角形的判定和性质，以及等边三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应角相等进行推导变形．举一反三：【变式1】 如图，AB CD ∥，BE 平分ABC Ð，CE 平分BCD Ð，点E 在AD 上，求证：BC AB CD =+.【分析】在BC 上取点F ，使BF=BA ，连接EF ，由角平分线的性质可以得出∠1=∠2，从而可以得出△ABE ≌△FBE ，可以得出∠A=∠5，进而可以得出△CDE ≌△CFE ，就可以得出CD=CF ，即可得出结论．证明：在BC 上取点F ，使BF=BA ，连接EF ，∵BE 、CE 分别是∠ABC 和∠BCD 的平分线，∴∠1=∠2，∠3=∠4，在△ABE 和△FBE 中，12AB FB BE BE =ìïÐ=Ðíï=î，∴△ABE ≌△FBE(SAS)，∴∠A=∠5，∵AB ∥CD ，∴∠A+∠D=180°，∴∠5+∠D=180，∵∠5+∠6=180°，∴∠6=∠D ，在△CDE 和△CFE 中，634D CE CE Ð=ÐìïÐ=Ðíï=î，∴△CDE ≌△CFE(AAS)，∴CF=CD ．∵BC=BF+CF ，∴BC=AB+CD．【点拨】本题考查了角平分线的性质的运用，全等三角形的判定及性质的运用，解答时运用截取法正确作辅助线是关键．【变式2】如图，在△ABC 中，60BAC Ð=°，40ACB Ð=°，P 、Q 分别在BC 、CA 上，并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线．求证：（1）BQ CQ =；（2）BQ AQ AB BP +=+．【答案】（1）见解析；（2）见解析【分析】（1）由三角形的内角和就可以得出∠ABC ＝80°，再由角平分线的性质就可以得出∠QBC ＝40°，就有∠QBC ＝∠C 而得出结论；（2）延长AB 至M ，使得BM ＝BP ，连结MP ，根据条件就可以得出∠M ＝∠C ，进而证明△AMP ≌△ACP 就可以得出结论．（1）证明：∵BQ 是ABC Ð的角平分线，∴12QBC ABC Ð=Ð．∵180ABC ACB BAC Ð+Ð+Ð=°，且60BAC Ð=°，40ACB Ð=°，∴80ABC Ð=°，∴180402QBC Ð=´°=°，∴QBC C Ð=Ð，∴BQ CQ =；（2）证明：延长AB 至M ，使得BM BP =，连结MP ．∴M BPM Ð=Ð，∵△ABC 中60BAC Ð=°，40C Ð=°，∴80ABC Ð=°，∵BQ 平分ABC Ð，∴40QBC C Ð=°=Ð，∴BQ CQ =，∵ABC M BPM Ð=Ð+Ð，∴40M BPM C Ð=Ð=°=Ð，∵AP 平分BAC Ð，∴MAP CAP Ð=Ð，在△AMP 和△ACP 中，∵M C MAP CAP AP AP Ð=ÐìïÐ=Ðíï=î，∴△AMP ≌△ACP ，∴AM AC =，∵AM AB BM AB BP =+=+，AC AQ QC AQ BQ =+=+，∴AB BP AQ BQ+=+【点拨】本题主要考查全等三角形的判定与性质的知识点，解答本题的关键是熟练掌握判定两个三角形全等的一般方法：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．。
