2020届江苏省高考数学预测卷(1)(有答案)(已纠错)
- 格式:doc
- 大小:670.50 KB
- 文档页数:25


2020届江苏省高考数学押题卷数学I一、填空题:本大题共14小题,每小题5分,计70分.请把答案写在答题纸的指定位置上.1.已知集合{|02}A x x =<<,{|11}B x x =-<<,则A B =U .2.设复数z 满足(1i)i z ⋅-=(其中i 为虚数单位),则z 的模为 .3.一组数据3,x ,5,6,7的均值为5,则方差为 .4.右图是一个算法的伪代码,其输出的结果为 .5.袋中有形状、大小都相同的5只球,其中2只白球,3只红球,从中一次随机摸出2只球,则这2只球颜色相同的概率为 .6.已知正四棱柱1111ABCD A B C D -中,AB =3,AA 1=2,P ,M 分别为BD 1,B 1C 1上的点. 若112BP PD =,则三棱锥M -PBC 的体积为______.7.在平面直角坐标系xOy 中,若双曲线)0,0(12222>>=-b a by a x 的一个焦点到一条渐近线的距离为2a ,则该双曲线的离心率为 .8. 若将函数f (x )的图象向右平移π6个单位后得到函数()π4sin 23y x =-的图象,则()π4f =______. 9. 已知函数()f x 是R 上的奇函数,当x ≥0时,f (x )=2x +m (m 为常数),则2(log 5)f -的值为______.10.已知函数2()e (1)x f x x ax =++的单调减区间为()ln ln e e b a ,,则a b 的值为______. 11.在平面直角坐标系xOy 中,A 为直线l :y =2x 上在第一象限内的点,B (5,0),以AB 为直径的 圆C 与直线l 交于另一点D .若AB ⊥CD ,则点A 的横坐标为 .12.设H 为三角形ABC 的垂心,且3450HA HB HC ++=u u u r u u u r u u u r r ,则cos BHC ∠= .13.已知函数f (x )满足1()+()x f x f x e'=,且f (0)=1,则函数[]21()3()()2g x f x f x =-的零点个数是 .14.若数列{}n a 满足21321111222n n a a a a a a --<-<<-<L L ,则称数列{}n a 为“差半递增”数列.若数列{}n a 为“差半递增”数列,其前n 项的和为n S ,且满足221()n n S a t n N *=+-∈,则实数t 的取值范围为 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出 文字说明、证明过程或演算步骤.15.(本小题满分14分)在三棱锥S —ABC 中,平面SAB ⊥平面SBC ,AB ⊥BC ,AS =AB ,过A 作AF ⊥SB ,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ‖平面ABC .(2)求证:BC ⊥SA .16.(本小题满分14分)已知△ABC 的内角的对边分别为a 、b 、c .(1)若π3B =,b =,△ABC 的面积S ,求a+c 值; (2)若()22cos C BA BC AB AC c ⋅+⋅=u u u v u u u v u u u v u u u v ,求角C .椭圆22221x y a b +=(a >b >0)的离心率为13,左焦点F 到直线l :x =9的距离为10, 圆G :(x -1)2+y 2=1.(1)求椭圆的方程;(2)若P 是椭圆上任意一点,EH 为圆G :(x -1)2+y 2=1的任一直径,求PE PH ⋅u u u r u u u r 的取值 范围;(3)是否存在以椭圆上点M 为圆心的圆M ,使得圆M 上任意一点N 作圆G 的切线,切点为T ,都满足NF NT =M 的方程;若不存在,请说明理由.18.(本小题满分16分)如图,在某商业区周边有两条公路1l 和2l ,在点O 处交汇;该商业区为圆心角π3, 半径3km 的扇形.现规划在该商业区外修建一条公路AB ,与12l l 、分别交于A B 、,要求AB 与扇形弧相切,切点T 不在12l l 、上.(1)设km,km,OA a OB b == 试用,a b 表示新建公路AB 的长度,求出,a b 满足的关系式,并写出,a b 的范围;(2)设α=∠AOT ,试用α表示新建公路AB 的长度,并且确定A B 、的位置,使得新建公路AB 的长度最短.已知函数f (x )=x 3-x +2x .(1)求函数y =f (x )在点(1,f (1))处的切线方程;(2)令g (x )2ln x +,若函数y =g (x )在(e ,+∞)内有极值,求实数a 的取值范围;(3)在(2)的条件下,对任意t ∈(1,+∞),s ∈(0,1),求证:1()()e 2eg t g s ->+- .20.(本小题满分16分)已知数列{a n },{b n }满足,2S n =(a n +2)b n ,其中n S 是数列{a n }的前n 项和.(1)若数列{a n }是首项为23,公比为13-的等比数列,求数列{b n }的通项公式; (2)若b n =n ,a 2=3,求证:数列{a n }满足a n +a n +2=2a n +1,并写出数列{a n }的通项公式;(3)在(2)的条件下,设 n n na cb =.试问,数列{c n }中的任意一项是否总可以表示成该数列其他两项之积?若可以,请证明之;若不可以,请说明理由.数学Ⅱ(附加题)满分40分考试时间30分钟21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答,每小题10分.若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.B.(选修4-2:矩阵与变换)已知线性变换T1是按逆时针方向旋转90︒的旋转变换,其对应的矩阵为M,线性变换T2:2,3x xy y'=⎧⎨'=⎩对应的矩阵为N.(1)写出矩阵M、N;(2)若直线l在矩阵NM对应的变换作用下得到方程为y=x的直线,求直线l的方程.C.选修4-4:坐标系与参数方程在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为,2sinxyαα⎧=⎪⎨=⎪⎩(α∈R,α为参数),曲线C2的极坐标方程为cos sin50ρθθ-=.(1)求曲线C1的普通方程和曲线C2的直角坐标方程;(2)设P为曲线C1上一点,Q曲线C2上一点,求线段PQ的最小值.【必做题】第22、23题,每小题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30︒,AE垂直BD于点E、F为A1B1的中点.(1)求异面直线AE与BF所成角的余弦值;(2)求平面BDF与平面AA1B1B所成二面角(锐角)的余弦值.23.(本小题满分10分)设集合S={1,2,3,…,n}(n≥5,n∈N*),集合A={a1,a2,a3}满足a1<a2<a3,且a3-a2≤2,A⊆S.(1)若n = 6,求满足条件的集合A的个数;(2)对任意的满足条件的n及A,求集合A的个数.。

2020年高考数学原创押题预测卷01(江苏卷)数学Ⅰ(考试时间:120分钟 试卷满分:160分)注意事项:1.本试卷均为非选择题(第1题~第20题,共20题).考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符. 4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、填空题(本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.) 1.已知集合{}062<--∈=x x Z x A ,{}1->=x x B ,则A B =I . 2.已知i R b a ,,∈是虚数单位,若i bibia =-+2,则ab 的值为 . 3.已知一组数据9,7,4,3,x 的平均数为5,则方差为 . 4.函数xy 15=的值域为 .5.执行如图所示的伪代码,输出的S 为 .6.双曲线12422=-y x 实轴的左端点为A ,虚轴的一个端点为B ,又焦点为F ,设点A 到直线BF 的距离为d ,则d 的值为 .7.将一个单位圆周六等分,得到6个不同的等分点,从任意取2个不同的等分点得到一条线段,则线段的长为3的概率为 .8.已知等比数列{}n a 的公比q 是正数,且352q a =,则当q a +1取得的最小时,q 值为 .9.现在有实心的正四棱柱铁器和实心的正四棱锥铁器各一个,已知它们的底面边长和高均相等,分别为n 和1.把它们在熔炉中熔化后重新铸造成一个底面半径为2,高为h 的实心圆锥体铁器(不计铸造过程中的损耗),则h 的值为 .10.已知点A,B 分别在以O 为圆心的两个同心圆上运动,且,2,1==OB OA 则-++的取值范围为 .11.若对任意正实数mab ab b Ina Inb a b a ≥+-+22)(,,恒成立,则实数m 的取值范围是 .12.已知函数),0(sin )(>=ωωx x f 若)4()4(),4()4(x f x f x f x f +=---=+-ππππ对任意的实数x 均恒成立,则ω的取值集合为 .13.已知x x ee xf 212)(-=的图象在点A 处的切线为)211(ln )(,1x x x xg l --=的图象在点B 处的切线为,2l 若21l l ⊥,则直线AB 的斜率为 . 14.在锐角三角形ABC 中,设A,B,C 的对边分别为cb a ,,成等差数列,则B accos 的取值范围为 .二、解答题(本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤) 15.(本小题满分14分)在三角形ABC 中,A 为钝角,且角A 的值和函数x y tan =与)3tan(x y -=π图象的一个公共点的横坐标相同. (1)求角A 的大小;(2)若,141sin cos sin =-C B A 求B sin 的值; 16.(本小题满分14分)如图,在六面体1111D C B A ABCD -中,已知从顶点A 出发的三条棱两两垂直,且四边形BA B A 11为矩形.(1)求证:⊥1AA 平面ABCD . (2)若11//DD BB ,求证:.//11CC AA17.(本小题满分14分)如图,椭圆)0(1:2222>>=+b a by a x C 的左、右顶点分别为21,A A ,离心率为32,其两条准线之间的距离为9. (1)求椭圆C 的标准方程;(2)设P 是曲线C 上一点,⎥⎦⎤⎢⎣⎡∈=∠3,421ππαA PA ,过2A 作P A R A 12⊥,交P A 1的延长线于点R A R 2,与C 交于点Q ,求直线PQ 斜率的取值范围.18.(本小题满分16分)如图,现要在边长为100 m 的正方形ABCD 内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为x m(x 不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为15x 2m 的圆形草地,为了保证道路畅通,岛口宽不小于60 m ,绕岛行驶的路宽均不小于10 m .(1)求x 的取值范围;(运算中2取1.4)(2)若中间草地的造价为a 元/m 2,四个花坛的造价为433ax 元/m 2,其余区域的造价为12a11元/m 2,当x 取何值时,可使“环岛”的整体造价最低?19.(本小题满分16分)已知函数f(x)=e x ,g(x)=ax 2+bx +1(a 、b ∈R ).(1)若a≠0,则a 、b 满足什么条件时,曲线y =f(x)与y =g(x)在x =0处总有相同的切线?(2)当a=1时,求函数h(x)=g(x)f(x)的单调减区间;(3)当a=0时,若f(x)≥g(x)对任意的x∈R恒成立,求b的取值的集合.20.(本小题满分16分)设等差数列{a n}的前n项和为S n,已知a1=2,S6=22.(1)求S n;(2)若从{a n}中抽取一个公比为q的等比数列{ak n},其中k1=1,且k1<k2<…<k n<…,k n∈N*.①当q取最小值时,求{k n}的通项公式;②若关于n(n∈N*)的不等式6S n>k n+1有解,试求q的值.数学Ⅱ(附加题)(考试时间:30分钟试卷满分:40分)注意事项:1.本试卷均为非选择题(第21题~第23题).考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.21.【选做题】本题包括A、B、C三小题,请选定其中两小题,并在相应的答题区域内...................作.答.,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.【选修4-2:矩阵与变换】(本小题满分10分)已知矩阵M =⎣⎢⎡⎦⎥⎤0 a b0满足:Mαi =λi αi ,其中λi (i =1,2)是互不相等的实常数,a i (i =1,2)是非零的平面列向量,λ1=1,α2=⎣⎢⎡⎦⎥⎤11,求矩阵M .B .【选修4-4:坐标系与参数方程】(本小题满分10分)已知两个动点P ,Q 分别在两条直线l 1:y =x 和l 2:y =-x 上运动,且它们的横坐标分别为角θ的正弦,余弦,θ∈[0,π].记OM →=OP →+OQ →,求动点M 的轨迹的普通方程.C .【选修4-5:不等式选讲】(本小题满分10分)解不等式:|x -1|+2|x|≤4x .【必做题】请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的A ,B ,C ,D ,E 五种商品有购买意向.已知该网民购买A ,B 两种商品的概率均为34,购买C ,D 两种商品的概率均为23,购买E 种商品的概率为12.假设该网民是否购买这五种商品中的任一种不受其他商品的影响.(1)求该网民至少购买4种商品的概率;(2)用随机变量η表示该网民购买商品的种数,求η的概率分布和数学期望.23.(本小题满分10分)设n 个正数a 1,a 2,…,a n 满足a 1≤a 2≤…≤a n (n ∈N *且n≥3). (1)当n =3时,证明:a 1a 2a 3+a 2a 3a 1+a 3a 1a 2≥a 1+a 2+a 3;(2)当n =4时,不等式a 1a 2a 3+a 2a 3a 4+a 3a 4a 1+a 4a 1a 2≥a 1+a 2+a 3+a 4也成立,请你将其推广到n(n ∈N *且n≥3)个正数a 1,a 2,…,a n 的情形,归纳出一般性的结论并用数学归纳法证明.2020年高考数学原创押题预测卷01(江苏卷)数学·全解全析1.【答案】{}2,1,0【解析】以题意知,{}{}{}2,1,0,132062-=<<-∈=<--∈=x Z x x x Z x A ,又{}1->=x x B ,所以B A ⋂={}2,1,0.2.【答案】4 【解析】因为i bibia =-+2,所以ib bi a 2+=+所以2==b a 所以ab 的值为4. 3.【答案】534 【解析】由题意可知,5)9743(51=++++x 解得2=x ,所以这组数据的方差为.534])59()57()54()53()52[(5122222=-+-+-+-+-⨯ 4.【答案】),1()1,0(+∞⋃ 【解析】令,1xt =则0≠t ,结合函数t y 5=的图象,可知函数x y 15=的值域是),1()1,0(+∞⋃.5. 【答案】42【解析】第一次循环,;17,17==S I 第二次循环;31,14==S I 第三次循环,42,11==S I 退出循环,输出的S 为42.6.【答案】262+ 【解析】易知)0,6(),0,2(F A -,由对称性不妨令)2,0(B ,则直线BF 的方程为063=-+y x 所以点A 到直线BF 的距离.262262=--=d7.【答案】52 【解析】由题意可得,不同的2个等分点构成的线段共有15条,其中满足线段长为3的线段有6条,根据古典概型的概率计算公式得,所求的概率为.52156= 8.【答案】2【解析】因为352q a =,所以3412q q a =因为q 为证数,所以,22222,211=⋅≥+=+=q qq q q a q a 当切仅当2=q 时取等号. 9.【答案】1【解析】由已知得, 实心的正四棱柱铁器和实心的正四棱锥铁器的体积之和为341)(311)(22πππ=⨯⨯+⨯,重新铸造成底面半径为2,高为h 的实心圆锥体铁器的体积为,342312h h ππ=⨯⨯所以h ππ3434=,所以.1=h 10.【答案】[4,【解析】设向量,的夹角为θ,则[],,0πθ∈OA OB OA OB ++-u u u r u u u r u u u r u u u r+=+=θθcos 45cos 45-++=.令θθcos 45cos 45-++=y ,则[],20,16cos 162521022∈-+=θy 据此可得OA OB OA OB ++-u u u r u u u r u u u r u u u r的取值范围为[4,.11.【答案】(]2,∞-【解析】因为对任意正实数mab ab b Ina Inb a b a ≥+-+22)(,,恒成立,∴对任意正实数(想)恒成立,a ba b b a a b a b b a m ln )ln (ln 1⋅+=-+≤-∴对任意正实数b a ,恒成立, .)ln (1min a b a b b a m ⋅+≤-∴令,x a b =则min )ln 1(1,0x x x m x +≤->.设,ln 1)(x x x x +=ϕ则.1ln 1)(2++-='x x x x ϕ令)()(x x g ϕ'=则)(,012)(3x x x x g ϕ'∴>+='在),0(+∞上单调递增,又∴=++-=',011ln 11)1(2ϕ当)1,0(∈x 时,,0)(<'x ϕ当),1(+∞∈x 时,ϕϕ∴>',0)(x )(x 在(0,1)上单调递减,在),1(+∞上单调递增,.2,11,1)1()(min ≤∴≤-∴==∴m m x ϕϕ12.【答案】{}N n n ∈+=,24ωω【解析】因为)4()4(),4()4(x f x f x f x f +=---=+-ππππ对任意的实数x 均恒成立,所以)(x f 的图像关于直线4π-=x 和直线4π=x 对称,所以).(2)4(4*∈=--N k k πππ).(*∈=N k kT π 因为,2ωπ=T 所以),(2*∈=N k k ω所以12sin )4(==ππk f 或1-,所以k 为正奇数,设,,12N n n k ∈+=所以ω的取值集合为{}N n n ∈+=,24ωω.13.【答案】23-【解析】易知21,l l 的斜率均存在,设直线21,l l 的斜率分别为1221)(21)(,,21=⋅⋅≥+='--x x x x e e e e x f k k ,当且仅当0=x 时等号成立,则.11≥k 因为21l l ⊥,所以121-=⋅k k ,所以.012<≤-k ,ln )(x x x g -='令,ln )(x x x h -=则11)(-='xx h ,令0)(='x h ,得1=x ,分析易知)(x h 在1=x 处取得最大值1-,所以12-≤k .因为012<≤-k ,所以1,112=-=k k ,所以,1,0==B A x x 可得A(0,0),)23,1(-B ,所以.23-=AB k14.【答案】)1,259(【解析】设,t ac= 若,c b a ≤≤则⎩⎨⎧>++=≥,,2,1222c b a c a b t 得;351<≤t 若,c b a ≥≥则⎪⎩⎪⎨⎧>+>++=≤,,,2,1222a c b a c b c a b t 得.153≤<t综上,.3553<<t ,41)1(83823324)(2cos 22222222-+=-+=+-+=-+=t t ac ac c a ac c a c a ac b c a B 所以,8348341)1(83cos 2+-=⎥⎦⎤⎢⎣⎡-+=t t t tt B a c 因为二次函数834832+-=t t y 图象的对称轴方程为,31=t 所以二次函数834832+-=t t y 在)35,53(上单调递增,所以,1259<<y 即.1cos 259<<B ac 15.(本小题满分14分)【解析】(1)由已知得)3tan(tan A A -=π,因为A 为钝角,所以),6,32(3),,2(πππππ-∈-∈A A 所以)3(A A -+=ππ,所以.32π=A (7分) (2)因为,141sin cos sin ,32=-=C B A A π 所以,141)3sin(cos 23=--B B π 所以,141)sin 3cos cos 3(sin cos 23=--B B B ππ 所以,141sin 21=B所以.71sin 21=B (14分) 16.(本小题满分14分)【解析】(1)因为从顶点A 出发的三条棱两两垂直, 所以.,11AD AA AB AA ⊥⊥因为⊂AD AB ,平面ABCD,且,A AD AB =⋂ 所以⊥1AA 平面ABCD.(7分)(2)因为11//DD BB ,⊄1BB 平面⊂111,DD CDD C 平面11CDD C , 所以//1BB 平面11CDD C ,因为平面⋂CB C B 11平面11CDD C ⊂=11,BB C C 平面,11CB C B 所以11//CC BB因为四边形BA B A 11为矩形,所以,//11BB AA 所以.//11CC AA (14分) 17.(本小题满分14分)【解析】(1)由椭圆C 的离心率为32,两条准线之间的距离为9得 ⎪⎪⎩⎪⎪⎨⎧==,92,322ca a c 得⎩⎨⎧==,2,3c a 结合222c b a +=,得5=b ,所以椭圆C 的标准方程为.15922=+y x (5分)(2)设直线P A 1的斜率为k,则,k ⎡∈⎣直线P A 1的方程是),3(+=x k y由⎪⎩⎪⎨⎧+==+)3(,15922x k y y x 消去y 得,0)59(954)59(2222=-+++k x k x k设P ,Q 的坐标分别是),(),,(2211y x y x ,由求根公式得22195)95(3kk x +-=,则219530k k y +=, 由P A R A 12⊥,得直线R A 2的方程为),3(1--=x k y 同理可得⎪⎪⎩⎪⎪⎨⎧+=+-=22222593059)59(3k k y k k x 所以)1(14559)59(395)95(3593095302222222121kk k k k k k kk k x x y y k PQ-=+--+-+-+=--=因为k k k g 1)(-=在[]3,1上单调递增,所以,2135,0⎥⎦⎤⎢⎣⎡∈PQ k 即直线PQ 的斜率的取值范围为.2135,0⎥⎦⎤⎢⎣⎡(14分)18. (本小题满分16分)【解析】(1) 由题意,得⎩⎨⎧x≥9,100-2x≥60,1002-2x -2×15x 2≥2×10,解得⎩⎪⎨⎪⎧x≥9,x≤20,-20≤x≤15,即9≤x≤15.所以x 的取值范围是[9,15].(6分) (2) 记“环岛”的整体造价为y 元,则由题意得 y =a×π×⎝⎛⎭⎫15x 22+433ax×πx 2+12a 11×[104-π×⎝⎛⎭⎫15x 22-πx 2] =a 11[π⎝⎛⎭⎫-125x 4+43x 3-12x 2+12×104], 令f(x)=-125x 4+43x 3-12x 2,则f′(x)=-425x 3+4x 2-24x =-4x ⎝⎛⎭⎫125x 2-x +6. 由f′(x)=0,解得x =0(舍去)或x =10或x =15, 列表如下:]^所以当x=10,y取最小值.答:当x=10 m时,可使“环岛”的整体造价最低.(16分)19. (本小题满分16分)【解析】(1)因为f′(x)=e x,所以f′(0)=1.又f(0)=1,所以y=f(x)在x=0处的切线方程为y=x+1.因为g′(x)=2ax+b,所以g′(0)=b.又g(0)=1,所以y=g(x)在x=0处的切线方程为y=bx+1.所以当a≠0且b=1时,曲线y=f(x)与y=g(x)在x=0处总有相同的切线.(4分)(2)由a=1,h(x)=x2+bx+1e x,所以h′(x)=-x2+(2-b)x+b-1e x=-(x-1)[x-(1-b)]e x.由h′(x)=0,得x=1或x=1-b.所以当b>0时,函数y=h(x)的减区间为(-∞,1-b),(1,+∞);当b=0时,函数y=h(x)的减区间为(-∞,+∞);当b<0时,函数y=h(x)的减区间为(-∞,1),(1-b,+∞).(10分)(3)由a=0,则φ(x)=f(x)-g(x)=e x-bx-1,所以φ′(x)=e x-b.①当b≤0时,φ′(x)>0,函数φ(x)在R上单调递增.又φ(0)=0,所以x∈(-∞,0)时,φ(x)<0,与函数f(x)≥g(x)矛盾.②当b>0时,由φ′(x)>0,得x>lnb;由φ′(x)<0,得x<lnb,所以函数φ(x)在(-∞,lnb)上单调递减,在(lnb,+∞)上单调递增.当0<b<1时,所以lnb<0.又φ(0)=0,所以φ(lnb)<0,与函数f(x)≥g(x)矛盾;当b>1时,同理φ(lnb)<0,与函数f(x)≥g(x)矛盾;当b=1时,lnb=0,所以函数φ(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.所以φ(x)≥φ(0)=0,故b=1满足题意.综上所述,b 的取值的集合为{1}.(16分) 20. (本小题满分16分)【解析】(1) 设等差数列的公差为d ,则S 6=6a 1+15d =22,因为a 1=2,解得d =23.(2分) 所以S n =n (n +5)3.(2分) (2) ① 因为数列{a n }是正项递增等差数列,所以数列{ak n }的公比q>1.要使q 最小,只需要k 2最小即可.若k 2=2,则由a 2=83,得q =a 2a 1=43,此时ak 3=2·⎝⎛⎭⎫432=329.由329=23(n +2),解得n =103N *,所以k 2>2.同理k 2>3.若k 2=4,则由a 4=4,得q =2,此时ak n =2n .因为ak n =23(k n +2),所以23(k n +2)=2n ,即k n =3×2n -1-2. 所以对任何正整数n ,ak n 是数列{a n }的第3·2n -1-2项, 所以最小的公比q =2,所以k n =3·2n -1-2.(9分) ② 因为ak n =2k n +43=2q n -1,所以k n =3q n -1-2(q>1).所以当q>1且q ∈N 时,所有的k n =3q n -1-2均为正整数,适合题意;当q>2且q N 时,k n =3q n -1-2∈N 不全是正整数,不合题意,所以q 为正整数. 而6S n >k n +1有解,所以2n (n +5)+23q n>1有解. 经检验,当q =2,q =3,q =4时,n =1都是2n (n +5)+23q n >1的解,适合题意. 下证当q≥5时,2n (n +5)+23q n >1无解,设b n =2n (n +5)+23q n , 则b n +1-b n =2[(1-q )n 2+(7-5q )n +7-q]3q n +1. 因为5q -72-2q <0,所以f(n)=2[(1-q)n 2+(7-5q)n +7-q]在n ∈N *上单调递减.因为f (1)<0,所以f(n)<0恒成立,所以b n +1-b n <0,所以b n ≤b 1恒成立.因为当q≥5时,b 1<1,所以当q≥5时,6S n >k n +1无解.综上所述,q 的取值为2,3,4.(16分)21.A .【选修4-2:矩阵与变换】(本小题满分10分)【解析】由题意,λ1,λ2是方程f(λ)=⎪⎪⎪⎪⎪⎪λ -a -b λ=λ2-ab =0的两根.因为λ1=1,所以ab =1. ①因为Mα2=λ2α2,所以⎣⎡⎦⎤0 a b 0⎣⎡⎦⎤11=λ2⎣⎡⎦⎤11,从而⎩⎪⎨⎪⎧a =λ2,b =λ2. 所以λ22=ab =1.因为λ1≠λ2,所以λ2=-1.从而a =b =-1.故矩阵M =⎣⎢⎡⎦⎥⎤0 -1-1 0.21.B .【选修4-4:坐标系与参数方程】(本小题满分10分)【解析】设M(x ,y),则⎩⎪⎨⎪⎧x =sinθ+cosθ,y =sinθ-cosθ,两式平方相加得x 2+y 2=2.又x =2sin ⎝⎛⎭⎫θ+π4,y =2sin ⎝⎛⎭⎫θ-π4,θ∈[0,π],所以x ∈[]-1,2,y ∈[]-1,2.所以动点M 轨迹的普通方程为x 2+y 2=2(x ,y ∈[]-1,2).21.C .【选修4-5:不等式选讲】(本小题满分10分)【解析】原不等式等价于⎩⎪⎨⎪⎧x≤0,1-x -2x≤4x 或⎩⎪⎨⎪⎧0<x≤1,1-x +2x≤4x 或⎩⎪⎨⎪⎧x >1,x -1+2x≤4x. 解⎩⎪⎨⎪⎧x≤0,1-x +2x≤4x ,得x ∈∅; 解⎩⎪⎨⎪⎧0<x≤1,1-x +2x≤4x ,得13≤x≤1; 解⎩⎪⎨⎪⎧x >1,x -1+2x≤4x ,得x >1. 所以原不等式的解集为⎣⎡⎭⎫13,+∞.22.(本小题满分10分)【解析】(1) 记“该网民购买i 种商品”为事件A i ,i =4,5, 则P(A 5)=34×34×23×23×12=18,P(A 4)=34×34×23×23×⎝⎛⎭⎫1-12+C 1234×⎝⎛⎭⎫1-34×23×23×12+C 1223×⎝⎛⎭⎫1-23×34×34×12=13, 所以该网民至少购买4种商品的概率为P(A 5)+P(A 4)=18+13=1124. 答:该网民至少购买4种商品的概率为1124.(2) 随机变量η的可能取值为0,1,2,3,4,5,P(η=0)=⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12=1288,P(η=1)=C 1234×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12+C 1223×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-12+12×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23=11288,P(η=2)=34×34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12+23×23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-12+C 12⎝⎛⎭⎫1-23×23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×12+C 1234×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×12+C 1234×⎝⎛⎭⎫1-34×C 1223×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12=47288,P(η=3)=1-P(η=0,1,2,4,5)=1-1288-11288-47288-13-18=97288, P(η=4)=P(A 4)=13,P(η=5)=P(A 5)=18. 所以,随机变量η的概率分布为故Eη=0×1288+1×11288+2×47288+3×97288+4×13+5×18=103.23.(本小题满分10分)【解析】(1)因为a n (n ∈N *且n≥3)均为正实数,左-右=12⎝⎛⎭⎫a 1a 3a 2+a 1a 2a 3-2a 1+12⎝⎛⎭⎫a 2a 3a 1+a 1a 2a 3-2a 2+12⎝⎛⎭⎫a 2a 3a 1+a 1a 3a 2-2a 3 ≥12⎝⎛⎭⎫2a 1a 3a 2×a 1a 2a 3-2a 1+12⎝⎛⎭⎫2a 2a 3a 1×a 1a 2a 3-2a 2+12⎝⎛⎭⎫2a 2a 3a 1×a 1a 3a 2-2a 3=0,所以,原不等式a 2a 3a 1+a 1a 3a 2+a 1a 2a 3≥a 1+a 2+a 3成立. (2)归纳的不等式为a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2≥a 1+a 2+…+a n (n ∈N *且n≥3). 记F n =a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2-(a 1+a 2+…+a n ), 当n =3(n ∈N *)时,由(1)知,不等式成立; 假设当n =k(k ∈N *且k≥3)时,不等式成立,即F k =a 1a 2a 3+a 2a 3a 4+…+a k -2a k -1a k +a k -1a k a 1+a k a 1a 2-(a 1+a 2+…+a k )≥0. 则当n =k +1时,F k +1=a 1a 2a 3+a 2a 3a 4+…+a k -2a k -1a k +a k -1a k a k +1+a k a k +1a 1+a k +1a 1a 2-(a 1+a 2+…+a k +a k +1) =F k +a k -1a k a k +1+a k a k +1a 1+a k +1a 1a 2-a k -1a k a 1-a k a 1a 2-a k +1=F k +a k -1a k ⎝⎛⎭⎫1a k +1-1a 1+a k +1⎝⎛⎭⎫a k a 1-1+a 1a 2(a k +1-a k )≥0+a 2k⎝⎛⎭⎫1a k +1-1a 1+a k +1⎝⎛⎭⎫a k a 1-1+a 1a k (a k +1-a k )=(a k +1-a k )⎝⎛⎭⎫a k a 1+a 1a k -a k +1+a k a k +1,因为a k +1≥a k ,a k a 1+a 1a k ≥2,a k +1+a k a k +1≤a k +1+a k +1a k +1=2, 所以F k +1≥0,所以当n =k +1,不等式成立.综上所述,不等式a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2≥a 1+a 2+…+a n (n ∈N *且n≥3)成立.。

2020年高考数学原创押题预测卷01(江苏卷)数学·参考答案1.{}2,1,02.43.5344.),1()1,0(+∞⋃5. 426.262+ 7.52 8.29.1 10.[4,11.(]2,∞-12.{}N n n ∈+=,24ωω13.23-14.)1,259(15.(本小题满分14分)【解析】(1)由已知得)3tan(tan A A -=π,因为A 为钝角,所以),6,32(3),,2(πππππ-∈-∈A A 所以)3(A A -+=ππ,所以.32π=A (7分) (2)因为,141sin cos sin ,32=-=C B A A π 所以,141)3sin(cos 23=--B B π 所以,141)sin 3cos cos 3(sin cos 23=--B B B ππ 所以,141sin 21=B 所以.71sin 21=B (14分)16.(本小题满分14分)【解析】(1)因为从顶点A 出发的三条棱两两垂直, 所以.,11AD AA AB AA ⊥⊥因为⊂AD AB ,平面ABCD,且,A AD AB =⋂ 所以⊥1AA 平面ABCD.(7分)(2)因为11//DD BB ,⊄1BB 平面⊂111,DD CDD C 平面11CDD C , 所以//1BB 平面11CDD C ,因为平面⋂CB C B 11平面11CDD C ⊂=11,BB C C 平面,11CB C B 所以11//CC BB因为四边形BA B A 11为矩形,所以,//11BB AA 所以.//11CC AA (14分) 17.(本小题满分14分)【解析】(1)由椭圆C 的离心率为32,两条准线之间的距离为9得 ⎪⎪⎩⎪⎪⎨⎧==,92,322ca a c 得⎩⎨⎧==,2,3c a 结合222c b a +=,得5=b ,所以椭圆C 的标准方程为.15922=+y x (5分)(2)设直线P A 1的斜率为k,则,k ⎡∈⎣直线P A 1的方程是),3(+=x k y由⎪⎩⎪⎨⎧+==+)3(,15922x k y y x 消去y 得,0)59(954)59(2222=-+++k x k x k 设P,Q 的坐标分别是),(),,(2211y x y x ,由求根公式得22195)95(3kk x +-=,则219530k k y +=, 由P A R A 12⊥,得直线R A 2的方程为),3(1--=x k y 同理可得⎪⎪⎩⎪⎪⎨⎧+=+-=22222593059)59(3k k y k k x所以)1(14559)59(395)95(3593095302222222121kk k k k k k kk k x x y y k PQ-=+--+-+-+=--=因为k k k g 1)(-=在[]3,1上单调递增,所以,2135,0⎥⎦⎤⎢⎣⎡∈PQ k即直线PQ 的斜率的取值范围为.2135,0⎥⎦⎤⎢⎣⎡(14分)18. (本小题满分16分)【解析】(1) 由题意,得⎩⎪⎨⎪⎧x≥9,100-2x≥60,1002-2x -2×15x 2≥2×10,解得⎩⎪⎨⎪⎧x≥9,x≤20,-20≤x≤15,即9≤x≤15.所以x 的取值范围是[9,15].(6分)(2) 记“环岛”的整体造价为y 元,则由题意得 y =a×π×⎝⎛⎭⎫15x 22+433ax×πx 2+12a 11×[104-π×⎝⎛⎭⎫15x 22-πx 2] =a 11[π⎝⎛⎭⎫-125x 4+43x 3-12x 2+12×104], 令f(x)=-125x 4+43x 3-12x 2,则f′(x)=-425x 3+4x 2-24x =-4x ⎝⎛⎭⎫125x 2-x +6. 由f′(x)=0,解得x =0(舍去)或x =10或x =15, 列表如下:]^所以当x =10,y 取最小值.答:当x =10 m 时,可使“环岛”的整体造价最低.(16分) 19. (本小题满分16分)【解析】(1)因为f′(x)=e x ,所以f′(0)=1.又f(0)=1, 所以y =f(x)在x =0处的切线方程为y =x +1. 因为g′(x)=2ax +b ,所以g′(0)=b.又g(0)=1,所以y =g(x)在x =0处的切线方程为y =bx +1.所以当a≠0且b =1时,曲线y =f(x)与y =g(x)在x =0处总有相同的切线.(4分) (2) 由a =1,h(x)=x 2+bx +1e x,所以 h′(x)=-x 2+(2-b )x +b -1e x =-(x -1)[x -(1-b )]e x . 由h′(x)=0,得x =1或x =1-b.所以当b>0时,函数y =h(x)的减区间为(-∞,1-b),(1,+∞);当b =0时,函数y =h(x)的减区间为(-∞,+∞);当b<0时,函数y =h(x)的减区间为(-∞,1),(1-b ,+∞).(10分) (3)由a =0,则φ(x)=f(x)-g(x)=e x -bx -1, 所以φ′(x)=e x -b.① 当b≤0时,φ′(x)>0,函数φ(x)在R 上单调递增.又φ(0)=0,所以x ∈(-∞,0)时,φ(x)<0,与函数f(x)≥g(x)矛盾.② 当b>0时,由φ′(x)>0,得x>lnb ;由φ′(x)<0,得x<lnb ,所以函数φ(x)在(-∞,lnb)上单调递减,在(lnb ,+∞)上单调递增. 当0<b<1时,所以lnb<0.又φ(0)=0,所以φ(lnb)<0,与函数f(x)≥g(x)矛盾; 当b>1时,同理φ(lnb)<0,与函数f(x)≥g(x)矛盾;当b =1时,lnb =0,所以函数φ(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增. 所以φ(x)≥φ(0)=0,故b =1满足题意. 综上所述,b 的取值的集合为{1}.(16分) 20. (本小题满分16分)【解析】(1) 设等差数列的公差为d ,则S 6=6a 1+15d =22,因为a 1=2,解得d =23.(2分) 所以S n =n (n +5)3.(2分) (2) ① 因为数列{a n }是正项递增等差数列,所以数列{ak n }的公比q>1.要使q 最小,只需要k 2最小即可.若k 2=2,则由a 2=83,得q =a 2a 1=43,此时ak 3=2·⎝⎛⎭⎫432=329.由329=23(n +2),解得n =103N *,所以k 2>2.同理k 2>3.若k 2=4,则由a 4=4,得q =2,此时ak n =2n .因为ak n =23(k n +2),所以23(k n +2)=2n ,即k n =3×2n -1-2. 所以对任何正整数n ,ak n 是数列{a n }的第3·2n -1-2项, 所以最小的公比q =2,所以k n =3·2n -1-2.(9分) ② 因为ak n =2k n +43=2q n -1,所以k n =3q n -1-2(q>1).所以当q>1且q ∈N 时,所有的k n =3q n -1-2均为正整数,适合题意;当q>2且q N 时,k n =3q n -1-2∈N 不全是正整数,不合题意,所以q 为正整数. 而6S n >k n +1有解,所以2n (n +5)+23q n>1有解. 经检验,当q =2,q =3,q =4时,n =1都是2n (n +5)+23q n >1的解,适合题意. 下证当q≥5时,2n (n +5)+23q n >1无解,设b n =2n (n +5)+23q n , 则b n +1-b n =2[(1-q )n 2+(7-5q )n +7-q]3q n +1. 因为5q -72-2q <0,所以f(n)=2[(1-q)n 2+(7-5q)n +7-q]在n ∈N *上单调递减.因为f (1)<0,所以f(n)<0恒成立,所以b n +1-b n <0,所以b n ≤b 1恒成立.因为当q≥5时,b 1<1,所以当q≥5时,6S n >k n +1无解. 综上所述,q 的取值为2,3,4.(16分) 21.A .【选修4-2:矩阵与变换】(本小题满分10分)【解析】由题意,λ1,λ2是方程f(λ)=⎪⎪⎪⎪⎪⎪λ -a -b λ=λ2-ab =0的两根.因为λ1=1,所以ab =1. ①因为Mα2=λ2α2,所以⎣⎢⎡⎦⎥⎤0a b0⎣⎢⎡⎦⎥⎤11=λ2⎣⎢⎡⎦⎥⎤11,从而⎩⎪⎨⎪⎧a =λ2,b =λ2.所以λ22=ab =1.因为λ1≠λ2,所以λ2=-1.从而a =b =-1.故矩阵M =⎣⎢⎡⎦⎥⎤0 -1-1 0.21.B .【选修4-4:坐标系与参数方程】(本小题满分10分)【解析】设M(x ,y),则⎩⎪⎨⎪⎧x =sinθ+cosθ,y =sinθ-cosθ, 两式平方相加得x 2+y 2=2.又x =2sin ⎝⎛⎭⎫θ+π4,y =2sin ⎝⎛⎭⎫θ-π4,θ∈[0,π],所以x ∈[]-1,2,y ∈[]-1,2.所以动点M 轨迹的普通方程为x 2+y 2=2(x ,y ∈[]-1,2). 21.C .【选修4-5:不等式选讲】(本小题满分10分)【解析】原不等式等价于⎩⎪⎨⎪⎧x≤0,1-x -2x≤4x 或⎩⎪⎨⎪⎧0<x≤1,1-x +2x≤4x 或⎩⎪⎨⎪⎧x >1,x -1+2x≤4x.解⎩⎪⎨⎪⎧x≤0,1-x +2x≤4x ,得x ∈∅; 解⎩⎪⎨⎪⎧0<x≤1,1-x +2x≤4x ,得13≤x≤1; 解⎩⎪⎨⎪⎧x >1,x -1+2x≤4x ,得x >1. 所以原不等式的解集为⎣⎡⎭⎫13,+∞.22.(本小题满分10分)【解析】(1) 记“该网民购买i 种商品”为事件A i ,i =4,5, 则P(A 5)=34×34×23×23×12=18,P(A 4)=34×34×23×23×⎝⎛⎭⎫1-12+C 1234×⎝⎛⎭⎫1-34×23×23×12+C 1223×⎝⎛⎭⎫1-23×34×34×12=13, 所以该网民至少购买4种商品的概率为P(A 5)+P(A 4)=18+13=1124. 答:该网民至少购买4种商品的概率为1124.(2) 随机变量η的可能取值为0,1,2,3,4,5,P(η=0)=⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12=1288,P(η=1)=C 1234×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12+C 1223×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-12+12×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23=11288,P(η=2)=34×34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12+23×23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-12+C 12⎝⎛⎭⎫1-23×23×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-34×12+C 1234×⎝⎛⎭⎫1-34×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-23×12+C 1234×⎝⎛⎭⎫1-34×C 1223×⎝⎛⎭⎫1-23×⎝⎛⎭⎫1-12=47288,P(η=3)=1-P(η=0,1,2,4,5)=1-1288-11288-47288-13-18=97288, P(η=4)=P(A 4)=13,P(η=5)=P(A 5)=18. 所以,随机变量η的概率分布为故Eη=0×1288+1×11288+2×47288+3×97288+4×13+5×18=103. 23.(本小题满分10分)【解析】(1)因为a n (n ∈N *且n≥3)均为正实数,左-右=12⎝⎛⎭⎫a 1a 3a 2+a 1a 2a 3-2a 1+12⎝⎛⎭⎫a 2a 3a 1+a 1a 2a 3-2a 2+12⎝⎛⎭⎫a 2a 3a 1+a 1a 3a 2-2a 3 ≥12⎝⎛⎭⎫2a 1a 3a 2×a 1a 2a 3-2a 1+12⎝⎛⎭⎫2a 2a 3a 1×a 1a 2a 3-2a 2+12⎝⎛⎭⎫2a 2a 3a 1×a 1a 3a 2-2a 3 =0,所以,原不等式a 2a 3a 1+a 1a 3a 2+a 1a 2a 3≥a 1+a 2+a 3成立. (2)归纳的不等式为a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2≥a 1+a 2+…+a n (n ∈N *且n≥3). 记F n =a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2-(a 1+a 2+…+a n ), 当n =3(n ∈N *)时,由(1)知,不等式成立; 假设当n =k(k ∈N *且k≥3)时,不等式成立,即F k =a 1a 2a 3+a 2a 3a 4+…+a k -2a k -1a k +a k -1a k a 1+a k a 1a 2-(a 1+a 2+…+a k )≥0. 则当n =k +1时,F k +1=a 1a 2a 3+a 2a 3a 4+…+a k -2a k -1a k +a k -1a k a k +1+a k a k +1a 1+a k +1a 1a 2-(a 1+a 2+…+a k +a k +1) =F k +a k -1a k a k +1+a k a k +1a 1+a k +1a 1a 2-a k -1a k a 1-a k a 1a 2-a k +1=F k +a k -1a k ⎝⎛⎭⎫1a k +1-1a 1+a k +1⎝⎛⎭⎫a k a 1-1+a 1a 2(a k +1-a k )≥0+a 2k⎝⎛⎭⎫1a k +1-1a 1+a k +1⎝⎛⎭⎫a k a 1-1+a 1a k (a k +1-a k )=(a k +1-a k )⎝ ⎛⎭⎪⎫a k a 1+a 1a k -a k +1+a k a k +1,因为a k +1≥a k ,a k a 1+a 1a k ≥2,a k +1+a k a k +1≤a k +1+a k +1a k +1=2, 所以F k +1≥0,所以当n =k +1,不等式成立.综上所述,不等式a 1a 2a 3+a 2a 3a 4+…+a n -2a n -1a n +a n -1a n a 1+a n a 1a 2≥a 1+a 2+…+a n (n ∈N *且n≥3)成立.。

2020年江苏省高考数学信息预测试卷(一)一、填空题(本大题共14小题,共70.0分)1.已知集合A={−1,1,2,4},B={−1,0,2},则A∩B=__________.2.若复数(a2−3a+2)+(a−2)i是纯虚数,则实数a的值为______ .3.执行如图所示的程序框图,则输出的结果是______ .4.样本数据18,16,15,16,20的方差s2=__________.5.从1,2,3,4,5五个数中随机取出2个数,则取出的两个数不是连续整数的概率是__.6.已知a=ln34,b=5lg3,c=3−12,则a,b,c的大小关系是__________.7.已知{a n}是等差数列,若2a7−a5−3=0,则a9的值是________.8.已知函数f(x)=2x−ax的图象在点(−1,f(−1))处的切线斜率是1,则此切线方程是_________.9.如图,直三棱柱ABC—A1B1C1中,∠CAB=90°,AC=AB=2,CC1=2,P是BC1的中点,则三棱锥C—A1C1P的体积为______.10.已知sinα+sin(π2+α)=2√55,则sin2α的值为______ .11. 已知圆A :x 2+y 2=1,圆B :(x −3)2+(y +4)2=10,P 是平面内一动点,过P 作圆A 、圆B 的切线,切点分别为D 、E ,若PE =PD ,则P 到坐标原点距离的最小值为______ .12. F 1、F 2为双曲线C :x 2a 2−y 2b2=1(a >0,b >0)的焦点,A 、B 分别为双曲线的左、右顶点,以F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M ,且满足∠MAB =30°,则该双曲线的离心率为______ .13. 已知AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =0,|AB ⃗⃗⃗⃗⃗ |=3,|AC ⃗⃗⃗⃗⃗ |=2,则|BC ⃗⃗⃗⃗⃗ |=______.14. 若关于x 的方程√1−x 2=|x −a|−a 有两个不相等的实数根,则实数a 的取值范围是______.二、解答题(本大题共6小题,共90.0分)15. 在△ABC 中,已知sin A :sin B :sin C =4:5:6,且a +b +c =30,求a .16. 四棱锥P −ABCD 中,底面ABCD 是正方形,PB ⊥BC ,PD ⊥CD ,E 点满足PE =13PD .(1)求证:PA ⊥平面ABCD ;(2)在线段BC 上是否存在点F 使得PF//面EAC ?若存在,确定F 的位置;若不存在,请说明理由.17.已知椭圆C:x2a2+y2b2=1(a>b>0)的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D(1,32)在椭圆C上(1)求椭圆C的方程;(2)直线MN过椭圆左焦点F1,A为椭圆短轴的上顶点,当直线AF1⊥MN时,求△MNA的面积.18.为美化校园,江苏省淮阴中学将一个半圆形的边角地改造为花园.如图所示,O为圆心,半径为1千米,点A、B、P都在半圆弧上,设∠NOP=∠POA=θ,∠AOB=2θ,且0<θ<π4.(1)请用θ分别表示线段NA、BM的长度;(2)若在花园内铺设一条参观线路,由线段NA、AB、BM三部分组成,则当θ取何值时,参观线路最长?(3)若在花园内的扇形..ONP和四边形OMBA内种满杜鹃花,则当θ取何值时,杜鹃花的种植总面积最大?19.已知函数f(x)=ln(ax+1)+1−x1+x,其中a>0.(1)若f(x)在x=1处取得极值,求a的值;(2)若f(x)的最小值为1,求a的取值范围.20.已知首项为3的数列{a n}满足:(a n+1−1)(a n−1)a n−a n+1=3,且b n=1a n−1.(1)求证:数列{b n}是等差数列;(2)求数列{2n⋅b n}的前n项和T n.【答案与解析】1.答案:{−1,2}解析:本题主要考查了集合的交集,属于基础题.利用交集定义求解即可.解:集合A={−1,1,2,4},B={−1,0,2},则A∩B={−1,2}.故答案为{−1,2}.2.答案:1解析:解:∵复数(a2−3a+2)+(a−2)i是纯虚数,∴a2−3a+2=0,a−2≠0,解得a=1.故答案为:1.利用纯虚数的定义即可得出.本题考查了纯虚数的定义,属于简单题.3.答案:20解析:解:模拟程序的运行,可得S=0,n=1执行循环体,S=3,n=2不满足条件S≥15,执行循环体,S=9,n=3不满足条件S≥15,执行循环体,S=20,n=4满足条件S≥15,退出循环,输出S的值为20.故答案为:20.由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查的知识点是循环结构的程序框图的应用,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.4.答案:3.2解析:由平均数和方差计算公式有x=15(18+16+15+16+20)=17,s2=15[(18−17)2+(16−17)2+(15−17)2+(16−17)2+(20−17)2]=3.2.5.答案:35解析:本题考查古典概型,属基础题.分别找出基本事件总数与事件“取出的两个数不是连续整数”包含的基本事件数,利用公式,即可得到最后结果.解:从1,2,3,4,5五个数中随机取出2个数,基本事件数有:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种;取出的两个数不是连续整数,包含的基本事件有:(1,3),(1,4),(1,5),(2,4),(2,5),(3,5),共6种;则取出的两个数不是连续整数的概率是610=35.故答案为35.6.答案:a<c<b解析:本题考查对数的性质,基础题型.解:a=ln34<ln1=0<c=3−12<30=1=50<b=5lg3,故答案为:a<c<b.7.答案:3解析:本题考查了等差数列的通项公式,考查了等差数列的性质,基本知识的考查.直接利用等差数列的性质结合已知得答案.解:设公差为d,则2(a1+6d)−(a1+4d)−3=0,即a1+8d=3,所以a9=3.8.答案:x−y−4=0解析:本题考查了利用导数求切线方程的应用,属于基础题.首先求出导函数,进而得到k=f′(−1)=1,得到a的值,进而得到f(−1),切线方程可求.解:因为f′(x)=−2x2−a,所以函数f(x)在点(−1,f(−1))处的切线斜率为k=f′(−1)=−2−a=1,所以a=−3,即f(−1)=−2+a=−5,所以切线方程为y=(x+1)−5=x−4,即x−y−4=0.故答案为x−y−4=0.9.答案:23解析:本题考查了棱锥的体积,先得出点A1到平面BB1C1C的距离为ℎ=√2,得出SΔPCC1=12×2×2√22=√2,由V C—A1C1P =V A1−PCC1即可得出结果.解:直三棱柱ABC—A1B1C1中,∠CAB=90°,AC=AB=2,∴点A1到平面BB1C1C的距离为ℎ=√2,∵AC=AB=2,CC1=2,P是BC1的中点,∴SΔPCC1=12×2×2√22=√2,∴V C—A1C1P =V A1−PCC1=13×SΔPCC1·ℎ=13×√2×√2=23,故答案为23.10.答案:−15解析:解:∵已知sinα+sin(π2+α)=2√55,即sinα+cosα=2√55,平方可得1+2sinαcosα=1+sin2α=2025=45,则sin2α=−15,故答案为:−15.利用同角三角函数的基本关系、二倍角公式、诱导公式,求得sin2α的值.本题主要考查同角三角函数的基本关系的应用,二倍角公式、诱导公式的应用,属于基础题.11.答案:85解析:解:设P(x,y),依题意,过P作⊙A、⊙B的切线,切点分别为D、E,PE=PD,所以x2+y2−1=(x−3)2+(y+4)2−10,整理得:3x−4y−8=0,P到坐标原点距离的最小值就是原点到3x−4y−8=0的距离,∴P到坐标原点距离的最小值为85故答案为85.设出P(x,y),依题意,求出P的坐标的轨迹方程,然后求方程上的点到原点距离的最小值.本题考查圆的切线方程,两点间的距离公式,轨迹方程问题,转化的数学思想,是难度较大的题目.12.答案:√213解析:本题主要考察双曲线的简单性质.解决本题得关键在于根据条件得到圆的方程以及渐近线方程,联立求出点M的坐标,结合∠MAB=30°求出a,b之间的关系.先根据条件得到圆的方程以及渐近线方程,联立求出点M的坐标,结合∠MAB=30°求出a,b之间的关系,进而求出离心率即可.解:由题得以F1F2为直径的圆的圆心是(0,0),半径为:c;故圆的标准方程为:x2+y2=c2;又双曲线的其中一条渐近线方程为:y =b a x ,联立{y =b a x x 2+y 2=c 2可得:{x =a y =b ,即M(a,b). 故MB 垂直于AB ;所以tan∠MAB =MB AB =b 2a =tan30°; 即b a =2√33⇒c a=√c 2a 2=√a 2+b 2a 2=√213. 故双曲线的离心率为√213.故答案为:√213. 13.答案:√13解析:解:由题意,AB ⃗⃗⃗⃗⃗ ⋅AC⃗⃗⃗⃗⃗ =0, ∴∠A =90°,三角形ABC 是直角三角形.∴|BC⃗⃗⃗⃗⃗ |=√|AB ⃗⃗⃗⃗⃗ |2+|AC ⃗⃗⃗⃗⃗ |2=√13. 故答案为:√13根据AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =0,可知角A 是直角.根据勾股定理即可求解|BC ⃗⃗⃗⃗⃗ |.本题考查了向量垂直与数量积的关系、向量的运算,属于基础题.14.答案:(−√22,12]解析:解:y =√1−x 2,表示以O 为圆心,半径为1的圆的上半圆, y =g(x)=|x −a|−a ={x −2a,x ≥a −x,x <a,图象关于x =a 对称,顶点为A(a,−a),若a <0,顶点A 位于第二象限.要使两个图象有两个交点,则A 只要在半圆内即可,即|OA|<1,即√a 2+a 2=√2a 2<1,得2a 2<1得a 2<12,得−√22<a <√22, ∵a <0,∴−√22<a <0, 当a =0时,半圆和y =|x|,一定有两个交点,满足条件.当a >0时,在x ≤a 时,y =g(x)=−x ,一定与半圆有一个交点,要使g(x)与半圆有两个交点,则只需要当x >a 时,g(x)=x −2a 与圆的右半圆有一个交点即可, 此时顶点A(a,−a)一定在第四象限,当x ≥a 时的直线g(x)=x −2a 经过B(1,0)时,1−2a =0,得a =12,此时对应的直线y =x −1,要使g(x)=x −2a 与圆的右半圆有一个交点即可,则满足−2a ≥−1,即a ≤12,∵a >0,∴0<a ≤12,综上−√22<a ≤12, 即实数a 的取值范围是(−√22,12], 故答案为:(−√22,12]. 根据函数与方程的关系作出y =√1−x 2和y =|x −a|−a 的图象,讨论a 的正负,结合绝对值函数的图象,利用数形结合进行求解即可.本题主要考查函数与方程的应用,利用条件转化为两个函数的图象交点个数问题,利用绝对值函数的图象,利用数形结合是解决本题的关键. 15.答案:解:∵sin A :sin B :sin C =4:5:6,由正弦定理可得:a:b:c=4:5:6,又∵a+b+c=30,∴a=30×44+5+6=8.解析:由sin A:sin B:sin C=4:5:6,利用正弦定理可得:a:b:c=4:5:6,即可得出.本题考查了正弦定理的应用,属于基础题.16.答案:(1)证明:在正方形ABCD中,AB⊥BC,又∵PB⊥BC,AB∩PB=B,AB⊂平面PAB,PB⊂平面PAB,∴BC⊥平面PAB,又PA⊂平面PAB,∴BC⊥PA,同理CD⊥PA,∵BC∩CD=C,BC⊂平面ABCD,CD⊂平面ABCD,∴PA⊥平面ABCD.(2)当F为BC中点时,PF//面EAC,理由如下:连接DF,PF,设DF与AC交于点M,连接EM,∵AD//FC,AD=2FC,∴FCAD =FMMD=12,又由已知有PEED =12,∴PF//EM,∵PF⊄平面EAC,EM⊂平面EAC,∴PF//平面EAC.解析:本题考查线面平行、线面垂直的证明,考查学生分析解决问题的能力,属于中档题. (1)证明BC ⊥PA ,CD ⊥PA ,即可证明:PA ⊥平面ABCD ;(2)连接DF ,PF ,设DF 与AC 交于点M ,连接EM ,当F 为BC 中点时,要说明PF//平面EAC 成立,证明PF//EM 即可.17.答案:解:(1)由题意可得{b c=√3a 2=b 2+c 21a 2+94b 2=1,解得a 2=4,b 2=3,c 2=1∴椭圆C 的方程为x 24+y 23=1.(2)∵A(0,√3),F 1(−1,0), ∴k AF 1=√3, ∵AF 1⊥MN , ∴k MN =√3,∴直线MN 的方程为y =3+1),将其代入x 24+y23=1整理可得13x 2+8x −32=0,设M(x 1,y 1),N(x 2,y 2), ∴x 1+x 2=−813,x 1x 2=−3213, ∴|MN|=√1+13⋅√(−813)2+4×3213=4813,∵|AF 1|=√12+(√3)2=2,∴S △MNA =4813解析:(1)由题意可得{b c=√3a 2=b 2+c 21a2+94b2=1,解得a 2=4,b 2=3,即可求出椭圆方程,(2)先求出直线MN 的方程,将其代入x 24+y 23=1整理可得13x 2+8x −32=0,根据弦长公式求出|MN|,即可求出三角形的面积本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.18.答案:解:(1)AN =2sinθ,BM =2cos2θ.(2)参观路线的长度l =4sinθ+2cos2θ=−4sin2θ+4sinθ+2,令,当t=12时,取得最大值,即θ=π6时,参观路线最长.(3)杜鹃花的种植总面积S=12θ+12sin4θ+12sin2θ,S′=12(1+4cos4θ+2cos2θ) =12(8cos22θ+2cos2θ−3)=12(2cos2θ−1)(4cos2θ+3),令S′=0得cos2θ=12,因为0<2θ<π2,所以2θ=π3,θ=π6,当θ∈(0,π6)时,S′>0,S单调递增;当θ∈(π6,π4)时,S′<0,S单调递减,所以θ=π6时,杜鹃花的种植总面积最大.解析:本题主要考查了导数在解决实际问题中的应用,利用导数研究闭区间上函数的最值,及三角函数的计算,属于中档题.(1)由题意直接解得AN=2sinθ,BM=2cos2θ.(2)参观路线的长度l=−4sin2θ+4sinθ+2,令,结合二次函数取可解答.(3)求得S=12θ+12sin4θ+12sin2θ,求解得导数,再令S′=0得cos2θ=12,根据导数的单调性即可求解.19.答案:解:(1)f(x)=ln(ax+1)+1−x1+x =ln(ax+1)+21+x−1,求导函数可得f′(x)=aax+1−2(1+x)2,∵f(x)在x=1处取得极值,∴f′(1)=0,∴aa+1−24=0,∴a=1;(2)设f′(x)=a ax+1−2(1+x)2>0,有ax 2>2−a ,若a ≥2,则f′(x)>0恒成立,f(x)在[0,+∞)上递增,∴f(x)的最小值为f(0)=1; 若0<a <2,则x >√2−a a,f′(x)>0恒成立,f(x)在(√2−a a,+∞)上递增,在(−∞,√2−a a)上递减,∴f(x)在x =√2−a a处取得最小值,f(√2−a a)<f(0)=1.综上知,若f(x)最小值为1,则a 的取值范围是[2,+∞).解析:(1)求导函数,根据f(x)在x =1处取得极值,可得f′(1)=0,即可求得a 的值;(2)设f′(x)=aax+1−2(1+x)2>0,有ax 2>2−a ,分类讨论:a ≥2,则f′(x)>0恒成立,f(x)在[0,+∞)上递增,f(x)的最小值为f(0)=1;0<a <2,可得f(x)在x =√2−a a处取得最小值,f(√2−a a)<f(0)=1,由此可得a 的取值范围.本题考查导数知识的运用,考查函数的单调性,考查函数的极值与最值,正确求导是关键.20.答案:解:(1)∵(a n+1−1)(a n −1)a n −a n+1=3,∴a n −a n+1(an+1−1)(a n−1)=13,∴b n+1−b n =1an+1−1−1a n −1=a n −a n+1(a n+1−1)(a n−1)=13. ∴数列{b n }是等差数列. (2)b 1=1a1−1=12,∴b n =12+13(n −1)=13n +16. ∴T n =2⋅12+22⋅56+23⋅76+24⋅96+⋯+2n ⋅2n+16,①①×2得:2T n =22⋅12+23⋅56+24⋅76+25⋅96+⋯+2n+1⋅2n+16,②①−②得:−T n =1+13⋅22+13⋅23+13⋅24+⋯+13⋅2n −2n+1⋅2n+16=1−2n+1⋅2n+16+13⋅4(1−2n−1)1−2=1−2n+1⋅2n+16+13⋅(2n+1−4)=−13−2n−16⋅2n+1.∴T n =13+2n−16⋅2n+1.解析:(1)计算b n+1−b n =a n −a n+1(an+1−1)(a n−1)=13; (2)求出b n 的通项公式,得出T n ,使用错位相减法求和. 本题考查了数列等差关系的判断,数列求和,属于中档题.。

绝密★启用前2020年普通高等学校全国统一招生考试(江苏卷)预测卷数学I注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.已知集合A={x|x<0},B={-2,-1,0,2},则A ∩B=___2.已知复数z 满足112z i i=++(i 是虚数单位),则复数z 的共轭复数为___ 3.某地区有小学生、初中生、高中生的人数见下表.采用分层抽样的方法调查学生的眼睛视力状况,在抽取的样本中初中生有320人,则该样本中的高中生人数为_____类别小学生 初中生 高中生 合计 人数 18000 16000 9000 430004.5.函数2()ln )(9f x x =-的定义域为____6.有3名学生甲、乙、丙,在分发数学作业时,从他们3人作业中各随机取出1份作业,则这3名学生恰好都拿到自己作业的概率为_____7.已知等比数列{}n a 满足11,2a =且2434(1),a a a =-则5a =____ 8.已知f(x)是定义在R 上的奇函数,当x>0时,2()log 3f x x =-,则f(f(-16))的值为_____9.某品牌汽车4S 店一年销售汽车4000辆,每次从汽车公司购置x 辆,运费为4万元/次,一年的总储存费用为0.4x 万元.要使一年的总运费与总储存费用之和最小的,则x 的值为_____.10.在平面直角坐标系xOy 中,已知抛物线220y px p =>的准线1与双曲线2221x y a a-=>0的两条渐近线围成等边三角形,且面积为3,则p+a=_____. 11.如图,在正四棱柱形容器内盛有水和相同高度的实心圆柱(其中圆柱底面内切于正四棱柱底面,水面恰与正四棱柱上底面齐平),将实心圆柱拿去后,则水面高度与正四棱高度比为____.(不计水的损耗)12.如图,△ABC 中,M 为AB 中点,AB=5,CM=3,EF 为圆心为C,半径为1的圆的动直径,则BE AF ⋅的取值范围是_____13.在平面直角坐标系xOy 中,圆221:4O x y +=与圆2222:(4)(0)O x y r r -+=>,在圆2O 上存在点Q,过点Q 作圆1O 的切线,切点为P,N,使得5,9QP QN ⋅=则实数r 的最小值为___. 14.已知函数3,1,(),1,x a x f x x ax x -≥⎧=⎨-<⎩若函数y=f[f(x)]恰有5个不同零点,则实数a 的取值范围是____. 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在平面直角坐标系xOy 中,以x 轴正半轴为始边作两个钝角α,β,它们的终边分别与单位圆交于A,B 两点.已知A,B 的横坐标分别为3102,.1010-- 求:(1)cos(α-β)的值;(2)2α-β的值.16.(本小题满分14分)如图,三棱锥P-ABC 中,已知PA ⊥底面ABC,AC ⊥BC,且PA=AC,点E,F 分别是棱PC,PB 的中点.(1)求证:AE ⊥BC;(2)点G 为棱AB 上一点,满足2,GB GA =求证:AE//平面CFG.17.(本小题满分14分)如图,在平面直角坐标系xOy 中,椭圆22221(0),x y a b a b +=>>圆C:222().4b x y b +-=A,B 分别为椭圆的左、右顶点,直线AC 交圆C 于D,P 两点(D 在线段AC 上),且2.AD DC =(1)求椭圆的离心率;(2)直线BP 与椭圆相交于点Q,直线AQ 被圆C 截得弦长为6,3求椭圆的标准方程. 18.(本小题满分16分)如图为某野生动物园一角,∠MOK 内区域为陆地动物活动区,∠NOK 内区域为水上动物活动区.为满足游客游览需要,现欲在OM,ON 上分别选一处A,B,修建一条贯穿两区域的直路AB,AB 与KO 相交于点P.若PA 段,PB 段每百米修路费用分别为1万元和2万元,已知∠NOK=30°,OM⊥OK,OP=2百米,设∠PAO=α.(1)试将修路费用表示为α的函数()S α(2)求修路费用()S α的最小值.19.(本小题满分16分)设等差数列{}n a 的前n 项和为,n S 且7146,54.a a S == (1)求数列{}n a 的通项公式;(2)是否存在正整数m,k,使得31,1,1m m k a a a +---依次成等比数列?并说明理由; (3)设数列{}n b 满足2*1()(),5n n a b n -=∈N 将{}n a 和{}n b 中相同的项按照从小到大的顺序依次排列,得到数列{},n c 求数列{}n c 的通项公式.20.(本小题满分16分)已知函数y=f(x)的定义域为D,若满足∀x ∈D,(x-1)f(x)≥0,则称函数f(x)为“L 型函数”.(1)判断函数xy e =和y=lnx 是否为“L 型函数”,并说明理由;(2)设函数f(x)=(x+1)lnx-(x-1)lna(a>0),记()().g x f x '=①若函数g(x)的最小值为1,求a 的值;②若函数f(x)为“L 型函数”,求a 的取值范围.21.[选做题]本题包括A 、B 、C 三小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-2:矩阵与变换(本小题满分10分) 已知矩阵记1040,10102A B ⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎣⎦记M=AB,求1.M B.选修4-4:坐标系与参数方程(本小题满分10分)在平面直角坐标系xOy 中,已知直线1,12x l y l=-+⎧⎨=-+⎩(l 为参数)与曲线cos ,cos 2x y θθ=⎧⎨=-⎩(θ为参数)的交点为A,B,求线段AB 的长.C.选修4-5:不等式选讲(本小题满分10分)已知x,y,z 均是正实数,且2229436.x y z ++=,求证:x+y+z ≤7.[必做题]第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图1,某电视台一档综艺节目的游戏挑战项目“蜂巢迷宫”的道具,游戏规定挑战者必须“蒙眼”进行现简化模型如图2所示,共有A,B,C,D,E,F 六个房间组成,每个房间各有六扇门分别与相邻房间或与外部相通,假设打开每扇门都是等可能的.现挑战者从房间A 出发,要求到达房间E.(1)求挑战者“打开两扇门完成挑战”的概率;(2)一次游戏中规定“只要走出道具外部或打开超过四扇门(含四扇)挑战失败”,得0分;“打开三扇门完成挑战”,得1分,“打开两扇门完成挑战”,得2分.挑战者共挑战1次,得分设为X,求随机变量X 的概率分布和数学期望E(X).23.(本小题满分10分)(1)用数学归纳法证明二项式定理:011()n n n n n a b C a C a b -+=++222*,.n r n r r n n n n n C a b C a b C b n --++++∈N(2)利用二项式定理求证:220()n k n n n k CC ==∑。

2020届全国普通高等学校招生统一考试模拟预测卷数学试题一、填空题1.现有7名数理化成绩优秀者,分别用1A ,2A ,3A ,1B ,2B ,1C ,2C 表示,其中1A ,2A ,3A 的数学成绩优秀,1B ,2B 的物理成绩优秀,1C ,2C 的化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛,则1A 和1B 不全被选中的概率为______________.2.若某几何体的三视图(单位:cm )如图所示,则该几何体的体积是________3cm .3.求值:()00sin 50180=______________.4.已知数列{}n a 成等差数列,且17134a a a π++=,则()212tan a a +=5.已知向量,a b 满足22b a ==,a 与b 的夹角为120,则4a b -=________.6.若曲线x y e =上点P 处的切线平行于直线210x y -+=,则点P 的坐标为______.7.阅读如图所示的程序框图,运行相应的程序,输出的结果i = .8.抛物线212y x =-的准线与双曲线22162x y -=的两条渐近线所围成的三角形的面积等 于 .9.已知一组数据6,7,8,9,m 的平均数是8,则这组数据的方差是_________.10.波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k (0k >且1k ≠)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有ABC ∆,4,sin 2sin AC C A ==,则当ABC ∆的面积最大时,AC 边上的高为_______________. 11.设集合{1,2,3}A =,{2,4,6}B =,则A B =__________.12.如图,三个相同的正方形相接,则tan ABC ∠的值为__________.13.下列四个命题中,正确命题的个数是___________.①0比i 小②两个复数互为共轭复数,当且仅当其和为实数③1x yi i +=+的充要条件为1x y ==④如果实数a 与ai 对应,那么实数集与纯虚数集一一对应14.已知函数()2ln 3a f x x x =+-,()322332g x x x x =-+-,对任意的1,23m ⎡⎤∈⎢⎥⎣⎦,都存在1,23n ⎡⎤∈⎢⎥⎣⎦,使得()()g m f n ≤成立,则实数a 的取值范围是______.二、解答题15.已知α,β为锐角,()12cos 13αβ+=,()3cos 25αβ+=,求cos α的值. 16.某单位科技活动纪念章的结构如图所示,O 是半径分别为1cm ,2cm 的两个同心圆的圆心,等腰△ABC 的顶点A 在外圆上,底边BC 的两个端点都在内圆上,点O ,A 在直线BC 的同侧.若线段BC 与劣弧BC 所围成的弓形面积为S 1,△OAB 与△OAC 的面积之和为S 2, 设∠BOC =2θ.(1)当3πθ=时,求S 2﹣S 1的值;(2)经研究发现当S 2﹣S 1的值最大时,纪念章最美观,求当纪念章最美观时,cos θ的值.(求导参考公式:(sin 2x )'=2cos 2x ,(cos 2x )'=﹣2sin 2x )17.已知四点12341112(3,),),(),(2223P P P P --中只有三点在椭圆C :22221x y a b +=上. (1)求椭圆C 的方程;(2)若直线l 的斜率为1,直线l 与圆221x y +=相切,且与椭圆C 交于点,A B ,求线段AB 的长.18.已知正项等差数列{}n a 满足:233312n n S a a a =+++,其中n S 是数列{}n a 的前n 项和. (1)求数列{}n a 的通项公式;(2)令()()()1412121n n n n n b a a -=--+,证明:122221n n b b b n ++++≤+. 19.现有6名奥运会志愿者,其中志愿者12,A A 通晓日语,12,B B 通晓俄语,12,C C 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.(1)求1A 被选中的概率;(2)求1B 和1C 不全被选中的概率;(3)若6名奥运会志愿者每小时派两人值班,现有两名只会日语的运动员到来,求恰好遇到12,A A 的概率.20.在等腰直角三角形ABC 中,AB =AC =3,点P 是边AB 上异于A ,B 的一点,光线从点P 出发,经BC ,CA 反射后又回到点P (如图),光线QR 经过ABC 的重心,若以点A 为坐标原点,射线AB ,AC 分别为x 轴正半轴,y 轴正半轴,建立平面直角坐标系.(1)AP 等于多少?(2)D (x ,y )是RPQ 内(不含边界)任意一点,求x ,y 所满足的不等式组,并求出D (x ,y )到直线2x +4y +1=0距离的取值范围.21.已知函数()2121f x x x =-++.(1)求函数()f x 的最小值m ;(2)若正实数,a b满足11a b +=,求证:2212m a b +≥. 22.已知曲线11:C y x=绕原点逆时针旋转45︒后可得到曲线222:2C y x -=, (I )求由曲线1C 变换到曲线2C 对应的矩阵1M ;.(II )若矩阵22003M ⎛⎫=⎪⎝⎭,求曲线1C 依次经过矩阵12,M M 对应的变换12,T T 变换后得到的曲线方程. 23.已知数列{}n a 满足22,2,n n n a n a a n ++⎧=⎨⎩为奇数为偶数,且*12,1,2n N a a ∈==. (1)求 {}n a 的通项公式;(2)设*1,n n n b a a n N +=⋅∈,求数列{}n b 的前2n 项和2n S ;(3)设()2121n n n n c a a -=⋅+-,证明:123111154n c c c c ++++< 24.已知函数12()4-=+x f x e ax ,曲线()y fx =在1x =处的切线方程为1y bx =+.(1)求实数a b 、的值;(2)0x >且1x ≠时,证明:曲线()y f x =的图象恒在切线1y bx =+的上方;(3)证明:不等式:12432ln 0----x xe x x x .25.如图所示,平面ABCD ⊥平面BCE ,四边形ABCD 为矩形, BC CE =,点F 为CE 的中点.(1)证明: //AE 平面BDF .(2)点M 为CD 上任意一点,在线段AE 上是否存在点P ,使得PM BE ⊥?若存在,确定点P 的位置,并加以证明;若不存在,请说明理由.【答案与解析】1.56列出从这7人中选出数学、物理、化学成绩优秀者各1名所有样本点,求出满足事件的样本点个数,即可求出结论.从这7人中选出数学、物理、化学成绩优秀者各1名,所有可能的结果组成的12个样本点为()111,,A B C ,()112,,A B C ,()121,,A B C ,()122,,A B C ,()211,,A B C ,()212,,A B C ,()221,,A B C ,()222,,A B C ,()311,,A B C ,()312,,A B C ,()321,,A B C ,()322,,A B C .“1A 和1B 全被选中”有2个样本点()111,,A B C ,()112,,A B C ,“1A 和1B 不全被选中”为事件N 共有10个样本点,概率为105126=. 故答案为:56. 本题考查古典概型的概率,列举样本点是解题的关键,属于基础题.2.144由三视图可知:该几何体是由一个长方体和正四棱台组成.其中长方体的长为4,宽为4,高为2,正四棱台的上底边长为4,下底边长为8,高为3,分别求得体积求和即可.由三视图可知:该几何体是由一个长方体和正四棱台组成.长方体的长为4,宽为4,高为2,所以V 长方体44232=⨯⨯= ;正四棱台的上底边长为4,下底边长为8,高为3,所以V 正四棱台()()1211166411233S S =++=++=. 所以该几何体的体积是144.故答案为:144本题主要考查三视图的应用以及几何体体积的求法,还考查了空间想象和运算求解的能力,属于基础题.3.1先利用同角基本关系将原式切化弦,再利用两角和的正弦公式,结合二倍角的正弦公式化简分子,进而再利用诱导公式变形,约分后即可得到结果.因为()()00sin501sin501︒=︒+=sin501︒+(1010sin cos ︒︒) =sin50︒=sin50︒•1210102210cos sin cos ⎛⎫︒+︒ ⎪⎝⎭︒=sin50︒•24010sin cos ︒︒ 2404010sin cos cos ︒︒=︒ 8010sin cos ︒=︒ 1010cos cos ︒=︒=1.故答案为1.本题考查了三角函数的化简求值问题,考查了两角和的正弦公式、同角三角函数间的基本关系,以及诱导公式的运用,熟练掌握公式是解本题的关键.4.先根据等差数列的等差中项的性质利用1713a a a ++的值求得7a 的值,进而利用等差中项的性质求得212a a +的值,代入()212tan a a +答案可得.1713734a a a a π++==743a π∴= ()212782tan tan 2tan tan 33a a a ππ∴+====故答案为本题主要考查了等差数列的性质、等差中项.作为等差数列的常用性质,在高考中常以填空和选择题出现. 解等差数列问题要注意应用等差数列的性质2p q m n r a a a a a +=+=(2p q m n r +=+=).5结合数量积的运算律可求得24a b -,进而求得结果. 2222248168cos12016186473a b a a b b a a b b -=-⋅+=-⋅+=++=, 473a b ∴-=.本题考查平面向量模长的求解问题,关键是熟练应用平面向量数量积的运算律求得模长的平方. 6.(ln 2,2)先设P (x ,y ),求出函数的导数,利用x e =2,求出x 并代入解析式求出y 可得P 的坐标. 设P (x ,y ),由题意得x y e =,∵'x y e =在点P 处的切线与直线210x y -+=平行,∴x e =2,解得x =ln 2,∴2x ln y e e ===2,故P (ln 2,2).故答案为:(ln 2,2).本题考查了导数的几何意义,即曲线在某点处切线的斜率是该点处的导数值,属于基础题. 7.5框图首先给变量a 和变量i 赋值,4a =,1i =.判断104=不成立,判断10是奇数不成立,执行1052a ==,112i =+=; 判断54=不成立,判断5是奇数成立,执行35116a =⨯+=,213i =+=;判断164=不成立,判断16是奇数不成立,执行1682a ==,314i =+=; 判断84=不成立,判断8是奇数不成立,执行842a ==,415i =+=; 判断44=成立,跳出循环,输出i 的值为5.8.试题分析:抛物线的准线方程为3x =,双曲线的渐近线方程为y x =,所以所要求的三角形的面积为132⨯⨯=;考点:1.抛物线的几何性质;2.双曲线的几何性质;9.2由平均数求得m ,根据方差计算公式求得结果. 由题意得:678985m ++++=,解得:10m = ∴方差()()()()()222222116878889810810255s ⎡⎤=⨯-+-+-+-+-=⨯=⎣⎦ 故答案为:2本题考查平均数与方差的计算方法,属于基础题.10.83ABC ∆,4,sin 2sin AC C A ==,即2c a=.根据阿波罗尼斯圆可得:点B 的轨迹为圆, 以线段AC 中点为原点,AC 所在直线为x 轴建立直角坐标系,求出B 的轨迹方程,进而得出结论. 解:||sin sin 2sin ,2||sin AB C C A CB A=∴==为非零常数, 根据阿波罗尼斯圆可得:点B 的轨迹是圆.以线段AC 中点为原点,AC 所在直线为x 轴建立直角坐标系则(2,0),(2,0)A C -,设(,)B x y ,∵2AB CB ==223320120x y x +-+=,整理得22210833x y ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭ 因此,当ABC ∆面积最大时,BC 边上的高为圆的半径83. 本题考查了阿波罗尼斯圆的应用、正弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.11.{2}{}{1,2,3}2,4,6A B ⋂=⋂={}212.17由两角差的正切公式可得,321tan 1327ABC -∠==+⨯,故答案为17.。
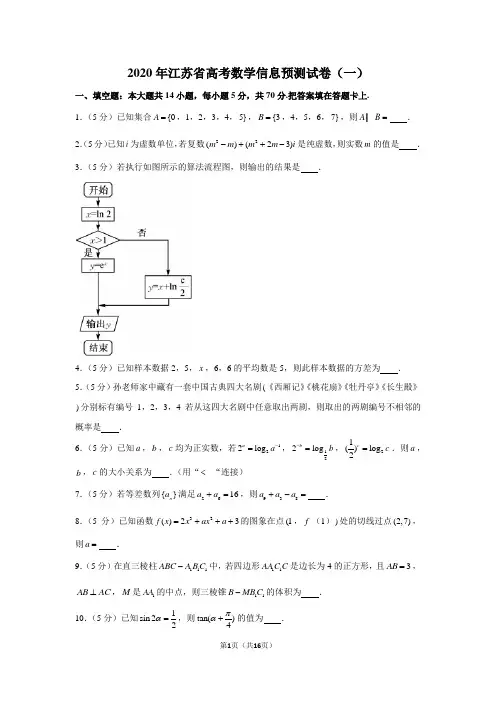
2020年江苏省高考数学信息预测试卷(一)一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题卡上.1.(5分)已知集合{0A =,1,2,3,4,5},{3B =,4,5,6,7},则A B =I . 2.(5分)已知i 为虚数单位,若复数22()(23)m m m m i -++-是纯虚数,则实数m 的值是 . 3.(5分)若执行如图所示的算法流程图,则输出的结果是 .4.(5分)已知样本数据2,5,x ,6,6的平均数是5,则此样本数据的方差为 . 5.(5分)孙老师家中藏有一套中国古典四大名剧(《西厢记》《桃花扇》《牡丹亭》《长生殿》)分别标有编号1,2,3,4若从这四大名剧中任意取出两剧,则取出的两剧编号不相邻的概率是 .6.(5分)已知a ,b ,c 均为正实数,若122log a a -=,122log b b -=,21()log 2c c =.则a ,b ,c 的大小关系为 .(用“< “连接) 7.(5分)若等差数列{}n a 满足2616a a +=,则938a a a +-= .8.(5分)已知函数32()23f x x ax a =+++的图象在点(1,f (1))处的切线过点(2,7),则a = .9.(5分)在直三棱柱111ABC A B C -中,若四边形11AA C C 是边长为4的正方形,且3AB =,AB AC ⊥,M 是1AA 的中点,则三棱锥11B MB C -的体积为 .10.(5分)已知1sin 22α=,则tan()4πα+的值为 .11.(5分)已知点P 是直线:0l x y b +-=上的动点,过点P 向圆22:1O x y +=作切线,切点分别为M ,N ,且90MPN ∠=︒,若点P 有且只有一个,则实数b = .12.(5分)已知过双曲线22219x y b-=的右焦点F 作圆229x y +=两条切线的切点分别为C ,D ,且双曲线的右顶点为E ,若105CEF ∠=︒,则该双曲线的离心率为 .13.(5分)已知四边形ABCD 满足AB DC =u u u r u u u r且||||||AB AD AB AD a ==-=u u u r u u u r u u u r u u u r ,P 是线段BD 上一点,则()PA PC PD +u u u r u u u r u u u rg 的最小值是 .14.(5分)已知函数21,0()|2|,0x x f x x x ⎧-+=⎨->⎩…,若关于x 的方程2()()0f x af x -=有且只有3个不同的实数根,则实数a 的取值范围是 .二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.(14分)已知锐角ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,且sin 23sin sin A B C =,4bc =,23a =.(1)求角A 的大小; (2)求ABC ∆的周长.16.(14分)如图,在四棱锥E ABCD -中,平面ABE ⊥平面ABCD ,//AB CD ,AB BC ⊥,22AB CD BC ==,EA EB =.(1)求证:AB DE ⊥;(2)线段EA 上是否存在点F 使//EC 平面FBD ?若存在,确定点F 的位置;若不存在,请说明理由.17.(14分)已知点O 为坐标原点,椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ,2,点I ,J 分别是椭圆C 的右顶点、上顶点,且IOJ ∆的边IJ 3. (1)求椭圆C 的标准方程;(2)过点(2,0)H -的直线交椭圆C 于A ,B 两点,若11AF BF ⊥,求直线AB 的方程.18.(16分)自20世纪以来,战争灾害、自然灾害给人类带来巨大损失.某地为解决重大紧急情况时人群疏散的需要,对一矩形ABMN 广场区域进行改造,其中AB 的长为60米,AN 的长为120米.现设计从边BM 上一点C 处,将CB 沿着直线CE (点E 在边AB 上)折叠,使点B 落在边AD 上点F 处,其中CEF ∆区域建在地上,CBE ∆区域往地下开挖并和其他区域相通,分地上地下用于疏散人群,令BCE θ∠=. (1)求θ的取值范围;(2)若CE 的长最小时,人群疏散效果最佳,求人群疏散效果最佳时线段CE 的长.19.(16分)已知函数2()()f x x ax lnx a R =+-∈. (1)若函数()f x 在1x =处取得极值,求实数a 的值;(2)令函数2()()((0,])g x f x x x e =-∈,是否存在实数a 使函数()g x 的最小值是4?若存在,求出a 的值;若不存在,请说明理由; (3)证明:25((0,])22lnx e x lnx x e ->+∈. 20.(16分)已知各项均为正数数列{}n a 满足33321212()n n a a a a a a ++⋯⋯+=++⋯⋯+. (1)求数列{}n a 的通项公式;(2)若等比数列{}n a 满足12b a =,24b a =,求12132121n n n n n a b a b a b a b a b ---+++⋯⋯++的值(用含n 的式子表示);(3)若113(*)n n n a c c n N ++=+∈,2352c c -=,求证:数列{}n c 是等差数列.2020年江苏省高考数学信息预测试卷(一)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.把答案填在答题卡上.1.(5分)已知集合{0A =,1,2,3,4,5},{3B =,4,5,6,7},则A B =I {3,4,5} .【解答】解:Q 集合{0A =,1,2,3,4,5},{3B =,4,5,6,7}, 则{3A B =I ,4,5}, 故答案为:{3,4,5}.2.(5分)已知i 为虚数单位,若复数22()(23)m m m m i -++-是纯虚数,则实数m 的值是 0 .【解答】解:复数22()(23)m m m m i -++-是纯虚数,20m m ∴-=,2230m m +-≠,解得:0m =. 故答案为:0.3.(5分)若执行如图所示的算法流程图,则输出的结果是 1 .【解答】解:分析程序的运行过程知,程序运行后输出,12,1x e x ln x y e x ⎧+⎪=⎨⎪>⎩…; 又21x ln =<,所以2212ey x ln ln lne ln =+=+-=.故答案为:1.4.(5分)已知样本数据2,5,x ,6,6的平均数是5,则此样本数据的方差为 125. 【解答】解:Q 样本数据2,5,x ,6,6的平均数是5, ∴1(2566)55x ++++=, 解得6x =,∴此样本数据的方差为:22222112[(52)(55)(56)(56)(56)]55-+-+-+-+-=. 故答案为:125. 5.(5分)孙老师家中藏有一套中国古典四大名剧(《西厢记》《桃花扇》《牡丹亭》《长生殿》)分别标有编号1,2,3,4若从这四大名剧中任意取出两剧,则取出的两剧编号不相邻的概率是13. 【解答】解:孙老师家中藏有一套中国古典四大名剧(《西厢记》《桃花扇》《牡丹亭》《长生殿》)分别标有编号1,2,3,4, 若从这四大名剧中任意取出两剧,基本事件总数246n C ==, 取出的两剧编号不相邻的包含的基本个数2m =, ∴取出的两剧编号不相邻的概率2163m p n ===. 故答案为:13.6.(5分)已知a ,b ,c 均为正实数,若122log a a -=,122log b b -=,21()log 2c c =.则a ,b ,c 的大小关系为 a b c << .(用“< “连接) 【解答】解:由题意可知,122a log a =,121()2b log b =,21()2c log c =,利用函数2x y =,1()2x y =,12log y x =,2log y x =的图象交点的位置,即可判断:a b c <<,故答案为:a b c <<.7.(5分)若等差数列{}n a 满足2616a a +=,则938a a a +-= 8 .【解答】解:设等差数列{}n a 的公差为d ,261162(3)a a a d +==+Q , 138a d ∴+=,则938138a a a a d +-=+=, 故答案为:8.8.(5分)已知函数32()23f x x ax a =+++的图象在点(1,f (1))处的切线过点(2,7),则a = 1- .【解答】解:32()23f x x ax a =+++Q ,f ∴(1)25a =+,2()62f x x ax '=+,()f x ∴在点(1,f (1))处切线的斜率k f '=(1)26a =+,()f x ∴在点(1,f (1))处切线的切线方程为(25)(26)(1)y a a x -+=+-. ()f x Q 在在点(1,f (1))处的切线过点(2,7), 7(25)(26)(21)a a ∴-+=+-,1a ∴=-.故答案为:1-.9.(5分)在直三棱柱111ABC A B C -中,若四边形11AA C C 是边长为4的正方形,且3AB =,AB AC ⊥,M 是1AA 的中点,则三棱锥11B MB C -的体积为 8 .【解答】解:如图,因为4AC =,3AB =,AB AC ⊥,5BC ∴=. 111111541022BB C S BB B C =⨯=⨯⨯=V , M 到面11BB C 的距离等于A 到面11BB C 的距离.在直三棱柱111ABC A B C -中,过A 作AD BC ⊥于D , 根据面面垂直的性质可得AD ⊥面11BB C , 1122AC AB BC AD ⨯=⨯,∴125AD =. 则三棱锥11B MB C -的体积为11210835V =⨯⨯=.故答案为:8.10.(5分)已知1sin 22α=,则tan()4πα+的值为 3± . 【解答】解:2222sin cos 2tan 1sin 212sin cos tan ααααααα===++Q , ∴整理可得:2tan 4tan 10αα-+=,解得tan 23α=±1tan tan()341tan πααα+∴+==±-.故答案为:3±.11.(5分)已知点P 是直线:0l x y b +-=上的动点,过点P 向圆22:1O x y +=作切线,切点分别为M ,N ,且90MPN ∠=︒,若点P 有且只有一个,则实数b = 2± . 【解答】解:解:过原点O 作0x y b +-=的垂线y x =,垂足为A , 由对称性可知当P 在A 处时,90MPN ∠=︒, OA Q 平分MPN ∠, 45OAM OAN ∴∠=∠=︒,∴过A 的水平线与竖直线为圆的两条切线,故(1,1)A 或(1,1)A --, 代入0x y b +-=可得2b =±. 故答案为:2±.12.(5分)已知过双曲线22219x y b-=的右焦点F 作圆229x y +=两条切线的切点分别为C ,D ,且双曲线的右顶点为E ,若105CEF ∠=︒,则该双曲线的离心率为 2 .【解答】解:由题意可得C ,E 在圆上,OC OE =,由105CEF ∠=︒可得75OEC OCE ∠=∠=︒,所以30COE ∠=︒,在OCF ∆中,CF 为切线,即OC CF ⊥,所以22c OF OC a ===, 所以双曲线的离心率为:22c=, 故答案为:213.(5分)已知四边形ABCD 满足AB DC =u u u r u u u r 且||||||AB AD AB AD a ==-=u u u r u u u r u u u r u u u r ,P 是线段BD 上一点,则()PA PC PD +u u u r u u u r u u u r g 的最小值是 2258a - .【解答】解:四边形ABCD 满足AB DC =u u u r u u u r且||||||AB AD AB AD ==-u u u r u u u r u u u r u u u r ,所以ABD ∆是正三角形,四边形ABCD 是菱形,画出图形如图,建立如图所示的坐标系,设2AB a =,(,0)A a -,(,0)D a ,3)B a ,(23)C a a ,设(,3)BP BD a a λλλ==-u u u r u u u r,[0λ∈,1],则(,33)P a a a λλ-+,所以(33)PA a a a a λλ=--u u u r ,(33)PD a a a a λλ=-u u u r ,(23)PC a a a λλ=-u u u r(32PC PD a a λ+=-u u u r u u u r,233)a a λ则22()(810)PA PC PD a λλ+=-u u u r u u u r u u u r g ,当58λ=时,()PA PC PD +u u u r u u u r u u u r g 取得最小值为:2258a -.故答案为:2258a -.14.(5分)已知函数21,0()|2|,0x x f x x x ⎧-+=⎨->⎩„,若关于x 的方程2()()0f x af x -=有且只有3个不同的实数根,则实数a 的取值范围是 (,0)[2-∞U ,)+∞ . 【解答】解:由题意,可知221,01,0()(2),02|2|,02,2x x x x f x x x x x x x ⎧-+⎧-+⎪==--<<⎨⎨->⎩⎪-⎩„„…,函数()f x 大致图象如右:Q 关于x 的方程2()()0f x af x -=有且只有3个不同的实数根,()[()]0f x f x a ∴-=g 有且只有3个不同的实数根,即()0f x =与()f x a =一共有3个不同的实数根,()0f x =Q 有1x =-与2x =两个实数根, ()f x a ∴=有且只有1个实数根,0a ∴<,或2a …. ∴实数a 的取值范围为(,0)[2-∞U ,)+∞.故答案为:(,0)[2-∞U ,)+∞.二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.(14分)已知锐角ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,且sin 23sin sin A B C =,4bc =,23a =(1)求角A 的大小; (2)求ABC ∆的周长.【解答】解:(1)sin 23sin sin A B C =Q ,显然sin 0A ≠, 2sin 23sin sin sin A A B C ∴=, ∴由正弦定理可得:223sin a bc A =,又4bc =Q ,23a =, 1283sin A ∴=,解得:3sin A =, (0,)2A π∈Q ,3A π∴=,(2)由(1)可知3A π=,可得:1cos 2A =, ∴由余弦定理可得:22222121cos 282b c a b c A bc +-+-===,2216b c ∴+=,222()224b c b c bc ∴+=++=,解得26b c +=, ABC ∴∆的周长2326a b c ++=.16.(14分)如图,在四棱锥E ABCD -中,平面ABE ⊥平面ABCD ,//AB CD ,AB BC ⊥,22AB CD BC ==,EA EB =.(1)求证:AB DE ⊥;(2)线段EA 上是否存在点F 使//EC 平面FBD ?若存在,确定点F 的位置;若不存在,请说明理由.【解答】解:(1)证明:取AB 中点O ,连结EO ,DO .因为EB EA =, 所以EO AB ⊥.因为四边形ABCD 为直角梯形,22AB CD BC ==,AB BC ⊥, 所以四边形OBCD 为正方形, 所以AB OD ⊥. 所以AB ⊥平面EOD . 所以AB ED ⊥.(2)线段EA 上存在点F 使//EC 平面FBD ,证明:连接AC 、BD 交于点M ,面ACE ⋂面FBD FM =. 因为//EC 平面FBD , 所以//EC FM .在梯形ABCD 中,有DMC BMA ∆∆∽,可得2MA MC =, 所以2AF FE =, 所以,13EF EA =.17.(14分)已知点O 为坐标原点,椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F 、2F ,2,点I ,J 分别是椭圆C 的右顶点、上顶点,且IOJ ∆的边IJ 3. (1)求椭圆C 的标准方程;(2)过点(2,0)H -的直线交椭圆C 于A ,B 两点,若11AF BF ⊥,求直线AB 的方程. 【解答】解:(Ⅰ)由题意可得:2c a =222a b c =+22132a b +=联立解得:22a =,1b c ==.∴椭圆C 的标准方程为:2212x y +=.(Ⅱ)设1(A x ,1)y ,2(B x ,2)y ,过点(2,0)H -的直线方程为2x ky =-,代入椭圆方程中,消x 可得22(2)420k y ky +-+=则△22168(2)0k k =-+>,解得2k >2k <-, 12242k y y k ∴+=+,12222y y k =+, 212121212(2)(2)2()4x x ky ky k y y k y y ∴=--=-++,1212()4x x k y y +=+-, 11AF BF ⊥Q , ∴110AF BF =u u u r u u u rg ,221212121212121212121212(1)(1)()12()4()41(1)()10x x y y x x x x y y k y y k y y k y y y y k y y k y y ∴+++=++++=-++++-++=+-++=即22222(1)41022k k k k +-+=++, 解得2k =±,故直线AB 的方程的方程为22x y =±-,即220x y ±+=18.(16分)自20世纪以来,战争灾害、自然灾害给人类带来巨大损失.某地为解决重大紧急情况时人群疏散的需要,对一矩形ABMN 广场区域进行改造,其中AB 的长为60米,AN的长为120米.现设计从边BM 上一点C 处,将CB 沿着直线CE (点E 在边AB 上)折叠,使点B 落在边AD 上点F 处,其中CEF ∆区域建在地上,CBE ∆区域往地下开挖并和其他区域相通,分地上地下用于疏散人群,令BCE θ∠=. (1)求θ的取值范围;(2)若CE 的长最小时,人群疏散效果最佳,求人群疏散效果最佳时线段CE 的长.【解答】解:(1)设CE l =,由题意可知Rt CFE Rt CBE ∆≅∆, ∴2BEC FEC πθ∠=∠=-,2FEA FEC BEC πθ∴∠=-∠-∠=,sin BE l θ∴=,cos sin cos2AE EF FEA l θθ=∠=g , sin cos2sin 60l l θθθ∴+=,23606030sin (1cos2)sin (22)sin l sin sin θθθθθθ∴===+--,(0,)2πθ∈,230sin 601BE l sin θθ∴==-„,∴212sin θ„,04πθ∴<„, 又330cos 60cos 120sin sin 2BC l sin θθθθθ===-Q „,1sin 22θ∴…,又Q (0,)2πθ∈,∴262ππθ剟,即124ππθ剟, 综上所求,[,]124ππθ∈;(2)令sin t θ=,Q [,]124ππθ∈,62[t -∴∈2, 则330l t t =-,设3()g t t t =-,62[t -∈2, 233()133()(g t t t t '∴=-=-, ∴当62[t -∈,3)时,()0g t '>,函数()g t 单调递增;当32(x ∈时,()0g t '<,函数()g t 单调递减, ∴当t =时,()g t取到最大值,最大值为g ,l ∴=即人群疏散效果最佳时线段CE的长为. 19.(16分)已知函数2()()f x x ax lnx a R =+-∈. (1)若函数()f x 在1x =处取得极值,求实数a 的值;(2)令函数2()()((0,])g x f x x x e =-∈,是否存在实数a 使函数()g x 的最小值是4?若存在,求出a 的值;若不存在,请说明理由; (3)证明:25((0,])22lnx e x lnx x e ->+∈. 【解答】解:(1)1()2f x x a x'=+-,Q 函数()f x 在1x =处取得极值, f ∴'(1)210a =+-=,解得1a =-.(2)2()()g x f x x ax lnx =-=-,(0,])x e ∈,假设存在实数a 使函数()g x 的最小值是4. 即4lnx a x+…,(0,])x e ∈,令4()lnx h x x+=,(0,])x e ∈, 23()lnx h x x +'=-,可得31x e=时,函数()h x 取得极大值即最大值.331()h e e =. 3a e ∴….∴存在实数3a e =,使函数()g x 的最小值是4.(3)证明:令25()22lnx u x e x lnx =---,(0x ∈,]e . 23()2u x e x '=-,令23()02u x e x '=-=,解得232x e=. 可得函数()u x 的极小值即最小值2333531()(32)23(433)0222222u ln ln ln e =---=-=->. 25022lnx e x lnx ∴--->,(0x ∈,]e . 即25((0,])22lnx e x lnx x e ->+∈. 20.(16分)已知各项均为正数数列{}n a 满足33321212()n n a a a a a a ++⋯⋯+=++⋯⋯+.(1)求数列{}n a 的通项公式;(2)若等比数列{}n a 满足12b a =,24b a =,求12132121n n n n n a b a b a b a b a b ---+++⋯⋯++的值(用含n 的式子表示);(3)若113(*)n n n a c c n N ++=+∈,2352c c -=,求证:数列{}n c 是等差数列.【解答】解:(1)各项均为正数数列{}n a 满足33321212()n n a a a a a a ++⋯⋯+=++⋯⋯+. 3211a a ∴=,解得11a =.2n …时,可得:32212121()()nn n a a a a a a a -=++⋯⋯+-++⋯+, 化为:3121(222)nn n n a a a a a a -=++⋯⋯++g , ∴22nn n a S a =-. 2n ∴…时,21112n n n a S a ---=-.相减可得:11n n a a --=. ∴数列{}n a 为等差数列.11n a n n ∴=+-=.(2)等比数列{}n a 满足122b a ==,244b a ==.可得公比422q ==. 2n n b ∴=.231121321212(1)2(3)2222n n n n n n n n T a b a b a b a b a b n n n ----=+++⋯⋯++=+-+-+⋯⋯++g g g g , 23122(1)2222n n n T n n +∴=+-+⋯⋯++g g g ,231124(21)2222222222421n n n n n n T n n n -++-∴=-+++⋯⋯+++=-+=---g .(3)证明:1113(*)n n n n a c c n N +++==+∈Q , 可得:2333c c =+,1223c c =+,又2352c c -=. 解得1516c =,2916c =,31316c =, 2n ∴…时,13n n n c c -=+.相减可得:11123n n n c c c +-=-+-. 12123n n n c c c ++∴=-+-,相减可得:21113()2()()n n n n n n c c c c c c +++--=-+-. 设1n n n d c c +=-,化为:1132n n n d d d +-=+. 又1214d d ==,可得314d =.以此类推可得:14n d =.即114n n n d c c +=-=. ∴数列{}n c 是等差数列.。

2020年江苏省高考押题卷数 学I 2020.6一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1. 已知集合M = {-1,0,1,2 },集合2{|20}N x x x =+-=,则集合M ∩N = ▲ .2. 已知复数22i 1iz =++(i 为虚数单位),则z 的共轭复数z =▲ .3. 为了解学生课外阅读的情况,随机统计了n 名学生的课外阅读时间,所得数据都在[50,150]中,其频率分布直方图如图所示.已知在[50 100),中的频数为24,则n 的值为 ▲ . 4. 如图,执行算法流程图,则输出的b 的值为 ▲ .5. 已知A 、B 、C 三人在三天节日中值班,每人值班一天,那么A 排在C 后一天值班的概率为 ▲ .6. 底面边长和高都为2的正四棱锥的表面积为 ▲ .7. 在平面直角坐标系xOy 中,已知双曲线经过点(36)-,,且它的两条渐近线方程是3y x =±,则该双曲线标准方程为 ▲ . 8.已知25sin cos αα+=,则sin2cos4αα+的值为 ▲ . 注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页包含填空题(第1~14题)、解答题(第15~20题).本卷满分为160分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.4.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5.请保持答题卡卡面清洁不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠(第4题)9. 设S n 为等差数列{a n }的前n 项和,若3521a a -=,10100S =,则20S 的值为 ▲ . 10. 埃及数学中有一个独特现象:除23用一个单独的符号表示以外,其它分数都要写成若干个单位分数和的形式.例如2115315=+可以这样理解:假定有两个面包,要平均分给5个人,如果每人 12,不够;每人13,余13,再将这13分成5份,每人得115,这样每人分得11315+.形如2n (n = 5,7,9,11,…)的分数的分解:2115315=+,2117428=+,2119545=+,按此规律,2n= ▲ (n = 5,7,9,11,…) . 11. 在平面直角坐标系xOy 中,已知圆22:(2)4C x y -+=,点P 是圆C 外的一个动点,直线P A ,PB 分别切圆C 于A ,B 两点.若直线AB 过定点(1,1),则线段PO 长的最小值为 ▲ . 12. 已知正实数x ,y 满足21()1,x x y y -=则1x y+的最小值为 ▲ . 13.如图,在平行四边形ABCD 中,AB =2AD ,E , F 分别为AD ,DC 的中点,AF 与BE 交于点O .若125OF OB AD AB u u u r u u u r u u u r u u u r⋅=⋅,则∠DAB 的余弦值为 ▲ . 14. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且431tan tan A B +=,则3c b的最大值为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知向量m =(b ,a - 2c ), n =(cos A - 2cos C ,cos B ),且m ⊥n . (1)求sin sin C A的值;(2)若a =2,35=m ,求△ABC 的面积.AB CD FEO16.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,12AC AA =,AC BC ⊥,D ,E 分别为A 1C 1,AB 的中点.求证:(1)AD ⊥平面BCD ;(2)A 1E ∥平面BCD .17.(本小题满分14分)如图,某大型厂区有三个值班室A ,B ,C .值班室A 在值班室B 的正北方向3千米处,值班室C 在值班室B 的正东方向4千米处.(1)保安甲沿CA 从值班室C 出发行至点P 处,此时PC =2,求PB 的距离;(2)保安甲沿CA 从值班室C 出发前往值班室A ,保安乙沿AB 从值班室A 出发前往值班室B ,甲乙同时出发,甲的速度为5千米/小时,乙的速度为3千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为3千米(含3千米),试问有多长时间两人不能通话?18.(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C :22221(0)y x a b a b+=>>过点()61,,离心率为2.A ,B 是椭圆上两点,且直线OA 与OB 的斜率之积为12. (1)求椭圆C 的方程; (2)求直线AB 的斜率; (3)设直线AB 交圆O :222x y a +=于C ,D 两点,且6AB CD =,求△COD 的面积.(第17题)19.(本小题满分16分)已知数列*{}()n a n ∈N 的前n 项和为S n ,()2n n nS a λ=+(λ为常数)对于任意的*n ∈N 恒成立.(1)若11a =,求λ的值; (2)证明:数列{}n a 是等差数列;(3)若22a =,关于m 的不等式|2|1m S m m -<+有且仅有两个不同的整数解,求λ的取值范围.20.(本小题满分16分)已知函数ln ()(1xf x a ax =∈+R ,且a 为常数). (1)若函数y =f (x )的图象在x =e 处的切线的斜率为21e(1e)-(e 为自然对数的底数),求a的值;(2)若函数y = f (x )在区间(1,2)上单调递增,求a 的取值范围; (3)已知x ,y ∈(1,2), 且x +y =3,求证:(23)ln (23)ln 11x x y yx y --+--≤0.2020年江苏省高考押题卷数 学II(附加题)21.【选做题】本题包括A ,B ,C 三小题,每小题10分. 请选定其中两.....小.题.,并在相应....的.答题区域....内作答....若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A. [选修4—2:矩阵与变换](本小题满分10分)曲线221x y +=在矩阵0(0,0)0a A a b b ⎡⎤=>>⎢⎥⎣⎦对应的变换下得到曲线221.9x y += (1)求矩阵A ;(2)求矩阵A 的特征向量.B. [选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,曲线C 的参数方程为2cos sin x y αα=⎧⎨=⎩,(α为参数).以原点O 为极点,以x 轴的非负半轴为极轴的极坐标系中,直线l 的极坐标方程为(sin cos )2ρθθ+=,直线l 与曲线C 相交于A ,B 两点,求线段AB 的值.C . [选修4-5:不等式选讲] (本小题满分10分)已知a ,b ,c 为正实数,满足a +b +c =3,求149a b c++的最小值.【必做题】第22题、第23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)五个自然数1、2、3、4、5按照一定的顺序排成一列. (1)求2和4不相邻的概率;(2)定义:若两个数的和为6且相邻..,称这两个数为一组“友好数”.随机变量X 表示上述五个自然数组成的一个排列中“友好数”的组数,求X 的概率分布和数学期望E (X ).23.(本小题满分10分)已知*2,,n n N ≥∈数列T 12:,,,n a a a L 中的每一项均在集合M ={1,2,…,n }中,且任意两项不相等,又对于任意的整数i ,j (1≤i <j ≤n ),均有.i j i a j a +≤+记所有满足条件的数列T 的个数为b n .例如n =2时,满足条件的数列T 为1,2或2,1,所以b 2=2.(1)求b 3; (2)求b n .。

2020年江苏省高考数学预测试卷本卷满分:160分试卷用时:120分钟一、填空题:本大题共14个小题;每小题5分,共70分。
1.设集合A,B是全集U的两个子集,则A⊂≠B是C U B⊂≠C U A的2.已知数列{a n}是首项为a1,公差为d(0<d<2π)的等差数列,若数列{c os a n}是等比数列,则其公比为3.某采访小组共8名同学,其中男生6名,女生2名。
现从中按性别分层随机抽取4名同学参加一项采访活动,则不同的抽取方法共有种4.已知函数=-'-'+=)31(,)31(2)(2fxfxxf则。
5.已知21[1,0)()1[0,1]x xf xx x+∈-⎧=⎨+∈⎩,,,则下列函数的图象错误..的是6.7某路段检查站监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如右图的频率分布直方图,则估计在这一时段内通过该站的汽车中速度不小于90k m/h 的约有辆7.过半径为2的球O 表面上一点A 作球O 的截面,若OA 与该截面所成的角是60°则该截面的面积是8.数列{a n }是等差数列,其前n 项和为S n ,若平面上的三个不共线的向量OC OB OA ,,满足,20061OC a OA a OB +=且A 、B 、C 三点共线,则S 2020=9.一条螺旋线是用以下方法画成:ABC ∆是边长为1的正三角形,曲线CA 1、A 1A 2、A 2A 3分别以A 、B 、C 为圆心,AC 、BA 1、CA 2为半径画的弧,曲线CA 1A 2A 3称为螺旋线,然后又以A 为圆心,AA 3为半径画弧L,这样画到第n 圈,则所得螺旋线112233231313,,,n n n n CA A A A A A A A A ---L 的总长度S n 为10.动点P 为椭圆22221(0)x y a b a b+=>>上异于椭圆顶点(,0)a ±的一点,F 1、F 2为椭圆的两个焦点,动圆C 与线段F 1P 、F 1F 2的延长线及线段PF 2相切,则圆心C 的轨迹为除去坐标轴上的点的11.函数y =f (x )的图象如右所示。
2020届江苏省新高考原创精准预测试卷(一)数学★祝考试顺利★ 注意事项:1、考试范围:高考范围。
2、试题卷启封下发后,如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况,应当立马报告监考老师,否则一切后果自负。
3、答题卡启封下发后,如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象,应当马上报告监考老师,否则一切后果自负。
4、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
6、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
7、保持答题卡卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
8、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、填空题(请把答案直接填写在答题卡...相应位置上) 1.设全集{}=1,2,3,4,5U ,若集合{}3,4,5A =,则U A =ð__________. 【答案】{}1,2 【解析】 【分析】利用补集定义直接求解即可.【详解】∵全集{}=1,2,3,4,5U ,集合{}3,4,5A =,∴{}12U A =,ð, 故答案为{}1,2.【点睛】本题考查补集的求法,是基础题,解题时要认真审题,注意补集定义的合理运用.2.命题“2,210x R x x ≥∃∈-+”的否定是__________. 【答案】2210x R x x ∀∈-+<,【解析】 【分析】直接利用特称命题的否定是全称命题写出结果即可. 【详解】因为特称命题的否定是全称命题,所以命题“2,210x R x x ≥∃∈-+”的否定命题:2210x R x x ∀∈-+<,, 故答案为:2210x R x x ∀∈-+<,.【点睛】本题主要考查命题的否定,全称命题与特称命题的否定关系,是基础题.3.已知向量(2,)a m =r ,(1,2)b =-r ,且a b ⊥r r,则实数m 的值是__________.【答案】1 【解析】 【分析】根据a b ⊥r r即可得出 220a b m ⋅=-=r r ,从而求出m 的值. 【详解】∵a b ⊥r r,∴ 220a b m ⋅=-=r r ;∴1m =,故答案为1.【点睛】本题主要考查向量垂直的充要条件,向量数量积的坐标运算,属于基础题.4.函数()lg(2)f x x =-+__________. 【答案】[)2,2- 【解析】 【分析】由偶次根式内部的代数式大于等于0,对数式的真数大于0联立不等式组求解. 【详解】由2020x x ->⎧⎨+≥⎩,得22x -≤<.∴函数()lg(2)f x x =-+[)2,2-. 故答案为[)2,2-.【点睛】本题主要考查了具体函数的定义域问题,属于基础题;常见的形式有:1、分式函数分母不能为0;2、偶次根式下大于等于0;3、对数函数的真数部分大于0;4、0的0次方无意义;5、对于正切函数tan y x =,需满足,2x k k Z ππ≠+∈等等,当同时出现时,取其交集.5.已知扇形的半径为6,圆心角为3π,则扇形的面积为__________. 【答案】6π 【解析】 【分析】先计算扇形的弧长,再利用扇形的面积公式可求扇形的面积. 【详解】根据扇形的弧长公式可得362l ππαr ==⨯=, 根据扇形的面积公式可得1126622S lr ππ==⋅⋅=, 故答案为6π.【点睛】本题主要考查扇形的弧长与面积公式,正确运用公式是解题的关键,属于基础题.6.已知等比数列{}n a 的前n 项和为n S ,424S S =,则84S S 的值是__________. 【答案】10 【解析】 【分析】根据等比数列前n 项和公式,由424S S =可得23q =,通过化简可得884411S q S q-=-,代入2q 的值即可得结果.【详解】∵424S S =,∴424S S =,显然1q ≠, ∴()()241111411a q a q qq--=--,∴214q +=,∴23q=,∴()()818484441111 110111a q S q q q S qa q q---===+=---,故答案为10. 【点睛】本题主要考查等比数列的前n 项和公式,本题解题的关键是看出数列的公比的值,属于基础题.7.设函数()sin()f x A x ωϕ=+(,,A ωϕ为常数,且0,0,0A ωϕ>><<π)的部分图象如图所示, 则ϕ的值是________.【答案】3π 【解析】 【分析】先由周期求出ω,再由五点法作图求出φ的值.【详解】根据函数f (x )=Asin (ωx +φ)(A ,ω,φ为常数,且A >0,ω>0,0<φ<π)的部分图象,可得34•2πω=712π+6π,∴ω=2. 再根据五点法作图可得2×(﹣6π)+φ=0,∴φ=3π,故答案为:3π.【点睛】本题主要考查由函数y=Asin (ωx +φ)的部分图象求解析式,由周期求出ω,由五点法求出φ的值,属于基础题.8.已知二次函数2()23f x x x =-++,不等式()f x m ≥的解集的区间长度为6(规定:闭区间[],a b 的长度为b a -),则实数m 的值是_______.【答案】5-【解析】 【分析】根据题意223x x m -++≥的解集为[],a b ,分析可得x a =和x b =是方程2230x x m -+-=的两根,将二次函数根与系数的关系与6b a -=相结合,可得m 的值.【详解】根据题意223x x m -++≥的解集为[],a b ,则x a =和x b =是方程223x x m -++=即2230x x m -+-=的两根, 则2a b +=,3ab m =-,不等式()f x m ≥的解集的区间长度为6,即6b a -=, 则有()()2444336a b ab m +-=--=,解可得5m =-, 故答案为5-.【点睛】本题主要考查函数的零点与方程根的关系,涉及一元二次不等式的解法,属于基础题.9.某工厂建造一个无盖的长方体贮水池,其容积为34800m ,深度为3m .如果池底每21m 的造价为150元,池壁每21m 的造价为120元,要使水池总造价最低,那么水池底部的周长为______m . 【答案】160 【解析】 【分析】设水池底面一边的长度为xm ,则另一边的长度为48003m x,由题意可得水池总造价()f x ,然后利用基本不等式求最值,可得水池总造价最低时的水池底部的周长. 【详解】设水池底面一边的长度为xm ,则另一边的长度为48003m x, 由题意可得水池总造价()48004800150120232333f x x x ⎛⎫=⨯+⨯+⨯⨯ ⎪⎝⎭()16002400007200x x x ⎛⎫=++> ⎪⎝⎭,则()1600720240000720240000f x x x ⎛⎫=++≥⨯ ⎪⎝⎭ 720240240000297600=⨯⨯+=,, 当且仅当1600x x=,即40x =时,()f x 有最小值297600, 此时另一边的长度为4800403m x=, 因此,当水池的底面周长为160m 时,水池的总造价最低,最低总造价是297600元, 故答案为160.【点睛】本题考查函数模型的构建,考查利用基本不等式求最值,考查利用数学知识解决实际问题,属于中档题.10.在ABC △中,sin 2sin cos 0A B C +=,则A 的最大值是______.【答案】6π 【解析】 【分析】利用三角形内角和定理与诱导公式化简可得3sin cos cos sin 0B C B C +=,即3tan tan B C =-,可得B 为锐角,C 为钝角,()tan tan A B C =-+展开代入利用基本不等式的性质即可得出tan A 的最大值,结合A 的范围即可得解. 【详解】∵sin 2sin cos 0A B C +=, ∴()sin 2sin cos 0B C B C ++=, ∴3sin cos cos sin 0B C B C +=, ∵cos 0C ≠,cos 0B ≠,∴3tan tan B C =-,可得B 为锐角,C 为钝角. ∴()()2tan 3tan tan tan tan tan 1tan tan 13tan B B B C A B C B C B --+=-+=-=-+213tan tan B B=≤=+,当且仅当tan B =时取等号, ∴tan A的最大值是3, ∵A 为锐角,∴A 的最大值是6π,故答案为6π. 【点睛】本题考查了三角形内角和定理、诱导公式、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.11.已知函数()2,1ln ,1x x ef x x x x⎧+<⎪⎪=⎨⎪≥⎪⎩,若()()()()123123f x f x f x x x x ==<<,则()13x f x 的取值范围是______. 【答案】21,0e ⎛⎫- ⎪⎝⎭【解析】 【分析】求得1x ≥时()f x 的导数,可得单调性和极值,画出()y f x =的图象,可得112e x e--<<,再由二次函数的单调性,可得所求范围. 【详解】由ln x y x =的导数为21ln xy x -'=, 当x e ≥,函数递减;当1x e ≤<时,可得函数递增, 即有x e =处函数取得极大值1e, 作出函数()2,1ln ,1x x ef x x x x⎧+<⎪⎪=⎨⎪≥⎪⎩的图象,可得112e x e --<<,由()()()()123123f x f x f x x x x ==<<,可得()()2213111112211x f x x f x x x x e e e ⎛⎫==+=+- ⎪⎝⎭,且在21,e e ⎛⎫-- ⎪⎝⎭递减,即有11x e =-时,()1321x f x e =-;12x e =-时,()130x f x =,可得()13x f x 的取值范围是21,0e ⎛⎫- ⎪⎝⎭.故答案为21,0e ⎛⎫-⎪⎝⎭.【点睛】本题考查分段函数的图象和应用:求范围,考查导数的运用:求单调性和极值,以及二次函数的单调性,考查运算能力,属于中档题.12.已知数列{}n a 的通项公式为51n a n =+,数列{}n b 的通项公式为2n b n =,若将数列{}n a ,{}n b 中相同的项按从小到大的顺序排列后看作数列{}n c ,则6c 的值为_______.【答案】256 【解析】 【分析】利用数列的通项公式列举数列的项,进一步利用共性求出结果. 【详解】数列{}n a 的通项公式为51n a n =+,数列的数据符合平方的数有:16,36,81,121,169,256.数列{}n b 的通项公式为2n b n =,当4n =,6,9,11,13,16时符合上面各个数.数列{}n a ,{}n b 中相同的项按从小到大的顺序排列后看作数列{}n c , 则6c 的值为256,故答案为256.【点睛】本题考查的知识要点:数列的通项公式的应用,列举法的应用,主要考查学生的运算能力和转化能力,属于基础题型.13.如图,在平面四边形ABCD中,AB BC⊥,AD CD⊥,60BCD∠=︒,23CB CD==.若点M为边BC上的动点,则AM DMuuu r uuu u r⋅的最小值为_______.【答案】214【解析】【分析】如图所示,以B为原点,以BA所在的直线为x轴,以BC所在的直线为y轴,求出A,D,C的坐标,根据向量的数量积和二次函数的性质即可求出.【详解】如图所示:以B为原点,以BA所在的直线为x轴,以BC所在的直线为y轴,过点D作DP x⊥轴,过点D作DQ y⊥轴,∵AB BC⊥,AD CD⊥,120BAD∠=︒,23CB CD==∴()00B,,()20A,,(0,23C,(3D,设()0,M a,则()2,AM a=-u u u u r,(3,3DM a=-u u u u r,故(22121 6244AM DM a a a ⎛⎫=+=-+≥ ⎪ ⎪⎝⎭⋅u u u u r u u u u r ,故答案为214. 【点睛】本题考查了向量在几何中的应用,考查了运算能力和数形结合的能力,属于中档题.14.函数()xf x e x a =-在(1,2)-上单调递增,则实数a 的取值范围是________.【答案】-1a ≤或3a ≥ 【解析】 【分析】首先根据单调性及最值可得()1,2a ∉-,分为1a ≤-和2a ≥两种情形,求出函数的导数,根据函数的单调性得到关于a 的不等式,解出取并集即可. 【详解】由题意得()()110a f x f e-->-=≥,()()01,2f a a =⇒∉-,①1a ≤-时,()()xf x ex a =-,()()10x f x e x a -+'=≥即()1,2x ∀∈-,()()10100g x x a g a a =-+≥⇒-=-≥⇒≤, 因此1a ≤-; ②2a ≥时,()()xf x ea x =-,()()10x f x e a x --'=≥即()1,2x ∀∈-,()()102303h x x a h a a =-+-≥⇒=-≥⇔≥ 因此3a ≥,综上可得(][),13,a ∈-∞-⋃+∞, 故答案为(][),13,-∞-+∞U .【点睛】本题主要考查了函数的单调性问题,考查导数的应用,分类讨论的数学思想,是一道综合题.二、解答题:请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤) 15.已知(2cos23,2sin2)αα=+m ,(sin ,cos )ββ=n . (1)若6πβ=,且()f α=⋅m n ,求()f α在[0,]2π上的取值范围;(2)若//m n ,且αβ+、α的终边不在y 轴上,求tan()tan αβα+的值. 【答案】(1)()17,22f α⎡⎤∈⎢⎥⎣⎦;(2)5-【解析】 【分析】(1)首先利用向量的数量积,对三角函数关系式进行变换,进一步利用函数的定义域求出值域;(2)利用向量的共线,建立等量关系,再利用角的恒等变换求出结果.【详解】(1)已知()2cos232sin 2ααm =+u r ,,() sin ,cos βn β=r ,由于6πβ=, ()()2cos23sin 2sin 2cos f αm n αβαβ=⋅=++⋅u r r3cos 222αα=++32262πsin α⎛⎫=++ ⎪⎝⎭,由于0,2απ⎡∈⎤⎢⎥⎣⎦,所以2]766[6πππα+∈,,故()17,22f α⎡⎤∈⎢⎥⎣⎦.(2)若 //m n u r r,且αβ+、α的终边不在y 轴上,故()2cos23cos 2sin 2sin 0αβαβ+⋅-⋅=, 即()2cos 23cos 0αββ++=,整理得()][()2cos 3cos []0αβααβα++++-=,化简为()5tan tan 0αβα++=,即()tan tan 5αβα+=-.【点睛】本题考查的知识要点:向量的数量积的应用,三角函数关系式的恒等变变换,正弦型函数性质的应用,主要考查学生的运算能力和转化能力,属于基础题型.16.已知等差数列{}n a 的前n 项和为n A ,35a =,636A =. 数列{}n b 的前n 项和为n B ,且21n n B b =-.(1)求数列{}n a 和{}n b 的通项公式;(2)设n n n c a b =⋅,求数列{}n c 的前n 项和n S . 【答案】(1)21n a n =-,12n n b -=;(2)()2323nn S n =⋅-+【解析】 【分析】(1)利用已知条件建立方程组,进一步求出数列的通项公式;(2)利用(1)的结论,进一步利用乘公比错位相减法求出数列的和.【详解】(1)等差数列{}n a 的前n 项和为n A ,35a =,636A =,设数列的首项为1a ,公差为d ,则316125656362a a d A a d =+=⎧⎪⎨⨯=+⋅=⎪⎩, 解得11a =,2d =,故21n a n =-. 由于数列{}n b 的前n 项和为n B ,且21n n B b =-.所以当2n ≥时,1121n n B b --=-, 整理得12n n b b -=,所以数列{}n b 是以11b =为首项,2为公比的等比数列. 故12n nb -=,首项符合通项,则12=n n b -.(2)由(1)得:()1212n n n n c a b n -=⋅=-⋅,所以()0111232212n n S n -⋅+⋅+⋅⋯+-=①,()1221232212n n S n ⋅+⋅+⋯+⋅-=②,①-②得:()()1112222212n nn S n --+⋅+⋯+⋅-=⋅-,所以()22121221n nn S n ⎛--+---⎫=⋅ ⎪⎝⎭,整理得()2323nn S n =⋅-+.【点睛】本题考查知识要点:数列的通项公式的求法及应用,乘公比错位相减法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型17.某湿地公园围了一个半圆形荷花塘如图所示,为了提升荷花池的观赏性,现计划在池塘的中轴线OC 上设计一个观景台D (D 与,O C 不重合),其中,,AD BD CD 段建设架空木栈道,已知2AB km =,设建设的架空木栈道的总长为ykm .(1)设(rad)DAO θ∠=,将y 表示成θ的函数关系式,并写出θ的取值范围; (2)试确定观景台的位置,使三段木栈道的总长度最短. 【答案】(1)21tan 0,cos 4πy θθθ⎛⎫=+-∈ ⎪⎝⎭,;(2)见解析 【解析】 【分析】(1)由2AB =,得1AO BO CO ===,可得1cos cos AO AD BD θθ===,进一步得到tan tan DO AO θθ==,1tan CD OC OD θ=-=-,则函数解析式可求;(2)求出原函数的导函数,得到函数的单调性,可得当6πθ=时,三段木栈道的总长度最短,由此得到观景台的位置.【详解】(1)由2AB =,则1AO BO CO ===, 由题意知:CO 为AB 的中垂线,可得1cos cos AO AD BD θθ===,tan tan DO AO θθ==, 则1tan CD OC OD θ=-=-,得21tan 0,cos 4πy θθθ⎛⎫=+-∈ ⎪⎝⎭,; (2)22sin 10,cos 4θπy θθ-⎛⎫'=∈ ⎪⎝⎭,, ∴当0,6πθ⎛⎫∈ ⎪⎝⎭时,0y '<,21sin cos y θθ=+-单调递减,当,64ππθ⎛⎫∈⎪⎝⎭时,0y '>,21sin cos y θθ=+-单调递增,∴当6πθ=时,即3OD km =时,三段木栈道的总长度最短. 【点睛】本题主要考查根据实际问题选择函数模型,训练了利用导数求最值,是中档题.18.已知()x x af x e e=-是奇函数,其中a 为常数. (1)求实数a 的值;(2)求函数222()x xy e e f x λ-=+-在[0,)x ∈+∞上的值域;(3)令()()2g x f x x =-,求不等式32(1)(13)0g x g x ++-<的解集.【答案】(1)1;(2)见解析;(3){|111x x x <<< 【解析】 【分析】(1)由题意可得()()f x f x -=-,代入可求a ;(2)令1x xt e e =-,然后转化为二次函数的值域求解;(3)结合()g x 为奇函数,及单调性可求不等式的解集. 【详解】(1)由题意可得()()f x f x -=-,1x xx xa ae e e e =--+, 整理可得,()110x x a e e ⎛⎫-+= ⎪⎝⎭, ∴1a =; (2)令1xxt e e =-, ∵[)0x ∈+∞,,∴[)1xe ∈+∞,, ∴0t ≥, ∴2222212222xx x x x xy ee λf x e e λe t λt e --⎛⎫=+-=+--=-+ ⎪⎝⎭(),0t ≥(),对称轴t λ=, ①0λ<时,222y t λt =-+在[)0+∞,上单调递增,∴2y ≥,值域为[)2,+∞; ②0λ≥时,222y t λt =-+在[)0+∞,上先减后增,当x λ=时函数有最小值22λ-,值域为)22,λ⎡-+∞⎣; (3)∵()()()()22g x f x x f x x g x -=-+=-+=-,x ∈R , ∴()g x 为奇函数, ∵()()321130g x g x++-<,∴()()()32211313g x g x g x +<--=-+,∵()120xx g x e e'+-≥=, ∴()g x 单调递增,∴32113x x +<-+, 即()()322321220x x x x x -+=---<,当1x >时,2220x x --<,解可得11x <<+ 当1x <时,2220x x -->,解可得1x < 综上可得,不等式的解集{|111x x x <-<<+.【点睛】本题主要综合考查了函数单调性,奇偶性等函数性质的综合应用,解题的关键是函数知识的熟练应用,属于中档题.19.已知数列{}n a 的首项为1,定义:若对任意的*n N ∈,数列{}n a 满足13n n a a +->,则称数列{}n a 为“M 数列”.(1)已知等差数列{}n a 为“M 数列”, 其前n 项和n S ,满足()2*S 22n n n n N <+∈,求数列{}n a 的公差d 的取值范围;(2)已知公比为正整数的等比数列{}n a 为“M 数列”,记数列{}n b 满足34n n b a =,且数列{}n b 不为“M 数列,求数列{}n a 的通项公式.【答案】(1)34d <≤;(2)15n n a -=,*n N ∈【解析】 【分析】(1)设公差为d 的等差数列{}n a 为“M 数列”,可得3d >,由等差数列的求和公式,解不等式可得d 的范围;(2)首先通过11(1)3n n n a a q q -+-=->得到q 至少为大于等于2的正整数,接着判断数列1{}--n n a a 单调递增,即可得213a a ->,所以4q >,同理可得213b b -≤,即5q ≤,即5q =,即可得到所求通项.【详解】(1)设公差为d 的等差数列{}n a 为“M 数列”,可得3d >,()21122n S n n n d n n =++<+, 即有412d d n -<+恒成立,即为402d d -≤+,解得34d <≤; (2)设数列{}n a 的公比为q ,则111n n n a a q q --==,因为公比为正整数的等比数列{}n a 为“M 数列”,所以1111(1)(1)3n n n n a a a q q q q --+-=-=->,所以q 至少为大于等于2的正整数;又112n nn n a a q a a +--=-≥,所以数列1{}--n n a a 单调递增, 所以在数列1{}--n n a a 中,21a a -为最小项,由{}n a 为“M 数列”,可知只需213a a ->,即13q ->,所以4q > 同理,在1{}n n b b --中,“21b b -”为最小项, 因为{}n b 不是“M 数列”,所以存在13m m b b --≤,又“21b b -”为最小项,所以213b b -≤, 即1(1)4a q -≤,所以5q ≤因为*q N ∈,所以5q =,15n n a -=.【点睛】本题考查新定义的理解和运用,考查等差数列的求和公式和等比数列的通项公式,考查转化思想和运算能力,属于中档题.20.设函数()1ln f x ax x =--,其中a 为常数.(1)当2a =时,求曲线()f x 在点(1,(1))f 处的切线方程;(2)若12,x x 为函数()f x 的两个零点,且12x x >. ①求实数a 的取值范围; ②比较12x x +与2a的大小关系,并说明理由. 【答案】(1)y x =;(2)①()0,1,②见解析 【解析】 【分析】(1)求出函数的导数,计算()1f ,()1f '的值,求出切线方程即可;(2)①求出函数的导数,通过讨论a 的范围,求出函数的单调区间,结合函数的零点的个数确定a 的范围即可;②求出1212ln ln x x a x x -=-,得到()121211221221ln 2x x x x x f x x x x x -⎛⎫+⎛⎫'=- ⎪ ⎪-+⎝⎭⎝⎭,设121x m x =>,则()()21ln 1m g m m m -=-+,根据函数的单调性证明即可.【详解】(1)2a =时,()21ln f x x x =--,()21f xx '=-, 故()()111f f ='=,故切线方程是y x =. (2)①()1f x a x'=-,当0a ≤时,()0f x <′恒成立, 即()f x 单调递减,不可能有2个零点, 故0a ≤不合题意;当0a >时,令()0f x '=,解得:1x=,列表如下:故()1min f x f lna a ⎛⎫==⎪⎝⎭,∵()f x 有2个零点,∴ln 0a <,解得:01a <<, 故10a f e e ⎛⎫=> ⎪⎝⎭,且 11e a <, 故存在211,x e a ⎛⎫∈ ⎪⎝⎭,使得()20f x =,244212ln f a aa ⎛⎫=-- ⎪⎝⎭,设()22a t =∈+∞,,则()()24212ln 2h t f t t t a ⎛⎫==--> ⎪⎝⎭,()220h t t'=->,故()h t 在()2,+∞递增, 故()()232ln 20h t h >=->, ∵2 41a a >,故存在1214,x a a ⎛⎫∈ ⎪⎝⎭,使得()10f x =, 综上,()01a ∈,;②∵()()120f x f x ==,故11221ln 1ln ax x ax x --=--, 即1212ln ln x x a x x -=-,()121211221221ln 2x x x x x f x x x x x -⎛⎫+⎛⎫'=- ⎪ ⎪-+⎝⎭⎝⎭, 设12 1x m x =>,则()()21ln 1m g m m m -=-+,则()()()22101m g m m m -'=>+,故()g m 递增,()()10g m g >=,∵120x x ->,∴()1212021x x f g m x x +⎛⎫'=>⎪-⎝⎭, 即1212x x a +>,故122x x a+>. 【点睛】本题考查了函数的单调性,最值问题,考查导数的应用以及分类讨论思想,转化思想,考查不等式的证明,属于难题. 21.如图,已知AD 是ABC ∆的外角EAC ∠的平分线,交BC 的延长线于点D ,延长DA 交ABC∆的外接圆于点F ,连结,FB FC .(1)求证:FB FC =;(2)若AB 是ABC ∆外接圆的直径,120EAC ∠=︒,6BC =,求AD 的长. 【答案】(1)见解析;(2)43 【解析】 【分析】(1)由已知得EAD DAC ∠=∠,DAC FBC ∠=∠,从而FBC FCB ∠=∠,由此能证明FB FC =;(2)由已知得90ACB ∠=︒,从而30ABC ∠=︒,1602DAC EAC ∠=∠=︒,由此能求出AD .【详解】证明:(1)因为AD 平分EAC ∠, 所以EAD DAC ∠=∠. 因为四边形AFBC 内接于圆, 所以DAC FBC ∠=∠, 因为EAD FAB FCB ∠=∠=∠, 所以FBC FCB ∠=∠,所以FB FC =.(2)因为AB 是圆的直径,所以90ACB ∠=︒, 又120EAC ∠=︒,所以30ABC ∠=︒,1602DAC EAC ∠=∠=︒, 因为6BC =,所以tan 23AC BC ABC =∠= 所以)43cos ACAD cm DAC==∠.【点睛】本题考查两线段长相等的证明,考查线段的求法,解题时要认真审题,注意圆的简单性质的合理运用,是中档题. 22.已知可逆矩阵273aA ⎡⎤=⎢⎥⎣⎦的逆矩阵为127b a --⎡⎤=⎢⎥-⎣⎦A ,求1A -的特征值.【答案】14λ=24λ= 【解析】 【分析】由110•01A A -⎡⎤=⎢⎥⎣⎦,求出5a =,3b =,从而13275A --⎡⎤=⎢⎥-⎣⎦,进而()281f λλλ=-+,由()0f λ=,能求出1A -的特征值.【详解】∵可逆矩阵273a A ⎡⎤=⎢⎥⎣⎦的逆矩阵为127b a --⎡⎤=⎢⎥-⎣⎦A , ∴12210 73701a b A A a --⎡⎤⎡⎤⎡⎤⋅==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦, ∴14172101431ab b a -=⎧⎪-=⎨⎪-+=⎩,解得5a =,3b =, ∴13275A --⎡⎤=⎢⎥-⎣⎦, ∴()2328175λf λλλλ-⎡⎤==-+⎢⎥-⎣⎦,由()0f λ=,得14λ=,24λ=.【点睛】本题主要考查逆变换与逆矩阵,考查矩阵特征值与特征向量的计算等基础知识,属于基础题. 23.在平面直角坐标系xOy 中,圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),以点O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求圆C 的极坐标方程;(2)过极点O 作直线与圆C 交于点A ,求OA 的中点所在曲线的极坐标方程. 【答案】(1)4cos ρθ=;(2)2cos ρθ= 【解析】 【分析】(1)直接利用转换关系,把参数方程直角坐标方程和极坐标方程之间进行转换;(2)设OA 的中点坐标为()00,ρθ,所以()00,2A ρθ,代入(1)中的结论即可得结果. 【详解】(1)圆C 的参数方程为22cos ,2sin x y αα=+⎧⎨=⎩(α为参数),转换为直角坐标方程为:()2224x y -+=, 转换为极坐标方程为:4cos ρθ=. (2)过极点O 作直线与圆C 交于点A ,设OA 的中点坐标为()00,ρθ,所以()00,2A ρθ, 所以0024cos ρθ=,即002cos ρθ=,所以OA 中点所在的曲线的极坐标方程为2cos ρθ=.【点睛】本题考查的知识要点:参数方程直角坐标方程和极坐标方程之间的转换,两点间的距离公式的应用,主要考查学生的运算能力和转化能力,属于基础题型24.[选修4—5:不等式选讲]已知函数()f x =()g x =x 使()()f x g x a +>成立,求实数a 的取值范围.【答案】(),8-∞ 【解析】试题分析:先将问题“ 存在实数x 使()()f x g x a +>成立”转化为“求函数()()f x g x +的最大值”,再借助柯西不等式求出()()f x g x +的最大值即可获解. 试题解析:存在实数x 使()()f x g x a +>成立,等价于()()f x g x +的最大值大于a , 因为,由柯西不等式:()()()2321143121464x xx x ⨯++⨯-≤+++-=,所以()()36148f x g x x x +=++-≤,当且仅当10x =时取“=”, 故常数a 的取值范围是(),8-∞.考点:柯西不等式即运用和转化与化归的数学思想的运用.25.如图,在四棱锥P ABCD -中, BC PB ⊥,AB BC ⊥,AD BC ∕∕,3AD =,22PA BC AB ===,3PB =.(1)求二面角P CD A --的余弦值;(2)若点E 在棱PA 上,且BE ∕∕平面PCD ,求线段BE 的长. 【答案】(1)105;(27【解析】 【分析】(1)推导出PB AB ⊥,以B 为原点,BA 为x 轴,BC 为y 轴,BP 为z 轴,建立空间直角坐标系,利用向量法能求出二面角P CD A --的余弦值;(2)由点E 在PA 上,得 AE λAP =u u u r u u u r,]1[0λ∈,,求出()10BE BA AE λ+=-=u u u u u r u u u r u r ,再由BE P 平面PCD ,可得 0E m B ⋅=u u u r u r,求出λ,得到 BE u u u r的坐标,则答案可求.【详解】(1)∵在四棱锥P ABCD -中,由22PA AB ==,PB = 得222PB AB PA +=,则PB AB ⊥, 又BC PB ⊥,AB BC ⊥,∴以B 为原点,BA 为x 轴,BC 为y 轴,BP 为z 轴,建立空间直角坐标系,则()000B ,,,()100A ,,,()020C ,,,()130D ,,,(00P , () 010CD =u u u r,,,(02PC =u u u r ,,, 由图可知,平面ABCD 的一个法向量为() 001n =r,,, 设平面PCD 的法向量为(),,x y z m =u r,则020m CD x y m PC y ⎧⋅=+=⎪⎨⋅==⎪⎩u u u v v u u uv v ,取2z =,得()m =u r , 设二面角P CD A --的平面角为α,则cos cos ,||5n m n mαn m ⋅====⋅r u rr u r r u r ,∴二面角P CD A --的余弦值为5; (2)∵点E 在棱PA 上,∴ AE λAP =u u u r u u u r,]1[0λ∈,,∵(10AP =-u u u r,∴() 0AE λ=-u u u r,()10BE BA AE λ+=-=u u u u u r u u u r u r, 又∵BE P 平面PCD ,m u r 为平面PCD 的法向量, ∴ 0E m B ⋅=u u u r u r,即)1=0λ-+,解得13λ=,∴23 BE ⎛= ⎝⎭u u u r,则BE BE ==u u u r .【点睛】本题主要考查利用空间向量求解二面角的大小,训练了利用空间向量证明线面平行,是中档题.26.已知函数0cos ()(0)xf x x x=>,设()n f x 是1()n f x -的导数,*n N ∈. (1) 求12πππ2()()222f f +的值;(2) 证明:对于任意*n N ∈,等式1πππ2()()4442n n nf f -+=都成立. 【答案】(1)0;(2)见解析 【解析】 【分析】(1)由于求两个函数的相除的导数比较麻烦,根据条件和结论先将原函数化为:()0cos f x x x =,然后两边求导后,根据条件两边再求导得:()()122cos x x f xf x +=-,把2x π=代入式子求值;(2)由(1)得,()()01sin f x xf x x +=-和()()122cos x x f xf x +=-,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后把4x π=代入所给的式子求解验证.【详解】(1)∵0cos ()xf x x=,∴()0cos f x x x =, 则两边求导,()()0[]cos xf x x '=',∵()n f x 为()1n f x -的导数,*n N ∈, ∴()()01sin f x xf x x +=-,两边再同时求导得,()()122cos x x f xf x +=-, 将2x π=代入上式得,1222202f f πππ⎛⎫⎛⎫⎪ ⎪⎝⎝⎭+=⎭; (2)证明:由(1)得,()()01sin cos 2πf x xf x x x ⎛⎫+=-=+⎪⎝⎭, 恒成立两边再同时求导得,()()()122sin cos 2πf x xf x x x π⎛⎫+=-+=+ ⎪⎝⎭, 再对上式两边同时求导得()()()2333sin cos 2πf x xf x x πx ⎛⎫+=-+=+⎪⎝⎭, 同理可得,两边再同时求导得,()()()3434sin cos 22πf x xf x x x π⎛⎫+=-+=+ ⎪⎝⎭, 猜想得,()()1cos 2n n n πnf x xf x x -⎛⎫+=+ ⎪⎝⎭对任意*n N ∈恒成立, 下面用数学归纳法进行证明等式成立: 当1n =时,()()01sin cos 2πf x xf x x x ⎛⎫+=-=+ ⎪⎝⎭成立,则上式成立; 假设*1n k k k N =>∈(且)时等式成立, 即()()1cos 2k k k πkf x xf x x -⎛⎫+=+⎪⎝⎭, ∵()()()()()11[]k k k k k kf x xf x kf x f x xf x --+'='++'()()()11k k k f x xf x +=++又()[1cos sin cos 2]22k πk πk πx x x +⎛⎫⎛⎫⎛⎫+'=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴那么1n k =+(1k >且*k N ∈)时.等式()()()()111cos 2k k k πk f xf x x x ++⎛⎫++=+ ⎪⎝⎭也成立,由①②得,()()1cos 2n n n πnf x xf x x -⎛⎫+=+⎪⎝⎭对任意*n N ∈恒成立.令4x π=代入上式得,1444424cos sin 2n n n ππππn ππf f -⎛⎫+==±⎛⎫⎛⎫+⎪ ⎪=± ⎭⎝⎭⎪⎭⎝⎝,所以,对于任意*n N ∈,等式1πππ()()4442n n nf f -+=都成立. 【点睛】本题考查了三角函数、复合函数的求导数公式和法则、诱导公式,以及数学归纳法证明命题、转化思想等,考查了学生观察问题、分析问题、解决问题的能力,以及逻辑思维能力.。
2020年普通高等学校全国统一招生考试 (江苏卷)预测卷数学I参考公式:1. 样本数据12,,,n c x x L 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑; 2.圆柱的体积V=Sh,其中S 是圆柱的底面圆面积,h 是高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.已知集合A={x|x<0}, B={-2,-1, 0, 2},则A ∩B=___2.已知复数z 满足112z i i=++(i 是虚数单位),则复数z 的共轭复数为___ 3.某地区有小学生、初中生、高中生的人数见下表.采用分层抽样的方法调查学生的眼睛视力状况,在抽取的样本中初中生有320人,则该样本中的高中生人数为_____类别小学生 初中生 高中生 合计 人数 18000 1 6000 9000 430004.5.函数2()ln )(9f x x =-的定义域为____6.有3名学生甲、乙、丙,在分发数学作业时,从他们3人作业中各随机取出1份作业,则这3名学生恰好都拿到自己作业的概率为_____7.已知等比数列{}n a 满足11,2a =且2434(1),a a a =-则5a =____ 8.已知f(x)是定义在R 上的奇函数,当x> 0时,2()log 3f x x =-,则f(f(-16))的值为_____9.某品牌汽车4S 店一年销售汽车4000辆,每次从汽车公司购置x 辆,运费为4万元/次,一年的总储存费用为0.4x 万元.要使一年的总运费与总储存费用之和最小的,则x 的值为_____.10.在平面直角坐标系xOy 中,已知抛物线220y px p =>的准线1与双曲线2221x y a a-=>0的两条渐近线围成等边三角形,且面积为3,则p+a=_____. 11.如图,在正四棱柱形容器内盛有水和相同高度的实心圆柱(其中圆柱底面内切于正四棱柱底面,水面恰与正四棱柱上底面齐平),将实心圆柱拿去后,则水面高度与正四棱高度比为____. (不计水的损耗)12.如图,△ABC 中, M 为AB 中点, AB=5, CM=3, EF 为圆心为C,半径为1的圆的动直径,则BE AF ⋅u u u r u u u r 的取值范围是_____13.在平面直角坐标系xOy 中,圆221:4O x y +=与圆2222:(4)(0)O x y r r -+=>,在圆2O 上存在点Q,过点Q 作圆1O 的切线,切点为P, N,使得5,9QP QN ⋅=u u u r u u u r 则实数r 的最小值为___. 14.已知函数3,1,(),1,x a x f x x ax x -≥⎧=⎨-<⎩若函数y=f[f(x)]恰有5个不同零点,则实数a 的取值范围是____.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)在平面直角坐标系xOy 中,以x 轴正半轴为始边作两个钝角α,β,它们的终边分别与单位圆交于A,B 两点.已知A,B 的横坐标分别为3102,.1010-- 求: (1) cos( α-β )的值;(2) 2α-β的值.16. (本小题满分14分)如图,三棱锥P- ABC 中,已知PA ⊥底面ABC,AC ⊥BC,且PA= AC,点E, F 分别是棱PC,PB 的中点.(1)求证:AE ⊥BC ;(2)点G 为棱AB 上一点,满足2,GB GA =求证:AE //平面CFG .17.(本小题满分14分)如图,在平面直角坐标系xOy 中,椭圆22221(0),x y a b a b +=>>圆C:222().4b x y b +-=A, B 分别为椭圆的左、右顶点,直线AC 交圆C 于D, P 两点(D 在线段AC 上),且2.AD DC =u u u r u u u r(1)求椭圆的离心率;(2)直线BP 与椭圆相交于点Q, 直线AQ 被圆C 截得弦长为6,求椭圆的标准方程.18. (本小题满分16分)如图为某野生动物园一角,∠MOK 内区域为陆地动物活动区,∠NOK 内区域为水上动物活动区.为满足游客游览需要,现欲在OM,ON 上分别选一处A,B,修建一条贯穿两区域的直路AB, AB 与KO 相交于点P.若PA 段,PB 段每百米修路费用分别为1万元和2万元,已知∠NOK=30°,OM ⊥OK, OP=2 百米,设∠PAO=α.(1)试将修路费用表示为α的函数()S α(2)求修路费用()S α的最小值.19. (本小题满分16分)设等差数列{}n a 的前n 项和为,n S 且7146,54.a a S == (1)求数列{}n a 的通项公式;(2)是否存在正整数m, k,使得31,1,1m m k a a a +---依次成等比数列?并说明理由; (3)设数列{}n b 满足2*1()(),5n n a b n -=∈N 将{}n a 和{}n b 中相同的项按照从小到大的顺序依次排列,得到数列{},n c 求数列{}n c 的通项公式.20. (本小题满分16分)已知函数y= f(x) 的定义域为D,若满足∀x ∈D,(x-1)f(x)≥0,则称函数f(x)为“L 型函数”.(1)判断函数xy e =和y=lnx 是否为“L 型函数”,并说明理由;(2)设函数f(x)=(x+1)lnx-(x-1)lna (a>0 ),记()().g x f x '=①若函数g(x)的最小值为1,求a 的值;②若函数f(x)为“L 型函数”,求a 的取值范围.21. [选做题]本题包括A 、B 、C 三小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-2:矩阵与变换(本小题满分10分) 已知矩阵记1040,10102A B ⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎣⎦记M=AB,求1.MB.选修4 -4:坐标系与参数方程(本小题满分10分)在平面直角坐标系xOy 中,已知直线1,12x l y l =-+⎧⎨=-+⎩(l 为参数)与曲线cos ,cos 2x y θθ=⎧⎨=-⎩(θ为参数)的交点为A,B,求线段AB 的长.C.选修4-5:不等式选讲(本小题满分10分)已知x, y, z 均是正实数,且2229436.x y z ++=,求证: x+y+z ≤7.[必做题]第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22. (本小题满分10分)如图1,某电视台一档综艺节目的游戏挑战项目“蜂巢迷宫”的道具,游戏规定挑战者必须“蒙眼”进行现简化模型如图2所示,共有A,B,C,D, E, F 六个房间组成,每个房间各有六扇门分别与相邻房间或与外部相通,假设打开每扇门都是等可能的.现挑战者从房间A 出发,要求到达房间E.(1)求挑战者“打开两扇门完成挑战”的概率;(2)一次游戏中规定“只要走出道具外部或打开超过四扇门(含四扇)挑战失败”,得0分;“打开三扇门完成挑战”,得1分,“打开两扇门完成挑战”,得2分.挑战者共挑战1次,得分设为X,求随机变量X 的概率分布和数学期望E(X).23. (本小题满分10分)(1)用数学归纳法证明二项式定理:011()n n n n n a b C a C a b -+=++222*,.n r n r r n n n n n C a b C a b C b n --++++∈L L N(2)利用二项式定理求证: 220()n k n n n k CC ==∑。
2020年全国普通高等学校招生统一考试(江苏卷)模拟预测卷数学试题一、填空题1.已知集合{}1A x x =>,{}1,2,3B =,则A B =______.【答案】{}2,3【分析】根据集合交集的定义和运算,即可求解. 【详解】由题意,集合{}1A x x =>,{}1,2,3B =, 根据集合交集的定义和运算,可得{}2,3A B ⋂=. 故答案为:{}2,3.【点睛】本题主要考查了集合交集的定义及运算,其中熟记集合交集的定义是解答的关键,属于容易题.2.已知复数2z i =+(其中i 为虚数单位),若(),za bi ab R i=+∈,则ab 的值为______. 【答案】-2【分析】根据已知求出,a b ,即得解. 【详解】由题得2z ai b i =-=+, 所以2,1b a -==, 所以1a =,2b =-, 所以2ab =-. 故答案为:-2【点睛】本题主要考查复数的运算和复数相等的概念,意在考查学生对这些知识的理解掌握水平.3.已知一组数据是4,a ,7,5,8的平均数为6,则该组数据的标准差是______.【分析】首先根据平均数公式计算得到a ,再根据标准差公式计算结果. 【详解】由平均数公式475865a ++++=得6a =,所以()()()()2222146076568625s ⎡⎤=-++-+-+-=⎣⎦. 故答案为:2【点睛】本题考查样本平均数和标准差,属于基础题型.4.在平面直角坐标系xOy 中,若双曲线1C :()2210x y m m-=>的一条准线与抛物线2C :22x y =的准线重合,则正数m 的值是___.【答案】3【分析】由已知可得双曲线的准线方程及其抛物线的准线方程,即可得出正数m . 【详解】抛物线2C :22x y =的准线方程为12y,双曲线1C :221x y m-=的一条准线方程为1y m =-+,根据题意得121m =+,解得3m =. 故答案为:3【点睛】本题考查了双曲线与抛物线的标准方程及其准线方程,属于基础题. 5.运行如图的程序框图,则输出的结果是______.【答案】13【分析】根据流程图的循环结构,计算输出结果. 【详解】根据流程图可知当1i =时进入循环,12a =,当2i =时,进入循环,1121312a ==+,当3i =时退出循环,输出13a =.故答案为:13.【点睛】本题考查循环结构,重点考查理性流程图,属于基础题型.6.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图所示,一与六共宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为5的概率为______.【答案】15【分析】根据阳数为1,3,5,7,9;阴数为2,4,6,8,10,利用古典概型的概率求法求解.【详解】∵阳数为1,3,5,7,9;阴数为2,4,6,8,10, ∴从阳数和阴数中各取一数的所有组合共有5×5=25个, 满足差的绝对值为5的有(1,6),(3,8),(5,10),(7,2),(9,4)共5个, 则其差的绝对值为5的概率为51255P == 故答案为:15【点睛】本题主要考查古典概型的概率求法,还考查了分析求解问题的能力,属于基础题.7.已知{}n a 为等差数列,n S 为其前n 项和,若2552a a +=,则15S 的值是______. 【答案】75【分析】由已知条件可解得85a =,再利用等差数列的性质即可求出.【详解】设等差数列的公差为d ,由2552a a +=,得()11524a d a d ++=+,即175a d +=,所以85a =, 则()1511581515752S a a a =+==. 故答案为:75.【点睛】本题考查等差数列性质的应用,属于基础题.8.圆柱形容器的内壁底半径是10cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为______2cm . 【答案】100π【分析】容器的水面下降部分的容积即为球的体积,由此计算出球的半径,再根据球的表面积公式即可求解.【详解】设实心铁球的半径为R ,则32451033R ππ=⨯⨯,得5R =, 故这个铁球的表面积为224100S R cm ππ==. 故填:100π.【点睛】本小题是立体几何的应用题,涉及圆柱的体积和球的表面积、体积的计算,考查考生理解、解决实际问题的能力. 9.若直线1y kx =+与曲线y =k 的值为______.【答案】14【分析】先求函数的导数,则0|x x k y ='==,写出切线方程与结合条件可得1,k =⎨⎪=⎪⎩,从而得出答案.【详解】y ''==,设切点为()00,x y,0y =则切线的斜率为0|x x k y ='==曲线y =()00,x y处的切线方程为y x =所以1,k =⎨⎪=⎪⎩解得14k =.故答案为:14【点睛】本题考查根据切线方程求参数的值,属于基础题. 104cos 122sin12=︒-︒______. 【答案】4-【分析】根据三角函数的基本关系式和两角和差的正弦函数公式,进行化简、运算,即可求解.【详解】原式()sin122sin 1260sin122sin 48cos12412cos 24sin122cos 24sin12cos12cos 24sin 24sin 482︒︒-︒︒︒-︒︒=====-︒︒︒︒︒︒︒︒.故答案为:4-【点睛】本题主要考查了三角函数的基本关系式,以及两角和与差的正弦公式的化简、求值,其中解答中熟记三角恒等变换的公式,准确运算是解答的关键,着重考查运算与求解能力.11.已知向量,a b ,满足3b =,a b a ⋅=,则a b -的最小值为______.【答案】【分析】利用222()2a b a b a b a b -=-=+-⋅化为数量积的运算,再代入已知条件可求得最小值.【详解】()222229218a ba b a b a a a -=+-⋅=+-=-+≥,当且仅当1a =时,等号成立,故a b -的最小值为故答案为:【点睛】本题考查求向量的模,解题关键是把向量的模转化向量数量积,然后结合函数知识得最小值.12.在平面直角坐标系xOy 中,已知A ,B 为圆C :()()2224-+-=x m y 上两个动点,且AB =若直线:2l y x =-上存在点P ,使得OC PA PB =+,则实数m 的取值范围为______.【答案】11⎡--+⎣【分析】根据题意求出AB 的中点Q 的轨迹,由2OC PA PB PQ =+=,设()00,P x y ,()11,Q x y ,进而求出点P 在以1,12D m ⎛⎫ ⎪⎝⎭为圆心,1为半径的圆D 上,根据点P 在直线l :2y x =-上,利用直线与圆的位置关系即可求解. 【详解】由题意知圆C 的圆心(),2C m ,半径2r .取AB 的中点Q ,连结CQ ,则CQ AB ⊥.所以1CQ ===, 所以点Q 在圆()()2221x m y -+-=上. 因为2OC PA PB PQ =+=,设()00,P x y ,()11,Q x y ,则()1010,PQ x x y y =--,(),2OC m =,所以()()10102,22,m x x y y ⎧=-⎪⎨=-⎪⎩则1010,21,m x x y y ⎧=+⎪⎨⎪=+⎩因为()11,Q x y 在圆()()2221x m y -+-=上, 所以()2200112m x m y ⎛⎫+-+-= ⎪⎝⎭, 即()2200112m x y ⎛⎫-+-= ⎪⎝⎭,所以点P 在以1,12D m ⎛⎫ ⎪⎝⎭为圆心,1为半径的圆D 上, 又点P 在直线l :2y x =-上,所以直线l 与圆D 有公共点,1≤,解得11m -≤-.故答案为:11⎡--⎣【点睛】本题考查了直线与圆的位置关系、轨迹问题,考查了基本知识以及知识的灵活应用,属于中档题.13.已知函数()31111,1,3442111,0,362x x x f x x x ⎧-+<≤⎪⎪=⎨⎪-+≤≤⎪⎩()()2x g x e ax a R =+-∈,若存在[]12,0,1x x ∈,使得()()12f x g x =成立,则实数a 的取值范围是______.【答案】[)2,e -+∞【分析】先利用导数求出()f x 的值域,设为集合A ,设()g x 的值域为B ,则本题等价于BA ≠∅,再求出()g x 的导数,讨论a 的范围结合()g x 的单调性和最值即可求出a 的范围.【详解】当102x ≤≤时,()f x 单调递减,()106f x ≤≤;当112x <≤时,()2104f x x '=-≥成立,()f x 单调递增,()1163f x <≤,所以()f x 的值域为10,3A ⎡⎤=⎢⎥⎣⎦. 设()g x 的值域为B ,因为存在1x ,[]20,1x ∈使得()()12f x g x =成立,所以B A ≠∅.()2x g x e ax =+-,()x g x e a '=+.①1a ≥-,任意[]0,1x ∈,()0g x '≥成立,()g x 在[]0,1单调递增, 所以()()min 01g x g ==-,()()max 12g x g e a ==+-,[]1,2B e a =-+-. 因为BA ≠∅,所以20e a +-≥,2a e ≥-;②a e ≤-,任意[]0,1x ∈,()0g x '≤成立,()g x 在[]0,1单调递减, 所以()()min 12g x g e a ==+-,()()max 01g x g ==-,[]2,1B e a =+--, 则B A ⋂=∅,不合题意; ③1e a -<<-,令()0x g x e a '=+=,()ln x a =-,()g x 在()()0,ln a -递减,()()ln ,1a -递增,所以()()()()min ln 2ln g x g a a a a =-=--+-,()()(){}max max 0,1g x g g =. 又()010g =-<,()120g e a =+-<,则B A ⋂=∅,不合题意. 综上所述,2a e ≥-.【点睛】本题考查利用导数解决能成立问题,属于较难题. 14.已知在锐角三角形ABC 中,AH BC ⊥于点H ,且()229449BA CA AH CA BA -=⋅-,若2BC =,则sin sin sin B CA的取值范围是______.【答案】5⎛⎫+∞ ⎪ ⎪⎝⎭【分析】由向量数量积的概念化简可得23BH CH =,BC 边上的高为h ,由tan ,tan B C 表示tan C ,结合三角形为锐角三角形,得h 的范围,由三角形面积公式和正弦定理结合可得2sin sin R B C h =,进而得出sin sin sin 2B C hA =,即可结果.【详解】由()229449BA CA AH CA BA -=⋅-,得229944BA AH BA CA CA AH +⋅=+⋅,所以94BA BH CA CH ⋅=⋅,即2294BH CH =,23BH CH =. 设BC 边上的高为h ,由2BC =,45BH =,6=5CH , 则5tan 4h B =,5tan 6hC =, 所以()2555046tan tan 0552524146h hh A B C h h h +=-+=-=>--⋅,所以h >因为ABC 的面积11sin 22S bc A ah ==,所以2sin sin R B C h =,所以sin sin sin 2B C h A =>.故答案为:⎫+∞⎪⎪⎝⎭.二、解答题15.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且3B π=.(1)若b =2a =,求c 的值; (2)若cos A ,求cos C 的值. 【答案】(1)4c =;(2)626-.【分析】(1)根据题中所给的条件,两边一角,利用余弦定理建立等量关系式,求得c 的值;(2)根据题中所给的条件13cos A =,利用同角三角函数关系式求得23sin A =,利用诱导公式和余弦和角公式求得结果. 【详解】(1)在ABC 中,3B π=,23b =,2a =,由余弦定理得2222cos b c a ac B =+-, 得21242c c =+-,即2280c c --=, 解之得4c =或2c =-(舍去). (2)由13cos 013A =>,得02A π<<, 所以221323sin 1cos 113A A ⎛⎫=-=-= ⎪ ⎪⎝⎭. 又因为3B π=,所以()()cos cos cos C A B A B π=--=-+cos cos sin sin A B A B =-+ 1312336132-=-⨯+⨯=. 【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有余弦定理解三角形,诱导公式和余弦和角公式,属于简单题目.16.已知直三棱柱111ABC A B C -,E ,F 分别是BC ,1AA 的中点,1CB CC =,AC BC ⊥.求证:(1)//EF 平面11BA C ; (2)1EF B C ⊥.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)设11,B C BC 交于O 点,连接1A O ,OE ,在1BB C △中,证得1//EF A O ,结合线面平行的判定定理,即可证得//EF 平面11BA C ;(2)由直三棱柱111ABC A B C -,所以1CC ⊥平面ABC ,得到1CC AC ⊥,再由AC ⊥平面11BCC B ,得到1AC B C ⊥,证得111AC B C ⊥,进而的得到1B C ⊥平面11BA C ,即可证得1EF B C ⊥.【详解】(1)设1B C ,1BC 交于O 点,连接1A O ,OE , 在1BB C △中,点O ,E 分别是1B C ,BC 中点, 所以1//OE B B 且112OE B B =, 因为直三棱柱111ABC A B C -,所以11//B B AA ,11B B AA =,又因为F 是1AA 中点,所以1OE FA =,1//OE FA ,所以1//EF A O ,因为1AO ⊂平面11BA C ,EF ⊄平面11BA C ,所以//EF 平面11BA C . (2)因为直三棱柱111ABC A B C -,所以侧面11BCC B 是矩形, 又因为1BC CC =,所以四边形1BCC B 是正方形,所以11B C BC ⊥, 因为直三棱柱111ABC A B C -,所以1CC ⊥平面ABC , 因为AC ⊂平面ABC ,所以1CC AC ⊥, 又因为BC AC ⊥,1BCCC C =,1CC ,BC ⊂平面11BCC B ,所以AC ⊥平面11BCC B ,因为1B C ⊂平面11BCC B ,所以1AC B C ⊥,因为直三棱柱111ABC A B C -,所以11//AC A C ,所以111AC B C ⊥, 因为1111BC AC C ⋂=,1BC ,11A C ⊂平面11BAC ,所以1B C ⊥平面11BA C , 因为1AO ⊂平面11BA C ,所以11A O B C ⊥, 因为1//EF A O ,所以1EF B C ⊥.【点睛】本题主要考查了直线与平面平行的判定,以及直线与平面垂直的性质的应用,其中解答中熟记空间几何体的结构特征,以及熟练应用线面位置关系的判定定理和性质定理是解答的关键,着重考查推理与论证能力,属于中档试题.17.如图,已知边长为2的正方形材料ABCD ,截去如图所示的阴影部分后,可焊接成一个正四棱锥的封闭容器.设FCB θ∠=.(1)用θ表示此容器的体积;(2)当此容器的体积最大时,求tan θ的值. 【答案】(1))2221tan tan V θθ=-,0,4πθ⎛⎫∈ ⎪⎝⎭;(2)1tan 5θ=. 【分析】(1)取BC 的中点M ,连接FM ,连接AC 交GF 于N ,根据题意可求出正方形EFGH 的边长,进而求出底面积和高,即可求出体积; (2)令tan t θ=求出()V t 的导数,利用导数判断其单调性,从而可求出其最大值,即得解.【详解】(1)取BC 的中点M ,连接FM ,连接AC 交GF 于N ,如图.由题意知FM BC ⊥,在直角三角形CFM 中,1cos CF θ=. 在直角三角形CFN 中,sin 4NF CF πθ⎛⎫=- ⎪⎝⎭, 所以22NF θ=-,所以22GF θ=. 因为cos 4CN CF πθ⎛⎫=- ⎪⎝⎭,所以22tan CN θ=+. 从而)222GFEH S θ=,正四棱锥高2222CO CN NO CN NF =-=-222222tan tan 2tan 2222θθθ⎛⎫⎛⎫=+--= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭所以正四棱锥的体积)211222tan 33GFEHV S CO θθ=⋅=⋅)2221tan tan θθ=-0,4πθ⎛⎫∈ ⎪⎝⎭.(2)令tan t θ=()0,1t ∈,则()))2253221233V t t t t t t =-=-+, ())()()4222222256151133V t t t t t '=-+=--. 令()0V t '=,得5t =. t50,5⎛⎫ ⎪⎝⎭555,15⎛⎫ ⎪ ⎪⎝⎭()V t '+-()V t↗ 极大值↘所以()V t 在50,⎛⎫⎪⎝⎭单调递增,在5,1⎛⎫ ⎪ ⎪⎝⎭单调递减, 所以()V t 在5t =时取到最大值,此时1tan 5θ=.【点睛】本题考查棱锥体积的求法,考查利用导数求最值,属于中档题.18.如图,点F 为椭圆C :()222210x y a b a b +=>>的左焦点,点A ,B 分别为椭圆C的右顶点和上顶点,点62,P ⎛⎫- ⎪ ⎪⎝⎭在椭圆C 上,且满足//OP AB .(1)求椭圆C 的方程; (2)过定点(),0T m ()2m <且与x 轴不重合的直线l 交椭圆C 于M ,N 两点,直线4x =分别交直线AM ,AN 于点D ,E ,求证:以DE 为直径的圆经过x 轴上的两定点(用m 表示).【答案】(1)22143x y +=;(2)证明见解析. 【分析】(1)由62,2P ⎛ ⎝⎭在椭圆上,可得222312a b +=,由//OP AB ,可得3ba=-,从而解出,a b 的值,得到答案. (2)设()11,M x y ,()22,N x y ,()00,Q x y 是以DE 为直径的圆上的任意一点,设出直线AM 的方程,得到点D 的纵坐标,同理得到点E 的纵坐标,由条件可得0DQ EQ ⋅=,得到()()()2120124422y y x x x -=---,设直线l 的方程为x ty m =+,与椭圆C 的方程22143x y +=联立,将韦达定理代入上述式子,可得答案.【详解】解:(1)由P ⎛ ⎝⎭在椭圆C :()222210x y a b a b +=>>上得222312a b +=①, 如图,由A 为C 的右顶点,B 为C 的上顶点可知(),0A a ,()0,B b , 因OPAB ,所以OP AB k k =,则b a=-②.联立①②得方程组22231,2,2a bb a ⎧+=⎪⎪⎨⎪-=-⎪⎩解得2,a b =⎧⎪⎨=⎪⎩故所求椭圆C 的方程为22143x y +=.(2)设()11,M x y ,()22,N x y ,又()2,0A , 所以直线AM 的方程为()1122y y x x =--,令4x =,得1122D yy x =-, 所以1124,2y D x ⎛⎫⎪-⎝⎭.同理2224,2y E x ⎛⎫ ⎪-⎝⎭. 设()00,Q x y 是以DE 为直径的圆上的任意一点,则0DQ EQ ⋅=,所以()21200012224022y y x y y x x ⎛⎫⎛⎫-+--= ⎪⎪--⎝⎭⎝⎭,令00y =,得()()()2120124422y y x x x -=---.设直线l 的方程为x ty m =+,与椭圆C 的方程22143x y+=联立,消去x 得()2223463120ty tmy m +++-=,所以122634tm y y t +=-+,212231234m y y t -=+, 所以()()()()12122222x x ty m ty m --=+-+-()()()()22212122422234m t y y t m y y m t -=+-++-=+.所以()()()()()()222212022122312432412334422242234m m y y m t x x x m m m t -+-+-=-=-==-----+, 因为22m -<<,所以04x =所以以DE 为直径的圆经过x 轴上两定点,其坐标分别为4⎛⎫⎪ ⎪⎝⎭和4⎛⎫⎪ ⎪⎝⎭. 【点睛】本题考查求椭圆的方程,考查直线与椭圆的位置关系,考查圆过定点问题,属于难题.19.若数列{}n c 满足:存在实数t ,使得()2212112m n m n c c c t m n --+-+=+-对任意m 、*n N ∈都成立,则称数列{}n c 为“t 倍等阶差数列”.已知数列{}n a 为“t 倍等阶差数列”.(1)若10a =,212a =-,31a =,求实数t 的值; (2)在(1)的条件下,设()*2121n n n b a a n N +-=-∈.①求数列{}n b 的通项公式;②设数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和为n S ,是否存在正整数p 、q ,且1p q <<,使得1S 、p S 、q S 成等比数列?若存在,求出p 、q 的值,若不存在,请说明理由.【答案】(1)2t =;(2)①87n b n =-;②存在2p =,36q =.【分析】(1)由题中定义可得出关于实数t 的等式,由此可解得实数t 的值; (2)①根据题中定义可推导出数列{}n b 为等差数列,确定该数列的首项和公差,由此可求得数列{}n b 的通项公式;②利用裂项相消法可求得n S ,由题意可得出2161988p p q+=+>,可得出关于正整数p的不等式,解出p 的取值范围,可求得正整数p 的值,进而可求得q 的值,由此可得出结论.【详解】(1)由数列{}n a 为“t 倍等阶差数列”, 令2m =,1n =,得()2312221a a a t +=+-,所以11022t ⎛⎫+=⨯-+ ⎪⎝⎭,解得2t =;(2)①以2n +代替m ,得23212128n nn a a a .则()()()21212112118n n n n a a a a +-+++-⎡⎤---=⎣⎦,即18n nb b +-=. 所以数列{}n b 是以8为公差的等差数列.又1311b a a =-=,所以()18187n b n n =+-=-.②因为()()111111878188781n n b b n n n n +⎛⎫==- ⎪-+-+⎝⎭, 所以111111111189917878188181n n S n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥-+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦, 则119S =,81p p S p =+,81q q S q =+. 假设1S 、p S 、q S 成等比数列,则2181981p qp q ⎛⎫=⋅⎪++⎝⎭, 因为216189988p q p q q ++==+>,所以281610p p --<, p <<又因为p 为大于1的整数,所以2p =,36q =, 所以存在2p =,36q =,使得1S 、p S 、q S 成等比数列.【点睛】本题考查数列的新定义,考查了等差数列的通项公式的求解、裂项相消法与数列的存在性问题的求解,考查计算能力,属于难题. 20.已知函数()()ln 0af x x x x=+>. (1)求函数()f x 的单调区间;(2)若函数()f x 在定义域内有两个零点,求a 的取值范围;(3)若对任意()0,x ∈+∞,不等式()()()2ln 112xm x x e x x x e++-≥-恒成立,求m的取值范围.【答案】(1)答案不唯一,见解析;(2)10,a e ⎛⎫∈ ⎪⎝⎭;(3)[)1,m ∈+∞. 【分析】(1)求导得()()20x af x x x -'=>,按0a ≤,0a >分类讨论得结果; (2)由题意得ln a x x -=在()0,∞+上有2个交点,令()ln h x x x =,则()'1ln h x x =+,得函数()h x 的单调性,最小值和最大值极限,即可得a 的取值范围;(3)由题意得()()1ln 12xm x e x e x ⎛⎫++-≥- ⎪⎝⎭,令()()1ln 21x F x m x x e e x ⎛⎫=++-+- ⎪⎝⎭,求导得()()21x m F x x e x ⎛⎫'=-+ ⎪⎝⎭,按0m ≥,0m <分类讨论得结果.【详解】(1)()()20x af x x x -'=>. 当0a ≤时,0x,得()0f x '>,所以()f x 在()0,∞+上单调增;当0a >时,令()0f x '>得x a >,所以()f x 在(),a +∞上单调增,令()0f x '<得0x a <<,所以()f x 在()0,a 上单调减.综上,当0a ≤时,()f x 的增区间为()0,∞+,无减区间; 当0a >时,()f x 的增区间为(),a +∞,减区间为()0,a . (2)令()ln 0af x x x=+=,得ln a x x -=,令()ln h x x x =,则()'1ln h x x =+, 0x,得()'0h x =的根为1=x e ,()h x ∴在10,e ⎛⎫ ⎪⎝⎭递减,在1,e ⎛⎫+∞ ⎪⎝⎭上递增,11h e e ⎛⎫∴=- ⎪⎝⎭,()0,0x h x →→,且(),x h x →+∞→+∞,要使函数()f x 有2个零点,则10a e -<-<,即10,a e ⎛⎫∈ ⎪⎝⎭;(3)0x,由()()()2ln 112xm x x e x x x e ++-≥-可得()()1ln 12x m x e x e x ⎛⎫++-≥- ⎪⎝⎭.令()()1ln 21xF x m x x e e x ⎛⎫=++-+- ⎪⎝⎭,()()()()22111x x m x m F x x e x e x x -⎛⎫'=+-=-+ ⎪⎝⎭. 当0m ≥时,20xme x+>,令()0F x '>得1x >,所以()f x 在()1,+∞上单调增; 令()0F x '<得01x <<,所以()f x 在()0,1上单调减.所以()()min 110F x F m ==-≥,得m 1≥.当0m <时,因为()()141774ln 414ln 41444F m e e m e ⎛⎫=--+-<--+- ⎪⎝⎭,即()1114ln 4044F m e ⎛⎫⎛⎫<---<⎪ ⎪⎝⎭⎝⎭,所以()0F x ≥在()0,x ∈+∞上不恒成立,则0m <舍去.综上可知,[)1,m ∈+∞.【点睛】本题主要考查了利用求导求原函数的单调性问题,同时也考查了参变分离求函数单调性与最值,进而求得参数的取值范围等,属于中档题.21.已知矩阵1002A ⎡⎤=⎢⎥⎣⎦,1201B ⎡⎤=⎢⎥⎣⎦,若直线l 依次经过变换A T ,B T 后得到直线l ':220x y +-=,求直线l 的方程.【答案】510x y +-=.【分析】本题可先设出直线l 上的任意一点(),P x y ,再设出这点经过变换T A ,T B 后得到的对应点(),P x y '''.然后根据变换对应的矩阵找到两个点的坐标的关系表达式,再根据点(),P x y '''在直线l '上,将两个点的坐标的关系表达式代入直线l '的方程即可得到直线l 的方程.【详解】解:设点(),P x y 是l 上的任意一点,其依次经过变换A T ,B T 后得到点(),P x y '''.则12100102x x y y '⎡⎤⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦,得42x x y y y '+⎡⎤⎡⎤=⎢⎥⎢⎥'⎣⎦⎣⎦,即4,2.x x y y y ''=+⎧⎨=⎩又点P '在直线l '上,所以220x y ''+-=,故()24220x y y ++-=,即510x y +-=, 所以直线的方程为:510x y +-=【点睛】本题主要考查一条直线经过一定的变换得到对应的直线,已知其中一条直线方程求另一条直线方程,本题可通过设对应点和变换对应的矩阵找到两个点的坐标的关系表达式来求出.本题属基础题.22.已知直线l的参数方程为1222x t y m ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),点P (1,2)在直线l 上.(1)求m 的值;(2)以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C :ρ=4与直线l 交于两点A ,B 两点,求|PA |·|PB |的值. 【答案】(1)2m =;(2)11.【分析】(1)根据点P (1,2)在直线l 上,将点的坐标代入直线的参数方程求解. (2)将曲线的极坐标方程转化为直角坐标方程,然后与直线的参数方程联立,再结合韦达定理利用参数的几何意义求解. 【详解】(1)因为()1,2P ,在直线l 上,所以112,22,t m ⎧=+⎪⎪⎨⎪=⎪⎩,解得2m =+.(2)因为曲线C :ρ=4,所以曲线C 的直角坐标方程为2216x y +=,将直线l的参数方程1122x t y ⎧=+⎪⎪⎨⎪=+⎪⎩代入C的方程得(21110t t ++-=,设A ,B 所对应的参数分别为1t ,2t ,则1211t t =-, 故1211PA PB t t ==⋅.【点睛】本题主要考查极坐标方程与直角坐标方程的转化直线与圆的位置关系以及参数的几何意义的应用,还考查了运算求解的能力,属于中档题.23.设,,a b c 都是正数,求证:222()()()4()+++++≥++b c c a a b a b c a b c.【答案】见解析【分析】利用柯西不等式证明即可; 【详解】证明:因为a ,b ,c 都是正数,所以()()()()222b c c a a b a b c a b c ⎡⎤+++++++⎢⎥⎢⎥⎣⎦222222⎡⎤⎡⎤=++++⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦2⎡⎤≥++⎢⎥⎣⎦()()()2b c c a a b =+++++⎡⎤⎣⎦ ()24a b c =++,所以()()()()2224b c c a a b a b c abc+++++≥++.【点睛】本题考查柯西不等式的应用,属于基础题.24.某商场准备在今年的“五一假”期间对顾客举行抽奖活动,举办方设置了,A B 两种抽奖方案,方案A 的中奖率为23,中奖可以获得2分;方案B 的中奖率为()0001P P <<,中奖可以获得3分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,并凭分数兑换奖品,(1)若顾客甲选择方案A 抽奖,顾客乙选择方案B 抽奖,记他们的累计得分为X ,若3≤X 的概率为79,求0P (2)若顾客甲、顾客乙两人都选择方案A 或都选择方案B 进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大? 【答案】(1)013P =(2)当0409P <<时,他们都选择A 方案进行抽奖时,累计得分的均值较大;当0419P <<时,他们都选择B 方案进行抽奖时,累计得分的均值较大;当049P =时,他们都选择A 方案或都选择B 方案进行抽奖时,累计得分的均值相等 【分析】(1)首先求解出对立事件“5X =”的概率,再根据对立事件概率公式求得结果;(2)利用二项分布均值公式求解出()1E X 和()2E X ,根据均值的性质求得两人全选A 方案或B 方案的均值,比较两个均值的大小,得到0P 不同取值的情况下应选取的方案.【详解】(1)由已知得,甲中奖的概率为23,乙中奖的概率为0P ,且两人中奖与否互不影响记“这2人的累计得分3≤X ”的事件为C ,则事件C 的对立事件为“5X =” ()0253P X P ==()()02715139P C P X P ∴=-==-= 013P ∴= (2)设甲、乙都选择A 方案抽奖的中奖次数为1X ,都选择B 方案抽奖的中奖次数为2X 则这两人选择A 方案抽奖累计得分的均值为()12E X ,选择B 方案抽奖累计得分的均值为()23E X 由已知可得:122,3X B ⎛⎫ ⎪⎝⎭,()202,X B P()124233E X ∴=⨯=,()202E X P = ()()118223E X E X ∴==,()()220336E X E X P == 若()()1223E X E X >,则0863P > 0409P ∴<< 若()()1223E X E X <,则0863P < 0419P ∴<< 若()()1223E X E X =,则0863P = 049P ∴= 综上所述:当0409P <<时,他们都选择A 方案进行抽奖时,累计得分的均值较大 当0419P <<时,他们都选择B 方案进行抽奖时,累计得分的均值较大 当049P =时,他们都选择A 方案或都选择B 方案进行抽奖时,累计得分的均值相等 【点睛】本题考查对立事件概率的求解、二项分布均值求解及均值性质的应用问题,利用均值来解决实际问题,属于常规题型.25.已知2020220200122020(1)....x a a x a x a x -=++++(1)求122020...a a a +++的值;(2)求01220201111...a a a a ++++的值.【答案】(1)1-;(2)20211011. 【分析】(1)根据已知条件,令0x =,求得0a ,令1x =,即可求得122020...a a a +++的值;(2)由二项式定理可得()20201k k k a C=-,求得1k n C ,由120202021202112021112022k k k C C C +⎛⎫=+ ⎪⎝⎭,进而求得202001k ka =∑,即可求得答案. 【详解】(1)()20202202001220201x a a x a x a x -=+++⋅⋅⋅+——①.在①中,令0x =,得01a =.在①中,令1x =,得01220200a a a a +++⋅⋅⋅+=,∴1220201a a a ++⋅⋅⋅+=-.(2)2020220200122020(1)....x a a x a x a x -=++++由二项式定理可得()20201k k k a C =-,0k =,1,2,⋅⋅⋅,2020.()()()()()()()!!!!2!!11111!21!21!k n k n k k n k n k n k k n k n n C n n n n n --+-+++-++==⋅=⋅++++ ()()()()()111!1!1!!111121!1!2k k n n k n k k n k n n n n n n C C +++⎡⎤+-+-⎛⎫++=+=+⎢⎥ ⎪++++⎢⎥⎝⎭⎣⎦, ∴202020202000002020202011(1)(1)kk k k k k k k a C C ===-==-∑∑∑ ()20200122020202020202020202011111C C C C =-+-⋅⋅⋅+-.120202021202112021112022k k k C C C +⎛⎫=+ ⎪⎝⎭, ∴20202020011220202021020212021202120212021202112021111111(1)2022k k a C C C C C C =⎡⎤⎛⎫⎛⎫⎛⎫=+-+++-+⎢⎥ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑ 0202120212021202111202120221011C C ⎛⎫=+= ⎪⎝⎭. 【点睛】本题解题关键是掌握组合数计算方法和根据二项式定理求各项系数和步骤,考查了分析能力和计算能力,属于难题.。
2020年江苏省南通市启东中学高考数学预测试卷(一)一、填空题(本大题共14小题,共70.0分)1.命题“∃x∈R,x≤1”的否定是______ .2.复数z=i1−i的共轭复数是______.3.在茎叶图中,样本的众数为__________4.某新媒体就我国提前进入“5G移动通信技术”商用元年的欢迎程度进行调查,参加调查的总人数为1000,其中持各种态度的人数如下表:态度很欢迎一般不欢迎人数72024040该媒体为进一步了解被调查者的具体想法,打算从中抽取50人进行更为详细的调查,则应抽取持“很欢迎”态度的人数为________.5.设x,y满足约束条件{x−y≥1x+y≥12x−y≤4,则z=x2+(y+2)2的最小值为_______.6.已知α为锐角,且cos(α+π4)=35,则sinα=__________.7.在四棱锥S−ABCD中,底面ABCD是边长为4的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若4√2≤SC≤8,则四棱锥S−ABCD的体积取值范围为______.8. 《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵ABC −A 1B 1C 1中,AA 1=AC =5,AB =3,BC =4,则阳马C 1−ABB 1A 1的外接球的表面积是______________9. 已知f(x)是定义在R 上的奇函数,满足f(2−x)=f(x).若当0≤x ≤1时,,则f(2019)= .10. 已知数列121×3,223×5,325×7,…,n 2(2n−1)×(2n+1),…S n 为其前n 项和,计算得S 1=13,S 2=35,S 3=67,S 4}=109.观察上述结果,归纳计算S n = ______ .11. 已知椭圆C :x 2a 2+y2b 2=1(a >b >0)的上顶点为A ,左焦点为F 1,延长AF 1与椭圆交于点B ,若以AB 为直径的圆经过椭圆的右焦点F 2,则椭圆的离心率为______.12. 在平面直角坐标系xOy 中,A(2,1),求过点A 与圆C:x 2+y 2=4相切的直线方程___.13. 在平行四边形ABCD 中,AB =8,AD =6,∠BAD =60°,点P 在CD 上,且CP ⃗⃗⃗⃗⃗ =3PD ⃗⃗⃗⃗⃗ ,则AP⃗⃗⃗⃗⃗ ⋅BP ⃗⃗⃗⃗⃗ =______.14. 已知xy =2x +y +2(x >1),则x +y 的最小值为______.二、解答题(本大题共10小题,共138.0分)15. 如图,在直三棱柱ABC −A 1B 1C 1中,AB ⊥BC ,BB 1=BC ,B 1C ∩BC 1=M ,N 为A 1B 的中点.(Ⅰ)求证:直线MN//平面ABC;(Ⅱ)求证:BC1⊥A1C.16.如图,已知角α的终边与单位圆相交于点P(35,45 ),求(1)sinα;(2)cosα.17.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为α(其中tanα=12)的斜坡前进√5km后到达D处,休息后继续行驶√5km到达山顶B.(1)求山的高度BE;(2)现山顶处有一塔CB=38km.从A到D的登山途中,队员在点P处测得塔的视角为θ(∠CPB=θ).若点P处高度PF为x km,则x为何值时,视角θ最大?18.已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右顶点分别为A,B,且长轴长为8,T为椭圆上任意一点,直线TA,TB的斜率之积为−34.(1)求椭圆C的方程;(2)设O 为坐标原点,过点M(0,2)的动直线与椭圆C 交于P ,Q 两点,求OP ⃗⃗⃗⃗⃗ ·OQ ⃗⃗⃗⃗⃗⃗ +MP ⃗⃗⃗⃗⃗⃗ ·MQ ⃗⃗⃗⃗⃗⃗⃗ 的取值范围.19. 已知函数f(x)=(ax −1)ln x +x 22.设函数g(x)=fˈ(x)有两个极值点x 1,x 2,其中x 1∈(0,e],求g(x 1)−g(x 2)的最小值.20. 设等差数列{a n }的公差为d ,点(a n ,b n )在函数f(x)=2x 的图象上(n ∈N ∗).(1)若a 1=−2,点(a 8,4b 7)在函数f(x)的图象上,求数列{a n }的前n 项和S n ; (2)若a 1=1,a 2=2,求数列{a nb n}的前n 项和T n .21. 已知矩阵M =[−12523],向量a ⇀=[416],求M 3a ⇀.22. 在平面直角坐标系xOy 中,已知直线l 的参数方程为{x =12t,y =√32t −1(t 为参数).在以坐标原点O 为极点,x 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C 的极坐标方程是ρ=2√2sin (π4+θ).(Ⅰ)求直线l 的普通方程与曲线C 的直角坐标方程;(Ⅱ)设点P(0,−1).若直线l 与曲线C 相交于两点A ,B.求|PA|+|PB|的值.23. 劲牌有限公司创建于1953年,历经六十余年的稳步发展,现已成为一家专业化的健康食品企业。
2020年江苏省南通市启东中学高考数学预测试卷(一)一、填空题(本大题共14小题,共70.0分) 1. 命题“∃x ∈R ,x 2+1<2x ”的否定是______ . 2. 复数z =(1−i1+i )4+2i 的共轭复数z =______. 3. 根据如图所示伪代码,最后输出的i 的值为______.4. “中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:在所有参与调查的人中,用分层随机抽样的方法抽取100人,则持“支持”态度的人中20岁及以上的有______人.支持 中立 不支持20岁以下 700 450 200 20岁及以上 200 150 3005. 已知x ,y 满足约束条件{x ≥yx +y ≤2y ≥0,则z =y+2x+1的取值范围为______.6. 已知锐角α满足sin2α−2cos2α=−1,则tan(α+π4)=______.7. 如图,在四棱锥P −ABCD 中,底面ABCD 是平行四边形,点E ,F 为PA ,PD 的中点,则面BCFE 将四棱锥P −ABCD 所分成的上下两部分的体积的比值为______.8. 《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著.其中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的四面体称之为鳖臑.已知直三棱柱A 1B 1C 1−ABC 中,AB ⊥BC ,AB =3,BC =4,AA 1=5√3,将直三棱柱沿一条棱和两个面的对角线分割为一个阳马和一个鳖臑,则鳖臑的体积与其外接球的体积之比为______.9. 函数f(x)是定义在R 上的奇函数,且满足f(x +1)=f(−x +1).当0<x ≤1时,f(x)=−log 2020x ,则f(12020)+f(2019)+f(2020)=______.10. T 1是一个边长为1的正三角形,T 2是将该正三角形沿三边中点连线等分成四份后去掉中间一份的正三角形后所形成的图形,依此类推T n+1是对T n 中所含有的所有正三角形都去掉中间一份(如图),记S n 为T n 的面积,Q n =S 1+S 2+⋯+S n ,则Q n =______.11. 如图,已知A 为椭圆x 2a 2+y 2b 2=1(a >b >0)上一点,它关于原点的对称点为B ,点F 为椭圆的右焦点,且以AB 为直径的圆过点F ,当∠ABF =π6时,该椭圆的离心率是______.12. 在平面直角坐标系xOy 中,已知圆C :(x −2)2+y 2=4,点A 是直线x −y +2=0上的一个动点,直线AP ,AQ 分别切圆C 于P ,Q 两点,则线段PQ 长的取值范围是______. 13. 如图,在四边形ABCD 中,AB =CD =1,点M ,N 分别是边AD ,BC 的中点,延长BA 和CD 交MN 的延长线于不同的两点P ,Q ,则PQ ⃗⃗⃗⃗⃗ ⋅(AB ⃗⃗⃗⃗⃗ −DC ⃗⃗⃗⃗⃗ )的值为______.14. 若实数x ,y 满足2cos 2(x +y −1)=(x+1)2+(y−1)2−2xyx−y+1,则xy 的最小值为______.二、解答题(本大题共10小题,共138.0分)15. 如图,矩形ACMN 所在平面与菱形ABCD 所在平面互相垂直,交线为AC ,AC ∩BD =O ,E 是MN 的中点.(1)求证:CE//平面NBD ;(2)若点F 在线段CM 上,且OF ⊥NO ,求证:NO ⊥平面FBD .16. 如图,点P 0是锐角α的终边与单位圆的交点,OP 0逆时针旋转π3得OP 1,OP 1逆时针旋转π3得OP 2,…,OP n−1逆时针旋转π3得OP n . (1)若P 0的坐标为(35,45),求点P 1的横坐标; (2)若点P 2020的横坐标为45,求sin(2α+2π3)的值.17.我国的“洋垃极禁止入境”政策已实施一年多.某沿海地区的海岸线为一段圆弧AB,对应的圆心角∠AOB=π,该地区为打击洋垃圾走私,在海岸线外侧20海里内的海域ABCD对不明船只进行识别查3证(如图:其中海域与陆地近似看作在同一平面内)在圆弧的两端点A,B分别建有监测站,A与B之间的直线距离为100海里.(1)求海域ABCD的面积;(2)现海上P点处有一艘不明船只,在A点测得其距A点40海里,在B点测得其距B点20√19海里.判断这艘不明船只是否进入了海域ABCD?请说明理由.18.已知椭圆C:x2a2+y2b2=1(a>b>0).(1)若椭圆的长轴长为4,离心率为√32,求椭圆的标准方程;(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围;(3)过原点O任意作两条互相垂直的直线与椭圆C:x2a2+y2b2=1(a>b>0)相交于P,S,R,Q四点,设原点O到四边形PQSR的一边距离为d,试求d=1时a,b满足的条件.19.已知函数f(x)=alnx(a≠0)与y=12ex2的图象在它们的交点P(s,t)处具有相同的切线.(1)求f(x)的解析式;(2)若函数g(x)=(x−1)2+mf(x)有两个极值点x1,x2,且x1<x2,求g(x2)x1的取值范围.20.设数列{a n}(n∈N∗)是公差不为零的等差数列,满足a3+a6=a9,a5+a72=6a9;数列{b n}(n∈N∗)的前n项和为S n,且满足4S n+2b n=3.(1)求数列{a n}、{b n}的通项公式;(2)在b1和b2之间插入1个数x11,使b1,x11,b2成等差数列;在b2和b3之间插入2个数x21,x22,使b2,x21,x22,b3成等差数列;……;在b n和b n+1之间插入n个数x n1,x n2,…,x nn,使b n,x n1,x n2,…x nn,b n+1成等差数列.(i)求T n=x11+x21+x22+⋯+x n1+x n2+⋯+x nn;(ii)是否存在正整数m,n,使T n=a m+12a m成立?若存在,求出所有的正整数对(m,n);若不存在,请说明理由.21.已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量e1⃗⃗⃗ =[23]并有特征值λ2=−1及属于特征值−1的一个特征向量e2⃗⃗⃗ =[1−1],α⃗=[−11],(Ⅰ)求矩阵M;(Ⅱ)求M5α⃗.22.在平面直角坐标系xOy中,曲线C的参数方程为{x=2+√3cosαy=√3sinα(α为参数,0≤α≤π).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,射线l的极坐标方程是θ=π6.(1)求曲线C的极坐标方程;(2)若射线l与曲线C相交于A,B两点,求|OA|⋅|OB|的值.23.冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现的新型冠状病毒(COVID−19)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中感染可导致肺奖、严重急性呼吸综合征、贤衰竭,甚至死亡.核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.根据统计发现,疑似病例核酸检测呈阳性的概率为p(0<p<1),现有4例疑似病例,分别对其取样、检测,多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下三种方案:方案一:逐个化验;方案二:四个样本混在一起化验;方案三:平均分成两组化验.在新冠肺炎爆发初期,由于检查能力不足,化检次数的期望值越小,则方案越“优”.(1)若p=1,求2个疑似病例样本混合化验结果为阳性的概率;4(2)若p=1,现将该4例疑似病例样本进行化验,请问:方案一、二,三中哪个最“优”?4(3)若对4例疑似病例样本进行化验,且“方案二”比“方案一”更“优”,求p的取值范围.24. 如图,已知点P 是x 轴下方(不含x 轴)一点,抛物线C :y =x 2上存在不同的两点A 、B 满足PD ⃗⃗⃗⃗⃗ =λDA ⃗⃗⃗⃗⃗ ,PE ⃗⃗⃗⃗⃗ =λEB ⃗⃗⃗⃗⃗ ,其中λ为常数,且D 、E 两点均在C 上,弦AB 的中点为M .(1)若P 点坐标为(1,−2),λ=3时,求弦AB 所在的直线方程; (2)在(1)的条件下,如果过A 点的直线l 1与抛物线C 只有一个交点,过B 点的直线l 2与抛物线C 也只有一个交点,求证:若l 1和l 2的斜率都存在,则l 1与l 2的交点N 在直线PM 上;(3)若直线PM 交抛物线C 于点Q ,求证:线段PQ 与QM 的比为定值,并求出该定值.答案和解析1.【答案】∀x∈R,x2+1≥2x【解析】解:因为特称命题的否定是求出你添,所以,命题“∃x∈R,x2+1<2x”的否定是:∀x∈R,x2+1≥2x.故答案为:∀x∈R,x2+1≥2x.利用特称命题的否定是全称命题写出结果即可.本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.2.【答案】1−2i【解析】【分析】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案.【解答】解:∵z=(1−i1+i )4+2i=[(1−i)2(1+i)(1−i)]4+2i=(−i)4+2i=1+2i,∴z=1−2i,故答案为:1−2i.3.【答案】7【解析】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:S=1+1;i=3;S=2+3,i=5;S=5+5≥10,i=7;故输出的i值为7.故答案为:7.分析程序中各变量、各语句的作用,再根据流程图所示的顺序,依次代入即可求出i的值.本题主要考查流程图的应用,根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.4.【答案】10【解析】解:参与调查的人数为700+200+450+150+200+300=2000,故持“支持”态度的人中20岁及以上的人数所占比例为2002000=0.1,∴采用分层抽样法抽取100人时,持“支持”态度的人中20岁及以上的人数为100×0.1=10.故答案为:10.先计算持“支持”态度的人中20岁及以上的人数占总人数的比列,再按比例计算选取人数.本题考查了分层抽样的特点,属于基础题.5.【答案】[23,2]【解析】解:z=y+2x+1的几何意义为点P(x,y)到点D(−1,−2)的斜率作出不等式组对应的平面区域如图:当P位于A(2,0)时,AD的斜率最小,此时z=0+22+1=23,当P位于O时,OD的斜率最大,此时OD的斜率z=0+20+1=2,故23≤k≤2,故答案为:[23,2].z=y+2x+1的几何意义为点(x,y)到点(−1,−2)的斜率,利用数形结合即可得到结论.本题主要考查线性规划的应用,根据直线的斜率公式,利用数形结合是解决本题的关键.6.【答案】2【解析】解:∵sin2α−2cos2α=−1,∴2sinαcosα−2(cos2α−sin2α)+sin2α+cos2α=0,化简得,3sin2α+2sinαcosα−cos2α=0,两边同时除以cos2α得,3tan2α+2tanα−1=0,解得,tanα=13或−1,∵α为锐角,∴tanα>0,∴tanα=13,∴tan(α+π4)=tanα+tanπ41−tanαtanπ4=13+11−13×1=2.故答案为:2.先利用二倍角公式对原等式进行化简,整理后得3sin2α+2sinαcosα−cos2α=0,两边同时除以cos2α得,3tan2α+2tanα−1=0,由于α为锐角,所以tanα>0,解方程即可得tanα的值,再结合正切的两角和公式进行运算即可得解.本题考查三角恒等变换公式的应用以及弦化切的思想,考查学生的逻辑推理能力和运算能力,属于基础题.7.【答案】35【解析】解:不妨设ABCD是正方形,PD⊥平面ABCD,AD=2a,则V P−ABCD=13×2a×2a×2a=83a3,连接FA,FB,则V EFABCD=12×83a3+13×12×a×a×2a=53a3,∴V P−EFBC=a3,∴四棱锥P−ABCD所分成的上下两部分的体积的比值为35.故答案为:35.不妨设ABCD是正方形,PD⊥平面ABCD,AD=2a,求出上下两部分的体积,即可得出结论.本题考查体积的计算,考查学生的计算能力,正确计算体积是关键.8.【答案】3√3:50π【解析】解:如图所示:,鳖臑为三棱锥B1−AA1C1,体积为13×12×3×4×5√3=10√3,因为鳖臑的四个面都为直角三角形,所以其外接球的球心为Rt △AA 1C 1的斜边的中点, 所以其外接球的半径为12AC 1=12×√52+(5√3)2=5,所以其外接球的体积为43π×53=5003π,所以鳖臑的体积与其外接球的体积之比为10√35003π=3√3:50π, 故答案为:3√3:50π.先画出直三棱柱A 1B 1C 1−ABC ,分割得到阳马和鳖臑,利用三棱锥体积公式求出鳖臑的体积,再利用球的体积公式求出其外接球的体积,从而得出结果.本题主要考查了三棱锥的体积公式以及三棱锥的外接球问题,考查了球的体积公式,是中档题.9.【答案】1【解析】 【分析】本题考查函数的奇偶性与周期性的综合应用,注意分析函数的周期性,属于基础题.根据题意,由足f(x +1)=f(−x +1)变形可得f(−x)=f(2+x),结合函数的奇偶性可得f(x +2)=−f(x),变形可得f(x +4)=−f(x +2)=f(x),即函数f(x)为周期为4的周期函数;据此可得f(2019)=f(−1+2020)=f(−1)=−f(1),f(2020)=f(0)=0,结合函数的解析式分析可得f(1)和f(12020)的值,计算即可得答案. 【解答】解:根据题意,函数f(x)满足f(x +1)=f(−x +1),则有f(−x)=f(2+x), 又由f(x)为奇函数,则f(−x)=−f(x),则有f(x +2)=−f(x),变形可得f(x +4)=−f(x +2)=f(x),即函数f(x)为周期为4的周期函数; f(2019)=f(−1+2020)=f(−1)=−f(1), f(2020)=f(0)=0,又由当0<x ≤1时,f(x)=−log 2020x ,则f(12020)=−log 202012020=log 20202020=1, f(1)=−log 20201=0,故f(12020)+f(2019)+f(2020)=1+0+0=1; 故答案为:1.10.【答案】√3(1−(34)n )【解析】解:对于T 1:三角形个数为30=1,边长为1, 对于T 2:三角形个数为31=3,边长为(12)1=12, 对于T 3:三角形个数为32=9,边长为(12)2=14, 对于T 4:三角形个数为33=27,边长为(12)3=18,……对于T n :三角形个数为3n−1,边长为(12)n−1, ∴S 1=1×√34×12=√34,S 2=3×√34×(12)2=√34×(√32)2,S 3=9×√34×(12)4=√34×(√32)4,S 4=27×√34×(12)6=√34×(√32)2n−2,……,S n =3n−1×√34×(12)2n−2, ∴数列{S n }是公比为(√32)2=34,首项为√34的等比数列,∴Q n =√34×[1−(34)n ]1−34=√3[1−(34)n ],故答案为:√3[1−(34)n ].观察图形得到三角形个数的规律,边长的规律,从而得到三角形的面积S n ,发现数列{S n }是公比为(√32)2=34,首项为√34的等比数列,再利用等比数列的前n 项和公式即可算出结果.本题主要考查了合情推理中的归纳推理,以及等比数列的性质,是中档题.11.【答案】√3−1【解析】解:如图所示:,由题意可知,以AB 为直径的圆过F ,点F 为椭圆的右焦点, 则∠AFB =90°,且AB =2c ,又∵∠ABF=π6,则AF=c,BF=√3c,设椭圆的左焦点为E,由椭圆的对称性可得AE=BF,由椭圆的定义得AF+BF=AE+AF=2a,则c+√3c=2a,即离心率e=ca =1+√3=√3−1,故答案为:√3−1.根据题意,由圆的圆周角的性质得出∠AFB=90°,且AB=2c,由于∠ABF=π6,则AF=c,BF=√3c,利用椭圆的定义得AF+BF=2a,即可得出a与c的关系式,从而求出椭圆的离心率.本题主要考查了椭圆的离心率和简单的几何性质,以及椭圆定义的应用和圆的性质的应用,是中档题.12.【答案】[2√2,4)【解析】解:如图,圆C:(x−2)2+y2=4的圆心到直线x−y+2=0的距离d=√2=2√2.设AC=x,则x≥2√2.由PC⊥AP,可知AP=√AC2−PC2=√x2−4,∵AC垂直平分PQ,∴PQ=2⋅PC⋅APAC =2⋅2⋅√x2−4x=4√1−4x2.∴当x=2√2时,PQ取得最小值2√2,又√1−4x2<1,∴线段PQ长的取值范围是[2√2,4).故答案为:[2√2,4).依题意画出图形,求出圆心C到直线的距离,设AC=x,则x≥2√2,由切割弦定理把PQ用含有x的关系式表示,由x的范围可得线段PQ长的取值范围.本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法,考查计算能力,是中档题.13.【答案】0【解析】解:设∠ABC =α,BC =a ,∠BCD =β,则A(cosα,sinα), B(0,0),C(a,0),D(a −cosβ,sinβ), ∴M(a+cosα−cosβ2,sinα+sinβ2),N(a2,0),∴NM⃗⃗⃗⃗⃗⃗⃗ =(cosα−cosβ2,sinα+sinβ2),AB ⃗⃗⃗⃗⃗ =(−cosα,−sinα),DC ⃗⃗⃗⃗⃗ =(cosβ,−sinβ),∴AB ⃗⃗⃗⃗⃗ −DC ⃗⃗⃗⃗⃗ =(−cosα−cosβ,−sinα+sinβ),∴NM ⃗⃗⃗⃗⃗⃗⃗ ⋅(AB ⃗⃗⃗⃗⃗ −DC ⃗⃗⃗⃗⃗ )=−12(cosα2−cos 2β)+12(sin 2β−sin 2α)=−12(cos 2α+sin 2α)+12(cos 2β+sin 2β)=0,又PQ ⃗⃗⃗⃗⃗ //NM⃗⃗⃗⃗⃗⃗⃗ , ∴PQ ⃗⃗⃗⃗⃗ ⋅(AB ⃗⃗⃗⃗⃗ −DC ⃗⃗⃗⃗⃗ )=0, 故答案为:0.建立坐标系,设∠ABC =α,BC =a ,∠BCD =β,求出MN ⃗⃗⃗⃗⃗⃗⃗ 和AB ⃗⃗⃗⃗⃗ −DC ⃗⃗⃗⃗⃗ 的坐标,即可得出结论. 本题考查了平面向量的数量积运算,建立坐标系可使运算较简单.14.【答案】14【解析】解:∵2cos 2(x +y −1)=(x+1)2+(y−1)2−2xyx−y+1,∴2cos 2(x +y −1)=x 2+2x +1+y 2−2y +1−2xyx −y +1∴2cos 2(x +y −1)=x 2+y 2+2x−2y−2xy+1+1x−y+1,故2cos 2(x +y −1)=(x−y+1)2+1x−y+1=(x −y +1)+1x−y+1,由基本不等式可得(x −y +1)+1x−y+1≥2,或(x −y +1)+1x−y+1≤−2, ∴2cos 2(x +y −1)≥2,由三角函数的有界性可得2cos 2(x +y −1)=2, 故cos 2(x +y −1)=1,即cos(x +y −1)=±1,此时x −y +1=1,即x =y ∴x +y −1=kπ,k ∈Z ,故x +y =2x =kπ+1,解得x =kπ+12,故xy =x ⋅x =(kπ+12)2,当k =0时,xy 的最小值14,故答案为:14配方可得2cos2(x+y−1)=(x−y+1)2+1x−y+1=(x−y+1)+1x−y+1,由基本不等式可得(x+y+1)+1x−y+1≤2,或(x−y+1)+1x−y+1≤−2,进而可得cos(x+y−1)=±1,x=y=kπ+12,由此可得xy的表达式,取k=0可得最值.本题考查基本不等式在最值问题中的应用,余弦函数的单调性,得出cos(x+y−1)=±1是解决问题的关键,属中档题.15.【答案】证明:(1)连结ON,∵矩形ACMN所在平面与菱形ABCD所在平面互相垂直,交线为AC,AC∩BD=O,E是MN的中点.∴O是AC的中点,∴NE−//CO,∴NECO是平行四边形,∴NO//CE,∵CE⊄平面NBD,ON⊂平面NBD,∴CE//平面NBD.(2)∵矩形ACMN所在平面与菱形ABCD所在平面互相垂直,交线为AC,AC∩BD=O,∴AC⊥BD,AN⊥AC,∴AN⊥平面ABCD,∴AN⊥BD,∵AN∩AC=A,∴BD⊥平面ACMN,∵OF⊂平面BDF,∴BD⊥OF,∵点F在线段CM上,且OF⊥NO,BD∩ON=O,∴NO⊥平面FBD.【解析】(1)连结ON,推导出NE−//CO,从面NECO是平行四边形,进而NO//CE,由此能证明CE//平面NBD.(2)推导出AC⊥BD,AN⊥AC,从而AN⊥平面ABCD,AN⊥BD,进而BD⊥平面ACMN,BD⊥OF,再由OF⊥NO,能证明NO⊥平面FBD.本题考查线面平行、线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.16.【答案】解:(1)因为点P0为(35,45),根据三角函数的定义可得sinα=45,cosα=35;根据题意可知点P1的横坐标为cos(α+π3)=cosαcosπ3−sinαsinπ3=35×12−45×√32=3−4√310;(2)根据题意可知点P 2020的横坐标为cos(α+2020π3)=cos(α+4π3)=45, 所以cos(α+π3)=−45; 又因为α是锐角,所以α+π3∈(π3,5π6),所以sin(α+π3)=35; 所以sin(2α+2π3)=2sin(α+π3)cos(α+π3)=−2425.【解析】(1)利用任意角的三角函数的定义,求得cosα、sinα的值,再利用两角和的余弦公式求得结论; (2)先根据点P 2020的横坐标cos(α+2020π3)的值求得cos(α+π3)=−45;再结合同角三角函数基本关系式以及二倍角公式求解结论.本题主要考查任意角的三角函数的定义,二倍角公式、诱导公式、两角和的余弦公式,属于基础题.17.【答案】解:(1)∵∠AOB =π3,在海岸线外侧20海里内的海域ABCD ,AB =100∴AD =BC =20,OA =OB =AB =100, ∴OD =OA +AD =100+20=120, ∴S ABCD =π32π⋅π(OD 2−OA 2)=16π(1202−1002)=2200π3(平方海里),(2)由题意建立平面直角坐标系,如图所示;由题意知,点P 在圆B 上,即(x −100)2+y 2=7600…①, 点P 也在圆A 上,即(x −50)2+(y −50√3)2=1600…②; 由①②组成方程组, 解得{x =30y =30√3或{x =90y =50√3;又区域ABCD 内的点满足{x 2+y 2≥10000x 2+y 2≤14400,由302+(30√3)2=3600<10000,∴点(30,30√3)不在区域ABCD 内, 由902+(50√3)2=15600>14400, ∴点(90,50√3)也不在区域ABCD 内; 即这艘不明船只没进入了海域ABCD .【解析】(1)利用扇环的面积公式求出海域ABCD 的面积;(2)由题意建立平面直角坐标系,利用坐标求出点P 的位置,判断点P 是否在海域ABCD 内. 本题考查了圆的方程模型应用问题,是中档题.18.【答案】解:(1)由题意可得{2a =4e =ca =√32a 2=b 2+c 2,解得a 2=4,b 2=1,c =√3.∴椭圆的标准方程为x 24+y 2=1;(2)直线l 的方程为y =kx +2,设A(x 1,y 1),B(x 2,y 2).联立{y =kx +2x 2+4y 2=4,化为(1+4k 2)x 2+16kx +12=0,由△=162k 2−48(1+4k 2)>0,解得k >√32或k <−√32.∴x 1+x 2=−16k 1+4k2,x 1x 2=121+4k 2. 若∠AOB 为锐角,则OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ >0,得x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2)=(1+k 2)x 1x 2+2k(x 1+x 2)+4>0,代入得12(1+k 2)1+4k 2+−32k 21+4k 2+4>0,化为k 2<4,解得−2<k <2.∴直线l 的斜率k 的取值范围为{x|−2<k <2}∩{x|k <−√32或k >√32}={k|−2<k <−√32或√32<x <2}.(3)如图所示,设P(x 1,y 1),Q(x 2,y 2),S(−x 1,−y 1),R(−x 2,−y 2).①当直线PS 与QR 的斜率都存在时,设直线PS :y =kx ,则直线QR :y =−1k x . 联立{y =kx b 2x 2+a 2y 2=a 2b 2,解得x 12=a 2b 2b 2+a 2k 2.(∗) 联立{y =−1k xb 2x 2+a 2y 2=a 2b 2,解得x 22=a 2b 2k 2a 2+b 2k 2.(∗∗)直线PR 的斜率存在时,则直线PR :y −y 1=y 2−y1x 2−x 1(x −x 1),化为(y 2−y 1)x +(x 1−x 2)y +x 2y 1−x 1y 2=0.∵d =1,∴|x 2y 1−x 1y 2|√(x1−x 2)2+(y 1−y 2)2=1,代入化为:(k +1k )2x 12x 22=k 2x 12+1k 2x 22+x 12+x 22.把(∗)(∗∗)代入上式:(k 2+1)2k 2⋅a 4b 4k 2(a 2+b 2k 2)(b 2+a 2k 2)=a 2b 2k 2b 2+a 2k 2+a 2b 2a 2+b 2k 2+a 2b 2b 2+a 2k 2+a 2b 2k 2a 2+b 2k 2.化为a 2b 2=a 2+b 2. 即1a 2+1b 2=1为定值.②当直线PS 与QR 的斜率有一个不存在时,直线PR 的斜率不存在时,经验证上式也成立.【解析】(1)由题意可得{2a =4e =ca =√32a 2=b 2+c 2,解得即可;(2)直线l 的方程为y =kx +2,设A(x 1,y 1),B(x 2,y 2).与椭圆方程联立,由△>0,解得k 的取值范围.可得根与系数的关系.若∠AOB 为锐角,则OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ >0,把根与系数的关系代入又得到k 的取值范围,取其交集即可. (3)如图所示,设P(x 1,y 1),Q(x 2,y 2),S(−x 1,−y 1),R(−x 2,−y 2).①当直线PS 与QR 的斜率都存在时,设直线PS :y =kx ,则直线QR :y =−1k x.与椭圆方程联立解得x 12,x 22.直线PR 的斜率存在时,则直线PR :y −y 1=y 2−y1x 2−x 1(x −x 1),化为(y 2−y 1)x +(x 1−x 2)y +x 2y 1−x 1y 2=0.由于d =1,利用点到直线的距离公式可得2112122122=1,化简并代入即可化为a 2b 2=a 2+b 2.②当直线PS 与QR 的斜率有一个不存在时,直线PR 的斜率不存在时,经验证上式也成立.熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立、直线的点斜式、分类讨论思想方法等是解题的关键.19.【答案】解:(1)根据题意,函数f(x)=alnx(a ≠0)与y =12e x 2可知f′(x)=ax ,y′=1e x ,两图象在点P(s,t)处有相同的切线,所以两个函数切线的斜率相等, 即1e ⋅s =as ,化简得s =√ae①, 将P(s,t)代入两个函数可得s 22e=alns②,综合上述两式①②可解得a =1,所以f(x)=lnx .(2)函数g(x)=(x −1)2+mf(x)=(x −1)2+mlnx ,定义域为(0,+∞), g′(x)=2(x −1)+m x=2x 2−2x+mx,因为x 1,x 2为函数g(x)的两个极值点,所以x 1,x 2是方程2x 2−2x +m =0的两个不等实根,由根与系数的关系知x 1+x 2=1,x 1x 2=m2,(∗), 又已知x 1<x 2,所以0<x 1<12<x 2<1,g(x 2)x 1=(x 2−1)2+mlnx 2x 1,将(∗)式代入得g(x 2)x 1=(x 2−1)2+2(1−x 2)x 2lnx 21−x 2=1−x 2+2x 2lnx 2,令ℎ(t)=1−t +2tlnt ,t ∈(12,1), ℎ′(t)=2lnt +1,令ℎ′(t)=0,解得:t =√e,当t ∈(12e )时,ℎ′(t)<0,ℎ(t)在(12e )单调递减; 当t ∈(e 1)时,ℎ′(t)>0,ℎ(t)在(e 1)单调递增; 所以ℎ(t)min =ℎ(√e )=1−√e =1−2√ee, ℎ(t)<max{ℎ(12),ℎ(1)},ℎ(12)=12−ln2<0=ℎ(1), 即g(x 2)x 1的取值范围是[1−2√ee,0).【解析】(1)求出函数的导数,得到关于a 的方程,解出即可求出f(x)的解析式; (2)求出x 1+x 2=1,x 1x 2=m2,(∗),得到g(x 2)x 1=(x 2−1)2+mlnx 2x 1,将(∗)式代入得g(x 2)x 1=1−x 2+2x 2lnx 2,令ℎ(t)=1−t +2tlnt ,t ∈(12,1),根据函数的单调性求出g(x 2)x 1的取值范围即可.本题考查了函数的单调性,最值问题,考查导数的应用以及转化思想,是一道综合题.20.【答案】解:(1)设数列{a n }的公差为d ,(d ≠0),则由a 3+a 6=a 9,得(a 1+2d)+(a 1+5d)=a 1+8d ,∴a 1=d ,∵a 5+a 72=6a 9,∴(a 1+4d)+(a 1+6d)2=6(a 1+8d),将a 1=d 代入上式,得5d +49d 2=54d ,∴49d 2=49d , ∵d ≠0,∴d =1,∴a n =n . 由4S n +2b n =3,①当n ≥2时,4S n−1+2b n−1=3,②①−②,得4b n +2b n −2b n−1=0,∴b n =13b n−1,(n ≥2), 又4b 1+2b 1=3,∴b 1=12≠0, ∴{b n }是首项为12,公比为13的等比数列,∴b n =12×(13)n−1,(n ∈N ∗).(2)(i)在b n 和b n−1之间插入n 个数x n 1,x n 2,…,x n n , ∵b n ,x n1,x n2,…x nm ,b n+1成等差数列,设公差为d n , ∴d n =b n+1−b n (n+2)−1=(12)(13)n −(12)(13)n−1n+1=−13n (n+1),则x nk =b n +kd n =12(13)n−1−k3n (n+1),∴∑x nk n k=1=12(13)n−1⋅n −13(n+1)⋅n(n+1)2=n3,∴T n =x 11+x 21+⋯+x n1+x n2+⋯+x nn =13+132+⋯+n 3n,①则13T n =132+133+⋯+n−13n +n3n+1,②①−②,得23T n =13+132+⋯+13n −n3n+1=13[1−(13)n ]1−13−n 3n+1=12(1−13n )−n3n+1,∴T n =34−14⋅3−n2⋅3=m+12m=12+12m .(ii)m =2⋅3n 3n −2n−3=2(3n −2n−3)+4n+63n −2n−3=2+4n+63n −2n−3,当n =1时,m =2+10−2=−3∉N ∗, 当n =2时,m =2+142=9∗,当n =3时,m =2+1=3∈N ∗,下证,当n ≥4(n ∈N ∗)时,有3n −2n −3>4n +6,即证3n −6n −9>0, 设f(x)=3x −6x −9,x ≥4,则f′(x)=3x ln3−6>3x −6>0, ∴f(x)在[4,+∞)上单调递增,故n ≥4时,3n −6n −9>34−6×4−9=48>0, ∴0<4n+63n −2n−3<1, ∴n ≥4时,m 不是整数,∴所有的正整数对(m,n)为(9,2)及(3,3).【解析】(1)设数列{a n }的公差为d ,(d ≠0),利用等差数列的通项公式求出d =1,从而a n =n.再由4S n +2b n =3,当n ≥2时,4S n−1+2b n−1=3,推导出{b n }是首项为12,公比为13的等比数列,由此能求出b n .(2)(i)在b n 和b n−1之间插入n 个数x n 1,x n 2,…,x n n ,推导出d n =b n+1−b n(n+2)−1=−13n (n+1),从而x nk =b n +kd n =12(13)n−1−k 3n (n+1),进而T n =x 11+x 21+⋯+x n1+x n2+⋯+x nn =13+132+⋯+n 3n,由此利用错位相沽法能求出T n . (ii)m =2⋅3n 3n −2n−3=2+4n+63n −2n−3,当n =1时,m =2+10−2=−3∉N ∗,当n =2时,m =2+142=9∗,当n =3时,m =2+1=3∈N ∗,再证明当n ≥4(n ∈N ∗)时,3n −6n −9>0,由此能求出所有的正整数对. 本题考查数列的通项公式、前n 项和、整数对的求法,考查等差数列、等比数列的性质、错位相减求和法、导数性质等基础知识,考查运算求解能力,是中档题.21.【答案】解:(Ⅰ)设M =[a b cd],则[a b c d ][23]=4[23]=[812],∴{2a +3b =82c +3d =12①,又[a b c d ][1−1]=(−1)[1−1]=[−11], ∴{a −b =−1c −d =1②,由①②可得a =1,b =2,c =3,d =2,∴M =[1232]; (Ⅱ)易知α⃗ =0⋅[23]+(−1)[1−1],∴M 5α⃗ =(−1)6α⃗ =[−11].【解析】(Ⅰ)利用矩阵的运算法则进行求解; (Ⅱ)利用矩阵的乘法法则进行求解.本题考查矩阵的运算法则,考查学生的计算能力,比较基础.22.【答案】解:(1)消去参数α得(x −2)2+y 2=3(y ≥0)将x =ρcosθ,y =ρsinθ代入得(ρcosθ−2)2+(ρsinθ)2=3,即ρ2−4ρcosθ+1=0.所以曲线C 的极坐标方程为ρ2−4ρcosθ+1=0(0≤θ≤π3). (2)法1:将θ=π6代入ρ2−4ρcosθ+1=0(0≤θ≤π3), 得ρ2−2√3ρ+1=0,设A(ρ1,π6),B(ρ2,π6),则ρ1ρ2=1.于是|OA|⋅|OB|=ρ1ρ2=1.法2:θ=π3与曲线C 相切于点M ,|OM|=2sin π3=1, 由切割线定理知|OA|⋅|OB|=|OM|2=1.【解析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换. (2)利用极径的应用和一元二次方程根和系数关系式的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,一元二次方程根和系数关系式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.【答案】解:(1)该混合样本呈阳性的概率是:P =1−(34)2=716.(2)方案一:逐个检测,数学期望为:4×14=1, 方案二:检测次数为X ,X 的可能取值为1,5, P(X =1)=81256, P(X =5)=175256,∴X 的分布列如下:方案二的期望为: EX =1×81256+5×175256=23964.方案三,由(1)知,每组两个样本检测时, 若呈阴性,则检测次数为1,概率为916, 若呈阳性则检测次数为3,概率为167,故方案二的检测次数记为Y ,Y 的可能取值为2,4,6, P(Y =2)=81256, P(Y =4)=126256,P =(Y =6)=49256,∴Y 的分布列为: Y 24 6P8125612625649256方案三的期望为E(Y)=2×81256+4×126256+6×49256=154,∵E(X)<E(Y),∴方案一、二,三中方案二最“优”. (3)方案二:记检测次数为X ,则X 的可能取值为1,5, X 15P(1−p)41−(1−p)4E(X)=(1−p)4+5[1−(1−p)4]=5−4(1−p)4, 由题意得E(X)=5−4(1−p)4<4,解得p <1−√22,∴0<p <1−√22时,方案二比方案一更优.【解析】(1)利用对立事件概率计算公式能求出该混合样本呈阳性的概率.(2)方案一:逐个检测,数学期望为:4×14=1,方案二:检测次数为X ,X 的可能取值为1,5,分求出相应的概率,由此能求出方案二的期望;方案三,每组两个样本检测时,若呈阴性,则检测次数为1,概率为916,若呈阳性则检测次数为3,概率为167,故方案二的检测次数记为Y ,Y 的可能取值为2,4,6,分别求出相应的概率,由此能求出方案三的期望,从而方案一、二,三中方案二最“优”.(3)方案二:记检测次数为X ,则X 的可能取值为1,5,分别求出概率得到X 得分布列,求出E(X)=(1−p)4+5[1−(1−p)4]=5−4(1−p)4,由此能求出方案二比方案一更优.本题考查概率的求法,考查最优方案的求法,考查离散型随机变量的分布列、数学期望等基础知识,是中档题.24.【答案】(1)解:设A(x 1,y 1),B(x 2,y 2),由PD ⃗⃗⃗⃗⃗ =3DA ⃗⃗⃗⃗⃗ ,PE ⃗⃗⃗⃗⃗ =3EB ⃗⃗⃗⃗⃗ , 可得D(1+3x 14,−2+3y 14),E(1+3x 24,−2+3y 24),由D 点在C 上可得:−2+3y 14=(1+3x 14)2,化简得:x 12−2x 1−3=0,同理可得:x 22−2x 2−3=0,∵A 、B 两点不同,不妨设A(3,9),B(−1,1), ∴弦AB 所在的直线方程为2x −y +3=0.(2)证明:由(1)可知,A(3,9),B(−1,1),设l 1:y −9=k 1(x −3), 与C :y 2=x 联立,并令△=0,可得k 1=6,同理l 2的斜率k 2=−2, ∴l 1:6x −y −9=0,l 2:2x +y +1=0,解方程组得:交点N(1,−3),而直线PM 的方程为x =1,得证.(3)证明:设P(x 0,y 0),A(x 1,x 12),B(x 2,x 22),由PD ⃗⃗⃗⃗⃗ =λDA ⃗⃗⃗⃗⃗ ,得D(x 0+λx 11+λ,y 0+λx 121+λ),代入y =x 2,化简得:λx 12−2λx 0x 1+(1+λ)y 0−x 02=0, 同理可得:λx 22−2λx 0x 2+(1+λ)y 0−x 02=0,显然x 1≠x 2,∴x 1、x 2是方程λx 2−2λx 0x +(1+λ)y 0−x 02=0的两个不同的根,∴x 1+x 2=2x 0,x 1⋅x 2=(1+λ)y 0−x 02λ,∴x M =x 1+x 22=x 0,即直线PM 的方程为x =x 0, ∵y M =x 12+x 222=(1+2λ)x 02−(1+λ)y 0λ,y Q =x 02,∴y M −y Q =(1+λ)x 02−(1+λ)y 0λ,y Q −y P =x 02−y 0, ∴线段PQ 与QM 的比为定值1+λλ.【解析】(1)设A(x 1,y 1),B(x 2,y 2),求出D 、E 坐标,设A(3,9),B(−1,1),然后判断求解弦AB 所在的直线方程.(2)设l 1:y −9=k 1(x −3),与C :y 2=x 联立,并令△=0,可得k 1=6,同理l 2的斜率k 2=−2,求出交点坐标,然后推出直线PM 的方程即可.(3)设P(x 0,y 0),设出A 、B 坐标,由PD ⃗⃗⃗⃗⃗ =λDA ⃗⃗⃗⃗⃗ ,求出D(x 0+λx 11+λ,y 0+λx121+λ),代入y =x 2,说明x 1、x 2是方程λx 2−2λx 0x +(1+λ)y 0−x 02=0的两个不同的根,利用韦达定理,求出P 、Q 坐标,然后求解线段比例即可.本题考查直线与抛物线的位置关系的应用,考查数形结合以及转化思想的应用,考查计算能力,是难题.。
2019年江苏省高考模拟考试数学试卷一、填空题(本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上).1.已知全集为R,集合M={﹣1,1,2,3,4},N={x|x2+2x>3},则M∩N=.2.已知复数z满足i•z=3﹣4i(其中i为虚数单位),则|z|=.3.某校为了解800名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取50名同学进行检查,将学生从1~800进行编号,现已知第17组抽取的号码为263,则第一组用简单随机抽样抽取的号码为.4.函数f(x)=ln(x+1)+的定义域是.5.袋中有2个黄球3个白球,甲乙两人分别从中任取一球,取得黄球得1分,取得白球得2分,两人总分和为X,则X=3的概率是.6.已知某程序框图如图所示,则该程序运行后输出的结果为.7.将函数的图象向右平移m(m>0)个单位长度,所得函数图象关于y轴对称,则m的最小值为.8.已知双曲线x2+ny2=1(n∈R)与椭圆有相同的焦点,则该双曲线的渐近线方程为.9.公差不为零的等差数列{a n}的前n项和为S n,若a4是a2与a7的等比中项,S5=50,则S8等于.10.若x,y满足不等式则的最大值是.11.已知椭圆的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若=0,则椭圆的离心率为.12.已知f(x)是定义在R上的函数,其导函数为f'(x),若2f(x)﹣f'(x)<2,f(0)=2018,则不等式f(x)>2019e2x+1(其中e为自然对数的底数)的解集为.13.在平面内,,动点P,M满足,,则的最大值是.14.已知函数,关于x的方程f(x)=m(m∈R)有四个不同的实数解x1,x2,x3,x4则x1x2x3x4的取值范围为.二、解答题(本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤).15.在△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,.(1)求角A的大小;(2)若,,求b+c的值.16.在正三棱柱ABC﹣A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且.(1)求证:A1C∥平面AB1D;(2)求证:平面AB1D⊥平面ABM.17.由于渤海海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为60米的水底进行作业,根据经验,潜水员下潜的平均速度为v(米/单位时间),每单位时间消耗氧气(升),在水底作业10个单位时间,每单位时间消耗氧气0.9(升),返回水面的平均速度为(米/单位时间),每单位时间消耗氧气1.5(升),记该潜水员完成此次任务的消耗氧气总量为y (升).(1)求y 关于v 的函数关系式;(2)若c ≤v ≤15(c >0),求当下潜速度v 取什么值时,消耗氧气的总量最少.18.已知过点且离心率为的椭圆C 的中心在原点,焦点在x 轴上.(1)求椭圆C 的方程;(2)设点P 是椭圆的左准线与x 轴的交点,过点P 的直线l 与椭圆C 相交于M ,N 两点,记椭圆C 的左,右焦点分别为F 1,F 2,上下两个顶点分别为B 2,B 1.当线段MN 的中点落在四边形F 1B 1F 2B 2内(包括边界)时,求直线l 斜率的取值范围.19.已知数列{a n }的前n 项和为S n ,∀n ∈N *满足,且a 1=1,正项数列{b n }满足b n +12﹣b n +1=b n 2+b n (n ∈N *),其前7项和为42. (1)求数列{a n }和{b n }的通项公式;(2)令c n =,数列{c n }的前n 项和为T n ,若对任意正整数n ,都有T n ≥2n +a ,求实数a的取值范围;(3)将数列{a n },{b n }的项按照“当n 为奇数时,a n 放在前面;当n 为偶数时,b n 放在前面”的要求进行排列,得到一个新的数列:a 1,b 1,b 2,a 2,a 3,b 3,b 4,a 4,a 5,b 5,b 6,…,求这个新数列的前n 项和P n .20.已知函数f (x )=.(1)求曲线y=f (x )与直线2x +y=0垂直的切线方程; (2)求f (x )的单调递减区间;(3)若存在x 0∈[e ,+∞),使函数g (x )=aelnx +•lnx•f (x )≤a 成立,求实数a 的取值范围.数学Ⅱ(理科加试)[选做题]本题包括A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A .[选修4-1:几何证明选讲](本小题满分0分)21.如图,A ,B ,E 是⊙O 上的点,过E 点的⊙O 的切线与直线AB 交于点P ,∠APE 的平分线和AE,BE分别交于点C,D.求证:(1)DE=CE;(2).B.[选修4-2:矩阵与变换](本小题满分0分)22.已知二阶矩阵M有特征值λ=8及对应的一个特征向量=,并且矩阵M将点(﹣1,3)变换为(4,16),求矩阵M.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线l的参数方程是(t为参数),曲线C的极坐标方程是ρcos2θ=4sinθ.(1)写出直线l的普通方程和曲线C的直角坐标方程;(2)设直线l与曲线C相交于A,B两点,点M为AB的中点,点P的极坐标为,求|PM|的值.D.[选修4-5:不等式选讲](本小题满分0分)24.若实数x,y,z满足4x+3y+12z=1,求x2+y2+z2的最小值.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤.25.底面是正方形的四棱锥中P﹣ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C﹣PD﹣G的余弦值为,若存在,请求出点G的位置;若不存在,请说明理由.26.设i为虚数单位,n为正整数,θ∈[0,2π).(1)用数学归纳法证明:(cosθ+isinθ)n=cosnθ+isinnθ;(2)已知,试利用(1)的结论计算z10.2019年江苏省高考数学预测卷(1)参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上).1.已知全集为R,集合M={﹣1,1,2,3,4},N={x|x2+2x>3},则M∩N={2,3,4} .【考点】1E:交集及其运算.【分析】根据题意,分化简集合B,进而求其交集可得答案.【解答】解:全集为R,集合M={﹣1,1,2,3,4},N={x|x2+2x>3}=(﹣∞,﹣3)∪(1,+∞),则M∩N={2,3,4},故答案为:{2,3,4}.2.已知复数z满足i•z=3﹣4i(其中i为虚数单位),则|z|=5.【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则、模的计算公式即可得出.【解答】解:复数z满足i•z=3﹣4i(其中i为虚数单位),∴﹣i•i•z=﹣i(3﹣4i),∴z=﹣3i﹣4.则|z|==5.故答案为:5.3.某校为了解800名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取50名同学进行检查,将学生从1~800进行编号,现已知第17组抽取的号码为263,则第一组用简单随机抽样抽取的号码为7.【考点】B2:简单随机抽样.【分析】根据系统抽样的特征,从800名学生从中抽取一个容量为50的样本,抽样的分段间隔为16,结合从第17组抽取的号码为263,可得第一组用简单随机抽样抽取的号码.【解答】解:∵从800名学生从中抽取一个容量为50的样本,∴系统抽样的分段间隔为16,设第一部分随机抽取一个号码为x,则抽取的第17编号为x+16×16=263,∴x=7.故答案为:7.4.函数f(x)=ln(x+1)+的定义域是(﹣1,).【考点】33:函数的定义域及其求法.【分析】根据对数的真数大于0,二次根式被开方数大于或等于0,分母不为0,列出不等式组求解集即可.【解答】解:函数f(x)=ln(x+1)+,∴,解得,即﹣1<x<;∴f(x)的定义域为(﹣1,).故答案为:(﹣1,).5.袋中有2个黄球3个白球,甲乙两人分别从中任取一球,取得黄球得1分,取得白球得2分,两人总分和为X,则X=3的概率是.【考点】CH:离散型随机变量的期望与方差.【分析】利用相互独立事件概率乘法公式、互斥事件概率加法公式求解.【解答】解:当X=3时,甲取到黄球,乙取到白球或甲取到白球,乙取到黄球,故P(X=3)==.故答案为:.6.已知某程序框图如图所示,则该程序运行后输出的结果为0.6.【考点】E8:设计程序框图解决实际问题.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出A值.模拟程序的运行过程,用表格对程序运行过程中各变量的值进行分析,不难得到最终的输出结果.【解答】解:程序在运行过程中各变量的值如下表示:是否继续循环 A n循环前/0.2 1第一圈是0.4 2第二圈是0.8 3第三圈是0.6 4第四圈是0.2 5第五圈是0.4 6…第4n圈是0.2/第4n+1圈是0.4/第4n+2圈是0.8/第4n+3圈是0.6/…第2007圈是0.6 2008第2008圈是0.2 2009第2009圈否故最终的输出结果为:0.6故答案为:0.67.将函数的图象向右平移m(m>0)个单位长度,所得函数图象关于y轴对称,则m的最小值为.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.【解答】解:将函数的图象向右平移m(m>0)个单位长度,所得图象对应的函数为y=sin(2x﹣2m﹣),再根据所得图象关于y轴对称,可得2m+=kπ+,k∈Z,即m=+,则m的最小值为,故答案为:.8.已知双曲线x2+ny2=1(n∈R)与椭圆有相同的焦点,则该双曲线的渐近线方程为y=±x.【考点】KC:双曲线的简单性质.【分析】根据题意,由椭圆的方程可得其椭圆的焦点坐标,再由双曲线的几何性质可得n<0,且1+(﹣)=4,解可得n的值,即可得双曲线的方程,由双曲线的几何性质,即可得答案.【解答】解:根据题意,椭圆的方程为,其焦点在x轴上,且c==2,即焦点在坐标为(±2,0),若双曲线x2+ny2=1的焦点在坐标为(±2,0),则有n<0,且1+(﹣)=4,则n=﹣,则双曲线的标准方程为:x2﹣=1,则其渐近线方程为:y=±x;故答案为:y=±x.9.公差不为零的等差数列{a n}的前n项和为S n,若a4是a2与a7的等比中项,S5=50,则S8等于104.【考点】85:等差数列的前n项和.【分析】利用等差数列通项公式、前n项和公式和等比中项定义,列出方程组,求出a1=6,d=2,由此能求出S8.【解答】解:∵公差不为零的等差数列{a n}的前n项和为S n,a4是a2与a7的等比中项,S5=50,∴,解得a1=6,d=2,∴S8==104.故答案为:104.10.若x,y满足不等式则的最大值是2.【考点】7C:简单线性规划.【分析】画出满足条件的平面区域,求出A的坐标,结合的几何意义,求出其最大值即可.【解答】解:画出x,y满足不等式的平面区域,如图示:由,解得A(2,4),而的几何意义表示过平面区域内的点与原点的直线的斜率,由图象得直线过OA时斜率最大,∴()max==2.故答案为:2.11.已知椭圆的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若=0,则椭圆的离心率为.【考点】K4:椭圆的简单性质.【分析】由题意画出图形,求出A的坐标,结合向量加法的坐标运算,求得C的坐标,代入椭圆方程可解e的值.【解答】解:如图,由题意,A(﹣c,﹣),F2(c,0),C(x,y),∵+2=0,(2c,)+2(﹣x+c,﹣y)=0,∴y=,x=2c.∴C(2c,),代入椭圆, +=1,由b2=a2﹣c2,整理得:5c2=a2,解得e==.椭圆的离心率.故答案为:.12.已知f(x)是定义在R上的函数,其导函数为f'(x),若2f(x)﹣f'(x)<2,f(0)=2018,则不等式f(x)>2019e2x+1(其中e为自然对数的底数)的解集为.【考点】6A:函数的单调性与导数的关系.【分析】构造函数g(x)=e﹣2x f(x)﹣e﹣2x,则g′(x)>0,g(x)单调递增,不等式f(x)>2019e2x+1两边同乘e﹣2x得出g(x)>2019,从而得出x的范围.【解答】解:设g(x)=e﹣2x f(x)﹣e﹣2x,则g′(x)=﹣2e﹣2x f(x)+e﹣2x f′(x)+2e﹣2x=﹣e﹣2x[2f(x)﹣f′(x)﹣2],∵2f(x)﹣f'(x)<2,∴g′(x)>0,∴g(x)在R上单调递增.∵f(x)>2019e2x+1,∴e﹣2x f(x)>2019+e﹣2x,即g(x)>2019,∵g(0)=f(0)﹣1=2019,∴x>2019.故答案为.13.在平面内,,动点P,M满足,,则的最大值是.【考点】9R:平面向量数量积的运算.【分析】由可知△ABC是边长为2的等边三角形,P在以A为圆心的圆上,建立坐标系,设出P点坐标,求出的坐标,根据模长公式即可得出||2关于θ的函数,利用三角恒等变换求出此函数的最大值即可.【解答】解:∵,∴=0,=0,=0,∴△ABC是等边三角形,设△ABC的边长为a,∴=a2cos60°==6,∴a=2.∵||=2,∴P在以A为圆心,以2为半径的圆上,∵,∴M是PC的中点,以BC为x轴,以BC的中垂线为y轴建立坐标系,则B(﹣,0),C(,0),A(0,3),设P(cosθ,3+sinθ),则M(, +sinθ),∴=(+cosθ, +sinθ),∴||2=(+cosθ)2+(+sinθ)2=cosθ+sinθ+=3sin(θ+)+,∴当sin(θ+)=1时,||2取得最大值.故答案为.14.已知函数,关于x的方程f(x)=m(m∈R)有四个不同的实数解x1,x2,x3,x4则x1x2x3x4的取值范围为(0,1).【考点】54:根的存在性及根的个数判断.【分析】作函数的图象,从而可得x3x4=1,推出x1x2的范围即可求解结果.【解答】解:作函数的图象如下,结合图象可知,﹣log2x3=log2x4,故x3x4=1,令﹣x2﹣2x=0得,x=0或x=﹣2,令﹣x2﹣2x=1得,x=﹣1;故x1x2∈(0,1),故x1x2x3x4∈(0,1).故答案为:(0,1).二、解答题(本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤).15.在△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,.(1)求角A的大小;(2)若,,求b+c的值.【考点】HT:三角形中的几何计算.【分析】(1)利用正弦定理化简已知条件,通过三角形内角求解A的大小即可.(2)由三角形的面积公式求出ab=2,再根据余弦定理即可求出b+c的值.【解答】解:(1)asinB=bcosA,由正弦定理可得sinAsinB=sinBcosA,∵B是三角形内角,∴sinB≠0,∴tanA=,A是三角形内角,∴A=.(2)∵S=bcsinA=,∴bc=2,由余弦定理a2=b2+c2﹣2bccosA,可得3=b2+c2﹣bc=(b+c)2﹣3bc=(b+c)2﹣6,∴b+c=3.16.在正三棱柱ABC﹣A1B1C1中,AA1=2AB,点D是BC的中点,点M在CC1上,且.(1)求证:A1C∥平面AB1D;(2)求证:平面AB1D⊥平面ABM.【考点】L Y:平面与平面垂直的判定;LS:直线与平面平行的判定.【分析】如图以A为原点,以AC,AA1为y、z轴建立空间直角坐标系.设AB=4,则AA1=8,CM=1.则A(0,0,0),B(2,2,0),C(0,4,0).A(0,0,8),B1(2,2,8),C1(0,4,8),D(,3,0),M(0,4,1),利用向量1法求解.【解答】解:如图以A为原点,以AC,AA1为y、z轴建立空间直角坐标系.设AB=4,则AA1=8,CM=1.则A(0,0,0),B(2,2,0),C(0,4,0).A(0,0,8),B1(2,2,8),C1(0,4,8),D(,3,0),M(0,4,1)1(1)设面AB1D的法向量为由可取,,则∵A1C⊄面AB1D,∴A1C∥平面AB1D(2)设面ABNM的法向量为,由,可取由(1)得面AB1D的法向量为,=+(﹣1)×(﹣3)+12×=0∴,∴平面AB1D⊥平面ABM17.由于渤海海域水污染严重,为了获得第一手的水文资料,潜水员需要潜入水深为60米的水底进行作业,根据经验,潜水员下潜的平均速度为v(米/单位时间),每单位时间消耗氧气(升),在水底作业10个单位时间,每单位时间消耗氧气0.9(升),返回水面的平均速度为(米/单位时间),每单位时间消耗氧气1.5(升),记该潜水员完成此次任务的消耗氧气总量为y(升).(1)求y关于v的函数关系式;(2)若c≤v≤15(c>0),求当下潜速度v取什么值时,消耗氧气的总量最少.【考点】36:函数解析式的求解及常用方法.【分析】(1)分别计算潜入水底用时用氧量,水底作业时用氧量和返回水面用时用氧量,即可得到总用氧量的函数y;(2)求导数y′,判断函数y的单调性,讨论c的取值,求出下潜速度v取什么值时消耗氧气的总量最少.【解答】解:(1)由题意,下潜用时单位时间,用氧量为[+1]×=+(升),水底作业时的用氧量为10×0.9=9(升),返回水面用时=单位时间,用氧量为×1.5=(升),∴总用氧量为y=++9(v>0);(2)求导数y′=﹣=,令y'=0,解得v=10,在0<v<10时,y'<0,函数y单调递减,在v>10时,y'>0,函数y单调递增;∴当c<10时,函数y在(0,10)上递减,在(10,15)上递增,此时v=10时用氧量最少;当c≥10时,函数y在[c,15]上递增,此时v=c时,总用氧量最少.18.已知过点且离心率为的椭圆C的中心在原点,焦点在x轴上.(1)求椭圆C的方程;(2)设点P是椭圆的左准线与x轴的交点,过点P的直线l与椭圆C相交于M,N两点,记椭圆C的左,右焦点分别为F1,F2,上下两个顶点分别为B2,B1.当线段MN的中点落在四边形F1B1F2B2内(包括边界)时,求直线l斜率的取值范围.【考点】KL:直线与椭圆的位置关系.【分析】(1)由过点且离心率为的椭圆C的中心在原点,焦点在x轴上,列出方程组,求出a=2,b=4,由此能求出椭圆C的方程.(2)设出直线的方程,将直线的方程与椭圆方程联立,利用二次方程的韦达定理得到弦中点的坐标,根据中点在正方形的内部,得到中点的坐标满足的不等关系,求出k的范围.【解答】解:(1)∵过点且离心率为的椭圆C的中心在原点,焦点在x轴上.∴设椭圆方程为=1(a>b>0),则,解得a=2,b=4,∴椭圆C的方程为=1.(2)椭圆C的左准线方程为x=﹣4,所以点P的坐标为(﹣4,0),由题意知直线l的斜率存在,所以设直线l的方程为y=k(x+4)如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0)由,得(1+2k2)x2+16k2x+32k2﹣8=0.①由△=(16k2)2﹣4(1+2k2)(32k2﹣8)>0,解得﹣<k<.②因为x1,x2是方程①的两根,所以x1+x2=﹣,于是x0==﹣,y0=k(x0+4)=.因为x0=﹣≤0,所以点G不可能在y轴的右边,又直线F1B2,F1B1方程分别为y=x+2,y=﹣x﹣2所以点G在正方形Q内(包括边界)的充要条件为,解得≤k ≤, 由②得:≤k ≤.故直线l 斜率的取值范围是[,].19.已知数列{a n }的前n 项和为S n ,∀n ∈N *满足,且a 1=1,正项数列{b n }满足b n +12﹣b n +1=b n 2+b n (n ∈N *),其前7项和为42. (1)求数列{a n }和{b n }的通项公式;(2)令c n =,数列{c n }的前n 项和为T n ,若对任意正整数n ,都有T n ≥2n +a ,求实数a的取值范围;(3)将数列{a n },{b n }的项按照“当n 为奇数时,a n 放在前面;当n 为偶数时,b n 放在前面”的要求进行排列,得到一个新的数列:a 1,b 1,b 2,a 2,a 3,b 3,b 4,a 4,a 5,b 5,b 6,…,求这个新数列的前n 项和P n .【考点】8E :数列的求和;8H :数列递推式.【分析】(1)数列{a n }的前n 项和为S n ,∀n ∈N *满足,且a 1=1,可得数列是等差数列,首项为1,公差为.利用通项公式可得S n .利用递推关系即可得出a n .正项数列{b n }满足b n +12﹣b n +1=b n 2+b n (n ∈N *),化为:(b n +1+b n )(b n +1﹣b n )=b n +1+b n ,可得b n +1﹣b n =1.再利用等差数列的求和公式即可得出.(2)c n ==2+2,利用裂项求和方法、数列的单调性即可得出.(3)n=2k 时,P n =P 2k =(a 1+a 2+…+a k )+(b 1+b 2+…+b k ).n=2k ﹣1时,2k 被2整除而不能被4整除时,P n =P 2k ﹣b k .2k 被4整除时,P n =P 2k ﹣a k .【解答】解:(1)数列{a n }的前n 项和为S n ,∀n ∈N *满足,且a 1=1,∴数列是等差数列,首项为1,公差为.∴=1+(n ﹣1),解得S n =.∴n ≥2时,a n =S n ﹣S n ﹣1=﹣=n ,n=1时也成立.正项数列{b n }满足b n +12﹣b n +1=b n 2+b n (n ∈N *),化为:(b n +1+b n )(b n +1﹣b n )=b n +1+b n , ∴b n +1﹣b n =1.∴数列{b n }是等差数列,公差为1.∵其前7项和为42,∴7b 1+×1=42,解得b 1=3.∴b n =3+n ﹣1=n +2.(2)c n ==2+2,∴数列{c n }的前n 项和T n =2n +2+…++=2n +2=2n +2,T n ≥2n +a ,化为:2≥a ,∴a ≤.∴实数a 的取值范围是.(3)n=2k 时,P n =P 2k =(a 1+a 2+…+a k )+(b 1+b 2+…+b k )=+=k 2+3k=+3×=.n=2k ﹣1时,2k 被2整除而不能被4整除时,P n =P 2k ﹣b k =﹣(k +2)=k 2+2k ﹣2.2k 被4整除时,P n =P 2k ﹣a k =﹣k=k 2+2k .20.已知函数f (x )=.(1)求曲线y=f (x )与直线2x +y=0垂直的切线方程; (2)求f (x )的单调递减区间;(3)若存在x 0∈[e ,+∞),使函数g (x )=aelnx +•lnx•f (x )≤a 成立,求实数a 的取值范围.【考点】6B :利用导数研究函数的单调性;6E :利用导数求闭区间上函数的最值;6H :利用导数研究曲线上某点切线方程.【分析】(1)设出切点坐标,求出切线方程即可;(2)求出函数的导数,由f′(x )<0得0<x <1或1<x <e ,即可求出单调递减区间; (3)由已知,若存在x 0∈[e ,+∞),使函数g (x )≤a 成立,则只需满足当x ∈[e ,+∞),g(x)min≤a即可.【解答】解:(1)f(x)=,f′(x)=,设出切点坐标(a,),而曲线y=f(x)与直线2x+y=0垂直的切线的斜率k=,故=,解得:a=e2,故切点坐标是:(e2,e2),故切线方程是:y﹣e2=(x﹣e2),即x﹣y+e2=0;(2)f′(x)=,由f′(x)<0,得0<x<1或1<x<e,所以函数f(x)的单调递减区间为(0,1)和(1,e);(3)因为g(x)=aelnx+x2﹣(a+e)x,由已知,若存在x0∈[e,+∞),使函数g(x)=aelnx+x2﹣•lnx•f(x)≤a成立,则只需满足当x∈[e,+∞),g(x)min≤a即可,又g(x)=aelnx+x2﹣(a+e)x,则g′(x)=,a≤e,则g′(x)≥0在x∈[e,+∞)上恒成立,∴g(x)在[e,+∞)上单调递增,∴g(x)min=g(e)=﹣,∴a≥﹣,∵a≤e,∴﹣≤a≤e,a>e,则g(x)在[e,a)上单调递减,在[a,+∞)上单调递增,∴g(x)在[e,+∞)上的最小值是g(a),∵g(a)<g(e),a>e,∴满足题意,综上所述,a≥﹣.数学Ⅱ(理科加试)[选做题]本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分0分)21.如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:(1)DE=CE;(2).【考点】NC:与圆有关的比例线段.【分析】(1)证明∠PEB=∠PAC,∠EPC=∠CPA,可得∠ECD=∠EDC,即可证明结论;(2)证明△EPB∽△APE,得=,PC是∠APE的平分线,得=,即可证明结论.【解答】证明:(1)∵PE是⊙O的切线,∴∠PEB=∠PAC,∵PC是∠APE的平分线,∴∠EPC=∠CPA,∴∠PEB+∠EPC=∠PAC+∠CPA,∴∠ECD=∠EDC,∴DE=CE;(2)∵∠PEB=∠PAC,∠EPB=∠APE,∴△EPB∽△APE,∴=,∵PC是∠APE的平分线,∴=,∴.B.[选修4-2:矩阵与变换](本小题满分0分)22.已知二阶矩阵M有特征值λ=8及对应的一个特征向量=,并且矩阵M将点(﹣1,3)变换为(4,16),求矩阵M.【考点】OV:特征值与特征向量的计算.【分析】设出矩阵,利用特征向量的定义,即二阶变换矩阵的概念,建立方程组,即可得到结论.【解答】解:设,∵特征值λ=8及对应的一个特征向量=,矩阵M将点(﹣1,3)变换为(4,16),∴,解得,∴M=…C.[选修4-4:坐标系与参数方程](本小题满分0分)23.以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线l的参数方程是(t为参数),曲线C的极坐标方程是ρcos2θ=4sinθ.(1)写出直线l的普通方程和曲线C的直角坐标方程;(2)设直线l与曲线C相交于A,B两点,点M为AB的中点,点P的极坐标为,求|PM|的值.【考点】Q4:简单曲线的极坐标方程.【分析】(1)消去参数t得直线l的普通方程,利用极坐标与直角坐标互化方法求曲线C的直角坐标方程;(2)求出M,P的直角坐标,即可求|PM|的值.【解答】解:(1)已知直线l的参数方程是(t为参数),普通方程为y=+3,曲线C的极坐标方程是ρcos2θ=4sinθ,化为ρ2cos2θ=4ρsinθ,∴x2=4y.…(2)由直线与抛物线方程,消去y得x2﹣4x﹣12=0…设A(x1,y1),B(x2,y2),则AB的中点M(2,9)…又点P的直角坐标为(2,6),…所以|PM|=3…D.[选修4-5:不等式选讲](本小题满分0分)24.若实数x,y,z满足4x+3y+12z=1,求x2+y2+z2的最小值.【考点】RA:二维形式的柯西不等式.【分析】利用条件x+2y+3z=1,构造柯西不等式(4x+3y+12z)2≤(x2+y2+z2)(42+32+122),变形即可得答案.【解答】解:根据题意,实数x,y,z满足4x+3y+12z=1,则有(4x+3y+12z)2≤(x2+y2+z2)(42+32+122),即1≤169(x2+y2+z2),即有x2+y2+z2≥;即x2+y2+z2的最小值为;故答案为:.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤.25.底面是正方形的四棱锥中P﹣ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,E,F分别为线段PC,DB的中点,问在线段AB上是否存在点G,使得二面角C﹣PD﹣G的余弦值为,若存在,请求出点G的位置;若不存在,请说明理由.【考点】MT:二面角的平面角及求法.【分析】取AD中点O,连结PO,以O为原点,OA为x轴,在平面ABCD中过O作AD的垂线为y轴,以OP为z轴,建立空间直角坐标系,利用向量法求出在线段AB上存在点G,使得二面角C﹣PD﹣G的余弦值为,且AG=.【解答】解:假设在线段AB上存在点G,使得二面角C﹣PD﹣G的余弦值为.取AD中点O,连结PO,∵底面是正方形的四棱锥中P﹣ABCD中,侧面PAD⊥底面ABCD,且△PAD是等腰直角三角形,其中PA=PD,∴PO⊥平面ABCD,以O为原点,OA为x轴,在平面ABCD中过O作AD的垂线为y轴,以OP为z轴,建立空间直角坐标系,设PA=PD=,则G(1,t,0)(0≤t≤2),C(﹣1,2,0),P(0,0,),D(﹣1,0,0),=(﹣1,0,﹣),=(﹣1,2,﹣),=(1,t,﹣),设平面PCD的法向量=(x,y,z),则,取x=,得=(,0,﹣1),设平面PDG的法向量=(a,b,c),则,取a=,得=(,﹣,﹣1),∵二面角C﹣PD﹣G的余弦值为,∴==,解得t=,∴在线段AB上存在点G,使得二面角C﹣PD﹣G的余弦值为,且AG=.26.设i为虚数单位,n为正整数,θ∈[0,2π).(1)用数学归纳法证明:(cosθ+isinθ)n=cosnθ+isinnθ;(2)已知,试利用(1)的结论计算z10.【考点】RG:数学归纳法.【分析】(1)利用数学归纳法即可证明,注意和差公式的应用.(2)利用(1)的结论即可得出.【解答】证明:(1)证明:1°当n=1时,左边=右边=cosθ+isinθ,所以命题成立;2°假设当n=k时,命题成立,即(cosθ+isinθ)k=coskθ+isinkθ,则当n=k+1时,(cosx+isinθ)k+1=(cosθ+isinθ)k•(cosθ+isinθ)=(coskθ+isinkθ)(cosθ+isinθ)=(coskθcosθ﹣sinkθsinθ)+i(sinkθcosθ+coskθsinθ)=cos(k+1)θ+isin(k+1)θ∴当n=k+1时,命题成立;综上,由1°和2°可得,(cosθ+isinθ)n=cosnθ+isinnθ.(2)=2(﹣)=2(cos+isin),∴z10=210(cosπ+isinπ)=210(cos+isin)=210(+i)=512+512i。