北京四中初二轴对称

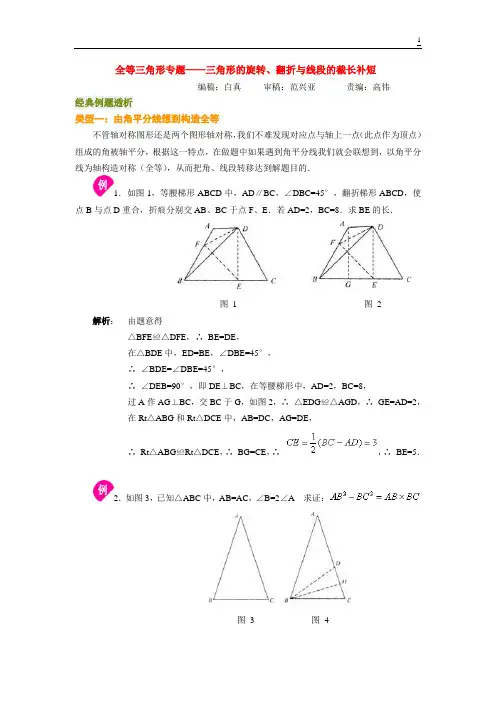
全等三角形专题——三角形的旋转、翻折与线段的截长补短编稿：白真审稿：范兴亚责编：高伟经典例题透析类型一：由角平分线想到构造全等不管轴对称图形还是两个图形轴对称，我们不难发现对应点与轴上一点（此点作为顶点）组成的角被轴平分，根据这一特点，在做题中如果遇到角平分线我们就会联想到，以角平分线为轴构造对称（全等），从而把角、线段转移达到解题目的．1．如图1，等腰梯形ABCD中，AD∥BC，∠DBC=45°，翻折梯形ABCD，使点B与点D重合，折痕分别交AB、BC于点F、E．若AD=2，BC=8．求BE的长．图1 图 2 解析：由题意得△BFE≌△DFE，∴BE=DE，在△BDE中，ED=BE，∠DBE=45°，∴∠BDE=∠DBE=45°，∴∠DEB=90°，即DE⊥BC，在等腰梯形中，AD=2，BC=8，过A作AG⊥BC，交BC于G，如图2，∴△EDG≌△AGD，∴GE=AD=2，在Rt△ABG和Rt△DCE中，AB=DC，AG=DE，∴Rt△ABG≌Rt△DCE，∴BG=CE，∴，∴BE=5．2．如图3，已知△ABC中，AB=AC，∠B=2∠A求证：图3图 4解析：如图4，作∠B的平分线交AC于D，则∠A=∠ABD，∠BDC=2∠A=∠C∴AD=BD=BC作BM⊥AC于M，则CM=DM．3．如图5，已知梯形ABCD中，AB∥CD，AD＞BC，求证：AC＞BD图5图6解析：如图6，作DE∥AC，DF∥BC，交BA或延长线于点E、F，四边形ACDE和四边形BCDF都是平行四边形．∴DE=AC，DF=BC，AE=CD=BF作DH⊥AB于H，根据勾股定理，，∵AD＞BC，AD＞DF∴AH＞FH，EH＞BH，∴DE＞BD，即AC＞BD.4．如图7，已知△ABC中，AD⊥BC，AB+CD=AC+BD．求证：AB=AC．图7解析：设AB、AC、BD、，CD分别为b、c、m、n，则c+n=b+m，c-b=m-n，∵AD⊥BC，根据勾股定理，得，∴，，∵c+b＞m+n，∴c-b=0即c=b，∴AB=AC．类型二：勾股定理的逆定理的运用5．如图8，P是正△ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A旋转后，得到，则点P与点之间的距离为________，∠APB=________．图8 图9 解析：如图9，连结，是由旋转得到的，所以≌所以. .所以三角形是等边三角形，．则在三角形中．所以是直角，．6．如图10，已知∠ABC=30°，∠ADC=60°，AD=DC．求证：．图10 图11解析：如图11，显然△ADC是等边三角形，以BC为边向右侧作等边三角形，则BC=BE，连接AE，则可证明△BCD≌△ACE，所以AE=DB，∠ABC+∠CBE=90°，根据勾股定理有，即．7．如图12，D为等腰△ABC的腰AB上的一点，E为另一腰AC延长线上的一点，且BD=CE，则A．DE=BC B．DE＞BCC．DE＜BC D．DE与BC大小关系决定于∠A的大小．图12 图13解析：如图13，分别过D和E点作到BC边的垂线，交BC及其延长线于G和H．则根据，可得到△BDG≌△ECH. 所以BG=CH．所以BC=GH．显然DE＞GH. 所以DE＞BC.8．如图14，已知等边△ABC内有一点N，ND⊥BC，NE⊥AB，NF⊥AC，D、E、F都是垂足，M是△ABC中异于N的另一点，若，，那么与的大小关系是________．图14图15 解析：如图15，作M到正三角形的各边上的高，根据面积相等的关系，有，，分别化简为所以．而根据直角三角形斜边与直角边的关系有，，．所以有．9．如图16，梯形ABCD中，AD∥BC，E是AB的中点，CE恰好是平分∠BCD，若AD=3，BC=4，则CD的长是A．5B．6C．7 D．8图16 图17 解析：如图17，延长CE交DA的延长线于F，则容易证明△BEC≌△AEF，于是可得到∠DCE=∠BCE=∠AFE，所以△FCD是等腰三角形，所以CD=AD+AF=7．10．如图18，在等腰直角△ABC中，∠BAC=90°，AD∥BC，在AD上取一点E，使∠EBC=30°，则BE和BC的大小关系是（）A．BE＞BC B．BE＜BC C．BE=BC D．不确定图18解析：作△ABC的高h，那么BC=2h．而BE=2h．所以BE=BC．11．已知三角形的两条边长分别为a=5，b=4，它们的高分别为，若，那么该三角形的面积是________．解析：根据三角形的面积公式，可知，而根据，可得到，所以．所以或．如果，则结合，可得到，矛盾．所以，结合，得到，所以，所以三角形的面积为．。

轴对称(2)编稿老师：李岩审稿老师：龚剑均责编:邵剑英(一)教学目标1、掌握线段的垂直平分线的性质定理和判定定理，能用它们解决相关问题．2、能利用轴对称变换求解最值问题．(二)知识要点1、线段的垂直平分线的概念垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线．2、线段垂直平分线的性质定理线段垂直平分线上的点到这条线段的两个端点的距离相等．[符号语言]如图，∵OP垂直平分线段AB，∴PA=PB．[作用]证明线段相等和作图的重要依据之一．3、线段垂直平分线的判定定理到线段两个端点的距离相等的点在这条线段的垂直平分线上．[符号语言] ∵PA=PB，∴点P在AB的垂直平分线上．[作用]证明点在线段的垂直平分线上的方法．4、线段垂直平分线可以看作是到线段两个端点距离相等的所有点的集合．5、三角形三边的垂直平分线的交点到三个顶点的距离相等，这个交点称为三角形的外心。

(三)典型例题1、(1)如图，在△ABC中，DE垂直平分线段AB，交AB于E，交AC于D，若AB=AC=32，BC=21，则△BCD的周长为________．(2)如图，在Rt△ABC中，∠C=90°，E为AB的中点，DE⊥AB交BC于D，若∠1：∠2=1：2，则∠B=________，∠BAC=________．解：(1)∵DE垂直平分线段AB，∴AD=BD．∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC．∵AC=32，BC=21，∴=53．(2)∵E为AB的中点，DE⊥AB，∴DE是AB的垂直平分线．∴AD=BD，∴∠2=∠B．∵∠C=90°，∴∠1+∠2+∠B=90°．∵∠1：∠2=1：2，∴∠1=18°，∠B=∠2=36°，∠BAC=∠1+∠2=54°．[小结]线段垂直平分线的性质在具体问题中的应用时，多数与等腰三角形性质联系在一起，因此应熟悉等腰三角形的一些基本性质．2、如图，△ABC中，AD平分∠BAC，EF垂直平分AD，垂足为H，交AB于E．交BC延长线于F，求证：∠B=∠CAF．证明：∵EF垂直平分AD∴AF=DF∴∠DAF=∠ADF。

一、选择题1．如图，已知30MON ︒∠=，点123,,...A A A 在射线ON 上，点123,,B B B …在射线OM 上，112223334,,...A B A A B A A B A ∆∆∆1n n n A B A +∆均为等边三角形，若11OA =，则778A B A ∆的边长为（ ）A ．16B ．32C ．64D ．128C解析：C【分析】 根据三角形的外角性质以及等边三角形的判定和性质得出OA 1=B 1A 1=1，OA 2=B 2A 2=2，OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，…进而得出答案．【详解】如图，∵△A 1B 1A 2是等边三角形，∴A 1B 1=A 2B 1，∠2=60°，∵∠MON=30°，∴∠MON=∠1=30°，∴OA 1=A 1B 1=1，∴A 2B 1= A 1A 2=1，∵△A 2B 2A 3是等边三角形，同理可得：OA 2=B 2A 2=2，同理；OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，OA 5=B 5A 5=4216=，…，以此类推：所以OA 7=B 7A 7=6264=，故选：C ．【点睛】本题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出OA 2=B 2A 2=2， OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，…进而发现规律是解题的关键．2．如图，ABC 中，45ABC ︒∠=，CD AB ⊥于D ，BE 平分ABC ∠，且BE AC ⊥于E ，与CD 相交于点F ，DH BC ⊥于H ，交BE 于G ，下列结论：①BD CD =；②AE BG =；③2CE BF =；④AD CF BD +=．其中正确的有（ ）A ．4个B ．3个C ．2个D ．1个B解析：B【分析】 根据∠ABC ＝45°，CD ⊥AB 可得出BD ＝CD ，利用ASA 判定Rt △DFB ≌Rt △DAC ，从而得出DF ＝AD ，BF ＝AC ．则CD ＝CF +AD ，即AD +CF ＝BD ；再利用ASA 判定Rt △BEA ≌Rt △BEC ，得出CE ＝AE ＝12AC ，又因为BF ＝AC 所以CE ＝12AC ＝12BF ，连接CG ．因为△BCD 是等腰直角三角形，即BD ＝CD ．又因为DH ⊥BC ，那么DH 垂直平分BC ．即BG ＝CG ． 在Rt △CEG 中，CG 是斜边，CE 是直角边，所以CE ＜CG ．即AE ＜BG ．【详解】解：∵CD ⊥AB ，∠ABC ＝45°，∴△BCD 是等腰直角三角形．∴BD ＝CD ．故①正确；连接CG ．∵△BCD 是等腰直角三角形，∴BD ＝CD又DH ⊥BC ，∴DH 垂直平分BC ．∴BG ＝CG在Rt △CEG 中，∵CG 是斜边，CE 是直角边，∴CE ＜CG ．∵CE ＝AE ，∴AE ＜BG ．故②错误．在Rt △BEA 和Rt △BEC 中∵BE 平分∠ABC ，∴∠ABE ＝∠CBE ．又∵BE ＝BE ，∠BEA ＝∠BEC ＝90°，∴Rt △BEA ≌Rt △BEC ．∴CE ＝AE ＝12AC ． 在Rt △DFB 和Rt △DAC 中，∵∠DBF ＝90°﹣∠BFD ，∠DCA ＝90°﹣∠EFC ，且∠BFD ＝∠EFC ，∴∠DBF ＝∠DCA ．又∵∠BDF ＝∠CDA ＝90°，BD ＝CD ，∴△DFB ≌△DAC ．∴BF ＝AC ，∴CE ＝12AC ＝12BF ， ∴2CE ＝BF ；故③正确；由③可得△DFB ≌△DAC ．∴BF ＝AC ；DF ＝AD ．∵CD ＝CF +DF ，∴AD +CF ＝BD ；故④正确；故选：B ．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、AAS 、ASA 、HL ．在复杂的图形中有45°的角，有垂直，往往要用到等腰直角三角形，要注意掌握并应用此点．3．如图所示，已知ABC 和DCE 均是等边三角形，点B 、C 、E 在同一条直线上，连接AE 、BD 、FG ，AE 与BD 交于点O ，AE 与CD 交于点G ，AC 与BD 交于点F ，则下列结论中：①AE BD =； ②AG BF =； ③FG//BE ； ④CF CG =，以上结论正确的有（ ）A．1个B．2个C．3个D．4个D解析：D【分析】首先根据等边三角形性质得出BC=AC，CD=CE，∠ACB=∠ECD=60°，即可证明△BCD与△ACE全等、△BCF与△ACG全等以及△DFC与△EGC全等，最后利用全等三角形性质以及等边三角形性质证明即可．【详解】∵△ABC与△CDE为等边三角形，∴BC=AC，CD=CE，∠ACB=∠ECD=60°，∴∠ACB+∠ACD=∠ACD+∠ECD，∠ACD=60°，即：∠ACE=∠BCD，在△BCD与△ACE中，∵BC=AC，∠ACE=∠BCD，CD=CE，∴△BCD≌△ACE(SAS)，∴AE=BD，即①正确；在△BCF与△ACG中，由①可知∠CBF=∠CAG，又∵AC=BC，∠BCF=∠ACG=60°，∴△BCF≌△ACG(ASA)，∴AG=BF，即②正确；在△DFC与△EGC中，∵△BCF≌△ACG，∴CF=CG．即④正确；∵∠GCF =60°，∴△CFG为等边三角形，∴∠CFG=∠FCB=60°，∴FG∥BE，即③正确；综上，①②③④都正确．故选：D．【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质以及平行线的判定，解题的关键是正确寻找全等三角形来解决问题，．4．如图，已知30MON ∠=︒，点1A ，2A ，3A ，…，在射线ON 上，点B ，1B ，2B ，3B ，…，在射线OM 上，112A B B ，223A B B △，334A B B △，…，均为等边三角形．若11OB =，则202020202021A B B △的边长为（ ）A ．20192B ．20202C ．20212D ．20222 A解析：A【分析】 先求出∠O=∠OA 1B 1=30°，从而A 1B 1=A 1B 2= OB 1=1，然后根据含30°角的直角三角形的性质求解即可．【详解】解：∵△A 1B 1B 2是等边三角形，∴∠A 1B 1B 2=∠A 1B 2O=60°，A 1B 1=A 1B 2，∵∠O=30°，∴∠A 2A 1B 2=∠O+∠A 1B 2O=90°，∵∠A 1B 1B 2=∠O+∠OA 1B 1，∴∠O=∠OA 1B 1=30°，∴OB 1=A 1B 1=A 1B 2=1，在Rt △A 2A 1B 2中，∵∠A 1A 2B 2=30°，∴A 2B 2=2A 1B 2=2，同法可得A 3B 3=22，A 4B 4=23，…，A n B n =2n-1，∴202020202021A B B △的边长=22019，故选：A ．【点睛】本题考查了图形类规律探究，等边三角形的性质，三角形外角的性质，含30角的直角三角形的性质等知识，解题的关键是学会探究规律的方法，属于中考常考题型．5．如图，在ABC ∆中，90,30C B ︒︒∠=∠= ，以A 为圆心，任意长为半径画弧分别交AB AC 、于点M 和N ，再分别以M N 、为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP ，并延长交BC 于点D ，则下列说法中正确的个数是（ ）①AD 是BAC ∠的平分线；②60ADC ︒∠=；③点D 在AB 的垂直平分线上﹔④若2AD =，则点D 到AB 的距离是1，:1:2DAC ABC S S ∆∆=A ．2B ．3C ．4D ．5B 解析：B【分析】先根据三角形内角和计算出∠BAC=60°，再利用基本作图对①进行判断；利用∠BAD=∠CAD=30°得到∠ADC=60°，则可对②进行判断；利用∠B=∠BAD 得到DA=DB ，根据线段垂直平分线的性质定理的逆定理可对③进行判断．利用30度角所对的直角边是斜边的一半、三角形的面积计算公式即可得出两个三角形的面积之比．【详解】解：由作法得，AD 平分∠BAC ，所以①正确；∵∠C=90°，∠B=30°，∴∠BAC=60°，∴∠BAD=∠CAD=12×60°=30°， ∴∠ADC=90°-∠CAD=60°，所以②正确；∵∠B=∠BAD ，∴DA=DB ，∴点D 在AB 的垂直平分线上，所以③正确；在直角△ACD 中，∠CAD=30°，∴CD=12AD ， ∴BC=CD+BD=12AD+AD=32AD ，1124DAC S AC CD AC AD ∆=⋅=⋅． ∴11332224ABC S AC BC AC AD AC AD ∆=⋅=⋅=⋅， ∴13::1:344DAC ABC S S AC AD AC AD ∆∆=⋅⋅=，故④错误． 所以，正确的结论有3个故选：B ．【点睛】 本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图．解题时需要熟悉等腰三角形的判定与性质．6．平面直角坐标系中，已知()1,1A ，()2,0B ．若在x 轴上取点C ，使ABC 为等腰三角形，则满足条件的点C 的个数是（ ）A ．2个B ．3个C ．4个D ．5个C解析：C【分析】分三种情况：当AB=AC 时，当BA=BC 时，当AC=AB 时，根据等腰三角形两边相等的性质分别作图即可得解．【详解】当AB=AC 时，点C 与点O 重合；当BA=BC 时，以点B 为圆心，AB 长为半径画弧，与x 轴有两个交点；当AC=AB 时，作线段AB 的垂直平分线，与x 轴有一个交点，共有4个点C ，故选：C ． ．【点睛】此题考查等腰三角形的性质，直角坐标系中作等腰三角形的方法，熟记等腰三角形的性质并利用其作图是解题的关键．7．如图，在ABC 中，90C =∠，30B ∠=，以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，连结AP 并延长交BC 于点D ，则:DAC ABC S S 等于（ ）A ．1:2B ．2:3C ．3D ．1:3D解析：D【分析】 先根据直角三角形的性质得出∠2=30°，CD=12AD ，再由三角形的面积公式即可得出结论．【详解】解：由作图过程可知：AP 平分∠BAC ，∵∠C=90°，∠B=30°，∴∠BAC=60°，∴∠1=∠2=∠B=30°，∴CD=12AD ，AD=BD ， ∴BC=BD+CD=AD+12AD=32AD ， S △DAC =12AC•CD=14AC•AD ， ∴S △ABC =12AC•BC=12AC•32AD=34AC•AD ， ∴S △DAC ：S △ABC =1：3，故选D ．【点睛】本题考查的是作图—基本作图，熟知角平分线的作法和性质，30°的直角三角形的性质是解答此题的关键．8．已知点(),3M a ，点()2,N b 关于x 轴对称，则2020()a b +的值（ ） A ．3-B ．1-C ．1D ．3C 解析：C【分析】根据关于坐标轴对称的规律，关于谁对称谁不变，另一个坐标变为相反数即可获得a 和b 的值，然后即可得解．【详解】∵点(),3M a ，点()2,N b 关于x 轴对称∴2a =，3b =-∴()()20182018231a b +=-= 故选：C ． 【点睛】本题考查了在坐标平面直角坐标系中关于x 轴对称的点的坐标的变化规律，点(),x y 关于x 轴对称的点的坐标为()x y -，，熟记规律即可得到正确答案．9．如图，AEC BED △△≌，点D 在AC 边上，AE 和BD 相交于点O ，若30AED ∠=︒，120∠=︒BEC ，则ADB ∠的度数为（ ）A ．45°B ．40°C ．35°D ．30°A解析：A【分析】 由△AEC ≌△BED 可知：EC=ED ，∠C=∠BDE ，∠BED=∠AEC ，根据等腰三角形的性质即可知∠C 的度数，从而可求出∠ADB 的度数．【详解】解：∵△AEC ≌△BED ，∴EC=ED ，∠C=∠BDE ，∠BED=∠AEC ，∴∠BEO+∠AED=∠CED+∠AED ，∴∠BEO=∠CED,∵∠AED=30°，∠BEC=120°，∴∠BEO=∠CED=120302︒-︒=45°， 在△EDC 中，∵EC=ED ，∠CED=45°，∴∠C=∠EDC=67.5°，∴∠BDE=∠C=67.5°，∴∠ADB=180°-∠BDE-∠EDC=180°-67.5°-67.5°=45°，故选A ．【点睛】本题考查全等三角形的性质，等腰三角形的性质，解题的关键是熟练运用全等三角形的性质．10．等腰三角形腰上的高与另一腰的夹角为30，则底角度数是（ ）A ．30B ．60︒C ．40︒或50︒D ．30或60︒D 解析：D【分析】由三角形的高可在三角形的内部，也可在三角形的外部，所以分锐角三角形和钝角三角形两种情况作出符合题意的图形，再结合等腰三角形的性质与三角形的内角和定理求解即可．【详解】解：如图，分两种情况：①如图，当三角形的高在三角形的内部时，AB=AC ，BD ⊥AC ，∠ABD=30°，∴∠A=60°，∴∠C=∠ABC=1802A ︒-∠ =60°； ②如图，当三角形的高在三角形的外部时，AB=AC ，BD ⊥AC ，∠ABD=30°，∴∠DAB=60°，∠BAC=120°，∴∠C=∠ABC=180302BAC ︒-∠=︒． 故选：D ．【点睛】本题考查了等腰三角形的性质和直角三角形的两锐角互余，三角形的内角和定理的应用，三角形的高的含义，分类讨论的数学思想，掌握分类讨论解决问题是解题的关键． 二、填空题11．如图，已知∠AOB =30°，点P 在射线OA 上，OP =16，点E 、点F 在射线OB 上，PE=PF ，EF =6．若点D 是射线OB 上一动点，当∠PDE =45°时，DF 的长为___________．5或11【分析】过点P 作PH ⊥OB 于点H 根据PE=PF 可得EH=FH=EF=3根据∠AOB=30°OP=16可得PH=OP=8当点D 运动到点F 右侧或当点D 运动到点F 左侧时分别计算可得DF 的长【详解】 解析：5或11【分析】过点P 作PH ⊥OB 于点H ，根据PE=PF ，可得EH=FH=12EF=3，根据∠AOB=30°，OP=16，可得PH=12OP=8，当点D 运动到点F 右侧或当点D 运动到点F 左侧时，分别计算可得DF 的长．【详解】如图，过点P作PH⊥OB于点H，∵PE=PF，∴EH=FH=1EF=3，2∵∠AOB=30°，OP=16，∴PH=1OP=8，2当点D运动到点F右侧时，∵∠PDE=45°，∴∠DPH=45°，∴PH=DH=8，∴DF=DH-FH=8-3=5；当点D运动到点F左侧时，D′F=D′H+FH=8+3=11．所以DF的长为5或11．故答案为：5或11．【点睛】本题考查了含30度角的直角三角形的性质、等腰三角形的性质，解决本题的关键是分两种情况画图解答．12．如图：已知在ABC中，90BAC︒∠=，在直线AC上找点P，使∠=，36ACB︒∠的度数为________．ABP△是等腰三角形，则APB72°或18°或108°或36°【分析】分四种情况：①AB＝BP1时②当AB＝AP3时③当AB＝AP2时④当AP4＝BP4时分别讨论根据等腰三角形的性质求出答案即可【详解】∵在Rt△ABC中∠C＝9解析：72°或18°或108°或36°【分析】分四种情况：①AB ＝BP 1时，②当AB ＝AP 3时，③当AB ＝AP 2时，④当AP 4＝BP 4时，分别讨论，根据等腰三角形的性质求出答案即可．【详解】∵在Rt △ABC 中，∠C ＝90°，∠A ＝36°，∴当AB ＝BP 1时，∠BAP 1＝∠BP 1A ＝36°，当AB ＝AP 3时，∠ABP 3＝∠AP 3B ＝12∠BAC ＝12×36°＝18°， 当AB ＝AP 4时，∠ABP 4＝∠AP 4B ＝12×（180°−36°）＝72°， 当AP 2＝BP 2时，∠BAP 2＝∠ABP 2，∴∠AP 2B ＝180°−36°×2＝108°，∴∠APB 的度数为：18°、36°、72°、108°．故答案为：72°或18°或108°或36°【点睛】此题主要考查了等腰三角形的性质，分类讨论思想的运用是解题关键．13．在平面直角坐标系中，O 为坐标原点，()1,1A ，在x 轴上确定一点P ，使AOP 为等腰三角形，则符合条件的等腰三角形的顶角度数为______．90°45°135°【分析】此题应该分情况讨论以OA 为腰或底分别讨论当A 是顶角顶点时P 是以A 为圆心以OA 为半径的圆与x 轴的交点共有1个当O 是顶角顶点时P 是以O 为圆心以OA 为半径的圆与x 轴的交点共有2解析：90°，45°，135°【分析】此题应该分情况讨论．以OA 为腰或底分别讨论．当A 是顶角顶点时，P 是以A 为圆心，以OA 为半径的圆与x 轴的交点，共有1个，当O 是顶角顶点时，P 是以O 为圆心，以OA 为半径的圆与x 轴的交点，共有2个，若OA 是底边时，P 是OA 的中垂线与x 轴的交点，有1个，进而求出对应等腰三角形的顶角度数，即可．【详解】（1）若AO 作为腰时，有两种情况，①当A 是顶角顶点时，P 是以A 为圆心，以OA 为半径的圆与x 轴的交点，此时，顶角度数为：90°；②当O 是顶角顶点时，P 是以O 为圆心，以OA 为半径的圆与x 轴的交点，此时，顶角度数为：45°或135°；（2）若OA 是底边时，P 是OA 的中垂线与x 轴的交点，此时，顶角度数为：90°． 综上所述，符合条件的等腰三角形的顶角度数为：90°，45°，135°，故答案是：90°，45°，135°．【点睛】此题主要考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论． 14．如图，ABC 中，45ABC ∠=︒，CD AB ⊥于D ，BE 平分ABC ∠，且BE AC ⊥于E 交CD 于点F ，H 是BC 边的中点，连接DH 交BE 于点G ，考察下列结论：①AC BF =；②2BF CE =；③ADGE GHCE S S =四四边形边形；④DGF △为等腰三角形．其中正确的有___．①②④【分析】只要证明△BDF ≌△CDA △BAC 是等腰三角形即可判断①②正确作GM ⊥BD 于M 只要证明GH ＜DG 即可判断③错误证明可判断④正确【详解】解：①又又∴是等腰直角三角形在和中故①正确；②平分解析：①②④【分析】只要证明△BDF ≌△CDA ，△BAC 是等腰三角形，即可判断①②正确，作GM ⊥BD 于M ，只要证明GH ＜DG 即可判断③错误，证明DGF DFG ∠=∠可判断④正确．【详解】解：①CD AB ⊥，90CDA BDF ∠∴∠==︒，18090DBF DFB BDF ︒∠+∠=-∠=︒，又BE AC ⊥，90BEA ∴∠=︒，18090DBF DAC BEA ∠+∠=-∠=∴︒︒，DAC DFB ∠=∠∴，又45ABC ∠=︒，18045DCB ABC BDF ∴∠=︒-∠-∠=︒，∴BCD △是等腰直角三角形，BD CD ∴=，在ACD △和FBD 中，DAC DFB CDA BDF CD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD FBD AAS ∴≅，AC BF ∴=．故①正确；②BE 平分ABC ∠，BE AC ⊥，ABE CBE ∴∠=∠，90BEA BEC ∠=∠=︒，∴在ABE △和CBE △中，ABE CBE BE BEBEA BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ASA ABE CBE ∴≅，AE CE ∴=，2AC AE CE CE ∴=+=，又AC BF =，2BF CE ∴=，故②正确；③如图所示，过G 作GM BD ⊥于点M ，H 为等腰直角BCD △斜边BC 的中点，DH BC ∴⊥，即90GHB ∠=︒，又BE 平分ABC ∠，GM BD ⊥，GM GH ∴=，又BD BH >，BDG BGH SS∴>， 又ABE CBE ≅ ABE CBE S S ∴=，ABE BDG ADGE S S S ∴=-四边形，CBE BGH GHCE S S S =-四边形，ADGE GHCE S S ∴<四边形四边形，故③错误；④18090HBG BGH GHB ∠+∠=︒-∠=︒，18090DBF DFG BDF ∠+∠=︒-∠=︒，HBG DBF ∠=∠，∴∠=∠，BGH DFG∠=∠，又BGH DGF∴∠=∠，DGF DFG∴为等腰三角形．DGF∴综上，答案为①②④．【点睛】此题是三角形综合题，考查了等腰三角形的性质，直角三角形的性质，全等三角形的性质和判定，三角形的面积等知识点的综合运用，第三个问题难度比较大，添加辅助线是解题关键．15．如图所示的网格是正方形网格，点A，B，C，D，O是网格线交点，那么AOB∠___________COD∠（填“＞”，“＜”或“＝”）．>【分析】如图过点B作BE⊥AC于E证明△BOE是等腰直角三角形得到∠BOE=过点C作CF⊥OC使FC=OC证明△OCF是等腰直角三角形得到∠FOC=由图知∠FOC>∠COD即可得到∠AOB>∠CO解析：>【分析】如图，过点B作BE⊥AC于E，证明△BOE是等腰直角三角形，得到∠BOE=45︒，过点C 作CF⊥OC，使FC=OC，证明△OCF是等腰直角三角形，得到∠FOC=45︒，由图知∠FOC>∠COD，即可得到∠AOB>∠COD．【详解】如图，过点B作BE⊥AC于E，∵OB=OE=2，∠BEO=90︒，∴△BOE是等腰直角三角形，∴∠BOE=45︒，过点C作CF⊥OC，使FC=OC，∴∠FCO=90︒，∴△OCF是等腰直角三角形，∴∠FOC=45︒，由图知∠FOC>∠COD，∴∠AOB>∠COD，故答案为：>．．【点睛】此题考查等腰直角三角形的判定及性质,角的大小比较，根据图形确定角的位置关系是解题的关键．16．已知等腰三角形的一边长为5，另一边长为10，则这个等腰三角形的周长为___________．25【分析】分腰长为10和腰长为5两种情况讨论不合题意的舍去据此即可求解【详解】解：当腰长为10时三边分别为10105构成三角形周长为10+10+5=25；当腰长为5时三边分别为5510∵5+5=1解析：25【分析】分腰长为10和腰长为5两种情况讨论，不合题意的舍去，据此即可求解．【详解】解：当腰长为10时，三边分别为10、10、5，构成三角形，周长为10+10+5=25；当腰长为5时，三边分别为5、5、10，∵5+5=10，无法构成三角形，不合题意．故答案为：25【点睛】本题考查了等腰三角形的定义和三角形的三边关系，熟知相关定理是解题关键．17．如图，在22的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的ABC为格点三角形，在图中最多能画出______个不同的格点三角形与ABC成轴对称．5【分析】画出所有与成轴对称的三角形【详解】解：如图所示：和对称和对称和对称和对称和对称故答案是：5【点睛】本题考查轴对称图形解题的关键是掌握画轴对称图形的方法解析：5【分析】画出所有与ABC成轴对称的三角形．【详解】解：如图所示：ABC和ADC对称，ABC和EBD△对称，ABC和DEF对称，ABC和DCB对称，ABC和CDA对称，故答案是：5．【点睛】本题考查轴对称图形，解题的关键是掌握画轴对称图形的方法．18．如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝20°，且AE＝AD，则∠CDE的度数是______．10°【分析】设∠B＝∠C＝x∠CDE＝y分别表示出∠DAE构建方程解方程即可求解【详解】解：设∠B＝∠C＝x∠EDC＝y∵AD＝AE∴∠ADE ＝∠AED＝x＋y∵∠DAE＝180°−2（x＋y）＝解析：10°【分析】设∠B＝∠C＝x，∠CDE＝y，分别表示出∠DAE，构建方程解方程即可求解．【详解】解：设∠B＝∠C＝x，∠EDC＝y，∵AD＝AE，∴∠ADE＝∠AED＝x＋y，∵∠DAE＝180 °−2（x＋y）＝180 °−20 °−2x，∴2y＝20 °，∴y＝10 °，∴∠CDE＝10 °．故答案为：10°【点睛】本题主要考查等腰三角形的判定与性质，还涉及三角形内角和等知识点，需要熟练掌握等腰三角形的判定与性质．⨯的正方形网格，每个小正方形的顶点称为格点，且边长为1，点,A B均在19．右图是44⨯的正方形网格的格点上，且格点上，在网格中建立平面直角坐标系．如果点C也在此44ABC ∆是等腰三角形，请写出一个满足条件的点C 的坐标_______；满足条件的点C 一共有_______个．（答案不唯一符合题意即可）8【分析】分别以AB 为圆心AB 为半径作圆弧寻找在圆弧上的格点即可【详解】①如图以A 为圆心AB 为半径作圆弧符合题意的格点有5个；②如图以B 为圆心AB 为半径作圆弧符合题意的格点解析：()2,2--（答案不唯一，符合题意即可） 8【分析】分别以A ，B 为圆心，AB 为半径作圆弧，寻找在圆弧上的格点即可．【详解】①如图，以A 为圆心，AB 为半径作圆弧，符合题意的格点有5个；②如图，以B 为圆心，AB 为半径作圆弧，符合题意的格点有3个；③如图，在AB 的垂直平分线上时，无符合题意的格点；综上，符合题意的格点共有8个，故答案为：()2,2--（答案不唯一，符合题意即可）；8．【点睛】本题考查在网格中作等腰三角形，根据已知边可作为底边或者腰进行分类讨论，熟练掌握尺规作图方法是解题关键．20．如图，网格纸上每个小正方形的边长为1，点A ，点C 均在格点上，点P 为x 轴上任意一点，则PAC △周长的最小值为________．【分析】根据勾股定理可得AC 的长度作点C 关于x轴的对称点C′连接AC′与x 轴交于点P 利用勾股定理求出AP+PC 的最小值从而得出答案【详解】AC=如图作点C 关于x 轴的对称点C′连接AC′与x 轴交于点P 解析：21022【分析】根据勾股定理可得AC 的长度，作点C 关于x 轴的对称点C′，连接AC′，与x 轴交于点P ，利用勾股定理求出AP+PC 的最小值，从而得出答案．【详解】 22222+=如图，作点C 关于x 轴的对称点C′，连接AC′，与x 轴交于点P ，则AP+PC=AP+PC′=AC′，此时AP+PC取得最小值，最小值为22+=，26210+，所以△PAC周长的最小值为21022+．故答案为：21022【点睛】本题主要考查了轴对称－最短路线问题，解题的关键是掌握轴对称变换的性质．三、解答题21．如图1，在直角△ABC中，∠C=90°，分别作∠CAB的平分线AP和AB的垂直平分线DP，交点为P．（1）如图2，若点P正好落在BC边上．①求∠B的度数；②求证：BC=3PC．（2）如图3，若点C、P、D恰好在一条直线上，线段AD、PD、BC之间的数量关系是否满足AD+PD=BC？若满足，请给出证明；若不满足，请说明理由．解析：（1）①∠B的度数是30°；②见解析；（2）满足，理由见解析【分析】（1）①由垂直平分线与角平分线的性质证明：∠PAD=∠PAC=∠B，再利用直角三角形的内角和定理即可得到答案；②先利用角平分线的性质证明PC=PD，再用∠B=30°证明BP=2PD，进而即可得到结论；（2）过点P作PE⊥AC于点E，由垂直平分线的性质可知AC=BC，∠ACD=∠BCD=45°，进而证明PE=CE，由角平分线的性质可知PE=PD，即可证明Rt△AEP≌Rt△ADP（HL），可得AE=AD，再利用线段的和差性质即可证明AD+PD=BC．【详解】（1）①∵DP是AB的垂直平分线，∴PA=PB ，∴∠PAD=∠B ，又∵AP 平分∠CAB ，∴∠PAD=∠PAC ，∴∠PAD=∠PAC=∠B ，设∠B=x°，则∠CAB=∠PAD+∠PAC=2x°，∵在Rt ABC 中，∠C=90°，∴∠B+∠BAC=90°，即3x=90，x=30，∴∠B 的度数是30°．②∵AP 平分∠CAB ，∠C=90°，DP ⊥AB ，∴PC=PD ，∵在Rt △BDP 中，∠B=30°，∴BP=2PD ，∴BC=BP+PC=3PC ．（2）如图，过点P 作PE ⊥AC 于点E ，∵CD 是AB 的垂直平分线，∴AC=BC ，∴∠ACD=∠BCD=12∠ACB=45°． ∵PE ⊥AC ，∴∠CPE=90°−∠PCE=90°−45°=45°=∠PCE ，∴PE=CE ，又∵AP 平分∠CAB ，PD ⊥AB ，PE ⊥AC ，∴PE=PD ，∴在Rt △AEP 和Rt △ADP 中， ,,AP AP PE PD =⎧⎨=⎩∴Rt △AEP ≌Rt △ADP （HL ），∴AE=AD ，∴AC=AE+EC=AD+PE=AD+PD ，又∵AC=BC ，∴AD+PD=BC ．【点睛】本题考查了角平分线的性质、垂直平分线的性质、三角形的内角和定理、锐角三角函数、等腰直角三角形的性质、直角三角形全等的判定与性质、含30°的直角三角形的性质、线段的和差性质，解答本题的关键是掌握并熟练运用以上知识．22．如图，△ABC 的三个顶点在边长为1的正方形网格中，已知A （−4，5），B （﹣3，1），C （−2，3）．（1）画出△ABC 及关于y 轴对称的△A 1B 1C 1，其中点B 1的坐标是________；（2）若点M 是x 轴上的动点，在图中画出使△B 1CM 周长最小时的点M ．解析：（1）图形见解析；B 1（3，2）；（2）见解析【分析】（1）分别找到A 、B 、C 点关于y 轴的对称点，然后连接即可；（2）找C 关于x 轴的对称点C′，连接1B C '交x 轴于一点M ，根据两点之间线段最短，可知此时的M 即为使1B CM △周长最小时的点M ．【详解】解：（1）111A B C △如图所示；根据图形可知B 1(3，2)，故答案为：(3，2)；（2）如图所示：找C 关于x 轴的对称点C′，则C′(-2，-3)，CM C M '=，连接1B C '交x 轴于一点M ，根据两点之间线段最短，可知此时的M 即为使1B CM △周长最小时的点M ．【点睛】本题考查作图-轴对称、最短路径问题，解题的关键是熟练掌握基础知识．23．如图，△ABC是等边三角形，E、F分别是边AB、AC上的点，且AE＝CF，且CE、BF 交于点P，且EG⊥BF，垂足为G．（1）求证：∠ACE＝∠CBF；（2）若PG＝1，求EP的长度．解析：（1）见解析；（2）PE＝2【分析】（1）证明△ACE≌△CBF（SAS），即可得到∠ACE＝∠CBF；（2）利用由（1）知∠ACE＝∠CBF，求出∠BPE＝60°，又EG⊥BF，即∠PGE＝90°，得到∠GEP＝30°，根据在直角三角形中，30°所对的直角边等于斜边的一半，可求出EP 的长．【详解】（1）证明：∵△ABC是等边三角形，∴AC＝BC，∠A＝∠BCF＝60°，AB＝AC，在△ACE与△BCF中，AC＝BC，∠A＝∠BCF，AE＝CF，∴△ACE≌△CBF（SAS），∴∠ACE＝∠CBF；（2）解：∵由（1）知，∠ACE＝∠CBF，又∠ACE＋∠PCB＝∠ACB＝60°，∴∠PBC＋∠PCB＝60°，∴∠BPE＝60°，∵EG⊥BF，即∠PGE＝90°，∴∠GEP ＝30°，∴在Rt △PGE 中，PE ＝2PG ，∵PG ＝1，∴PE ＝2．【点睛】本题考查了全等三角形的性质定理与判定定理、等边三角形的性质，含30度的直角三角形的性质，解决本题的关键是证明△ACE ≌△CBF ．24．已知：如图，MON ∠为锐角，点A 在射线OM 上．求作：射线AC ，使得//AC ON ．小静的作图思路如下：①以点A 为圆心，AO 为半径作弧，交射线ON 于点B ，连接AB ；②作MAB ∠的角平分线AC ．射线AC 即为所求的射线．（1）使用直尺和圆规，按照小静的作图思路补全图形（保留作图痕迹）；（2）完成下面的证明．证明：OA AB =，O ABO ∴∠=∠（__________）．MAB ∠是AOB 的一个外角，MAB ∴∠=∠_________+∠__________．12ABO MAB ∴∠=∠． AC 平分MAB ∠，12BAC MAB ∴∠=∠． ABO BAC ∴∠=∠．//AC ON ∴（__________）．解析：（1）见解析；（2）等边对等角；O ；ABO ；内错角相等，两直线平行【分析】（1）按照步骤作图即可；（2）由作法知，OA=AB ，AC 是∠MAB 的平分线，然后根据等腰三角形的性质，三角形外角的性质，以及角平分线的定义说明即可．【详解】解：（1）作图如下：（2）证明：OA AB =，O ABO ∴∠=∠（等边对等角）．MAB ∠是AOB 的一个外角，MAB O ABO ∴∠=∠+∠12ABO MAB ∴∠=∠． AC 平分MAB ∠，12BAC MAB ∴∠=∠. ABO BAC ∴∠=∠.//AC ON ∴（内错角相等，两直线平行）．故答案为：等边对等角；O ；ABO ；内错角相等，两直线平行．【点睛】本题考查了作一条线段等于已知线段，作角的角平分线，以及等腰三角形的性质，三角形外角的性质，以及角平分线的定义等知识，熟练掌握各知识点是解答本题的关键． 25．如图，在平面直角坐标系中，ABC 三个顶点坐标分别为()3,3A ，()1,1B ，()4,1C -．（1）画出ABC ，并求出ABC 的面积；（2）在图中作出ABC 关于y 轴对称的图形111A B C △，并写出2B 、1C 两点的坐标．解析：（1）画图见解析；5 （2）画图见解析；()11,1B -，()14,1C --【分析】（1）先根据A 、B 、C 三点坐标描点，再顺次连接即可得到ABC ，再运用割补法即可求出ABC 的面积；（2）分别作出A 、B 、C 三点关于y 轴的对称点，再顺次连接即可，根据作图即可写出2B 、1C 两点的坐标．【详解】解：（1）ABC 如图所示： 111341422235222ABC S =⨯-⨯⨯-⨯⨯-⨯⨯=△；（2）111A B C △如图所示：()11,1B -，()14,1C --．【点睛】本题主要考查作图-轴对称变换，解题的关键是掌握轴对称变换的定义和性质． 26．在平面直角坐标系中，点(0,)A a ，点(,0)B b ，点(3,0)C -，且a 、b 满足269||0a a a b -++-=．（1）点A 坐标为______，点B 坐标为______，ABC 是______三角形．（2）如图，过点A 作射线l （射线l 与边BC 有交点），过点B 作BD l ⊥于点D ，过点C 作CE l ⊥于点E ，过点E 作EF DC ⊥于点F 交y 轴于点G ．①求证：BD AE =；②求点G 的坐标．（3）如图，点P 是x 轴正半轴上一动点，APO ∠的角平分线交y 轴于点Q ，点M 为线段OP 上一点，过点M 作//MN PQ 交y 轴于点N ；若45AMN ∠=︒，请探究线段AP 、AN 、PM 三者之间的数量关系，并证明你的结论．解析：（1）(0,3)A ，(3,0)B ，等腰直角；（2）①见解析；②点 (0,3)G -；（3）AP AN PM =+，证明见解析．【分析】（1）根据偶次方与绝对值的非负性，解得a b 、的值，即可解得点A 、B 的坐标，继而根据等腰直角三角形的判定方法解题；（2）①由等角的余角相等，解得BAD ACE =∠∠，结合（1）中结论，进而证明AEC BDA ≌△△(AAS)，即可解题；②由AEC BDA ≌△△可证CAE ABD ∠=∠，继而得到GAE CBD ∠=∠，设CF 交y 轴于点H ，根据等角的余角相等，得到HGE OCH ∠=∠，继而证明AGE BCD ≌△△(AAS)解得AG 、OG 的长即可解题；（3）在AP 上截取AH AN =，连接MH ，设NMO α∠=，分别解得45AMO α∠=︒+，=45NAM α∠︒-，由角平分线的性质解得2APO α∠=，45HAM α∠=︒-，进而得到NAM HAM ∠=∠，即可证明AMN AMH ≌(SAS)，继而证明PMH PHM ∠=∠，PH PM =即可解题．【详解】（1）269||0a a a b -++-=2(3)||0a a b ∴-+-=3,3a b a ∴===(0,3)A ∴，(3,0)B ，(3,0)C -,AO OB CO AO ∴==90AOB AOC ∠=∠=︒45ACO ABO ∴∠=∠=︒90CAB ∴∠=︒()AOC AOB SAS ∴≅AC AB ∴=ABC ∴为等腰直角三角形，故答案为：(0,3)A ，(3,0)B ，等腰直角； （2）①BD l ⊥，CE l ⊥90BDA AEC ∴∠=∠=︒90,90BAD CAE CAE ACE ∠+∠=︒∠+∠=︒ BAD ACE ∴∠=∠AC AB =AEC BDA ∴≌(AAS)，∴BD AE =．②AEC BDA ≌ CAE ABD ∴∠=∠45CAO ABO ∠=∠=︒GAE CBD ∴∠=∠，设CF 交y 轴于点HEF DC ⊥90CFG ∴∠=︒90FGH FHG ∴∠+∠=︒90COH ∠=︒90OCH CHO ∴∠+∠=︒∴ CHO FHG ∠=∠HGE OCH ∴∠=∠又∵AE BD =∴AGE BCD ≌△△(AAS) ∴6AG BC ==又∵3AO =，∴3OG =∴点(0,3)G -．（3）AP AN PM =+．证明过程如下： 在AP 上截取AH AN =，连接MH ，设NMO α∠=，45AMN ∠=︒45AMO α∴∠=︒+，∴()904545NAM αα∠=︒-︒+=︒-， 又∵//MN PQ∴QPO NMO α∠=∠=，∵PQ 平分APO ∠∴2APO α∠=∴45245HAM ααα∠=︒+-=︒- ∴NAM HAM ∠=∠又∵AN AH =，AM AM =∴AMN AMH ≌(SAS)∴45AMH AMN ∠=∠=︒ ∴90PMH α∠=︒-， 又∵()454590PHM αα∠=︒+︒-=︒- ∴PMH PHM ∠=∠∴PH PM =∴AP AH PH AN PM =+=+．【点睛】本题考查全等三角形的判定与性质、等腰直角三角形、角平分线的性质、平行线的性质、绝对值的非负性、偶次方的非负性等知识，是重要考点，难度一般，掌握相关知识是解题关键．27．已知：(0,1),(2,0),(4,4)A B C -．（1）在图中所示的坐标系中描出各点，画出ABC ，并求ABC 的面积．（2）若ABC 各顶点的横坐标不变，纵坐标都乘以1-，在同一坐标系中描出对应的点A '，B '，C '，并依次连结这三个点得A B C '''，并写出ABC 与A B C '''有怎样的位置关系？解析：（1）图见解析，3；（2）ABC 与A B C '''关于x 轴对称【分析】（1）根据点坐标确定其在坐标系中的位置，顺次连线即可得到ABC ，利用割补法求面积；（2）根据点A 、B 、C 纵坐标都乘以1-，得到对应的点A '，B '，C '的坐标，再确定各点位置，即可得到两个三角形的关系．【详解】（1）如图，ABC 即为所求，111451245(15)23222ABC S =⨯-⨯⨯-⨯⨯-⨯+⨯=；（2）∵(0,1),(2,0),(4,4)A B C -，∴A '（0，-1），B '（2,0），C '（4,4），∴ABC 与A B C '''关于x 轴对称．．【点睛】此题考查点坐标的确定，坐标与图形，图形的变换关系，正确根据点的坐标确定其在直角坐标系中的位置是解题的关键．28．如图，在ABC 中，45B ︒∠=，60C ︒∠=，点E 为线段AB 的中点，点F 在边AC 上，连结EF ，沿EF 将AEF 折叠得到PEF ．（1）如图1，当点P 落在BC 上时，求AEP ∠的度数．（2）如图2，当PF AC ⊥时，求BEP ∠的度数．解析：（1）90°；（2）60°【分析】（1）证明BE=EP ，可得∠EPB=∠B=45°解决问题．（2）根据折叠的性质求出∠AFE=45°，根据三角形内角和求出∠BAC ，从而得到∠AEF 和∠PEF ，再根据平角的定义求出∠BEP ．【详解】解：（1）如图1中，∵折叠，∴△AEF ≌△PEF ，∴AE=EP ，∵点E 是AB 中点，即AE=EB ，∴BE=EP ，∴∠EPB=∠B=45°，∴∠PEB=90°，∴∠AEP=180°-90°=90°．（2）∵PF⊥AC，∴∠PFA=90°，∵沿EF将△AEF折叠得到△PEF．∴△AEF≌△PEF，∴∠AFE=∠PFE=45°，∵∠B=45°，∠C=60°，∴∠BAC=180°-45°-60°=75°，∴∠AEF=∠PEF=180°-75°-45°=60°，∴∠BEP=180°-60°-60°=60°．【点睛】本题考查了折叠的性质，三角形内角和，全等三角形的性质，解题的关键是根据折叠的性质得到相等的线段和角．。

北京市第四中学2020-2021学年八年级上学期数学期中试卷一、单选题（共10题；共20分）1.下列轴对称图形中，有4条对称轴的图形是（）A. B. C. D.2.下列运算正确的是（）A. B. C. D.3.下列变形属于因式分解的是（）A. B.C. D.4.在平面直角坐标系上，已知点A关于直线x＝1对称的点为B（﹣2，4），则点A的坐标为（）A. （4，4）B. （﹣2，﹣2）C. （2，4）D. （3，4）5.电子文件的大小常用等作为单位，其中，某视频文件的大小约为等于（）A. B. C. D.6.已知，则a2+4b2的值是（）A. 110B. 120C. 125D. 1307.图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是( )A. B. C. D.8.如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（）A. SSSB. SASC. AASD. ASA9.我们利用尺规作图可以作一个角等于已知角，如下所示：（1）作射线；（2）以为圆心，任意长为半径作弧，交于，交于；（3）以为圆心，为半径作弧，交于；（4）以为圆心，为半径作弧，交前面的弧于；（5）连接作射线则就是所求作的角．以上作法中，错误的一步是（）A.（2）B.（3）C.（4）D.（5）10.△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）A. △ABC的周长B. △AFH的周长C. 四边形FBGH的周长D. 四边形ADEC的周长二、填空题（共10题；共13分）11.分解因式：________．12.在正方形网格中，的位置如图所示，则点中在的平分线上是________点．13.若3x+2y﹣2=0，则等于________．14.如图,在△ABC中,点D在BC上,将点D分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.根据图中标示的角度,则∠EAF=________°.15.已知关于的代数式，设代数式的值为，则．下表中列出了当分别取…，…，…时对应的值．··· -1 0 1 2 3 4 5 ········· 10 5 2 1 2 5 ······（1）表中n的值为________；（2）当________时，有最小值，最小值是________；（3）________ ．（填）16.已知等腰三角形一个外角的度数为108°，则顶角度数为________.17.已知锐角如图⑴在射线上取一点，以点为圆心，长为半径作弧，交射线于点，连接；⑵分别以点为圆心，长为半径作弧，两弧交于点连接；⑶作射线交于点．根据以上作图过程及所作图形，下列结论中正确的是________；；；；18.如图，已知每个小方格的边长为两点都在小方格的顶点上（即为格点），请在图中找一个格点，使为等腰三角形，则这样的格点有________个．19.若为正奇数，则________ (底数中含k个k)；若为正偶数，则________ (底数中含k个k)；20.用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD．则正方形ABCD的面积为________（用含a，b的代数式表示）．三、解答题（共9题；共85分）21.分解因式：（1）；（2）．22.计算：（1）（2）；（3）；（4）．23.先化简，再求值：，其中24.如图，，和相交于点，．求证：．25.小宇遇到了这样一个问题：已知：如图，，点A，B分别在射线OM，ON上，且满足．求作：线段OB上的一点C，使的周长等于线段的长．以下是小宇分析和求解的过程，请补充完整：首先画草图进行分析，如图1所示，若符合题意得点C已经找到，即得周长等于OB的长，那么由，可以得到________．对于这个式子，可以考虑用截长得办法，在BC上取一点D，使得，那么就可以得到________．若连接AD，由________．（填推理依据）．可知点C在线段AD得垂直平分线上，于是问题得解法就找到了．请根据小宇得分析，在图2中完成作图（尺规作图，不写做法，保留作图痕迹）．________26.阅读材料小明遇到这样一个问题：求计算所得多项式的一次项系数.小明想通过计算所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法.他决定从简单情况开始，先找所得多项式中的一次项系数，通过观察发现：也就是说，只需用中的一次项系数1乘以中的常数项3，再用中的常数项2乘以中的一次项系数2，两个积相加，即可得到一次项系数.延续上面的方法，求计算所得多项式的一次项系数，可以先用的一次项系数1，的常数项3，的常数项4，相乘得到12；再用的一次项系数2，的常数项2，的常数项4，相乘得到16；然后用的一次项系数3，的常数项2的常数项3，相乘得到18.最后将12，16，18相加，得到的一次项系数为46.参考小明思考问题的方法，解决下列问题：（1）计算所得多项式的一次项系数为________.（2）计算所得多项式的一次项系数为________.（3）若是的一个因式，求、的值.27.如图1，点是等腰三角形外一点，过点作于点．（1）依据题意，补全图形．（2）求证：．（3）如图2，与交于点，当是的中点时，翻折得到，连接求证：两点到直线的距离相等．28.小明同学研究如下问题：从，…，为整数，且）这个整数中任取个整数，这个整数之和共有多少种不同的结果？他采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找出解决问题的方法．他进行了如下几个探究：（1）探究一：从这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？所取的2个整数 1,2 1,3 2,32个整数之和 3 4 5如上表，所取的2个整数之和可以为，也就是从3到5的连续整数，其中最小是3最大是5所以共有3种不同的结果．（2）从这4个整数中任取2个整数，这2个整数之和共有多少种不同的结果？所取的2个整数 1,2 1,3 1,4 2,3 2,4 3,42个整数之和 3 4 5 5 6 4如上表，所取的2个整数之和可以为，也就是从3到7的连续整数，其中最小是3，最大是7，所以共有5种不同的结果．（3）从这个整数中任取个整数，这个整数之和共有_________种不同的结果．（4）从，…，为整数，且）这个整数中任取个整数，这个整数之和共有__________种不同的结果．（5）探究二：从这个整数中任取个整数，这个整数之和共有________种不同的结果．（6）从，…，为整数，且）这个整数中任取个整数，这个整数之和共有________种不同的结果．（7）探究三：从，…，为整数，且这个整数中任取个整数，这个整数之和共有________种不同的结果．归纳结论：从，…，为整数，且这个整数中任取个整数，这个整数之和共有________种不同的结果．拓展延伸：从，…，这个整数中任取________个整数，使得取出的这些整数之和共有种不同的结果？（写出解答过程）29.如图，中，，将线段绕点逆时针旋转得到点，点与点关于直线对称，连接．（1）依题意补全图形；（2）判断的形状，并证明；（3）请问在直线上是否存在点，使得成立？若存在，请用文字描述出点的准确位置，并画图证明：若不存在，请说明理由．答案解析部分一、单选题1.【答案】D2.【答案】B3.【答案】D4.【答案】A5.【答案】A6.【答案】B7.【答案】C8.【答案】D9.【答案】（1）C10.【答案】A二、填空题11.【答案】3m（a2-b）12.【答案】Q13.【答案】414.【答案】13415.【答案】（1）10（2）2；1（3）＜16.【答案】72°或36°17.【答案】②③④18.【答案】819.【答案】；20.【答案】三、解答题21.【答案】（1）解：4x2-9，=（2x）2-32，=（2x+3）（2x-3）；（2）解：，=-b（4a2-4ab+b2），=-b（2a-b）2．22.【答案】（1）解：（x-3y）（-6x）=-6x2+18xy；（2）解：（6x4-8x2y）÷2x2=3x2-4y；（3）解：（x-1）（x+2）=x2+2x-x-2=x2+x-2；（4）解：（x+y-3）（x-y+3）=[x+（y-3）][x-（y-3）]=x2-（y-3）2=x2-y2+6y-9．23.【答案】解：原式=a2-b2+a2-2ab+b2-2a2+3ab=ab，当a= ，b=1时，原式= ．24.【答案】解：，，，在和中，，，25.【答案】BC；DC；线段的垂直平分线的判定；26.【答案】（1）19（2）1（3）解：由x4+ax2+bx+2中4次项系数为1、常数项为2可设另一个因式为x2+mx+2，则（x2-3x+1）（x2+mx+2）=x4+ax2+bx+2，解得：27.【答案】（1）解：如图3所示即为所求：（2）证明：如图4，过点A作AH⊥CD，交DC的延长线于H，∵AE⊥BD，AH⊥DH，∴∠AED＝∠H＝90°．∴∠EDH＋∠EAH＝180°．∵AB＝AC，∴∠ABC＝∠ACB．∵∠BAC＋∠ABC＋∠ACB＝180°，∴∠BAC＋2∠ABC＝180°．又∵∠BDC＝2∠ABC，∴∠BDC＋∠BAC＝180°．∴∠BAC＝∠EAH．∴∠BAC-∠CAE＝∠EAH-∠CAE．即∠BAE＝∠CAH．在△ABE和△ACH中，∠AEB＝∠H，∠BAE＝∠CAH，AB＝AC，∴△ABE≌△ACH（AAS）．∴AE＝AH，BE＝CH．在Rt△AED和Rt△AHD中，AE＝AH，AD＝AD，∴Rt△AED≌Rt△AHD（HL）．∴DE＝DH．∴DE＝BE＋CD；（3）证明：如图5，过点A作AG⊥BC于点G，连接GD交BC的延长线于点N，∵翻折△BCD得到△BCG，∴BN⊥GD，GN＝DN，∵F是AD的中点，∴AF＝DF，在△AGF和△DNF中，∠AFG＝∠DFN，∠AGF＝∠DNF，AF＝DF，∴△AGF≌△DNF（AAS）．∴AG＝DN．∴AG＝GN．∴A，G两点到直线BC的距离相等．28.【答案】（1）解：根据探究一：从1，2，3这3个整数中任取2个整数，这2个整数之和共有3种不同的结果；（2）解：从1，2，3，4这4个整数中任取2个整数，这2个整数之和共有5种不同的结果；（3）7（4）（2n-3）（5）4（6）（3n-8）（7）（4n-15）；（an-a2+1）；7或2929.【答案】（1）解：补全图形如图1：（2）解：△CDE为等边三角形，理由如下：连接BD，设BC与DE交于F，如图2：∵AB=AC，∴∠ABC=∠ACB，∵线段AB绕点A逆时针旋转60°得到点D，∴AD=AB=AC，∠BAD=60°，∴△ABD是等边三角形，∠ACD=∠ADC，∴∠ABD=∠ADB=60°，∴∠ABC+∠DBC=60°，∴∠ACB+∠DBC=60°，在△BCD中，∠DBC+∠BDC+∠DCB=180°，∴∠DBC+∠ADB+∠ADC+∠DCB=180°，∴∠DBC+∠ADB+∠ACD+∠DCB=180°，∴∠DBC+∠ADB+∠ACB+∠DCB+∠DCB=180°，即60°+60°+2∠DCB=180°，∴∠DCB=30°，∵点E与点D关于直线BC对称，∴∠ECF=∠DCB=30°，CD=CE，∴∠DCE=60°．∴△CDE是等边三角形；（3）解：存在，作AG⊥BC于G，直线CE与AG的交点即为点P，理由如下：延长AG、CD交于点Q，连接QB，BD，由（2）可知，∠PCQ=60°，点P与Q关于BC对称，∴PC=QC，∴△PCQ为等边三角形，∴∠QPC=60°，∴∠APC=120°，∵AG⊥BC，AC=AB，∴AG垂直平分BC，PG=QG，∴PB=PC=QB=QC，∴四边形PBQC是菱形，∴CP=BQ=CQ=PB，∠PBQ=∠PCQ=60°，∠DQB=120°=∠APC，∵QB=QC，∴∠QBC=∠QCB，∴∠ABQ=∠ACQ，由（2）得：△ABD为等边三角形，∴∠ABD=60°=∠PCQ，∴∠ABQ-∠ABD=∠ACQ-∠PCQ，∴∠DBQ=∠ACP，在△ACP和△DBQ中，，∴△ACP≌△DBQ（ASA），∴AP=DQ，∵PB=CQ，CQ-DQ=CD，∴PB-AP=CD即PB-PA=CD成立．。

北京四中重点中学2024年中考数学全真模拟试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．下面的图形中，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ．2．下列图形中，不是中心对称图形的是（ ）A ．平行四边形B ．圆C ．等边三角形D ．正六边形3．3-的倒数是（ ）A ．13-B ．3C ．13D ．13± 4．已知A(x 1，y 1)，B(x 2，y 2)是反比例函数y ＝(k≠0)图象上的两个点，当x 1＜x 2＜0时，y 1＞y 2，那么一次函数y ＝kx －k 的图象不经过( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．如图，已知BD 是ABC △的角平分线，ED 是BC 的垂直平分线，90BAC ∠=︒，3AD =，则CE 的长为（ ）A ．6B ．5C ．4D ．336．如图所示的几何体，它的左视图是（ ）A ．B ．C ．D ．7．小红上学要经过两个十字路口，每个路口遇到红、绿灯的机会都相同，小红希望上学时经过每个路口都是绿灯，但实际这样的机会是（ ）A ．12B ．13C ．14D ．348．一个不透明的布袋里装有5个红球，2个白球，3个黄球，它们除颜色外其余都相同，从袋中任意摸出1个球，是黄球的概率为（ ）A ．310B ．15C ．12D ．7109．若点A （2，1y ），B （-3，2y ），C （-1，3y ）三点在抛物线24y x x m =--的图象上，则1y 、2y 、3y 的大小关系是（ ）A ．123y y y ＞＞B ．213y y y ＞＞C ．231y y y ＞＞D ．312y y y ＞＞10．如图是二次函数2y ax bx c =++的图象，有下面四个结论：0abc >①；0a b c ②-+>；230a b +>③；40c b ->④，其中正确的结论是( )A ．①②B ．①②③C ． ①③④D ． ①②④二、填空题（共7小题，每小题3分，满分21分）11．八位女生的体重（单位：kg ）分别为36、42、38、40、42、35、45、38，则这八位女生的体重的中位数为_____kg ．12．因式分解：3a 2-6a+3=________．13．如图，在一次数学活动课上，小明用18个棱长为1的正方体积木搭成一个几何体，然后他请小亮用其他棱长为1小明所搭几何体的形状）．请从下面的A 、B 两题中任选一题作答，我选择__________．A 、按照小明的要求搭几何体，小亮至少需要__________个正方体积木．B 、按照小明的要求，小亮所搭几何体的表面积最小为__________．14．某种商品因换季准备打折出售，如果按定价的七五折出售将赔25元，而按定价的九折出售将赚20元，则商品的定价是______元.15．如图，在平面直角坐标系中，抛物线212y x =可通过平移变换向__________得到抛物线2122y x x =-，其对称轴与两段抛物线所围成的阴影部分（如图所示）的面积是__________．16．小刚家、公交车站、学校在一条笔直的公路旁（小刚家、学校到这条公路的距离忽略不计）．一天，小刚从家出发去上学，沿这条公路步行到公交站恰好乘上一辆公交车，公交车沿这条公路匀速行驶，小刚下车时发现还有4分钟上课，于是他沿着这条公路跑步赶到学校（上、下车时间忽略不计），小刚与学校的距离s （单位：米）与他所用的时间t （单位：分钟）之间的函数关系如图所示．已知小刚从家出发7分钟时与家的距离是1200米，从上公交车到他到达学校共用10分钟．下列说法：①公交车的速度为400米/分钟；②小刚从家出发5分钟时乘上公交车；③小刚下公交车后跑向学校的速度是100米/分钟；④小刚上课迟到了1分钟．其中正确的序号是_____．17．如图，点A 的坐标为（3，7），点B 的坐标为（6，0），将△AOB 绕点B 按顺时针方向旋转一定的角度后得到△A′O′B ，点A 的对应点A′在x 轴上，则点O′的坐标为_____．三、解答题（共7小题，满分69分）18．（10分）某数学社团成员想利用所学的知识测量某广告牌的宽度（图中线段MN 的长），直线MN 垂直于地面，垂足为点P ．在地面A 处测得点M 的仰角为58°、点N 的仰角为45°，在B 处测得点M 的仰角为31°，AB ＝5米，且A 、B 、P 三点在一直线上．请根据以上数据求广告牌的宽MN 的长．（参考数据：sin58°＝0.85，cos58°＝0.53，tan58°＝1.1，sin31°＝0.52，cos31°＝0.86，tan31°＝0.1．）19．（5分）计算：（-13）-2 – 234）+ 112 20．（8分）如图，抛物线21y x bx 2c =-++与x 轴交于A ，B ，与y 轴交于点C （0，2），直线1x 22y =-+经过点A ，C .（1）求抛物线的解析式；（2）点P 为直线AC 上方抛物线上一动点；①连接PO ，交AC 于点E ，求PE EO的最大值； ②过点P 作PF ⊥AC ，垂足为点F ，连接PC ，是否存在点P ，使△PFC 中的一个角等于∠CAB 的2倍？若存在，请直接写出点P 的坐标；若不存在，请说明理由.21．（10分） (1)解方程组31021x y x y +=⎧⎨-=⎩(2)若点A 是平面直角坐标系中坐标轴上的点，( 1 )中的解 , x y 分别为点B 的横、纵坐标,求AB 的最小值及AB 取得最小值时点A 的坐标.22．（10分）如图，菱形ABCD 中，,E F 分别是,BC CD 边的中点．求证：AE AF =.23．（12分）先化简再求值：2()(2)x y y y x -++，其中2x =3y =24．（14分）学了统计知识后，小红就本班同学上学“喜欢的出行方式”进行了一次调查，图（1）和图（2）是她根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：（1）补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数．（2）若由3名“喜欢乘车”的学生，1名“喜欢骑车”的学生组队参加一项活动，现欲从中选出2人担任组长（不分正副），求出2人都是“喜欢乘车”的学生的概率，（要求列表或画树状图）参考答案一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1、B【解题分析】试题解析：A. 是轴对称图形但不是中心对称图形B.既是轴对称图形又是中心对称图形；C.是中心对称图形，但不是轴对称图形；D.是轴对称图形不是中心对称图形；故选B.2、C【解题分析】根据中心对称图形的定义依次判断各项即可解答.【题目详解】选项A、平行四边形是中心对称图形；选项B、圆是中心对称图形；选项C、等边三角形不是中心对称图形；选项D、正六边形是中心对称图形；故选C．【题目点拨】本题考查了中心对称图形的判定，熟知中心对称图形的定义是解决问题的关键.3、A解：3-的倒数是13-． 故选A ．【题目点拨】本题考查倒数，掌握概念正确计算是解题关键．4、B【解题分析】试题分析：当x 1＜x 2＜0时，y 1＞y 2，可判定k ＞0，所以﹣k ＜0，即可判定一次函数y=kx ﹣k 的图象经过第一、三、四象限，所以不经过第二象限，故答案选B ．考点：反比例函数图象上点的坐标特征；一次函数图象与系数的关系．5、D【解题分析】根据ED 是BC 的垂直平分线、BD 是角平分线以及∠A=90°可求得∠C=∠DBC=∠ABD=30°，从而可得CD=BD=2AD=6，然后利用三角函数的知识进行解答即可得.【题目详解】∵ED 是BC 的垂直平分线，∴DB=DC ，∴∠C=∠DBC ，∵BD 是△ABC 的角平分线，∴∠ABD=∠DBC ，∵∠A=90°，∴∠C+∠ABD+∠DBC=90°，∴∠C=∠DBC=∠ABD=30°，∴BD=2AD=6，∴CD=6，∴故选D ．【题目点拨】本题考查了线段垂直平分线的性质，三角形内角和定理，含30度角的直角三角形的性质，余弦等，结合图形熟练应用相关的性质及定理是解题的关键.6、D分析：根据从左边看得到的图形是左视图，可得答案．详解：从左边看是等长的上下两个矩形，上边的矩形小，下边的矩形大，两矩形的公共边是虚线，故选D ．点睛：本题考查了简单组合体的三视图，从左边看得到的图形是左视图．7、C【解题分析】列举出所有情况，看每个路口都是绿灯的情况数占总情况数的多少即可得.【题目详解】画树状图如下，共4种情况，有1种情况每个路口都是绿灯，所以概率为14． 故选C ．8、A【解题分析】让黄球的个数除以球的总个数即为所求的概率． 【题目详解】解：因为一共10个球，其中3个黄球，所以从袋中任意摸出1个球是黄球的概率是310． 故选：A ．【题目点拨】本题考查概率的基本计算，用到的知识点为：概率等于所求情况数与总情况数之比．9、C【解题分析】首先求出二次函数24y x x m =--的图象的对称轴x=2b a-=2，且由a=1＞0，可知其开口向上，然后由A （2，1y ）中x=2，知1y 最小，再由B （-3，2y ），C （-1，3y ）都在对称轴的左侧，而在对称轴的左侧，y 随x 得增大而减小，所以23y y ＞．总结可得231y y y ＞＞．故选C ．20y ax bx c a =++≠（）的图象性质． 10、D【解题分析】根据抛物线开口方向得到a 0>，根据对称轴02b x a=->得到b 0<，根据抛物线与y 轴的交点在x 轴下方得到c 0<，所以0abc >；1x =-时，由图像可知此时0y >，所以0a b c -+>；由对称轴123b x a =-=，可得230a b +=；当2x =时，由图像可知此时0y >，即420a b c ++>，将23a b =-代入可得40c b ->.【题目详解】①根据抛物线开口方向得到0a >，根据对称轴02b x a=->得到b 0<，根据抛物线与y 轴的交点在x 轴下方得到c 0<，所以0abc >，故①正确.②1x =-时，由图像可知此时0y >，即0a b c -+>，故②正确. ③由对称轴123b x a =-=，可得230a b +=，所以230a b +>错误，故③错误； ④当2x =时，由图像可知此时0y >，即420a bc ++>，将③中230a b +=变形为23a b =-，代入可得40c b ->，故④正确.故答案选D.【题目点拨】本题考查了二次函数的图像与系数的关系，注意用数形结合的思想解决问题。

北京市北京四中数学轴对称填空选择单元复习练习(Word版含答案)一、八年级数学全等三角形填空题（难）1．将一副三角板按如图所示的方式摆放，其中△ABC为含有45°角的三角板，直线AD是等腰直角三角板的对称轴，且斜边上的点D为另一块三角板DMN的直角顶点，DM、DN分别交AB、AC于点E、F．则下列四个结论：①BD＝AD＝CD；②△AED≌△CFD；③BE+CF＝EF；④S四边形AEDF＝14BC2．其中正确结论是_____（填序号）．【答案】①②【解析】分析：根据等腰直角三角形的性质可得AD=CD=BD，∠CAD=∠B=45°，故①正确；根据同角的余角相等求出∠CDF=∠ADE，然后利用“ASA”证明△ADE≌△CDF，判断出②，根据全等三角形的对应边相等，可得DE=DF=AF=AE，利用三角形的任意两边之和大于第三边，可得BE+CF＞EF，判断出③，根据全等三角形的面积相等，可得S△ADF=S△BDE，从而求出四边形AEDF的面积，判断出④.详解：∵∠B=45°，AB=AC∴点D为BC的中点，∴AD=CD=BD故①正确；由AD⊥BC，∠BAD=45°可得∠EAD=∠C∵∠MDN是直角∴∠ADF+∠ADE=∠CDF+∠ADF=∠ADC=90°∴∠ADE=∠CDF∴△ADE≌△CDF（ASA）故②正确；∴DE=DF，AE=CF，∴AF=BE∴BE+AE=AF+AE∴AE+AF＞EF故③不正确；由△ADE≌△CDF可得S△ADF=S△BDE∴S四边形AEDF=S△ACD=12×AD×CD=12×12BC×12BC=18BC2，故④不正确.故答案为①②.点睛：此题主要查了等腰三角形的性质和全等三角形的判定与性质，以及三角形的三边关系，关键是灵活利用等腰直角三角形的边角关系和三线合一的性质.2．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为48和36，求△EDF的面积________.【答案】6【解析】【分析】作DM=DE交AC于M，作DN⊥AC，利用角平分线的性质得到DN=DF，将三角形EDF的面积转化为三角形DNM的面积来求．【详解】作DM=DE交AC于M，作DN⊥AC，∵AD是△ABC的角平分线，DF⊥AB，∴DF=DN，∵DE=DG，∴DG=DM，∴Rt△DEF≌Rt△DMN（HL），∵DG=DM， DN⊥AC，∴MN=NG，∴△DMN≌△DNG，∵△ADG和△AED的面积分别为48和36，∴S△MDG=S△ADG-S△ADM=48-36=12，∴S△DEF=12S△MDG=1212=6，故答案为：6【点睛】本题考查了角平分线的性质及全等三角形的判定及性质，正确地作出辅助线，将所求的三角形的面积转化为另外的三角形的面积来求是解题关键．3．在ABC中给定下面几组条件：①BC=4cm，AC=5cm，∠ACB=30°；②BC=4cm，AC=3cm，∠ABC=30°；③BC=4cm，AC=5cm，∠ABC=90°；④BC=4cm，AC=5cm，∠ABC=120°．若根据每组条件画图，则ABC能够唯一确定的是___________（填序号）.【答案】①③④【解析】【分析】根据全等三角形的判定方法进行分析，从而得到答案．【详解】解：①符合全等三角形的判定定理SAS，即能画出唯一三角形，正确；②根据BC=4cm，AC=3cm，∠ABC=30°不能画出唯一三角形，如图所示△ABC和△BCD，错误；③符合全等三角形的判定定理HL，即能画出唯一三角形，正确；④∵∠ABC为钝角，结合②可知，只能画出唯一三角形，正确.故答案为：①③④．【点睛】本题考查的是全等三角形的判定方法；解答此题的关键是要掌握三角形全等判定的几种方法即可，结合已知逐个验证，要找准对应关系．4．如图，在等边△ABC中，AB=10，BD=4，BE=2，点P从点E出发沿EA方向运动，连结PD，以PD为边，在PD的右侧按如图所示的方式作等边△DPF，当点P从点E运动到点A 时，点F运动的路径长是________．【答案】8【解析】【分析】作FG ⊥BC 于点G ，DE’⊥AB 于点E’，易证E 点和E’点重合，则∠FGD=∠DEP=90°；由∠EDB+∠PDF=90°可知∠EDP+∠GFD=90°，则易得∠EPD=∠GDF ，再由PD=DF 易证△EPD ≌△GDF ，则可得FG=DE ，故F 点的运动轨迹为平行于BC 的线段，据此可进行求解.【详解】解：作FG ⊥BC 于点G ，DE’⊥AB 于点E’，由BD=4、BE=2与∠B=60°可知DE ⊥AB ，即∠∵DE’⊥AB ，∠B=60°，∴BE’=BD×12=2， ∴E 点和E’点重合，∴∠EDB=30°，∴∠EDB+∠PDF=90°，∴∠EDP+∠GFD=90°=∠EDP+∠DPE ， ∴∠DPE=∠GFD∵∠DEP=∠FGD=90°，FD=GP ，∴△EPD ≌△GDF ，∴FG=DE ，DG=PE ，∴F 点运动的路径与G 点运动的路径平行，即与BC 平行，由图可知，当P 点在E 点时，G 点与D 点重合，∵DG=PE ，∴F 点运动的距离与P 点运动的距离相同，∴F 点运动的路径长为：AB-BE=10-2=8，故答案为8.【点睛】通过构造垂直线段构造三角形全等，从而确定F 点运动的路径，本题有一些难度.5．如图，ABC ∆中，090,,2ACB AC BC AB ∠===G 为AC 中点，连接BG ，CE BG ⊥于F ，交AB 于E ，连接GE ，点H 为AB 中点，连接FH ，以下结论：①ACE ABG ∠=∠；②5CF =；③AGE CGB ∠=∠；④FH 平分BFE ∠。

北京四中八年级第一学期期末数学试题（附答案）作者：学大教育编辑整理 来源：网络一、选择（本题共30分，每小题3分） 1．下列说法正确的是（ ）．A ．4的平方根是2B ．9的算术平方根是C ．8的立方根是D ．的立方根是2．计算的结果是（ ）．A ．B ．C ．21D ．3．下列图形中，轴对称图形的个数是（ ）．A ．1B ．2C ．3D ．4 4．下列变形正确的是（ ）．A ．B ．C ．D ．5．若函数（k≠0）的图象如图所示，则关于x的不等式≤0的解集在数轴上表示正确的是（）．6．如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）．A．SSS B．SAS C．AAS D．HL7．若将直线(k≠0)的图象向上平移3个单位后经过点(2，7)，则平移后直线的解析式为（）．A．B．C．D．8．如图，等边三角形ABC中，D为BC的中点，BE平分∠ABC交AD于E，若△CDE的面积等于1，则△ABC的面积等于（）．A ．2B ．4C ．6D ．12 9．已知一次函数，其中，则所有符合条件的一次函数的图象一定都经过（ ）．A ．第一、二象限B ．第二、三象限C ．第三、四象限D ．第一、四象限10．如图，D 为△ABC 内一点，CD 平分∠ACB ，BD ⊥CD ，∠A ＝∠ABD ，若AC ＝5，BC ＝3，则BD 的长为（ ）．A ．1B ．1.5C ．2D ．2.5二、填空（本题共18分，第15题4分，其余每小题各2分） 11．函数2-=x y 中，自变量x 的取值范围是_________．12．在，，，327这四个实数中，无理数是_________．13．如图，△ABC 中，D 为AC 边上一点，AD ＝BD ＝BC ，若∠A ＝40°，则∠CBD ＝_____．14．若直线（k ≠0）经过点（1，3），则该直线关于x 轴对称的直线的解析式为____15 . Rt △ABC 中，∠C ＝90°，∠A ＝30°，P 为AC 边上一点，PC ＝2，∠PBC ＝30°．（1）若PD ⊥AB 于D ，在图中画出线段PD ；（2）点P 到斜边AB 的距离等于_________．16．下图是按一定规律排列的一组图形，依照此规律，第n 个图形中的个数为_____．（n 为正整数）17．如图，钝角三角形纸片ABC 中，∠BAC ＝110°，D 为AC 边的中点．现将纸片沿过点D 的直线折叠，折痕与BC 交于点E ，点C 的落点记为F ．若点F 恰好在BA 的延长线上，则∠ADF ＝_________°．18．对于三个数a 、b 、c ，用}c b min{、、a 表示这三个数中最小的数， 例如，，那么观察图象，可得到的最大值为_________．三、（本题共17分，第19、21题各5分，第20题3分，第22题4分） 19．因式分解：（1）； （2）．20．计算：．21．先化简再求值：，其中x=3．22．解分式方程：．四、（本题共11分，第23题6分，第24题5分）23．已知：如图，D为△ABC内一点，AC=BC，CD平分∠ACB．求证：∠ABD＝∠BAD．24．已知：如图，在∠POQ内部有两点M、N，∠MOP＝∠NOQ．（1）画图并简要说明画法：在射线OP上取一点A，使点A到点M和点N的距离和最小；在射线OQ上取一点B，使点B到点M和点N的距离和最小；（2）直接写出AM＋AN与BM＋BN的大小关系．解：（1）画法：（2）答：AM＋AN_________BM＋BN．（填“＞”、“＝”或“＜”）五、（本题共12分，每小题6分）25．在平面直角坐标系xOy中，一动点从点出发，在由，四点组成的正方形边线上（如图①所示），按一定方向匀速运动．图②是点P运动的路程s与运动时间t（秒）之间的函数图象，图③是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分．请结合以上信息回答下列问题：（1）图②中，s与t之间的函数关系式是_________（t≥0）；（2）与图③中的折线段相对应的点P的运动路径是→_________→_________→_________；（填“A”、“B”、“C”、“D”、“M”或“N”）（3）当4≤s≤8时，直接写出y与s之间的函数关系式，并在图③中补全相应的函数图象．26．某中学初二年级300名同学在“爱心包”活动中，集资购买一批学习用品（书包和文具盒），捐赠给灾区90名学生，所买的书包每个54元，文具盒每个12元．现每名同学只购买一种学习用品，而且每2人合买一个文具盒，每6人合买一个书包．若x名同学购买书包，全年级共购买了y件学习用品．（1）求y与x之间的函数关系式（不要求写出自变量x的取值范围）；（2）若捐赠学习用品的总金额超过2300元，且灾区90名学生每人至少得到一件学习用品，问：同学们如何设计购买方案，才能使所购买的学习用品件数最多？学习用品最多能买多少件？六、解答题（本题共12分，每小题6分）27．已知：如图，平面直角坐标系xOy中，点A、B的坐标分别为，，P为y轴上B点下方一点，PB＝m（m＞0），以AP为边作等腰直角三角形APM，其中PM＝PA，点M落在第四象限．（1）求直线AB的解析式；（2）用m的代数式表示M点的坐标；（3）若直线MB与x轴交于点Q，判断点Q的坐标是否随m的变化而变化，写出你的结论并说明理由．28．如图，等腰直角三角形ABC中，∠BAC＝90°，D、E分别为AB、AC边上的点，AD＝AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．（1）求证：△EGM为等腰三角形；（2）判断线段BG、AF与FG的数量关系并证明你的结论．（1）证明：（2）答：线段BG、AF与FG的数量关系为_________．证明：北京四中八年级第一学期期末数学试题（附答案）参考答案一、选择（本题共30分，每小题3分）题号 1 2 3 4 5 6 7 8 9 10 答案 D D B B B D A C B A二、填空（本题共18分，第15题4分，其余每小题各2分）11．x≥2．12．．13．20．14．．15．（1）答案见图1；（2）2．16．．17．40．18．1．三、计算（本题共17分，第19、21题各5分，第20题3分，第22题4分）19．（1）解：．（2）解：．20．解：．21．解：．当x= 3时，原式=．22．解：去分母，得．2x=2．x=1．经检验，x=1是原方程的解．所以，原方程的解为x=1．四、认真做一做（本题共11分，第23题6分，第24题5分）23．证法一：如图2-1．∵CD平分∠ACB，∴∠1＝∠2．在△ACD与△BCD中，∴△ACD≌△BCD．∴AD＝BD．∴∠ABD＝∠BAD．证法二：如图2-2．延长CD交AB于点E．∵AC＝BC，CD平分∠ACB，∴CE垂直平分AB．∵点D在CE上，∴AD＝BD．∴∠ABD＝∠BAD．24．解：（1）答案图如图3所示．画法：1．作点M关于射线OP的对称点，连结交OP于点A．2．作点N关于射线OQ的对称点，连结交OQ于点B．（2）＝．五、仔细想一想（本题共12分，每小题6分）25．（1）（2）M→D→A→N；（3）26．解：（1）．（2）由题意得解得＜x≤180．又因为x为6的倍数，所以x等于168，174，180．因为随x的增大而减小，所以当x等于168，即168名同学购买书包，132名同学购买文具盒时，所购买的学习用品件数最多．因为时，，所以最多可买94件学习用品．此时168名同学购买书包，132名同学购买文具盒。

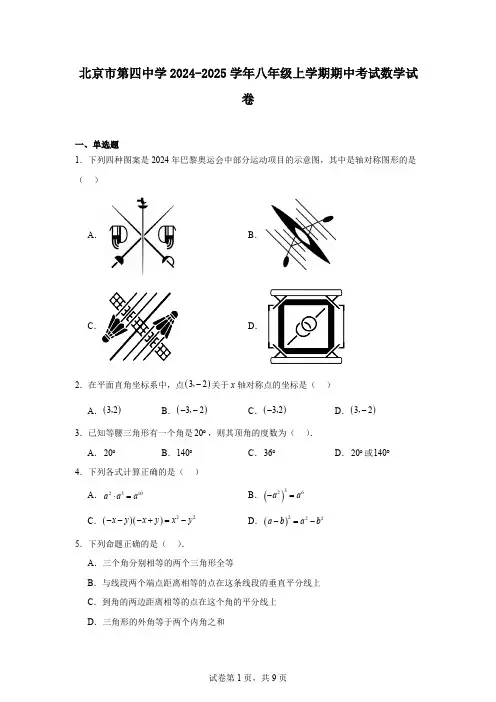
北京市第四中学2024-2025学年八年级上学期期中考试数学试卷一、单选题1．下列四种图案是2024年巴黎奥运会中部分运动项目的示意图，其中是轴对称图形的是（ ）A ．B ．C ．D ．2．在平面直角坐标系中，点()32-，关于x 轴对称点的坐标是（ ）A ．()32，B ．()32--，C ．()32-，D ．()32-，3．已知等腰三角形有一个角是20︒，则其顶角的度数为（ ）．A ．20︒B ．140︒C ．36︒D ．20︒或140︒4．下列各式计算正确的是（ ）A ．2510a a a ⋅=B ．()326a a -=C ．()()22x y x y x y ---+=-D ．()222a b a b -=-5．下列命题正确的是（ ）．A ．三个角分别相等的两个三角形全等B ．与线段两个端点距离相等的点在这条线段的垂直平分线上C ．到角的两边距离相等的点在这个角的平分线上D ．三角形的外角等于两个内角之和6．如图，在ABC V 和BDE V 中，AB BD =，再添一个条件不能使ABC V 和BDE V 全等的是（ ）A ．AE DC=B ．DE AC =C ．E C ∠=∠D ．EAF CDF∠=∠7．三条公路将A ，B ，C 三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是（ ）．A ．三条高线的交点B ．三条中线的交点C ．三条角平分线的交点D ．三边垂直平分线的交点8．如图，在ABC V 中，BD 是AC 边上的高，CE 是ACB ∠的平分线，BD ，CE 交于点F ．若80AEC ∠=︒，128BFC ∠=︒，则ABC ∠的度数是（ ）A ．28︒B ．38︒C ．42︒D ．62︒9．在如图的三个图形中，根据尺规作图的痕迹，能判断射线AD 平分BAC ∠的是（ ）A ．①②B ．①③C ．②③D ．只有①10．如图，边长为4的等边ABC V ，F 是边AC 的中点，点D 是线段BF 上的动点，连接AD ，在AD 的右侧作等边ADE V ，连接CD ，CE ，EF ，给出如下结论：①BF AC ⊥；②DEC DCE ∠=∠；③AE CD =；④ADE V 的周长最小值为6；⑤当AEF △周长最小时，60AFE ∠=︒；⑥ACE ∠的大小随着点D 的移动而变化；上述结论中正确的有（ ）个．A ．3B ．4C ．5D ．6二、填空题11．若一个三角形两边长分别为2、5，则此三角形的周长c 的取值范围为 ．12．若正多边形的每一个内角为135 ，则这个正多边形的边数是 ．13．若2320x y +-=，则48x y ⋅= ．14．如图所示，有一根高为18米的松树（垂直于地面）在A 处断裂，松树顶部落在地面C 处，通过测量可知30ACB ∠=︒，则松树断裂处A 离地面的距离AB 的长为 米．15．如图，在ABC V 中，点D 在边BC 上，AB AD DC ==，36C ∠=︒，则BAC ∠= ．16．若244230a a b +++-=，则a b += ．17．如图所示，点A 、B 、C 、D 均在正方形网格格点上，则ABC ADC ∠+∠= ．18．2019年11月，联合国教科文组织将每年的3月14日定为“国际数学日”，也被许多人称为“π节”．某校今年“π节”策划了五个活动，规则见下图：小云参与了所有活动．（1）若小云只挑战成功一个，则挑战成功的活动名称为 ；（2）若小云共挑战成功两个，且她参与的第四个活动成功，则小云最终剩下的“π币”数量的所有可能取值为 ．三、解答题19．化简：(1)()23332xy x y xy -；(2)()42322261233x y x y x y x y +-÷；(3)()()33a b a b +-；(4)()()22a b a b -+++．20．已知22770x x --=，求代数式()()()223321x x x ---+的值．21．如图，在平面直角坐标系中，ABC V 的顶点()1,4A -，B (−2,1)，()4,3C -．(1)已知ABC V 与111A B C △关于y 轴对称，111A B C △与222A B C △关于x 轴对称，请在坐标系中画出111A B C △和222A B C △；(2)在y 轴有一点P ，使得12PA B △周长最短，请画出点P 的位置（保留画图的痕迹）．22．已知，如图，AC BC BD AD AC ⊥⊥，，与BD 交于点O ，且AC BD =．求证：OA OB =．23．数学课上，李老师提出了如下问题：尺规作图：作ABC V 中边BC 上的高线．已知：如图，ABC V ．求作：ABC V 中BC 边上的高线AD ．下面是小婷设计的“作ABC V 中BC 边上的高线”的尺规作图过程．作法：如图，①以点B 为圆心，以BA 长为半径作弧，以点C 为圆心，以CA 长为半径作弧，两弧在BC 下方交于点E ；②连接AE 交BC 于点D ，则线段AD 是ABC V 中BC 边上的高线．李老师肯定了小婷的作法，请你根据她设计的尺规作图过程，完成下列问题．(1)使用直尺和圆规，补全图形．（保留作图痕迹）(2)小齐和小郭两位同学对小婷的作法给出了证明，请将证明过程补充完整．小齐证明：连接BE CE ，．∵BE BA =，CE CA =，∴点B ，C 分别在线段AE 的垂直平分线上．（______①______）∴BC 垂直平分线段AE ．∴线段AD 是ABC V 中BC 边上的高线．小郭证明：连接BE CE ，．∵BE BA =，CE CA =，BC BC =，∴ABC EBC ≌△△．∴ABC EBC ∠=∠．又∵BE BA =，∴BD AE ⊥．（______②______）线段AD 是ABC V 中BC 边上的高．(3)若AB BC =，40ABC ∠=︒，则CAE ∠的度数为______．24．在ABC V 中，AD 平分,BAC E ∠是BC 上一点，,//BE CD EF AD =交AB 于F 点，交CA 的延长线于,//P CH AB 交AD 的延长线于点H ．（1）求证：APF 是等腰三角形；（2）猜想AB 与PC 的大小有什么关系？证明你的猜想．25．如图1是一个长为2m 、宽为2n 的长方形()m n >，沿图中虚线用剪刀均匀分成四块小长方形，然后按图2形状拼成一个正方形．(1)请分别用两种不同的方法表示图2中阴影部分的面积：方法一：______；方法二：______；(2)观察图2，直接写出代数式()2m n +，()2m n -，mn 之间的关系：_______(3)利用（2）的结论，尝试解决以下问题：①已知7m n +=，6mn =，则()2m n -的值为______；②已知：()()456x x --=，求()292x -的值；(4)两个正方形ABCD AEFG ，如图3摆放，边长分别为x ，y ，若22x y 34+=，2BE =，求图中阴影部分面积和．26．已知，平面内线段AB ，点C ，M ，N ，满足：180CAM CBN ∠+∠=︒，AC AM =，BC BN =，连接MN ，D 为MN 的中点，连接AD 、BD ．(1)如图1，当点C 在线段AB 上时，直接写出AD 与BD 的位置关系．(2)如图2，当点C 在线段AB 上方时，若2AB BD =，求MAC ∠的度数．(3)线段AC 从图2的位置出发，绕着点A 顺时针转到线段AB 下方，且使线段AB 同时落在CAM ∠和CBN ∠的内部，在AC 运动的过程中，下列说法始终正确的有______．AD BD ⊥①AD ②平分MAB ∠ABD ADM BDN S S S ≤+③ 2NBC DBA∠=∠④27．数表操作：设A 是由m n ⨯个实数组成的m 行n 列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．(1)数表A 如表1所示，若经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负实数，请写出每次“操作”后所得的数表；1-3-416-023-表1第一次操作后的数表第二次操作后的数表→(2)数表A 如表2所示，若该数表必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和均为非负数，则实数a 的取值范围是______．表221a +1a -1a 13a -1-a -28．在平面直角坐标系xOy 中，直线l 为过点()2,0且和y 轴平行的直线，对于点P 和正方形ABCD ，给出如下定义：记点P 关于直线l 的对称点为P '，若点P '到正方形ABCD 的边所在直线的最大距离是最小距离的k 倍，则称点P 是正方形ABCD 的“k 倍距离点”．已知：点(),A a a --，(),B a a -，(),C a a ，其中0a >．(1)当2a =时，①点D 的坐标是______；②在()13,1P ，()21,1P -，()34,0P 三个点中，______是正方形ABCD 的“3倍距离点”；(2)当3a =时，点()5,P n 是正方形ABCD 的“2倍距离点”，求n 的取值范围；(3)点()6,2M -，()1,3N ，若线段MN 上至少存在3个点是正方形ABCD 的“2倍距离点”，直接写出a 的取值范围．。

一、选择题1．如图，在ABC 中，6AB =，8AC =，10BC =，EF 是BC 的垂直平分线，P 是直线EF 上的一动点，则PA PB +的最小值是（ ）．A ．6B ．8C ．10D ．112．如图，在ABC ∆中，90,30C B ∠=︒∠=︒，以点A 为圆心，任意长为半径画弧分别交,AB AC 于点M 和N ，再分别以,M N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ，则下列结论不正确的是（ ）A ．AD 是∠BAC 的平分线B ．60ADC ∠=︒ C ．点D 在AB 的垂直平分线上 D ． : 1:3DAC ABD S S ∆∆=3．如图，已知30MON ∠=︒，点1A ，2A ，3A ，…，在射线ON 上，点B ，1B ，2B ，3B ，…，在射线OM 上，112A B B ，223A B B △，334A B B △，…，均为等边三角形．若11OB =，则202020202021A B B △的边长为（ ）A ．20192B ．20202C ．20212D ．20222 4．如图，在△ABC 中，∠BAC ＝90°，AD 是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，下面说法：①△ABE 的面积＝△BCE 的面积；②∠AFG ＝∠AGF ；③∠FAG ＝2∠ACF ；④BH ＝CH ．其中正确的是（ ）A ．①②③④B ．①②③C ．②④D ．①③ 5．如图，在Rt ABC ∆中， 90,30,ACB A CD ︒︒∠=∠=是斜边AB 上的高，2BD =，那么AD 的长为（ ）A ．2B ．4C ．6D ．86．平面直角坐标系中，已知()1,1A ，()2,0B ．若在x 轴上取点C ，使ABC 为等腰三角形，则满足条件的点C 的个数是（ ）A ．2个B ．3个C ．4个D ．5个 7．已知点(),3M a ，点()2,N b 关于x 轴对称，则2020()a b +的值（ ）A ．3-B ．1-C ．1D ．3 8．如图，在ABC 中，87,A ABC ∠=︒∠的平分线BD 交AC 于点,DE 是BC 中点，且DE BC ⊥，那么C ∠的度数为（ ）A ．16︒B ．28︒C ．31︒D ．62︒9．如图所示，D 为 BC 上一点，且 AB ＝AC ＝BD ，则图中∠1 与∠2 的关系是（ ）A ．∠1＝2∠2B ．∠1+∠2＝180°C ．∠1+3∠2＝180°D ．3∠2﹣∠1＝180° 10．如图，∠MON =30°，点A 1、A 2、A 3…在射线ON 上，点B 1、B 2、B 3…在射线OM 上，△A 1B 1A 2、△A 2B 2A 3、△A 3B 3A 4…均为等边三角形，从左起第1个等边三角形的边长记为a 1，第2个等边三角形的边长记为a 2，以此类推．若OA 1=1，则a 2019=（ ）A ．22017B ．22018C ．22019D ．2202011．已知一个等腰三角形ABC 的两边长为5，7，另一个等腰三角形ABC 的两边为23x -，35x -，若两个三角形全等，则x 的值为（ ）A ．5B ．4C ．4或5D ．10312．如图，ABC 中，AC AD BD ==，80CAD ︒∠=，则B 等于（ ）A ．25︒B ．30︒C ．35︒D ．40︒13．如图，已知等腰三角形ABC 中，AB AC =，15DBC ∠=︒，分别以A 、B 两点为圆心，以大于12AB 的长为半径画圆弧，两弧分别交于点E 、F ，直线EF 与AC 相交于点D ，则A ∠的度数是（ ）A ．50°B ．60°C ．75°D ．45°14．如图，在ABC ∆中，5AC =，线段AB 的垂直平分线交AC 于点,D BCD ∆的周长是9，则BC 的长为（ ）A．3B．4C．5D．615．如图，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD 相交于点F，DH⊥BC于H，交BE于G，下列结论：①BD＝CD；②AD+CF＝BD；③CE＝1BF；④AE＝BG．其中正确的是（）2A．①②B．①③C．①②③D．①②③④二、填空题16．若等腰三角形的顶角为30°，腰长为10，则此等腰三角形的面积为_________．17．如图：已知在ABC中，90∠=，在直线AC上找点P，使BAC︒ACB︒∠=，36∠的度数为________．ABP△是等腰三角形，则APB18．如图在钝角△ABC中，已知∠BAC=135°，边AB、AC的垂直平分线分别交BC于点D、E，连接AD、AE，则∠DAE=_____19．如图，等边△ABC的边长为4，点D在边AC上，AD＝1．（1）△ABC的周长等于_____；（2）线段PQ在边BA上运动，PQ＝1，BQ＞BP，连接QD，PC，当四边形PCDQ的周长取得最小值时，请在如图所示的矩形区域内，用无刻度的直尺和圆规，画出线段PC ，QD ，并简要说明点P 和点Q 的位置是如何找到的（保留作图痕迹，不要求证明）_____．20．如图，在ABC 中，AB AC =，36ABC ∠=︒，DE 是线段AC 的垂直平分线，连接AE ，若BE a =，EC b =，则用含有a ，b 的代数式表示ABC 的周长是______．21．如图，在△ACB 中，∠ACB ＝∠90°，AB 的垂直平分线DE 交AB 于E ，交AC 于D ，∠DBC ＝30°，DC ＝4cm ，则D 到AB 的距离为________cm ．22．如图，在ABC 中，AB=AC ，40A ∠=，CD //AB ，则BCD ∠的度数是______°．23．如图，AOB 与COB △关于边OB 所在的直线成轴对称，AO 的延长线交BC 于点D .若46BOD ∠=︒，22C ∠=︒，则ADC ∠=______°．24．如图，E 是腰长为2的等腰直角ABC 斜边上一点，且BE BC P =，为CE 上任意一点，PQ BC ⊥于点Q PR BE ⊥，于点R ，则PQ PR +的值是___________．25．含30角的直角三角板与直线1l ，2l 的位置关系如图所示，已知12//l l ，30A ∠=︒，160∠=︒，若6AB =，CD 的长为__________．26．如图，在△ABC 中，AD 平分∠BAC ，交BC 于点D ，BE ⊥AD 于E ，AB =6，AC =14，∠ABC =3∠C ，则BE =____．三、解答题27．如图，,A B AE BE ∠=∠=，点D 在AC 边上，12,AE ∠=∠和BD 相交于点O ． （1）求证：AEC BED ∆≅∆（2）若70BDE ︒∠=，求1∠的度数．28．在等边三角形ABC 中，点E 为线段AB 上一动点，点E 与A ，B 不重合，点D 在CB 的延长线上，且ED ＝EC ．（1）当E 为边AB 的中点时，如图1所示，确定线段AE 与BD 的大小关系，并证明你的结论；（2）如图2，当E 不是边AB 的中点时，（1）中的结论是否成立？若不成立，请直接写出BD 与AE 的数量关系；若成立，请给予证明；（提示：过E 作//EF BC 交AC 于点F ） （3）在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED ＝EC ，ABC 的边长为1，AE ＝2，请直接写出CD 的长．29．在等边ABC ∆中，（1）如图1，P ，Q 是BC 边上两点，AP AQ =，20BAP ∠=︒，求AQB ∠的度数； （2）点P ，Q 是BC 边上的两个动点（不与B ，C 重合），点P 在点Q 的左侧，且AP AQ =，点Q 关于直线AC 的对称点为M ，连接AM ，PM ．①依题意将图2补全；②求证：PA PM =．30．如图，,ABC AEF ∆∆均为等边三角形，连接BE ，连接并延长CF 交BE 于点D ． （1）求证：CAF BAE ∆≅∆;（2）连接AD ，求证DA 平分CDE ∠.。

轴对称周末练习
习题：
1．填空
（1）一个圆形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是（）图形，折痕所在的
这条（）叫做（）。

（2）在轴对称图形中，对称轴两侧相对的点到对称轴的距离（）。

（3）长方形有2条（）轴，正方形有（）条对称轴，等腰三角形、等腰梯形、扇形只
有（）条对称轴，圆、环形有（）条对称轴，等边三角形有（）条对称轴。

2.（1）下面每个网格内的两个图形（如图所示）都是成轴对称的，请画出它们的对称轴；
（2）画出如图所示的图形关于直线l的对称图形.
3. 在直角坐标系中,已知A（2,0）,B（1,-2）则线段AB关于坐标系原点的对称线段的图象是下图中
的（）.
4. 如图所示,将一张正方形纸片经过两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是（）
5. 已知点A（3，-2），B（-4，1），点M与点A关于x轴对称，点N与点B关于y轴对称，求M，N两点坐标.
6. 如图,已知:AD为△ABC的高,∠B=2∠C,利用轴对称的性质证明CD=AB+BD.
参考答案：
1．（1）轴对称；直线；对称轴；（2）相等（3）对称；4；1 ；无数；3；
2．（略）
3．A．
4．D
５.M（3，2），N（4，1）
６．提示：取点B关于AD的对称点E，连结AE。

轴对称周末练习（2）1．将一张矩形的纸对折，然后用笔尖在上面扎出“B”，再把它铺平，你可见到（）2．在平面镜里看到背后墙上，电子钟示数如图示，这时的时间应是（）(A)21：05 (B)21：15(C)20：15 (D)20：053．在△ABC中，边AB的垂直平分线交AC于E，若△ABC和△BEC的周长分别为24和14，则AB=________。

4．如图，△ABC的周长为19，AC的垂直平分线DE交BC于D，E为垂足，AE=3，则△ABD的周长为_______。

5．如图所示，△ABC中，BC边的垂直平分线DE交BC于D，交AC于E，BE=5，△BCE的周长是18，则BC= ________。

6．如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿AD对折，点C落在点的位置，则与BC之间的大小关系是________。

7．在△ABC中，∠BAC=110°，AB、AC的垂直平分线交BC于D、E两点，求∠DAE的度数。

8．如图，在正方形网格纸上有一个△ABC(1)作△ABC关于直线MN的对称图形；(2)若网格上最小正方形边长为1，求△ABC的面积。

9．如图，P在∠AOB内，点M、N分别是点P关于OA、OB的对称点，MN分别交OA、OB于E、F，若△PEF的周长是20cm，求MN的长。

10．在△ABC中，DE是AB的垂直平分线，交BC于D，交AB于E，若∠ACB=80°，且∠CAD：∠CAB=1：3，求∠B的度数。

参考答案：1．C2．A3．104．135．86．7．40°8．（1）略（2）3 9．20cm10．40°。

2015-2016学年北京四中八年级（上）期中数学试卷一、选择题（本题共30分，每小题3分）1．下列图形中，不是轴对称图形的是( )A．B．C．D．2．把a2﹣4a多项式分解因式，结果正确的是( )A．a（a﹣4）B．（a+2）（a﹣2）C．a（a+2）（a﹣2）D．（a﹣2）2﹣43．使分式有意义，则x的取值范围是( )A．x≠1 B．x=1 C．x≤1 D．x≥14．点A（2，3）关于y轴成轴对称的点的坐标是( )A．（3，﹣2）B．（﹣2，3）C．（﹣2，﹣3）D．（2，﹣3）5．在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，添加下列条件中的一个，不能使△ABC≌△A′B′C′一定成立的是( )A．AC=A′C′B．BC=B′C′C．∠B=∠B′ D．∠C=∠C′6．下列各式中，正确的是( )A．B．C．=D．7．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为( )A．12 B．15 C．12或15 D．188．如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是( )A．18°B．24°C．30°D．36°9．如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为( )A．30°B．45°C．60°D．75°10．如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于( )A．50°B．75°C．80°D．105°二、填空题（本题共20分，每小题2分）11．已知某种植物花粉的直径为35000纳米，即0.000035米，把0.000035用科学记数法表示为__________．12．因式分解：3x2﹣6x+3=__________．13．计算的结果是__________．14．如图，在Rt△ABC中，∠C=90°，∠B=30°，AD平分∠CAB交BC于D，DE⊥AB于E．若DE=1cm，则BC=__________cm．15．如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=__________度．16．如图，△ABC中，BO、CO分别平分∠ABC、∠ACB，OM∥AB，ON∥AC，BC=10cm，则△OMN的周长=__________．17．已知，则代数式的值为__________．18．如图△ABC中，AD平分∠BAC，AB=4，AC=2，且△ABD的面积为3，则△ACD的面积为__________．19．如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD 最小时，∠PCD=__________°．20．如图所示，矩形ABCD中，AB=4，BC=，点E是折线段A﹣D﹣C上的一个动点（点E与点A不重合），点P是点A关于B E的对称点，在点E运动的过程中，使△PCB 为等腰三角形的点E的位置共有__________个．三、解答题21．分解因式．（1）x2（m﹣2）+9y2（2﹣m）（2）（x2+1）2﹣4x2．22．计算：（1）．（2）．23．先化简，再求值：（1﹣）÷，其中a=﹣1．24．解方程：．25．已知：如图，AD=AE，AB=AC，∠DAE=∠BAC．求证：BD=CE．26．甲、乙两名学生练习计算机打字，甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同．已知甲每分钟比乙每分钟多打5个字．问：甲、乙两人每分钟各打多少字？27．小明在做课本“目标与评定”中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？小明的做法是：如图2，画PC∥a，量出直线b与PC的夹角度数，即直线a，b所成角的度数．（1）请写出这种做法的理由；（2）小明在此基础上又进行了如下操作和探究（如图3）：①以P为圆心，任意长为半径画圆弧，分别交直线b，PC于点A，D；②连结AD并延长交直线a于点B，请写出图3中所有与∠PAB相等的角，并说明理由；（3）请在图3画板内作出“直线a，b所成的跑到画板外面去的角”的平分线（画板内的部分），只要求作出图形，并保留作图痕迹．28．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D、E．证明：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线l 上，且∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立；请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是直线l上的两动点（D、A、E三点互不重合），点F 为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，求证：DF=EF．附加题（满分20分，计入总分）29．已知：a﹣b=2，2a2+a﹣4=0，则=__________．30．已知：，则（b﹣c）x+（c﹣a）y+（a﹣b）z的值为__________．31．等腰Rt△ABC中，∠BAC=90°，点A、点B分别是x轴、y轴两个动点，直角边AC 交x轴于点D，斜边BC交y轴于点E；（1）如图（1），若A（0，1），B（2，0），求C点的坐标；（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB=∠CDE （3）如图（3），在等腰Rt△ABC不断运动的过程中，若满足BD始终是∠ABC的平分线，试探究：线段OA、OD、BD三者之间是否存在某一固定的数量关系，并说明理由．2015-2016学年北京四中八年级（上）期中数学试卷一、选择题（本题共30分，每小题3分）1．下列图形中，不是轴对称图形的是( )A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解．【解答】解：A、不是轴对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误．故选A．【点评】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．把a2﹣4a多项式分解因式，结果正确的是( )A．a（a﹣4）B．（a+2）（a﹣2）C．a（a+2）（a﹣2）D．（a﹣2）2﹣4【考点】因式分解-提公因式法．【分析】直接提取公因式a即可．【解答】解：a2﹣4a=a（a﹣4），故选：A．【点评】此题主要考查了提公因式法分解因式，关键是掌握找公因式的方法：当各项系数都是整数时，公因式的系数应取各项系数的最大公约数；字母取各项的相同的字母，而且各字母的指数取次数最低的；取相同的多项式，多项式的次数取最低的．3．使分式有意义，则x的取值范围是( )A．x≠1 B．x=1 C．x≤1 D．x≥1【考点】分式有意义的条件．【分析】根据分式有意义的条件：分母不等于0，即可求解．【解答】解：根据题意得：x﹣1≠0，解得：x≠1．故选：A．【点评】本题主要考查了分式有意义的条件，正确理解条件是解题的关键．4．点A（2，3）关于y轴成轴对称的点的坐标是( )A．（3，﹣2）B．（﹣2，3）C．（﹣2，﹣3）D．（2，﹣3）【考点】关于x轴、y轴对称的点的坐标．【分析】根据关于y轴对称的两点纵坐标相等，横坐标互为相反数，由此可求出．【解答】解：点A（2，3）关于y轴成轴对称的点的坐标是（﹣2，3）．故选：B．【点评】本题考查了关于坐标轴对称的两点的坐标关系，根据关于y轴对称的两点的性质得出是解题关键．5．在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，添加下列条件中的一个，不能使△ABC≌△A′B′C′一定成立的是( )A．AC=A′C′B．BC=B′C′C．∠B=∠B′ D．∠C=∠C′【考点】全等三角形的判定．【专题】证明题．【分析】全等三角形的判定定理有SAS，ASA，AAS，SSS，根据图形和已知看看是否符合即可．【解答】解：A、∠A=∠A′，AB=A′B′AC=A′C′，根据SAS能推出△ABC≌△A′B′C′，故A选项错误；B、具备∠A=∠A′，AB=A′B′，BC=B′C′，不能判断△ABC≌△A′B′C′，故B选项正确；C、根据ASA能推出△ABC≌△A′B′C′，故C选项错误；D、根据AAS能推出△ABC≌△A′B′C′，故D选项错误．故选：B．【点评】本题考查了对全等三角形判定的应用，注意：判定两三角形全等的方法有ASA，SAS，AAS，SSS，而SSA，AAA都不能判断两三角形全等．6．下列各式中，正确的是( )A．B．C．=D．【考点】分式的基本性质．【专题】计算题．【分析】利用分式的基本性质对各式进行化简即可．【解答】解：A、已经是最简分式，故本选项错误；B、，故本选项错误；C、=，故本选项错误；D、利用分式的基本性质在分式的分子与分母上同时乘以x+y即可得到，故本选项正确；故选D．【点评】本题考查了分式的基本性质，解题的关键是在进行分式的运算时要同时乘除．7．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为( )A．12 B．15 C．12或15 D．18【考点】等腰三角形的性质；三角形三边关系．【分析】因为已知长度为3和6两边，没有明确是底边还是腰，所以有两种情况，需要分类讨论．【解答】解：①当3为底时，其它两边都为6，3、6、6可以构成三角形，周长为15；②当3为腰时，其它两边为3和6，∵3+3=6=6，∴不能构成三角形，故舍去，∴答案只有15．故选B．【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．8．如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是( )A．18°B．24°C．30°D．36°【考点】等腰三角形的性质．【分析】根据已知可求得两底角的度数，再根据三角形内角和定理不难求得∠DBC的度数．【解答】解：∵AB=AC，∠A=36°，∴∠ABC=∠ACB=72°∵BD是AC边上的高，∴BD⊥AC，∴∠DBC=90°﹣72°=18°．故选A．【点评】本题主要考查等腰三角形的性质，解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题，此题难度一般．9．如图，∠3=30°，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证∠1的度数为( )A．30°B．45°C．60°D．75°【考点】生活中的轴对称现象；平行线的性质．【专题】压轴题．【分析】要使白球反弹后能将黑球直接撞入袋中，则∠2=60°，根据∠1、∠2对称，则能求出∠1的度数．【解答】解：要使白球反弹后能将黑球直接撞入袋中，∠2+∠3=90°，∵∠3=30°，∴∠2=60°，∴∠1=60°．故选：C．【点评】本题是考查图形的对称、旋转、分割以及分类的数学思想．10．如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于( )A．50°B．75°C．80°D．105°【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线性质得出BP=AP，CQ=AQ，推出∠B=∠BAP，∠C=∠QAC，求出∠B+∠C，即可求出∠BAP+∠QAC，即可求出答案．【解答】解：∵MP和QN分别垂直平分AB和AC，∴BP=AP，CQ=AQ，∴∠B=∠PAB，∠C=∠QAC，∵∠BAC=130°，∴∠B+∠C=180°﹣∠BAC=50°，∴∠BAP+∠CAQ=50°，∴∠PAQ=∠BAC﹣（∠PAB+∠QAC）=130°﹣50°=80°，故选：C．【点评】本题考查了等腰三角形的性质，线段垂直平分线性质，三角形的内角和定理，注意：线段垂直平分线上的点到线段两个端点的距离相等，等边对等角．二、填空题（本题共20分，每小题2分）11．已知某种植物花粉的直径为35000纳米，即0.000035米，把0.000035用科学记数法表示为3.5×10﹣5米．【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.000035米=3.5×10﹣5米．故答案为：3.5×10﹣5米．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．12．因式分解：3x2﹣6x+3=3（x﹣1）2．【考点】提公因式法与公式法的综合运用．【分析】先提取公因式3，再对余下的多项式利用完全平方公式继续分解．【解答】解：3x2﹣6x+3，=3（x2﹣2x+1），=3（x﹣1）2．【点评】本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．13．计算的结果是4．【考点】实数的运算；零指数幂；负整数指数幂．【专题】计算题．【分析】分别计算负整数指数幂、零指数幂及绝对值，然后合并即可得出答案．【解答】解：原式=2﹣1+3=4．【点评】此题考查了零指数幂及负整数指数幂的知识，属于基础题，解答本题的关键是熟练掌握各部分的运算法则．14．如图，在Rt△ABC中，∠C=90°，∠B=30°，AD平分∠CAB交BC于D，DE⊥AB于E．若DE=1cm，则BC=3cm．【考点】含30度角的直角三角形；角平分线的性质．【专题】计算题．【分析】根据角平分线性质求出CD的长和∠DAE的度数，根据含30度角的直角三角形性质求出BD，代入BC=BD+CD求出即可．【解答】解：∵AD平分∠CAB，∠C=90°，DE⊥AB，∴CD=DE=1，∵∠B=30°，∴BD=2DE=2，∴BC=1+2=3，故答案为：3．【点评】本题考查了对含30度角的直角三角形的性质和角平分线性质的应用，求出CD和BD的长是解此题的关键．15．如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=15度．【考点】等边三角形的性质；三角形的外角性质；等腰三角形的性质．【专题】几何图形问题．【分析】根据等边三角形三个角相等，可知∠ACB=60°，根据等腰三角形底角相等即可得出∠E的度数．【解答】解：∵△ABC是等边三角形，∴∠ACB=60°，∠ACD=120°，∵CG=CD，∴∠CDG=30°，∠FDE=150°，∵DF=DE，∴∠E=15°．故答案为：15．【点评】本题考查了等边三角形的性质，互补两角和为180°以及等腰三角形的性质，难度适中．16．如图，△ABC中，BO、CO分别平分∠ABC、∠ACB，OM∥AB，ON∥AC，BC=10cm，则△OMN的周长=10cm．【考点】等腰三角形的判定与性质；平行线的性质．【分析】由BO为∠ABC的平分线，得到一对角相等，再由OM与AB平行，根据两直线平行内错角相等得到一对角相等，等量代换得到∠MBO=∠MOB，再由等角对等边得到OM=BM，同理ON=CN，然后利用三边之和表示出三角形OMN的周长，等量代换得到其周长等于BC的长，由BC的长即可求出三角形OMN的周长．【解答】解：∵BO平分∠ABC，∴∠ABO=∠DBO，又OM∥AB，∴∠ABO=∠MOB，∴∠MBO=∠MOB，∴OM=BM，同理ON=CM，∵BC=10cm，则△OMN的周长c=OM+MN+ON=BM+MN+NC=BC=10cm．故答案为10cm．【点评】此题考查了等腰三角形的判定与性质，以及平行线的性质，利用了等量代换的思想，熟练掌握性质是解本题的关键．17．已知，则代数式的值为4．【考点】分式的加减法．【专题】计算题．【分析】已知等式左边通分并利用同分母分式的减法法则计算，得出关系式，所求式子变形后代入计算即可求出值．【解答】解：解法一：∵﹣=﹣=3，即x﹣y=﹣3xy，则原式===4．解法二：将原式的分子和分母同时除以xy，===4故答案为：4．【点评】此题考查了分式的加减法，分式加减法的关键是通分，通分的关键是找最简公分母．18．如图△ABC中，AD平分∠BAC，AB=4，AC=2，且△ABD的面积为3，则△ACD的面积为．【考点】角平分线的性质．【专题】探究型．【分析】过点D作DE⊥AB，DF⊥AC，由角平分线的性质可得出DE=DF，再由AB=4，△ABD 的面积为3求出DE的长，由AC=2即可得出△ACD的面积．【解答】解：过点D作DE⊥AB，DF⊥AC，∵AD平分∠BAC，∴DE=DF，∵AB=4，△ABD的面积为3，∴S△ABD=AB•DE=×4×DE=3，解得DE=；∴DF=，∵AC=2，∴S△ACD=AC•DF=×2×=．故答案为：．【点评】本题考查的是角平分线的性质，根据题意作出辅助线，利用数形结合求解是解答此题的关键．19．如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD 最小时，∠PCD=45°．【考点】轴对称-最短路线问题．【分析】根据当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC即可得出∠PCD的度数．【解答】解：∵当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC，AC为正方形对角线，根据正方形的性质得出∠PCD=45°，∴∠PCD=45°．故答案为：45°．【点评】此题主要考查了轴对称求最短路线问题，根据已知得出D点关于MN的对称点，正好是A点是解题关键．20．如图所示，矩形ABCD中，AB=4，BC=，点E是折线段A﹣D﹣C上的一个动点（点E与点A不重合），点P是点A关于BE的对称点，在点E运动的过程中，使△PCB为等腰三角形的点E的位置共有4个．【考点】矩形的性质；等腰三角形的判定；轴对称的性质．【专题】压轴题．【分析】分为三种情况：①以BC为底时，有两个，是BC的垂直平分线与以B为圆心BA 为半径的圆的交点；②以BP为底，C为顶点时，有两个，是以B为圆心BA为半径的圆与以C为圆心BC为半径的圆的交点；③以CP为底，B为顶点时，没有，∵是以B为圆心BA为半径的圆与以B为圆心BC为半径的圆没有交点．【解答】解：分为三种情况：①以BC为底时，有两个，是BC的垂直平分线与以B为圆心BA为半径的圆的交点；②以BP为底，C为顶点时，有两个，是以B为圆心BA为半径的圆与以C为圆心BC为半径的圆的交点；③以CP为底，B为顶点时，没有，∵是以B为圆心BA为半径的圆与以B为圆心BC为半径的圆没有交点；综上满足要求的P有4个，故答案为：4．【点评】本题考查了矩形的性质，等腰三角形的判定，轴对称的性质等知识点，主要考查学生的理解能力和动手操作能力．三、解答题21．分解因式．（1）x2（m﹣2）+9y2（2﹣m）（2）（x2+1）2﹣4x2．【考点】提公因式法与公式法的综合运用．【专题】计算题；因式分解．【分析】（1）原式变形后，提取公因式，再利用平方差公式分解即可；（2）原式利用平方差公式及完全平方公式分解即可．【解答】解：（1）原式=x2（m﹣2）+9y2（m﹣2）=（m﹣2）（x2﹣9y2）=（m﹣2）（x﹣3y）（x+3y）（2）原式=（x2+1+2x）（x2+1﹣2x）=（x﹣1）2（x+1）2．【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．22．计算：（1）．（2）．【考点】分式的混合运算．【专题】计算题；分式．【分析】（1）原式先计算乘方运算，再计算乘除运算即可得到结果；（2）原式通分并利用同分母分式的加法法则计算即可得到结果．【解答】解：（1）原式=••=﹣；（2）原式===．【点评】此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．23．先化简，再求值：（1﹣）÷，其中a=﹣1．【考点】分式的化简求值．【专题】探究型．【分析】先根据整式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．【解答】解：原式=÷=×=a+1．当a=﹣1时，原式=﹣1+1=．【点评】本题考查的是分式的混合运算，熟知分式混合运算的法则是解答此题的关键．24．解方程：．【考点】解分式方程．【专题】计算题．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：（x+3）（x+1）﹣8=x2﹣1，去括号得：x2+4x+3﹣8=x2﹣1，移项合并得：4x=4，解得：：x=1，经检验x=1是原方程的增根，分式方程无解．【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．25．已知：如图，AD=AE，AB=AC，∠DAE=∠BAC．求证：BD=CE．【考点】全等三角形的判定与性质．【专题】证明题．【分析】根据角与角之间的等量关系求出∠BAD=∠CAE，根据SAS证△BAD≌△CAE，根据全等三角形的性质推出即可．【解答】证明：∵∠DAE=∠BAC，∴∠DAE﹣∠BAE=∠EAC﹣∠BAE，∴∠BAD=∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴BD=EC．【点评】本题考查了全等三角形的判定与性质，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等．26．甲、乙两名学生练习计算机打字，甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同．已知甲每分钟比乙每分钟多打5个字．问：甲、乙两人每分钟各打多少字？【考点】分式方程的应用．【专题】应用题．【分析】设乙每分钟打x个字，则甲每分钟打（x+5）个字，再由甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同，可得出方程，解出即可得出答案．【解答】解：设乙每分钟打x个字，则甲每分钟打（x+5）个字，由题意得，=，解得：x=45，经检验：x=45是原方程的解．答：甲每分钟打50个字，乙每分钟打45个字．【点评】本题考查了分式方程的应用，解答本题的关键是设出未知数，找到等量关系，根据等量关系建立方程，注意不要忘记检验．27．小明在做课本“目标与评定”中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？小明的做法是：如图2，画PC∥a，量出直线b与PC的夹角度数，即直线a，b所成角的度数．（1）请写出这种做法的理由；（2）小明在此基础上又进行了如下操作和探究（如图3）：①以P为圆心，任意长为半径画圆弧，分别交直线b，PC于点A，D；②连结AD并延长交直线a于点B，请写出图3中所有与∠PAB相等的角，并说明理由；（3）请在图3画板内作出“直线a，b所成的跑到画板外面去的角”的平分线（画板内的部分），只要求作出图形，并保留作图痕迹．【考点】作图—应用与设计作图；平行线的性质；等腰三角形的性质．【分析】（1）根据平行线的性质得出即可；（2）根据题意，有3个角与∠PAB相等．由等腰三角形的性质，可知∠PAB=∠PDA；又对顶角相等，可知∠BDC=∠PDA；由平行线性质，可知∠PDA=∠1．因此∠PAB=∠PDA=∠BDC=∠1；（3）作出线段AB的垂直平分线EF，由等腰三角形的性质可知，EF是顶角的平分线，故EF即为所求作的图形．【解答】解：（1）PC∥a（两直线平行，同位角相等）；（2）∠PAB=∠PDA=∠BDC=∠1，如图，∵PA=PD，∴∠PAB=∠PD A，∵∠BDC=∠PDA（对顶角相等），又∵PC∥a，∴∠PDA=∠1，∴∠PAB=∠PDA=∠BDC=∠1；（3）如图，作线段AB的垂直平分线EF，则EF是所求作的图形．【点评】本题涉及到的几何基本作图包括：（1）过直线外一点作直线的平行线，（2）作线段的垂直平分线；涉及到的考点包括：（1）平行线的性质，（2）等腰三角形的性质，（3）对顶角的性质，（4）垂直平分线的性质等．本题借助实际问题场景考查了学生的几何基本作图能力，是一道好题．题目篇幅较长，需要仔细阅读，理解题意，正确作答．28．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D、E．证明：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线l 上，且∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立；请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是直线l上的两动点（D、A、E三点互不重合），点F 为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，求证：DF=EF．【考点】全等三角形的判定与性质．【分析】（1）由条件可证明△ABD≌△CAE，可得DA=CE，AE=BD，可得DE=BD+CE；（2）由条件可知∠BAD+∠CAE=180°﹣α，且∠DBA+∠BAD=180°﹣α，可得∠DBA=∠CAE，结合条件可证明△ABD≌△CAE，同（1）可得出结论．（3）由（2）知，△ADB≌△CAE，得到BD=EA，∠DBA=∠CAE，再△DBF≌△EAF（SAS），得到DF=EF，∠BFD=∠AFE，求出∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，所以△DEF 为等边三角形．即可得到DF=EF．【解答】解：（1）∵BD⊥l，CE⊥l，∴∠BDA=∠AEC=90°又∵∠BAC=90°，∴∠BAD+∠CAE=90°，∠BAD+∠ABD=90°，∴∠CAE=∠ABD在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD；（2）成立∵∠BD A=∠AEC=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α，∴∠CAE=∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE；（3）由（2）知，△ADB≌△CAE，∴BD=EA，∠DBA=∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°，∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE，∵BF=AF在△DBF和△EAF中，，∴△DBF≌△EAF（SAS），∴DF=EF，∠BFD=∠AFE，∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形．∴DF=EF．【点评】本题主要考查全等三角形的判定和性质，由条件证明三角形全等是解题的关键．附加题（满分20分，计入总分）29．已知：a﹣b=2，2a2+a﹣4=0，则=﹣2．【考点】分式的化简求值．【专题】计算题；分式．【分析】由a﹣b=2可得b=a﹣2，代入变为只含有a的代数式，由2a2+a﹣4=0可得，再代入前面化简后的式子，即可解答本题．【解答】解：∵a﹣b=2，∴b=a﹣2．∴=+==．∵2a2+a﹣4=0，∴．∴=．故答案为：﹣2．【点评】本题考查分式的化简求值，解题的关键是可以将题目中的式子灵活变化，变为所求式子需要的条件30．已知：，则（b﹣c）x+（c﹣a）y+（a﹣b）z的值为0．【考点】分式的混合运算；解三元一次方程组．【专题】计算题；整体思想．【分析】设=k，从而可得b+c﹣a=①，c+a﹣b=②，a+b﹣c=③，然后用k、x、y、z分别表示出a、b、c，代入所求代数式就可解决问题．【解答】解：设=k，则b+c﹣a=①，c+a﹣b=②，a+b﹣c=③．由①+②+③得：a+b+c=④，由④﹣①得：a=，由④﹣②得：b=，由④﹣③得：c=，则原式=•x+•y+•z==0．故答案为0．【点评】本题考查了分式的混合运算，解三元一次方程组等知识，运用整体思想是解决本题的关键．31．等腰Rt△ABC中，∠BAC=90°，点A、点B分别是x轴、y轴两个动点，直角边AC 交x轴于点D，斜边BC交y轴于点E；（1）如图（1），若A（0，1），B（2，0），求C点的坐标；（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB=∠CDE （3）如图（3），在等腰Rt△ABC不断运动的过程中，若满足BD始终是∠ABC的平分线，试探究：线段OA、OD、BD三者之间是否存在某一固定的数量关系，并说明理由．【考点】全等三角形的判定与性质；等腰三角形的性质；直角三角形的性质．【分析】（1）过点C作CF⊥y轴于点F通过证△ACF≌△ABO得CF=OA=1，AF=OB=2，求得OF的值，就可以求出C的坐标；（2）过点C作CG⊥AC交y轴于点G，先证明△ACG≌△ABD就可以得出CG=AD=CD，∠DCE=∠GCE=45°，再证明△DCE≌△GCE就可以得出结论；（3）在OB上截取OH=OD，连接AH，由对称性得AD=AH，∠ADH=∠AHD，可证∠AHD=∠ADH=∠BAO=∠BEO，再证明△ACE≌△BAH就可以得出结论．【解答】（1）解：过点C作CF⊥y轴于点F，∴∠AFC=90°，∴∠CAF+∠ACF=90°．∵△ABC是等腰直角三角形，∠BAC=90°，∴AC=AB，∠CAF+∠BAO=90°，∠AFC=∠BAC，∴∠ACF=∠BAO．在△ACF和△ABO中，，∴△ACF≌△ABO（AAS）∴CF=OA=1，AF=OB=2∴OF=1∴C（﹣1，﹣1）；（2）证明：过点C作CG⊥AC交y轴于点G，∴∠ACG=∠BAC=90°，∴∠AGC+∠GAC=90°．∵∠CAG+∠BAO=90°，∴∠AGC=∠BAO．∵∠ADO+∠DAO=90°，∠DAO+∠BAO=90°，∴∠ADO=∠BAO，∴∠AGC=∠ADO．在△ACG和△ABD中∴△ACG≌△ABD（AAS），∴CG=AD=CD．∵∠ACB=∠ABC=45°，∴∠DCE=∠GCE=45°，在△DCE和△GCE中，，∴△DCE≌△GCE（SAS），∴∠CDE=∠G，∴∠ADB=∠CDE；（3）解：在OB上截取OH=OD，连接AH由对称性得AD=AH，∠ADH=∠AHD．∵∠ADH=∠BAO．∴∠BAO=∠AHD．∵BD是∠ABC的平分线，∴∠ABO=∠EBO，∵∠AOB=∠EOB=90°．在△AOB和△EOB中，，∴△AOB≌△EOB（ASA），∴AB=EB，AO=EO，∴∠BAO=∠BEO，∴∠AHD=∠ADH=∠BAO=∠BEO．∴∠AEC=∠BHA．在△AEC和△BHA中，，∴△ACE≌△BAH（AAS）∴AE=BH=2OA∵DH=2OD∴BD=2（OA+OD）．【点评】本题考查了全等三角形的判定与性质的运用，等腰直角三角形的性质的运用，直角三角形的性质的运用，解答时证明三角形的全等是关键．。

数学试卷考生须知1.本试卷共7页，第一部分共24道小题，第二部分共2道小题，满分110考分.考试时间100分钟.2.在试卷和答题卡上准确填写班级、姓名和学号.3.答案一律填写在答题卡上，在试卷上作答无效.4.在答题卡上，选择题和作图题用2B铅笔作答，其他试卷用黑色字迹签字笔作答.第一部分一、选择题(本大题共8小题，每小题2分，共16分)1.下列博物院的标识中是轴对称图形的是（）A. B. C. D.2.如图，用三角板作ABC的边AB上的高线，下列三角板的摆放位置正确的是（）A. B. C. D.3.下列计算正确的是（）A.()22244ab a b= B.236a a a⋅=C.224a a a+= D.()236239a b a b-=4.如图，ABC被木板遮住了一部分，其中6AB=，则AC BC+的值不可能是（）A.11B.9C.7D.55.根据分式的基本性质，分式aa b--可变形为（）A.aa b- B.aab+ C.aa b--D.ab a-6.如图，已知AD∥BC，欲用“边角边”证明△ABC≌△CDA，需补充条件（）A.AB=CDB.∠B=∠DC.AD=CBD.∠BAC=∠DCA7.如图，等腰直角三角形ABC 中，∠ABC ＝90°，BA ＝BC ，将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，连结CP ，过点A 作AH ⊥CP 交CP 的延长线于点H ，连结AP ，则∠PAH 的度数（）A.随着θ的增大而增大B.随着θ的增大而减小C.不变D.随着θ的增大，先增大后减小8.用两种或两种以上的正多边形没有重叠、没有缝隙地填充一个平面，并且每个顶点周围的多边形排列是相同的，所得到的图案叫做“半正密铺”图案．下图所示的三个“半正密铺”图案可以依次用记号()4,8,8，()3,6,3,6，()3,3,4,3,4表示．下列记号中，不能表示“半正密铺”图案的是（）A.()3,12,12B.()3,4,6,4 C.()3,3,4,12 D.()3,3,3,6二、填空题(本大题共8小题，每小题2分，共16分)9.计算：()0π 3.14-=______；132-=⎛⎫- ⎪⎝⎭______.10.要使分式53x -有意义，则x 的取值范围是______．11.已知一个多边形的每个内角都等于150°，则这个多边形的边数是___________．12.等腰三角形一腰上的高与另一腰的夹角是20°，则等腰三角形的顶角等于_____．13.如图，60ABC ∠=︒，3AB =，动点P 从点B 出发，以每秒1个单位长度的速度沿射线BC 运动，设点P 的运动时间为t 秒，当ABP 是直角三角形时，t =______．14.有两个正方形A 、B ，现将B 放在A 的内部得图甲，将A 、B 并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和10，则正方形A ，B 的面积之和为______．15.数学课上，老师提出问题，任意画两条长度不等的线段a 、b ，利用尺规作图作Rt △ABC ，使线段a 、b 分别为三角形的一条直角边和斜边，小勇所作之图如下：请你回答下列问题：（1）在以下作图步骤中，小勇的作图顺序可能是_____；（只填序号）①以B 为圆心，BA 的长为半径画弧，交射线AG 于点D ．②画直线BF ．③分别以点A ，D 为圆心，大于线段AB 的长为半径画弧，交于点F ．④以点A 为圆心，线段b 的长为半径画弧，交直线BF 于点C ，连接AC ．⑤画射线AG ，并在AG 上截取线段AB=a（2）∠ABC=90°的理由是_____．16.在等边ABC 中，M 、N 、P 分别是边AB 、BC 、CA 上的点（不与端点重合），对于任意等边ABC ，下面四个结论中：①存在无数个MNP △是等腰三角形；②存在无数个MNP △是等边三角形；③存在无数个MNP △是等腰直角三角形；④存在一个MNP △在所有MNP △中面积最小．所有正确结论的序号是_____________．二、解答题(本大题共8小题，第17题每小题4分，共24分，第18，19，20，21，23题每题6分，第22，24题每题7分，共68分)17.（1）计算：()2384ab a b ⎛⎫-⋅ ⎪⎝⎭；（2）计算：2202220202024-⨯(需简便运算)；（3）计算：()2215105x y xyxy -÷；（4）计算：()()()22322x y x y x y +-+-；（5）因式分解：()()22x m x n +-+；（6）因式分解：22363ax axy ay ++．18.如图，A ，C ，D 三点共线，ABC 和CDE 落在AD 的同侧，AB CE ∥，BC DE =，B D ∠=∠，求证：（1）ABC CDE △≌△；（2）AB CE AD+=.19.先化简：222142x x x÷--，再从0，1-，2-，2中选择一个合适的数作为x 的值代入求值．20.如图所示的正方形网格中，每个小正方形的边长都是1，ABC 顶点都在网格线的交点上，点A 坐标为()4,1--，点B 坐标为()1,1--，点C 坐标为()3,3-.（1）画出ABC 关于y 轴的对称图形111A B C △；（2）请写出点B 关于x 轴对称点的坐标为______；（3）点P 在y 轴上，且ABP 与ABC 的面积相等，则点P 的坐标为______.21.中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编（图1），书中记载了大量几何作图题，所有内容均用浅近的文言文表述，第一编记载了这样一道几何作图题：原文释义甲乙丙为定直角．以乙为圆心，以任何半径作丁戊弧；以丁为圆心，以乙丁为半径画弧得交点己；再以戊为圆心，仍以原半径画弧得交点庚；乙与己及庚相连作线．如图2，ABC∠为直角．以点B为圆心，以任意长为半径画弧，交射线BA，BC分别于点D，E；以点D为圆心，以BD长为半径画弧与 DE交于点F；再以点E为圆心，仍以BD长为半径画弧与DE交于点G；作射线BF，BG．（1）根据以上信息，请你用不带刻度的直尺和圆规，在图2中完成这道作图题（保留作图痕迹，不写作法）；（2）根据（1）完成的图，直接写出DBG∠，GBF∠，FBE∠的大小关系．22.如图(1)，等边ABC中，D是AB边上的动点，作等边DCE△使得点B和点E位于CD两侧，连接AE.（1）DBC△与EAC全等吗？请说明你的理由；（2）求证：AE BC∥；（3）如图（2），将（1）动点D运动到边BA的延长线上，其余条件不变，请问是否仍有AE BC∥？证明你的猜想.23.阅读下列材料：对于多项式22x x+-，如果我们把1x=代入此多项式，发现22x x+-的值为0，这时可以确定多项式中有因式()1x-；同理，可以确定多项式中有另一个因式()2x+，于是我们可以得到：()()2212x x x x+-=-+．又如：对于多项式2232x x--，发现当2x=时，2232x x--的值为0，则多项式2232x x--有一个因式()2x-，我们可以设()()22322x x x mx n--=-+，解得2m=，1n=．于是我们可以得到：()()2232221x x x x --=-+．请你根据以上材料，解答以下问题：（1）当x =______时，多项式265x x --的值为0，所以多项式265x x --有因式______，从而因式分解265x x --=______；（2）以上这种因式分解的方法叫“试根法”，常用来分解一些比较复杂的多项式，请你尝试用试根法分解多项式：376x x -+．24.如图，已知ABC 是等边三角形，点E 在射线AB 上且2ACE a Ð=，在射线CE 上取点D 使得CD CA =，连接AD 并延长交射线CB 于点F ．（1）当0260α︒<<︒时，①DAB ∠=______；(请用含α的代数式表示)②求证：CE BE CF +=；（2）当602120α︒<<︒时，请根据题意补全图形，并写出线段CE ，BE ，CF 间的数量关系______.第二部分附加题(共10分)25.找规律.第1组：114133+=，222435+=；第2组：1183515+=，22281517+=；第3组：11125735+=，222123537+=；……（1）请写出第4组等式_____，_______；（2）请写出第n 组等式______，______；（3）若()222960396050k k +=>，则k =______．26.为了比较两个实数的大小，常用的方法是判定这两个数的差的符号，我们称这种方法为“作差比较法”．要比较两个代数式的大小，同样可以采用类似的方法，因此，可以利用不等式比较大小．如果要证明A B >，只需要证明0A B ->；同样的，要证明A B <，只需要证明0A B -<．例如：小明对于命题：任意的实数a 和b ，总有222a b ab +≥，当a b =并且只有a b =时，等号成立，给出了如下证明：证明：∵()22220a b ab a b +-=-≥，∴222a b ab +≥，当a b =并且只有a b =时，等号成立．（1）请仿照小明的证明方法，证明如下命题：若a ，b ，x ，0y ≥，且a x ≥，则()()()2222a x b y a b x y -+-≤+-+．（2）若120n a a a ≥≥≥≥ ，120n b b b ≥≥≥≥ ，且12121n n a a a b b b +++=+++= ，求()()()2221122n n a b a b a b -+-++- 的最大值．数学试卷第一部分一、选择题(本大题共8小题，每小题2分，共16分)1.下列博物院的标识中是轴对称图形的是（）A. B. C. D.【答案】B【分析】根据轴对称的定义进行判断即可.【详解】解：根据轴对称图形的概念可知,选项A 、C 、D 不是轴对称图形,故选B.【点睛】本题考查轴对称图形的概念.判定轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.如图，用三角板作ABC 的边AB 上的高线，下列三角板的摆放位置正确的是（）A. B. C. D.【答案】B【分析】根据三角形高的画法进行判断即可．【详解】解：选项A ，C ，D 中都不是ABC 的边AB 上的高，故选：B ．【点睛】此题考查了三角形的高，熟练掌握三角形高的画法是解题的关键．3.下列计算正确的是（）A.()22244ab a b = B.236a a a ⋅=C.224a a a+= D.()236239a b a b -=【答案】D 【分析】根据同底数幂的乘法法则、积的乘方、合并同类项等知识点逐项判定即可．【详解】解：A ．()222416ab a b =，故A 错误，不符合题意；B ．235a a a ⋅=，故B 错误，不符合题意；C ．2222a a a +=，故C 错误，不符合题意；D ．()236239a ba b -=，故D 正确，符合题意．故选D ．【点睛】本题主要考查了同底数幂的乘法、积的乘方、合并同类项法则等知识点，熟练掌握相关运算法则是解答本题关键．4.如图，ABC 被木板遮住了一部分，其中6AB =，则AC BC +的值不可能是（）A.11B.9C.7D.5【答案】D 【分析】根据三角形三边关系判断即可．【详解】解：∵AB =6，∴AC +BC ＞AB =6，∴11，9，7都满足，5不满足，故选D ．【点睛】本题考查了三角形三边关系，解题的关键是掌握三角形两边之和大于第三边．5.根据分式的基本性质，分式a ab --可变形为（）A.a a b - B.aa b + C.aa b -- D.ab a-【答案】D【分析】根据分式的基本性质即可求出答案．【详解】a a a b b aa ab ----==-，故选：D ．【点睛】本题考查分式的基本性质，解题的关键是熟练运用分式的基本性质，本题属于基础题型．6.如图，已知AD ∥BC ，欲用“边角边”证明△ABC ≌△CDA ，需补充条件（）A.AB =CDB.∠B =∠DC.AD =CBD.∠BAC =∠DCA【答案】C 【分析】由平行线的性质可知DAC BCA ∠=∠，再由AC 为公共边，即要想利用“边角边”证明△ABC ≌△CDA ，可添加AD =CB 即可．【详解】∵AD ∥BC ，∴DAC BCA ∠=∠．∵AC 为公共边，∴只需AD =CB ，即可利用“边角边”证明△ABC ≌△CDA ．故选：C ．【点睛】本题考查平行线的性质，三角形全等的判定．理解“边角边”即为两边及其夹角是解答本题的关键．7.如图，等腰直角三角形ABC 中，∠ABC ＝90°，BA ＝BC ，将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，连结CP ，过点A 作AH ⊥CP 交CP 的延长线于点H ，连结AP ，则∠PAH 的度数（）A.随着θ的增大而增大B.随着θ的增大而减小C.不变D.随着θ的增大，先增大后减小【答案】C【分析】由旋转的性质可得BC ＝BP ＝BA ，由等腰三角形的性质和三角形内角和定理可求∠BPC +∠BPA ＝135°＝∠CPA ，由外角的性质可求∠PAH ＝135°﹣90°＝45°，即可求解．【详解】解：∵将BC 绕点B 顺时针旋转θ（0°＜θ＜90°），得到BP ，∴BC ＝BP ＝BA ，∴∠BCP ＝∠BPC ，∠BPA ＝∠BAP ，∵∠CBP +∠BCP +∠BPC ＝180°，∠ABP +∠BAP +∠BPA ＝180°，∠ABP +∠CBP ＝90°，∴∠BPC +∠BPA ＝135°＝∠CPA ，∵∠CPA ＝∠AHC +∠PAH ＝135°，∴∠PAH ＝135°﹣90°＝45°，∴∠PAH 的度数是定值，故选：C ．【点睛】本题考查了旋转的性质，等腰三角形的性质，三角形的外角性质，灵活运用这些性质解决问题是本题的关键．8.用两种或两种以上的正多边形没有重叠、没有缝隙地填充一个平面，并且每个顶点周围的多边形排列是相同的，所得到的图案叫做“半正密铺”图案．下图所示的三个“半正密铺”图案可以依次用记号()4,8,8，()3,6,3,6，()3,3,4,3,4表示．下列记号中，不能表示“半正密铺”图案的是（）A.()3,12,12B.()3,4,6,4C.()3,3,4,12D.()3,3,3,6【答案】D【分析】本题考查的是密铺，正多边形的内角度数，解题的关键是要掌握“密铺图形的公共顶点处的角的度数和为360︒”【详解】解：观察可知“半正密铺”图案记号()4,8,8，则表示由一个正方形和两个正八边形组成的；A.()3,12,12是由一个正三角形、两个正十二边形组成，正三角形的一个内角为60︒，正十二边形的每一个内角为：(122)18015012-⨯︒=︒，∴60150150360︒+︒+︒=︒，能表示“半正密铺”图案，则不符合题意；B.()3,4,6,4是由一个正三角形、两个正方形和一个正六边形组成，正三角形的一个内角为60︒，正方形的内角为90︒，正六边形的内角为：(62)1801206-⨯︒=︒，∴60902120360︒+︒⨯+︒=︒，能表示“半正密铺”图案，则不符合题意；C.()3,3,4,12是由两个正三角形、一个正方形、一个正十二边形组成，正三角形的一个内角为60︒，正方形的内角为90︒，正十二边形的每一个内角为：(122)18015012-⨯︒=︒，60290150360∴︒⨯+︒+︒=︒，能表示“半正密铺”图案，则不符合题意；D.()3,3,3,6是由三个正三角形、一个正六边形组成，正三角形的一个内角为60︒，正六边形的内角为：(62)1801206-⨯︒=︒，603120300∴︒⨯+︒=︒，不能表示“半正密铺”图案，符合题意；故选：D ．二、填空题(本大题共8小题，每小题2分，共16分)9.计算：()0π 3.14-=______；132-=⎛⎫- ⎪⎝⎭______.【答案】①.1②.23-【分析】直接利用零指数幂的性质以及负整数指数幂的性质计算，即可得出答案．【详解】解：()0π 3.141-=；13322-⎛⎫- ⎪=-⎝⎭．故答案为：1；23-10.要使分式53x -有意义，则x 的取值范围是______．【答案】x ≠3【分析】根据分式有意义，分母不为0，列不等式求解即可.【详解】解：根据题意，要使分式53x -有意义，必须使x-3≠0,解得：x ≠3故答案为：x ≠3【点睛】本题考查了分式有意义，分母不为0．11.已知一个多边形的每个内角都等于150°，则这个多边形的边数是___________．【答案】12##十二【分析】根据正n 边形的每个内角的度数为()2180n n-⋅︒，列出方程进行计算即可．【详解】解：由题意，得：()2180150n n -⋅︒=⋅︒，解得：12n =，∴这个多边形的边数是12；故答案为：12．【点睛】本题考查正多边形的内角问题．熟练掌握正n 边形的每个内角的度数为()2180n n -⋅︒，是解题的关键．12.等腰三角形一腰上的高与另一腰的夹角是20°，则等腰三角形的顶角等于_____．【答案】110°或70°【分析】等腰三角形的高相对于三角形有三种位置关系：三角形内部；三角形的外部；三角形的边上．根据条件可知第三种高在三角形的边上这种情况不成立，因而应分两种情况进行讨论．【详解】当高在三角形内部时（如图1），∠ABD =20°，∴∠A =90°-∠ABD =70°，∴顶角是70°；当高在三角形外部时（如图2），∠ABD =20°，∴∠CAB =90°+∠ABD =110°，∴顶角是110°．故答案为：70°或110°．【点睛】此题主要考查等腰三角形的性质，熟记三角形的高相对于三角形的三种位置关系是解题的关键，本题易出现的错误是只是求出70°一种情况，把三角形简单的认为是锐角三角形．因此此题属于易错题．13.如图，60ABC ∠=︒，3AB =，动点P 从点B 出发，以每秒1个单位长度的速度沿射线BC 运动，设点P 的运动时间为t 秒，当ABP 是直角三角形时，t =______．【答案】32或6【分析】此题考查含30︒的直角三角形的性质，关键是根据在直角三角形中，30︒角所对的直角边等于斜边的一半解答．【详解】解：①当90APB ∠=︒时，过A 作⊥AP BC ，∵60ABC ∠=︒，3AB =，∴1322BP AB ==，∴33122t =÷=，②当90BAP '∠=︒时，过A 作P A AB '⊥时，∵60ABC ∠=︒，3AB =，∴26BP AB '==，∴616t =÷=，故答案为：32或6．14.有两个正方形A 、B ，现将B 放在A 的内部得图甲，将A 、B 并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和10，则正方形A ，B 的面积之和为______．【答案】11【点睛】设正方形A 的边长为a ，正方形B 的边长为b ，由图形得出关系式求解即可．【详解】解：设正方形A 的边长为a ，正方形B 的边长为b ，由图甲得()2221a b b a b ---=即2221a b ab +-=，由图乙得()22210a b a b +--=即210ab =，∴2211a b +=，故答案为：11．【分析】本题主要考查了完全平方公式的几何背景，解题的关键是根据图形得出数量关系．15.数学课上，老师提出问题，任意画两条长度不等的线段a 、b ，利用尺规作图作Rt △ABC ，使线段a 、b 分别为三角形的一条直角边和斜边，小勇所作之图如下：请你回答下列问题：（1）在以下作图步骤中，小勇的作图顺序可能是_____；（只填序号）①以B 为圆心，BA 的长为半径画弧，交射线AG 于点D ．②画直线BF ．③分别以点A ，D 为圆心，大于线段AB 的长为半径画弧，交于点F ．④以点A 为圆心，线段b 的长为半径画弧，交直线BF 于点C ，连接AC ．⑤画射线AG ，并在AG 上截取线段AB=a（2）∠ABC=90°的理由是_____．【答案】（1）⑤①③②④；（2）到线段两端点距离相等的点在线段垂直平分线上．【分析】（1）根据尺规作直角三角形的方法进行判断即可；（2）根据线段垂直平分线的性质即可判断．【详解】解：（1）根据尺规作图的方法可知作图的顺序为：⑤①③②④，故答案为⑤①③②④；（2）根据作图方法可知BC 是线段AD 的垂直平分线，根据线段垂直平分线的性质可知∠ABC=90°，故∠ABC=90°的理由是：到线段两端点距离相等的点在线段垂直平分线上，故答案为：到线段两端点距离相等的点在线段垂直平分线上．【点睛】本题考查了尺规作图——复杂作图、线段垂直平分线的性质等，掌握基本作图的方法是解题的关键．16.在等边ABC 中，M 、N 、P 分别是边AB 、BC 、CA 上的点（不与端点重合），对于任意等边ABC ，下面四个结论中：①存在无数个MNP △是等腰三角形；②存在无数个MNP △是等边三角形；③存在无数个MNP △是等腰直角三角形；④存在一个MNP △在所有MNP △中面积最小．所有正确结论的序号是_____________．【答案】①②③【分析】根据题意作图，根据所画图形判定即可解决问题．【详解】解：如图1中，满足AM ＝BN ＝PC ，∵ABC 是等边三角形∴AB =BC =CA ，∠A =∠C =∠B =60°∴AB -AM =BC -BN =CA -CP∴AP =CN =BM又∠A =∠C =∠B =60°∴△AMP ≌△CNP ≌△BMN∴MP =PN =MN∴△PMN 是等边三角形，这样的三角形有无数个．如图2中，当NM ＝NP ，∠MNP ＝90°时，△MNP 是等腰直角三角形，这样的三角形有无数个（见图3）．故①②③正确，△PNM 的面积不存在最小值．故答案为①②③．【点睛】本题考查等腰三角形的判定和性质，等边三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．二、解答题(本大题共8小题，第17题每小题4分，共24分，第18，19，20，21，23题每题6分，第22，24题每题7分，共68分)17.（1）计算：()2384ab a b ⎛⎫-⋅ ⎪⎝⎭；（2）计算：2202220202024-⨯(需简便运算)；（3）计算：()2215105x y xyxy -÷；（4）计算：()()()22322x y x y x y +-+-；（5）因式分解：()()22x m x n +-+；（6）因式分解：22363ax axy ay ++．【答案】（1）326a b -；（2）4；（3）32x y -；（4）21210xy y +；（5）()()2x m n m n ++-（6）()23a x y +．【分析】（1）根据单项式乘以单项式法则求解即可；（2）利用平方差公式求解即可；（3）根据多项式除以单项式法则求解即可；（4）首先利用平方差公式和完全平方公式求解，然后合并同类项即可；（5）利用平方差公式分解因式即可；（6）先提公因式，然后利用完全平方公式分解因式即可．【详解】（1）()2384ab a b ⎛⎫-⋅ ⎪⎝⎭326a b =-；（2）2202220202024-⨯()()220222022220222=--+()222202220222=--222202220222=-+4=；（3）()2215105x y xy xy-÷32x y =-；（4）()()()22322x y x y x y +-+-()222241294x xy y x y =++--x xy y x y 222212944=-+++21210xy y =+；（5）()()22x m x n +-+()()x m x n x m x n =++++--()()2x m n m n =++-；（6）22363ax axy ay ++()2232a x xy y =++()23a x y =+．【点睛】此题考查了单项式乘以单项式，平方差公式，多项式除以单项式，完全平方公式，因式分解，解题的关键是熟练掌握以上知识点．平方差公式：()()22a b a b a b +-=-，完全平方公式：()2222a b a ab b +=++，因式分解的方法有：提公因式法，平方差公式法，完全平方公式法，十字相乘法等．18.如图，A ，C ，D 三点共线，ABC 和CDE 落在AD 的同侧，AB CE ∥，BC DE =，B D ∠=∠，求证：（1）ABC CDE △≌△；（2）AB CE AD +=.【答案】18.证明见解析19.证明见解析【分析】本题考查了全等三角形的判定和性质，（1）根据平行线的性质可得A DCE ∠=∠，再利用AAS 证明ABC CDE △≌△即可；（2）利用全等三角形“对应边相等”的性质结合线段的和与差可得结论．【小问1详解】证明：∵AB CE ∥，A ECD ∴∠=∠，在ABC 和CDE 中，A ECDB D BC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS ABC CDE ∴ ≌；【小问2详解】证明：ABC CDE ≌△△，AB CD ∴=，AC CE =，AB CE CD AC AD ∴+=+=．19.先化简：222142x x x ÷--，再从0，1-，2-，2中选择一个合适的数作为x 的值代入求值．【答案】22x x +，=1x -时，原式2=-【分析】根据分式的运算法则化简计算即可．【详解】222142x x x÷--()()()2222x x x x =⨯-+-22x x =+．∵2x ≠±，∴=1x -时，()2122212x x ⨯-==-+-+．【点睛】本题考查了分式的化简求值，正确化简，适当选值是解题的关键．20.如图所示的正方形网格中，每个小正方形的边长都是1，ABC 顶点都在网格线的交点上，点A 坐标为()4,1--，点B 坐标为()1,1--，点C 坐标为()3,3-.（1）画出ABC 关于y 轴的对称图形111A B C △；（2）请写出点B 关于x 轴对称点的坐标为______；（3）点P 在y 轴上，且ABP 与ABC 的面积相等，则点P 的坐标为______.【答案】（1）作图见解析；（2）(11)-，（3）(03)，或(05)-，【分析】本题考查了坐标与图形，关于坐标轴对称的点的坐标特征，“关于x 轴对称，x 不变，关于y 轴对称，y 不变”，以及作轴对称图象，采用数形结合的方法，熟练掌握轴对称的性质以及面积相等采用同底等高的方法是解题的关键．【小问1详解】解： 点A 坐标为()4,1--，点B 坐标为()1,1--，点C 坐标为()3,3-.∴1(41)A -，，1(11)B -，，1(33)C ，，【小问2详解】解： 点B 坐标为()1,1--，∴点B 关于x 轴对称点的坐标为：(11)-，，故答案为：(11)-，；【小问3详解】解： ABP 与ABC 的面积相等，()111141222ABP ABC c P S S AB y AB AB y ∴==⨯⨯+=⨯⨯=⨯⨯+ ，∴5P y =-或3．又 点P 在y 轴上，当点P 在y 轴的正半轴时，P ∴的坐标为：(03)，当点P 在y 轴负半轴时，P ∴的坐标为：(05)-，，故答案为：(03)，或(05)-，21.中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编（图1），书中记载了大量几何作图题，所有内容均用浅近的文言文表述，第一编记载了这样一道几何作图题：原文释义甲乙丙为定直角．以乙为圆心，以任何半径作丁戊弧；以丁为圆心，以乙丁为半径画弧得交点己；再以戊为圆心，仍以原半径画弧得交点庚；乙与己及庚相连作线．如图2，ABC ∠为直角．以点B 为圆心，以任意长为半径画弧，交射线BA ，BC 分别于点D ，E ；以点D 为圆心，以BD 长为半径画弧与 DE 交于点F ；再以点E 为圆心，仍以BD 长为半径画弧与 DE 交于点G ；作射线BF ，BG ．（1）根据以上信息，请你用不带刻度的直尺和圆规，在图2中完成这道作图题（保留作图痕迹，不写作法）；（2）根据（1）完成的图，直接写出DBG ∠，GBF ∠，FBE ∠的大小关系．【答案】（1）见解析（2）DBG GBF FBE∠=∠=∠【分析】（1）根据题意作出图形即可；（2）连接DF ，EG ，可得BDF V 和BEG 均为等边三角形，60DBF EBG ∠=∠=︒，进而可得30DBG GBF FBE ∠=∠=∠=︒．【小问1详解】解：（1）如图：【小问2详解】DBG GBF FBE ∠=∠=∠．理由：连接DF ，EG 如图所示则BD =BF =DF ，BE =BG =EG即BDF V 和BEG 均为等边三角形∴60DBF EBG ∠=∠=︒∵90ABC ∠=︒∴30DBG GBF FBE ∠=∠=∠=︒【点睛】本题考查了尺规作图，根据题意正确作出图形是解题的关键．22.如图(1)，等边ABC 中，D 是AB 边上的动点，作等边DCE △使得点B 和点E 位于CD 两侧，连接AE .（1）DBC △与EAC 全等吗？请说明你的理由；（2）求证：AE BC ∥；（3）如图（2），将（1）动点D 运动到边BA 的延长线上，其余条件不变，请问是否仍有AE BC ∥？证明你的猜想.【答案】（1）会全等，理由见解析（2）证明见解析（3）AE BC ∥；证明见解析【分析】本题主要考查了全等三角形的判定和性质．（1）首先证明BCD ACE ∠=∠，然后利用SAS 证明DBC EAC △≌△即可；（2）根据全等的性质可得60EAC B ∠=∠=︒，进而可得EAC ACB ∠=∠，从而可得AE BC ∥；（3）利用等边三角形的性质可得BC AC =，DC CE =，60BCA DCE ∠=∠=︒，然后再证明DBC EAC △≌△，再推出EAC ACB ∠=∠，进而可得AE BC ∥．【小问1详解】解：DBC △和EAC 会全等；理由：60ACB ∠=︒ ，60DCE ∠=︒，60BCD ACD ∴∠=︒-∠，60ACE ACD ∠=︒-∠，BCD ACE ∴∠=∠，在DBC △和EAC 中，BC AC BCD ACE EC DC =⎧⎪∠=∠⎨⎪=⎩()SAS DBC EAC ∴ ≌；【小问2详解】证明：DBC EAC ≌，60EAC B ∴∠=∠=︒，又60ACB ∠=︒，EAC ACB ∴∠=∠，∴AE BC ∥；【小问3详解】解：结论：AE BC ∥理由：ABC 、EDC △为等边三角形BC AC ∴=，DC CE =，60BCA DCE ∠=∠=︒，BCA ACD DCE ACD ∠+∠=∠+∠，即BCD ACE ∠=∠，在DBC △和EAC 中，BC AC BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩，()SAS DBC EAC ∴ ≌，60EAC B ∴∠=∠=︒，又60ACB ∠=︒ ，EAC ACB ∴∠=∠，∴AE BC ∥．23.阅读下列材料：对于多项式22x x +-，如果我们把1x =代入此多项式，发现22x x +-的值为0，这时可以确定多项式中有因式()1x -；同理，可以确定多项式中有另一个因式()2x +，于是我们可以得到：()()2212x x x x +-=-+．又如：对于多项式2232x x --，发现当2x =时，2232x x --的值为0，则多项式2232x x --有一个因式()2x -，我们可以设()()22322x x x mx n --=-+，解得2m =，1n =．于是我们可以得到：()()2232221x x x x --=-+．请你根据以上材料，解答以下问题：（1）当x =______时，多项式265x x --的值为0，所以多项式265x x --有因式______，从而因式分解265x x --=______；（2）以上这种因式分解的方法叫“试根法”，常用来分解一些比较复杂的多项式，请你尝试用试根法分解多项式：376x x -+．【答案】（1）1，()1x -，()()165x x -+（2）()()()376132x x x x x -+=-+-【分析】本题考查多项式乘以多项式，因式分解；熟练掌握多项式与多项式，理解阅读材料的方法，借助多项式乘法进行因式分解是解题的关键．因式分解的方法有：提公因式法，平方差公式法，完全平方公式法，十字相乘法等．【小问1详解】（1）当1x =时，多项式265x x --的值为0，所以多项式265x x --有因式()1x -，设()()()22165x mx n mx n m x n x x -++---==-∴6m =，5n =，∴因式分解()()256165x x x x -=+-，故答案为：1，()1x -，()()165x x -+；【小问2详解】当1x =时，3760x x -+=∴376x x -+有有一个因式()1x -，当3x =-时，3760x x -+=∴设()()()37613x x x x ax b -+=-++∵()()()13x x ax b -++()()223x x ax b =+-+3222233ax bx ax bx ax b=+++--()()322233ax b a x b a x b=+++--∴()()233272633ax b a x b a x b x x -+=+++--∴1a =，36b -=，即2b =-∴()()()376132x x x x x -+=-+-．24.如图，已知ABC 是等边三角形，点E 在射线AB 上且2ACE a Ð=，在射线CE 上取点D 使得CD CA =，连接AD 并延长交射线CB 于点F ．（1）当0260α︒<<︒时，①DAB ∠=______；(请用含α的代数式表示)②求证：CE BE CF +=；（2）当602120α︒<<︒时，请根据题意补全图形，并写出线段CE ，BE ，CF 间的数量关系______.【答案】（1）①30α︒-；②见解析（2）CE CF BE=+【分析】（1）①根据等边三角形的性质得出()11802902CAD CDA a a ∠=∠=︒-=︒-，根据角度关系得出906030DAB CAD CAB a a ∠=∠-∠=︒--︒=︒-；②延长BA ，使EG CE =，连接CG ，证明CBG ACF ≌，得出CF BG =，根据BG BE GE BE CE =+=+，即可证明结论；（2）根据题意补全图形，在CE 上截取EG BE =，连接BG ，证明BCG D CF ≌，得出CG CF =，即可证明CE CF BE =+．【小问1详解】解：①∵ABC 是等边三角形，∴AC AB BC ==，60ACB ABC CAB ∠=∠=∠=︒，∵CD CA =，2ACE a Ð=，∴()11802902CAD CDA a a ∠=∠=︒-=︒-，∴906030DAB CAD CAB a a ∠=∠-∠=︒--︒=︒-，故答案为：30α︒-．②延长BA ，使EG CE =，连接CG ，如图所示：则CGE ECG ∠=∠，∵602CEB CGE ECG CAB ACE a ∠=∠+∠=∠+∠=︒+，∴1302CGE ECG CEB a ∠=∠=∠=︒+，∵ADC DCF CFD ∠=∠+∠，∴()9060230CFD ADC DCF a a a ∠=∠-∠=︒--︒-=︒+，∴CGE CFD ∠=∠，∵AC BC =，60CBG ACF ∠=∠=︒，∴CBG ACF ≌，∴CF BG =，∵BG BE GE BE CE =+=+，∴CE BE CF +=；【小问2详解】解：CE CF BE =+，理由如下：在CE 上截取EG BE =，连接BG ，如图所示：∵ABC 是等边三角形，∴AC AB BC ==，60ACB ABC CAB ∠=∠=∠=︒，∵CD CA =，2ACE a Ð=，∴()11802902ADC CAD a a ∠=∠=︒-=︒-，∵1801202E CAE ACE a ∠=︒-∠-∠=︒-，又∵BE EG =，∴()1180302EBG BGE E a ∠=∠=︒-∠=︒+，∴18090CBG ABC EBG a ∠=︒-∠-∠=︒-，∴CBG CDA ∠=∠，∵AC CD =，AC BC =，∴BC DC =，∵BCG DCB ∠=∠，∴BCG D CF ≌，∴CG CF =，∴CE CG EG CG BE CF BE =+=+=+．故答案为：CE CF BE =+．【点睛】本题主要考查了等边三角形的性质，三角形全等的判定和性质，等腰三角形的判定和性质，三角形内角和定理，三角形外角的性质，解题的关键是作出辅助线，数形结合，熟练掌握三角形全等的判定方法，证明BCG D CF ≌．第二部分附加题(共10分)25.找规律.第1组：114133+=，222435+=；第2组：1183515+=，22281517+=；第3组：11125735+=，222123537+=；……（1）请写出第4组等式_____，_______；（2）请写出第n 组等式______，______；（3）若()222960396050k k +=>，则k =______．【答案】（1）11167963+=，222166365+=（2）2114212141n n n n +=-+-，()()()2222244141n n n +-=+（3）196【分析】（1）根据所给算式可直接写出第4组等式；（2）由所给算式可知，第n 组的第一个等式左边是()21n -和()21n +的倒数和，右边的分子是()21n -与()21n +的和，分母是()21n -与()21n +的积；第二个等式左边是第一个等式右边分子、分母的平方和，右边是()21n -与()21n +的积加上2再平方；（3）根据296034491=⨯-，296054491=⨯+，结合（2）中规律可得449196k =⨯=．【小问1详解】解：第4组等式为：11167963+=，222166365+=，故答案为：11167963+=，222166365+=；【小问2详解】解：由分析可知，第n 组等式为：()()211212142121212141n n n n n n n n -+++==-+-+-，()()()()222222244141241n n n n +-=-+=+，故答案为：2114212141n n n n +=-+-，()()()2222244141n n n +-=+；【小问3详解】解：∵296034491=⨯-，296054491=⨯+，∴()()()22222449144910k k +⨯-=⨯+>，由（2）可知()()()2222244141n n n +-=+，∴449196k =⨯=，故答案为：196．【点睛】本题考查了数字类规律探索，根据所给算式，总结归纳出一般性规律是解题的关键．26.为了比较两个实数的大小，常用的方法是判定这两个数的差的符号，我们称这种方法为“作差比较法”．要比较两个代数式的大小，同样可以采用类似的方法，因此，可以利用不等式比较大小．如果要证明A B >，只需要证明0A B ->；同样的，要证明A B <，只需要证明0A B -<．例如：小明对于命题：任意的实数a 和b ，总有222a b ab +≥，当a b =并且只有a b =时，等号成立，给出了如下证明：证明：∵()22220a b ab a b +-=-≥，∴222a b ab +≥，当a b =并且只有a b =时，等号成立．（1）请仿照小明的证明方法，证明如下命题：若a ，b ，x ，0y ≥，且a x ≥，则()()()2222a x b y a b x y -+-≤+-+．（2）若120n a a a ≥≥≥≥ ，120n b b b ≥≥≥≥ ，且12121n n a a a b b b +++=+++= ，求()()()2221122n n a b a b a b -+-++- 的最大值．。

一、选择题1．如图，在等腰三角形ABC 中，,36,AB AC A D =∠=是AC 的中点，ED AC ⊥交AB 于点E ，已知6,2AC DE ==，则BC 的长为（ ）A ．13B ．32C ．40D ．20 2．已知锐角AOB ∠，如图（1）在射线OA 上取一点C ，以点O 为圆心，OC 长为半径作弧MN ，交射线OB 于点D ，连接CD ；（2）分别以点,C D 为圆心，CD 长为半径作弧，两弧交于点P ，连接,CP DP ； （3）作射线OP 交CD 于点Q ．根据以上作图过程及所作图形，有如下结论：①//CP OB ；②2CP QC =；③AOP BOP ∠=∠；④CD OP ⊥．其中正确的有（ ）A ．①②③④B ．②③④C ．③④D ．③3．下列命题中，是假命题的是（ ）A ．能够完全重合的两个图形全等B ．两边和一角对应相等的两个三角形全等C ．三个角都相等的三角形是等边三角形D ．等腰三角形的两底角相等4．如图，在ABC 中，90C ∠=︒，30B ∠=︒，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M 和N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ．则下列说法中正确的个数是（ ） ①AD 是BAC ∠的平分线；②60ADC ∠=︒；③点D 在AB 的中垂线上；④:2:5DAC ABC S S =△△A ．1B ．2C ．3D ．45．如图，在ABC 中，34B ∠=︒，BCA ∠的平分线CD 交AB 于点D ，若DE 垂直平分BC 交BC 于点E ，则A ∠的度数为（ ）A ．90°B ．68°C ．78°D ．88°6．如图，ABC ∆和CDE ∆都是等边三角形，且62EBD ∠=，则AEB ∠的度数是（ ）A ．124B ．122C ．120D ．118 7．若a ，b 为等腰ABC 的两边，且满足350a b --=，则ABC 的周长为（ ）A ．11B ．13C ．11或13D ．9或15 8．等腰三角形两边长为2和4，则其周长为（ ） A ．8 B ．10 C ．8或10D ．12 9．已知点(),3M a ，点()2,N b 关于x 轴对称，则2020()a b +的值（ ）A ．3-B ．1-C ．1D ．3 10．如图，ABC 中，AB AC =，AB 的垂直平分线DE 分别交AB 、AC 于点E 、D ，若52BAC ∠=︒，则DBC ∠=（ ）．A ．12︒B ．14︒C ．16︒D ．18︒11．如图，在ABC 中，18cm AC =，20cm BC =，点M 从点A 出发以每秒2cm 的速度向点C 运动，点N 从点C 出发以每秒1.6cm 的速度向点B 运动，其中一个动点到达终点时，另一个动点也随之停止运动，当CMN △是以MN 为底的等腰三角形时，则这时等腰三角形的腰长是（ ）A ．5cmB ．6cmC ．7cmD ．8cm 12．在直角坐标系中，已知A （2，－2），在y 轴上确定一点P ，使△AOP 为等腰三角形，则符合条件的点P 共有（ ）A ．2个B ．3个C ．4个D ．5个二、填空题13．如图，长方形纸片ABCD ，点E ，F 分别在边AB ，CD 上，连接EF ，将BEF ∠对折B 落在直线EF 上的点'B 处，得折痕EM ；将AEF ∠对折，点A 落在直线EF 上的点'A 得折痕EN ，若6215'BEM ∠=︒，则AEN ∠=____．14．如图，在ABC 中，AB 的垂直平分线DE 分别与,AB BC 交于点,D E ，AC 的垂直平分线FG 分别与,BC AC 交于点,F G ，10,3BC EF ==，则AEF 的周长是________．15．如图，点C 在DE 上，,,45B E AB AE CAD BAE ∠=∠=∠=∠=︒，则ACB =∠_____________．16．如图，在ABC 中，AB=AC ，40A ∠=，CD //AB ，则BCD ∠的度数是______°．17．如图所示的网格是正方形网格，点A ，B ，C ，D ，O 是网格线交点，那么AOB ∠___________COD ∠（填“＞”，“＜”或“＝”）．18．如图，在22⨯的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形．图中的ABC 为格点三角形，在图中最多能画出______个不同的格点三角形与ABC 成轴对称．19．如图，已知 O 为△ABC 三边垂直平分线的交点，且∠A ＝50°，则∠BOC 的度数为_____度．20．如图，在ABC 中，30EFD ∠=︒，且AEF AFE ∠=∠，CFD CDF ∠=∠，则B 的度数为______．三、解答题21．如图，在Rt ABC △中，90ACB ∠=︒，CA CB =，M 是AB 的中点，点D 在BM 上，AE CD ⊥，BF CD ⊥，垂足分别为E ，F ，连接EM ．（1）求证：CE BF =；（2）求证：AEM DEM ∠=∠．22．如图，在ABC 中，90,C AC BC ∠=︒>，D 为AB 的中点，E 为CA 延长线上一点，连接DE ，过点D 作DF DE ⊥，交BC 的延长线于点F ，连接EF ．作点B 关于直线DF 的对称点G ，连接DG ．（1）依题意补全图形；（2）若ADF α∠=．①求EDG ∠的度数（用含α的式子表示）；②请判断以线段,,AE BF EF 为边的三角形的形状，并说明理由．23．如图，90BAD CAE ∠=∠=︒，AB AD =，AE AC =，AF CB ⊥，垂足为F ．（1）求证：ABC ADE △≌△；（2）求FAE ∠的度数．24．如图，（1）在网格中画出ABC ∆关于y 轴对称的111A B C ∆；（2）写出ABC ∆关于x 轴对称的222A B C ∆的各顶点坐标；（3）在y 轴上确定一点P ，使PAB ∆周长最短．只需作图，保留作图痕迹．25．如图，在ABC 中，90C ∠=︒．（1）用尺规作出BAC ∠的平分线，并标出它与边BC 的交点D （保留作图痕迹，不写作法）；（2）若30B ∠=︒，1CD =，求BD 的长．26．如图，在平面直角坐标系中，(1,5)A -，(1,0)B -，(4,3)C -．（1）作出ABC 关于y 轴的对称图形A B C '''；（2）写出点A '，B '，C '的坐标；（3）在y 轴上找一点P ，使PA PC +最短（不写作法）．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE ，然后根据等边对等角可得∠ECD=∠A ，再根据三角形内角和等于180°求出∠B=72°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BEC=72°，然后根据等角对等边的性质和勾股定理解答．【详解】解：∵D 是AC 的中点，ED AC ⊥交AB 于点E ，∴ED 垂直平分AC ，∴AE=CE ，∴∠ECD=∠A ，∵∠A=36°，∴∠ECD=36°，∵AB=AC ，∠A=36°，∴∠B=12（180°-36°）=72°， ∵∠ECD=∠A=36°，∴∠BEC=∠ECD+∠A=36°+36°=72°，∴∠B=∠BEC ，∴BC=CE ，∵AE=CE ，ED ⊥AC ，∴CD=12AC =3， 在Rt △CED 中，∴故选A ．【点睛】本题考查了等腰三角形三线合一的性质，勾股定理，线段垂直平分线上的点到线段两端点的距离相等的性质，等边对等角以及等角对等边的性质，熟练掌握有关性质是解题的关键． 2．B解析：B【分析】由作图易判断射线OP 为AOB ∠的角平分线，又为CD 的垂直平分线，CDP 为等边三角形，由它们的性质逐项判断即可．【详解】由作图（1）（2）可知OC=OD ，CP=DP ，∴射线OP 为AOB ∠的角平分线，又为CD 的垂直平分线．∴即=AOP BOP ∠∠，CD OP ⊥，故③④正确；由作图（2）可知CP=CD=DP ，即CDP 为等边三角形，又∵CD OP ⊥，∴CP=2CQ ，故②正确；若//CP OB ，则=CPO BOP ∠∠，又∵=AOP BOP ∠∠，∴=CPO AOP ∠∠，∴OC=PC ，故只有当OC=PC 时，//CP OB ，故①错误．综上，正确的有②③④．故选：B ．【点睛】本题考查角平分线的判定和性质，线段垂直平分线的判定和性质，等边三角形的判定和性质．理解作图步骤隐藏的已知信息是解答本题的关键．3．B解析：B【分析】根据全等三角形的定义去判断A ，全等三角形性质去判断B ，等边三角形和等腰三角形性质判断C 、D ，依次分析解答即可．【详解】解：A.由全等三角形的定义得到：能够完全重合的两个图形全等，此命题是真命题；B.两边和一角对应相等且该角是两边的夹角的两个三角形全等，此命题是假命题；C. 三个角都相等的三角形是等边三角形，此命题是真命题；D. 等腰三角形的两底角相等，此命题是真命题；故选B ．【点睛】此题主要考查了命题的真假，关键是掌握相关定义和性质．注意SAS 时，一角必须是两边的夹角．4．C解析：C【分析】根据题意作图可知：AD 是BAC ∠的平分线，由此判断①正确；先求得∠BAC=60︒，由AD 是BAC ∠的平分线，求得∠CAD=∠BAD=30B ∠=︒，即可得到60ADC ∠=︒，判断②正确；过点D 作DE ⊥AB 于E ，根据∠BAD=30B ∠=︒，证得△ABD 是等腰三角形，得到AE=BE ，即可判断③正确；证明Rt △ACD ≌Rt △AED ，得到S △ACD =S △AED ，根据等底同高得到S △AED =S △BED ，即可得到:1:3DAC ABC S S =，判断④错误．【详解】解：由题意得：AD 是BAC ∠的平分线，故①正确；∵90C ∠=︒，30B ∠=︒，∴∠BAC=60︒，∵AD 是BAC ∠的平分线，∴∠CAD=∠BAD=30B ∠=︒，∴60ADC ∠=︒，故②正确；过点D 作DE ⊥AB 于E ，∵∠BAD=30B ∠=︒，∴AD=BD ，∴△ABD 是等腰三角形，∴AE=BE ，∴点D 在AB 的中垂线上，故③正确；∵AD 是BAC ∠的平分线，DC ⊥AC ，DE ⊥AB ，∴CD=DE ，∠C=∠AED=90︒，又∵AD=AD ，∴Rt △ACD ≌Rt △AED ，∴S △ACD =S △AED ，∵AE=BE ，DE ⊥AB ，∴S △AED =S △BED ，∴:1:3DAC ABC S S =，故④错误；故选：C ．．【点睛】此题考查角平分线的作图方法及性质应用，全等三角形的判定及性质，线段垂直平分线的判定，等腰三角形的判定及性质，三角形内角和定理，熟练掌握各部分知识并综合应用是解题的关键．5．C解析：C【分析】由垂直平分线的性质，可得∠DCB=34B ∠=︒，由角平分线的定义得∠ACB=2∠DCB=68°，进而即可求解．【详解】∵DE 垂直平分BC 交BC 于点E ，∴DB=DC ，∴∠DCB=34B ∠=︒，∵CD 是BCA ∠的平分线，∴∠ACB=2∠DCB=68°，∴∠A=180°-34°-68°=78°，【点睛】本题主要考查垂直平分线的性质，等腰三角形的性质，角平分线的定义以及三角形内角和定理，熟练垂直平分线的性质定理，是解题的关键．6．B解析：B【分析】由等边三角形的性质，得到AC=BC ，CE=CD ，∠ACB=∠ECD=60°，然后证明△ACE ≌△BCD ，则∠CAE=∠CBD ，由角的关系，求出∠ABE+∠BAE=58°，即可得到答案．【详解】解：如图：∵ABC ∆和CDE ∆都是等边三角形，∴AC=BC ，CE=CD ，∠ACB=∠ECD=60°，∴∠ACE+∠BCE=∠BCD+∠BCE=60°，∴∠ACE=∠BCD ，∴△ACE ≌△BCD ，∴∠CAE=∠CBD ，即6062BAE EBC ︒-∠=︒-∠，∵60EBC ABE ∠=︒-∠，∴6062(60)BAE ABE ︒-∠=︒-︒-∠，∴58ABE BAE ∠+∠=︒，∴18058122AEB ∠=︒-︒=︒；故选：B ．【点睛】本题考查了等边三角形的性质，全等三角形的判定和性质，三角形的内角和定理，以及角的和差关系，解题的关键是掌握所学的知识，正确求出58ABE BAE ∠+∠=︒． 7．C解析：C【分析】根据非负数的意义列出关于a 、b 的方程并求出a 、b 的值，再根据b 是腰长和底边长两种情况讨论求解．解：根据题意得a-3=0，b-5=0，解得a=3，b=5，（1）若3是腰长，则三角形的三边长为：3、3、5，能组成三角形，周长为：3+3+5=11；（2）若3是底边长，则三角形的三边长为：3、5、5，能组成三角形，周长为3+5+5=13．故选：C ．【点睛】本题考查了等腰三角形的性质、非负数的性质及三角形三边关系；解题主要利用了非负数的性质，分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形作出判断．8．B解析：B【分析】由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析．【详解】解：①当2为腰时，2+2=4，不能构成三角形，故此种情况不存在；②当4为腰时，符合题意，则周长是2+4+4=10．故选：B ．【点睛】本题考查的是等腰三角形的性质和三边关系，解答此题时注意分类讨论，不要漏解． 9．C解析：C【分析】根据关于坐标轴对称的规律，关于谁对称谁不变，另一个坐标变为相反数即可获得a 和b 的值，然后即可得解．【详解】∵点(),3M a ，点()2,N b 关于x 轴对称∴2a =，3b =-∴()()20182018231a b +=-= 故选：C ． 【点睛】本题考查了在坐标平面直角坐标系中关于x 轴对称的点的坐标的变化规律，点(),x y 关于x 轴对称的点的坐标为()x y -，，熟记规律即可得到正确答案．10．A【分析】由在△ABC 中，AB ＝AC ，∠BAC ＝52°，又由DE 是AB 的垂直平分线，即可求得∠ABD 的度数，继而求得答案．【详解】在ABC 中，AB AC =，52BAC ∠=︒，()11802ABC ACB BAC ∴∠=∠=⨯︒-∠ ()1180522=⨯︒-︒64=︒， DE 为AB 的中垂线，AD BD ∴=，52ABD BAC ∴∠=∠=︒，12DBC ABC ABD ∴∠=∠-∠=︒．故选A ．【点睛】此题考查了线段垂直平分线的性质以及等腰三角形的性质．此题难度适中，注意掌握数形结合思想的应用．11．D解析：D【分析】要求运动后得到的等腰三角形的腰长，首先要求出动点所运动的时间．我们可以设M 、N 运动的时间为x 秒．【详解】设M 、N 运动的时间为x 秒．当CMN △是以MN 为底的等腰三角形时，,182, 1.6CM CN CM x CN x ==-= 即182 1.6x x -=，解得5x =．∴腰长为5 1.68cm ⨯=故选D ．【点睛】此题主要考查学生对等腰三角形的性质这一知识点的理解和掌握，此题涉及到动点，有一定的拔高难度．12．C解析：C【分析】如果OA 为等腰三角形的腰，有两种可能，①以O 为圆心OA 为半径的圆弧与y 轴有两个交点，以A 为圆心AO 为半径的圆弧与y 轴有一个交点；②如果OA 为等腰三角形的底，只有一种可能，作线段OA 的垂直平分线，与y 轴有一个交点，所以符合条件的点一共4个．分二种情况进行讨论：①当OA为等腰三角形的腰时，以O为圆心OA为半径的圆弧与y轴有两个交点，以A为圆心OA为半径的圆弧与y轴有一个交点；②当OA为等腰三角形的底时，作线段OA的垂直平分线，与y轴有一个交点，∴符合条件的点一共4个，故选：C．【点睛】本题考查等腰三角形的性质，解题关键是根据两腰相等，分四种情况进行讨论．二、填空题13．【分析】先根据折叠的性质求出∠B′EM根据邻补角求出∠AEA′再根据折叠的性质即可求出∠AEN【详解】解：根据折叠可知：EM平分∠BEB′∴∠B′EM=∠BEM=62°15′∴∠AEA′=180°-解析：2745'【分析】先根据折叠的性质求出∠B′EM，根据邻补角求出∠AEA′，再根据折叠的性质即可求出∠AEN．【详解】解：根据折叠可知：EM平分∠BEB′，∴∠B′EM=∠BEM=62°15′，∴∠AEA′=180°-2×62°15′=55°30′，EN平分∠AEA′，∴∠AEN=∠A′EN=12∠AEA′=12×55°30′=27°45′，故答案为：27°45′．【点睛】本题考查了折叠的性质，邻补角的定义，以及角的计算、度分秒的换算，解决本题的关键是掌握折叠的性质．14．16【分析】根据线段的垂直平分线的性质得到EB＝EAAF＝FC根据三角形的周长公式计算得到答案【详解】解：∵DE是AB边的垂直平分线∴EB＝EA∵FG是AC边的垂直平分线∴AF＝FC∴△AEF的周长解析：16【分析】根据线段的垂直平分线的性质得到EB＝EA、AF＝FC，根据三角形的周长公式计算，得到答案．【详解】解：∵DE是AB边的垂直平分线，∴EB ＝EA ，∵FG 是AC 边的垂直平分线，∴AF ＝FC ，∴△AEF 的周长=AF+AE+EF=FC+BE+EF=EC+EF+BE+EF=BC+2EF=10+6=16，故答案为：16．【点睛】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．15．【分析】由条件可证得△ABC ≌△AED 则可求得∠ACB=∠ADEAD=AC 再利用等腰三角形的性质可求得答案【详解】解：∵∠CAD=∠BAE ∴∠CAD+∠CAE=∠BAE+∠CAE 即∠BAC=∠DAE解析：67.5【分析】由条件可证得△ABC ≌△AED ，则可求得∠ACB=∠ADE ，AD=AC ，再利用等腰三角形的性质可求得答案．【详解】解：∵∠CAD=∠BAE ，∴∠CAD+∠CAE=∠BAE+∠CAE ，即∠BAC=∠DAE ，在△ABC 和△AED 中，B E AB AEBAC EAD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△AED （ASA ），∴AD=AC ，∠ACB=∠ADE ，∴∠ACD=∠ADC ，∵∠CAD=45°，∴∠ADC=67.5°，∴∠ACB=67.5°，故答案为：67.5．【点睛】本题主要考查全等三角形的判定和性质及等腰三角形的性质，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（全等三角形的对应边相等、对应角相等）是解题的关键．16．110【分析】根据等腰三角形的性质求出∠B=70º再根据平行线的性质求出的度数【详解】解：∵AB=AC ∴∠B=∠ACB==70º∵//∴+∠B=180º∴=110º故答案为：110【点睛】本题考查了解析：110【分析】根据等腰三角形的性质，求出∠B=70º，再根据平行线的性质，求出BCD ∠的度数．【详解】解：∵AB=AC ，40A ∠=，∴∠B=∠ACB=180402︒-︒=70º， ∵CD //AB ， ∴BCD ∠+∠B=180º，∴BCD ∠=110º，故答案为：110．【点睛】本题考查了等腰三角形的性质和平行线的性质，熟练运用已知条件，准确推理计算，是解决这类题的关键．17．>【分析】如图过点B 作BE ⊥AC 于E 证明△BOE 是等腰直角三角形得到∠BOE=过点C 作CF ⊥OC 使FC=OC 证明△OCF 是等腰直角三角形得到∠FOC=由图知∠FOC>∠COD 即可得到∠AOB>∠CO解析：>【分析】如图，过点B 作BE ⊥AC 于E ，证明△BOE 是等腰直角三角形，得到∠BOE=45︒，过点C 作CF ⊥OC ，使FC=OC ，证明△OCF 是等腰直角三角形，得到∠FOC=45︒，由图知∠FOC>∠COD ，即可得到∠AOB>∠COD ．【详解】如图，过点B 作BE ⊥AC 于E ，∵OB=OE=2，∠BEO=90︒，∴△BOE 是等腰直角三角形，∴∠BOE=45︒，过点C 作CF ⊥OC ，使FC=OC ，∴∠FCO=90︒，∴△OCF 是等腰直角三角形，∴∠FOC=45︒，由图知∠FOC>∠COD ，∴∠AOB>∠COD ，故答案为：>．．【点睛】此题考查等腰直角三角形的判定及性质,角的大小比较，根据图形确定角的位置关系是解题的关键．18．5【分析】画出所有与成轴对称的三角形【详解】解：如图所示：和对称和对称和对称和对称和对称故答案是：5【点睛】本题考查轴对称图形解题的关键是掌握画轴对称图形的方法解析：5【分析】画出所有与ABC成轴对称的三角形．【详解】解：如图所示：ABC和ADC对称，ABC和EBD△对称，ABC和DEF对称，ABC和DCB对称，ABC和CDA对称，故答案是：5．【点睛】本题考查轴对称图形，解题的关键是掌握画轴对称图形的方法．19．100【分析】连接AO延长交BC于D根据线段垂直平分线的性质可得OB=OA=OC再根据等腰三角形的等边对等角和三角形的外角性质可得∠BOC=2∠A即可求解【详解】解：连接AO延长交BC于D∵O为△A解析：100【分析】连接AO延长交BC于D，根据线段垂直平分线的性质可得OB=OA=OC，再根据等腰三角形的等边对等角和三角形的外角性质可得∠BOC=2∠A，即可求解．【详解】解：连接AO延长交BC于D，∵O 为△ABC 三边垂直平分线的交点，∴OB=OA=OC，∴∠OBA=∠OAB ，∠OCA=∠OAC ，∵∠BOD=∠OBA+∠OAB=2∠OAB ，∠COD=∠OCA+∠OAC=2∠OAC ，∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2∠BAC ，∵∠BAC=50°，∴∠BOC=100°．故答案为：100．【点睛】本题考查线段垂直平分线的性质、等腰三角形的性质、三角形的外角性质，属于基础题型，熟练掌握它们的性质和运用是解答的关键．20．120°【分析】设∠ABC=根据等腰三角形的性质以及三角形的内角和定理即可得到结论【详解】设∠ABC=∴∵∴∴∴∴∴∴故答案为：120°【点睛】本题考查了三角形内角和定理等腰三角形的性质等知识解题的解析：120°【分析】设∠ABC=x ，根据等腰三角形的性质以及三角形的内角和定理即可得到结论．【详解】设∠ABC=x ，∴180A C x ∠+∠=︒-．∵AFE AEF ∠=∠，CFD CDF ∠=∠，∴2180A AFE ∠+∠=︒，2180C CFD ∠+∠=︒，∴()()22360A C AFE CFD ∠+∠+∠+∠=︒，∴22180AFE CFD x ∠+∠=︒+， ∴1902AFE CFD x ∠+∠=︒+， ∴118090302EFD x ⎛⎫∠=︒-︒+=︒ ⎪⎝⎭， ∴120x =︒，故答案为：120°．【点睛】本题考查了三角形内角和定理，等腰三角形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 三、解答题21．（1）证明见解析；（2）证明见解析【分析】（1）先证明CAE BCF ∠=∠，再证明CAE BCF ≌△△，从而可得结论；（2）连接CM ，FM ，先证明ECM FBM ∠=∠，再证明CME BMF ≌△△，可得EM FM =，EMC FMB ∠=∠，再证明FME 是等腰直角三角形，可得45MED ∠=︒，从而可得结论．【详解】证明：（1）AE CD ⊥，BF CD ⊥，90AEC CFB ∴∠=∠=︒．90ACB ∠=︒， 90BCF ACE ACE EAC ∴∠+∠=︒=∠+∠CAE BCF ∴∠=∠．CA BC =．()CAE BCF AAS ∴≌△△．CE BF ∴=．（2）连接CM ，FM在Rt ABC △中，CA CB =，点M 是AB 的中点，90,ACB ∠=︒BM AM ∴=，CM AB ⊥，CM 平分ACB ∠，45ACM BCM CBM CAM ∴∠=∠=∠=∠=︒，CM BM AM ==，由CAE BCF ≌△△可得：ACE CBF ∠=∠．,ACM ECM CBM MBF ∴∠+∠=∠+∠ECM FBM ∴∠=∠．又CE BF =，()CME BMF SAS ∴≌△△．EM FM ∴=，EMC FMB ∠=∠．90EMF FMB DME CME DME ∠=∠+∠=∠+∠=︒．FME ∴△是等腰直角三角形．45MED ∴∠=︒，90AED ∠=︒，45AEM DEM ∴∠=∠=︒．【点睛】本题考查的的三角形全等的判定与性质，等腰直角三角形的判定与性质，掌握以上知识是解题的关键．22．（1）补图见解析；（2）①90EDG α∠=︒-；②以线段,,AE BF EF 为边的三角形是直角三角形，理由见解析．【分析】(1)根据题意画出图形解答即可；(2) ①根据轴对称的性质解答即可；②根据轴对称的性质和全等三角形的判定和性质得出AE GE =，进而解答即可．【详解】解：（1）补全图形，如图所示，（2）①∵ADF α∠=，∴180BDF α∠=︒-，由轴对称性质可知，180GDF BDF α∠=∠=︒-，∵DF DE ⊥，∴90EDF ∠=︒，∴1809090EDG GDF EDF αα∠=∠-∠=︒--︒=︒-，②以线段,,AE BF EF 为边的三角形是直角三角形，如图,连接,GF GE ，由轴对称性质可知，,GF BF DGF B =∠=∠，∵D 是AB 的中点，∴AD BD =，∵GD BD =，∴AD GD =，∵90,GDE EDA DE DE α∠=∠=︒-=，∴GDE ADE ≌，∴,EGD EAD AE GE ∠=∠=，∵90EAD B ∠=︒+∠，∴90EGD B ∠=︒+∠，∴9090EGF EGD DGF B B ∠=∠-∠=︒+∠-∠=︒， ∴以线段,,GE GF EF 为边的三角形是直角三角形，∴以线段,,AE BF EF 为边的三角形是直角三角形．【点睛】此题考查全等三角形的判定和性质，关键是根据轴对称的性质和全等三角形的判定和性质解答．23．（1）见解析；（2）135FAE ∠=︒．【分析】（1）根据题意和题目中的条件可以找出△ABC ≌△ADE 的条件；（2）根据（1）中的结论和等腰直角三角形的定义可以得到∠FAE 的度数．【详解】证明：（1）∵∠BAD=∠CAE=90°，∴∠BAC+∠CAD=90°，∠CAD+∠DAE=90°，∴∠BAC=∠DAE ，在△BAC 和△DAE 中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAC ≌△DAE （SAS ）；（2）∵∠CAE=90°，AC=AE ，∴∠E=45°，由（1）知△BAC ≌△DAE ，∴∠BCA=∠E=45°，∵AF ⊥BC ，∴∠CFA=90°，∴∠CAF=45°，∴∠FAE=∠FAC+∠CAE=45°+90°=135°．【点睛】本题考查全等三角形的判定与性质及等腰三角形的性质，解答本题的关键是明确题意，找出全等所需要的条件．24．（1）如图所示，见解析；（2）222(3,2)(4,3)(1,1)A B C -----、、；（3）如图所示，见解析．【分析】（1）直接利用关于y 轴对称点的性质得出答案；（2）直接利用关于x 轴对称点的性质得出答案；（3）利用轴对称求最短路线的方法得出P 点位置即可．【详解】解：(1)如图所示：（2）∵A （-3，2），B （4-，3-），C （1-，1），∴关于x 轴对称的点分别为：222(3,2)(4,3)(1,1)A B C -----、、；（3）如图所示：【点睛】此题主要考查了利用轴对称求短路线以及轴对称变换，正确得出对应点位置是解题关键． 25．（1）见解析；（2）2【分析】（1）根据尺规作图的基本步骤进行画图，即可得到答案；（2）过点D 作DE AB ⊥，垂足为E ，由角平分线的性质定理，得到1DE CD ==，再由含30度直角三角形的性质，即可求出答案．【详解】（1）解：如图所示：（2）过点D 作DE AB ⊥，垂足为E ． AD 为BAC ∠的平分线，90C AED ∠=∠=︒．1DE CD ∴==．在Rt BED △中，30B ∠=︒，22BD DE ∴==．【点睛】本题考查了尺规作图——作角平分线，角平分线的性质，以及含30度的直角三角形的性质，解题的关键是掌握所学的知识，正确的作出图形．26．（1）见解析；（2）(1,5)A '，(1,0)B '，3)(4,C '；（3）见解析【分析】（1）根据轴对称的性质确定点,,A B C '''，顺次连线即可得到图形；（2）根据点的位置直接得解；（3）连接AC '与y 轴交于一点即为点P ，连接PC ，此时AP+PC 最短．【详解】解：（1）如图所示，A B C '''为所求作．（2）由图可得，(1,5)A '，(1,0)B '，4,3)C '．（3）如图所示，点P 即为所求作．【得解】此题考查轴对称的性质，轴对称作图，点的坐标，最短路径问题，正确理解轴对称的性质作出图形是解题的关键．。

北京四中初二上期中数学试卷DA B C ....2).把多项式.分解因式，结果正确的是( 2aa4 ?2)a 2)(a a(2)2)(a ((a 4)a a4(a 2) DB A C ....2 . ) 3•分式的取值范围是(有意义，则 x _______ 1 x B C DA1x 1 xx 1x 1 .... ).4 •点关于轴成轴对称的点的坐标是(y3)A(2,3)2) (2,(3, 3), 3)( 2,( 2 C A BD ....△中，已知 AA CAB 幻使5.在和，添加下列条件中的一个，不能， B AB A ABCABC △△ . . △). 一定成立的是( CABC ADB . . . . C B CAC ACC BCB B.)6 .下列各式中，正确的是( y yx a b1 bx A B .. --------------------------- -------------22abb 22yx yx 1x 3 D C . . ---------------------- --------- -------- ---------- 22) xy(x y3 9x x，则这个等腰三角形的周长为( ).7.等腰三角形的两边长分别为和63B C D A181515 ...或.1212的度数是(边上的高，则是， ，中，如图，8. ) BDDBC ACABC △ AB A36ACA 18 .B . 24C 30 .D 36.一、选择题1 •下列图形中，不是轴对称图形的是 ()•，为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证A 50.二、填空题 用科学记数法表示为•已知某种植物花粉的直径为纳米，即米，把 110.000035350000.000035 __________ ..12 .分解因式： 6x 3x3，在同一直线上，且、、、，是等边三角形，点 15.如图，已知 DE DFEBDCD91 30 3 . ). ，若A 30 .B 45.17数为（10•如图，和分别垂直平分和，则等于（ABMPPAQ QNAC130C 60 .D 75 . BAC度.的度•如图, ABCC 90△ Rt ，cm1DEB 75.C 80.D 105 .C △ ABCCG 贝 U•计算：.13 3|)|( 2 1) (一 20 1，中，、分别平分，、•如图，16ABC0 ABCBOACB II OMABC △.，则___________ ，的周长OMNIOcmBCACON II △ cm2112x 14xy 2y 3 __________ . 17 •已知，则代数式的面积为，则，且，平分如图18. 中，，的面积为4ABADACDABD3 △△ ABCAC三角运动的过程中，能使，点是点关于的对称点.在点与点不重合）最小时，是正方形点是直线上的一个动点，当PPDMNABCD PCMN上的一个动点（点，点是折线段20 •如图所示，长方形中,，E4EAB 3 4BCCA DABCD 为等腰—xyx 2xy yBAC2 △EPAABEPCB △.... 的位oA置共有__________ 个.形的点、解答题分解因式22)y(2 m92)mx( . . 21222xx( 1)4 . 22.计算abb32b )( . 23.4b3a9ax12 . 24. ----------------------------2x1 1 xal」］.25.先化简，再求值：，其中1 a 3 (1 ) ------------------------------ -------- 21 12aa a 83x 1 .解方程：26 . 21 x1x.,27 .已知：如图，,AE ADBAC AB AC DAE .求证：CEBD28. 列分式方程解应用题甲、乙两名学生练习计算机打字，甲打一篇字的文章与乙打一篇字的文章所用的时间相同•已9001000知甲每分钟比乙每分钟多打个字•问：甲、乙两人每分钟各打多少字？529. 小明在做课本中的一道题：如图，直线，所成的角跑到画板外面去了，你有什么办法量岀这1b a两条直线所成的角的度数？小明的做法是：如图，画，量岀直线与的夹角度数，即2PCbCP II a直线，所成角的度数. b a ()请写岀这种做法的理由. 1 ()小明在此基础上又进行了如下操作和探究(如图)：①以为圆心，任意长为半径画圆弧，分P23别交直线，于点，•②连结并延长交直线于点，请直接写岀图中所有与相PABADBA D3PCb a等的角.（）请在图画板内作岀“直线，所成的跑到画板外面去的角”的平分线（画板内的部分） 求b33a 作岀图形，并保留作图痕迹.30. （本题8分）（）如图（），已知：在中，，，直线经过点，丄直线，丄 BDA11CE △ ABC BAC 90 ACABII 直 线，垂足分别为点、•证明：.EDCEBD DE I （）如图（），将（）中的条件改为：在中，，、、三 点都在直线上，EAD221AC △ ABC ABI ，其中为任意锐角或钝角•请问结论且是否成立？如成 CE BDBDA AEC BAC DE 立•请你给岀证明•若不成立，请说明理由.（）拓展与应用：如图（），、是直线上的两动点（、、三点互不重合），点为EEAFDD BAC33I 平分线上的一点，且和均为等边三角形，连接、 ，若，BDBAC ACF CEAEC △ ABFBDA △求证：.EF DF，只要附加题2122 a b042a a •已知：.， ____________ 则 1 , ------------ b lazxy 2 .已知：的值为，贝U __________ , zb）（yac ）（bcx（） a -------- -------------- 「-------- ccb ab caa by，中，直角边3•等腰轴两个动点，交轴于点轴、、点，点分别是BADAC BAC 90ABCRt △ xx斜边•交轴于点yEBC点的坐标•，，求），若）如图（（0）B（2,,1）（0A11C 恰为，运动到使点连接当等腰），（）（如图中点时，求证：• DED22CDE ADBAC △ RtABC的平分线，试探究：）如图（不断运动的过程中，若满足（），在等腰始终是BDABCABC △ Rt33、三者之间是否存在某一固定的数量关系，并说明理由. 、线段BDODOA 6北京四中初二上期中数学试卷参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10答案 A A A B B D B A C C二、填空题 5 1 1. 103.5 2l)3(x 12.13. 4 14. 3 15. 15 16. 10 . 174 . 181.5 . 1945 . 204三、解答题22)x2)(m 9ym(2 21 .解:22)yx 9 (m 2)(.)y33 y)(x (m 2)(x222X 1)4 (x 22 .解：22)1 2x (x 1 2x)(x221)x( x 1)(.ab3b2b3.解：23 )( ----------- ------- ------ 4b9a 3a3ab39ab ---------- — ------------ 43bb227a2a3b _ _______ 32b6a1 . ___ ab2x21 .解：24 -------------------------- 2X1 x1x 1x2 ----------------------- ) )(1 (1xx81 . ------ x1a1 1a . 解:原式25 ( ) ____________ _____ ____ 21aa 1a a 1 2a11 aa1a 1 a. 』叮时，原式当.31 11 3a 321aa a122 1 aa21 8 x(x 3)(x 1)•解：，26 221 8 x 4x 3 x ，4x 4，1x ，1 x是原方程的增根，所以原方程无解•经检验：,27 .证明：J, BAE BAEBAC DAE , 即EACBAE DAB DAE BAE BAC 中，在和ADB △ AEC △ AE AD , EAC DAB ACAB ), •〜 (SAS △△ AECADB /.. CEBD个字，则甲每分钟打个字，28•解：设乙每分钟打5)(x X9001000 ,由题意得，——------------ xx 5得：，45 x检验：是原方程的解，且符合题意. 45x 个字，乙每分钟打个字•答：甲每人每分钟打455029 •解：（）两直线平行，同位角相等.1BDA(),2190AECPDA BDC9PAB ,）作线段（的垂直平分线EFAB3 是所求作的图形•则EF解：（1丨IBD CE •••,)v,,30.,又90 B AC , •••,90 BAD BAD CAE 90 ABD ? * •• ABD CAE中，在和CAE△ △ ABDCAE ABD ,90ADB CEA AC AB ),〈垄（・•• AAS △△ ABDCAE , •,AEBD> CE AD , •/ AE DE AD . •BD DE CE ()成立， 2 ,•/ AEC BAC BDA , •CAE 180 BAD BAD DBA •,ABD CAE在和中，CEA △ ADB △ABD CAE ,CEA ADB AB AC •••幻(),AAS △ ADBCEA △•-•, , BDAE CEAD •.DE AD BD CE AE()由()知，幻，2CEA △△ ADB3 /., , BD AECAE DBA 二•和均为等边三角形，ACF △△ABF •••,60 CAF ABF /., CAF CAE DBA ABF /., FAEDBF v, AFBF 在和中，EAFDBF △△ FB FA , FAE FBD BD AE •••和(),SAS △ DBF △ EAF ••,, AFEBFD DF EF •, BFD 60DFA DFA AFE DFE •为等边三角形. DEF △ •. EFDF附加题：10a2, 1 •解：由题可知，2a b a2—212 • _ ___________ ba 1a 2 2(a 1) -------------------------------2)a a 1)((3a ------------------ 22aa 3a ------------------------- a a 22_ 2. 2xyz，解：令2k ---------------------- --------------- --------------- c abb c a bc a则，，)bk(c ay )b c k(ax k(b c a) z 代入zb)y (a c)x (c a)(b , )ca b b) (a b)( b c)(bc a) (c a)(c a (222222 ,y //<“ F/ —Jbc ab a b cb ab ac cac a bc• 1OF卜AA7AcQG1,轴于点（）如图，过点作交，y2GCACCG 圍（2）轴于点,3.（）如图，过点作yCF F1C ），则幻（AASACFABO• 1) (C△ △,,••• 2OB 1AF CF OA，幻()贝0 ASA △△ ACGABD , •, GCG AD △ DCEGCE △，二G CDE . • CDE ADB CD ADB , •/ DCE GCE 45 ,) •心(SAS ()如图，在上截取，连接，AHOD3 OBOH ,(7),△ ABC 无法判定幻，、B CBC BACBBAAB A A △ 判定可利用幻 CBACJA占〉由对称性得，AHD AD AH ADH S(3) •••, BEO BAO ADH AHD •••, BHA AEC ,，又:ABH ABACCAEAASACE △△ BAH)OD BD2(OA12北京四中初二上期中数学试卷部分答案解析一、选择题1A【答案】.【解析】轴对称图形，是指在平面内沿一条直线折叠, 图形，这条直 选项经过折叠后不能重合•线就叫做对称轴. 直线两旁的部分能够完全重合的 A A .故选:2A【答案】.2 4a aa(a 4).【解析】A .故选：3A 【答案】.2 1x 1 Ox •，解得【解析】分式有意义，则分母 B------- x 1 A .故选:4【答案】.y3) A(2,3)y 3(2, 2x .【解析】点轴成轴对称的点的坐标其， ，即关于 B •故选:B5【答案】.△ ABC △ SAS ，幻，【解析】、，条件判定可利用 A CAAC ACBBAB A AAABC △ CSAS ,,、，条件(7),ACAB A A AAB △ ABCASA △.条件判定可利用，、，幻DCAB C CB AB AA AB .故选：6D【答案】.a bl b ，本选项错误，、【解析】A ----------------- --------- abb x yx y ，本选项错误，、B -------- ------------ 22x 31 C, 本选项错误，、 ------- -------- 2 9xx 3?2yyx x 、，本选项正确. D.故选：----------------------------------- ------------------------------ 2) y y(xx D7B【答案】.6 3363不能构成三角形.，底边为【解析】若腰为，贝9 1315 6 3636 •故腰为，则周长为，底边为B .故选:8A【答案】• AC AB ,【解析】•/ 1 B C (180 A) 72 , •••_ 2 AC BD , •/18C 90 DBC A .故选：9C【答案】.60 3 1 2 90.【解析】 C .故选：10C【答案】.130 A，【解析】J 50 C B, • QN AC ,和和分别垂直平分J ABMPAQ CQ •••, APBP QAC C ,•••, BPAB PAB QAC B C 50 , •PAQ BAC ( PAB QAC) 80 . • C .故选：二、填空题11 5【答案】.103.5 n iioio< a，这种记【解析】把一个绝对值小于(或者大于等于的形式(其中)的实数记为)110a 5 0.000035 .数法叫做科学记数法.把用科学记数法表示为103.5 5 .故答案为：10 3.521) 3(x 12【答案】.2221)X 1) XX 3 3(3( 2x3x 6 .【解析】2“ 3(x .故答案为：13【答案】.41 ••10() (2 1) | 3| 2 13 4 .【解析】一2 .故答案为：41414 3【答案】.DC CABAC ,,，平分【解析】•/ ABDEAD 1 DECD , •30B Rt△ BDE ,中，又•••在，二2 BD 2DE 3cmBD BC CD . • 3.故答案为：15 15【答案】.ABC △是等边三角形，【解析】J 120 ACD ACB 60,二，CDCG，又丁150 FDE CDG 30, •，又丁DEDF 15 E . •15.故答案为：16 10【答案】.ABC BO，平分【解析】J MBO ABO , • AB II OM，又丁BOM ABO , • MOB MBO , • OBOM , • NCON，同理可得10cmBC NC ON MN BM MN △ OMNOM .的周长为• 10.故答案为：17【答案】.411xy3 ，【解析】将等式两边同时乘以_ _ xyxy 3xy ，得y14xy 2 2X•----------------------- yxy x2xy 2(xy) 14 ---------------------------------- xyy 2 xxyxy 6 14 ---------------------------- xy 3 xy2 . 4 .故答案为：41518 1.5【答案】.ACDF，作，【解析】过ABDE D 是AD , • DFDE 13 AB SDE , J △—ADC 2 1.5.故答案为：BAC的平分线，J■ ABD23 DE，•一23 DF，•一21 SDF 1.5AC1945【答案】.，【解析】连结PB.¥SBCMN，垂直平分J PC PB,「. PBPC PD PD，二•两点之间直线最短，BD PD< PB ,••• BD PD< PC,「. PDPC，即的最短距离为BD BCDPC ，此时平分45PCD .二45.故答案为：20【答案】.4为等腰三角形一腰长时，【解析】①BP个，符合点的位置有E2 BC •的垂直平分线与以为圆心是为半径的圆的交点即是点PBBA C为顶点时，为底边时，② BP个，的位置有符合点E2 BCC •为圆心为半径的圆与以是以为圆心为半径的圆的交点即是点PBBA PC为顶点时，这样的等腰三角形不存在，③以为底边， B BC为半径的圆没有交点•为半径的圆与以为圆心因为以为圆心BBBA 16•故答案为：417。

一、选择题1．如图，已知30MON ︒∠=，点123,,...A A A 在射线ON 上，点123,,B B B …在射线OM 上，112223334,,...A B A A B A A B A ∆∆∆1n n n A B A +∆均为等边三角形，若11OA =，则778A B A ∆的边长为（ ）A ．16B ．32C ．64D ．1282．如图，AD 是ABC 的角平分线，DE AC ⊥，垂足为E ，//BF AC 交ED 的延长线于点F ，若BC 恰好平分ABF ∠，2AE BF =．下列四个结论中：①DE DF =；②DB DC =；③AD BC ⊥；④3AB BF =．其中正确的结论共有（ ）A ．4个B ．3个C ．2个D ．1个3．如图，在ABC 中，34B ∠=︒，BCA ∠的平分线CD 交AB 于点D ，若DE 垂直平分BC 交BC 于点E ，则A ∠的度数为（ ）A ．90°B ．68°C ．78°D ．88°4．如图，已知AD 为ABC 的高线，AD BC =，以AB 为底边作等腰Rt ABE △，且点E 在ABC 内部，连接ED ，EC ，延长CE 交AD 于F 点，下列结论：①EBD DAE ∠=∠；②ADE BCE ≌△△；③BD AF =；④BDE ACE S S =△△，其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个 5．平面直角坐标系中，点A (3，2)与点B 关于y 轴对称，则点B 的坐标为（ ） A ．(3，－2) B ．(－3，－2) C ．(－3，2) D ．(－2，3) 6．如图，已知点D 为ABC 内一点，CD 平分ACB ∠，BD CD ⊥，A ABD ∠=∠，若6AC =，4BC =，则BD 的长为（ ）A ．2B ．1.5C ．1D ．2.5 7．下列推理中，不能判断ABC 是等边三角形的是（ ） A ．A B C ∠=∠=∠B ．,60AB AC B =∠=︒ C ．60,60A B ∠=︒∠=︒D ．AB AC =，且B C ∠=∠8．已知一个等腰三角形ABC 的两边长为5，7，另一个等腰三角形ABC 的两边为23x -，35x -，若两个三角形全等，则x 的值为（ ）A ．5B ．4C ．4或5D ．1039．如图，已知AD 为ABC 的高线，AD BC =，以AB 为底边作等腰Rt ABE △，连接ED ，EC 延长CE 交AD 于F 点，下列结论：①DAE CBE ∠=∠；②CE DE ⊥；③BD AF =；④AED 为等腰三角形；⑤BDE ACE S S =△△，其中正确的有（ ）A ．①③⑤B ．①②④C ．①③④D ．①②③⑤ 10．如图，在Rt △ABC 中，∠BAC ＝90°，∠ACB ＝45°，点D 是AB 中点，AF ⊥CD 于点H ，交BC 于点F ，BE ∥AC 交AF 的延长线于点E ，给出下列结论：①∠BAE ＝∠ACD ，②△ADC ≌△BEA ，③AC ＝AF ，④∠BDE ＝∠EDC ，⑤BC ⊥DE ．上述结论正确的序号是（ ）A ．①②⑤B ．②④⑤C ．①②④D ．①②③ 11．下列图案中，是轴对称图形的是（ ）A ．B ．C ．D ．12．如图，△ABC 中，∠ABC ＝45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，DH ⊥BC 于H ，交BE 于G ，下列结论：①BD ＝CD ；②AD +CF ＝BD ；③CE ＝12BF ；④AE ＝BG ．其中正确的是（ ）A ．①②B ．①③C ．①②③D ．①②③④二、填空题13．如图，等腰ABC 的周长为36，底边上的高12AD ，则ABD △的周长为________．14．如图，在ABC 中，22A ∠=︒，D 为AB 边中点，E 为AC 边上一点，将ADE 沿着DE 翻折，得到A DE '，连接A B '．当A B A D ''=时，A EC '∠的度数为______．15．如图，ABC 中，AB BC =，点D 在线段BC 上（不与点,B C 重合）． 作法如下：①连接AD ，作AD 的垂直平分线分别交直线,AB AC 于点,P Q ，连接,DP DQ ，则APQ DPQ △≌△；②过点D 作AC 的平行线交AB 于点P ，在线段AC 上截取AQ ，使AQ DP =，连接,PQ DQ ，则APQ DQP △≌△；③过点D 作AC 的平行线交AB 于点P ，过点D 作AB 的平行线交AC 于点Q ，连接PQ ，则APQ DQP △≌△；④过点D 作AB 的平行线交AC 于点Q ，在直线AB 上取一点P ，连接DP ，使DP AQ =，连接PQ ，则APQ DPQ △≌△．以上说法一定成立的是__________．（填写正确的序号）16．如图，点A 为线段BC 外一动点，4BC =，1AB =，分别以AC 、AB 为边作等边ACD △、等边ABE △，连接BD ．则线段BD 长的最大值为______．17．如图，等边ABC 的边长为4，AD 是BC 边上的中线，F 是AD 边上的动点，E 是AC 边上一点．若2AE =，当EF CF +取最小值时，ECF ∠的度数为___________度．18．在△ABC 中，按以下步骤作图：①分别以A ，C 为圆心，以大于12AC 的同样长为半径画弧，两弧相交于两点M ，N ； ②作直线MN 交AB 于点D ，连结CD ．请回答：若BC=DC ，∠B=100°，则∠ACB 的度数为____． 19．如图，在四边形ABCD 中，130DAB ∠=︒，90D B ∠=∠=︒，点M ，N 分别是CD ，BC 上两个动点，当AMN 的周长最小时，AMN ANM ∠+∠的度数为_________．20．如图，在等边三角形ABC 中，CM 平分ACB ∠交AB 于点M ．（1）ACM ∠的大小=__________（度）；（2）AMC ∠的大小=__________（度）；（3）已知4AB =，点D 为射线CM 上一点，作∠DCE=60︒，()CE CD CD AB =≠，连接DE 交射线CB 于点F ，连接BD ，BE 当以B ，D ，M 为顶点的三角形与BEF 全等时，线段CF 的长为__________．三、解答题21．如图，△ABC 是等边三角形，E 、F 分别是边AB 、AC 上的点，且AE ＝CF ，且CE 、BF 交于点P ，且EG ⊥BF ，垂足为G ．（1）求证：∠ACE ＝∠CBF ；（2）若PG ＝1，求EP 的长度．22．已知在ABC 中，CAB ∠的平分线AD 与BC 的垂直平分线DE 交于点D ，DM AB ⊥于M ，DN AC ⊥交AC 的延长线于N ．（1）证明：BM CN =；（2）当80BAC ∠=︒时，求DCB ∠的度数．23．如图，在ABC 中，AB AC =，D 为AC 的中点，DE AB ⊥于点E ，DF BC ⊥于点F ，且DE DF =，连接BD ，点G 在BC 的延长线上，且CD CG =．（1）求证：ABC 是等边三角形；（2）若2CG =，求BC 的长．24．在如图所示的方格纸中，（1）作出ABC 关于MN 对称的111A B C △；（2）222A B C △是由111A B C △经过怎样的平移得到的？并求出111A B C △在平移过程中所扫过的面积．25．在ABC 中，AB AC =，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作ADE ，使AD AE =，DAE BAC ∠=∠，连接CE ． （1）如图，当点D 在线段BC 上，如果90BAC ∠=︒，则BCE ∠=______度．（2）设BAC α∠=，BCE β∠=．①如图，当点D 在线段BC 上移动时，α、β之间有怎样的数量关系？请直接写出你的结论．②如图，当点D 在线段BC 的反向延长线上移动时，α、β之间有怎样的数量关系？请说明理由．26．如图，点E 、F 在BC 上，BE CF =，AB DC =，B C ∠=∠，AF 与DE 交于点G ，求证：GE GF =．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据三角形的外角性质以及等边三角形的判定和性质得出OA 1=B 1A 1=1，OA 2=B 2A 2=2，OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，…进而得出答案．【详解】如图，∵△A 1B 1A 2是等边三角形，∴A 1B 1=A 2B 1，∠2=60°，∵∠MON=30°，∴∠MON=∠1=30°，∴OA 1=A 1B 1=1，∴A 2B 1= A 1A 2=1，∵△A 2B 2A 3是等边三角形，同理可得：OA 2=B 2A 2=2，同理；OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，OA 5=B 5A 5=4216=，…，以此类推：所以OA 7=B 7A 7=6264=，故选：C ．【点睛】本题主要考查了等边三角形的性质以及等腰三角形的性质，根据已知得出OA 2=B 2A 2=2， OA 3=B 3A 3=224=，OA 4=B 4A 4=328=，…进而发现规律是解题的关键．2．A解析：A【分析】根据角平分线的定义、平行线的性质得到∠ABC=∠C ，得到AC=AB ，根据等腰三角形的性质得到DB=DC ，AD ⊥BC ，证明△CDE ≌△BDF ，根据全等三角形的性质证明得到答案．【详解】解：∵BC 平分∠ABF ，∴∠ABC=∠FBC ，∵BF ∥AC ，∴∠C=∠FBC ，∴∠ABC=∠C ，∴AC=AB ，∵AC=AB ，AD 是△ABC 的角平分线，∴DB=DC ，AD ⊥BC ，故②、③说法正确；在△CDE 和△BDF 中，C DBF CD DBCDE BDF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△CDE ≌△BDF （ASA ），∴DE=DF ，故①说法正确；∵△CDE ≌△BDF ，∴BF=CE ，∵AE=2BF ，∴AB=AC=3BF ，故④说法正确；故选：A ．【点睛】本题考查的是等腰三角形的性质、全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．3．C解析：C【分析】由垂直平分线的性质，可得∠DCB=34B ∠=︒，由角平分线的定义得∠ACB=2∠DCB=68°，进而即可求解．【详解】∵DE 垂直平分BC 交BC 于点E ，∴DB=DC ，∴∠DCB=34B ∠=︒，∵CD 是BCA ∠的平分线，∴∠ACB=2∠DCB=68°，∴∠A=180°-34°-68°=78°，故选C ．【点睛】本题主要考查垂直平分线的性质，等腰三角形的性质，角平分线的定义以及三角形内角和定理，熟练垂直平分线的性质定理，是解题的关键．4．D解析：D【分析】由AD 为△ABC 的高线，可得∠CBE+∠ABE+∠BAD=90°，Rt △ABE 是等腰直角三角形， 可得90ABE BAD DAE ∠+∠+∠=︒，从而可判断①；由等腰Rt ABE △可得AE BE =，结合AD BC =，∠DAE=∠CBE ，可判断②；由△ADE ≌△BCE ，可得,ADE BCE ∠=∠ 再证明∠BDE=∠AFE ，结合EBD DAE ∠=∠，AE BE =， 证明△AEF ≌△BED ，可判断③；由△ADE ≌△BCE ，可得,DE CE = 由△AEF ≌△BED ，,EF DE = 证明,EF CE =从而可判断④．【详解】解：∵AD 为△ABC 的高线，∴∠CBE+∠ABE+∠BAD=90°，∵Rt △ABE 是等腰直角三角形，∴90ABE BAD DAE ∠+∠+∠=︒，∴∠DAE=∠CBE ，即EBD DAE ∠=∠，故①正确；∵Rt △ABE 是以AB 为底等腰直角三角形，∴AE=BE ，在△ADE 和△BCE 中，AE BE DAE CBE AD BC =⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△BCE （SAS ）； 故②正确；△ADE ≌△BCE ，,ADE BCE ∴∠=∠∵∠BDE=∠ADB+∠ADE ，∠AFE=∠ADC+∠ECD ，90ADB ADC ∠=∠=︒，∴∠BDE=∠AFE ，在△AEF 和△BED 中，FAE DBE AFE BDE AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△BED （AAS ），∴AF BD =； 故③正确；∵△ADE ≌△BCE ，∴,DE CE =△AEF ≌△BED ，,,AEF BED EF DE SS ∴== ,EF CE ∴=∴,AEF ACE SS = ∴ ,BDE ACES S =故④正确； 综上：正确的有①②③④．故选：D ．【点睛】本题考查的是三角形的内角和定理，三角形的中线与高的性质，三角形全等的判定与性质，等腰直角三角形的性质，掌握以上知识是解题的关键．5．C解析：C【分析】根据“关于y 轴对称的点，纵坐标相同，横坐标互为相反数”解答即可．【详解】解：点A （3，2）关于y 轴对称点的坐标为B （−3，2）．故选：C ．【点睛】本题考查了关于x 轴、y 轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x 轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y 轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．6．C解析：C【分析】延长BD与AC交于点E，由题意可推出BE=AE，依据等角的余角相等，即可得等腰三角形BCE，可推出BC=CE，AE=BE=2BD，根据AC=6，BC=4，即可推出BD的长度．【详解】解：延长BD与AC交于点E，∵∠A=∠ABD，∴BE=AE，∵BD⊥CD，∴BE⊥CD，∵CD平分∠ACB，∴∠BCD=∠ECD，∴∠EBC=∠BEC，∴△BEC为等腰三角形，∴BC=CE，∵BE⊥CD，∴2BD=BE，∵AC=6，BC=4，∴CE=4，∴AE=AC-EC=6-4=2，∴BE=2，∴BD=1．故选：C．【点睛】本题主要考查等腰三角形的判定与性质，比较简单，关键在于正确地作出辅助线，构建等腰三角形，通过等量代换，即可推出结论．7．D解析：D【分析】根据等边三角形的定义、判定定理以及三角形内角和定理进行判断．【详解】A、由“三个角都相等的三角形是等边三角形”可以判断△ABC是等边三角形，故本选项不符合题意；B 、由“有一个角是60°的等腰三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；C 、由“∠A ＝60°，∠B ＝60°”可以得到“∠A ＝∠B ＝∠C ＝60°”，则由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；D 、由“AB ＝AC ，且∠B ＝∠C”只能判定△ABC 是等腰三角形，故本选项符合题意． 故选：D ．【点睛】本题主要考查了等边三角形的判定和三角形内角和定理，属于基础题．（1）由定义判定：三条边都相等的三角形是等边三角形．（2）判定定理1：三个角都相等的三角形是等边三角形．（3）判定定理2：有一个角是60°的等腰三角形是等边三角形．8．B解析：B【分析】根据等腰ABC 的两边长为5，7，得到ABC 的三边长为5，7，7；或5,5,7；之后根据全等分2x-3=5，2x-3=7，3x-5=5，3x-5=7四种情况分类讨论，舍去不合题意的即可求解．【详解】解：∵等腰ABC 的两边长为5，7，∴ABC 的三边长为5，7，7；或5,5,7；由题意得另一个等腰三角形的两边为23x -，35x -，且与等腰ABC 全等（1）当2x-3=5时，解得x=4，则3x-5=7，符合题意；（2）当2x-3=7时，解得x=5，则3x-5=10，不合题意；（3）当3x-5=5时，解得103x =，则2x-3=113，不合题意； （4）当3x-5=7时，解得x=4，则2x-3=5，符合题意；综上所述：x 的值为4．故答案为：B【点睛】 本题考查了等腰三角形的定义，全等三角形的性质，根据题意分类讨论是解题关键． 9．D解析：D【分析】①由等腰直角三角形的性质可得出结论；②证明△ADE ≌△BCE ，可得∠AEC=∠DEB ，即可求得∠AED=∠BEG ，即可解题； ③证明△AEF ≌△BED 即可；④AE≠DE ，故④不正确；⑤易证△FDC 是等腰直角三角形，则CE=EF ，S △AEF =S △ACE ，由△AEF ≌△BED ，可知S △BDE =S △ACE ，所以S △BDE =S △ACE ．【详解】解：①∵AD 为△ABC 的高线，∴∠CBE+∠ABE+∠BAD=90°，∵Rt △ABE 是等腰直角三角形，∴∠ABE=∠BAE=∠BAD+∠DAE=45°，AE=BE ，∴∠CBE+∠BAD=45°，∴∠DAE=∠CBE ，故①正确②在△DAE 和△CBE 中，AE BE DAE CBE AD BC =⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△BCE （SAS ）；∴∠EDA=∠ECB ，∵∠ADE+∠EDC=90°，∴∠EDC+∠ECB=90°，∴∠DEC=90°，∴CE ⊥DE ；故②正确；③∵∠BDE=∠ADB+∠ADE ，∠AFE=∠ADC+∠ECD ，∴∠BDE=∠AFE ，∵∠BED+∠BEF=∠AEF+∠BEF=90°，∴∠BED=∠AEF ，在△AEF 和△BED 中，BDE AFE BED AEF AE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEF ≌△BED （AAS ），∴BD=AF ；故③正确；④∵AE≠DE ，∴△ADE 不是等腰三角形，⑤∵AD=BC ，BD=AF ，∴CD=DF ，∵AD ⊥BC ，∴△FDC 是等腰直角三角形，∵DE ⊥CE ，∴EF=CE ，∴S △AEF =S △ACE ，∵△AEF ≌△BED ，∴S △AEF =S △BED ，∴S △BDE =S △ACE ．故⑤正确；故选：D ．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，熟练掌握全等三角形的判定方法是解题的关键．10．A解析：A【分析】由90BAE FAC ∠+∠=︒，90ACD FAC ，得出BAE ACD ∠=∠，①正确；由ASA 证明ADC BEA ∆≅∆，②正确；由AC AB AF ，得出③不正确；由全等三角形的性质得出AD BE =，由AD BD =，得出BE BD =，45BDE EDC ，④不正确；由等腰直角三角形的三线合一性质得出⑤正确；即可得出结论．【详解】90BAC ∠=︒，45ACB ∠=︒，ABC ∴是等腰直角三角形，90BAE FAC ∠+∠=︒，AB AC ∴=，45CBA ACB ，AF CD ⊥，90AHC ∴∠=︒，90ACD FAC ，BAE ACD ∴∠=∠，①正确；//BE AC ，180ABE BAC ，90ABE ∴∠=︒，在ADC ∆和BEA ∆中，90CADABE ACAB ACD BAE()ADCBEA ASA ，②正确； AC AB AF ，∴③不正确； ADC BEA ， AD BE ∴=，点D 是AB 中点，AD BD ∴=，BE BD ∴=，45BDE EDC ，④不正确；90ABE ∠=︒，BE BD =，45CBA ∠=︒，45EBP，即BP平分ABE∠，△BDE为等腰直角三角形，∴根据“三线合一”可得BC⊥DE，⑤正确．故选：A．【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质、平行线的性质等知识，熟悉相关性质是解题的关键．11．C解析：C【分析】如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，据此进行判断即可．【详解】解：A、不是轴对称图形，故本选项不合题意；B、不是轴对称图形，故本选项不合题意；C、是轴对称图形，故本选项符合题意；D、不是轴对称图形，故本选项不合题意；故选：C．【点睛】本题主要考查了轴对称图形，判断轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．12．C解析：C【分析】根据∠ABC=45°，CD⊥AB可得出BD=CD，利用ASA判定Rt△DFB≌Rt△DAC，从而得出DF=AD，BF=AC．则CD=CF+AD，即AD+CF=BD；再利用ASA判定Rt△BEA≌Rt△BEC，得出CE=AE=12AC，又因为BF=AC所以CE=12AC=12BF，连接CG．因为△BCD是等腰直角三角形，即BD=CD．又因为DH⊥BC，那么DH垂直平分BC．即BG=CG．在Rt△CEG中，CG是斜边，CE是直角边，所以CE＜CG．即AE＜BG．【详解】解：∵CD⊥AB，∠ABC＝45°，∴△BCD是等腰直角三角形．∴BD＝CD．故①正确；在Rt△DFB和Rt△DAC中，∵∠DBF＝90°﹣∠BFD，∠DCA＝90°﹣∠EFC，且∠BFD＝∠EFC，∴∠DBF＝∠DCA．又∵∠BDF＝∠CDA＝90°，BD＝CD，∴△DFB≌△DAC．∴BF＝AC；DF＝AD．∵CD＝CF+DF，∴AD+CF＝BD；故②正确；在Rt△BEA和Rt△BEC中∵BE平分∠ABC，∴∠ABE＝∠CBE．又∵BE＝BE，∠BEA＝∠BEC＝90°，∴Rt△BEA≌Rt△BEC．∴CE＝AE＝12AC．又由（2），知BF＝AC，∴CE＝12AC＝12BF；故③正确；连接CG．∵△BCD是等腰直角三角形，∴BD＝CD又DH⊥BC，∴DH垂直平分BC．∴BG＝CG在Rt△CEG中，∵CG是斜边，CE是直角边，∴CE＜CG．∵CE＝AE，∴AE＜BG．故④错误．∴正确的选项有①②③；故选：C．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL．在复杂的图形中有45°的角，有垂直，往往要用到等腰直角三角形，要注意掌握并应用此点．二、填空题13．30【分析】根据等腰三角形的性质可求得AB+BD=18再结合AD=12即可求得的周长【详解】∵△ABC 为等腰三角形AD 为底边上的高∴AB=ACBD=DC ∵△ABC 的周长等于36∴AB+BD+DC+A解析：30【分析】根据等腰三角形的性质可求得AB+BD=18，再结合AD=12，即可求得ABD △的周长．【详解】∵△ABC 为等腰三角形，AD 为底边上的高，∴AB=AC ，BD=DC ，∵△ABC 的周长等于36，∴AB+BD+DC+AC=36，即AB+BD=18，∵AD=12，∴△ABD 的周长等于=AD+BD+AB=12+18=30．故答案为：30．【点睛】本题考查等腰三角形的性质．掌握等腰三角形三线合一（底边上的中线、底边上的高线，顶角的平分线重合）是解题关键．14．【分析】根据折叠的性质可得根据及折叠的性质可得为等边三角形再根据三角形的外角性质求解即可【详解】在中将沿着翻折交于点得到如图；∴∴∵为边中点∴为等边三角形∴∴∵即∴故答案为：【点睛】本题考查了全等三 解析：16【分析】根据折叠的性质可得AED A ED '≅，根据A B A D ''=及折叠的性质可得A BD '为等边三角形，再根据三角形的外角性质求解即可【详解】在ABC 中，22A ∠=︒，将ADE 沿着DE 翻折，A D '交AC 于点F ,得到A DE '，如图；∴AED A ED '≅ ∴1=,222AD A D AB EA D A ''===∠∠, ∵A B A D ''=，D 为AB 边中点，∴A B A D DB ''==,A BD '为等边三角形， ∴=60A DB '∠，∴60A AFD +=∠∠，∵=AFD EA D A EC ''+∠∠∠即()60A EA D A EC ''++=∠∠∠∴=16A EC '∠.故答案为：16【点睛】本题考查了全等三角形的性质，等边三角形的性质，三角形外角的性质等知识点，解题的关键是根据折叠找到对应的边角关系15．①②③【分析】根据题意画出图形再根据垂直平分线的性质平行线的性质和三角形全等的判定可以得证【详解】解：①如图∵PQ 为AD 的垂直平分线∴PA=PDQA=QD ∴在△APQ 和△DPQ 中∴△APQ ≌△DPQ解析：①②③【分析】根据题意画出图形，再根据垂直平分线的性质，平行线的性质和三角形全等的判定可以得证．【详解】解：①如图，∵PQ 为AD 的垂直平分线，∴PA=PD ，QA=QD ，∴ 在△APQ 和△DPQ 中，PA PD PQ PQ QA QD =⎧⎪=⎨⎪=⎩，∴△APQ ≌△DPQ （SSS ），①正确；②如图，∵PD ∥AC ， ∴∠DPQ=∠AQP ， ∴在△APQ 和△DQP 中， AQ DP AQP DPQ QP PQ =⎧⎪∠=∠⎨⎪=⎩， ∴△APQ ≌△DQP （SAS ），②正确 ； ③如图，∵PD ∥AC ， ∴∠DPQ=∠AQP ， 同理∠DQP=∠APQ ， ∴在△APQ 和△DQP 中， DPQ AQP PQ PQ DQP APQ ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△APQ ≌△DQP （ASA ），③正确 ； ④如图，△APQ ≌△DPQ 不成立，④错误；故答案为①②③．【点睛】本题考查三角形与平行线的综合应用，熟练掌握垂直平分线的性质，平行线的性质和三角形全等的判定是解题关键．16．5【分析】连接CE 根据等边三角形的性质得到AE ＝ABAC ＝AD ∠CAD ＝∠BAE ＝60°再利用SAS 推出△BAD ≌△EAC 由全等三角形的性质得到BD ＝EC 由于线段BD 长的最大值＝线段EC 的最大值即可解析：5【分析】连接CE,根据等边三角形的性质得到AE ＝AB ，AC ＝AD ，∠CAD ＝∠BAE ＝60°，再利用SAS 推出△BAD ≌△EAC ，由全等三角形的性质得到BD ＝EC ，由于线段BD 长的最大值＝线段EC 的最大值，即可得到结果．【详解】解：连接CE ，∵△ACD 与△ABE 是等边三角形，∴AE ＝AB ，AC ＝AD ，∠CAD ＝∠BAE ＝60°，∴∠CAD ＋∠BAC ＝∠BAE ＋∠BAC ，即∠BAD ＝∠EAC ，在△BAD 与△EAC 中，AD AC BAD EAC AB AE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BAD ≌△EAC （SAS ），∴BD ＝EC ；∵线段BD 长的最大值＝线段EC 的最大值，当线段EC 的长取得最大值时，点E 在CB 的延长线上，且BC ＝4，AB ＝1，∴线段BD 长的最大值为BE ＋BC ＝AB ＋BC ＝5．故答案为：5．【点睛】本题考查了三角形的综合问题，掌握等边三角形的性质、全等三角形的判定与性质，并正确的作出辅助线构造全等三角形是解题的关键．17．30【分析】由等边三角形三线合一可知：点B 和点C 关于AD 成轴对称连接BE 交AD 于点F 此时取得最小值进而求出的度数即可【详解】∵是等边三角形是边上的中线∴AD ⊥BCAD 平分∠BAC ∴点B 和点C 关于AD解析：30【分析】由等边三角形三线合一，可知：点B 和点C 关于AD 成轴对称，连接BE 交AD 于点F ，此时，EF CF +取得最小值，进而，求出ECF ∠的度数即可．【详解】∵ABC ∆是等边三角形，AD 是BC 边上的中线，∴AD ⊥BC ，AD 平分∠BAC ，∴点B 和点C 关于AD 所在直线成轴对称，连接BE 交AD 于点F ，则BF=CF ，∴EF CF +=EF+BF=BE ，即：此时，EF CF +取得最小值，∵等边ABC ∆的边长为4，2AE =，∴E 是AC 的中点，∴BE 平分∠ABC ，∵点F 是角平分线AD 与BE 的交点，∴CF 平分∠BCA ，即：∠FCA=12∠ACB=12×60°=30°， ∴∠ECC=30°．故答案是：30．【点睛】本题主要考查等边三角形中，两线段和最小时，求角的度数，通过轴对称，把两线段和化为两点之间的一条线段的长，是解题的关键．18．30°【分析】依据等腰三角形的性质即可得到∠BDC 的度数再根据线段垂直平分线的性质即可得出∠A 的度数进而得到∠ACB 的度数【详解】解：根据题意如图：∵BC=DC ∠ABC=100°∴∠BDC=∠CBD解析：30°【分析】依据等腰三角形的性质，即可得到∠BDC的度数，再根据线段垂直平分线的性质，即可得出∠A的度数，进而得到∠ACB的度数．【详解】解：根据题意，如图：∵BC=DC，∠ABC=100°，∴∠BDC=∠CBD=180°-100°=80°，根据题意得：MN是AC的垂直平分线，∴CD=AD，∴∠ACD=∠A，∴∠A=1(18080)50⨯︒-︒=︒，2∴∠ACB=∠CBD-∠A=80°-50°=30°．故答案为：30°．【点睛】此题主要考查了线段垂直平分线的性质以及等腰三角形的性质．解题时注意线段垂直平分线上任意一点，到线段两端点的距离相等．19．100°【分析】作点A关于BC的对称点A′关于CD的对称点A″根据轴对称确定最短路线问题连接A′A″与BCCD的交点即为所求的点MN利用三角形的内角和定理列式求出∠A′+∠A″再根据轴对称的性质和三解析：100°【分析】作点A关于BC的对称点A′，关于CD的对称点A″，根据轴对称确定最短路线问题，连接A′A″与BC、CD的交点即为所求的点M、N，利用三角形的内角和定理列式求出∠A′+∠A″，再根据轴对称的性质和三角形的一个外角等于与它不相邻的两个内角的和可得∠AMN+∠ANM=2（∠A′+∠A″），然后计算即可得解．【详解】解：如图，作点A关于BC的对称点A′，关于CD的对称点A″，连接A′A″与BC、CD的交点即为所求的点M、N，∵∠BAD=130°，∠B=∠D=90°，∴∠A′+∠A″=180°-∠130°=50°，由轴对称的性质得：A′N= AN，A″M=AM∴∠A′=∠A′AN，∠A″=∠A″AM，∴∠AMN+∠ANM=2（∠A′+∠A″）=2×50°=100°．故答案为：100°【点睛】本题考查了轴对称确定最短路线问题，轴对称的性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，确定出点M、N的位置是解题的关键，要注意整体思想的利用．20．2或6或【分析】（1）根据等边三角形的性质及角平分线的性质求解；（2）根据等边三角形的三线合一的性质解答；（3）根据题意分两种情况：当点D在线段CM上时当点D在线段CM的延长线上时分别画出图形利用全解析：3090︒ 2或6或23【分析】（1）根据等边三角形的性质及角平分线的性质求解；（2）根据等边三角形的三线合一的性质解答；（3）根据题意分两种情况：当点D在线段CM上时，当点D在线段CM的延长线上时，分别画出图形，利用全等三角形的性质解答．【详解】（1）∵△ABC是等边三角形，∴∠ACB=60︒，∵CM平分ACB∠，∴∠ACM=1∠ACB=30，2故答案为：30；∠，（2）∵△ABC是等边三角形，CM平分ACB∴CM⊥AB，∴∠AMC=90︒，故答案为：90︒；（3）∵∠DCE=60︒，CD=CE，∴△CDE是等边三角形，∴DE=CE=CD，∵∠BCM=∠ACM=30，∴∠BCE=30，∴CF平分∠DCE，∵CD=CE，∴CB垂直平分DE，①当点D在线段CM上时，当△BDM≌△BEF时，如图1，∴BF=BM=2，∴CF=CB-BF=4-2=2；当△BDM≌△EBF时，如图1，则EF=BM=2，∴CD=DE=4，,∵AB=4，CD<CM<4,∴此种情况不成立，舍去；②当点D在线段CM的延长线上时，当△BDM≌△BEF时，如图2，∴BF=BM=2，∴CF=BC+BF=4+2=6,；当△BDM≌△EBF时，如图3，则EF=BM=2，∴CE=2EF=4，∴2223=-=，CF CE EF故答案为： 2或6或23．．【点睛】此题考查等边三角形的性质，利用三线合一的性质进行证明，全等三角形的性质，熟记等边三角形的性质是解题的关键．三、解答题21．（1）见解析；（2）PE＝2【分析】（1）证明△ACE≌△CBF（SAS），即可得到∠ACE＝∠CBF；（2）利用由（1）知∠ACE＝∠CBF，求出∠BPE＝60°，又EG⊥BF，即∠PGE＝90°，得到∠GEP＝30°，根据在直角三角形中，30°所对的直角边等于斜边的一半，可求出EP 的长．【详解】（1）证明：∵△ABC是等边三角形，∴AC＝BC，∠A＝∠BCF＝60°，AB＝AC，在△ACE与△BCF中，AC＝BC，∠A＝∠BCF，AE＝CF，∴△ACE≌△CBF（SAS），∴∠ACE＝∠CBF；（2）解：∵由（1）知，∠ACE＝∠CBF，又∠ACE＋∠PCB＝∠ACB＝60°，∴∠PBC＋∠PCB＝60°，∴∠BPE＝60°，∵EG⊥BF，即∠PGE＝90°，∴∠GEP＝30°，∴在Rt△PGE中，PE＝2PG，∵PG＝1，∴PE＝2．【点睛】本题考查了全等三角形的性质定理与判定定理、等边三角形的性质，含30度的直角三角形的性质，解决本题的关键是证明△ACE≌△CBF．22．（1）证明见解析；（2）∠DCB=40°．【分析】（1）根据角平分线的性质和线段垂直平分线的性质可得到DM=DN，DB=DC，根据HL证明Rt△DMB≌Rt△DNC，即可得出BM=CN；（2）根据角平分线的性质得到DM=DN，根据全等三角形的性质得到∠ADM=∠ADN，线段垂直平分线的性质和等腰三角形的性质得到∠EDC=50°于是得到结论．【详解】（1）证明：连接BD，DC，如图所示：∵AD 是∠CAB 的平分线，DM ⊥AB ，DN ⊥AC ，∴DM=DN ，∵DE 垂直平分BC ，∴DB=DC ，在Rt △DMB 和Rt △DNC 中，DB DC DM DN =⎧⎨=⎩， ∴Rt △DMB ≌Rt △DNC （HL ），∴BM=CN ；（2）解：由（1）得：∠BDM=∠CDN ，∵AD 是∠CAB 的平分线，DM ⊥AB ，DN ⊥AC ，∴DM=DN ，在Rt △DMA 和Rt △DNA 中，DA DA DM DN =⎧⎨=⎩∴Rt △DMA ≌Rt △DNA （HL ），∴∠ADM=∠ADN ，∵∠BAC=80°，∴∠MDN=100°，∠ADM=∠ADN=50°，∵∠BDM=∠CDN ，∴∠BDC=∠MDN=100°，∵DE 是BC 的垂直平分线，∴DB=DC ，∴∠EDC=12∠BDC=50°， ∴∠DCB=90°-∠EDC=40°，∴∠DCB=40°．【点睛】本题主要考查了全等三角形的判定与性质、角平分线的性质、线段垂直平分线的性质，熟悉角平分线的性质和线段垂直平分线的性质，证明三角形全等是解决问题的关键． 23．（1）见解析 （2）4【分析】（1）只要证明Rt △ADE ≌Rt △CDF ，推出∠A=∠C ，推出BA=BC ，又AB=AC ，即可推出AB=BC=AC ；（2）证明BD 是等边三角形的∠ABC 的平分线，得∠DBC =30゜，再利用直角三角形的性质求解即可．【详解】解：（1）证明：∵DE ⊥AB ，DF ⊥BC ，垂足分别为点E ，F ，∴∠AED=∠CFD=90°，∵D 为AC 的中点，∴AD=DC ，在Rt △ADE 和Rt △CDF 中，AD DC DE DF ⎧⎨⎩＝＝， ∴Rt △ADE ≌Rt △CDF ，∴∠A=∠C ，∴BA=BC ，∵AB=AC ，∴AB=BC=AC ，∴△ABC 是等边三角形．（2）∵DE ⊥AB ，DF ⊥BC ，且DE DF =，∴BD 平分ABC ∠，∵ABC 是等边三角形，∴60ABC ACB ∠=∠=︒，∴BD AC ⊥，30CBD ∠=︒， ∴2BC CD =，∵CD CG =，2CG =∴24BC CG ==．【点睛】本题考查全等三角形的判定和性质、等边三角形的判定和性质、直角三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题．24．（1）图见解析；（2）先向右平移6个单位，再向下平移2个单位，面积是16【分析】（1）作点A 、B 、C 关于MN 的对称点1A 、1B 、1C ，即可得到111A B C △；（2）先向右平移6个单位，再向下平移2个单位可以得到222A B C △，画出平移的图象，求出扫过的面积．【详解】解：（1）如图所示，（2）如图所示，111A B C △先向右平移6个单位，再向下平移2个单位，得到222A B C △，111A B C △在平移过程中所扫过的面积是图中阴影部分，16242124162S =⨯+⨯⨯=+=． 【点睛】本题考查轴对称和平移，解题的关键是掌握轴对称图形的画法和图形平移的方法． 25．（1）90；（2）①180αβ+=︒，理由见解析；②αβ=，理由见解析【分析】（1）由等腰直角三角形的性质可得∠ABC=∠ACB=45°，由“SAS”可证△BAD ≌△CAE ，可得∠ABC=∠ACE=45°，可求∠BCE 的度数；（2）①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ，再用三角形的内角和即可得出结论；②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ，再用三角形外角的性质即可得出结论．【详解】（1）∵AB=AC ，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠DAE=∠BAC ，∴∠BAD=∠CAE ，在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAE （SAS ）∴∠ABC=∠ACE=45°，∴∠BCE=∠ACB+∠ACE=90°，故答案为：90；（2）①180αβ+=︒．理由：∵∠BAC=∠DAE ，∴∠BAC-∠DAC=∠DAE-∠DAC ．即∠BAD=∠CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ），∴∠B=∠ACE ．∴∠B+∠ACB=∠ACE+∠ACB ．∵∠ACE+∠ACB=β，∴∠B+∠ACB=β，∵α+∠B+∠ACB=180°，∴α+β=180°；② 当点D 在射线BC 的反向延长线上时，αβ=． 理由如下：∵DAE BAC ∠=∠，∴DAB EAC ∠=∠，在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△≌△ADB AEC(SAS)， ∴ABD ACE ∠=∠，∵ABD BAC ACB ∠=∠+∠，ACE BCE ACB ∠=∠+∠， ∴BAC ABD ACB ∠=∠-∠，BCE ACE ACB ∠=∠-∠，∴BAC BCE ∠=∠，即αβ=．【点睛】此题考查了全等三角形的判定和性质，等腰直角三角形的性质，三角形的内角和定理，以及三角形外交的性质，证明△ABD ≌△ACE 是解本题的关键．26．见详解【分析】由题意，根据SAS 证明△ABF ≌△DCE ，得到∠AFB=∠DEC ，即可得到GE GF =．【详解】解：根据题意，如图：∵BE CF =∴BE EF CF EF +=+，∴BF CE =，∵AB DC =，B C ∠=∠，∴△ABF ≌△DCE ，∴∠AFB=∠DEC ，∴GE GF =．【点睛】本题考查了全等三角形的判定和性质，等角对等边，解题的关键是掌握所学的知识，证明△ABF ≌△DCE ．。