北京四中初二全等三角形专题——三角形的旋转、翻折与线段的截长补短

全等三角形-截长补短法全等三角形截长补短法在初中数学的几何学习中，全等三角形是一个重要的知识点，而解决全等三角形相关问题时，截长补短法是一种非常实用且巧妙的方法。

首先，咱们来聊聊什么是截长补短法。

简单来说，截长补短就是通过在图形中截取或者延长某条线段，使得图形中的线段关系发生变化，从而构造出全等三角形，帮助我们解决问题。

比如说，有一个三角形 ABC，其中∠B ＝ 2∠C，要证明 AB ＝ AC ＋ CD。

这时候，我们就可以考虑使用截长补短法。

如果使用截长的思路，就在 AB 上截取 AE ＝ AC，然后连接 DE。

这样一来，因为 AE ＝AC，再加上公共边 AD，以及已知的∠CAD ＝∠EAD，就可以证明△ACD 和△AED 全等。

然后通过一系列的角度推导，就能得出结论。

要是用补短的方法呢，就是延长 AC 至 E，使 CE ＝ CD，连接 DE。

通过角度关系证明∠E ＝∠CDE，进而得出∠B ＝∠BDE，再证明△ABD 和△AED 全等。

接下来，咱们通过几个具体的例子来更深入地理解截长补短法。

例 1：在△ABC 中，AB ＞ AC，AD 平分∠BAC，P 为 AD 上一点。

求证：AB AC ＞ PB PC。

我们来用截长的方法解决。

在 AB 上截取 AE ＝ AC，连接 PE。

因为 AD 平分∠BAC，所以∠BAD ＝∠CAD。

又因为 AE ＝ AC，AP 是公共边，所以△APE ≌△APC。

那么 PC ＝ PE。

在△PBE 中，根据三角形两边之差小于第三边，有 PB PE ＜ BE。

而 BE ＝ AB AE ＝ AB AC，所以 AB AC ＞ PB PC。

例 2：已知在正方形 ABCD 中，∠MAN ＝ 45°，∠MAN 绕点 A 顺时针旋转，它的两边分别交 CB、DC 于点 M、N。

求证：BM ＋ DN ＝MN。

这道题我们用补短的方法。

延长 CB 至 E，使 BE ＝ DN，连接 AE。

CCBA全等三角形问题中常见的辅助线——截长补短法例1、如图，中，AB =2AC ，AD 平分，且AD =BD ，ABC ∆BAC ∠求证：CD ⊥AC例2、如图，AD ∥BC ， AE , BE 分别平分∠DAB ,∠CBA ，CD 过点E ，求证;AB ＝AD +BC例3、如图，已知在内，，，P ，Q 分别在BC ，CA 上，ABC 060BAC ∠=040C ∠=并且AP ，BQ 分别是，的角平分线。

求证：BQ +AQ =AB +BPBAC ∠ABC ∠B A DO E CB A 例4、如图，在四边形ABCD 中，BC ＞BA ,AD ＝CD ，BD 平分，ABC ∠求证： 0180=∠+∠C A 例5、如图在△ABC 中，AB ＞AC ，∠1＝∠2，P 为AD 上任意一点，求证;AB －AC ＞PB －PC例6、已知中，，、分别平分和，、ABC ∆60A ∠= BD CE ABC ∠.ACB ∠BD CE交于点，试判断、、的数量关系，并加以证明．O BE CD BC例7、如图，点为正三角形的边所在直线上的任意一点(点除外)，作M ABD AB B ，射线与外角的平分线交于点，与有怎样的数60DMN ∠=︒MN DBA ∠N DM MN 量关系?变式练习：如图，点为正方形的边上任意一点，且与外角的平分M ABCD AB MN DM ⊥ABC ∠线交于点，与有怎样的数量关系？N MD MN 例8、如图所示．已知正方形ABCD 中，M 为CD 的中点，E 为MC 上一点，且∠BAE =2∠DAM ．求证：AE =BC +CE ．NEB M A DMEDCB A NCD EB M ANMD CB A FEDC B A DN M CB A例9、已知：如图，ABCD 是正方形，∠FAD =∠FAE .求证：BE +DF =AE .例10、如图所示，是边长为2的正三角形，是顶角为的等腰三ABC ∆BDC ∆120 角形，以为顶点作一个的，点、分别在、上，求D 60 MDN ∠M N AB AC的周长．AMN ∆变式练习如图所示，是边长为4的正三角形，是顶角为的等腰三角形，以ABC ∆BDC ∆120为顶点作一个的，点、分别在、上，求的周长．D 60MDN ∠M N AB AC AMN ∆CE DB A例11、五边形ABCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：DA平分∠CDE例12、如图，在四边形ABCD中，AD∥BC,点E是AB上一个动点，若∠B=600，AB=BC，且∠DEC=60O,判断AD+AE与BC的关系并证明你的结论。

全等三角形模型之截长补短法若遇到证明线段的和差倍分关系时，通常考虑“截长补短法“”，构造全等三角形.（1）截长法：在较长线段中截取一段等于另两条较短线段中的一条，然后证明剩下部分等于另一条.即证明“短1＋短2＝长”，“截长法”是在“长”线段上截取一条和“短1”相等长度的线段，再证明剩下的部分和“短2”等长.（2）补短法：将一条较短线段延长，延长部分等于另一条较短线段，然后证明新线段等于较长线段.即证明“短1＋短2＝长”，“补短法”是将“短1”线段延长，延长的长度等于“短2”的长度，再证明新线段与“长”线段长度相等.【典型例题】1．【模型分析】当题目中出现线段的和差关系时，考虑用截长补短法，该类题目中常出现等腰三角形、角平分线等关键词句，采用截长补短法进行证明．问题：如图，在△ABC中，AD平分∠BAC交BC于点D，且∠B＝2∠C，求证：AB+BD＝AC．截长法：在AC上截取AE＝AB，连接DE，证明CE＝BD即可．补短法：延长AB至点F，使AF＝AC，连接DF，证明BF＝BD即可．请结合【模型分析】证明结论．求证：AB+BD＝AC．【截长法】【补短法】2．已知△ABC中，AB＝AC，∠A＝108°，BD平分∠ABC，求证：BC＝AB+CD．3．课堂上，老师提出了这样一个问题：如图1，在△ABC中，AD平分∠BAC交BC于点D，且AB+BD＝AC．求证：∠ABC＝2∠ACB．小明的方法是：如图2，在AC上截取AE，使AE＝AB，连接DE，构造全等三角形来证明结论．（1）小天提出，如果把小明的方法叫做“截长法”，那么还可以用“补短法”通过延长线段AB构造全等三角形进行证明．辅助线的画法是：延长AB至F，使BF＝BD，连接DF．请补全小天提出的辅助线的画法，并在图1中画出相应的辅助线；（2）小芸通过探究，将老师所给的问题做了进一步的拓展，给同学们提出了如下的问题：如图3，点D在△ABC的内部，AD，BD，CD分别平分∠BAC，∠ABC，∠ACB，且AB+BD ＝AC．求证：∠ABC＝2∠ACB．请你解答小芸提出的这个问题；（3）小东将老师所给问题中的一个条件和结论进行交换，得到的命题如下：如果在△ABC中，∠ABC＝2∠ACB，点D在边BC上，AB+BD＝AC，那么AD平分∠BAC．小东判断这个命题也是真命题，老师说小东的判断是正确的．请你利用图4对这个命题进行证明．4．阅读：探究线段的和差倍分关系是几何中常见的问题，解决此类问题通常会用截长法或补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明．（1）请完成下题的证明过程：如图1，在△ABC中，∠B＝2∠C，AD平分∠BAC．求证：AB+BD＝AC．证明：在AC上截取AE＝AB，连接DE（2）如图2，AD∥BC，EA，EB分别平分∠DAB，∠CBA，CD过点E，求证：AB＝AD+BC．【小试牛刀】1．如图，△ABC中，∠C＝2∠A，BD平分∠ABC交AC于D，求证：AB＝CD+BC．（用两种方法）2．如图，△ABC中，∠B＝2∠A，∠ACB的平分线CD交AB于点D，已知AC＝16，BC＝9，则BD的长为．3．已知，如图，BD是△ABC的角平分线，AB＝AC，（1）若BC＝AB+AD，请你猜想∠A的度数，并证明；（2）若BC＝BA+CD，求∠A的度数？（3）若∠A＝100°，求证：BC＝BD+DA．4．已知：如图所示，四边形ABCD中，AD∥BC，O是CD上一点，且AO平分∠BAD，BO 平分∠ABC．（1）求证：AO⊥BO；（2）若AO＝3，BO＝4，求四边形ABCD的面积．5．如图，已知△ABC中，∠A＝60°，D为AB上一点，且AC＝2AD+BD，∠B＝4∠ACD，则∠DCB的度数是．。

在本次活动中，教师应重点关注：
⑴学生能否熟练运用截长法和补短法。
⑵学生的辅助线选择是否正确，思路是否清晰．
⑶学生的表达能力．
要求学生口述作图方法
通过练习，及时反馈学生学习的情况，便于教师把握授课效果，并能及时查漏补缺，进一步优化教学，
本次活动注重学生的亲身体验，从实践中获得结论，提高学生的参与意识和数学兴趣，培养学生自主探索、发现、概括规律的能力
情感态度
１、使学生经历探索线段的和问题的解决过程，感受数学活动充满探索以及数学方法确定性。
２、培养学生积极主动参与学习数学活动的意识，增强学好数学的信心。培养学生与他人合作交流的意识和能力。
重点
正确的辅助线作法。
难点
运用截长补短法解决线段和问题。
教学流程安排
活动流程图
活动内容和目的
活动１ 竞赛活动，复习旧知
⑵学生是否能清晰、准确概括出所学知识。
学生回顾、总结本节课的学习内容，教师积极评价，去粗取精，巩固升华。
学生独立完成作业，进一步巩固所学知识。
板书设计
“截长补短法”分析线段和问题
补短法：合二为一.
截长法：一分为二.
教学设计说明
本节主要内容是截长补短法在解决线段和问题中的应用．要求学生掌握此类问题的解决方法，还要提高学生的动手操作能力，使学生重视作图的准确性和规范性。
活动4
小结
截长补短法思路分析
布置作业：
1、活动3中题运用补短法证明
2、拓展作业Biblioteka 在五边形ABCDE中，AB=AE, BC+DE =CD，∠BAE=∠BCD=120°,∠ABC+∠AED=180°,连接AD。
求证：AD平分∠CDE.
学生思考小结，教师最后补充完整．

2、三角线的中线：在三角形中，连结一个顶点和它对边中点的线段叫做三
角形的中线．
符号语言：
∵AD是△ABC的中线，
∴BD=CD.
三角形的三条中线交于一点.
重要结论：若AD为△ABC的中线，则S△ABD=S△ACD.
3、三角形的高：从三角形一个顶点向对边画垂线，顶点和垂足之间的线段
叫三角形的高．
符号语言：∵AD是△ABC中BC边上的高，
∴∠ADB＝∠ADC＝90°．
三角形的三条高线所在直线交于一点.
例3、如图，
（1）图中有几个三角形？请把它们表示出来；
（2）∠C是哪个三角形的内角？
（3）若AD⊥BC于D，则AD是哪个三角形的高？
（4）若F是AD的中点，则BF是哪个三角形的中线？
例4、等腰三角形一腰上的中线把它的周长分为15和18两部分，求三边
的长．
例5、有一块三角形优良品种试验田，现引进四个品种进行对比试验，需
将这块土地分成面积相等的四块，请你制定出两种以上的方案供选择.
例1、判断下列三条线段能否构成三角形.
(1) 3，4，5；(2) 3，5，9；(3) 5，5，8.
小结：如何真正来使用这条定理呢？
①ห้องสมุดไป่ตู้条较短边之和大于最长边；
②等腰三角形两腰之和大于第三边；
③等边一定可以．
例2、（1）已知三角形的两边分别为5cm和6cm，求第三边c的取值范围；
（2）已知等腰三角形的周长是18cm，其中一条边长为4cm，求其它两条
2、三角形的分类
（1）按三个内角的大小分，三角形可分为锐角三角形、直角三角形、钝角
三角形三类．
（2）按边的相等关系分类如下：
3、三边关系
[活动]（1）试画一个三角形使其三边分别为：a=3，b=2，c=4．

向量与矩阵
向量与矩阵是高等数学中的重要概念，它们在解决几何问 题，特别是涉及旋转、平移等变换的问题时具有广泛的应 用。
THANKS FOR WATCHING
感谢您的观看
全等三角形的性质
对应边相等
对应角相等 面积相等
周长相等
判定三角形全等条件
01
02
03
04
SSS（边边边）
三边分别相等的两个三角形全 等。
SAS（边角边）
两边和它们之间的夹角分别相 等的两个三角形全等。
ASA（角边角）
两角和它们之间的夹边分别相 等的两个三角形全等。
AAS（角角边）
两角和一角的对边分别相等的 两个三角形全等。
04 复杂图形中三角形全等问 题解决方法
分析复杂图形中隐藏信息
观察图形特点
挖掘隐藏条件
注意图形的对称性、角的度数、边的 长度等，这些可能是解决问题的关键。
根据已知信息和图形特点，挖掘出可 能对解决问题有帮助的隐藏条件。
寻找潜在的全等三角形
通过观察和分析，尝试找出可能的全 等三角形，以便利用全等三角形的性 质解决问题。
应注意准确理解和运用各种判定定理。
02
旋转操作中的误区
在运用旋转证明三角形全等时，学生可能忽略旋转前后的图形关系，导
致证明失败。应注意保持旋转前后的图形对应关系。
03
截长补短法的使用不当
学生可能在不适当的场合使用截长补短法，或者在使用时未能正确构造
出全等三角形。应注意分析问题的具体条件，合理运用截长补短法。
截取法
通过截取线段，使得两个三角形在对应边上相等。例如，在证明两三角形全等 时，可以截取其中一个三角形的一条边，使得这条边与另一个三角形的一条边 相等。

《三角形的证明》全章复习与巩固（基础）【学习目标】1.经历回顾与思考的过程，深刻理解和掌握定理的探索和证明.2.结合具体实例感悟证明的思路和方法，能运用综合、分析的方法解决有关问题.3.能正确运用尺规作图的基本方法作已知线段的垂直平分线和角的平分线，以及绘制特殊三角形.【知识网络】【要点梳理】要点一、等腰三角形1.三角形全等的性质及判定全等三角形的对应边相等，对应角也相等.判定：SSS、SAS、ASA、AAS、HL.2.等腰三角形的判定、性质及推论性质：等腰三角形的两个底角相等（等边对等角）判定：有两个角相等的三角形是等腰三角形（等角对等边）推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）3.等边三角形的性质及判定定理性质定理：等边三角形的三个角都相等，并且每个角都等于60°；等边三角形是轴对称图形，有3条对称轴.判定定理：有一个角是60°的等腰三角形是等边三角形；三个角都相等的三角形是等边三角形.4.含30°的直角三角形的边的性质定理：在直角三角形中，如果一个角等于30°，那么它所对的直角边等于斜边的一半. 要点诠释：等边三角形是中考中常考的知识点，并且有关它的计算也很常见，因此对于等边三角形的特殊数据要熟记于心，比如边长为a 的等边三角形它的高是2a ，面积是24a ；含有30°的直角三角形揭示了三角形中边与角的关系，打破了以往那种只有角或边的关系，同时也为我们学习三角函数奠定了基础.要点二、直角三角形1.勾股定理及其逆定理定理：直角三角形的两条直角边的平方和等于斜边的平方.逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.2.命题与逆命题命题包括题设和结论两部分；逆命题是将原命题的题设和结论交换位置得到的；3.直角三角形全等的判定定理定理：斜边和一条直角边对应相等的两个直角三角形全等（HL ）.要点诠释：①勾股定理的逆定理在语言叙述的时候一定要注意，不能说成“两条边的平方和等于斜边的平方”，应该说成“三角形两边的平方和等于第三边的平方”.②直角三角形的全等判定方法，还有SSS,SAS,ASA,AAS,HL 一共有5种判定方法. 要点三、线段的垂直平分线1.线段垂直平分线的性质及判定性质：线段垂直平分线上的点到这条线段两个端点的距离相等.判定：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.2.三角形三边的垂直平分线的性质三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.3.如何用尺规作图法作线段的垂直平分线分别以线段的两个端点A 、B 为圆心，以大于12AB 的长为半径作弧，两弧交于点M 、N ；作直线MN ，则直线MN 就是线段AB 的垂直平分线.要点诠释：①注意区分线段的垂直平分线性质定理和判定定理,注意二者的应用范围；②利用线段的垂直平分线定理可解决两条线段的和距离最短问题.要点四、角平分线1.角平分线的性质及判定定理性质：角平分线上的点到这个角的两边的距离相等；判定：在一个角的内部，且到角的两边的距离相等的点，在这个角的平分线上.2.三角形三条角平分线的性质定理性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等.3.如何用尺规作图法作出角平分线要点诠释：①注意区分角平分线性质定理和判定定理,注意二者的应用范围；②几何语言的表述，这也是证明线段相等的一种重要的方法.遇到角平分线时，要构造全等三角形.【典型例题】类型一、 三角形的证明1. 已知：点D 是△ABC 的边BC 的中点，DE⊥AC，DF⊥AB，垂足分别为E ，F ，且BF=CE ． 求证：△ABC 是等腰三角形．【思路点拨】欲证△ABC 是等腰三角形，又已知DE ⊥AC ，DF ⊥AB ，BF=CE ，可利用三角形中两内角相等来证明．【答案与解析】证明：∵D 是BC 的中点，∴BD=CD，∵DE⊥AC，DF⊥AB，∴△BDF 与△CDE 为直角三角形，在Rt△BDF 和Rt△CDE 中，,BF CE BD CD =⎧⎨=⎩∴Rt△BFD≌Rt△CED（HL ），∴∠B=∠C，∴AB=AC，∴△ABC 是等腰三角形．【总结升华】考查等腰三角形的判定方法及全等三角形的判定及性质；充分利用条件证明三角形全等是正确解答本题的关键．举一反三：【变式1】在四边形ABCD 中，AB=2，CD=1，∠A=60°，∠B=∠D=90°，求BC 和AD ．【答案】解：延长AD 与BC ，两延长线交于点E ，如图所示，∵∠B=90°，∠A=60°，∴∠E=30°，在Rt△CDE 中，CD=1，∴CE=2CD=2，根据勾股定理得：223CE CD -=在Rt△ABE 中，AB=2，∴AE=2AB=4，根据勾股定理得：2223AE AB -=则BC=BE ﹣3﹣2，AD=AE ﹣DE=43【变式2】如图，在△ABC中，AB=AC，D、E在BC上，且AD=AE，求证：BD=CE．【答案】证明：∵AB=AC，AD=AE，∴∠B=∠C，∠ADE=∠AED，∵∠ADE=∠B+∠BAD，∠AED=∠C+∠EAC，∴∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE，∴ BD=CE．类型二、直角三角形2. 如图，已知，在Rt△ABC中，∠C=90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．（1）当∠A满足什么条件时，点D恰为AB的中点写出一个你认为适当的条件，并利用此条件证明D为AB的中点；（2）在（1）的条件下，若DE=1，求△ABC的面积．【思路点拨】（1）根据折叠的性质：△BCE≌△BDE，BC=BD，当点D恰为AB的重点时，AB=2BD=2BC，又∠C=90°，故∠A=30°；当添加条件∠A=30°时，由折叠性质知：∠EBD=∠EBC=30°，又∠A=30°且ED⊥AB，可证D为AB的中点；（2）在Rt△ADE中，根据∠A及ED的值，可将AE、AD的值求出，又D为AB的中点，可得AB的长度，在Rt△ABC中，根据AB、∠A的值，可将AC和BC的值求出，代入S△ABC=AC×BC进行求解即可．【答案与解析】解：（1）添加条件是∠A=30°．证明：∵∠A=30°，∠C=90°，所以∠CBA=60°，∵C 点折叠后与AB 边上的一点D 重合，∴BE 平分∠CBD，∠BDE=90°，∴∠EBD=30°，∴∠EBD=∠EAB，所以EB=EA ；∵ED 为△EAB 的高线，所以ED 也是等腰△EBA 的中线，∴D 为AB 中点．（2）∵DE=1，ED⊥AB，∠A=30°，∴AE=2．在Rt△ADE 中，根据勾股定理，得AD=22213-=，∴AB=23，∵∠A=30°，∠C=90°，∴BC=12AB=3． 在Rt△ABC 中，AC=22AB BC -=3，∴S△ABC =12×AC×BC=332． 【总结升华】考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，根据轴对称的性质，折叠前后图形的形状和大小不变．3. 小林在课堂上探索出只用三角尺作角平分线的一种方法：如图，在已知∠AOB 的两边上分别取点M ，N ，使OM=ON ，再过点M 作OB 的垂线，过点N 作OA 的垂线，垂足分别为C 、D ，两垂线交于点P ，那么射线OP 就是∠AOB 的平分线．老师当场肯定他的作法，并且表扬他的创新．但是小林不知道这是为什么．①你能说明这样做的理由吗？也就是说，你能证明OP 就是∠AOB 的平分线吗？②请你只用三角板设法作出图∠AOB 的平分线，并说明你的作图方法或设计思路．【思路点拨】①在Rt △OCM 与Rt △ODN 中，依据ASA 得出OC=OD;在Rt △O CP 与Rt △O DP 中，因为OP=OP ，OC=OD 得出Rt△O CP ≌Rt△O DP （HL ），所以∠C OP=∠DOP ，即OP 平分∠AOB． ②可作出两个直角三角形，利用HL 定理证明两角所在的三角形全等．【答案与解析】①证明：在Rt △OCM 和Rt △ODN 中，COM DON OCM ODN OM ON ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△OCM ≌△ODN （AAS ），∴OC=OD ，在△OCP 与△ODP 中，∵,OC OD OP OP=⎧⎨=⎩∴Rt △OCP ≌Rt △ODP （HL ），∴∠COP=∠DOP ，即OP 平分∠AOB ；②解：①利用刻度尺在∠AOB 的两边上分别取OC=OD ；②过C ，D 分别作OA ，OB 的垂线，两垂线交于点E ；③作射线OE ，OE 就是所求的角平分线．∵CE⊥OA，ED⊥OB，∴∠OCE=∠ODE=90°，在Rt△OCE 与Rt△ODE 中，∵OC OD OE OE=⎧⎨=⎩，∴Rt△OCE≌Rt△ODE（HL ），∴∠EOC=∠EOD，∴OE 为∠AOB 的角平分线．【总结升华】主要考查了直角三角形的判定，利用全等三角形的性质得出∠EOC=∠EOD 是解题关键．类型三、线段垂直平分线4. 撑伞时，把伞“两侧的伞骨”和支架分别看作AB 、AC 和DB 、DC ，始终有AB=AC ，DB=DC ，请大家考虑一下伞杆AD 与B 、C 的连线BC 的位置关系为 ．【思路点拨】根据到线段两端点的距离相等的点在线段的垂直平分线上得出A 、D 都在线段BC 的垂直平分线上，根据两点确定一条直线得出AD 是线段BC 的垂直平分线即可．【答案】垂直．【解析】解：连接BC 、AD ，∵AB=AC，DB=DC ，∴A 在线段BC 的垂直平分线上，D 在线段BC 的垂直平分线上，∴根据两点确定一条直线得出AD是线段BC的垂直平分线，即AD⊥BC，【总结升华】考查了线段的垂直平分线定理和两点确定一条直线等知识点，注意：①到线段两端点的距离相等的点在线段的垂直平分线上；②两点确定一条直线．举一反三：【变式】如图所示，AD是△ABC中∠BAC的平分线，AD的垂直平分线EF交BC的延长线于F，试说明∠BAF=∠ACF的理由．【答案】解：∵EF垂直平分AD，∴AF=DF，∴∠FAD=∠FDA．又∵AD平分∠BAC，∴∠BAD=∠CAD，∵∠BAF=∠BAD+∠FAD，∠ACF=∠DAC+∠FDA，∴∠BAF=∠ACF．类型四、角平分线5. 如图，在△ABC中，∠BAC=80°，延长BC到D，使AC=CD，且∠ADB=20°，DE平分∠ADB交AC于F，交AB于E，连接CE，求∠CED的度数．【思路点拨】作EG⊥DA，EH⊥BD，EP⊥AC，根据角平分线的性质得到EG=EH，根据△EGA≌△EPA，得出∠ECB，就可以得到∠CED的度数．【答案与解析】证明：作EG⊥DA交DA的延长线于G，再作EH⊥BD，EP⊥AC，垂足分别为H，P，则EG=EH ∵∠ADC=20°，AC=CD，∴∠CAD=20°，而∠BAC=80°，∴∠GAE=180°﹣20°﹣80°=80°，∴Rt△EGA≌Rt△EPA，∴EG=EP∴EP=EH，∴∠ECB=∠ECA=12∠BCA=12×40°=20°∴∠CED=∠BCE﹣∠BDE=20°﹣10°=10°【总结升华】主要考查了角平分线的性质定理及逆定理、三角形全等的性质和判定；做题中两次用到角平分线的知识是正确解答本题的关键．举一反三：【变式】如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（）A．1处B．2处 C．3处 D．4处【答案】D．解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角两两平分线的交点，共三处．。

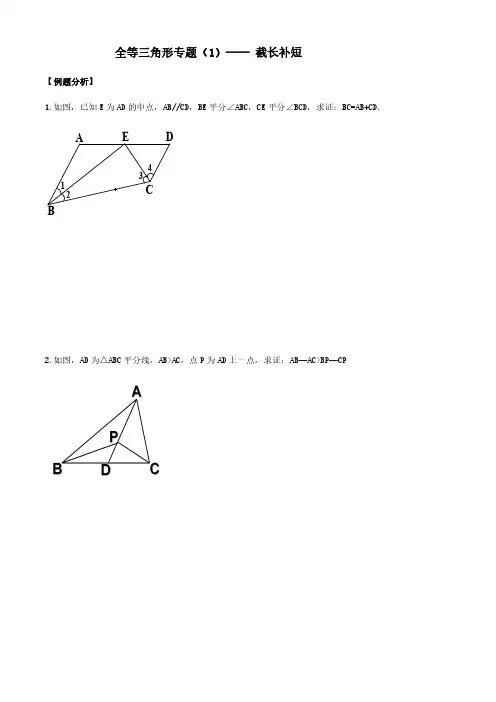
全等三角形专题（1）——截长补短【例题分析】1.如图，已知E 为AD 的中点，AB//CD，BE 平分∠ABC，CE 平分∠BCD，求证：BC=AB+CD.2.如图，AD 为△ABC 平分线，AB>AC，点P 为AD 上一点，求证：AB—AC>BP—CP3.如图，已知B（﹣1，0），C（1，0），A为y轴正半轴上一点，点D为第二象限一动点，E在BD的延长线上，CD交AB于F，且∠BDC=∠BAC．（1）求证：∠ABD=∠ACD；（2）求证：AD平分∠CDE；（3）若在D点运动的过程中，始终有DC=DA+DB，在此过程中，∠BAC的度数是否变化？如果变化，请说明理由；如果不变，请求出∠BAC的度数？【巩固练习】1.在△ABC 中,∠ACB＝90o,AC＝BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN 于E.⑴当直线MN 绕点C 旋转到图⑴的位置时,求证:DE＝AD＋BE；⑵当直线MN 绕点C 旋转到图⑵的位置时,求证:DE＝AD－BE；⑶当直线MN 绕点C 旋转到图⑶的位置时,试问DE、AD、BE 具有怎样的等量关系？并证明。

2.如图在△ABC 中，∠ABC=600，AD、CE 分别平分∠BAC 和∠ACB，求证：AC=AE+CD.654321O ED CBA3.五边形ABCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD平分∠CDE4.（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD.求证：EF=BE+FD；（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？说明理由.。

三角形全等之截长补短 (整理)三角形全等之截长补短一、知识点概述截长补短是指在几何题目中，当出现线段和的情况时，可以考虑通过截取一段线段并加上一段等于原线段的线段，将原问题转化为线段等量的问题。

二、例题讲解1.已知：如图，在△ABC中，∠1=∠2，∠B=2∠C．求证：AC=AB+BD．证明：可以通过截长法和补短法两种方法证明。

截长法：在AC上截取AF=AB，连接DF。

在△ABD和△AFD中，根据SAS准则可以得到△ABD≌△AFD，进而得到∠B=∠AFD，BD=FD。

又因为∠B=2∠C，所以∠AFD=2∠C。

因为∠AFD是△DFC的一个外角，所以∠AFD=∠C+∠XXX。

因为∠1=∠2，所以∠XXX∠C，进而得到∠AFD=2∠C=∠B。

因此，根据三角形内角和定理，可以得到∠A=180°-∠B-∠C=∠AFD+∠XXX∠C=2∠C+∠C+∠C=4∠C。

在△ABC中，∠B=2∠C，所以∠A=60°。

在△ADE和△ADC中，因为∠E=∠C，∠1=∠2，AD=AD，所以△ADE≌△ADC （AAS），进而得到AE=AC。

因此，AC=AB+BD。

补短法：延长AB到E，使BE=BD，连接DE。

因为BE=BD，所以∠XXX∠BDE。

因为∠ABD是△XXX的一个外角，所以∠ABD=∠E+∠BDE=2∠E。

因为∠ABD=2∠C，所以∠XXX∠C。

在△ADE和△ADC中，因为∠E=∠C，∠1=∠2，AD=AD，所以△ADE≌△ADC（AAS），进而得到AE=AC。

因此，XXX。

2.如图，在四边形ABCD中，∠A=∠B=90°，点E为AB边上一点，且DE平分∠ADC，CE平分∠BCD．求证：XXX．证明：在△ADE和△BCE中，因为∠A=∠B=90°，所以AD=BC。

因为DE平分∠ADC，CE平分∠BCD，所以∠AED=∠DEC，∠XXX∠XXX。

因为∠AED+∠BCE=180°，所以∠DEC+∠CDE=180°。

全等三角形截长补短法的经典例题（最新版）目录1.截长补短法的概念2.截长补短法的两种方法：截长法和补短法3.截长补短法在全等三角形中的应用4.经典例题解析4.1 例题一4.2 例题二4.3 例题三5.截长补短法的优点和意义正文一、截长补短法的概念截长补短法是一种在几何问题中添加辅助线的方法，主要用于解决全等三角形的问题。

截长指的是在较长的线段上截取一段较短的线段，补短则是在较短线段上补一段线段，使其和较长的线段相等。

截长补短法的目的是将问题合理地转化为更容易解决的形式，从而简化结论。

二、截长补短法的两种方法截长补短法包括两种方法：截长法和补短法。

1.截长法：在较长的线段上截取与较短线段相等的线段。

2.补短法：在较短线段上补一段线段，使其和较长的线段相等。

三、截长补短法在全等三角形中的应用在全等三角形的证明中，截长补短法是非常常用的一种方法。

通过添加适当的辅助线，可以将问题转化为更容易证明的形式，从而得出结论。

下面通过几个经典例题来具体讲解截长补短法在全等三角形中的应用。

四、经典例题解析1.例题一已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

解：通过截长补短法，我们可以在 BC 上截取 BE=CF，连接 AD 和 CE。

由于 AB=DE，BC=EF，且∠ABC=∠DEF，根据三角形全等的 SAS 条件，可得三角形 ABC≌三角形 DEF。

2.例题二已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

解：这次我们可以在 AB 上截取 AD=DF，连接 CE 和 BD。

同样地，由于 AB=DE，BC=EF，且∠ABC=∠DEF，根据三角形全等的 SAS 条件，可得三角形 ABC≌三角形 DEF。

3.例题三已知三角形 ABC 和三角形 DEF 满足条件：AB=DE，BC=EF，∠ABC=∠DEF，求证三角形 ABC 与三角形 DEF 全等。

ADBCE图2-1截长补短法人教八年级上册课本中，在全等三角形部分介绍了角的平分线的性质，这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法，在无法进行直接证明的情形下，利用此种方法常可使思路豁然开朗.请看几例.例1. 已知，如图1-1，在四边形ABCD 中，BC ＞AB ，AD =DC ，BD 平分∠ABC .求证：∠BAD +∠BCD =180°.分析：因为平角等于180°，因而应考虑把两个不在一起的通过全等转化成为平角，图中缺少全等的三角形，因而解题的关键在于构造直角三角形，可通过“截长补短法”来实现.证明：过点D 作DE 垂直BA 的延长线于点E ，作DF ⊥BC 于点F ，如图1-2 ∵BD 平分∠ABC ，∴DE =DF ，在Rt △ADE 与Rt △CDF 中，⎩⎨⎧==CDAD DFDE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°，∴∠BAD +∠DCF =180°， 即∠BAD +∠BCD =180°例2. 如图2-1，AD ∥BC ，点E 在线段AB 上，∠ADE =∠CDE ，∠DCE =∠ECB .求证：CD =AD +BC .分析：结论是CD =AD +BC ，可考虑用“截长补短法”中的“截长”，即在CD 上截取CF =CB ，只要再证DF =DA 即可，这就转化为证明两线段相等的问题，从而达到简化问题的目的.证明：在CD 上截取CF =BC ，如图2-2在△FCE 与△BCE 中，⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE （SAS ）,∴∠2=∠1.ABCD图1-1FEDCBA图1-2ADB CEF1234图2-2又∵AD ∥BC ，∴∠ADC +∠BCD =180°，∴∠DCE +∠CDE =90°， ∴∠2+∠3=90°，∠1+∠4=90°，∴∠3=∠4. 在△FDE 与△ADE 中，⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE （ASA ），∴DF =DA ， ∵CD =DF +CF ，∴CD =AD +BC .例3. 已知，如图3-1，∠1=∠2，P 为BN 上一点，且PD ⊥BC 于点D ，AB +BC =2BD .求证：∠BAP +∠BCP =180°.分析：与例1相类似，证两个角的和是180°，可把它们移到一起，让它们是邻补角，即证明∠BCP =∠EAP ，因而此题适用“补短”进行全等三角形的构造.证明：过点P 作PE 垂直BA 的延长线于点E ，如图3-2∵∠1=∠2，且PD ⊥BC ，∴PE =PD ， 在Rt △BPE 与Rt △BPD 中，⎩⎨⎧==BPBP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ，∴AB +BD +DC =BD +BE ，∴AB +DC =BE 即DC =BE -AB =AE . 在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例4. 已知：如图4-1，在△ABC 中，∠C ＝2∠B ，∠1＝∠2.求证：AB =AC +CD .ABCDP12N图3-1P12NABCDE 图3-2DCB A 12图4-1分析：从结论分析，“截长”或“补短”都可实现问题的转化，即延长AC 至E 使CE =CD ，或在AB 上截取AF =AC . 证明：方法一（补短法）延长AC 到E ，使DC =CE ，则∠CDE ＝∠CED ，如图4-2∴∠ACB ＝2∠E ，∵∠ACB ＝2∠B ，∴∠B ＝∠E ， 在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED （AAS ）,∴AB =AE . 又AE =AC+CE =AC +DC ，∴AB =AC +DC . 方法二（截长法）在AB 上截取AF =AC ，如图4-3 在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD （SAS ）,∴DF =DC ，∠AFD ＝∠ACD . 又∵∠ACB ＝2∠B ，∴∠FDB ＝∠B ，∴FD =FB . ∵AB =AF +FB =AC +FD ，∴AB =AC +CD .上述两种方法在实际应用中，时常是互为补充，但应结合具体题目恰当选择合适思路进行分析。

初二数学 全全等三角形截长补短知识点总结及解析一、全等三角形截长补短1．已知ABC 是等边三角形，6AB =．（1）如图1，点M 是BC 延长线上一点，60AMN ∠=︒，MN 交ABC 的外角平分线于点N ，求CN CM -的值；（2）如图2，过点A 作AD BC ⊥于点D ，点P 是直线AD 上一点，以CP 为边，在CP 的下方作等边CPQ ，连接DQ ，求DQ 的最小值．2．阅读与理解：折纸，常常能为证明一个命题提供思路和方法．例如，在ABC 中，AB AC >（如图），怎样证明C B ∠>∠呢？分析：把AC 沿A ∠的角平分线AD 翻折，因为AB AC >，所以，点C 落在AB 上的点C '处，即AC AC '=，据以上操作，易证明ACD AC D '△△≌，所以AC D C '∠=∠，又因为AC D B '∠>∠，所以C B ∠>∠．感悟与应用：（1）如图（a ），在ABC 中，90ACB ∠=︒，30B ∠=︒，CD 平分ACB ∠，试判断AC 和AD 、BC 之间的数量关系，并说明理由；（2）如图（b ），在四边形ABCD 中，AC 平分BAD ∠，16AC =，8AD =，12DC BC ==，①求证：180B D ∠+∠=︒；②求AB 的长．3．如图，在△ABC 中，AB ＝AC ，∠BAC ＝30°，点D 是△ABC 内一点，DB ＝DC ，∠DCB ＝30°，点E 是BD 延长线上一点，AE ＝AB ．（1）求∠ADB 的度数；（2）线段DE ，AD ，DC 之间有什么数量关系？请说明理由．4．如图，在ABC 中，AB AC =，30ABC ∠<︒，D 是边BC 的中点，以AC 为边作等边三角形ACE ，且ACE △与ABC 在直线AC 的异侧，连接BE 交DA 的延长线于点F ，连接FC 交AE 于点M ．（1）求证：FB FC =；（2）求证：FEA FCA ∠=∠；（3）若8FE =，2AD =，求AF 的长．5．阅读题：如图1，OM 平分AOB ∠，以O 为圆心任意长为半径画弧，交射线OA ，OB 于C ，D 两点，在射线OM 上任取一点E （点O 除外），连接CE ，DE ，可证OCE ODE △△≌，请你参考这个作全等的方法，解答下列问题：（1）如图2，在ABC 中，2A B ∠=∠，CD 平分ACB ∠交AB 于点D ，试判断BC 与AC 、AD 之间的数量关系；（2）如图3，在四边形ABCD 中，AC 平分BAD ∠，10BC CD ==，20AB =，8AD =，求ABC 的面积．6．如图所示，//AB DC AB AD BE ⊥，，平分ABC CE ∠，平分BCD ∠；（1）求AB CD 、与BC 的数里关系，并说明你的理由．（2）若把AB AD ⊥条件去掉，则（1）中AB CD 、与BC 的数里关系还成立吗?并说明你的理由．7．在菱形ABCD 中，射线BM 从对角线BD 所在的位置开始绕着点B 逆时针旋转，旋转角为()0180αα︒<<︒，点E 在射线BM 上，DEB DAB ∠=∠．（1）当60DAB ∠=︒时，BM 旋转到图①的位置，线段BE ，DE ，AE 之间的数量关系是______；（2）在（1）的基础上，当BM 旋转到图②的位置时，探究线段BE ，DE ，AE 之间的数量关系，并证明；（3）将图②中的60DAB ∠=︒改为90DAB ∠=︒，如图③，其他条件不变，请直接写出线段BE ，DE ，AE 之间的数量关系．8．如图，//AD BC ，点E 在线段AB 上，DE 、CE 分别是ADC ∠、BCD ∠的角平分线，若3AD =，2BC =，求CD 的长．9．如图，正方形ABCD 的对角线相交于点O ．点E 是线段DO 上一点，连接CE ．点F 是∠OCE 的平分线上一点，且BF ⊥CF 与CO 相交于点M ，点G 是线段CE 上一点，且CO=CG ．（1）若OF=4，求FG 的长；（2）求证：BF=OG+CF ．10．在数学活动课上，数学老师出示了如下题目：如图①，在四边形ABCD中，E是边CD的中点，AE是BAD∠的平分线，AD BC∥．求证：AB AD BC=+．小聪同学发现以下两种方法：方法1：如图②，延长AE、BC交于点F．方法2：如图③，在AB上取一点G，使AG AD=，连接EG、CG．（1）请你任选一种方法写出这道题的完整的证明过程；（2）如图④，在四边形ABCD中，AE是BAD∠的平分线，E是边CD的中点，60 BAD∠=︒，11802D BCD∠+∠=︒，求证：CB CE=．【参考答案】***试卷处理标记，请不要删除一、全等三角形截长补短1．（1）6；（2）3 2【分析】（1）在CN上截取点H，使CH=CM，先证出△CMH为等边三角形，然后利用ASA证出△AMC ≌△NMH ，从而得出AC=NH ，从而求出结论；（2）连接BQ ，利用SAS 证出△QCB ≌△PCA ，从而得出∠CBQ=∠CAP ，然后根据三线合一和等量代换即可求出∠CBQ=30°、∠ABQ =90°，从而判断出点Q 的运动轨迹，然后根据垂线段最短即可得出当DQ ⊥BQ 时，DQ 最短，然后利用30°所对的直角边是斜边的一半即可得出结论．【详解】解：（1）在CN 上截取点H ，使CH=CM ，连接MH∵△ABC 为等边三角形∴∠ACB=60°，AC=AB=6∴∠ACM=180°－∠ACB=120°∵CN 平分∠ACM∴∠MCN=12∠ACM=60° ∴△CMH 为等边三角形 ∴CM=HM ，∠CMH=∠CHM=60°∴∠NHM=180°－∠CHM=120°，∠AMC ＋∠AMH=60°∴∠ACM=∠NHM∵60AMN ∠=︒∴∠NMH ＋∠AMH=60°∴∠AMC=∠NMH在△AMC 和△NMH 中AMC NMH CM HMACM NHM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AMC ≌△NMH∴AC=NH∴CN CM -=CN －CH=NH=AC=6（2）连接BQ∵△ABC 和△CPQ 都是等边三角形∴BC=AC ，QC=PC ，∠PCQ =∠ACB=∠ABC=∠BAC =60°∴∠PCQ －∠PCB=∠ACB －∠PCB∴∠QCB=∠PCA在△QCB 和△PCA 中BC AC QCB PCA QC PC =⎧⎪∠=∠⎨⎪=⎩∴△QCB ≌△PCA∴∠CBQ=∠CAP∵AD BC ⊥∴∠CAP=12∠BAC=30°，BD=12BC=3 ∴∠CBQ=30°∴∠ABQ=∠ABC ＋∠CBQ=90°∴点Q 在过点B 作AB 的垂线上运动 根据垂线段最短可得：当DQ ⊥BQ 时，DQ 最短此时在Rt △BDQ 中，∠QBD=30°∴DQ=12BD=32即DQ 的最小值为32． 【点睛】 此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、直角三角形的性质和垂线段最短的应用，掌握构造全等三角形的方法、全等三角形的判定及性质、等边三角形的判定及性质、30°所对的直角边是斜边的一半和垂线段最短是解决此题的关键． 2．（1）BC−AC ＝AD ；理由详见解析；（2）①详见解析；②AB=14【分析】（1）在CB 上截取CE ＝CA ，连接DE ，证△ACD ≌△ECD 得DE ＝DA ，∠A ＝∠CED ＝60°，据此∠CED ＝2∠CBA ，结合∠CED ＝∠CBA ＋∠BDE 得出∠CBA ＝∠BDE ，即可得DE ＝BE ，进而得出答案；（2）①在AB 上截取AM ＝AD ，连接CM ，先证△ADC ≌△AMC ，得到∠D ＝∠AMC ，CD ＝CM ，结合CD ＝BC 知CM ＝CB ，据此得∠B ＝∠CMB ，根据∠CMB ＋∠CMA ＝180°可得； ②设BN ＝a ，过点C 作CN ⊥AB 于点N ，由CB ＝CM 知BN ＝MN ＝a ，CN 2＝BC 2−BN 2＝AC 2−AN 2，可得关于a 的方程，解之可得答案．【详解】解：（1）BC−AC ＝AD ．理由如下：如图（a ），在CB 上截取CE ＝CA ，连接DE ，∵CD 平分∠ACB ，∴∠ACD ＝∠ECD ，又CD ＝CD ，∴△ACD ≌△ECD （SAS ），∴DE ＝DA ，∠A ＝∠CED ＝60°，∴∠CED ＝2∠CBA ，∵∠CED ＝∠CBA ＋∠BDE ，∴∠CBA ＝∠BDE ，∴DE ＝BE ，∴AD ＝BE ，∵BE ＝BC−CE ＝BC−AC ，∴BC−AC ＝AD ．（2）①如图（b ），在AB 上截取AM ＝AD ，连接CM ，∵AC 平分∠DAB ，∴∠DAC ＝∠MAC ，∵AC ＝AC ，∴△ADC ≌△AMC （SAS ），∴∠D ＝∠AMC ，CD ＝CM ＝12，∵CD ＝BC ＝12，∴CM ＝CB ，∴∠B ＝∠CMB ，∵∠CMB ＋∠CMA ＝180°，∴∠B ＋∠D ＝180°；②设BN ＝a ，过点C 作CN ⊥AB 于点N ，∵CB ＝CM ＝12，∴BN ＝MN ＝a ，在Rt △BCN 中，2222212CN BC BN a --＝＝，在Rt △ACN 中，2222216(8)CN AC AN a --+＝＝，则22221216(8)a a --+＝，解得：a ＝3，即BN ＝MN ＝3，则AB ＝8+3+3=14，∴AB=14．【点睛】本题考查了四边形的综合题，以及全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质；本题有一定难度，需要通过作辅助线证明三角形全等才能得出结果． 3．（1）120°；（2）DE ＝AD +CD ，理由见解析【分析】（1）根据三角形内角和定理得到∠ABC ＝∠ACB ＝75°，根据全等三角形的性质得到∠BAD ＝∠CAD ＝15°，根据三角形的外角性质计算，得到答案；（2）在线段DE 上截取DM ＝AD ，连接AM ，得到△ADM 是等边三角形，根据△ABD ≌△AEM ，得到BD ＝ME ，结合图形证明结论【详解】解：（1）∵AB ＝AC ，∠BAC ＝30°，∴∠ABC ＝∠ACB ＝12（180°﹣30°）＝75°， ∵DB ＝DC ，∠DCB ＝30°，∴∠DBC ＝∠DCB ＝30°，∴∠ABD ＝∠ABC ﹣∠DBC ＝45°，在△ABD 和△ACD 中，AB AC DB DC AD AD =⎧⎪=⎨⎪=⎩，∴△ABD ≌△ACD （SSS ），∴∠BAD ＝∠CAD ＝12∠BAC ＝15°， ∴∠ADE ＝∠ABD +∠BAD ＝60°，∴∠ADB ＝180°﹣∠ADE ＝180°﹣60°＝120°；（2）DE ＝AD +CD ，理由如下：在线段DE 上截取DM ＝AD ，连接AM ，∵∠ADE ＝60°，DM ＝AD ，∴△ADM 是等边三角形，∴∠ADB ＝∠AME ＝120°．∵AE ＝AB ，∴∠ABD ＝∠E ，在△ABD 和△AEM 中，ABD E ADB AME AB AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△AEM （AAS ），∴BD ＝ME ，∵BD ＝CD ，∴CD ＝ME ．∵DE ＝DM +ME ，∴DE ＝AD +CD ．【点睛】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．4．（1）见解析；（2）见解析；（3）4【分析】（1）利用AD 所在直线是BC 的垂直平分线，点F 在直线AD 上即可得出结论． （2）由ACE △是等边三角形，得AC=AE=AB 推得ABF FEA ∠=∠．易证ABF ≌ACF （SSS ），ABF FCA FEA ∠=∠=∠即可，（3）延长AD 至点P 处，使DP AD ，连接CP ．先证直角三角形ADC ≌PDC△（SAS ），推出AC CP CE ==，ACD PCD ∠=∠．再证60EFC EAC ∠=∠=︒．求出，FBD 30FCD ∠=∠=︒．用ACD ∠表示30ECF ACD ∠=︒+∠．而30FCP ACD ∠=︒+∠，得ECF FCP ∠=∠．可证ECF △≌PCF （SAS ），可推得AF EF AP =-即可．【详解】（1）证明：∵AB AC =，D 是边BC 的中点，∴AD 所在直线是BC 的垂直平分线，又∵点F 在直线AD 上∴FB FC =．（2）证明：∵ACE △是等边三角形， ∴60EAC ACE ∠=∠=︒，AC AE =． ∵AB AC =，∴AB AE =，∴ABF FEA ∠=∠．由（1）可知，FB FC =， 又∵AF AF =，AB AC =，∴ABF ≌ACF （SSS ），∴ABF FCA ∠=∠，∴FEA FCA ∠=∠． （3）解：如图，延长AD 至点P 处，使DP AD ，连接CP ．∵AB AC =，D 是边BC 的中点， ∴90ADC PDC ∠=∠=︒． ∵ACE △是等边三角形，∴AC CE =，60EAC ∠=︒． ∵AD DP =，ADC PDC ∠=∠，CD CD =，∴ADC ≌PDC △（SAS ），∴AC CP CE ==，ACD PCD ∠=∠． 由（2）可知，FEA FCA ∠=∠， ∵AMC FME ∠=∠，∴60EFC EAC ∠=∠=︒． 由（1）可知，BF CF =， ∴()18060260BFD CFD ∠=∠=︒-︒÷=︒， ∴906030FCD ∠=︒-︒=︒． ∵FCA FCD ACD ∠=∠-∠， ∴30FCA ACD ∠=︒-∠． ∵ECF ECA FCA ∠=∠-∠， ∴()303030ECF ECA ACD ECA ACD ACD ∠=∠-︒-∠=∠-︒+∠=︒+∠． ∵FCP FCD PCD ∠=∠+∠，∴30FCP ACD ∠=︒+∠，∴ECF FCP ∠=∠．∵FC FC =，CE CP =，∴ECF △≌PCF （SAS ），∴FE FP =，∴2FE FA AP AF AD =+=+，∴2822=4AF EF AD =-=-⨯．【点睛】本题考查线段垂直平分线性质，等边三角形性质，三角形全等判定与性质，掌握线段垂直平分线性质，等边三角形性质，三角形全等判定与性质，会利用引辅助线构造三角形全等转化线与线关系，角与角关系来解决问题．5．（1）BC=AC+AD ；（2）△ABC 的面积为80．【分析】（1）在CB 上截取CE=CA ，则由题意可得AD=DE ，∠CED=∠A ，再结合∠A=2∠B 可得DE=BE ，从而得到BC=AD+AC ；（2）在AB 上截取AE=AD ，连结CE ，过C 作CF ⊥AB 于F 点，由题意可得EC=BC ，从而得到EF 的长度，再由勾股定理根据EC 、EF 的长度求得CF 的长度，最后根据面积公式可以得到解答 ．【详解】解：（1）如图，在CB 上截取CE=CA ，则由题意得：△CAD ≌△CED ，∴AD=DE ，∠CED=∠A ，∵∠A=2∠B ，∴∠CED=2∠B ，又∠CED=∠B+∠EDB ，∴∠B+∠EDB=2∠B ，∴∠EDB=∠B ，∴DE=BE ，∴BC=BE+CE=DE+CE=AD+AC ；（2）如图，在AB 上截取AE=AD ，连结CE ，过C 作CF ⊥AB 于F 点，∴由题意可得：△CDA ≌△CEA ，∴EC=CD=BC=10，AE=AD=8，∵CF ⊥AB ，∴EF=FB=208622AB AE --==，∴8CF ==， ∴112088022ABC S AB CF =⨯=⨯⨯=． 【点睛】本题考查三角形全等的综合运用，熟练掌握三角形全等的判定和性质、等腰三角形的判定和性质、勾股定理是解题关键．6．（1）AB CD BC +=，见解析；（2）成立，见解析【分析】（1）先写出数量关系，过E 作EF BC ⊥于F ，然后证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得结论了．（2）成立, 在BC 上截取CF CD =证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得到结论．【详解】()1AB CD BC +=理由是：过E 作EF BC ⊥于FCE 为角平分线DCE FCE ∴∠=∠//AB DC AB AD ⊥，90D ∴∠=EF BC ⊥D CFE ∴∠=∠CE CE =()CDE CFE AAS ∆≅∆CD CF ∴=同理可证()ABE FBE AAS ∆≅∆AB BF ∴=CF BF AB +=AB CD BC ∴+=()2成立理由：在BC 上截取CF CD =CE 为角平分线DCE FCE ∴∠=∠CE CE =()CDE CFE SAS ∆≅∆CD CF ∴= D CFE ∠=∠//AB DC180D A ∴∠+∠=又180CFE EFB ∠+=A EFB ∴∠=∠又BE 是角平分线ABE FBE ∴∠=∠BE BE =()BAE BFE AAS ∆≅∆AB FB ∴=∴ CF BF AB +=AB CD BC ∴+=7．（1）BE DE AE =+；（2）BE DE AE =-，证明见解析；（3）2BE DE =【分析】（1）在射线BM 上截取BF DE =，连接AF ，首先利用菱形的性质证明ADE ABF ≌，然后利用全等三角形的性质及等边三角形的性质得出EF AE =，从而可得出结论BE DE AE =+；（2）在DE 上截取DG BE =，连接AG ，首先利用菱形的性质证明ADG ABE ≌，然后利用全等三角形的性质及等边三角形的性质得出EG AE =，从而可得出结论BE DE AE =-；（3）在DE 上截取DH BE =，连接AH ，首先利用正方形的性质证明ADH ABE △≌，然后利用全等三角形的性质及等腰直角三角形的性质得出2EH AE =，从而可得出结论2BE DE AE =-．【详解】（1）解：BE DE AE =+；如图①，在射线BM 上截取BF DE =，连接AF ，60DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是菱形，AB AD ∴=．()ADE ABF SAS ∴△≌△，AE AF ∴=，EAD BAF ∠=∠．60DAB DAF BAF DAF EAD EAF ∴∠=∠+∠=∠+∠=∠=︒．AEF ∴是等边三角形，EF AE ∴=．BE BF EF =+，BE DE AE ∴=+．图①（2）BE DE AE =-．证明：如图②，在DE 上截取DG BE =，连接AG ，60DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是菱形，AB AD ∴=．()ADG SAS ∴△≌△ABE ．AE AG ∴=，DAG BAE ∠∠=．60DAB DAG BAG BAE BAG EAG ∴∠=∠+∠=∠+∠=∠=︒． ∴AEG 是等边三角形．EG AE ∴=．DG DE EG =-，BE DE AE ∴=-；图②（3）2BE DE AE =-．如图③，在DE 上截取DH BE =，连接AH ，90DEB DAB ∠=∠=︒，EDA ABE ∴∠=∠．四边形ABCD 是正方形，AB AD ∴=．()ADH ABE SAS ∴△≌△．AE AH ∴=，HAD BAE ∠=∠．90DAB DAH BAH BAE BAH EAH ∴∠=∠+∠=∠+∠=∠=︒．AEH ∴是等腰直角三角形．2EH AE ∴=．DH DE EH =-，2BE DE AE ∴=-．图③【点睛】本题主要考查全等三角形的判定及性质，等腰直角三角形和等边三角形的性质，正方形和菱形的性质，合理的作出辅助线是解题的关键．8．5【分析】如图，在DC 上截取DF DA =，连接EF ，先证明ADE FDE △≌△，得到AE EF =，5A ∠=∠，然后证明CEF CEB △≌△，得到CF BC =，即可求出答案．【详解】解：如图，在DC 上截取DF DA =，连接EF ，DE 是ADC ∠的角平分线，12∠∠∴=，在△ADE 和△FDE 中，,12,,AD DF DE DE =⎧⎪∠=∠⎨⎪=⎩()ADE FDE SAS ∴△≌△，AE EF ∴=，5A ∠=∠，//AD BC ，180A B ∴∠+∠=︒，56180∠+∠=︒，6B ∴∠=∠， CE 是BCD ∠的角平分线，34∴∠=∠，在CEF △和CEB △中，6,34,,B CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()CEF CEB AAS ∴△≌△，CF BC ∴=，325CD DF CF AD BC ∴=+=+=+=．【点睛】本题考查了角平分线的性质，平行线的性质，全等三角形的判定和性质，证明ADE FDE △≌△是解题关键．9．（1）4；（2）见解析【分析】（1）根据条件证明△OCF ≌△GCF ，由全等的性质就可以得出OF=GF 而得出结论； （2）在BF 上截取BH=CF ，连接OH ，通过条件可以得出△OBH ≌△OCF ，可以得出OH=OF ，从而得出OG ∥FH ，OH ∥FG ，进而可以得出四边形OHFG 是平行四边形，就可以得出结论．【详解】解：（1）∵CF 平分∠OCE ，∴∠OCF=∠ECF ．∵OC=CG ，CF=CF ，∵在△OCF 和△GCF 中，OC GC OCF ECF CF CF ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△OCF ≌△GCF （SAS ），∴FG=OF=4即FG 的长为4．（2）证明：在BF 上截取BH=CF ，连接OH ．∵四边形ABCD 为正方形，∴AC ⊥BD ，∠DBC=45°，∴∠BOC=90°，∴∠OCB=180°-∠BOC-∠DBC=45°．∴∠OCB=∠DBC ．∴OB=OC ．∵BF ⊥CF ，∴∠BFC=90°．∵∠OBH=180°-∠BOC-∠OMB=90°-∠OMB ，∠OCF=180°-∠BFC-∠FMC=90°-∠FMC ，且∠OMB=∠FMC ，∴∠OBH=∠OCF ．∵在△OBH 和△OCF 中OB OC OBH OCF BH CF ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△OBH ≌△OCF （SAS ）．∴OH=OF ，∠BOH=∠COF ．∵∠BOH+∠HOM=∠BOC=90°，∴∠COF+∠HOM=90°，即∠HOF=90°． ∴1180452OHF OFH HOF ∠=∠=︒-∠=︒（）∴∠OFC=∠OFH+∠BFC=135°．∵△OCF ≌△GCF ，∴∠GFC=∠OFC=135°，∴∠OFG=360°-∠GFC-∠OFC=90°． ∴1180452FGO FOG OFG ∠=∠=︒-∠=︒（） ， ∴∠GOF=∠OFH ，∠HOF=∠OFG ．∴OG ∥FH ，OH ∥FG ，∴四边形OHFG 是平行四边形（两组对边分别平行的四边形是平行四边形）．∴OG=FH ．∵BF=FH+BH ，∴BF=OG+CF【点睛】本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，平行四边形的判定及性质的运用，解答时采用截取法作辅助线是关键．10．（1）方法1：证明见解析；方法2：证明见解析；（2）证明见解析．【分析】（1）方法1：先根据角平分线的定义、平行线的性质得出BAF DAE F ∠=∠=∠，再根据等腰三角形的性质可得AB BF =，根据三角形全等的判定定理与性质得出AD FC =，然后根据线段的和差即可得证；方法2：先根据角平分线的定义得出DAE GAE ∠=∠，再根据三角形全等的判定定理与性质可得,DE GE D AGE =∠=∠，然后根据线段中点的定义、等腰三角形的性质可得ECG EGC ∠=∠，最后根据平行线的性质、平角的定义可得BCG BGC ∠=∠，由等腰三角形的定义可得BG BC =，由此根据线段的和差即可得证；（2）如图（见解析），参照方法1构造辅助线，先根据等腰三角形的性质得出EF 平分AFG ∠，从而有12EFC AFG ∠=∠，再根据平行线的性质、角的和差得出60EFC BFC ∠=∠=︒，ECF BCF ∠=∠，然后根据三角形全等的判定定理与性质即可得证．【详解】（1）方法1：如图②，延长AE 、BC 交于点FAE ∵是BAD ∠的平分线BAF DAE ∴∠=∠//AD BCDAE F ∴∠=∠BAF F ∴∠=∠AB BF FC BC ∴==+E 是边CD 的中点DE CE ∴=在ADE 和FCE △中，DAE F AED FEC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADE FCE AAS ∴≅AD FC ∴=AB FC BC AD BC ∴=+=+；方法2：如图③，在AB 上取一点G ，使AG AD =，连接EG 、CGAE ∵是BAD ∠的平分线DAE GAE ∴∠=∠在ADE 和AGE 中，AD AG DAE GAE AE AE =⎧⎪∠=∠⎨⎪=⎩()ADE AGE SAS ∴≅,DE GE D AGE ∴=∠=∠E 是边CD 的中点DE CE ∴=CE GE ∴=ECG EGC ∴∠=∠//AD BC180D BCD ︒∴∠+∠=，即180D ECG BCG ∠+∠+∠=︒180AGE EGC BCG ∴∠+∠+∠=︒，即180AGC BCG ∠+∠=︒又180AGC BGC ∠+∠=︒BCG BGC ∴∠=∠BG BC ∴=AB AG BG AD BC ∴=+=+；（2）如图，过点C 作//CG AD ，交AE 延长线于点G ，延长GC 交AB 于点F ，连接EF 由方法1可知：,AF GF AE GE ==AFG ∴是等腰三角形EF ∴平分AFG ∠12EFC AFG ∴∠=∠ //CG AD ，60BAD ∠=︒60,180120BFC BAD AFG BAD ∴∠=∠=︒∠=︒-∠=︒60EFC ∴∠=︒//CG AD180D ECF ∴∠+∠=︒ 11802D BCD ︒∠+∠=，即1()1802D ECF BCF ∠+∠+∠=︒ 1()2ECF ECF BCF ∴∠=∠+∠ ECF BCF ∴∠=∠在ECF △和BCF △中，60EFC BFC CF CF ECF BCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()ECF BCF ASA ∴≅CB CE ∴=．【点睛】本题考查了角平分线的定义、平行线的性质、三角形全等的判定定理与性质等知识点，较难的是题（2），参照方法1，通过作辅助线，构造全等三角形是解题关键．。

专训2 构造全等三角形的六种常用方法【名师点睛】在进行几何题的证明或计算时，有时需要在图形中添加一些辅助线，辅助线能使题目中的条件比较集中，比较溶液找到一些量之间的关系，使数学问题较轻松的解决。

常见的辅助线作法有：翻折法、构造基础三角形法、旋转法、平行线法、倍长中线法和截长补短法，目的都是构造全等三角形。

[方法1]翻折法1.如图，在△ABC中，BE是∠ABC的角平分线，AD⊥BE，垂足为D，求证：∠2=∠1+∠C. 解答：证明：∵BE是∠ABC的角平分线，AD⊥BE∴AB=FB∴∠2=∠AFB∵∠AFB=∠1+∠C∴∠2=∠1+∠C.[方法2]构造基础三角形法2.如图,在Rt△ABC中,∠ACB=90∘,AC=BC,∠ABC=45∘，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF.求证：∠ADC=∠BDF.解答：证明：作BG⊥CB,交CF的延长线于点G,如图所示：∵∠CBG=90∘，CF⊥AD∴∠CAD+∠ADC=∠BCG+∠ADC=90∘∴∠CAD=∠BCG在△ACD和△CBG中∠CAD=∠BCGAC=BC∠ACD=∠CBG=90∘∴△ACD≌△CBG(ASA)∴CD=BG，∠CDA=∠CGB∵CD=BDBF=BF∴△BFG≌△BFD(SAS)∴∠FGB=∠FDB∴∠ADC=∠BDF.[方法3]旋转法3.正方形ABCD中，E为BC上的一点，F为CD上的一点，BE+DF=EF，求∠EAF的度数。

解答：延长EB使得BG=DF，连接AG，在△ABG和△ADF中由AB=AD，∠ABG=∠ADF=90∘，BG=DF可得△ABG≌△ADF(SAS)∴∠DAF=∠BAG，AF=AG又∵EF=DF+BE=EB+BG=EG，AE=AE在△AEG和△AEF中，AE=AE，GE=FE，AG=AF∴△AEG≌△AEF(SSS)∴∠EAG=∠EAF∵∠DAF+∠EAF+∠BAE=90∘∴∠EAG+∠EAF=90∘∴∠EAF=45∘.[方法4]平行线法4.如图，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC 交AC于点Q，且AP与BQ相交于点O.求证：AB+BP=BQ+AQ.解答：证明：过点O作OD∥BC交AB于点D.∵OD∥BC∴∠ADO=∠ABC∵∠BAC=60°，∠C=40°∴∠ABC=80°∴∠ADO=80°∵BQ平分∠ABC∴∠ABQ=∠QBC=40°∴∠AQB=∠C+∠QBC=80°∴∠ADO=∠AQB∵AP平分∠BAC∴∠DAO=∠QAO=30°又∵OA=OA∴△ADO≌△AQO∴OD=OQ，AD=AQ又∵OD∥BP∴∠PBO=∠DOB又∵∠PBO=∠DBO∴∠DBO=∠DOB∴△DOB是等腰三角形∴BD=OD∴BD=OQ∵∠BAP=30°，∠ABQ=40°∴∠BOP=70°∵∠BAP=30°，∠ABC=80°∴∠APB=70°∴∠BOP=∠APB∴△BOP是等腰三角形∴BO=BP∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ，即AB+BP=BQ+AQ.[方法5]倍长中线法5.如图，△ABC中，D为BC的中点。

初二数学全全等三角形截长补短知识点总结含答案一、全等三角形截长补短1．如图，在△ABC中，AB＝AC，∠BAC＝30°，点D是△ABC内一点，DB＝DC，∠DCB＝30°，点E是BD延长线上一点，AE＝AB．（1）求∠ADB的度数；（2）线段DE，AD，DC之间有什么数量关系？请说明理由．2．已知在四边形ABCD中，∠ABC＋∠ADC＝180°，∠BAD＋∠BCD＝180°，AB＝BC（1）如图1，连接BD，若∠BAD＝90°，AD＝7，求DC的长度．（2）如图2，点P、Q分别在线段AD、DC上，满足PQ＝AP＋CQ，求证：∠PBQ＝∠ABP ＋∠QBC（3）若点Q在DC的延长线上，点P在DA的延长线上，如图3所示，仍然满足PQ＝AP ＋CQ，请写出∠PBQ与∠ADC的数量关系，并给出证明过程．3．（1）问题背景：如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC，CD上的点且∠EAF＝60°，探究图中线段BE、EF、FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G．使DG＝BE．连结AG，先证明ABE≌ADG，再证明AEF≌AGF，可得出结论，他的结论应是______________；（2）探索延伸：如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E，F分别是BC ，CD 上的点，且∠EAF 12=∠BAD ，上述结论是否仍然成立，并说明理由； （3）实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O 处）北偏西30°的A 处，舰艇乙在指挥中心南偏东70°的B 处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以45海里/小时的速度前进，同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进，2小时后，指挥中心观测到甲、乙两地分别到达E 、F 处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．4．如图，在ABC 中，AB AC =，30ABC ∠<︒，D 是边BC 的中点，以AC 为边作等边三角形ACE ，且ACE △与ABC 在直线AC 的异侧，连接BE 交DA 的延长线于点F ，连接FC 交AE 于点M ．（1）求证：FB FC =；（2）求证：FEA FCA ∠=∠；（3）若8FE =，2AD =，求AF 的长．5．问题提出，如图1所示，等边△ABC 内接于⊙O ，点P 是AB 上的任意一点，连结PA ，PB ，PC ．线段PA 、PB 、PC 满足怎样的数量关系?（尝试解决）为了解决这个问题，小明给出这样种解题思路：发现存在条件CA=CB ，∠ACB=60°，从而将CP 绕点逆时针旋转60°交PB 延长线于点M ，从而证明△PAC ≌△MBC ，请你完成余下思考，并直接写出答案：PA 、PB 、PC 的数量关系是 ； （自主探索）如图2所示，把原问题中的“等边△ABC”改成“正方形ABCD”，其余条件不变，①PC 与PA ，PB 有怎样的数量关系?请说明理由：②PC+PD 与PA ，PB 的数量关系是 ．（直接写出结果）（灵活应用）把原问题中的“等边△ABC”改成“正五边形ABCDE”，其余条件不变，则PC+PD+PE 与PA+PB 的数量关系是 ．（直接写出结果）6．如图所示，//AB DC AB AD BE ⊥，，平分ABC CE ∠，平分BCD ∠； （1）求AB CD 、与BC 的数里关系，并说明你的理由．（2）若把AB AD ⊥条件去掉，则（1）中AB CD 、与BC 的数里关系还成立吗?并说明你的理由．7．（1）如图①，Rt ABC 中，AB AC =，90BAC ∠=︒，D 为BC 边上的一点，将ABD △绕点A 逆时针旋转90°至ACF ，作AE 平分DAF ∠交BC 于点E ，易证明：222BD CE DE +=．若2DE BD =，则以BD 、DE 、EC 为边的三角形的形状是______；（2）如图②，四边形ABCD 中，90BAD BCD ∠=∠=︒，AB AD =，若四边形ABCD 的面积是32，2CD =，求BC 的长度；（3）ABC 是以BC 为底的等腰直角三角形，点D 是ABC 所在平面内一点，且满足4=AD ，6BD =，2CD =，请画草图并求ADC ∠的度数．8．数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．∠AEF=90°，且EF 交正方形外角∠DCG 的角平分线CF 于点F ，求证：AE=EF ．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．9．如图，在等边△ABC中，BD＝CE，连接AD、BE交于点F．（1）求∠AFE的度数；（2）求证：AC•DF＝BD•BF；（3）连接FC，若CF⊥AD时，求证：BD＝12 DC．10．已知平行四边形ABCD中，N是边BC上一点，延长DN、AB交于点Q，过A作AM⊥DN于点M，连接AN，则AD⊥AN．（1）如图①，若tan∠ADM＝34，MN＝3，求BC的长；（2）如图②，过点B作BH∥DQ交AN于点H，若AM＝CN，求证：DM＝BH+NH．【参考答案】***试卷处理标记，请不要删除一、全等三角形截长补短1．（1）120°；（2）DE＝AD+CD，理由见解析【分析】（1）根据三角形内角和定理得到∠ABC＝∠ACB＝75°，根据全等三角形的性质得到∠BAD ＝∠CAD＝15°，根据三角形的外角性质计算，得到答案；（2）在线段DE上截取DM＝AD，连接AM，得到△ADM是等边三角形，根据△ABD≌△AEM，得到BD＝ME，结合图形证明结论【详解】解：（1）∵AB＝AC，∠BAC＝30°，∴∠ABC＝∠ACB＝12（180°﹣30°）＝75°，∵DB＝DC，∠DCB＝30°，∴∠DBC＝∠DCB＝30°，∴∠ABD＝∠ABC﹣∠DBC＝45°，在△ABD和△ACD中，AB AC DB DC AD AD=⎧⎪=⎨⎪=⎩，∴△ABD≌△ACD（SSS），∴∠BAD＝∠CAD＝12∠BAC＝15°，∴∠ADE＝∠ABD+∠BAD＝60°，∴∠ADB＝180°﹣∠ADE＝180°﹣60°＝120°；（2）DE＝AD+CD，理由如下：在线段DE上截取DM＝AD，连接AM，∵∠ADE＝60°，DM＝AD，∴△ADM是等边三角形，∴∠ADB＝∠AME＝120°．∵AE＝AB，∴∠ABD＝∠E，在△ABD和△AEM中，ABD EADB AME AB AE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△AEM（AAS），∴BD＝ME，∵BD＝CD，∴CD＝ME．∵DE＝DM+ME，∴DE＝AD+CD．【点睛】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．2．（1）7DC =；（2）见解析；（3）1902PBQ ADC ∠=︒+∠，证明见解析 【分析】（1）根据已知条件得出BDC 为直角三角形，再根据HL 证出△≌△Rt BAD Rt BCD ，从而证出AD CD =即可得出结论；（2）如图2，延长DC 到 K ，使得CK=AP ，连接BK ，通过证△BPA ≌△BCK （SAS ）得到：∠1=∠2，BP=BK ．然后根据SSS 证明得≌PBQ BKQ ，从而得出21PBQ CBQ CBQ ∠=∠+∠=∠+∠，然后得出结论；（3）如图3，在CD 延长线上找一点K ，使得KC=AP ，连接BK ，构建全等三角形：△BPA ≌△BCK （SAS ），由该全等三角形的性质和全等三角形的判定定理SSS 证得：△PBQ ≌△BKQ ，则其对应角相等：∠PBQ=∠KBQ ，结合四边形的内角和是360°可以推得：∠PBQ=90°+12∠ADC ． 【详解】（1）证明：如图1，∵180ABC ADC ∠+∠=︒，90BAD ∠=︒，∴90BCD BAD ∠=∠=︒，在Rt BAD 和Rt BCD 中，BD BD AB BC=⎧⎨=⎩ ∴()△≌△Rt BAD Rt BCD HL ，∴AD DC =，∴7DC =；（2）如图2，延长DC 至点K ，使得CK AP =，连接BK∵180ABC ADC ∠+∠=︒，∴180BAD BCD ∠+∠=︒，∵180BCD BCK ∠+∠=︒，∴BAD BCK ∠=∠，∵AP CK =，AB BC =，∴()△≌△BPA BCK SAS ， ∴12∠=∠，BP BK =，∵PQ AP CQ =+，QK CK CQ =+，∴PQ QK =，∵BP BK =，BQ BQ =，∴()≌PBQ BKQ SSS ，∴21PBQ CBQ CBQ ∠=∠+∠=∠+∠，∴PBQ ABP QBC ∠=∠+∠；（3）1902PBQ ADC ∠=︒+∠； 如图3，在CD 延长线上找一点K ，使得KC AP =，连接BK ，∵180ABC ADC ∠+∠=︒，∴180BAD BCD ∠+∠=︒，∵180BAD PAB ∠+∠=︒，∴PAB BCK ∠=∠，在BPA △和BCK 中，AP CK BAP BCK AB BC =⎧⎪∠=∠⎨⎪=⎩∴()△≌△BPA BCK SAS ， ∴ABP CBK ∠=∠，BP BK =，∴PBK ABC ∠=∠，∵PQ AP CQ =+，∴PQ QK =，在PBQ △和BKQ 中，BP BK BQ BQ PQ KQ =⎧⎪=⎨⎪=⎩∴()≌PBQ BKQ SSS ，∴PBQ KBQ ∠=∠，∴22360PBQ PBK PBQ ABC ∠+∠=∠+∠=︒，∴()2180360PBQ ADC ∠+︒-∠=︒， ∴1902PBQ ADC ∠=︒+∠． ．【点睛】本题考查了全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．3．（1）EF ＝BE +DF ；（2）结论EF ＝BE +DF 仍然成立；（3）此时两舰艇之间的距离是210海里【分析】（1）延长FD 到点G ，使DG=BE ．连结AG ，即可证明ABE ≌ADG ，可得AE=AG ，再证明AEF ≌AGF ，可得EF=FG ，即可解题； （2）延长FD 到点G ，使DG=BE ．连结AG ，即可证明ABE ≌ADG ，可得AE=AG ，再证明AEF ≌AGF ，可得EF=FG ，即可解题； （3）连接EF ，延长AE 、BF 相交于点C ，然后与（2）同理可证．【详解】解：（1）EF ＝BE +DF ，证明如下：在ABE 和ADG 中，B ADG AB AD ⎪∠=∠⎨⎪=⎩， ∴ABE ≌ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF 12=∠BAD ， ∴∠GAF ＝∠DAG +∠DAF ＝∠BAE +∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ， ∴∠EAF ＝∠GAF ，在AEF 和GAF 中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴AEF ≌AGF （SAS ），∴EF ＝FG ，∵FG ＝DG +DF ＝BE +DF ，∴EF ＝BE +DF ；故答案为 EF ＝BE +DF ．（2）结论EF ＝BE +DF 仍然成立；理由：延长FD 到点G ．使DG ＝BE ．连结AG ，如图2，在ABE 和ADG 中，DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩，∴ABE ≌ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠EAF 12=∠BAD ， ∴∠GAF ＝∠DAG +∠DAF ＝∠BAE +∠DAF ＝∠BAD ﹣∠EAF ＝∠EAF ，∴∠EAF ＝∠GAF ，在AEF 和GAF 中，EAF GAF AF AF ⎪∠=∠⎨⎪=⎩， ∴AEF ≌AGF （SAS ），∴EF ＝FG ，∵FG ＝DG +DF ＝BE +DF ，∴EF ＝BE +DF ；（3）如图3，连接EF ，延长AE 、BF 相交于点C ，∵∠AOB ＝30°+90°+（90°﹣70°）＝140°，∠EOF ＝70°，∴∠EOF 12=∠AOB ， 又∵OA ＝OB ，∠OAC +∠OBC ＝（90°﹣30°）+（70°+50°）＝180°，∴符合探索延伸中的条件，∴结论EF ＝AE +BF 成立，即EF ＝2×（45+60）＝210（海里）．答：此时两舰艇之间的距离是210海里．【点睛】本题考查了全等三角形的判定以及全等三角形对应边相等的性质，本题中求证△AEF ≌△AGF 是解题的关键．4．（1）见解析；（2）见解析；（3）4【分析】（1）利用AD 所在直线是BC 的垂直平分线，点F 在直线AD 上即可得出结论． （2）由ACE △是等边三角形，得AC=AE=AB 推得ABF FEA ∠=∠．易证ABF ≌ACF （SSS ），ABF FCA FEA ∠=∠=∠即可，（3）延长AD 至点P 处，使DP AD ，连接CP ．先证直角三角形ADC ≌PDC△（SAS ），推出AC CP CE ==，ACD PCD ∠=∠．再证60EFC EAC ∠=∠=︒．求出，FBD 30FCD ∠=∠=︒．用ACD ∠表示30ECF ACD ∠=︒+∠．而30FCP ACD ∠=︒+∠，得ECF FCP ∠=∠．可证ECF △≌PCF （SAS ），可推得AF EF AP =-即可．【详解】（1）证明：∵AB AC =，D 是边BC 的中点，∴AD 所在直线是BC 的垂直平分线，又∵点F 在直线AD 上∴FB FC =．（2）证明：∵ACE △是等边三角形，∴60EAC ACE ∠=∠=︒，AC AE =．∵AB AC =，∴AB AE =，∴ABF FEA ∠=∠．由（1）可知，FB FC =，又∵AF AF =，AB AC =，∴ABF ≌ACF （SSS ），∴ABF FCA ∠=∠，∴FEA FCA ∠=∠． （3）解：如图，延长AD 至点P 处，使DP AD ，连接CP ．∵AB AC =，D 是边BC 的中点，∴90ADC PDC ∠=∠=︒．∵ACE △是等边三角形，∴AC CE =，60EAC ∠=︒．∵AD DP =，ADC PDC ∠=∠，CD CD =，∴ADC ≌PDC △（SAS ），∴AC CP CE ==，ACD PCD ∠=∠．由（2）可知，FEA FCA ∠=∠，∵AMC FME ∠=∠，∴60EFC EAC ∠=∠=︒．由（1）可知，BF CF =， ∴()18060260BFD CFD ∠=∠=︒-︒÷=︒，∴906030FCD ∠=︒-︒=︒．∵FCA FCD ACD ∠=∠-∠，∴30FCA ACD ∠=︒-∠．∵ECF ECA FCA ∠=∠-∠，∴()303030ECF ECA ACD ECA ACD ACD ∠=∠-︒-∠=∠-︒+∠=︒+∠． ∵FCP FCD PCD ∠=∠+∠，∴30FCP ACD ∠=︒+∠，∴ECF FCP ∠=∠．∵FC FC =，CE CP =，∴ECF △≌PCF （SAS ）， ∴FE FP =， ∴2FE FA AP AF AD =+=+，∴2822=4AF EF AD =-=-⨯．【点睛】本题考查线段垂直平分线性质，等边三角形性质，三角形全等判定与性质，掌握线段垂直平分线性质，等边三角形性质，三角形全等判定与性质，会利用引辅助线构造三角形全等转化线与线关系，角与角关系来解决问题．5．【尝试解决】PA+PB=PC ；【自主探索】①PC PA =；理由见解析；②1)()PC PD PA PB +=+；【灵活应用】2)()PC PD PE PA PB ++=+．【分析】尝试解决：利用旋转性质证明△PAC ≌△MBC ，得到PA=BM ，得到PM 等于PB 与PA 的和，再证明△PCM 是等边三角形，得到PM 等于PC ，即可得到结果；自主探索：①在PC 上截取QC=PA ，证出△CBQ 全等于△ABP ，得到△PBQ 是等腰直角三角形，PQ 等于PB 倍，即可得到结果；②同①方法，即可得到PD 与PA 和PB 的关系，即可求出PC+PD 与PA 和PB 的关系； 灵活应用：类比（自主探索）中的方法证明PC 与PA 和PB 的关系，再用同样的方法证明PE 与PA 和PB 的关系，构造△CDM 全等于△CBP ，得到PD 与PC 的关系，进一步得到PD 与PA 和PB 的关系，最终求出PD+PE+PC 的和即可得到与PA 和PB 的关系．【详解】尝试解决：PA+PB=PC ；证明：因为∠ACP+∠PCB=60°，∠MCB+∠PCB=60°，∴∠ACP=∠MCB ，又∵CP=CM ，AC=MC ，∴△ACP ≌△BCM ，所以PA=BM ，∠CBM=∠CAP ，∵四边形APBC 内接于圆O ，∴∠CAP+∠CBP=180°，∴∠CBM+∠CBP=180° ，∴P 、B 、M 三点共线，∴△PCM 是等边三角形，∴PM=PC ，∴PC=PM=PB+BM=PB+PA ；自主探索：①PC 与PA 、PB 的数量关系为2PC PA PB =+；理由：截取CQ=PA ，，如图，∵四边形ABCD 是正方形，∴BC=AB ，∠ABC=∠BCD=∠CDA=∠DAB=90°，∵PA=CQ ，∠BCQ=BAP ，BC=AB∴△BCQ ≌△BAP ，∴∠CBQ=∠ABP ，BQ=BP ， ∵∠CBQ+∠ABQ=90°，∴90ABP ABQ ∠+∠=︒，∴△PBQ 是等腰直角三角形，∴2PB ，∴2PC CQ PQ PA PB =+=+；②21)()PC PD PA PB +=+证明：在PD 上截取DH=PB ，∵DH=PB ，∠ADH=∠ABP ，AD=AB∴△ADH ≌△ABP∴∠DAH=∠BAP ，AH=AP ，∵∠DAH+∠HAP=90°， ∴∠BAP+∠HAP=90°，∴△HAP 是等腰直角三角形，∴2，∴2PA ，∴21)()PC PD PA PB +=+．灵活应用：52)()PC PD PE PA PB ++=+．证明：在PC 上截取FC=PA ，∵五边形ABCDE 是正五边形，∴BC=AB=CD=DE=AE ，∠ABC=∠EAB=108°，∵PA=CF ，AB=BC ，∠FCB=∠BAP ，∴△BAP ≌△BCF ，∴BF=PB ，∠CBF=∠ABP ，∵∠CBF+∠FBA=108°，∴∠ABP+∠FBA=108°，∴△FBP 是顶角为108°的等腰三角形，∴15+PB ， ∴15+PB+PA ， 同理可证15+PA+PB ， 延长PD 至点M 使DM=PB ，∵∠MDC+∠CDP=180°，∠CDP+∠PBC=180°，∴∠CDM=∠CBP又∵CD=BC ，∴△CDM ≌△CBP∴CM=CP ，∠MCD=∠BCP ，又∵∠PCB+∠PCD=108°，∴∠MCD+∠PCD=108°，∴△MCP 是顶角108°的等腰三角形，∴PM=152+PC ， ∴15+PC-PB ， ∴PC+PD+PE 15+15+35+15+PB+PA ）+152+PA=()()2525PA PB +++=()()25PA PB ++ 【点睛】 本题考查旋转性质、圆的有关性质、圆内接四边形、正五边形有关性质、三角形全等的相关性质和判定，综合性强，难度较大是一道好题，属中考压轴题型．6．（1）AB CD BC +=，见解析；（2）成立，见解析【分析】（1）先写出数量关系，过E 作EF BC ⊥于F ，然后证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得结论了．（2）成立, 在BC 上截取CF CD =证明CDE CFE ∆≅∆和ABE FBE ≅∆∆，便可得到结论．【详解】()1AB CD BC +=理由是：过E 作EF BC ⊥于FCE 为角平分线DCE FCE ∴∠=∠//AB DC AB AD ⊥，90D ∴∠=EF BC ⊥D CFE ∴∠=∠CE CE =()CDE CFE AAS ∆≅∆CD CF ∴=同理可证()ABE FBE AAS ∆≅∆AB BF ∴=CF BF AB +=AB CD BC ∴+=()2成立理由：在BC 上截取CF CD =CE 为角平分线DCE FCE ∴∠=∠CE CE =()CDE CFE SAS ∆≅∆CD CF ∴= D CFE ∠=∠//AB DC180D A ∴∠+∠=又180CFE EFB ∠+=A EFB ∴∠=∠ 又BE 是角平分线 ABE FBE ∴∠=∠BE BE =()BAE BFE AAS ∆≅∆AB FB ∴=∴ CF BF AB +=AB CD BC ∴+=7．（1）等腰直角三角形；（2）723）图见解析，135°或45°【分析】（1）要判断以BD 、DE 、EC 为边的三角形形状，根据题干中所给条件，只需证明BD EC =即可；（2）先构造出ABE ADC △≌△，进而判断出CAE 是等腰直角三角形，四边形的面积等于ACE △的面积，由此求出AC ，CE 即可；（3）分情况讨论：①当点D 在ABC 内时，作AE AD ⊥，使AE AD =，连接CE ，DE ，利用全等三角形的性质以及勾股定理的逆定理解决问题；②当点D 在ABC 外时，作AE AD ⊥，使AE AD =，连接CE ，DE ，利用全等三角形的性质以及勾股定理的逆定理解决问题．【详解】解：（1）222BD CE DE +=，∴以BD 、DE 、EC 为边的三角形是直角三角形，2DE BD =，设BD a =，则2DE a =，2222a EC a ∴+=，EC a ∴=，BD EC ∴=，∴以BD 、DE 、EC 为边的三角形的形状是等腰直角三角形． 故答案：等腰直角三角形．（2）如图①，延长CB 至E ，使BE CD =，连接AE ，在四边形ABCD 中，90BAD BCD ∠=∠=︒，180ABC ADC ∴∠+∠=︒，180ABC ABE ∠+∠=︒，ABE ADC ∴∠=∠，在ABE △和ADC 中，,,,AB AD ABE ADC BE CD =⎧⎪∠=∠⎨⎪=⎩()ABE ADC SAS ∴△≌△，AE AC ∴=，BAE DAC ∠=∠，90CAE BAE BAC DAC BAC ∴∠=∠+∠=∠+∠=︒，212ACE S AC ∴=△， 四边形ABCD 的面积为32，ACE ABCD S S =△四边形，21322AC ∴=， 8AC ∴=（负值已舍），282EC AC ∴==，82272BC EC BE ∴=-=-=．图①（3）①画图如图②，③．当点D 在ABC 内时，如图②，过点A 作AE AD ⊥，使AE AD =，连接CE ，DE ， 90BAC DAE ∠=∠=︒，BAD CAE ∴∠=∠，在BAD 和CAE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，()BAD CAE SAS ∴≌，6BD CE ∴==，2DE ==2CD =，222EC ED CD ∴=+，90EDC ∴∠=︒，45ADE ∠=︒，4590135ADC ∴∠=︒+︒=︒；②当点D 在ABC 外时，如图③，过点A 作AE AD ⊥，使AE AD =，连接CE ，DE ，90BAC DAE ∠=∠=︒，BAD CAE ∴∠=∠，在BAD 和CAE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，()BAD CAE SAS ∴≌，6BD CE ∴==，2DE ==2CD =，222EC ED CD ∴=+，90EDC ∴∠=︒，45ADE ∠=︒，45ADC ∴∠=︒．综上所述，ADC ∠的度数为135°或45°．图② 图③【点睛】本题考查了等腰三角形的判定和性质，全等三角形的判定和性质，勾股定理以及逆定理等知识，解题的关键是利用旋转法添加辅助线，构造全等三角形解决问题，用分类讨论的思想思考问题，属于中考压轴题．8．（1）正确．证明见解析；（2）正确．证明见解析.【分析】（1）在AB 上取一点M ，使AM EC =，连接ME ，根据已知条件利用ASA 判定AME ECF ，因为全等三角形的对应边相等，所以AE EF =． （2）在BA 的延长线上取一点N ，使AN CE =，连接NE ，根据已知利用ASA 判定ANE ECF ，因为全等三角形的对应边相等，所以AE EF =． 【详解】 解：（1）正确．证明：在AB 上取一点M ，使AM EC =，连接ME ．BM BE ∴=，45BME ∴∠=°，135AME ， CF 是外角平分线，45DCF ∴∠=︒，135ECF ∴∠=°，AME ECF ，90AEB BAE ，90AEB CEF ∠+∠=︒， BAE CEF ∴∠=∠， ()AME ECF ASA ，AE EF ∴=．（2）正确．证明：如图示，在BA 的延长线上取一点N ，使AN CE =，连接NE ．BN BE ∴=，45N NEC ， CF 平分DCG ∠，45FCE ，N ECF ，四边形ABCD 是正方形，//AD BE ∴，DAE BEA ，即9090DAE BEA ，NAE CEF ， ()ANE ECF ASA ，AE EF ∴=．【点睛】此题主要考查了正方形的性质，角平分线的性质及全等三角形的判定方法，熟悉相关性质是解题的关键．9．（1）60°；（2）证明见解析；（3）证明见解析【分析】（1）证明△ABD ≌△BCE （SAS ），得出∠BAD ＝∠CBE ，则∠BFD ＝∠AFE ＝∠ABC ＝60°； （2）证明△ADB ∽△BDF ，得出=AB BD BF DF，由AB ＝AC 可得出结论； （3）延长BE 至H ，使FH ＝AF ，连接AH ，CH ，证明△BAF ≌△CAH （SAS ），得出∠ABF ＝∠ACH ，CH ＝BF ，可证明AF ∥CH ，得出1=2BF BD FH CD =，进而即可得出答案． 【详解】解：（1）∵△ABC 是等边三角形，∴AB ＝AC ＝BC ，∠ABD ＝∠BCE ＝60°，在△ABD 和△BCE 中， ABD BC AB BC BD CE E =⎧=∠∠⎪⎨⎪⎩＝，∴△ABD ≌△BCE （SAS ），∴∠BAD ＝∠CBE ，∵∠ADC ＝∠CBE+∠BFD ＝∠BAD+∠ABC ，∴∠BFD ＝∠AFE ＝∠ABC ＝60°；（2）证明：由（1）知∠BAD ＝∠DBF ，又∵∠ADB ＝∠BDF ，∴△ADB ∽△BDF ，∴=AB BD BF DF， 又AB ＝AC ， ∴=AC BD BF DF， ∴AC•DF ＝BD•BF ；（3）证明：延长BE 至H ，使FH ＝AF ，连接AH ，CH ，由（1）知∠AFE ＝60°，∠BAD ＝∠CBE ，∴△AFH 是等边三角形，∴∠FAH ＝60°，AF ＝AH ，∴∠BAC ＝∠FAH ＝60°，∴∠BAC ﹣∠CAD ＝∠FAH ﹣∠CAD ，即∠BAF ＝∠CAH ，在△BAF 和△CAH 中，BAF CA AB AC AF AH H =⎧=∠∠⎪⎨⎪⎩＝,∴△BAF ≌△CAH （SAS ），∴∠ABF ＝∠ACH ，CH ＝BF ，又∵∠ABC ＝∠BAC ，∠BAD ＝∠CBE ，∴∠ABC ﹣∠CBE ＝∠BAC ﹣∠BAD ，即∠ABF ＝∠CAF ，∴∠ACH ＝∠CAF ，∴AF ∥CH ，∵∠AFC ＝90°，∠AFE ＝60°，∴CF ⊥CH ，∠CFH ＝30°，∴FH ＝2CH ，∴FH ＝2BF ，∵FD ∥CH ， ∴1=2BF BD FH CD ， ∴BD ＝12DC ． 【点睛】本题考查等边三角形的性质、全等三角形的判定及其性质、相似三角形的判定及其性质，解题的关键熟练掌握全等三角形的判定方法和相似三角形的判定方法．10．（1）BC ＝203；（2）见解析. 【分析】（1）如图①中，设AM ＝3k ，DM ＝4k ，则AD ＝5k ，由△ADM ∽△NDA ，可得AD 2＝DM •AN ，由此构建方程即可解决问题．（2）如图②中，连接CH ，在DM 上取一点K ，使得DK ＝BH ．证明△ADK ≌△CBH （SAS ），推出AK ＝CH ，再证明Rt △AMK ≌Rt △CNH （HL ），推出MK ＝HN 即可解决问题．【详解】（1）解：如图①中，∵AM ⊥DN ，∴∠AMD ＝90°，∵tan ∠ADM ＝AII DN ＝34， ∴可以假设AM ＝3k ，DM ＝4k ，则AD ＝5k ，∵AD⊥AN，∴∠DAN＝90°＝∠AMD，∵∠ADM＝∠ADN，∴△ADM∽△NDA，∴AD2＝DM•AN，∴（5k）2＝4k（4k+3），解得k＝43，∴AD＝203，∵四边形ABCD是平行四边形，∴BC＝AD＝203．（2）证明：如图②中，连接CH，在DM上取一点K，使得DK＝BH．∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠ADK＝∠BNQ，∵BH∥DQ，∴∠CBH＝∠BNQ，∴∠ADK＝∠CBH，∵DK＝BH，DA＝BC，∴△ADK≌△CBH（SAS），∴AK＝CH，∵AM⊥DQ，AN⊥AD，AD∥BC，∴AN⊥BC，∴∠AMK＝∠CNH＝90°，∵AM＝CN，∴Rt△AMK≌Rt△CNH（HL），∴MK＝NH，∴DM＝DK+MK＝BH+HN．【点睛】本题考查了三角形的综合问题，掌握解直角三角形、相似三角形的性质以及判定定理、全等三角形的性质以及判定定理是解题的关键．。