力学竞赛静力学1
- 格式:pdf
- 大小:707.20 KB
- 文档页数:23

第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学(静止流体中的压强)【内容讲解】一.物体的重心1.常见物体的重心:质量均匀分布的三角板的重心在其三条中线的交点;质量均匀分布的半径R的半球体的重心在其对称轴上距球心3R/8处;质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.重心:在xyz 三维坐标系中,将质量为m的物体划分为质点m1、m2、m3……m n.设重心坐标为(x0,y0,z0),各质点坐标为(x1,y1,z1),(x2,y2,z2)……(x n,y n,z n).那么:mx0=∑m i x i my0=∑m i y i mz0=∑m i z i【例题】1、(1)有一质量均匀分布、厚度均匀的直角三角板ABC,∠A=30°∠B=90°,该三角板水平放置,被A、B、C三点下方的三个支点支撑着,三角板静止时,A、B、C三点受的支持力各是N A、N B、N C,则三力的大小关系是.(2)半径为R的均匀球体,球心为O点,今在此球内挖去一半径为0.5R的小球,且小球恰与大球面内切,则挖去小球后的剩余部分的重心距O点距离为.2、如图所示,质量分布均匀、厚度均匀的梯形板ABCD,CD=2AB,求该梯形的重心位置。
3、在质量分布均匀、厚度均匀的等腰直角三角形ABC(角C为直角)上,切去一等腰三角形APB,如图所示。
如果剩余部分的重心恰在P点,试证明:△APB的腰长与底边长的比为5:4.4、(1)质量分别为m,2m,3m……nm的一系列小球(可视为质点),用长均为L的细绳相连,并用长也是L的细绳悬于天花板上,如图所示。
求总重心的位置5、如图所示,质量均匀分布的三根细杆围成三角形ABC,试用作图法作出其重心的位置。
6、如图所示,半径为R圆心角为θ的一段质量均匀分布的圆弧,求其重心位置。
7、论证质量均匀分布的三角形板的重心在三条中线的交点上8、求半径为R的厚薄均匀的半圆形薄板的重心9、均匀半球体的重心问题10、均匀圆锥体的重心11、如图所示,有一固定的半径为R 的光滑半球体,将一长度恰好等于R 21、质量为m 的均匀链条搭在球体上,其一端恰在球体的顶点上,并用水平拉力拉住链条使之静止,求拉力的大小。
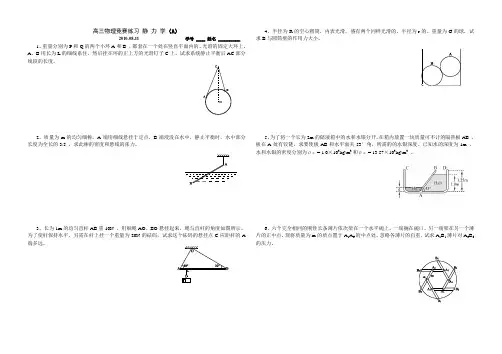
高三物理竞赛练习静力学(A)2010-08-11 学号 ____ 姓名 __________1、重量分别为P和Q的两个小环A和B ,都套在一个处在竖直平面内的、光滑的固定大环上。
A、B用长为L的细线系住,然后挂在环的正上方的光滑钉子C上。
试求系统静止平衡后AC部分线段的长度。
2、质量为m的均匀细棒,A端用细线悬挂于定点,B端浸没在水中,静止平衡时,水中部分长度为全长的3/5 ,求此棒的密度和悬线的张力。
3、长为1m的均匀直杆AB重10N ,用细绳AO、BO悬挂起来,绳与直杆的角度如图所示。
为了使杆保持水平,另需在杆上挂一个重量为20N的砝码,试求这个砝码的悬挂点C应距杆的A 端多远。
4、半径为R的空心圆筒,内表光滑,盛有两个同样光滑的、半径为r的、重量为G的球,试求B与圆筒壁的作用力大小。
5、为了将一个长为2m的储液箱中的水和水银分开,在箱内放置一块质量可不计的隔热板AB ,板在A处有铰链,求要使板AB和水平面夹53°角,所需的的水银深度。
已知水的深度为1m 、水和水银的密度分别为ρ水= 1.0×103kg/m3和ρ汞= 13.57×103kg/m3。
6、六个完全相同的刚性长条薄片依次架在一个水平碗上,一端搁在碗口,另一端架在另一个薄片的正中点。
现将质量为m的质点置于A1A6的中点处,忽略各薄片的自重,试求A1B1薄片对A6B6的压力。
静力学(A ) 提示与答案:1、提示:本题应用共点力平衡知识,正确画出两个小环的受力,做出力的矢量三角形,利用力三角形和空间几何三角形相似求解。
答案:QP Q+L 。
2、提示:本题利用力矩平衡知识求解,列方程注意转动点(或转动轴)应根据所求问题正确选取,另注意浮力的作用点在浸没段的中心点。
答案:2521ρ水;72mg 。
3、提示:本题利用刚体平衡条件求解,列出力的平衡方程和力矩平衡方程求解,列力矩平衡方程注意转动点(或转动轴)应根据所求问题正确选取。

⾼中物理竞赛静⼒学静⼒学1如图所⽰,⼀个半径为R 的四分之⼀光滑球⾯放在⽔平桌⾯上,球⾯上放置⼀光滑均匀铁链,其A 端固定在球⾯的顶点,B 端恰与桌⾯不接触,铁链单位长度的质量为ρ.试求铁链A 端受的拉⼒T.2:图3—9中,半径为R 的圆盘固定不可转动,细绳不可伸长但质量可忽略,绳下悬挂的两物体质量分别为M 、m.设圆盘与绳间光滑接触,试求盘对绳的法向⽀持⼒线密度.3、质量为m ,⾃然长度为2πa ,弹性系数为k 的弹性圈,⽔平置于半径为R 的固定刚性球上,不计摩擦。
⽽且a = R/2 。
(1)设平衡时圈长为2πb ,且 b = 2a ,试求k 值;(2)若k = R 2mg 2 ,求弹性圈的平衡位置及长度。
4、均质铁链如图2悬挂在天花板上,已知悬挂处的铁链的切线与天花板的夹⾓为θ,⽽铁链总重为G , 试求铁链最底处的张⼒。
5、如图3所⽰,两不计⼤⼩的定滑轮被等⾼地固定在天花板上,跨过滑轮的轻绳悬挂三部分重物。
A 、B 部分的重量是固定的,分别是A G = 3⽜顿和B G = 5⽜顿,C G 则可以调节⼤⼩。
设绳⾜够长,试求能维持系统静⽌平衡的C G 取值范围。
6、如图5所⽰,长为L 、粗细不均匀的横杆被两根轻绳⽔平悬挂,绳⼦与⽔平⽅向的夹⾓在图上已标⽰,求横杆的重⼼位置。
7、如图所⽰,⼀个重量为G 的⼩球套在竖直放置的、半图 2θA B C 图 3径为R 的光滑⼤环上,另⼀轻质弹簧的劲度系数为k ,⾃由长度为L (L <2R ),⼀端固定在⼤圆环的顶点A ,另⼀端与⼩球相连。
环静⽌平衡时位于⼤环上的B 点。
试求弹簧与竖直⽅向的夹⾓θ。
思考:若将弹簧换成劲度系数k ′较⼤的弹簧,其它条件不变,则弹簧弹⼒怎么变?环的⽀持⼒怎么变?8、光滑半球固定在⽔平⾯上,球⼼O 的正上⽅有⼀定滑轮,⼀根轻绳跨过滑轮将⼀⼩球从图中所⽰的A 位置开始缓慢拉⾄B 位置。
试判断:在此过程中,绳⼦的拉⼒T 和球⾯⽀持⼒N 怎样变化?9、如图所⽰,⼀个半径为R 的⾮均质圆球,其重⼼不在球⼼O 点,先将它置于⽔平地⾯上,平衡时球⾯上的A 点和地⾯接触;再将它置于倾⾓为30°的粗糙斜⾯上,平衡时球⾯上的B 点与斜⾯接触,已知A 到B 的圆⼼⾓也为30°。

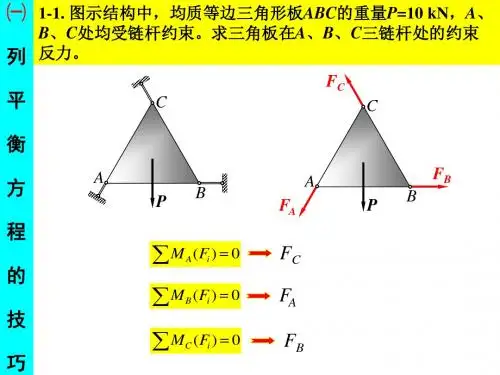

第一讲:力、物体的平衡补充:杠杆平衡(即力矩平衡),对任意转动点都平衡。
一、力学中常见的三种力1.重力、重心 重心的定义:++++=g m g m gx m gx m x 212211,当坐标原点移到重心上,则两边的重力矩平衡。
问题:半径R =30cm 的均匀圆板上挖出一个半径r =15cm 的内切圆板,如图a 所示,求剩下部分的重心。
2.弹力、弹簧的弹力(F =kx ,或F =-kx )(1)两弹簧串联总伸长x ,F =?由x 1+x 2=x ,k 1x 1=k 2x 2,得2112k k x k x +=,所以kx k k x k k x k F =+===212122. (2)并联时F =(k 1+k 2)x .(3)把劲度系数为k 的弹簧均分为10段,每段劲度系数k '=?(10k )1. 一个重为G 的小环,套在竖直放置的半径为R 的光滑大圆上。
一个劲度系数为k ,自然长度为L (L <2R )的轻质弹簧,其上端固定在大圆环最高点,下端与小环相接,不考虑一切摩擦,小环静止时弹簧与竖直方向的夹角为: . (答案:GkR kL 22cos 1--)3.摩擦力(1)摩擦力的方向:①静摩擦力的方向:跟运动状态与外力有关。
②滑动摩擦力的方向:跟相对运动方向相反。
2. 如图所示,在倾角θ=300的粗糙斜面上放一物体,物体的重力为G ,现用与斜面底边平行的水平作用力F (F =G /2)推物体,物体恰好在斜面上作匀速直线运动,则物体与斜面的动摩擦因数为 . (答案:36)(2)摩擦角:f 和N 的合力叫全反力,全反力的方向跟弹力的方向的最大夹角(f 达到最大)叫摩擦角,摩擦角ϕ=tan -1f /N =tan -1μ。
摩擦角与摩擦力无关,对一定的接触面,ϕ是一定的。
水平地面上有一质量为m 的物体,受斜向上的拉力F 作用而匀速移动,物体与地面间的动摩擦因数为μ,则为使拉力F 最小,F 与水平地面间的夹角多大?F 的最小值为多少?二、物体的平衡1.三力平衡特点 (1)任意两个的合力与第三个力是一对平衡力(2)三力汇交原理:互不平行的三个力处于平衡,这三个力的作用线必交于一点。


静力学1如图所示,一个半径为R 的四分之一光滑球面放在水平桌面上,球面上放置一光滑均匀铁链,其A 端固定在球面的顶点,B 端恰与桌面不接触,铁链单位长度的质量为ρ.试求铁链A 端受的拉力T.2:图3—9中,半径为R 的圆盘固定不可转动,细绳不可伸长 但质量可忽略,绳下悬挂的两物体质量分别为M 、m.设圆盘与 绳间光滑接触,试求盘对绳的法向支持力线密度.3、质量为m ,自然长度为2πa ,弹性系数为k 的弹性圈,水平置于半径为R 的固定刚性球上,不计摩擦。
而且a = R/2 。
(1)设平衡时圈长为2πb ,且b = 2a ,试求k 值;(2)若k =R2mg2 ,求弹性圈的平衡位置及长度。
4、均质铁链如图2悬挂在天花板上,已知悬挂处的铁链的切线与天花板的夹角为θ,而铁链总重为G , 试求铁链最底处的张力。
5、如图3所示,两不计大小的定滑轮被等高地固定在天花板上,跨过滑轮的轻绳悬挂三部分重物。
A 、B 部分的重量是固定的,分别是A G = 3牛顿和B G = 5牛顿,C G 则可以调节大小。
设绳足够长,试求能维持系统静止平衡的C G 取值范围。
6、如图5所示,长为L 、粗细不均匀的横杆被两根轻绳水平悬挂,绳子与水平方向的夹角在图上已标示,求横杆的重心位置。
θ图 37、如图所示,一个重量为G 的小球套在竖直放置的、半径为R 的光滑大环上,另一轻质弹簧的劲度系数为k ,自由长度为L (L <2R ),一端固定在大圆环的顶点A ,另一端与小球相连。
环静止平衡时位于大环上的B 点。
试求弹簧与竖直方向的夹角θ。
思考:若将弹簧换成劲度系数k ′较大的弹簧,其它条件不变,则弹簧弹力怎么变?环的支持力怎么变?8、光滑半球固定在水平面上,球心O 的正上方有一定滑轮,一根轻绳跨过滑轮将一小球从图中所示的A 位置开始缓慢拉至B 位置。
试判断:在此过程中,绳子的拉力T 和球面支持力N 怎样变化?9、如图所示,一个半径为R 的非均质圆球,其重心不在球心O 点,先将它置于水平地面上,平衡时球面上的A 点和地面接触;再将它置于倾角为30°的粗糙斜面上,平衡时球面上的B 点与斜面接触,已知A 到B 的圆心角也为30°。



周培源力学竞赛公式周培源力学竞赛公式是指的周培源力学竞赛所囊括的各种力学公式,这些公式覆盖了力学的各个方面,包括静力学、动力学、功与能等。
在力学竞赛中,运用这些公式可以帮助我们快速计算、分析和推导问题,从而解决相应的力学问题。
下面是一些常见的周培源力学竞赛公式。
一、静力学公式1.牛顿第一定律(惯性定律):物体在没有外力或合力为零的情况下,保持匀速直线运动或静止。
2. 牛顿第二定律(运动定律):F=ma,表示物体的运动状态与作用在其上的力的大小和方向成正比。
3.牛顿第三定律(作用-反作用定律):任何两个物体之间的相互作用力都满足大小相等、方向相反、作用在不同物体上的特点。
二、动力学公式1. 动能(动能定理):K=(1/2)mv²,表示物体的动能与其质量和速度平方成正比。
2.位移与速度的关系:v=∆s/∆t,表示速度是位移关于时间的导数。
3. 速度与加速度的关系:a=dv/dt,表示加速度是速度关于时间的导数。
4.加速度与位移的关系:a=∆v/∆t=∆(∆s/∆t)/∆t=∆²s/∆t²,表示加速度是位移关于时间的二阶导数。
5. 弹簧力和弹性势能:F=-kx,U=(1/2)kx²,其中F表示弹簧的弹力,k表示弹簧的劲度系数,x表示弹簧的伸长或压缩量,U表示弹簧的弹性势能。
6.圆周运动的加速度:a=v²/r,表示物体在圆周运动中的加速度与速度平方和半径的倒数成正比。
三、功与能公式1.功:W=Fs,表示力对物体所做的功等于力与物体位移方向上的距离的乘积。
2. 功率:P=dW/dt,表示功率等于单位时间内所做的功。
3.机械能守恒定律:E=K+U,表示物体的机械能等于其动能和势能之和,在没有外力做功的情况下保持不变。
4. 转动惯量(转动引力矩):I=mr²,表示物体的转动惯量与其质量和距离旋转轴的平方成正比。
5.力矩:τ=Fr,表示力矩等于力与力臂的乘积,力臂是力的作用线与旋转轴之间的垂直距离。
第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学(静止流体中的压强)【内容讲解】一.物体的重心1.常见物体的重心:质量均匀分布的三角板的重心在其三条中线的交点;质量均匀分布的半径R的半球体的重心在其对称轴上距球心3R/8处;质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.重心:在xyz 三维坐标系中,将质量为m的物体划分为质点m1、m2、m3……m n.设重心坐标为(x0,y0,z0),各质点坐标为(x1,y1,z1),(x2,y2,z2)……(x n,y n,z n).那么:mx0=∑m i x i my0=∑m i y i mz0=∑m i z i【例题】1、(1)有一质量均匀分布、厚度均匀的直角三角板ABC,∠A=30°∠B=90°,该三角板水平放置,被A、B、C三点下方的三个支点支撑着,三角板静止时,A、B、C三点受的支持力各是N A、N B、N C,则三力的大小关系是.(2)半径为R的均匀球体,球心为O点,今在此球内挖去一半径为0.5R的小球,且小球恰与大球面内切,则挖去小球后的剩余部分的重心距O点距离为.2、如图所示,质量分布均匀、厚度均匀的梯形板ABCD,CD=2AB,求该梯形的重心位置。
3、在质量分布均匀、厚度均匀的等腰直角三角形ABC(角C为直角)上,切去一等腰三角形APB,如图所示。
如果剩余部分的重心恰在P点,试证明:△APB的腰长与底边长的比为5:4.4、(1)质量分别为m,2m,3m……nm的一系列小球(可视为质点),用长均为L的细绳相连,并用长也是L的细绳悬于天花板上,如图所示。
求总重心的位置5、如图所示,质量均匀分布的三根细杆围成三角形ABC,试用作图法作出其重心的位置。
6、如图所示,半径为R圆心角为θ的一段质量均匀分布的圆弧,求其重心位置。
7、论证质量均匀分布的三角形板的重心在三条中线的交点上8、求半径为R的厚薄均匀的半圆形薄板的重心9、均匀半球体的重心问题10、均匀圆锥体的重心11、如图所示,有一固定的半径为R 的光滑半球体,将一长度恰好等于R 21、质量为m 的均匀链条搭在球体上,其一端恰在球体的顶点上,并用水平拉力拉住链条使之静止,求拉力的大小。
一.一般物体的平衡条件1.共点力的平衡条件2.有固定转动轴的物体的平衡条件 力矩(M ):力(F )和力臂(L )的乘积。
即:M =F ·L 。
力矩是描述物体转动效果的物理量。
物体转动状态发生变化,才肯定受力矩的作用。
当物体绕固定轴转动时,力矩只有两种可能的方向,所以可用正负号来表示。
一般规定:使物体沿逆时针方向转动的力矩为正;使物体沿顺时针方向转动的力矩为负。
因此作用于有固定轴的转动物体上的几个力矩的合力矩就等于它们的代数和。
这个代数和将决定物体是处于平衡状态,还是非平衡状态。
在国际单位制中,力矩的单位是牛顿·米,注意不能写成焦耳。
力偶、力偶矩:(1)力偶:两个大小相等、方向相反的力,并且力的作用线互相平行而不重合,这样的一对力称为力偶。
力偶中两力的垂直距离称为力偶臂,力偶所在的平面称力偶作用面。
如用手旋钥匙、水龙头时,所施加的作用常是力偶。
(2)力偶矩:表示由两个力组成的力偶,每个力的大小均为F ,相距为i ,从整体上看,其合力为零:因为合力为零,所以力偶不能改变物体平动状态,力偶的作用效果仅仅是使物体转动状态发生改变。
力偶的转动效应决定于力偶的力矩,简称力偶矩。
力偶矩是力偶对某一转动轴的合力矩。
一个力偶矩的大小跟所选取的转轴无关,它仅由力偶中的任意一个力和力偶臂的乘积决定。
如果有几个力偶同时作用在物体上,则物体的转动效果将由力偶矩的代数和决定。
力偶矩代数和为零时,物体将保持角速度不变或保持静止。
3.一般物体的平衡条件4.稳度稳度:是指物体处于稳定平衡状态的稳定程度,稳度的大小由物体重心的高度和支持面的大小决定。
重心低,支持面大的物体稳度大,反之则稳度小。
所谓支持面是指物体各部分所围成的面积。
如站在行驶车厢里的人,为了增大稳度,往往把两腿叉开,这样两脚所围成的面积就增加了,支持面增加了(同时重心也降低了),稳度增大了。
又如一块砖平放和竖放相比较,平放时重心低,支持面积大,所以稳度就大。
第一章 静力学例题:如图均匀带轴的直角弯杆,质量为m ,OA 段长度是AB 段长度的2倍,对杆施力F ,使杆静止在如图的位置,求F 的最小值 (在计算重力矩时,可分别计算OA 、AB 部分的重力矩。
)解: mgl l mg l F 322315+= 15F N = 例题:如图,半径为R 的匀质球体,内部挖去半径为R/2的球,求剩余部分重心的位置。
提示:设球的密度为ρ 挖去部分的质量 31432R m πρ⎛⎫= ⎪⎝⎭剩余部发的质量 33244332R m R πρπρ⎛⎫=- ⎪⎝⎭376R πρ= 则 124R m m x =(x 为m 2到球心间距) 3317266R R R x πρπρ= 14R x = 例题:一薄壁烧杯,半径为r ,质量为m ,重心位于中心线上,离杯底的距离为H ,今将水慢慢注入杯中,问烧杯连同杯内的水共同重心最低时,水面离杯底的距离等于多少?为什么?(设水的密度为ρ)解:当烧杯连同杯内的水共同重心在水面上时,就处于最低位置。
有 ()222h mgH g r hm g r h gh ρπρπ+=+ 22()2h mgH g r h mg g r h h ρπρπ+⋅⋅=+h = 例题:两个轻弹簧,劲度系数为k 1、k 2,按图所示连接,并在下面悬挂一重物G ,滑轮质量不计,把滑轮和两个弹簧等效一个弹簧,求等效弹簧的劲度系数。
解:设悬挂上重物G 后滑轮的位置比未悬挂重物G 时的位置下降了x ∆,而弹簧k 1和k 2分别伸长了1x ∆和2x ∆122x x x ∆+∆=∆而 1122k x k x ∆=∆滑轮受力平衡 1122k x k x G ∆+∆=等效弹簧的劲度系数 G k x =∆21214k k k k += 例题:如图所示,质量为m 的物体放在摩擦因数为µ的水平面上,对物体施加一和水平方向成θ的力F 的作用,要使物体运动,求力F 的大小范围?解:要使物体运动,应符合)sin (cos θμθF mg F +>mg F μθμθ>-)sin (cos若θμcot <,则θμθμsin cos ->mg F 若θμcot ≥,则用再大的力也推不动物体。
静力学竞赛习题详解1.图1—23所示的上大下小的杯中,盛有密度均匀的混合液体.其密度为ρ经过一段时间后变成密度分别为ρ1,ρ2的两层均匀液体.如果总体积不变,试讨论杯底所受液体的压强有何变化?[解]: 取以杯底为底面积的竖直水柱为研究对象,在均匀混合时,该体积内两种密度的液体各占一半.而分层后,由于密度较大的一半液体分布在杯子的底部,由于平均底面积较小,而体的总高度不变,2.底边为a θ当θ动或翻倒.试分别求出发生滑动和翻倒时的θ,并说明在什么条件下出现的是滑动情况,在什么条件下出现的是翻倒情况.[解]物体恰好沿斜面下滑的条件是:sin cos mg mg θμθ=即tan μθ=若物体不下滑而翻倒,此时重心的延长线恰好过物体的左下角如图解2-2所示.此时角θ满足tan a bθ=若a u b <, 当1tan θμ-= 时, 先开始滑动.若a u b>, 当1tan a b θ-=时,先翻倒.3.一物体质量为m ,置于倾角为的斜面上,物体与斜面间的动摩擦4.一轻绳跨过两个等高的轻定滑轮,两端分别挂上质量m l =4kg 和m 2=2kg 的物体,如图1-25所示.在滑轮之间的绳上悬挂物体m ,为使三个物体能图1-25保持平衡,求m 的取值范围. [解]:m 最大值:的夹角α接近因此1m m <+ m 的最小值m 的夹角近90由此解得: m 综合以上:5.质量为M =1多少?[解]当物体在斜面运动时,物体所受的力并不在同一平面内.在垂直斜面的平面内,物体的受力如解2-5-1所示.沿斜面平面内受力如解2-5-2所示.由图可知。
N =mg cos30°因为物体做匀速直线运动,所以在两个方向合力都为0,即有21sin F f mg f θ=⎧⎨=⎩f 1、f 2分别为物体所受摩擦力的两个分量。
f 2解2-5-2f =求得f =又由f N μ=可求得μ=6.如图1-27线的夹角为θ[解]可。