当前位置：文档之家 › 平面向量单元复习课件

平面向量单元复习课件

  • 格式：ppt
  • 大小：810.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

平面向量复习课课件

平面向量复习课课件
是指将两个向量相加得到一个新的向量。减法是加法的逆操 作。学习了解平面向量的加减法，将帮助我们更好地理解向量的运算法则。
平面向量的数量积和向量积
数量积（点积）和向量积（叉积）是平面向量的两种重要运算。数量积用来计算向量的夹角和向量之间 的投影，而向量积则得到两个向量构成的新向量。让我们研究它们的性质和应用。
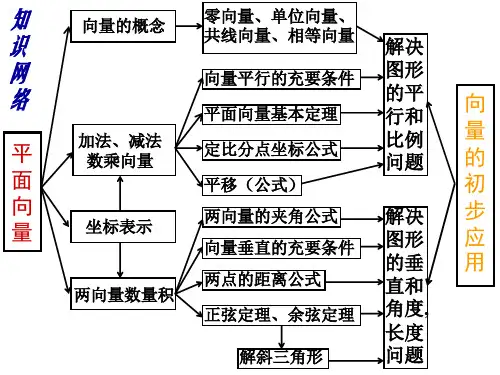
平面向量复习课ppt课件
欢迎来到平面向量复习课ppt课件！本课程将介绍平面向量的定义、表示、运 算和应用，以及与向量相关的数学概念。让我们开始学习吧！
什么是平面向量
平面向量是具有大小和方向的量，可以用箭头或有向线段表示。它们在物理、工程和几何中具有广泛的 应用。让我们深入了解平面向量的定义和基本概念。
平面向量的线性相关和线性无关性质
向量的线性相关性描述了向量之间的依赖关系，线性无关性表示没有一组向量可以由其他向量线性表示。 了解这些性质将帮助我们分析向量的维度和空间关系。
平面向量的基底和坐标
基底是向量空间中的一组线性无关的向量，坐标表示一个向量在基底上的投 影。通过基底和坐标，我们可以更好地描述向量和进行向量运算。
平面向量的向量方程
向量方程将一组向量相加得到等于零的表达式，这可以用来解决线性方程组和求解几何问题。学习向量 方程将提供更灵活的分析和数学工具。
向量的模、单位向量和方向角
向量的模指向量的长度或大小，单位向量是模等于1的向量。方向角描述了向 量相对于某一方向的偏离程度。学习这些概念将帮助我们准确表示和操作向 量。
平面向量的投影和正交分解
向量的投影是指一个向量在另一个向量上的映射，正交分解将一个向量拆分为在另一个向量上的投影和 与之正交的部分。这些概念有助于我们理解向量的复杂性质。

高一数学平面向量知识点复习ppt公开课获奖课件

高一数学平面向量知识点复习ppt公开课获奖课件
=（3-2λ，-12） =（-2，μ） ∴ 3-2λ=-2 μ=-12
∴ λ= 5 ，μ=-12 2
第8页
三、两个重要定理
1、向量共线充要条件
向量b 与非零向量 a 共线充要条件是有且只有
一个实数λ，使得 b a
注意：这是判断两个向量共线（平行）重要措施。
2、平面向量基本定理
假如 e1, e2 是同一个平面内两个不共线向量，
（2）函数 y cos(x ) 2图象通过怎样
平移，可以得到函数 y 3cos x图象？
第14页
六、正弦定理及其变形公式
a b c 2R sin A sin B sin C
S ABC
1 bc sin 2
A
1 ca sin 2
B
1 2
ab sin C
a 2R sin A,b 2R sin B, c 2R sin C
使 k a b=λ (a 3b，) 由（k-3，2k+2）= λ（10，-4）
k 3 10 2k 2 4
解得 k 1 , 1
3
3
反向
第12页
五、两个重要公式
1、定比分点坐标公式
设P（x，y），P1（x1，y1），P2（x2，y2），且
P1P PP2，则
x
x1 x2 1
（3）（a b） a b
2、平面向量数量积运算律
思索：你能将此 运算律用坐标表 达出来吗？
（1）a b b a
(2)(a) b (a b) a ( b)
(3)(a b) c a c b c
第6页
例1 判断如下命题及其逆命题真假：
1、若| a|= | b| ，则 a 与 b是共线向量； 2、若 a∥b ，则 a在 b方向上投影是 ；a 3、若 | a || b | 1 ，则 a b 1 ； 4、若a 0，则 0且a 0

2025届高中数学一轮复习课件《平面向量基本定理及坐标表示》ppt

2025届高中数学一轮复习课件《平面向量基本定理及坐标表示》ppt

)
高考一轮总复习•数学
第10页
2．已知平面向量 a＝(1,1)，b＝(1，－1)，则向量12a－32b＝( )
A．(－2，－1) B．(－2,1)
C．(－1,0)
D．(－1,2)
解析：因为 a＝(1,1)，b＝(1，－1)，所以12a－32b＝12(1，1)－32(1，－1)＝12，12－32，－32 ＝(－1,2)．
∴54<k<32.即 k 的取值范围为54，32.
高考一轮总复习•数学
第23页
题型
平面向量的坐标运算
典例 2(1)已知 A(－2,5)，B(10，－3)，点 P 在直线 AB 上，且 P→A ＝－13P→B ，则点 P 的
由线性关系，转化到坐标运算．
坐标是( )
A．(－8,9)
B．(1,3)
C．(－1，－3) D．(8，－9)
高考一轮总复习•数学
第3页
01 理清教材 强基固本 02 重难题型 全线突破 03 限时跟踪检测
高考一轮总复习•数学
第4页
理清教材 强基固本
高考一轮总复习•数学
第5页
一 平面向量基本定理 如果 e1，e2 是同一平面内的两个不共线向量，那么对这一平面内的任一向量 a，有且只 有一对实数 λ1，λ2，使 a＝λ1e1＋λ2e2，若 e1，e2 不共线，我们把{e1，e2}叫做表示这一平面内 所有向量的一个基底．若 e1，e2 互相垂直，则称这个基底为正交基底；若 e1，e2 分别为与 x 轴、y 轴方向相同的两个单位向量，则称这个基底为单位正交基底．
高考一轮总复习•数学
第22页
解析：如图，分别取 BD，AE 的中点 G，N，连接 GN 交 EF 于 H，

平面向量复习课件共21页PPT资料

平面向量复习课件共21页PPT资料

向量
c
(4，
7) 共线
2 2 3
4 7
2
［点评］本题考查向量的共线问题、向量的数乘运算， 坐标运算，属容易题。
考题剖析
例 5、(2008 江西文)如图，正六边形 ABCDEF 中，有下列四个命题：
uuur uuur uuur
A． AC AF 2BC
E
D
uuur uuuur uuur
B． C．
故选 C；
［点评］此题重点考察向量加减、数乘的坐标运算； 准确应用向量的坐标运算公式是解题的关键；
考题剖析
例 4、(2008 全国Ⅱ卷文、理)设向量 a (1，2)，b (2，3) ，
若向量 a b 与向量 c (4， 7) 共线，则
．
解： a b = ( 2,2 3) ，则向量 a b 与
考题剖析
r
r
例 r3、(2r008 四川文)设平面向量 a 3,5,b 2,1 ，
则 a 2b ( )
（Ａ）（7，3） （Ｃ）（1，7）
（Ｂ）（07x，7,）cosx4 （Ｄ）（1，32） 5
解:
∵
r a
3,
5
,
r b
2,1
rr
∴ a 2b 3,5 22,1 3 4，5 2 7，3
考题剖析
例 1、如图，△ ABC 中，D，E，F 分别是边 BC，AB，CA
的中点，在以 A、B、C、D、E、F 为端点的有向线段中所表示
的向量中，
uuur
（1）与向量 FE 共线的有
．
（2）与向量
uuur DF
的模相等的有
．
（3）与向量
uuur ED
相等的有

《平面向量高三复习》课件

《平面向量高三复习》课件
,
汇报人：
目录
向量的表示和定义
向量：具有大小和方向的量 向量的表示：用有向线段表示，线段的长度表示向量的大小，箭头的方向表示向量的方向 向量的定义：向量是数学中的基本概念，是研究线性代数的基础 向量的性质：向量的加法、减法、数乘、向量积等
向量的模
向量的模：向量的长度，表示向量的大小 计算公式：|v|=√(x^2+y^2+z^2) 几何意义：向量的模表示向量在空间中的长度 物理意义：向量的模表示向量在空间中的位移或力
向量的向量积的方向与两个向量的 方向有关，可以通过右手定则来确 定
添加标题
添加标题
添加标题
添加标题
向量的向量积的长度等于两个向量 的长度的乘积
向量的向量积的应用广泛，如物理 中的力矩、电场强度等
向量的向量积的运算律
交换律： a×b=b×a
结合律： (a×b)×c=a×(b× c)
分配律： a×(积的定义
向量的数量积 也称为点积或
内积
两个向量的数 量积等于它们 的模的乘积再 乘以它们夹角
的余弦值
向量的数量积 是一个实数， 其符号取决于 两个向量的夹
角
向量的数量积 在物理中常用 于计算力矩、
功等物理量
向量的数量积的几何意义
向量的数量积 表示两个向量
的夹角
向量的数量积 等于两个向量 的长度乘以两 个向量的夹角
向量的数量积的性质
向量的数量积是一个实数 向量的数量积满足交换律 向量的数量积满足结合律 向量的数量积满足分配律
向量的向量积的定义
向量的向量积是一个向量
向量的向量积的长度等于两 个向量的长度的乘积
向量的向量积是指两个向量 的乘积
向量的向量积的方向与两个 向量的方向有关

高一数学平面向量复习课件

高一数学平面向量复习课件
详细描述
向量数量积的几何意义在于它表示了两个向量的长度和它们之间的夹角之间的关系。具体来说，当两个非零向量 的夹角为锐角时，它们的数量积为正；当夹角为直角时，数量积为零；当夹角为钝角时，数量积为负。
向量数量积的运算律
总结词
掌握向量数量积的运算律，包括 交换律、结合律和分配律。
详细描述
向量数量积满足交换律，即 a·b=b·a；结合律，即 (a+b)·c=a·c+b·c；分配律，即 (λa)·b=λ(a·b)，其中λ是标量。
向量积的性质
向量积的性质
1. 向量积的方向与两个向量的夹角和大小有 关，其方向垂直于两个给定向量所确定的平 面；2. 向量积的模长为|a×b|=|a||b|sinθ； 3. 向量积满足结合律但不满足交换律；4. 向量积可以用来表示向量的旋转关系。
性质的应用
在解析几何中，向量积可以用来解决与旋转 、速度和加速度有关的问题；在物理中，向 量积可以用来描述力矩、角速度等物理量。 通过理解这些性质和应用，学生可以更好地
向量积的运算律
向量积的运算律
交换律a×b=-b×a，分配律 (a+b)×c=a×c+b×c。这些运算律与标量积 的运算律类似，但要注意向量积不满足结合 律。
运算律的理解
交换律表明向量积的方向与夹角有关，而分 配律表明向量积与向量的线性组合是可分配 的。这些运算律对于理解向量积的性质和计 算非常重要。
混合积的性质
非负性
向量a、b、c的混合积为非负数，当且仅当a、b、c三个 向量共面时取值为0。
线性性质
混合积满足线性性质，即对于任意标量m和n，有 $(mvec{a} + nvec{b}) cdot vec{c} = mvec{a} cdot vec{c} + nvec{b} cdot vec{c}$。

平面向量复习课PPT课件


二、基 本 知 识
1. 向量的概念
为平行向量，记作 a // b. 因为向量可以进行任意平移，平行向量总可以平移到 同一直线上，故又称共线向量.
2. 向量的运算
(1)向量的加法: 平行四边形法则；三角形法则(首尾相接). 坐标表示: a + b = (x1+ x2，y1+ y2)． 运算律：交换律；结合律。 → → → 重要结论: AB + BC = AC． (2)向量的减法: 三角形法则(指向被减数)． 坐标表示: a - b = (x1- x2， y1- y2)． → → → → → 重要结论: a – b = a +(– b)， AB =– BA，PB – PC = CB． (3)实数与向量的积: λ a． 规定: 1) |λ a| =|λ ||a| ; 2) λ ＞0时与a同向; λ ＜0时与a反向; λ =0时, λ a = 0． 坐标表示: λ a = (λ x，λ y)． 运算律：λ (μ a ) = (λ μ )a ; (λ +μ )a = λ a +μ a ; λ (a + b ) = λ a +λ b. (4)两个向量的数量积: a • b = |a | | b| cosθ= x1 x2 + y1 y2． 重要性质及运算律：见课本 P119.
→ →
｛
x’ = x + h， y’ = y + k．
(6)正弦定理、余弦定理: (略)
例1. 已知a = (1, 2), b = ( 3, 2), 当 k 为何值时, (1) ka + b与 a 3 b垂直; (2) ka + b与 a 3 b平行, 平行时它们是同向还是反向? 分析: ka + b = ( k 3, 2k + 2 ), a 3 b = (10, 4 )． (1) 当(ka + b )•(a 3 b ) = 0时, 两向量互相垂直; (2) 存在唯一的实数λ, 使 ( ka + b ) = λ( a 3 b )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(5)0 a a 0 a
(6)0 0 (7)0 a 0
3.单位向量
a 与非零向量a共线的单位向量a0
|a| 3
一.基本概念 区分向量平行、共线与几何平行、共线
4.平行向量 (共线向量) 方向相同或相反的非零向量叫做平行向量
5.相等向量 长度相等且方向相同的向量叫做相等向量.
在保持长度和方向不变的前提下, 向量可以平行移动.平移先后两向量相等 任一组平行向量都可平移到同一直线上
且方向相同，
A
B
uuur
uuur
所以 AD 与 BC 夹角是 0
uuur uuur uuur uuur
所以 AD BC | AD || BC | cos 0o 3 31 9
uuur uuur （2）因为 AB 与 AD
uuur 的夹角是60o ，所以 AB
与
uuur DA
的夹角为120o
所以
uuur uuur uuur uuur AB DA | AB || DA | cos120o
b
B
[0, ]
θ O
向量夹角：首要的是通过向
a B1
A
量平移,使两个向量共起点。
向量数量积的几何意义
r
rr
| b | cos 叫做向量b在a方向上的投影
ab |a|
可正可负可为零
7
平面向量的数量积a·b的性质: ①e·a=a·e=|a|cosθ
②a⊥b a·b=0
③a，b同向a·b=|a||b|反向时a·b=|a|·|b|
分析：先求OM、ON.
14
五.应用举例 平面向量的数量积
例4、如图，在平行四边形ABCD中，已知
uuur
uuur
，| AB | 4，| AD | 3
DAB ，60求o ：
（1） uuur ；uuur （2） AD BC
uu；ur uuur AB DA
D
F
C
E
解：
（1）因为
uuur AD
∥
uuur BC
r
r
1ar.向// br量a和有非唯零一向的量实b数，使ar
r b
xr 1
y
r2x2源自y102r .非r零向r量ar和b
a b a b 0 x1 x2 y1 y2 0
10
四.一个基本定理
平面向量基本定理
如 果e1、e 2 是 同 一 平 面 内 的 两 个 不共 线 的 向量, 那么对于这一平面内的任一向量a, 有且只有一对实数1 , 2 , 使a 1e1 2 e2 把 不 共 线 的 向 量e1、e 2叫 做 表 示 这 一 平 面 内 所 有 向 量 的 一 组基 底.
（2）原式= AB + BD + DA －（BC + CA）
= 0－BA = AB
13
五.应用举例
平面向量基本定理
例3.如图平行四边形OADB的对角线OD、AB相交 点C,线段BC上有一点M满足BC=3BM,线段CD上有 点N满足CD=3CN,
uuur r uuur r r r uuuur 设OA a,OB b,试用a,b表示MN
rr
(x1, y1 )
4)a b x1 x2 y1 y2
r rr 5) | a | a a
rr
x12 y12
6) cos uaurbr x1 x2 y1 y2
|a||b|
x12
y
2 1
x
2 2
y
2 2
9
三.两个等价条件
若a (x1, y1),b (x2 , y2 ),则
b a +b
Aa
B
3.向量减法的三角形法则
共起点
r r uuur uuur uuur a b AB AD DB
首同尾连向被减
5
二.基本运算（向量途径） 4.实数与向量的积 a 是一个向量
a是一个与a
共线的向量
6
二.基本运算（向量途径）
rr
5.两个非零向量
rr r
a与r b
的数量积
a b | a | | b | cos
利用向量分解的“唯一性”来构建实系数方程组
11
五.应用举例
向量的有关概念
例 1 给出下列命题：
①若 a·b = 0 ，则 a、b 中至少有一个为 0 .
②若 A，B，C，D 是不共线的四点，则A→B＝D→C 是四边形 ABCD 为平行四边形的充要条件；
③若 a＝b，b＝c，则 a＝c； ④a＝b 的充要条件是|a|＝|b|且 a∥b； ⑤若 a∥b，b∥c，则 a∥c. 其中正确的序号是___②__③___．
a2
a2=a·a=|a|2(a·a= )
ab
④cosθ= |a||b|
⑤|a·b|≤|a|·|b|
8
二r.基本运算（r坐标途径）
若a r
( r
x1,
y1 ),
b
(
x2
,
y2
),
则
1)a b (x1 x2 , y1 y2 ) rr
2)a b r
(x1 x2 , y1 y2 )
3)a
6.相反向量 (a) a,a (a) 0
长度相等且方向相反的向量叫做相反向量. 4
二.基本运算（向量途径）
C
1.向量加法的三角形法则
r r uuur uuur uuur
a +b b
a b AB BC AC A首a尾相连B 首尾连
2.向量加法的平行四边形法则 D
C
r r uuur uuur uuur ，a b AB AD AC
课题：
平面向量复习课
学习导航:向量是近代数学重要工具,准确掌握向量 的运算及其性质是利用向量为工具解决平面几何, 三角,空间几何等其它分支学科的基础.故同学们应 重视复习和巩固向量的知识,并强化建系处理问题 或基底处理向量问题的意识.
1
一.基本概念
1.向量及向量的模、向量的表示方法
B
1)图形表示
A
有向线段AB
2)字母表示 a AB r uuur
3)坐标表示
r uuur
r
向量的模
rr
:|
a
||
AB
|
a xi y j (x, y)
ar OuuAuur (x, y) 点A(x, y)
a MN (xN xM , yN yM )
2
一.基本概念
2.零向量及其特殊性
(1)0方向任意(2)0 // a(3)0 0(4) 0 0
4 3 ( 1) 6
2
思考：若E、F分别是BC，DC的中点，
试求AE AF的值。 20 15
12
五.应用举例
向量加减法则
例2 化简（1）（AB + MB）+ BO + OM
（2） AB + DA + BD －BC－CA 利用加法减法运算法则，借助结论
AB=AP+PB；AB=OB－OA；AB+BC+CA=0
进行变形.
解：（1）原式= AB +（BO + OM + MB） = AB + 0 = AB