平面向量基本定理应用

平面向量基本定理的应用——力的合成应用背景力的合成是力学中的一个重要概念，用于描述多个力共同作用时的结果。

力的合成在物理学、工程学等领域都有广泛的应用，例如在建筑结构设计、机械运动分析、航空航天工程等方面都需要对力的合成进行分析和计算。

平面向量基本定理是力的合成的一种基本方法，它通过将力表示为平面向量的形式，利用向量加法的性质进行计算，从而得到力的合成结果。

平面向量基本定理的应用可以简化力的合成的计算过程，提高计算的效率和准确性。

应用过程假设有两个力F1和F2作用在同一物体上，力F1的大小为F1的模为|F1|，方向与x轴的夹角为θ1；力F2的大小为F2的模为|F2|，方向与x轴的夹角为θ2。

要求计算两个力合成后的结果力F的大小和方向。

首先，根据平面向量基本定理，可以将力F1和F2表示为平面向量的形式。

假设x轴和y轴是我们选择的坐标轴，F1可以表示为F1 = F1x * i + F1y * j，其中F1x和F1y分别为F1在x轴和y轴上的分量，i和j分别为x轴和y轴的单位向量。

同样，F2可以表示为F2 = F2x * i + F2y * j。

其次，根据平面向量基本定理，可以得到合成力F的表达式。

合成力F等于F1和F2的矢量和，即F = F1 + F2。

根据向量加法的性质，可以得到F = (F1x + F2x) * i + (F1y + F2y) * j。

最后，根据合成力F的表达式，可以计算出合成力F的大小和方向。

合成力F的大小等于F的模|F|，可以通过计算F的模来得到。

合成力F的方向可以通过计算F与x轴的夹角θ来得到。

夹角θ可以通过计算F在x轴上的分量F_x和F在y轴上的分量F_y的比值来得到，即tanθ = F_y / F_x。

应用效果平面向量基本定理的应用可以简化力的合成的计算过程，提高计算的效率和准确性。

通过将力表示为平面向量的形式，可以将力的合成问题转化为向量加法的问题，利用向量加法的性质进行计算。

平面向量基本定理1. 介绍平面向量是平面上具有大小和方向的量，广泛应用于数学、物理和工程等领域。

平面向量基本定理是关于平面向量的一个重要定理，它是矢量运算的基础，对于解析几何和向量代数具有重要的指导作用。

本文将详细介绍平面向量基本定理的定义、性质以及应用。

2. 定义在平面上，一个向量可以表示为有向线段，具有大小和方向。

平面向量基本定理是指对于任意两个平面向量，它们的和（或差）可以用三角形规则来表示。

即，对于平面向量 $\\vec{a}$ 和 $\\vec{b}$，它们的和（或差）向量 $\\vec{c}$ 可以通过如下方式得到：$$ \\vec{c} = \\vec{a} + \\vec{b} \\quad \\text{或} \\quad \\vec{c} = \\vec{a} - \\vec{b} $$其中，$\\vec{c}$ 的起点与 $\\vec{a}$ 的起点相同，终点与 $\\vec{b}$ 的终点相同。

3. 性质平面向量基本定理具有以下性质：3.1 交换律对于任意两个平面向量 $\\vec{a}$ 和 $\\vec{b}$，它们的和（或差）向量满足交换律，即：$$ \\vec{a} + \\vec{b} = \\vec{b} + \\vec{a} \\quad \\text{或} \\quad \\vec{a} - \\vec{b} = -\\vec{b} + \\vec{a} $$3.2 结合律对于任意三个平面向量 $\\vec{a}$、$\\vec{b}$ 和 $\\vec{c}$，它们的和（或差）向量满足结合律，即：$$ (\\vec{a} + \\vec{b}) + \\vec{c} = \\vec{a} + (\\vec{b} + \\vec{c}) \\quad \\text{或} \\quad (\\vec{a} - \\vec{b}) - \\vec{c} = \\vec{a} - (\\vec{b} + \\vec{c}) $$3.3 零向量存在一个特殊的向量，其大小为零，记作 $\\vec{0}$，称为零向量。

平⾯向量基本定理的推论及其应⽤平⾯向量基本定理的推论及其应⽤梅州市五华县⽔寨中学邓定扬我们知道，平⾯上任意两个不共线的向量可作为平⾯向量基底，该平⾯上的任⼀向量OM 必有：OM xOA yOB =+，关于此式，我们有三个推论。

推论1：,x y 唯⼀存在，推论2：1x y M AB +=?在直线上，推论3：12x y M AB ==是中点。

在解题中，⽤好这三个推论常常会收到事半功倍的效果。

例题1：如图1，在边长为1的等边ABC ,,D AB G CD 是中点是中点，,,G AB AC E F AE AB AF AC λµ==过点的直线与线段，相交于点，设。

（1）⽤µ表⽰λ，求出λ和µ的取值范围，（2）求出AEF ⾯积的最⼩值。

解：(1) 11112242AG AD AC AB AC =+=+1142AG AE AF λµ∴=+,因为点G EF 在直线上，所以11142λµ+=,即=42λµ-,由题意易知[1,2]λ∈,342[1,2][1,]2µµ∴-∈?∈.(2) 1||||sin 23ABCSAE AF π===, 所以当=1µ时，⾯积最⼩为8。

评：利⽤推论2快速建⽴了,µλ的关系式。

例题2：四边形OABC 是边长为1的正⽅形，3OD =,P 为BCD 内（含边界）的动点，设OP OC OD αβ=+,则+αβ的取值范围。

解：由向量数乘运算的⼏何意义可知当点P 在边界上时取得最⼤最⼩值，当P 在线段CD 上时显然1αβ+=图1BB当P 在线段CB 上时OP OC OD αβ=+，由平⾏四边形法则可知11,[0,]3αβ=∈，所以4[1,]3αβ+∈当P 在线段BD 上时()3x OP xOB yOD xOC y OD =+=++，则,3xx y αβ==+1x y +=，133x x x y αβ+=++=+，因为[0,1]x ∈，所以4[1,]3αβ+∈综上可知4[1,]3αβ+∈评：当P 在线段BD 上时，巧妙利⽤推论2减少变量，快速解题。

一、平面向量的基本定理（1）平面向量基本定理：如果1e 和2e 是一平面内的两个不平行的向量，那么该平面内的任一向量a ，存在唯一的一对实数1a ，2a ，使a =1122a e a e +．（2） 基底：我们把不共线向量1e ，2e 叫做表示这一平面内所有向量的一组基底，记作{}12,e e ．1122a e a e +叫做向量a 关于基底{}12,e e 的分解式． 注：①定理中1e ，2e 是两个不共线向量；②a 是平面内的任一向量，且实数对1a ，2a 是惟一的； ③平面的任意两个不共线向量都可作为一组基底．（3）平面向量基本定理的证明：在平面内任取一点O ，作11OE e =，22OE e =，OA a =．由于1e 与2e 不平行，可以进行如下作图：过点A 作2OE 的平行（或重合）直线，交直线1OE 于点M ，过点A 作1OE 的平行（或重合）直线，交直线2OE 于点N ，于是依据平行向量基本定理，存在两个唯一的实数1a 和2a 分别有11OM a e =，22ON a e =，所以1122a OA OM ON a e a e ==+=+证明表示的唯一性：如果存在另对实数x ，y 使12OA xe ye =+，则112212a e a e xe ye +=+，即1122()()0x a e y a e -+-=，由于1e 与2e 不平行，如果1x a -与2y a -中有一个不等于0，不妨设20y a -≠，则1212x a e e y a -=--，由平行向量基本定理，得1e 与2e 平行，这与假设矛盾，因此10x a -=，20y a -=，即1x a =，2y a =．二、向量的正交分解与向量的直角坐标运算：（1）向量的直角坐标：如果基底的两个基向量1e ，2e 互相垂直，则称这个基底为正交基底．在正交基底下分解向量，叫做正交分解．（2）向量的坐标表示：在直角坐标系中，一点A 的位置被点A 的位置向量OA 所唯一确定．设点A 的坐标为(,)x y ，由平面向量基本定理，有12(,)OA xe ye x y =+=，即点A 的位置向量OA 的坐标(,)x y ，也就是点A 的坐标；反之，点A 的坐标也是点A 相对于坐标原点的位置向量OA 的坐标．E 2E 1e 2e 1O ANMae1e 2axyO O yxae 2e 1平面向量的基本定理及坐标运算（3）向量的直角坐标运算：设12(,)a a a =，12(,)b b b =，则 ①1122(,)a b a b a b +=++；②1122(,)a b a b a b -=--；③1212(,)(,)a a a a a λλλλ==注：①两个向量的和与差的坐标等于两个向量相应坐标的和与差；②数乘向量的积的坐标等于数乘以向量相应坐标的积．（4）若11(,)A x y ，22(,)B x y ，则向量2121(,)AB OB OA x x y y =-=--；即：一个向量的坐标等于向量的终点的坐标减去始点的坐标．（5）用平面向量坐标表示向量共线条件：设12(,)a a a =，12(,)b b b =，则12210a b a b -=就是两个向量平行的条件．若向量b 不平行于坐标轴，即10b ≠，20b ≠，则两个向量平行的条件是，相应坐标成比例．题型一、平面向量的基本定理【例1】 若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是（ ）A ．1e 与2e -B ．31e 与22eC ．1e ＋2e 与1e —2eD ．1e 与21e【例2】 线段与互相平分，则可以表示为（ ）A ．B ．C ．D ． 【例3】 已知ABCD □的两条对角线交于点O ，设AB a =，AD b =，用向量a 和b 表示向量BD ，AO ．【例4】 如图，平行四边形ABCD 中，E F 、分别是BC DC 、的中点，G 为DE BF 、的交点，若AB =a ，AD =b ，试以a ，b 为基底表示DE 、BF 、CG ．AB CD BD AB CD -1122AB CD -+1()2AB CD -()AB CD --GFE DCBA【例5】 设P 是正六边形OABCDE 的中心，若OA a =，OE b =，试用向量a ，b 表示OB 、OC 、OD【例6】 已知向量a ，b 不共线，()R c ka b k =+∈，d a b =-，如果c d ∥，那么（ ）A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向【例7】 已知四边形ABCD 是菱形，点P 在对角线AC 上（不包括端点A ，C ），则AP 等于（ ）A ．()AB AD λ+，(01)λ∈， B ．()AB BC λ+，202λ⎛⎫∈ ⎪ ⎪⎝⎭， C ．()AB AD λ+，202λ⎛⎫∈ ⎪ ⎪⎝⎭，D ．()AB BC λ-，202λ⎛⎫∈ ⎪ ⎪⎝⎭， 【例8】 已知向量a b ，不共线，m n ，为实数，则当0ma nb +=时，有m n += 【例9】 在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点．若AC AE AF λμ=+，其中λ，R μ∈，则λμ+= ．【例10】证明：若向量,,OA OB OC 的终点A B C 、、共线，当且仅当存在实数,λμ满足等式1λμ+=，使得OC OB OA λμ=+．POE DCBAFEDCBAOCBA题型二、平面向量的坐标表示与运算【例11】设向量(23),AB =，且点A 的坐标为(12),，则点B 的坐标为 ． 【例12】若(21),a =，(34),b =-则34a b +的坐标为_________． 【例13】设平面向量()()3,5,2,1a b ==-，则2a b -=（ ）A ．()6,3B ．()7,3C ．()2,1D ．()7,2【例14】已知(2,3),(1,2)a x b y =-=+，若a b =，则x = ，y = ． 【例15】若()0,1A ，()1,2B ，()3,4C ，则AB -2BC = 【例16】若()3,2M -，()5,1N --且12MP =MN ，求P 点的坐标．【例17】已知向量()1,0a =，()0,1b =，()R c ka b k =+∈，d a b =-，如果那么（ ）A ．且与同向B ．且与反向C ．且与同向D ．且与反向【例18】已知向量()11a =，，()2b x =，若a b +与42b a -平行，则实数的值是（ ） A ．2- B ．0 C ．1 D ．2【例19】在平面直角坐标系xoy 中，四边形ABCD 的边AB DC ∥，AD BC ∥，已知点()2,0A -，()6,8B ，()8,6C ，则D 点的坐标为___________．【例20】已知向量()3,1a =，()1,3b =，(),7c k =，若()a c -∥b ，则= ． 【例21】已知()12a =，，()32b =-，，当ka b +与3a b -平行，k 为何值（ ）A ．14 B ．－14 C ．－13 D ．13【例22】已知(1,2),(3,2)a b ==-，当实数k 取何值时，k a ＋2b 与2a -4b 平行？//c d 1k =c d 1k =c d 1k =-c d 1k =-c d x k【例23】点(23),A 、(54),B 、(710),C ，若()R AP AB AC λλ=+∈，试求λ为何值时，点P 在一、三象限角平分线上．【练1】 在ABC △中，AB c =，AC b =．若点D 满足2BD DC =，则AD =（ ）A ．2133b c +B ．5233c b -C ．2133b c -D ．1233b c +【练2】 如图，在ABC △中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M N ，，若AB mAM =，AC nAN =，则m n +的值为．【练3】 已知两个向量()()121a b x ==，，，，若a b ∥，则x 的值等于（ ） A ．12-B ．12C ．2-D ．2【练4】 若平面向量a ，b 满足1a b +=，a b +平行于轴，()21b =-，，则a = ．DCBAONMCBAx 随堂练习【题1】 若向量()1,1a =，()1,1b =-，()4,2c =，则c = （ ）A ．3a +bB ． 3a -bC ．-a +3bD ．a +3b【题2】 已知a ＝（4，2），b ＝（x ，3），且a ∥b ，则x 等于（ ）A ．9B ．6C ．5D ．3【题3】 已知平面向量a ＝（x ，1），b ＝（－x ，x 2），则向量a ＋b （ ）A ．平行于x 轴B ．平行于第一、三象限的角平分线C ．平行于y 轴D ．平行于第一、四象限的角平分线【题4】 已知向量e 1与e 2不共线，实数x ，y 满足（3x －4y ）e 1＋（2x －3y ）e 2＝6e 1＋3e 2，则x －y 等于（ ）A ．3B ．－3C ．0D ．2【题5】 已知向量(1,2)a =，(0,1)b =，设u a kb =+，2v a b =-，若u ∥v ，则实数k 的值为（ ）A ．－1B ．－12C ．12D ．1【题6】 设点A （2，0），B （4，2），若点P 在直线AB 上，且|AB |＝2|AP |，则点P 的坐标为（ ）A ．（3，1)B ．（1，－1）C ．（3，1）或（1，－1)D ．无数多个【题7】 设(1,2),(2,3),a b ==若向量a b λ+与向量(4,7)c =--共线，则λ=．【题8】 已知向量a ＝（2，－1），b ＝（－1，m ），c ＝（－1，2），若（a ＋b ）∥c ，则m ＝________．【题9】 已知A （－2，4），B （3，－1），C （－3，－4）．设AB →＝a ，BC →＝b ，CA →＝c ，且CM →＝3c ，CN→＝－2b ．（1）求：3a ＋b －3c ；（2）求满足a ＝m b ＋n c 的实数m ，n ．【题10】 在平行四边形ABCD 中，AC 与BD 交于点O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F ．若AC →＝a ，BD →＝b ，则AF →＝（ ） A ．14a ＋12b B ．23a ＋13b C ．12a ＋14bD ．13a ＋23b课后作业。

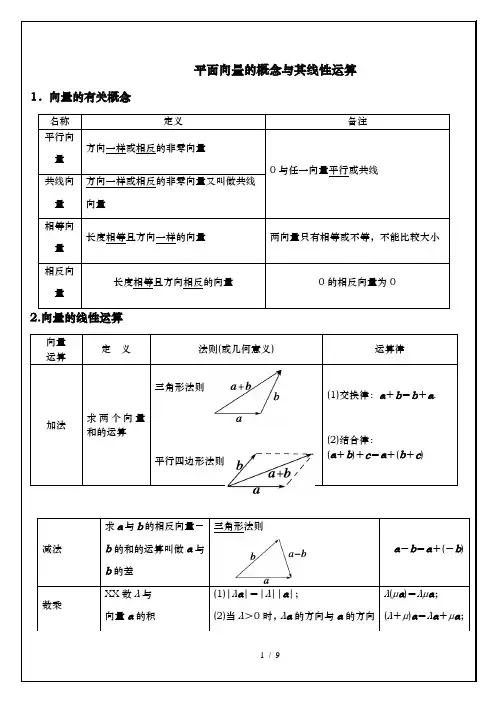
平面向量的概念与其线性运算1．向量的有关概念名称定义备注平行向量方向一样或相反的非零向量0与任一向量平行或共线共线向量方向一样或相反的非零向量又叫做共线向量相等向量长度相等且方向一样的向量两向量只有相等或不等，不能比较大小相反向量长度相等且方向相反的向量0的相反向量为02.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算三角形法则平行四边形法则(1)交换律：a＋b＝b＋a.(2)结合律：(a＋b)＋c＝a＋(b＋c)减法求a与b的相反向量－b的和的运算叫做a与b的差三角形法则a－b＝a＋(－b)数乘XX数λ与向量a的积(1)|λa|＝|λ||a|；(2)当λ＞0时，λa的方向与a的方向λ(μa)＝λμa；(λ＋μ)a＝λa＋μa；[例3]在△ABC 中，点O 在线段BC 的延长线上，且与点C 不重合，若AO →＝xAB →＋(1－x )AC →， 则实数x 的取值X 围是( )．A ．(－∞，0) B ．(0，＋∞)C．(－1,0) D ．(0,1)[例4]若点O 是△ABC 所在平面内的一点，且满足|OB →－OC →|＝|OB →＋OC →－2OA →|，则△ABC的形状为________．[例5]在△ABC 中，E ，F 分别为AC ，AB 的中点，BE 与CF 相交于G 点，设AB →＝a ，AC →＝b ， 试用a ，b 表示AG →.[课堂巩固]1．如图，设P 、Q 为△ABC 内的两点，且2155AP AB AC =+， AQ ＝23AB ＋14AC ，则△ABP 的面积与△ABQ的面积之比为( )A ．15B ．45C ． 14 D ．13A3．如图，在△ABC 中，已知2AB =，3BC =，60ABC ∠=︒，AH BC ⊥于H ，M 为AH 的中点，若AM AB BC λμ=+，则λμ+=.3、向量a ,b ,c 在正方形网格中的位置如图所示.若c =λa +μb (λ,μ∈R),则λμ=_________.3、ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m 的值是多少？4、在△ABC 中，过中线AD 的中点E 任作一条直线分别交AB ，AC 于M ，N 两点，若AM →＝xAB →，AN →＝yAC →，求y x +4的最小值。

浅谈平面向量基本定理及其应用作者：楼可飞来源：《中学教学参考·理科版》2013年第10期向量是数学研究的一种重要工具，尤其是解决几何问题，常有独到之处.下面我们来看看平面向量基本定理在几何中的应用.一、平面向量基本定理如果e1、e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1、λ2，使a=λ1e1+λ2e2.我们把不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底（base）.二、平面向量基本定理的推论图1如图1，已知P1、P、P2三点共线，O是空间任一点，则存在实数x，y，使OP=xOP1+yOP2，且x+y=1.三、三点共线图2【例1】如图2，三个向量a、b、c有公共起点，且满足c=λa+μb，λ、μ∈R，求证：三个向量的终点共线的充要条件是λ+μ=1.分析：设向量a、b、c的公共起点是O，终点分别是A、B、C，则AC=c-a，AB=b-a.必要性：如果A、B、C三点共线，则存在一个实数m，使AC=mAB，即c-a=m（b-a），即c=（1-m）a+mb.令λ=1-m，μ=m，则c=λa+μb，所以三个向量的终点共线的必要条件是λ+μ=1.充分性：如果λ+μ=1，则λ=1-μ，代入c=λa+μb，得c=（1-μ）a+μb=a+μ（b-a）=a+μAB，即c-a=μAB，AC=μAB，得AC与AB共线，所以三个向量的终点共线的充分条件是λ+μ=1.综上所述，三个向量的终点共线的充要条件是λ+μ=1.注：（1）题中的c=λa+μb是大前提，在证充分性与必要性时都可以应用它；（2）当点c 为线段AB的中点时，则有c=a+b2.【例2】如图3，设点O是△ABC的外接圆的圆心，AO=xAB+yAC且|AB|=c，|AC|=b，y=kx-k2，求AB·AC的值.图4分析：由y=kx-k2，AO=xAB+（kx-k2）AC，AO+k2AC=x（AB+kAC）.设AE=-k2AC，AF=-kAC，上式等价于AO-AE=x（AB-AF），即EO=xFB，EO∥FB，如图4.延长AO 交圆于点D.现AEAF=-k2÷（-k）=12，得AEAF=AOAD，EO∥FD，所以FB∥FD，这说明F、D、B三点共线，而直径所对的圆周角是直角，∠ABD=90°.在Rt△ABF中，∠BAC=∠BAF，cos∠BAC=ABAF=c-kb.在△ABC中，由向量数量积的定义，得AB·AC=|AB|·|AC|·cos∠BAC=c·b·c-kb=c2-k.（责任编辑黄春香）。

2023年高考数学----平面向量基本定理及其应用规律方法与典型例题讲解【规律方法】1、应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．2、用基底表示某个向量的基本方法：（1）观察各向量的位置；（2）寻找相应的三角形或多边形；（3）运用法则找关系；（4）化简结果．【典型例题】例1．（2022·全国·模拟预测）如图，在ABC 中，点D 是边AB 上一点且2BD AD =，E 是边BC 的中点，直线AE 和直线CD 交于点F ，若BF 是ABC ∠的平分线，则BCBA =（ ）A ．4B ．3C ．2D ．12 【答案】C【解析】因为BF 是ABC ∠的平分线，所以存在一个实数λ使得BA BC BF BA BC λ⎛⎫ ⎪=+ ⎪⎝⎭，（根据角平分线的条件，选择合适的基底）因为E 是边BC 的中点，所以2BA BE BF BA BC λ⎛⎫ ⎪ ⎪⎝⎭=+，又点A ，E ，F 共线，所以21BA BC λλ+=①．（三点共线的应用：OA OB OC λμ=+（λ，μ为实数），若A ，B ，C 三点共线，则1λμ+=） 因为2BD AD =，所以32BD BC BF BABC λ⎛⎫ ⎪=+ ⎪ ⎪⎝⎭，又点C ，F ，D 共线，所以312BA BC λλ+=②，联立①②，得112BA BC =，则2BC BA =，即2BC BA =.故选：C ． 例2．（2022·全国·模拟预测）如图，在平行四边形ABCD 中，点E 在线段BD 上，且EB mDE =（m R ∈），若AC AE AD λμ=+（λ，μ∈R ）且20λμ+=，则m =（ ）A ．13B ．3C ．14D ．4【答案】B 【解析】方法1：在平行四边形ABCD 中，因为EB =mDE ，所以()AB AE m AE AD −=−，所以11AE AB m =++1m AD m +， 又∵AB DC AC AD ==−，∴()111m AE AC AD AD m m =−+++， ∴()()11AC m AE m AD =++−，又∵AC AE AD λμ=+，∴1m λ=+，1m μ=−，（平面向量基本定理的应用）又∵20λμ+=，∴()1210m m ++−=，解得3m =，故选：B.方法2：如图，以A 为坐标原点，AB 所在直线为x 轴建立平面直角坐标系，则()0,0A ，设(),0B a ，(),D b c ，∵AB DC = 则 (),C a b c +，又∵EB mDE =，设(),E x y ，则()()11mb a x a x m x b m y m y c mc y m ⎧+⎧=⎪⎪−=−⎪⎪+⇒⎨⎨−=−⎪⎪=⎪⎪+⎩⎩即：,11mb a mc E m m +⎛⎫ ⎪++⎝⎭∴,11mb a mc AE m m +⎛⎫= ⎪++⎝⎭，(),AC a b c =+，(),AD b c =， 又∵AC AE AD λμ=+，20λμ+=∴2AC AE AD μμ=−+∴()(),=2,,11mb a mc a b c b c m m μμ+⎛⎫+−+ ⎪++⎝⎭∴2()121a bm a b b m mc c c m μμμμ−+⎧+=+⎪⎪+⎨−⎪=+⎪+⎩①② 由②得1=1m mμ+−，将其代入①得3m =， 故选：B. 例3．（2022·北京·牛栏山一中高三期中）在平行四边形ABCD 中，E 是边CD 的中点，AE 与BD 交于点F ．若AB a =，AD b =，则AF =（ ）A ．1344a b +B ．2133a b +r rC ．3144a b +D ．1233a b + 【答案】D【解析】12AE AD DE AD AB =+=+. 设AF AE λ=()01λ<<， 则1122BF AF AB AD AB AB AD AB λλλ⎛⎫⎛⎫=−=+−=+− ⎪ ⎪⎝⎭⎝⎭, 又BD AD AB =−，且,,B F D 三点共线，则,BF BD 共线，即R μ∃∈，使得BF BD μ=，即12AD AB AD AB λλμμ⎛⎫+−=− ⎪⎝⎭， 又,AB AD 不共线，则有12λμλμ=⎧⎪⎨−=−⎪⎩，解得2323λμ⎧=⎪⎪⎨⎪=⎪⎩，所以，22112123323333AF AE AD AB AB AD a b ⎛⎫==+=+=+ ⎪⎝⎭. 故选：D.例4．（2022·广东广州·高三期中）如图，在平行四边形ABCD 中，,M N 分别为,AB AD 上的点，且42,53AM AB AN AD ==，连接,AC MN 交于P 点，若AP AC λ=，则λ的值为（ ）A ．35B ．57C ．411D ．815【答案】C 【解析】设MP kMN = 则45AP AM MP AB kMN =+=+ 显然2435MN AN AM AD AB =−=− 得()42424153535k AP AB k AD AB AD k AB ⎛⎫=+−=+− ⎪⎝⎭ 显然AC AD AB =+因为AP AC λ= 所以有()()24135k AD k AB AD AB λ+−=+ 即()24135k AD k AB AD AB λλ+−=+ 根据向量的性质可知()23415k k λλ⎧=⎪⎪⎨⎪−=⎪⎩ 解得611411k λ⎧=⎪⎪⎨⎪=⎪⎩故选：C例5．（2022·安徽省舒城中学模拟预测（文））已知平面向量OA ，OB 满足2OA OB ==，2OA OB ⋅=−，点D 满足2DA OD =，E 为AOB 的外心，则OB ED ⋅的值为（ ）A ．83− B ．83 C ．163− D ．163 【答案】A 【解析】2OA OB ==uu r uu u r Q ，cos 4c 2os OA O OA OB B AOB AOB ⋅=−∴⋅∠=∠=uu r uu u r uu r uu u r ，1cos 2AOB ∴∠=−，23AOB π∴∠=， 以O 为原点，OA ，垂直于OA 所在直线为x ，y 轴建立平面直角坐标系，如图所示，则()0,0O ，()2,0A ，(B −，设(),0D x 又2DA OD =，知()(),022,0x x =−，解得23x =，2,03D ⎛⎫∴ ⎪⎝⎭ 又E 为AOB 的外心，123AOE AOB π∴∠=∠=，OE EA =3AOE EAO OEA π∴∠=∠=∠=，AOE ∴为等边三角形，(E ，∴1,3ED ⎛=− ⎝，∴83OB ED ⋅=−． 故选：A例6．（多选题）（2022·湖北·华中师大一附中高三期中）如图，ABC 中，13BD BC =，12AE AC =，AD 与BE 交于点F ，则下列说法正确的是（ ）A ．1233AD AB AC =+ B ．12BF BE = C ．:1:3BFD AFE S S =△△D ．20AF BFCF ++=【答案】BCD 【解析】为了判断下面的有关结论，先引入三点共线向量形式的充要条件，设,,A B C 三点共线，O 为线外一点，则()1OB mOC m OA =+−， 即OA 与OC 前系数和为1，证：,,A B C 三点共线，AB mAC ∴=，()OB OA m OC OA ∴−=−， ()1OB mOC m OA ∴=+−．()11213333AD AB BD AB BC AB AC AB AB AC =+=+=+−=+， 故A 错； ,,B F E 三点共线，()()112AF AB AE AB AC λλλλ−∴=+−=+， ,,A F D 三点共线，233AF AD AB AC μμμ∴==+， 23132μλμλ⎧=⎪⎪∴⎨−⎪=⎪⎩， 解得1234λμ⎧=⎪⎪⎨⎪=⎪⎩，1122AF AB AE ∴=+， ∴ F 为BE 的中点， 12BF BE ∴=，故B 对； 111443BFD ABD ABC S S S ==⨯⋅△△△， 111222AFE ABE ABC S S S ==⨯⋅△△△， :1:3BFD AFE S S ∴=△△，故C 对；取AB 中点G ，BC 中点H ，如下图，则,,G F H 三点共线，()()()()2AF BF CF AF BF BF CF FB FB F FA C ⎡⎤∴++=−++++=++⎣⎦ ()()220FG FH EA EC =−+=−+=，故D 对． 故选：BCD ．例7．（2022·黑龙江·哈尔滨三中模拟预测）在ABC 中，13A A D B =，34A A E C =，BE 与DC 交于点F ，若AF AB AC λμ=+，则λμ+的值为__________. 【答案】79【解析】由已知可得，13A A D B =，34A A E C =. 因为，,,D F C 三点共线，设DF mDC =uuu r uuu r ，01m <<. 13DC AC AD AC AB =−=−uuu r uuu r uuu r uuu r uu u r ，则111333m AF AD DF AB m AC AB AB mAC −⎛⎫=+=+−=+ ⎪⎝⎭uu u r uuu r uuu r uu u r uuu r uu u r uu u r uuu r . 1233m m BF AF AB AB mAC AB AB mAC −+=−=+−=−+uu u r uu u r uu u r uu u r uuu r uu u r uu u r uuu r ， 又34BE AE AB AB AC =−=−+uur uu u r uu u r uu u r uuu r ，因为,,B E F 三点共线，则存在R n ∈，使得BF nBE =uu u r uur ，即233344m n AB mAC n AB AC nAB AC +⎛⎫−+=−+=−+ ⎪⎝⎭uu u r uuu r uu u r uuu r uu u r uuu r ， 因为，,AB AC 不共线，所以有2334m n n m +⎧−=−⎪⎪⎨⎪=⎪⎩，解得2389m n ⎧=⎪⎪⎨⎪=⎪⎩， 所以，1293AF AB AC =+uu u r uu u r uuu r ，即19λ=，23μ=，79λμ+=. 故答案为：79.例8．（2022·全国·高三专题练习）根据毕达哥拉斯定理，以直角三角形的三条边为边长作正方形，从斜边上作出的正方形的面积正好等于在两直角边上作出的正方形面积之和．现在对直角三角形CDE 按上述操作作图后，得如图所示的图形，若AF AB AD x y =+，则x y −=____________．【答案】12− 【解析】如图，以A 为原点，分别以,AB AD 为,x y 轴建立平面直角坐标系，设正方形ABCD 的边长为2a ，则正方形DEHI，正方形EFGC 边长为a 可知()0,0A ，()2,0B a ，()0,2D a，)1DF a =则)1cos30F x a =⋅，)1sin 302F y a a =⋅+，即F ⎫⎪⎪⎝⎭ 又AF AB AD x y =+，()()()2,00,22,2x a y a ax ay ⎫∴=+=⎪⎪⎝⎭即22ax ay ⎧=⎪⎪⎨⎪=⎪⎩，即22ax ay −=，化简得12x y −=− 故答案为：12−。

平面向量基本定理的应用问题一、利用平面向量基本定理表示未知向量平面向量基本定理的内容：如果1e ,2e 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a ,有且只有一对实数λ1,λ2使a=λ11e +λ22e ,平面内选定两个不共线向量为基底,可以表示平面内的任何一个向量．【例1】如图,平面内有三个向量,,OA OB OC ,其中OA 与OB 的夹角为120︒,OA 与OC 的夹角为30︒,且3||2,||,||232OA OB OC ===,若(,)OC OA OB λμλμ=+∈R ,则（ ） A. 4,2λμ== B. 83,32λμ==C. 42,3λμ==D. 34,23λμ== ABCO【分析】平面向量基本定理实质上是“力的分解原理”,过点C 分别作直线,OA OB 的平行线,分别与直线,OB OA 相交,利用向量加法的平行四边形法则和平面向量共线定理将OC 用,OA OB 表示．【解析】设与,OA OB 同方向的单位向量分别为,a b ,依题意有42OC a b =+,又2OA a =,32OB b =,则423OC OA OB =+,所以42,3λμ==.故选C.【点评】利用平面向量基本定理表示未知向量时,向量加法的三角形法则、平行四边形法则以及必要的平面几何知识是必要的．【小试牛刀】【2016届重庆市巴蜀中学高三上学期期中】在ABC ∆中,若点D 满足DC BD 2=,则=AD （ ）A ．AB AC 3231+ B ．AC AB 3235- C ．3132- D ．3132+二、利用平面向量基本定理确定参数的值、取值范围问题平面向量基本定理是向量坐标的理论基础,通过建立平面直角坐标系,将点用坐标表示,利用坐标相等列方程,寻找变量的等量关系,进而表示目标函数,转化为函数的最值问题．【例2】【2016届浙江省绍兴市一中高三9月回头考】已知向量,OA OB 满足1OA OB ==,,(,,)OA OB OC OA OB R λμλμ⊥=+∈若M 为AB 的中点,并且1MC =,则λμ+的最大值是（ ）A ．13-B ．12+C ．5D ．13+【分析】首先利用已知条件建立适当的直角坐标系,并写出点,A B 的坐标,然后运用向量的坐标运算计算出点C 的坐标,再由1MC =可得,λμ所满足的等式关系即圆的方程,设t λμ=+,将其代入上述圆的方程并消去μ得到关于λ的一元二次方程,最后运用判别式大于等于0即可得出所求的答案．【解析】因为向量,OA OB 满足1OA OB ==,OA OB ⊥,所以将,A B 放入平面直角坐标系中,令(1,0),(0,1)A B ,又因为M 为AB 的中点,所以11(,)22M ．因为(,,)OC OA OB R λμλμ=+∈,所以(1,0)(0,1)(,)OC OA OB λμλμλμ=+=+=,即点(,)C λμ．所以11(,)22MC λμ→=--,因为1MC =,所以2211()()122λμ-+-=,即点(,)C λμ在以11(,)22为圆心,1为半径的圆上．令t λμ=+,则t μλ=-,将其代入圆2211()()122λμ-+-=的方程消去μ得到关于λ的一元二次方程：22122()02t t t λλ-+--=,所以221(2)42()02t t t ∆=-⨯--≥,解之得2121t -+≤≤+,即λμ+的最大值是12+．故应选B ．【点评】若题中有互相垂直的单位向量,大多可建立坐标系,转化为代数问题.【小试牛刀】如图,在正方形ABCD 中,E 为AB 的中点,P 为以A 为圆心,AB 为半径的圆弧上的任意一点,设向量的最小值为则μλμλ++=,AP DE AC ．三、三点共线向量式设,,A B C 是共线三点,O 是平面内任意一点,则(1)OB OA OC λλ=+-,其特征是“起点一致,终点共线,系数和为1”,利用向量式,可以求交点位置向量或者两条线段长度的比值．【例3】如图所示,已知点G 是△ABC 的重心,过G 作直线与AB 、AC 两边分别交于M 、N 两点,且,AM x AB AN y AC ==,则xyx y+的值为 . NMGCBA【分析】g (x )在区间(－2,－1)内存在单调递减区间可转化为'()0g x ≤在区间(－2,－1)有解,且不是唯一解,参变分离为2a x+x≤,只需求右侧函数的最大值,再检验等号． 【解析】这题应该用到这个结论：O 是直线AB 外一点,OC mOA nOB =+,则,,A B C 三点共线的充要条件是1m n +=．本题中就是设AG mAM nAN =+,则1m n +=,由于G 是ABC ∆的重心,有AG =1()3AB AC +,又AG mxAB ny AC =+,根据平面向量基本定理得13mx ny ==,即13x m =,13y n=,代入得13xy x y =+． 【点评】本题实质是不等式的有解问题,可先参变分离,转化为求函数的最值问题,但是需注意因为函数单调是对于某一区间而言的,故还需检验解不是唯一．【小试牛刀】若点M 是∆ABC 所在平面内一点,且满足：3144AM AB AC =+. （1）求∆ABM 与∆ABC 的面积之比.（2）若N 为AB 中点,AM 与CN 交于点O,设BD xBM yBN =+,求,x y 的值. 四、平面向量基本定理在解析几何中的应用【例4】【2016届安徽省六安一中高三上第五次月考】设双曲线22221x y a b-=(0,0)a b >>的右焦点为F ,过点F 与x 轴垂直的直线l 交两渐近线于A ,B 两点,与双曲线的其中一个交点为P ,设坐标原点为O,若OP mOA nOB =+(,)m n R ∈,且29mn =,则该双曲线的渐近线为（ ） A ．34y x =±B ．24y x =±C ．12y x =±D ．13y x =±【分析】过双曲线的右焦点(),0F c 并与x 轴垂直的直线:l x c =,与渐近线by x a=±的交点坐标为,,bc A c c ⎛⎫ ⎪⎝⎭ ,,bc B c c ⎛⎫- ⎪⎝⎭代入向量运算得到点P 的坐标,再代入双曲线方程求出离心率,从而渐近线方程可求．【解析】由题意可知,,bc A c c ⎛⎫ ⎪⎝⎭,,bc B c c ⎛⎫- ⎪⎝⎭代入OP mOA nOB =+,得()(),bc P m n c m n a ⎛⎫+- ⎪⎝⎭,代入双曲线方程22221x y a b -=中,整理得241e mn =；又因为29mn =,可得2322,144b e e a =∴=-=,所以该双曲线的渐近线为24y x =±,故B 为正确答案． 【点评】解析几何中基本量的计算要注意方程思想的应用和运算的准确性.【小试牛刀】【2016届河北省邯郸市一中高三一轮收官考试】已知A 是双曲线22221x y a b-=（0a >,0b >）的左顶点,1F 、2F 分别为左、右焦点,P 为双曲线上一点,G 是12FF ∆P 的重心,若1G F λA =P ,则双曲线的离心率为（ ）A ．2B ．3C ．4D ．与λ的取值有关【迁移运用】1.如图,在平行四边形ABCD 中,a AB =,b AD =,NC AN 3=,则BN =（ ）(用a ,b 表示)A ．→→-b a 4341 B ．→→-b a 4143C ．→→-a b 4341 D ．→→-a b 4143 2．设向量)20cos ,20(sin ),25sin ,25(cos oo oo b a ==→→,若→→→+=b t a c (t ∈R),则2()c 的最小值为（ ） A ．22D.213.【2016届广西武鸣县高中高三8月月考】直线过抛物线的焦点,且交抛物线于两点,交其准线于点,已知,则（ ）A.2B.C.D.44．已知,OA OB 是两个单位向量,且OA OB ⋅=0．若点C 在∠AOB 内,且∠AOC=30°,则(,),OC mOA nOB m n R =+∈则nm（ ） A ．13 B ．3 C 3 D ．3 5．在△ABC 中,M 为边BC 上任意一点,N 为AM 中点,AN ＝λAB ＋μAC ,则λ＋μ的值为( ) A.12 B.13 C.14D.16. 已知b a OB b a OA a +=-=-=,),3,1(,若AOB ∆是以O 为直角顶点的等腰直角三角形,则AOB ∆的面积是（ ）A ．3B ．2C ．22D ．4[来源:学#科#网]7.过坐标原点O 作单位圆221x y +=的两条互相垂直的半径OA OB 、,若在该圆上存在一点C ,使得OC aOA bOB =+（a b R ∈、）,则以下说法正确的是（ ）A ．点(),P a b 一定在单位圆内B ．点(),P a b 一定在单位圆上C ．点(),P a b 一定在单位圆外D ．当且仅当0ab =时,点(),P a b 在单位圆上8. 在平面上,⊥,||=||=1,=+．若||<,则||的取值范围是( ) A ．(0,] B ．(,] C ．(,] D ．(,]9.在平面直角坐标系中,O 为坐标原点,直线:10l x ky -+=与圆22:4C x y +=相交于, A B 两点,OM OA OB =+．若点M 在圆C 上,则实数k =（ ） A ．2- B ．1- C ．0 D ．110.如图,在扇形OAB 中,60AOB ︒∠=,C 为弧AB 上的一个动点．若OC -→xOA y OB -→-→=+,则y x 4+的取值范围是 ．11. 如图,四边形OABC 是边长为1的正方形,3=OD ,点P 为BCD ∆内（含边界）的动点,设(,)OP OC OD R αβαβ=+∈,则αβ+的最大值等于12.（2015北京理13）在ABC △中,点M ,N 满足2AM MC =,BN NC =.若MN x AB y AC =+,则x = ；y = .。

第9讲 平面向量共线定理、平面向量基本定理的应用问题一、共线向量定理1．对空间任意两个向量a ，b (a ≠0)，a 与b 共线的充要条件是存在实数λ，使得b ＝λa .2．对于三点共线有以下结论：对于平面上的任一点O ，OA →，OB →不共线，满足OP →＝xOA →＋yOB →(x ，y ∈R )，则P ，A ，B 共线⇔x ＋y ＝1.例1 如图所示，在△ABO 中，OC →＝14OA →，OD →＝12OB →，AD 与BC 相交于点M ，设OA →＝a ，OB →＝b .试用a 和b 表示向量OM →. 例2如图，在△ABC 中，3BAC π∠=，2AD DB =,P 为CD 上一点，且满足12AP mAC AB =+，若△ABC 的面积为AP 的最小值为（ ）A. C. 3D.43【针对练习 】如图，经过△OAB 的重心G 的直线与OA ，OB 分别交于点P ，Q ，设OP →＝mOA →，OQ →＝nOB →，m ，n ∈R ，则1n ＋1m 的值为________．例3 在△ABC 中，点P 满足2BP PC =，过点P 的直线与AB ，AC 所在直线分别交于点M ，N ，若AM mAB =，AN nAC =(m ＞0，n ＞0)，则m +2n 的最小值为（ ） A ．3 B ．4C ．83D ．103例4 已知数列{a n }为等差数列，且满足32015BA a OB a OC =+，若()AB AC R λλ=∈，点O 为直线BC 外一点，则12017a a += ( ) A. 0 B. 1C. 2D. 4例5 已知圆O 的半径为2，A ，B 是圆上两点且∠AOB 23π=，MN 是一条直径，点C 在圆内且满足(1)(01)OC OA OB λλλ=+-<<，则CM CN ⋅的最小值为（ ）A ．－3B ．C ．0D ．2例6 O 是平面上一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λAB →|AB →|＋AC →|AC →|，λ∈[0，＋∞)，则P 的轨迹一定通过△ABC 的( ) A ．外心 B ．内心 C ．重心 D ．垂心【针对练习】 1．已知点G 为ABC △的重心，过点G 作直线与AB ，AC 两边分别交于,M N两点，且,AM xAB = ,AN y AC = ,x y R ∈，则2．如图所示，已知点G 是ABC ∆的重心，过点G 作直线与,AB AC 两边分别交于,M N 两点，且,AM xAB AN y AC ==,则x y +的最小值为（ ）A ．2BC D3．设A 1，A 2，A 3，A 4是平面直角坐标系中两两不同的四点，若A 1A 3→＝λA 1A 2→(λ∈R )，A 1A 4→＝μA 1A 2→(μ∈R )，且1λ＋1μ＝2，则称A 3，A 4调和分割A 1，A 2.已知点C (c ，0)，D (d ，0)(c ，d ∈R )调和分割点A (0，0)，B (1，0)，则下面说法正确的是( )A ．C 可能是线段AB 的中点 B ．D 可能是线段AB 的中点C ．C ，D 可能同时在线段AB 上D ．C ，D 不可能同时在线段AB 的延长线上二、平面向量基本定理如果1e ,2e 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2使a=λ11e +λ22e ,平面内选定两个不共线向量为基底,可以表示平面内的任何一个向量．例7 如图,平面内有三个向量,,OA OB OC ,其中OA 与OB 的夹角为120︒,OA 与OC 的夹角为30︒,3||2,||,||23OA OB OC ===若(,)OC OA OB λμλμ=+∈R ,则（ ）A. 4,2λμ==ABCO例8 两个非零向量OA →，OB →不共线，且OP →＝mOA →，OQ →＝nOB →(m ，n >0)，直线PQ 过△OAB 的重心，则m ，n 满足( )A ．m ＋n ＝32B ．m ＝1，n ＝12 C.1m ＋1n＝3 D ．以上全不对例9 如图，AB 是圆O 的直径，C ，D 是圆O 上的点，60CBA ∠=，45ABD ∠=，CD xOA yBC =+，则x y +的值为（ ）A ．13-B．3- C ．23D．【针对练习】 1．在△ABC 中，点D ，E 分别在边BC ，AC 上，且2BD DC =，3CE EA =，若AB a =，AC b =，则DE =（ ） A 15a b +B 113a b -C 15a b -D 113a b +2．在梯形ABCD 中，已知AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点．若AB→＝λAM →＋μAN →，则λ＋μ＝________．3．已知平面向量,m n 的夹角为3π且1,2m n ==，在△ABC 中，22AB m n =+，26AC m n =-，D 为BC 中点，则AD =( )A. B. C.6 D.12三、利用平面向量基本定理确定参数的值、取值范围问题例10 已知向量,OA OB 满足1OA OB ==,,(,,)OA OB OC OA OB R λμλμ⊥=+∈若M 为AB 的中点,1MC =,则λμ+的最大值是（ ）A例11 在Rt ABC ∆中，AB AC ⊥，1AB =，2AC =，点P 为△ABC 内（包含边界）的点，且满足AP xAB y AC =+（其中x ，y 为正实数），则当xy 最大时，yx的值是（ ） A ．12B ．1 C.2 D ．与∠A 的大小有关例12 △ABC 中，35,5==BC AB ，3π=A ，点P 是ABC ∆内（包括边界）的一动点，且)(5253R AC AB AP ∈-=λλ的最大值为____________例13 如图，四边形ABCD 是正方形，延长CD 至E ，使得DE ＝CD ，若动点P 从点A 出发，沿正方形及三角形的边按如下路线运动：A →B →C →D →E →A →D ，其中AP →＝λAB →＋μAE →.给出下列说法：①当P 为BC 的中点时λ＋μ＝2； ②满足λ＋μ＝1的点P 恰有3个；③λ＋μ的最大值为3；④若满足λ＋μ＝k 的点P 有且只有2个，则k ∈(1，3)． 其中，说法正确的序号是________．【针对练习】 1．如图所示，A ，B ，C 是圆O 上不同的三点，线段CO 的延长线与线段BA 交于圆外的一点D ，若OC OA OB λμ=+（R λ∈，R μ∈），则λμ+的取值范围是（ ）A ．(0,1)B ．(1,)+∞C ．(),1-∞-D ．()1,0-2．如图，已知,B C 是以原点O 为圆心，半径为1的圆与x 轴的交点，点A 在劣 弧PQ （包含端点）上运动，其中30POx ∠=，OP OQ ⊥，作AH BC ⊥于H ．若记AH xAB y AC =+，则xy 的取值范围是( )A. 1(0,]4B. 11[,]164C. 13[,]1616 D. 31[,]164四、平面向量基本定理在解析几何中的应用例14 F ,过点F 与x 轴垂直的直线l 交两渐近线于A ,B 两点,与双曲线的其中一个交点为P ,设坐标原点为O,若OP mOA nOB =+(,)m n R ∈,则该双曲线的渐近线为（ ）A B C D【针对练习】已知A 是双曲线（0a >,0b >）的左顶点,1F 、2F 分别为左、右焦点,P 为双曲线上一点,G 是12F F ∆P 的重心,若1G F λA =P ,则双曲线的离心率为（ ） A ．2 B ．3 C ．4 D ．与λ的取值有关【精品练习】1．在△ABC 中，点D 是线段BC 上任意一点，M 是线段AD 的中点，若存在实数λ和μ，使得BM AB AC =+λμ，则λμ+= .2．已知平面直角坐标系内的两个向量()3,2a m =-，()1,2b m =-，且平面内的任一向量c 都可以唯一地表示成c a b λμ=+(λ，μ为实数)，则实数m 的取值范围是( ) A.(－∞,2)B.6,5⎛⎫+∞ ⎪⎝⎭C.(－∞,－2)∪(－2,+∞)D.66,,55⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭3．如图，在△ABC 中，点D ，E 是线段BC 上两个动点，且AD AE x AB y AC +=+，则14x y+的最小值为（ ）A ． 32B ．2C ．52D ．924．已知3AB =uu u v ，A ，B 分别在y 轴和x 轴上运动，O 为原点，1233OP OA OB =+uu u v uu v uu u v,点P 的轨迹方程为( )A.2214x y +=B.2214y x +=C.2219x y +=D.2219y x += 5．如图4-25-1所示，在平行四边形ABCD 中，E 和F 分别在边CD 和BC 上，且DC →＝3DE →，BC →＝3BF →，若AC →＝mAE →＋nAF →，其中m ，n ∈R ，则m ＋n ＝________．6．如图4-25-3，在四边形ABCD 中，AB ＝BC ＝CD ＝1，且∠B ＝90°，∠BCD ＝135°，记向量AB →＝a ，AC →＝b ，则AD →＝( )图4-25-3A.2a －1＋22b B ．－2a ＋1＋22b C ．－2a ＋1－22b D.2a ＋1－22b7．已知A ，B ，C 是圆x 2＋y 2＝1上不同的三点，且OA →·OB →＝0(O 为坐标原点)，若存在实数λ，μ满足OC →＝λOA →＋μOB →，则实数λ，μ的关系满足( ) A.1λ＋1μ＝1 B ．λ2＋μ2＝1 C ．λμ＝1 D ．λ＋μ＝1。