3.4.3球赛积分表问题
- 格式:ppt
- 大小:1.16 MB
- 文档页数:59

人教版七年级数学上册3.4 第3课时《球赛积分表问题》说课稿2一. 教材分析《球赛积分表问题》是人教版七年级数学上册第3.4节的内容,主要是让学生掌握用一元一次方程解决实际问题的方法。
这部分内容是学生学习数学的转折点,从理论过渡到实际应用,培养学生运用数学知识解决生活问题的能力。
本节内容通过分析球赛的积分表,引导学生发现问题的规律,建立方程,求解问题。
二. 学情分析七年级的学生已经掌握了基本的代数知识,对于一元一次方程有一定的理解。
但是,将实际问题转化为数学模型,并用方程求解问题的能力还不够成熟。
因此,在教学过程中,需要引导学生发现问题的规律,培养学生运用数学知识解决实际问题的能力。
三. 说教学目标1.知识与技能:学生能够理解球赛积分表的规律,会用一元一次方程解决实际问题。
2.过程与方法:学生通过分析球赛积分表,培养观察、思考、表达的能力。
3.情感态度与价值观:学生体验数学在生活中的应用,培养学习数学的兴趣。
四. 说教学重难点1.教学重点:学生能够分析球赛积分表的规律,建立方程,求解问题。
2.教学难点:引导学生发现问题的规律,培养学生运用数学知识解决实际问题的能力。
五. 说教学方法与手段1.教学方法:采用问题驱动法,引导学生自主探究,合作交流。
2.教学手段:多媒体课件,球赛积分表实例,数学软件。
六. 说教学过程1.导入新课:通过一个具体的球赛积分表,引导学生发现问题的规律。
2.探究规律:学生分组讨论,总结球赛积分表的规律。
3.建立方程:引导学生用一元一次方程表达球赛积分表的规律。
4.求解问题:学生自主解决实际问题,教师进行指导。
5.巩固练习:设计一些类似的实际问题,让学生运用所学知识解决。
6.课堂小结:学生总结本节课的收获,教师进行点评。
七. 说板书设计板书设计如下:球赛积分表问题1.分析球赛积分表的规律2.用一元一次方程表达规律3.求解实际问题八. 说教学评价教学评价主要从学生的知识掌握、能力培养、情感态度三个方面进行。


人教版七年级数学上册3.4 第3课时《球赛积分表问题》教学设计2一. 教材分析球赛积分表问题是人教版七年级数学上册3.4章节的一部分,主要让学生学会通过已知信息推断未知信息,培养学生解决问题的能力。
本节课通过分析球赛积分表,让学生理解并掌握用方程和不等式解决实际问题的方法。
二. 学情分析七年级的学生已经掌握了方程和不等式的基本知识,具备一定的逻辑思维能力。
但解决实际问题时,部分学生可能会对题目理解不深,不能很好地将数学知识与实际问题结合。
因此,在教学过程中,教师需要引导学生深入理解问题,培养学生的解决问题的能力。
三. 教学目标1.让学生理解球赛积分表问题,学会用方程和不等式解决实际问题。
2.培养学生收集、处理信息的能力,提高学生解决问题的能力。
3.培养学生合作学习的意识,提高学生的团队协作能力。
四. 教学重难点1.重点:让学生学会用方程和不等式解决实际问题。
2.难点:引导学生深入理解问题,找出问题的关键信息。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动思考问题。
2.使用案例分析法,让学生通过分析球赛积分表,掌握解决实际问题的方法。
3.采用合作学习法,让学生在团队中共同探讨问题,提高团队协作能力。
六. 教学准备1.准备球赛积分表的相关案例,用于教学演示。
2.准备与球赛积分表问题相关的练习题,用于巩固所学知识。
3.准备黑板,用于板书关键步骤和答案。
七. 教学过程1.导入(5分钟)教师通过向学生介绍球赛积分表的背景,激发学生的学习兴趣,引导学生思考如何通过已知信息推断未知信息。
2.呈现(10分钟)教师展示球赛积分表案例,让学生观察并找出关键信息。
教师提出问题,引导学生思考如何解决问题。
3.操练(10分钟)教师引导学生列出方程或不等式,解决球赛积分表问题。
教师讲解解题过程,让学生理解并掌握解题方法。
4.巩固(10分钟)教师给出类似的球赛积分表问题,让学生独立解决。
教师选取部分学生的答案进行讲评,巩固所学知识。

人教版七年级数学上册3.4 第3课时《球赛积分表问题》教案2一. 教材分析球赛积分表问题是人教版七年级数学上册3.4节的内容,主要让学生通过实际问题情境,理解并掌握用方程和不等式解决实际问题的方法。
这部分内容既联系了生活实际,又锻炼了学生的数学思维能力。
二. 学情分析七年级的学生已经具备了一定的数学基础,对用方程和不等式解决实际问题已经有了一定的了解。
但学生在解决实际问题时,往往会因为对问题的理解不深入,找不到等量关系,或者列出的方程不正确,导致解题困难。
因此,在教学过程中,需要引导学生正确理解问题,找到等量关系,列出正确的方程。
三. 教学目标1.让学生通过实际问题情境,理解并掌握用方程和不等式解决实际问题的方法。
2.培养学生观察、分析、解决问题的能力。
3.培养学生合作交流、归纳总结的能力。
四. 教学重难点1.教学重点:理解并掌握用方程和不等式解决实际问题的方法。
2.教学难点:找到问题的等量关系,列出正确的方程。
五. 教学方法采用问题驱动法,引导学生通过观察、分析、归纳、总结,自主探索解决问题的方法。
在教学过程中,注重让学生说理,培养学生的逻辑思维能力。
六. 教学准备1.准备相关的球赛积分表问题案例。
2.准备黑板、粉笔等教学用具。
七. 教学过程1.导入(5分钟)通过一个实际的球赛积分表问题,引导学生思考如何用数学方法解决这个问题。
例如,某校举行篮球比赛,甲、乙、丙、丁四支球队进行了循环赛,每队胜一场得2分,负一场得1分,弃权一场不得分,请问哪支球队得分最高?2.呈现(10分钟)呈现球赛积分表问题,让学生观察并思考问题。
引导学生发现,要解决这个问题,需要找到每支球队的比赛场次、胜负情况以及得分。
3.操练(10分钟)让学生分组讨论,尝试解决呈现的球赛积分表问题。
教师在这个过程中,引导学生找到问题的等量关系,列出方程。
4.巩固(10分钟)对学生的解答进行讲解,让学生理解并掌握用方程解决实际问题的方法。

设胜一场积x分,从表中其他任何一行可以列方程,求出x的值,例如从第三行得方程.解方程,得用表中其他行可以验证,得出结论,负一场积1分,胜一场积2分.(1)如果一个队胜m场,则负(14-m)场,胜场积分2m,负场积分为14-m,总积分为2m+(14-m)=m+14.(2)问题(2),学生可能通过计算积分榜中各队的胜场总积分和负场总积分,说明某队的胜场总积分不能等于它的负场总积分.你能用方程,说明上述结论吗?如果设一个队胜了x场,则负了(14-x)场,•如果这个队的胜场总积分等于负场总积分,那么列方程为由此,解得x=想一想,x表示什么量?它可以是分数吗?由此你能得出什么结论?这里x表示一个队所胜的场数,它是一个整数,所以x=不符合实际意义.•由此可以判定没有哪个队的胜场总积分等于负场总积分.这个问题说明:利用方程不仅能求出具体数值,而且还可以进行推理判断,是否存在某种数量关系.另外,上面问题还说明,用方程解决实际问题时,不仅要注意方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.拓展延伸如果删去积分榜的最后一行,你还能用式子表示总积分与胜、负场数之间的数量关系吗?我们可以从积分榜中积分不相同的两行数据列方程求得胜、负一场各得几分,例如,从第一、三行.设胜一场积x分,则前进队胜场积分为10x,负场积分为(24-10x)分,•他负了4场,所以负一场积分为,同理从第三行得到负一场积分为,从中找出相等关系(1)试判断A队胜、平各几场?(2)若每赛一场每名队员均得出场费50元,那么A队的每一名队员所得奖金与出场费的和是多少元?五、教学反思:本节课的主要内容是球赛积分问题,问题与实际情况更接近,也比较复杂,例题中还包含了需要利用反证法来解决的问题,具有一定难度,我在本次教学重以学生为主体,以探究为主线,采取生生合作交流、师生合作的探究式学习法,教师设计小问题,来逐步引导学生找出积分表中的数量,以及数量之间的基本关系,找出有用的数据信息,探索列出方程的相等关系,这种启发式引导可增强学生学习的主动性,引发学生浓厚的学习兴趣,使学生的知识得到巩固的同时,也使生活经验、学习方法等得到提高,在问题情境引题中,我创设学生熟悉且感兴趣的球赛问题,激发学生的学习兴趣,使得学生能更快地投入到对问题的讨论中,同时我也明确了本节课要学的主要内容,本节课的每一个问题都鼓励学生积极动手动口,以达到教学要求,促进思维能力的发展,增强学生的自主学习能力,本节课学生对表格中有效信息的筛选会产生疑惑,不知道该找出哪些有用的信息。
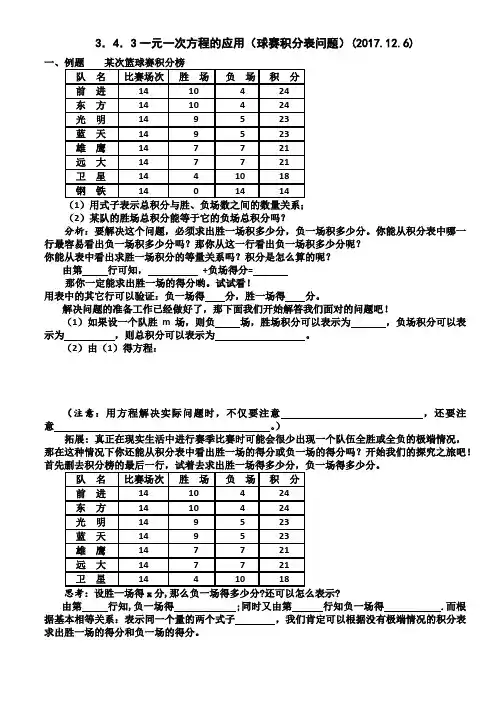
3.4.3一元一次方程的应用(球赛积分表问题)(2017.12.6)(2)某队的胜场总积分能等于它的负场总积分吗?分析:要解决这个问题,必须求出胜一场积多少分,负一场积多少分。
你能从积分表中哪一行最容易看出负一场积多少分吗?那你从这一行看出负一场积多少分呢?你能从表中看出求胜一场积分的等量关系吗?积分是怎么算的呢?由第行可知,+负场得分=那你一定能求出胜一场的得分哟。
试试看!用表中的其它行可以验证:负一场得分,胜一场得分。
解决问题的准备工作已经做好了,那下面我们开始解答我们面对的问题吧!(1)如果设一个队胜m场,则负场,胜场积分可以表示为,负场积分可以表示为,则总积分可以表示为。
(2)由(1)得方程:(注意:用方程解决实际问题时,不仅要注意,还要注意。
)拓展:真正在现实生活中进行赛季比赛时可能会很少出现一个队伍全胜或全负的极端情况,那在这种情况下你还能从积分表中看出胜一场的得分或负一场的得分吗?开始我们的探究之旅吧!?由第行知,负一场得;同时又由第行知负一场得.而根据基本相等关系:表示同一个量的两个式子,我们肯定可以根据没有极端情况的积分表求出胜一场的得分和负一场的得分。
二、课堂练习 1. 下表记录了一次实验中时间和温度的数据:(1)如果温度的变化是均匀的,21分的温度是多少?(2)什么时间的温度是34℃?2.某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章价格各是多少元?五、课堂检测1、郑逸是学校的篮球明星,在一场篮球比赛中,他一人得了23分,如果他投进的2分球比3分球多4个,那么他一共投进了___个2分球。
2分,并且没有负一场。
(1)试判断A队胜、平各几场?(2) 若每赛一场每名队员均得出场费50元,那么A 队的每一名队员所得奖金与出场费的和是多少元?共计145元。


新区中学数学导学案课题 3.4.3球赛积分表问题课型新授备课教师李晓男审核人闫功邦课时 3 年班时间编号学习目标1.会根据实际问题中数量关系列方程解决实际问题,熟练掌握一元一次方程的解法2.培养学生数学建模能力,分析问题、解决问题的能力。
(重点)用一元一次方程解决球赛积分表问题。
(难点)实际问题中,如何建立等量关系,并根据等量关系列出方程。
学习流程一、自学质疑1、球队积分:一支球队经过一个赛季的比赛,其成绩是由它的积分决定的,积分越多,名次就越 _________2、积分的原则:不同的比赛有不同的积分办法。
(1)如篮球、排球等比赛,其结果只有胜或负,通常胜一场得2分,负一场得1分,故有:总积分=_________×2+_________×1(2)如足球比赛,其结果有胜、平或负,通常胜一场得3分,平一场得1分,负一场得0分,则:总积分=_________。
二、精讲点拨知识点1:球赛积分问题例:某球队参加了10场足球赛,共积17分,已知胜一场得3分,平一场得1分,负一场得0分,其中该队输了3场,该队胜了几场?知识点2:图表信息问题例:某飞机停机前的运行速度v(米/秒)和运行时间t(秒)之间的关系如下表:三、练习点评课后习题四、课堂总结1、球队积分2、积分的原则五、布置作业t 0 1 1 2 3 …v 42 39 36 33 30 …课后反思这类问题中积分多少与胜、负的场数相关,同时也与比赛积分规定有关,需要先弄清规定胜一场积几分,平一场积几分,负一场积几分。
且这类问题中的基本等量关系为:比赛总场数=胜场数+负场数+平场数;比赛总积分=胜场积分+负场积分+平场积分解图表信息题的一般方法:(1)图表信息题是一种通过表格或图形的形式给出数据信息,然后通过读图识表,从图表中获得足够信息,再利用一元一次方程解决问题的题型。
(2)解图表信息题的关键是仔细观察图表,分析图表,从图表中获取有用的信息,比如表格应用题,就应当搞清楚每一横行、每一竖行,以及每一横行和竖行交叉处的单元格各表示什么意思,读懂表格之后,再分析表格中量与量之间的关系,方可解题1、下表是足球比赛的得分规则:输赢胜一场平一场负一场积分 3 1 0某足球队踢了14场球,负了5场,得19分,那么这个球队胜了多少场球?2、在学校的一场篮球赛中,我班以16:9胜利了,现知道2分球的个数比3分球多3个,总共是16分,那么3分球有多少个?3、某次知识竞赛共有20道题,每一道题答对5分,答错或不答题都扣3分,小明考了68分,那么小明答对多少道题?4、如图是2014年9月份的日历表,任意圈出一竖列上相邻的三个数,则这三个数的和可能是()A.35B.75C.84D.42综合提升某小组8名同学参加一次知识竞赛,共答10道题,每题分值相同。

前言:
该导学案(导学单)由多位一线国家特级教师根据最新课程标准的要求和教学对象的特点结合教材实际精心编辑而成。
实用性强。
高质量的导学案(导学单)是高效课堂的前提和保障。
(最新精品导学案)
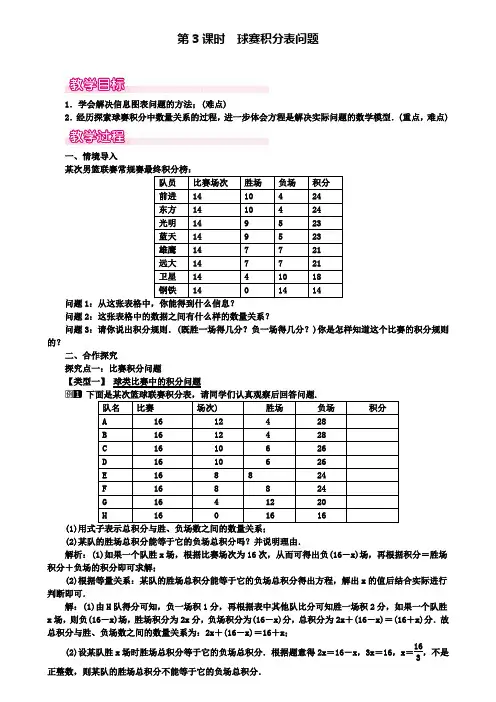
第3课时球赛积分表问题
1.学会解决信息图表问题的方法;(难点)
2.经历探索球赛积分中数量关系的过程,进一步体会方程是解决实际问题的数学模型.(重)
点,难点
一、情境导入
某次男篮联赛常规赛最终积分榜:
队员比赛场次胜场负场积分
前进1410424
东方1410424
光明149523
蓝天149523
雄鹰147721
远大147721
卫星1441018
钢铁1401414
问题1:从这张表格中,你能得到什么信息?
问题2:这张表格中的数据之间有什么样的数量关系?
问题3:请你说出积分规则.(既胜一场得几分?负一场得几分?)你是怎样知道这个比赛的积分规则的?
二、合作探究
探究点一:比赛积分问题
【类型一】球类比赛中的积分问题
1。
第3课时 球赛积分表问题1.学会解决信息图表问题的方法;(难点) 2.经历探索球赛积分中数量关系的过程,进一步体会方程是解决实际问题的数学模型.(重点,难点)一、情境导入某次男篮联赛常规赛最终积分榜:问题1:从这张表格中,你能得到什么信息?问题2:这张表格中的数据之间有什么样的数量关系?问题3:请你说出积分规则.(既胜一场得几分?负一场得几分?)你是怎样知道这个比赛的积分规则的?二、合作探究探究点一:比赛积分问题【类型一】 球类比赛中的积分问题(1)(2)某队的胜场总积分能等于它的负场总积分吗?并说明理由.解析:(1)如果一个队胜x 场,根据比赛场次为16次,从而可得出负(16-x)场,再根据积分=胜场积分+负场的积分即可求解;(2)根据等量关系:某队的胜场总积分能等于它的负场总积分得出方程,解出x 的值后结合实际进行判断即可.解:(1)由H 队得分可知,负一场积1分,再根据表中其他队比分可知胜一场积2分,如果一个队胜x 场,则负(16-x)场,胜场积分为2x 分,负场积分为(16-x)分,总积分为2x +(16-x)=(16+x)分.故总积分与胜、负场数之间的数量关系为:2x +(16-x)=16+x ;(2)设某队胜x 场时胜场总积分等于它的负场总积分.根据题意得2x =16-x ,3x =16,x =163,不是正整数,则某队的胜场总积分不能等于它的负场总积分.方法总结:解答本题的关键是根据表格得出胜一场、负一场各自所得的积分.【类型二】学习竞赛中的积分问题某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分.某选手在这次竞赛中共得116分,那么他答对几道题?解析:设选手答对了x道题,则有(20-x)道题答错或不答,根据答对题目的得分减去答错或不答题目的扣分是116分,即可得到一个关于x的方程,解方程即可.解:设答对了x道题,则有(20-x)道题答错或不答,由题意得:8x-(20-x)×3=116,8x+3x=116+60,11x=176,x=16.答:他答对16道题.方法总结:解这类题关键是找准相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列方程求解.探究点二:其他图表类问题有一批货物需要从A地运往B地,货主准备租用甲、乙两种货车,已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付50元计算,问货主应付运费多少元?解析:设乙种货车每辆每次运x吨,则甲种货车每辆每次运(11.5-3x)吨,根据现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付50元计算可列方程求解.解:设乙种货车每辆每次运x吨,则甲种货车每辆每次运(11.5-3x)吨,6x+5×(11.5-3x)=35,x =2.5,11.5-3x=4(吨),3×4+5×2.5=24.5(吨).50×24.5=1225(元).答:货主应付运费1225元.方法总结:解决本题的关键是读懂表格,找到相应的等量关系列出方程.三、板书设计1.球类比赛中的积分问题2.表格信息类问题本节课主要是借球赛积分表问题学习数学知识的应用.由于本节问题的背景和表达都比较贴近实际,因为其中的有些数量关系比较隐蔽,所以在探究过程中正确建立方程是难点,教师要恰当的引导,让学生弄清问题背景,分析清楚有关数量关系,找出可作为方程依据的主要相等关系,但教师不要代替学生的思考.要鼓励学生自主探究.2019-2020学年七年级数学上学期期末模拟试卷一、选择题1.如图,点A 、B 在线段EF 上,点M 、N 分别是线段EA 、BF 的中点,EA :AB :BF =1:2:3,若MN =8cm ,则线段EF 的长是( )A.10 cmB.11 cmC.12 cmD.13 cm2.如图所示,两个直角∠AOB ,∠COD 有公共顶点O ,下列结论:(1)∠AOC =∠BOD ;(2)∠AOC +∠BOD =90°;(3)若OC 平分∠AOB ,则OB 平分∠COD ;(4)∠AOD 的平分线与∠COB 的平分线是同一条射线.其中正确的个数是( )A.1B.2C.3D.43.下列说法正确的是( )①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的封面是长方形. A .①②B .①③C .②③D .①②③4.书架上,第一层的数量是第二层书的数量的2倍,从第一层抽8本到第二层,这时第一层剩下的数量恰比第二层的一半多3本,设第二层原有x 本,则可列方程( ) A.2x=12x+3 B.2x=12(x+8)+3 C.2x ﹣8= 12x+3 D.2x ﹣8=12(x+8)+3 5.把方程12x x --=225x +-去分母,正确的是( ) A.10x -5(x -1)=2-2(x +2) B.10x -5(x -1)=20-2(x +2)C.10x -5(x -1)=20-(x +2)D.10x -(x -1)=2-2(x +2)6.下列各题中,合并同类项结果正确的是( ) A.2a 2+3a 2=5a 2B.2a 2+3a 2=6a 2C.4xy-3xy=1D.2m 2n-2mn 2=07.如图,题中图形是用棋子按照一定规律摆成的,按照这种摆法,第n 个图形中共有棋子( )A .2n 枚B .(n 2+1)枚C .(n 2-n )枚D .(n 2+n )枚8.若x=-3是方程2(x-m )=6的解,则m 的值为( ) A.6B.6-C.12D.12-9.若x 1=时,3ax bx 7++式子的值为2033,则当x 1=-时,式子3ax bx 7++的值为( )A .2018B .2019C .2019-D .2018-10.下列说法正确的个数有( ) ①负分数一定是负有理数 ②自然数一定是正数 ③﹣π是负分数 ④a 一定是正数 ⑤0是整数 A .1个B .2个C .3个D .4个11.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则50!48! 的值为( ) A.5048B.49!C.2450D.2!12.若a 与b 互为相反数,则a ﹣b 等于( )A .2aB .﹣2aC .0D .﹣2 二、填空题13.一个正方体的六个面上分别标有1、2、3、4、5、6,根据图中从各个方向看到的数字,解答下面的问题:“?”处的数字是_____.14.上午9点钟的时候,时针和分针成直角,则下一次时针和分针成直角的时间是_____.15.整理一批图书,由一个人完成做40h 完成,现计划由一部分人先做4h ,然后增加2人与他们一起做8h ,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?设先安排人先做4h .据题意列出方程为_______________________16.一个长方形的长为xcm ,周长为30cm ,如果长减少2cm ,宽增加1cm ,那么整个长方形就成了一个正方形,则这个长方形的面积是_____cm 2. 17.若13x 2y m 与2x n y 6是同类项,则m+n= . 18.如图,某广场用正方形地砖铺地面,第一次拼成图(1)所示的图案,需要4块地砖;第二次拼成图(2)所示的图案,需要12块地砖,第三次拼成图(3)所示的图案,需要24块地砖,第四次拼成图(4)所示的图案,需要_____块地砖…,按照这样的规律进行下去,第n 次拼成的图案共用地砖_____块.19.若|-m|=2018,则m=_____.20.23=________.三、解答题21.已知:如图,∠AOB=2∠BOC=60°,OD是∠AOC的平分线,求∠BOD的度数.22.如图,AB、CD交于点O,OE⊥AB,且OC平分∠AOE.(1)如图1,求∠BOD的度数;(2)如图2,过O点作射线OF,且∠DOF=4∠AOF,求∠FOC的度数.23.食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输。

3.4.3 球赛中的积分问题知识要点1.比赛总场数=胜场数+平场数+________;2.比赛总积分=胜场积分+___________+负场积分基础训练1.小明在一场篮球比赛中,他一人得25分,如果他投3分球比投2分球少5个,而且他没投罚球,那么他投2分球_____个.2.爷爷和小磊下棋,爷爷胜一盘得1分,小磊胜一盘得3分,下了8盘,没有平局,而且两人得分相同,则小磊胜______盘.3.一次数学小测试共有25道选择题,评分标准如下:对一题得4分,错一题得-1分,不答得0分.小明不答的题比比答错的题多1道,他的得分是87分,则他答对_____道题.4.NBA的一场比赛中,姚明22投14中得28分,除了3个3分球全中外,他还投了____个2分球,_____个罚球.5.某市收取水费按以下规定:每户每月用水不超过20立方米,则每立方米收费1.2元;若超过20立方米,则超过部分每立方米收2元.如果某户居民某月所交水费为平均每立方米1.5元,那么他家这个月用水()A.28m³B.30m³C.32m³D.36m³6.康伟是校篮球小明星,在一场比赛中,他一人得21分,如果他投中的2分球比3分球多3个,没有罚球,那么他投的2分球的个数是()A.2B.3C.6D.77.某校九年级11个班开展篮球单循环赛(每班进行10场比赛).比赛规则是:每场比赛都要分出胜负,胜一场得3分,负一场得-1分,已知(2)班在所有的比赛中得14分,若设该班胜x场,则x应满足的方程是()A.3x+(10-x)=14 B.3x-(10-x)=14C.3x+x=14D.3x-x=148.小明和小丽出生于2002年12月,他们的生日不是同一天,但都是星期四,且小明出生日期早,两人出生日期的和是24,那么小丽的出生日期是()A.5号 B.15号C.19号D.20号基础训练9.一个两位数,十位上的数字比各位上的数字小1,十位和个位上的数字之和是这个两位数的51,求这个两位数。