第2章一阶动态电路的暂态分析

一阶动态电路分析在一阶动态电路分析中，通常需要考虑以下几个步骤：1.确定电路拓扑结构：首先需要确定电路中的元件和它们的连接方式，以建立电路的拓扑结构。

2.建立电路微分方程：根据电路中的元件和连接方式，可以通过基尔霍夫定律、欧姆定律等来建立电路的微分方程。

对于电容和电感元件，可以利用其电压和电流的关系（即电压-电流特性）得到微分方程。

- 对于电容元件，根据电容的定义（Q=C*dV/dt），可以得到微分方程：C*dV/dt = I，其中C为电容值，V为电容的电压，t为时间，I为电流。

- 对于电感元件，根据电感的定义（V=L*di/dt），可以得到微分方程：L*di/dt = V，其中L为电感值，i为电感的电流，t为时间，V为电压。

3.求解微分方程：根据所建立的微分方程，可以通过分离变量、积分等方法对方程进行求解。

求解过程中需要考虑初始条件，即在其中一时刻电容的电压或电感的电流的初始值。

4.分析电路响应：根据微分方程的解，可以得到电路中电容的电压或电感的电流随时间的变化曲线。

根据这些曲线可以分析电路的稳定状态、暂态响应和频率响应。

在分析电路响应时，可以根据不同的输入信号类型进行分类，常见的输入信号包括：-直流输入：当输入信号为直流信号时，可以将微分方程简化为代数方程进行求解。

此时电路响应主要包括稳态响应和过渡过程。

-正弦输入：当输入信号为正弦信号时，可以利用拉普拉斯变换将微分方程转换为代数方程。

通过求解代数方程和对频率的分析，可以得到电路的频率响应。

-脉冲输入：当输入信号为脉冲信号时，可以将微分方程进行离散化，转化为差分方程进行求解。

此时电路响应主要包括脉冲响应和响应序列的叠加。

总结来说，一阶动态电路分析是通过建立微分方程，求解微分方程，分析电路响应的一种方法。

通过这种方法，可以了解电路的稳定状态、暂态响应和频率响应等特性。

同时，对于不同类型的输入信号，还可以通过不同的数学工具和方法进行求解和分析。

这种分析方法可以广泛应用于电子电路、控制系统等领域的研究和应用中。

第1章 直流电路一、填 空 题1.4.1 与之联接的外电路；1.4.2 1-n ，)1(--n b ；1.4.3 不变；1.4.4 21W ，负载；1.4.5 Ω1.65A ，　；1.4.6 1A 3A ，　； 1.4.7 3213212)(3)23(R R R R R R R +++=； 1.4.8 1A ；1.4.9 Ω4.0，A 5.12；1.4.10 电压控制电压源、电压控制电流源、电流控制电压源、电流控制电流源；1.4.11 3A ；1.4.12 3A ；1.4.13 Ω2；1.4.14 15V ，Ω5.4；1.4.15 V 6S =U 。

二、单 项 选 择 题1.4.16 C ； 1.4.17 B ； 1.4.18 D ； 1.4.19 A ；1.4.20 A ； 1.4.21 C ； 1.4.22 B ； 1.4.23 D 。

第2章一阶动态电路的暂态分析一、填 空 题2.4.1 短路，开路；2.4.2 零输入响应；2.4.3 短路，开路；2.4.4 电容电压，电感电流；2.4.5 越慢；2.4.6 换路瞬间；2.4.7 三角波；2.4.8 s 05.0，k Ω25； 2.4.9 C R R R R 3232+； 2.4.10 mA 1,V 2。

二、单 项 选 择 题2.4.11 B ； 2.4.12 D ； 2.4.13 B ；2.4.14 D ； 2.4.15 B ； 2.4.16 C 。

第3章 正弦稳态电路的分析一、填 空 题3.4.1 ︒300.02s A 10，　，　； 3.4.2 V )13.532sin(25)(︒+=t t u ；3.4.3 容性， A 44；3.4.4 10V ，2V3.4.5 相同；3.4.6 V 30，20V ；3.4.7 A 44，W 7744；3.4.8 A 5；3.4.9 减小、不变、提高；3.4.10 F 7.87μ；3.4.11 20kVA ，12kvar -；3.4.12 带通，带阻3.4.13不变、增加、减少；3.4.14电阻性，电容性； 3.4.15 LC π21，阻抗，电流；3.4.16 1rad/s ，4；3.4.17 Ω10；3.4.18 P L U U =，P L 3I I =，︒-30； 3.4.19 P L 3U U =，P L I I =，超前。

电路的暂态分析(总18页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第8章电路的暂态分析含有动态元件L和C的线性电路，当电路发生换路时，由于动态元件上的能量不能发生跃变，电路从原来的一种相对稳态过渡到另一种相对稳态需要一定的时间，在这段时间内电路中所发生的物理过程称为暂态，揭示暂态过程中响应的规律称为暂态分析。

本章的学习重点：暂态、稳态、换路等基本概念；换路定律及其一阶电路响应初始值的求解；零输入响应、零状态响应及全响应的分析过程；一阶电路的三要素法；阶跃响应。

换路定律1、学习指导（1）基本概念从一种稳定状态过渡到另一种稳定状态需要一定的时间，在这一定的时间内所发生的物理过程称为暂态；在含有动态元件的电路中，当电路参数发生变化或开关动作等能引起的电路响应发生变化的现象称为换路；代表物体所处状态的可变化量称为状态变量，如i L和u C就是状态变量，状态变量的大小显示了储能元件上能量储存的状态。

（2）基本定律换路定律是暂态分析中的一条重要基本规律，其内容为：在电路发生换路后的一瞬间，电感元件上通过的电流i L和电容元件的极间电压u C，都应保持换路前一瞬间的原有值不变。

此规律揭示了能量不能跃变的事实。

（3）换路定律及其响应初始值的求解一阶电路响应初始值的求解步骤一般如下。

①根据换路前一瞬间的电路及换路定律求出动态元件上响应的初始值。

②根据动态元件初始值的情况画出t=0＋时刻的等效电路图：当i L(0＋)=0时，电感元件在图中相当于开路；若i L(0＋)≠0时，电感元件在图中相当于数值等于i L(0＋)的恒流源；当u C(0＋)=0时，电容元件在图中相当于短路；若u C(0＋)≠0，则电容元件在图中相当于数值等于105106u C (0＋)的恒压源。

根据t = 0＋时的等效电路图，求出各待求响应的初始值。

2、学习检验结果解析（1）何谓暂态何谓稳态您能说出多少实际生活中存在的过渡过程现象解析：在含有动态元件电容的电路中，电容未充电，原始储能为零时是一种稳态，电容充电完毕，储能等于某一数值时也是一种稳态。

实验四 一阶动态电路暂态过程的研究一. 实验目的1.研究一阶RC 电路的零输入响应、零状态响应和全响应的变化规律和特点。

2、研究一阶电路在阶跃激励和方波激励情况下, 响应的基本规律和特点。

测定一阶电路的时间常数 ,了解电路参数对时间常数的影响。

3.掌握积分电路和微分电路的基本概念。

4.研究一阶动态电路阶跃响应和冲激响应的关系。

5.学习用示波器观察和分析电路的响应。

二. 实验原理1.含有动态元件的电路, 其电路方程为微分方程。

用一阶微分方程描述的电路, 为一阶电路。

图6－1所示为一阶RC 电路。

首先将开关S 置于1使电路处于稳定状态。

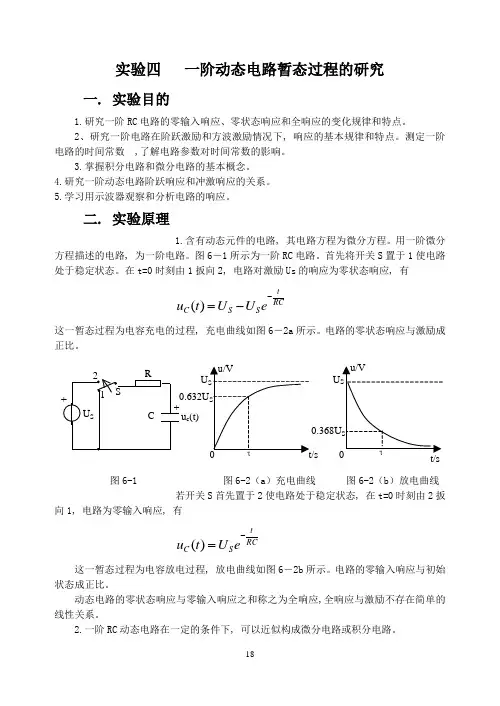
在t=0时刻由1扳向2, 电路对激励Us 的响应为零状态响应, 有RCt S S C eU U t u --=)(这一暂态过程为电容充电的过程, 充电曲线如图6－2a 所示。

电路的零状态响应与激励成正比。

U U u c (t) 图6-1 图6-2（a ）充电曲线 图6-2（b ）放电曲线若开关S 首先置于2使电路处于稳定状态, 在t=0时刻由2扳向1, 电路为零输入响应, 有RCt S C eU t u -=)(这一暂态过程为电容放电过程, 放电曲线如图6－2b 所示。

电路的零输入响应与初始状态成正比。

动态电路的零状态响应与零输入响应之和称之为全响应,全响应与激励不存在简单的线性关系。

2.一阶RC 动态电路在一定的条件下, 可以近似构成微分电路或积分电路。

当时间常数 (=RC)远远小于方波周期T 时, 图6－3(a)所示为微分电路。

输出电压u0(t)与方波激励uS(t)的微分近似成比例, 输入输出波形如6－3(b)所示。

从中可见, 利用微分电路可以实现从方波到尖脉冲波形的转变。

+ u O_uC图6－3（a ） 图6－3（b ）当时间常数 (=RC)远远大于方波周期T 时, 图6－4(a)所示为积分电路, 输出电压uO(t)与方波激励uS 的积分近似成比例。

输入、输出波形如图6－4(b)所示。

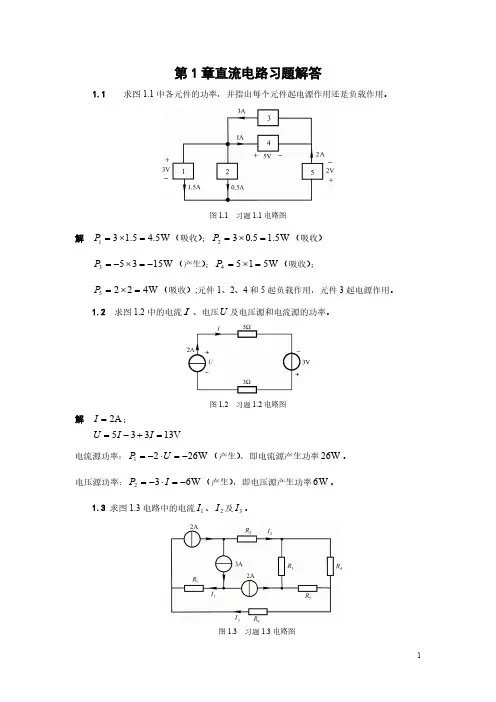
第1章直流电路习题解答1.1 求图1.1中各元件的功率，并指出每个元件起电源作用还是负载作用。

图1.1 习题1.1电路图解 W 5.45.131=×=P （吸收）；W 5.15.032=×=P （吸收） W 15353−=×−=P （产生）；W 5154=×=P （吸收）； W 4225=×=P （吸收）;元件1、2、4和5起负载作用，元件3起电源作用。

1.2 求图1.2中的电流I 、电压U 及电压源和电流源的功率。

图1.2 习题1.2电路图解 A 2=I ；V 13335=+−=I I U电流源功率：W 2621−=⋅−=U P （产生），即电流源产生功率6W 2。

电压源功率：W 632−=⋅−=I P （产生），即电压源产生功率W 6。

1.3 求图1.3电路中的电流1I 、2I 及3I 。

图1.3 习题1.3电路图解 A 1231=−=I ;A 1322−=−=I由1R 、2R 和3R 构成的闭合面求得：A 1223=+=I I 1.4 试求图1.4所示电路的ab U 。

图1.4 习题1.4电路图解 V 8.13966518ab −=×+++×−=U 1.5 求图1.5中的I 及S U 。

图1.5 习题1.5电路图解 A 7152)32(232=×+−×+−=IV 221021425)32(22S =+−=×+−×+=I U1.6 试求图1.6中的I 、X I 、U 及X U 。

图1.6 习题1.6电路图解 A 213=−=I ；A 31X −=−−=I I ; V 155X −=⋅=I UV 253245X X −=×−−⋅=I U1.7 电路如图1.7所示：（1）求图(a)中的ab 端等效电阻；（2）求图(b)中电阻R 。

图1.7 习题1.7电路图解 (1) Ω=+=+++×+×+×+=1046418666661866666ab R (2) Ω=−−=712432383R1.8 电路如图1.8所示：（1）求图(a)中的电压S U 和U ；（2）求图(b)中V 2=U 时的电压S U 。

4.5 一阶RC 电路的暂态过程分析一、实验目的1．学习用示波器观察和分析RC 电路的响应。

2．了解一阶RC 电路时间常数对过渡过程的影响，掌握用示波器测量时间常数。

3．进一步了解一阶微分电路、积分电路和耦合电路的特性。

二、实验原理1．一阶RC 电路的全响应=零状态响应+零输入响应。

当一阶RC 电路的输入为方波信号时，一阶RC 电路的响应可视为零状态响应和零输入响应的多次重复过程。

在方波作用期间，电路的响应为零输入响应，即为电容的充电过程；在方波不作用期间，电路的响应为零输入响应，即为电容的放电过程。

方波如图4.5.1所示。

图4.5.1 方波电压波形 图4.5.4 测常数和积分电路接线2．微分电路如图4.5.2所示电路，将RC 串联电路的电阻电压作为输出U 0，且满足τ ‹‹ t w 的条件，则该电路就构成了微分电路。

此时，输出电压U 0近似地与输入电压U i 呈微分关系。

dt du RC U i O 图4.5.2 微分电路和耦合电路接线 图4.5.3 微分电路波形微分电路的输出波形为正负相同的尖脉冲。

其输入、输出电压波形的对应关系如图4.5.3所示。

在数字电路中，经常用微分来将矩形脉冲波形变换成尖脉冲作为触发信号。

3．积分电路积分电路与微分电路的区别是：积分电路取RC 串联电路的电容电压作为输出U 0，如图4.5.4所不电路，且时间常数满τ ››t w 。

此时只要取τ＝RC ››t w ，则输出电压U 0近似地与输入电压U i 成积分关系，即⎰≈t i O d u RC U 1积分电路的输出波形为锯齿波。

当电路处于稳态时，其波形对应关系如图3.5.5所示。

注意：U i 的幅度值很小，实验中观察该波形时要调小示波器Y 轴档位。

图4.5.5 积分电路波形 图4.5.6 耦合电路波形4．耦合电路RC 微分电路只有在满足时间常数τ＝RC ‹‹ t w 的条件下，才能在输出端获得尖脉冲。

如果时间常数τ＝RC ››t w ，则输出波形已不再是尖脉冲，而是非常接近输出电压U i 的波形，这就是RC 耦合电路，而不再是微分电路。

第
4章
一阶线性电路的暂态分析 67
图4.2.5 RC 电路的零状态响应
4.2.2 一阶动态电路暂态分析的三要素法
通过前面的分析可知，零输入响应和零状态响应可看成是全响应的特例。

直流电源激励下的一阶动态电路中的电压或电流，其全响应总是由初始值开始，按指数规律变化而接近于稳态值。

则全响应f (t )可表示为
()()[(0)()]e t
f t f f f τ−+=+−∞∞ （4.2.12）
只要知道了初始值f (0+)、稳态值f (∞)和时间常数τ 这三个要素，就可以通过式（4.2.12）直接写出直流电源激励下的一阶动态电路的全响应，这种方法称为三要素法。

时间常数 L RC R ττ⎛⎞==⎜⎟⎝
⎠或，其中R 为等效电阻，是换路后从储能元件C （或L ）两端看进去的除源网络外的入端电阻，即戴维宁或诺顿等效电路的等效电阻。

三要素法具有方便、实用和物理概念清楚等特点，是求解一阶电路常用的方法。

例4.2.1 在图4.2.6（a ）所示的电路中，U S =180 V ，R 1=30Ω，R 2=60Ω，C =100μF ，电容初始电压为0，t =0时开关S 合上。

试求换路后的u C (t )
、i
1(t
)。

图4.2.6 例4.2.1题图
解：利用三要素法求解。

（1）求初始值u C (0+)、i 1(0+)
由换路定律知
u C (0+) = u C (0-) = 0
由于u C (0+ ) = 0，此时电容可视为短路，因此有换路后t = 0+时的等效电路，如图4.2.6（b ）所示。

则有。

第3章电路的暂态分析【教学提示】暂态过程是电路的一种特殊过程，持续时间一般极为短暂，但在实际工作中却极为重要。

本章介绍了电路暂态过程分析的有关概念和定律，重点分析了RC和RL一阶线性电路的暂态过程，由RC电路的暂态过程归纳出了一阶电路暂态分析的三要素法。

最后讨论了RC的实际应用电路一-积分和微分电路。

【教学要求】了解一阶电路的暂态、稳态、激励、响应等的基本概念理解电路的换路定律和时间常数的物理意义了解用经典法分析RC电路、RL电路的方法掌握一阶电路暂态分析的三要素法了解微分电路和积分电路的构成及其必须具备的条件3.1暂态分析的基本概念暂态分析的有关概念是分析暂态过程的基础，理解这些概念能更好地理解电路的暂态过程。

1•稳态在前面几章的讨论中，电路中的电压或电流，都是某一稳定值或某一稳定的时间函数，这种状态称为电路的稳定状态，简称稳态( steady state)。

2•换路当电路中的工作条件发生变化时，如电路在接通、断开、改接、元件参数等发生突变时，都会引起电路工作状态的改变，就有可能过渡到另一种稳定状态。

把上述引起电路工作状态发生变化的情况称为电路的换路(switching circuit )。

3•暂态换路后，电路由原来的稳定状态转变到另一个稳定状态。

这种转换不是瞬间完成的，而是有一个过渡过程，电路在过渡过程中所处的状态称为暂态( transient state)。

4•激励激励(excitation )又称输入，是指从电源输入的信号。

激励按类型不同可以分为直流激励、阶跃信号激励、冲击信号激励以及正弦激励。

5•响应电路在在内部储能或者外部激励的作用下，产生的电压和电流统称为响应。

按照产生响应原因的不同，响应又可以分为：(1)零输入响应(zero input response):零输入响应就是电路在无外部激励时，只是由内部储能元件中初始储能而引起的响应。

(2)零状态响应(zero state respo ns©:零状态响应就是电路换路时储能元件在初始储能为零的情况下，由外部激励所引起的响应。