一阶线性电路暂态分析的三要素法

第3章电路的暂态分析本章教学要求：1．理解电路的暂态和稳态、零输入响应、零状态响应、全响应的概念，以及时间常数的物理意义。

2．掌握换路定则及初始值的求法。

3．掌握一阶线性电路分析的三要素法。

4．了解微分电路和积分电路。

重点：1．换路定则；2．一阶线性电路暂态分析的三要素法。

难点：1．用换路定则求初始值；2．用一阶线性电路暂态分析的三要素法求解暂态电路；3．微分电路及积分电路的分析。

稳定状态：在指定条件下电路中电压、电流已达到稳定值。

暂态过程：电路从一种稳态变化到另一种稳态的过渡过程。

换路: 电路状态的改变。

如：电路接通、切断、短路、电压改变或参数改变。

电路暂态分析的内容：(1) 暂态过程中电压、电流随时间变化的规律。

(2) 影响暂态过程快慢的电路的时间常数。

研究暂态过程的实际意义：1. 利用电路暂态过程产生特定波形的电信号，如锯齿波、三角波、尖脉冲等，应用于电子电路。

2. 控制、预防可能产生的危害，暂态过程开始的瞬间可能产生过电压、过电流使电气设备或元件损坏。

3.1 电阻元件、电感元件及电容元件3.1.1 电阻元件 描述消耗电能的性质。

根据欧姆定律：u = R i ，即电阻元件上的电压及通过的电流成线性关系。

电阻的能量： 表明电能全部消耗在电阻上，转换为热能散发。

电阻元件为耗能元件。

3.1.2 电感元件描述线圈通有电流时产生磁场、储存磁场能量的性质。

电流通过一匝线圈产生 （磁通），电流通过N 匝线圈产生（磁链），电感： ，L 为常数的是线性电感。

自感电动势：其中：自感电动势的参考方向及电流参考方向相同，或及磁通的参考方向符合右手螺旋定则。

根据基尔霍夫定律可得：0d d 00≥==⎰⎰t Ri t ui W t2tΦN Φψ=tiL t ψe d d d )d(d )d(d d -=-=-=-=t Li t N ΦL 21ti将上式两边同乘上 i ，并积分，则得：磁场能W =即电感将电能转换为磁场能储存在线圈中，当电流增大时，磁场能增大，电感元件从电源取用电能；当电流减小时，磁场能减小，电感元件向电源放还能量。

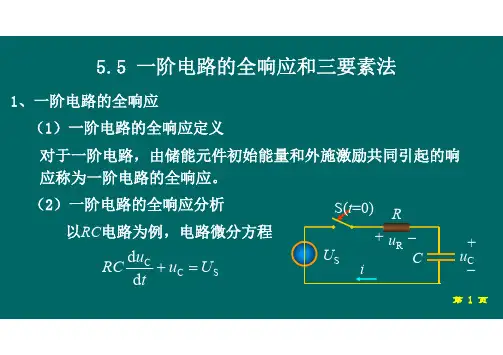
8.4 RC和RL电路的暂态过程8.4.1 储能元件和换路定则8.4.2 一阶线性电路暂态分析的三要素法电容电路： )0()0(-+=C C u u 注：换路定则仅用于换路瞬间来确定暂态过程中 u C 、 i L 初始值。

设：t=0 — 表示换路瞬间 (定为计时起点)t =0-—表示换路前的终了瞬间t=0+—表示换路后的初始瞬间（初始值）1.换路定则电感电路：)0()0(-+=L L ιι2.初始值的确定求解要点：初始值：电路中各 u 、i 在 t =0+ 时的数值。

(1) u C ( 0+)、i L ( 0+) 的求法。

1) 先由t =0-的电路求出 u C ( 0– ) 、i L ( 0– )；2) 根据换路定律求出 u C ( 0+)、i L ( 0+) 。

暂态过程初始值的确定 例1．解： (1)由换路前电路求 )0(),0(--L C i u 由已知条件知 0000==--)(,)(L C i u 根据换路定则得： 0)0()0(==-+C C u u 0)0()0(==-+L L ιι 已知：换路前电路处稳态，C 、L 均未储能。

试求：电路中各电压和电流的初始值。

C R 2 S (a)U R 1 t =0 + - L暂态过程初始值的确定 例1: 00=-)(C u , 换路瞬间，电容元件可视为短路。

00=-)(L ι , 换路瞬间，电感元件可视为开路。

R U C ==++)()(001ιι )0)0((=-C ι 0)0(2=+u U u u L ==++)0()0(1)0)0((=-L u i C 、u L 产生突变 (2) 由t =0+电路，求其余各电流、电压的初始值 C R 2 S (a) U R 1 t =0 + -L i L (0+ ) U i C (0+ ) u C (0+) u L (0+) _ u 2(0+) u 1(0+) i 1(0+ ) R 2 R 1 + + + _ _ + - (b) t = 0+等效电路结论1.换路瞬间，u C、i L不能跃变, 但其它电量均可以跃变。

第三章 电路的暂态分析含有电感或电容储能元件的电路，在换路时会出现暂态过程。

本章研究了暂态过程中电压与电流的变化规律。

主要内容：1．暂态过程的基本概念。

2．换路定则：在换路瞬间，电容电流和电感电压为有限值的情况下，电容电压 和电感电流在换路前后的瞬间保持不变。

3．RC 电路的零输入响应、零状态响应和全响应。

4．RL 电路的零输入响应、零状态响应和全响应。

5．一阶线性电路暂态分析的三要素法：一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。

6．暂态过程的应用：对于RC 串联电路，当输入矩形脉冲，若适当的选择参数 和输出，可构成微分电路或积分电路。

[练习与思考]解答3-1-1什么是稳态？什么是暂态？解：当电路的结构、元件参数及激励一定时，电路的工作状态也就一定，且电流和电压为某一稳定的值，此时电路所处的工作状态就称为稳定状态，简称为稳态。

在含有储能元件的电路中，当电路的发生换路时，由于储能元件储的能量的变化，电路将从原来的稳定状态经历一定时间变换到新的稳定状态，这一变换过程称为过渡过程，电路的过渡过程通常是很短的，所以又称暂态过程。

3-1-2什么是暂态过程？产生暂态过程的原因是什么？解：含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程（过渡过程）。

暂态过程产生的内因是电路中含有储能元件，外因是电路发生换路。

3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值？解：初始值是暂态过程的+=0t 时刻的值，稳态值是暂态过程的∞=t 时刻的值。

3-2-2 如何求暂态过程的初始值？解：求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路，求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。

对直流电路，如果换路前电路处于稳态，则电容相当于开路，电感相当于短路。

线性含源电阻网络C 线性含源电阻网络L C u+-C R ocu 1. 三要素公式的推导oc 0d d (0)C C C u RC u u t u U +⎧+=⎪⎨⎪=⎩sc 0d d (0)L L L i GL i i t i I +⎧+=⎪⎨⎪=⎩sc i L L i G 0d ()()()d (0)f t f t g t t f F τ+⎧+=⎪⎨⎪=⎩RC τ=/GL L Rτ==或p h ()()()f t f t f t =+d ()()0d f t f t tτ+=/p ()e t f t A τ-=+定Ap (0)(0)f f A ++=+p (0)(0)A f f ++=-定解 /p p ()()[(0)(0)]e t f t f t f f τ-++=+-三要素公式 三要素 (1) 初始值 (0)f +(2) 特解 p ()f t (3) 时间常数 τ2. 三要素中特解的求取方法(1) 换路后电路中无独立电源时 p ()0f t =(2) 换路后电路为直流激励时，换路后电路可 达到新的稳态，特解是稳态解且是恒定量。

p p ()(0)()f t f f +==∞/()()[(0)()]e t f t f f f τ-+=∞+-∞(3) 换路后电路为正弦交流电源时，换路后电 路可达到新的稳态，特解是稳态解，是与 电源同频率的正弦量，可用相量法求得。

(4) 换路后电路为非正弦周期性电源时，换路后电路可达到新的稳态，特解是稳态解，并且是非正弦周期量，可用叠加定理求得。

(5) 换路后电路为非上述激励源情况时，电路不一定能达到新的稳态，这时特解不是稳态解。

f t()决定于独立源g t()与初值无关；p有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）)(t g p ()f t )/1(e τ≠-b K bt bt A -e )/1(e τ=-b K bt bt Bt A -+e)(cos()K t ωϕ+cos()A t ωθ+ 形式形式 KA KtA+Bt Kt 2A+Bt+Ct 2 p ()f t ()g t 强制量与 的对应关系。

一阶线性电路暂态分析的三要素法
仅含一个储能元件或可等效为一个储能元件的线性电路, 且由一阶微分方程描述，称为一阶线性电路。

在直流电源激励的情况下，一阶线性电路微分方程解的通用表达式：
式中, f(t) 代表一阶电路中任一电压、电流函数
利用求三要素的方法求解暂态过程，称为三要素法。

一阶电路都可以应用三要素法求解，在求得、和t 的基础上, 可直接写出电路的响应( 电压或电流) 。

电路响应的变化曲线
三要素法求解暂态过程的要点
(1) 求初始值、稳态值、时间常数；
(2) 将求得的三要素结果代入暂态过程通用表达式；
(3) 画出暂态电路电压、电流随时间变化的曲线。

响应中“三要素”的确定
(1) 稳态值f(∞) 的计算
求换路后电路中的电压和电流，其中电容 C 视为开路, 电感L 视为短路，即求解直流电阻性电路中的电压和电流。

(2) 初始值f(0+)的计算
(3) 时间常数t 的计算
注意：
1) 对于简单的一阶电路，R 0 = R ;
2) 对于较复杂的一阶电路，R 0 为换路后的电路除去电源和储能元件后，在储能元件两端所求得的无源二端网络的等效电阻。