多边形面积练习题及答案

北师大版五年级数学上册第四单元《多边形的面积》练习题及答案一、我会填1.一个平行四边形的底是12 cm,高是8 cm,这个平行四边形的面积是( )cm2,与它等底等高的三角形的面积是( )cm2。

2.有一张上底是7 cm,下底是12 cm,高是8 cm的梯形纸片,现在要把这张纸片的一面涂上红色,涂色部分的面积是( )cm2。

3.把一个平行四边形的底扩大到原来的3倍,高不变,得到的平行四边形的面积是原来的( )倍。

4.一个三角形的面积是24 dm2,底是8 dm,它的高是( ),一个平行四边形的面积和底都与这个三角形相等,这个平行四边形的高是( )。

5.一张三角形纸片的底是9 cm,底是高的1.5倍,这张三角形纸片的面积是( )。

二、我会判断(对的在括号里画“√”,错的画“✕”)1.两个面积相等的三角形可以拼成一个平行四边形。

( ）2.直角三角形只有一条高。

( )3.把一个平行四边形框架拉成一个长方形框架,面积会变大。

( )4.面积相等的两个平行四边形,它们的底和高一定都相等。

( )5.平行四边形的面积是梯形面积的2倍。

( )三、我会选(把正确答案的序号填在括号里)1.下图中阴影部分的面积与空白部分的面积相比,( )。

A. 阴影部分的面积大B. 空白部分的面积大C. 一样大2.一个梯形的上底与下底的总和是12 dm,高是5 dm,它的面积是( )dm2。

A. 30B. 60C. 1203.平行四边形有( )条高。

A. 1B. 2C. 无数4.把一个三角形的底扩大到原来的2倍,高扩大到原来的4倍,面积会扩大到原来的( )倍。

A. 6B. 8C. 25.( )图形与其余2个的面积不一样大。

四、求出下列图形的面积五、请在下面的方格纸中画出一个三角形、一个平行四边形和一个梯形,使它们的面积都是6cm2。

(每个方格表示1cm2)六、解决问题1.一块平行四边形菜地的面积是600平方米,它的底是15米,这块菜地的高是多少米?2.在公路中间有一块直角三角形的草坪(如下图),1平方米草坪的价格是12元,种这块草坪需要多少钱?3.一个果园的形状近似梯形,它的上底是120米,下底是180米,高是80米,如果每棵果树占地10平方米,这个果园共有多少棵果树?4.下图中梯形的面积是360 cm2。

人教版五年级上册数学第六单元《多边形面积》同步练习一.选择题1.如图,一个长方形分成甲、乙两部分,下面说法正确的是（）。

A.甲、乙周长相等,面积不相等B.甲、乙周长和面积都不相等C.甲、乙周长和面积都相等2.图中,甲、乙两点分别为长方形宽的中点,那么图中面积相等的所有三角形是（）。

A.A、B、CB.A、BC.B、C3.一个三角形和一个平行四边形面积相等,底也相等,若平行四边形的高是6厘米,则三角形的高是（）厘米。

A.3B.6C.124.两个完全一样的平行四边形拼在一起,可以拼成（）。

A.长方形B.梯形C.平行四边形5.在一个长方形内画一个最大的三角形,这个三角形的面积（）长方形面积的一半。

A.大于B.小于C.等于二.判断题1.等底等高平行四边形的面积是三角形面积的2倍。

（）2.我们可以用割补的方法将三角形转化成平行四边形,推导出三角形的面积计算公式。

（）3.如果两个三角形的面积相同,那么它们的形状一定相同。

（）4.两个完全一样的直角梯形既可以拼成一个长方形也可以拼成一个梯形。

（）5.在一个长方形内,画一个最大的三角形,这个三角形的面积等于长方形面积的一半。

（）三.填空题1.梯形的上底是8分米,下底与高相等,都是10分米,它的面积是（）平方分米。

2.两个完全一样的等腰梯形可以拼成一个（）。

3.拼成平行四边形的两个三角形（）。

4.一块平行四边形草坪的面积是105平方米,测得它的高是2.5m,这块草坪的底边长是（）m。

5.比较图形面积的大小．(单位：厘米)_____最大_____最小_____和_____相等。

四.解答题1.一堆水泥电线杆堆成一个梯形,最上层有4根,最下层有12根,一共有9层。

两堆这样的电线杆一共有多少根？2.一个正方形花坛的周长是4.8米,与这个正方形花坛面积相等的一块三角形底边长1.2米,那么高是多少？3.如图是一块长方形草地,长16m、宽10m,中间有两条路,一条是平行四边（一边长2m）,一条是长方形（宽2m）。

多边形的面积练习3.梯形的面积等于上底与下底的和乘高。

( ) 一、填空。

4.梯形的上、下底越长，面积就越大。

1.一个平行四边形的底是1.2米，面积是15平方米，这个平行四边形对应底边上的高是( )米。

2.一个三角形的底扩大到原来的5倍，高() 5.计算组合图形的面积时，可以把组合图形分成几个简单的图形，然后再进行计算。

( )缩小到原来的,它的面积( )。

6.周长相等的长方形与平行四边形，面积也相等。

( )50平方千米=( )公顷4.在一个长方形内画一个面积最大的三三、求下图中阴影部分的面积。

(单位：角形，这个三角形的面积等于长方形面厘米)积的( )。

1.5.一个梯形的下底是15分米，上底和高相等，都是12分米，它的面积是( )平方分米。

6.一个梯形的上底、下底和高同时扩大到原来的5倍，这个梯形的面积扩大到原来的( )倍。

7.一个直角梯形的下底是8cm, 如果把上底增加3cm, 它就变成了一个正方形。

这个梯形的面积是( )cm²。

二、判断。

(对的打“√”,错的打“×”)1.两个面积相等的梯形一定能拼成一个平行四边形。

( )2.任何一个梯形都可以分成两个等高的三角形。

( )3 .3公顷=( )平方米四、图中每个小方格的面积是1cm ², 估算老虎头像的面积。

( )cm²五、解决问题。

1.王师傅开垦了一块平行四边形的草地， 它的高是80米，底是125米，这块草地 的面积是多少公顷?2.一块梯形菜地，它的上底是100米，下 底是140米，高是80米，平均每平方米 种的蔬菜收入1.5元，这块菜地可以收 入多少元?4.公园里有两块空地，计划分别种玫瑰和 牡丹。

玫瑰每棵占地0.5m², 每棵6元；牡丹每棵占地1.2m², 每棵10元。

玫瑰 园占地多少平方米?种玫瑰一共需要 多少元?六、拓展题。

如图，已知三角形ABC 的面积是 32.4cm², 是三角形EFB 面积的3倍。

多边形的面积综合练习题学校:___________姓名：___________班级：___________考号：___________一、选择题1．梯形的面积为S，上底为a，下底为b，高为（）。

A．S÷（a＋b）B．S÷（a＋b）÷2C．S×2÷（a＋b）2．梯形的上底是3.8厘米，高是4厘米，已知它的面积是20平方厘米，下底是() A．6.2厘米B．3.1厘米C．1.2厘米3．一个平行四边形操场的底是150米，高是20米，它的面积是（）平方米。

A．30B．300C．30004．在两条平行线之间有三个不同的图形（如下图），把它们按面积从小到大的顺序排列是（）。

A．①＜①＜①B．①＜①＜①C．①＜①＜①D．①＜①＜①二、填空题5．如下图，大平行四边形的底是20厘米，底上的高是10厘米，小平行四边形的顶点是大平行四边形各边上的中点，小平行四边形的面积是( )平方厘米。

6．如图，每个小正方形的面积是1cm2，请你数一数，图形E的面积是( )cm2。

（不满1格的按半格算）7．一个平行四边形与一个三角形等底，若三角形的面积是256dm2，且平行四边形的高是三角形的3倍，则平行四边形的面积是( )dm2。

8．学校有一条长60米的小道，计划在道路的一旁栽树，每隔3米栽一棵，如果两端都各栽一棵树，那么共需( )棵树苗；如果两端都不栽树，那么共需( )棵树苗；如果只有一端栽树，那么共需( )棵树苗。

9．梯形上底为a，下底为b，高为h，则梯形的面积S＝________。

10．一个三角形的面积是S平方厘米，高是5厘米，它的底是( )厘米。

11．一个直角三角形的三条边分别是6厘米、8厘米和10厘米，这个三角形的面积是( )平方厘米。

三、判断题12．一个直角三角形的面积是30cm2，一条直角边长10cm，则另一条直角边长3cm。

( )13．上底和下底都相等的梯形面积不一定相等。

多边形的面积练习题及答案一、选择题1. 下列哪个图形是不规则多边形？A. 正方形B. 三角形C. 长方形D. 梯形2. 以下哪个公式可用于计算正方形的面积？A. S = a * bB. S = 1/2 * a * bC. S = a^2D. S = (a + b) * h3. 如图所示，一块田地被修建成了如下图形，哪个图形的面积最大？A. 正方形B. 正三角形C. 圆形D. 正五边形二、计算题1. 计算下列多边形的面积：a) 一个正方形的边长为5cm;b) 一个边长为6cm的正三角形;c) 一个边长分别为4cm和6cm，高为3cm的梯形;d) 一个有6个边，每个边长为4cm的正六边形。

2. 计算下述图形的面积，保留两位小数：a) 一个边长为9cm的正方形的周长为36cm;b) 一个边长为6cm的正三角形的外接圆半径为10cm。

三、解答题1. 如图所示，一个边长为6cm的正方形被切割成4个等边三角形和1个小正方形，请计算小正方形的面积。

[示意图]2. 已知一个正方形的面积为36cm²，求其边长。

[解答]四、答案1. 选择题1. B2. C3. C2. 计算题1.a) 正方形的面积为 S = a^2 = 5^2 = 25cm²b) 正三角形的面积为 S = (sqrt(3) / 4) * a^2 = (sqrt(3) / 4) * 6^2 =9sqrt(3) cm² (约为 15.59cm²)c) 梯形的面积为 S = (a + b) * h / 2 = (4 + 6) * 3 / 2 = 15cm²d) 正六边形的面积为 S = (3 * sqrt(3) / 2) * a^2 = (3 * sqrt(3) / 2) * 4^2 = 24sqrt(3) cm² (约为 41.57cm²)2.a) 正方形的边长为 9cm / 4 = 2.25cm，面积为 2.25^2 = 5.06cm²b) 正三角形的外接圆半径为 a / (2sqrt(3)) = 6 / (2sqrt(3)) = 1.73cm，面积为(sqrt(3) / 4) * (2.66)^2 ≈ 6cm²三、解答题1. 小正方形的边长等于等边三角形的边长，即6cm，所以小正方形的面积为 6^2 = 36cm².2. 已知正方形的面积为36cm²，设其边长为 a，则 a^2 = 36，解得 a = 6cm，所以正方形的边长为6cm。

一、单选题1.把一个平行四边形拉成一个长方形，周长不变，面积（）。

A. 变小了B. 变大了C. 不变D. 不确定2.( )的两个梯形一定能拼成一个平行四边形。

A. 面积相等B. 周长相等C. 完全相同D. 任意3.如图，从两张完全相同的梯形纸上剪下一个平行四边形和一个长方形，剪下的图形的面积（）A. 平行四边形的大B. 长方形的大C. 一样大D. 无法判断4.一个梯形的上底增加2厘米，下底减少2厘米，高不变，这时的面积与原来的面积相比( )。

A. 变大了B. 变小了C. 不变D. 不知道高，所以无法比较二、判断题5.两个面积相等的梯形可以拼成一个平行四边形．（）6.一个梯形的上、下底和高都扩大到原来的2倍，这个梯形的面积扩大到原来的8倍。

（）7.面积相等的两个平行四边形的形状一定一样。

（）8.两个完全一样的梯形可以拼成一个平行四边形．（）三、填空题9.下面平行四边形的面积________．10.一个梯形，上底是2.4分米，下底是3.6分米，高是1.5分米，这个梯形的面积是________平方分米11.求图中阴影部分的面积为________ (结果保留π)．12.如图，一个平行四边形被分成了四个小平行四边形，其中三个的面积分别是5平方厘米、8平方厘米、10平方厘米，第四个小平行四边形的面积是________平方厘米．四、解答题13.如果现在有个三年级小朋友请教你：为什么梯形的面积S=（a+b）×h÷2。

你会怎样做一个小老师，帮助他推导出梯形的面积计算公式呢？请你以下面直角梯形为例写出两种不同角度的三角形面积推导过程。

14.计算图形的面积五、应用题15.求下图阴影面积．(单位：分米)参考答案一、单选题1.【答案】B【解析】【解答】把一个平行四边形拉成一个长方形，周长不变，面积变大了.故答案为：B.【分析】把一个平行四边形拉成一个长方形，拉伸后底不变，高变大，根据公式S=ah，所以面积变大，据此解答.2.【答案】C【解析】【解答】完全相同的两个梯形一定能拼成一个平行四边形.故答案为：C.【分析】根据梯形面积公式可知，两个完全一样的梯形，将其中一个倒置，就可以拼成一个平行四边形，据此解答.3.【答案】C【解析】【解答】解：剪下的图形的面积相等。

北师大版五年级上册数学第四单元《多边形的面积》练习题一、选择题1．一个三角形的面积是36cm2，底是6cm，高是（）cmA．6 B．8 C．10 D．122．一个平行四边形，底不变，高扩大到原来的2倍，它的面积（）A．扩大到原来的2倍B．扩大到原来的4倍C．缩小到原来的1 23．把三角形的底和高都扩大为原来的2倍，则面积扩大为原来的（）倍。

A．2 B．4 C．6 D．84．一个梯形的面积是36cm2，它的高是4cm，上底是6cm，下底是（）cm A．9 B．12 C．14 D．165．一个平行四边形的两条边分别为12厘米和8厘米，其中一条边上的高是10厘米，这个平行四边形的面积是（）平方厘米。

A．96 B．120 C．80 D．80或1206．下图平行线中三个图形的面积（）A．都相等B．三角形面积大C．梯形面积小D．平行四边形面积大二、填空题7．一个直角三角形的两条直角边分别是3cm和4cm，斜边长5cm，这个直角三角形的面积是( )cm2，斜边上的高是( )cm8．一个平行四边形的面积是60cm2，底是10cm，高是( )cm9．一个平行四边形的面积是60dm2，底是5dm，这条底边对应的高是( )dm 10．一个平行四边形的底和高都是8分米，它的面积是( )平方分米，和它等底等高的三角形的面积是( )平方分米。

11．梯形的上底变为原来的2倍，下底也变为原来的2倍，高不变，它的面积就变为原来的( )倍。

12．一个梯形的高是8cm，在它的同一侧给上底和下底都增加3cm，则梯形面积增加( ) 13．一个平行四边形的底是4cm，高是6cm，它的面积是( )，与它等底等高的三角形的面积是( )14．一个平行四边形的面积是30cm2，高扩大2倍，底不变，面积是( )cm215．一个三角形的面积是48cm2，与它等底等高的平行四边形的面积是( )cm2 16．在一个底是12厘米，高是8厘米的平行四边形纸片中剪一个最大的三角形，这个三角形的底是( )厘米，高是( )厘米，面积是( )平方厘米。

人教版五年级上册数学《多边形的面积》专项练习（含答案）1.填空题。

（1）用两个完全一样的梯形拼成一个底是5.4cm，高是2.5cm的平行四边形，每个梯形上、下底的和是（）cm，面积是（）cm2。

（2）一个三角形的面积是18.2cm2，底是5.2cm，它的高是（）cm。

（3）如图，平行四边形的面积与三角形的面积相等。

如果AB＝6cm，那么CD＝（）cm。

（4）一个三角形的面积比和它等底等高的平行四边形的面积少 3.8dm2，这个平行四边形的面积是（）dm2。

（5）把一个长、宽分别是15cm和10cm的长方形，拉成一个高是12cm的平行四边形，它的面积是（）cm2。

2.计算下列各图形的面积。

（单位：dm）3.判断题。

（1）三角形的底和高都扩大到原来的2倍，它的面积就扩大到原来的4倍。

（）（2）拼成一个平行四边形的两个梯形一定完全相同。

（）（3）下面面积相等的平行四边形、长方形和等腰三角形中，阴影部分面积相等。

（）（4）面积相等的长方形和平行四边形，长方形的周长长一些。

（）4.填空题。

（1）如图，梯形的下底是上底的2倍，把这个梯形分成一个平行四边形和一个三角形。

如果这个梯形的面积是18cm2，那么平行四边形的面积是（）cm2，三角形的面积是（）cm2。

（2）如图，正方形的周长是80dm，那么阴影部分平行四边形的面积是（）dm2。

5.选择题。

（1）如图，梯形ABCD中，D共有8个三角形，其中面积相等的三角形有（）对。

A.1B.2C.3D.4（2）在下列各图形中，每个小正方形的边长都是1cm，则图中阴影部分面积最大的是（）。

（3）一个直角梯形上、下底之和是20分米，两腰分别长6分米和10分米。

求这个梯形面积，正确列式是（）。

A.20×6÷2B.20×10÷2C.（6＋10）×20÷26.小红家有一块三角形麦田，底是600米，高是240米，今年她家共收获小麦48.6吨，平均每公顷收小麦多少吨？7.如图，已知阴影部分的面积是35cm2，求图中三角形的面积。

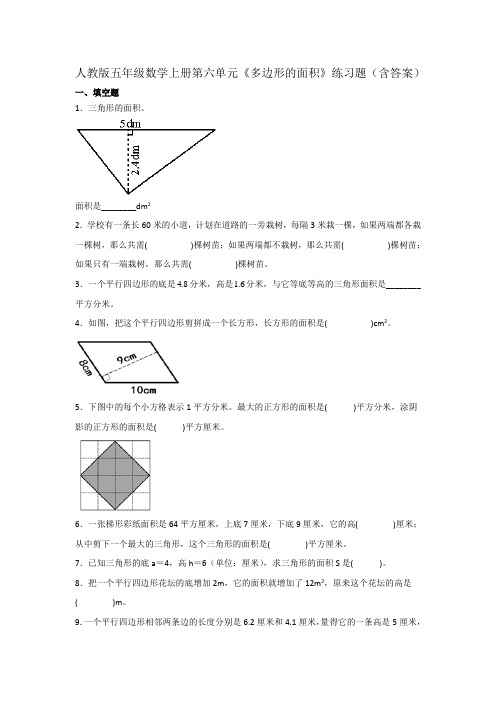
人教版五年级数学上册第六单元《多边形的面积》练习题（含答案）一、填空题1．三角形的面积。

面积是________dm22．学校有一条长60米的小道，计划在道路的一旁栽树，每隔3米栽一棵，如果两端都各栽一棵树，那么共需( )棵树苗；如果两端都不栽树，那么共需( )棵树苗；如果只有一端栽树，那么共需( )棵树苗。

3．一个平行四边形的底是4.8分米，高是1.6分米，与它等底等高的三角形面积是________平方分米。

4．如图，把这个平行四边形剪拼成一个长方形，长方形的面积是( )cm2。

5．下图中的每个小方格表示1平方分米。

最大的正方形的面积是( )平方分米，涂阴影的正方形的面积是( )平方厘米。

6．一张梯形彩纸面积是64平方厘米，上底7厘米，下底9厘米，它的高( )厘米；从中剪下一个最大的三角形，这个三角形的面积是( )平方厘米。

7．已知三角形的底a＝4，高h＝6（单位：厘米），求三角形的面积S是( )。

8．把一个平行四边形花坛的底增加2m，它的面积就增加了12m2，原来这个花坛的高是( )m。

9．一个平行四边形相邻两条边的长度分别是6.2厘米和4.1厘米，量得它的一条高是5厘米，这个平行四边形的面积是( )平方厘米。

10．一个三角形的底是8分米，高是3分米，与它等底等高的平行四边形的面积是( )平方分米。

二、判断题11．图中甲、乙两个三角形的面积相等。

( )12．梯形的面积等于上底加下底乘高除以2。

( )13．面积相等的两个三角形，周长可能不相等。

( )14．把一个木条钉成的平行四边形拉成长方形，它的面积变大了，周长没变。

( ) 15．两个等底等高的三角形，面积相等，形状也一定完全相同。

( )三、选择题16．在下图中，三个图形A、B、C的面积，图形面积最大的是（）。

A．A B．B C．C17．每个小方格面积是1平方厘米，估测下面不规则图形的面积大约是（）平方厘米。

A．20 B．50 C．11 D．3518．一条红领巾的面积是1650平方厘米，它的高是33厘米，则它的底是（）厘米。

多边形面积练习题答案一、选择题1. 下列哪个公式可以用来计算三角形的面积？A. 底×高÷2B. 底×高C. 周长×半径D. 底×高×2答案：A2. 一个平行四边形的底是10厘米，高是5厘米，它的面积是多少平方厘米？A. 25B. 50C. 75D. 100答案：B3. 一个正六边形的边长是a，它的面积可以用以下哪个公式表示？A. 6a²B. 3√3a²C. 2√3a²D. √3a²答案：B二、填空题1. 如果一个梯形的上底是3厘米，下底是7厘米，高是4厘米，那么它的面积是________平方厘米。

答案：202. 一个正五边形的外接圆半径是r，它的面积是________。

答案：(5/4)r²√5π三、计算题1. 一个正三角形的边长是6厘米，求它的面积。

解：根据正三角形面积公式，面积 = (边长²√3) / 4。

代入边长6厘米，面积 = (6²√3) / 4 = 54√3 / 4 = 27√3 平方厘米。

2. 一个矩形的长是15厘米，宽是8厘米，求它的面积。

解：矩形面积 = 长× 宽。

代入长15厘米，宽8厘米，面积= 15 × 8 = 120 平方厘米。

四、解答题1. 一个不规则四边形，已知它的四个顶点坐标分别是A(1,2)，B(4,6)，C(7,3)，D(4,0)。

求这个四边形的面积。

解：首先，我们可以将这个四边形分割成两个三角形，例如三角形ABD和三角形BCD。

然后分别计算这两个三角形的面积，最后将它们相加。

对于三角形ABD，底AD = 3厘米，高为从A到BD的垂直距离，即2厘米，面积= 3 × 2 ÷ 2 = 3平方厘米。

对于三角形BCD，底CD = 3厘米，高为从C到BD的垂直距离，即3厘米，面积= 3 × 3 ÷ 2 = 4.5平方厘米。

苏教版五年级上册数学第二单元多边形的面积一、选择题1．国家体育场“鸟巢”的占地面积大约是（）A．21平方分米B．21平方米C．21公顷D．21平方千米2．一个梯形上底与下底都扩大到原来的3倍，高不变，它的面积就扩大到原来的（）倍。

A．6 B．3 C．9 D．123．在一个平行四边形中剪去一个最大的三角形，余下的面积与剪去的面积比较（）A．余下的面积大B．剪去的面积大C．一样大D．无法比较4．一个长方形的长去掉4厘米后，面积就减少了20平方厘米，剩下的部分正好是一个正方形，原来的长方形的面积是（）平方厘米。

A．25 B．45 C．5 D．205．周长相等的长方形和正方形，（）的面积大一些。

A．长方形B．正方形C．不一定6．一个直角三角形的三条边长分别是8厘米，10厘米，6厘米，斜边上的高是（）A．4.8厘米B．5厘米C．2.4厘米7．一块直角三角形菜地，三条边长分别是30米、40米、50米，这块菜地的面积是（）A．1200平方米B．1000平方米C．600平方米D．250平方米8．下图中有（）个四边形。

A．4 B．5 C．9二、填空题9．在括号里填上适当的面积单位。

（1）足球场的面积是8000( )（2）天安门广场是中国最大的广场，它占地44( )（3）香港特别行政区的面积大约是1100( )10．0.07升＝( )毫升25平方米＝( )公顷68克＝( )千克3分米5厘米＝( )米11．一个平行四边形的底是1.6分米，高是4分米，平行四边形的面积是( )平方分米。

12．一个长方形的长是18分米，宽是12分米，在这个长方形里画一个最大的三角形，三角形的面积是( )平方分米。

13．已知梯形的下底长是上底长的2倍，高为5厘米，面积为15平方厘米，那么梯形的上底长是( )厘米。

14．一个平行四边形，底为10分米，高为4分米，如果底不变，高增加2分米，那么面积增加( )平方分米。

15．一个梯形的面积是60平方厘米，上底是8厘米，下底是12厘米，高是( )厘米。

多边形面积练习题及答案一、选择题1. 一个平行四边形的底是8米，高是5米，它的面积是（）平方米。

A. 30B. 40C. 50D. 602. 一个三角形的底是10厘米，高是6厘米，它的面积是（）平方厘米。

A. 30B. 40C. 50D. 603. 一个梯形的上底是4厘米，下底是8厘米，高是5厘米，它的面积是（）平方厘米。

A. 20B. 25C. 30D. 354. 一个圆的半径是3厘米，它的面积是（）平方厘米。

A. 28.26B. 36C. 45D. 545. 一个长方形的长是12米，宽是5米，它的面积是（）平方米。

A. 50B. 60C. 72D. 80二、填空题6. 如果一个平行四边形的面积是60平方米，底是15米，那么它的高是________米。

7. 一个三角形的面积是48平方厘米，底是12厘米，那么它的高是________厘米。

8. 一个梯形的面积是40平方厘米，上底是6厘米，下底是10厘米，那么它的高是________厘米。

9. 一个圆的面积是78.5平方厘米，它的半径是________厘米。

10. 一个长方形的面积是180平方米，长是15米，那么它的宽是________米。

三、计算题11. 计算下列多边形的面积：- 平行四边形：底=10米，高=6米。

- 三角形：底=8米，高=4米。

- 梯形：上底=5米，下底=10米，高=3米。

- 圆：半径=4米。

- 长方形：长=20米，宽=6米。

12. 已知一个平行四边形的面积是100平方米，底是20米，求高。

13. 已知一个三角形的面积是75平方厘米，底是15厘米，求高。

14. 已知一个梯形的面积是150平方厘米，上底是10厘米，下底是20厘米，求高。

15. 已知一个圆的面积是314平方厘米，求半径。

16. 已知一个长方形的面积是360平方米，长是24米，求宽。

四、解答题17. 某学校操场是一个长方形，长是200米，宽是100米。

请计算操场的面积，并说明如果学校要在操场上铺设草坪，需要多少平方米的草坪。

多边形的面积计算测验题及答案题目一：将下列多边形的面积计算结果填入空格。

1. 正方形的边长为5cm，面积是 ________ 平方厘米。

2. 长方形的长为8cm，宽为4cm，面积是 ________ 平方厘米。

3. 三角形的底边长为6cm，高为3cm，面积是________ 平方厘米。

4. 平行四边形的底边长为7cm，高为5cm，面积是 ________ 平方厘米。

5. 梯形的上底长为6cm，下底长为10cm，高为4cm，面积是________ 平方厘米。

答案：1. 252. 323. 94. 355. 24题目二：计算下列多边形的面积。

1. 一个边长为5cm的正五边形的面积是多少？（保留两位小数）2. 一个底边长为6cm，高为8cm的三角形的面积是多少？（保留一位小数）3. 一个边长为9cm，高为5cm的正六边形的面积是多少？（保留两位小数）4. 一个底边长为10cm，高为7cm的平行四边形的面积是多少？（保留一位小数）5. 一个上底长为7cm，下底长为12cm，高为5cm的梯形的面积是多少？（保留一位小数）答案：1. 43.012. 24.03. 116.174. 70.05. 47.5题目三：根据提供的图形，计算多边形的面积。

（图形中有一个梯形，上底长为6cm，下底长为12cm，高为8cm；一个正方形，边长为5cm；一个平行四边形，底边长为7cm，高为4cm；一个三角形，底边长为6cm，高为3cm）1. 计算梯形的面积。

2. 计算正方形的面积。

3. 计算平行四边形的面积。

4. 计算三角形的面积。

5. 将以上四个多边形的面积相加，得到总面积。

答案：1. 722. 253. 284. 95. 134题目四：小明做了一个实验，用橡皮圈围成了不同形状的图形，请根据提供的图形，计算多边形的面积。

（图形有一个正方形，边长为4cm；一个长方形，长为6cm，宽为3cm；一个等腰梯形，上底长为5cm，下底长为9cm，高为4cm）1. 计算正方形的面积。

五年级数学上册第二单元多边形面积的计算一、基础知识测试。

1、把一个平行四边形转变为一个长方形，它的面积与本来平行四边形的面积(相等) ，这个长方形的长等于原平行四边形的(底) ，这个长方形的宽等于原平行四边形的(高) 。

长方形的面积等于长乘宽，因此平行四边形的面积等于(底) 乘 (高) ，用字母表示的公式为(S=A*H) 。

2、一个平行四边形的底为形底为 12 分米，面积为3、一个平行四边形的底扩大高扩大 3 倍，则面积 (15 分米，高为18 分米，面积为180 平方分米，则高为 (154 倍，高减小 2 倍，则面积 (不变) 。

( 270) 分米。

扩大两倍) 平方分米。

假如一个平行四边) ；假如它的底减小 3 倍，4、一个梯形的面积是42 平方米，它的上下底之和与一个平行四边形的底边相等，高与平行四边形的高相等，这个平行四边形的面积是( 84) 平方米。

5、一个梯形的面积是22 平方分米，上、下底之和为11 分米，它的高是 (4) 分米。

6、一个梯形的面积是24 平方分米，下底是 5 分米，高是 4 分米，上底是 (7) 分米。

7、一个平行四边形的面积为64 平方厘米，高为8 厘米，底为 ( 8) 厘米。

8、一块直角三角形的地，两条直角边的长分别是36 米、 27 米，这块地的面积是 ( 486) 平方米。

9、一个三角形，它的面积为36 平方分米，高为8 分米，则它的底为 (9) 分米。

10、一块直角梯形的地，它的下底是40 米，假如上底增添38 米，这块地就变为了正方形，原梯形的面积是 ( 4602) 平方米。

11、一个长方形木框，长10dm，宽 8dm，将它拉成一个平行四边形，面积变(小) ，这个平行四边形的周长为 (36)dm。

12、三角形有一条边的长为 9 厘米，这条边上的高为 4 厘米，另一条边长 6 厘米，这条边上的高是 ( 6)厘米。

13、一个三角形的面积为10 平方分米，若底扩大 2 倍，高减小 4 倍，则此刻的面积为 (5) 平方分米。

多边形的面积练习题及答案练习题一：三角形面积计算题目：已知一个三角形的底边长为10厘米，高为6厘米，求该三角形的面积。

解答：根据三角形面积公式，面积 = (底边长× 高) / 2。

代入数值得面积= (10 × 6) / 2 = 30平方厘米。

练习题二：平行四边形面积计算题目：一个平行四边形的底边长为8厘米，高为5厘米，求该平行四边形的面积。

解答：平行四边形的面积公式为面积 = 底边长× 高。

代入数值得面积= 8 × 5 = 40平方厘米。

练习题三：梯形面积计算题目：一个梯形的上底长为4厘米，下底长为8厘米，高为6厘米，求该梯形的面积。

解答：梯形的面积公式为面积 = (上底 + 下底) × 高 / 2。

代入数值得面积= (4 + 8) × 6 / 2 = 18平方厘米。

练习题四：正多边形面积计算题目：一个正六边形的边长为5厘米，求该正六边形的面积。

解答：正六边形可以被划分为6个等边三角形，每个三角形的底边长等于正六边形的边长。

因此，每个三角形的面积= (5 × 5 ×sin(60°)) / 2。

正六边形的总面积= 6 × 每个三角形的面积 = 6× (5 × 5 × √3 / 4) = 75√3 / 2 ≈ 64.95平方厘米。

练习题五：不规则多边形面积估算题目：一个不规则多边形，已知其所有顶点的坐标，如何估算其面积？解答：可以通过将其划分为多个三角形，然后计算每个三角形的面积并求和。

如果顶点坐标已知，可以使用多边形面积公式，即根据顶点坐标计算多边形的面积。

练习题六：圆内接多边形面积计算题目：一个圆的半径为10厘米，求其内接正六边形的面积。

解答：圆内接正六边形的边长等于圆的半径。

因此，正六边形的面积= 6 × (半径× 半径× sin(60°)) / 2 = 6 × (10 × 10 ×√3 / 4) = 150√3 ≈ 259.81平方厘米。

五年级数学多边形的面积计算公式汇总+练习题（附答案）面积计算公式1、长方形的面积=长×宽字母表示：S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长b=S÷a2、正方形的面积=边长×边长字母表示: S= a²3、平行四边形的面积=底×高字母表示：S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2字母表示：S=ah÷2三角形的高= 2×面积÷底h=2S÷a三角形的底= 2×面积÷高a=2S÷h5、梯形的面积=（上底+下底）×高÷2字母表示：S=(a+b)·h ÷2梯形的高=2×面积÷（上底+下底）h=2S÷(a+b)梯形的上底=2×面积÷高—下底a=2S÷h-b梯形的下底=2×面积÷高—上底b=2S÷h-a1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方米=10000平方厘米1米=10分米=100厘米多边形面积同步试题一、填空1．完成下表。

考查目的：平行四边形、三角形和梯形的面积计算及变式练习。

答案：解析：直接利用公式计算这三种图形的面积，对于学生来说完成的难度不大。

对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习，可引导学生进行比较，理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。

2．下图是一个平行四边形，它包含了三个三角形，其中两个空白三角形的面积分别是15 平方厘米和25 平方厘米。

中间涂色三角形的面积是（）。

考查目的：等底等高的三角形和平行四边形的面积之间的关系。

多边形面积练习题及答案多边形面积练习题及答案多边形是几何学中常见的图形，它由若干条线段组成，每条线段称为边，相邻两边的交点称为顶点。

多边形的面积是几何学中的一个重要概念，它表示多边形所占据的平面区域的大小。

在学习多边形面积的过程中，练习题是非常重要的一部分，下面将给出一些多边形面积的练习题及答案，希望能对你的学习有所帮助。

练习题一：计算下列多边形的面积：1. 一个正三角形，边长为5cm。

2. 一个矩形，长为8cm，宽为4cm。

3. 一个正五边形，边长为6cm。

答案一：1. 正三角形的面积可以使用公式S = (边长^2 * √3) / 4来计算，代入边长5cm，得到S = (5^2 * √3) / 4 ≈ 10.83cm²。

2. 矩形的面积可以使用公式S = 长 * 宽来计算，代入长8cm和宽4cm，得到S= 8 * 4 = 32cm²。

3. 正五边形的面积可以使用公式S = (边长^2 * √25 + 10 * √5) / 4来计算，代入边长6cm，得到S = (6^2 * √25 + 10 * √5) / 4 ≈ 61.66cm²。

练习题二：计算下列多边形的面积：1. 一个等边五边形，边长为10cm。

2. 一个正六边形，边长为7cm。

3. 一个梯形，上底长为5cm，下底长为8cm，高为6cm。

答案二：1. 等边五边形的面积可以使用公式S = (边长^2 * √25 + 10 * √5) / 4来计算，代入边长10cm，得到S = (10^2 * √25 + 10 * √5) / 4 ≈ 172.05cm²。

2. 正六边形的面积可以使用公式S = (3 * √3 * 边长^2) / 2来计算，代入边长7cm，得到S = (3 * √3 * 7^2) / 2≈ 91.14cm²。

3. 梯形的面积可以使用公式S = (上底 + 下底) * 高 / 2来计算，代入上底5cm、下底8cm和高6cm，得到S = (5 + 8) * 6 / 2 = 39cm²。

五年级数学多边形面积的计算试题答案及解析1.一块三角形的稻田占地8公顷，它的一条直角边长800米，另一条直角边长多少米？【答案】100【解析】直角三角形的面积等于两条直角边相乘，面积8公顷=80000平方千米，80000÷800=100（米）。

【考点】面积单位公顷与平方米之间的换算。

总结：应用题中出现面积单位时，注意单位之间的换算。

2.在图中，梯形的上底是6cm，下底4cm，阴影部分的面积是10cm2，空白部分的面积是（）cm2。

A．12.5B．25C．50D．15【答案】D【解析】阴影部分的面积已知，先利用三角形的面积公式求出阴影部分的高，也就是梯形的高，梯形的上底和下底已知，利用梯形的面积公式即可求出梯形的面积，再据空白部分的面积=梯形的面积-阴影部分的面积即可求解。

解：10×2÷4=5（厘米），（6+4）×5÷2，=10×5÷2，=50÷2，=25（平方厘米）；25-10=15（平方厘米）；答：空白部分的面积是15平方厘米．故选：D．【考点】梯形的面积。

总结：此题主要考查三角形和梯形的面积的计算方法，关键是明白：阴影部分的高就等于梯形的高。

3.将图中的平行四边形分成一个三角形和一个梯形，已知梯形比三角形面积大40平方厘米，梯形的下底CD是多少厘米？【答案】5厘米【解析】先依据平行四边形的面积公式求出平行四边形的面积，再用平行四边形的面积减去40，就是两个三角形的面积，于是可以得出1个三角形的面积，从而利用三角形的面积公式即可求解。

解：三角形的面积：（25×8-40）÷2，=（200-40）÷2，=160÷2，=80（平方厘米），BC的长度：80×2÷8=20（厘米），所以CD的长度为25-20=5（厘米）；答：梯形的下底CD是5厘米。

【考点】梯形的面积。