2018年中考数学复习第4单元图形的初步认识与三角形第17课时图形的认识及平行线相交线课件湘教版
- 格式:ppt
- 大小:2.13 MB
- 文档页数:30
第17课时图形的初步认识一、知识点1.立体图形:视图,平面展开图;2.平面图形:点和线,两点之间线段最短。
(1)角:对顶角相等,等角的补角相等,等角的余角相等;(2)平行线:两位角相等,两直线平行;两直线平行,同位角相等。
二、中考课标要求三、中考知识梳理1.立体图形的展开图这类问题,主要考查对立体图形与平面图形的关系的认识,因此要求掌握常用多面体的平面展开图的识别及逆向判断。
2.角的有关计算这类问题一般主要考查互余、互补、对顶角的性质及平行线的性质的运用,首先根据已知条件观察图形,分析角与角之间的数量关系,从中找到解决问题的思路及途径,在中考中通常和三角形的内角和定理,内外角性质,或特殊三角形相联系。
3.平行线的性质与判定的运用平行线的特征与识别是互逆的,有时易混淆,在中考中往往综合运用,也经常与后续知识,平行四边形、相似形等相联系,是中考的重点之一。
四、中考题型例析题型一 有关立体图形例 1 在图所示的长方体中,和平面A1 C1 垂直的平面有( )A.4个B.3个C.2个D.1个 解析:利用长方体的特征判断即可。
答案:A 。
例2如图是一个正方体的展开图,每个图内都标注了字母,则展开与面E 相对的是( ) A.面D B.面B C.面C D.面A解析:已知这是一个正方体的表面展开图,共有6个面,其中和D 相邻的有4 个面,它们是:A 、C 、F 、B ,因此和E 相对的只有D 。
答案:A 点评:为了培养空间的相象能力:一时要动手操作,仔细观察;二是要善于想象,把想象的样子亲自折一折,经过训练,就会大大提高自己的空间想象能力,另外,善于总结规律,会提高识别能力。
题型二 角的有关计算例3如查∠a=20°,那么∠a 的补角等于( ) A.20° B.70° C.110° D.160° 解析:利用补角的定义,即可得出结果。
答案:D例4如图,AB ∥CD ,EF 分别交AB 、CD 于点E 、F ,∠1=70°,则∠2=___________。

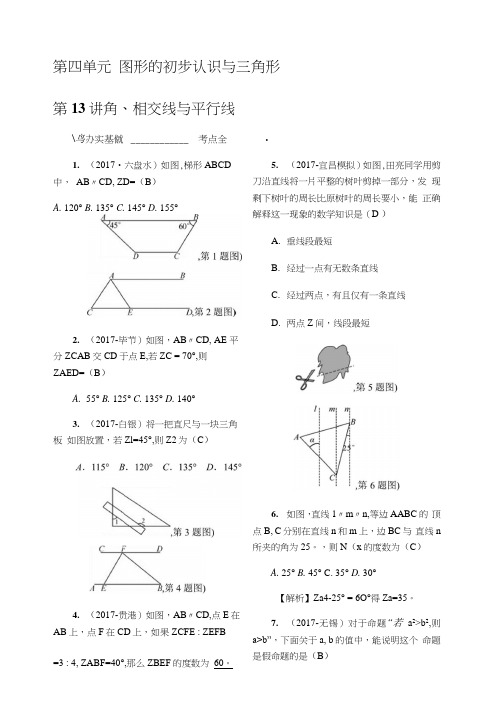
第四单元图形的初步认识与三角形第13讲角、相交线与平行线\鸟办实基僦____________ 考点全1.(2017•六盘水)如图,梯形ABCD 中,AB〃CD, ZD=(B)A. 120°B. 135°C. 145°D. 155°2.(2017-毕节)如图,AB〃CD, AE 平分ZCAB交CD于点E,若ZC = 70°,则ZAED=(B)A.55°B. 125°C. 135°D. 140°3.(2017-白银)将一把直尺与一块三角板如图放置,若Zl=45°,则Z2为(C)4.(2017-贵港)如图,AB〃CD,点E在AB上,点F在CD上,如果ZCFE : ZEFB=3 : 4, ZABF=40°,那么ZBEF的度数为60。
•5.(2017-宜昌模拟)如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是(D )A.垂线段最短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点Z间,线段最短6.如图,直线1〃m〃n,等边AABC的顶点B, C分别在直线n和m上,边BC与直线n 所夹的角为25。
,则N(x的度数为(C)A. 25°B. 45°C. 35°D. 30°【解析】Za4-25° = 6O°得Za=35。
7.(2017-无锡)对于命题“若a2>b2,则a>b”,下面关于a, b的值中,能说明这个命题是假命题的是(B)A. a = 3, b=2 B• a= —3, b=2C. a=3, b= —1D. a= —1, b = 38.(2017-贵港)下列命题屮假命题是(C)A,正六边形的外角和等于360。
B,位似图形必泄相似C.样本方差越大,数据波动越小D.方程x2+x+l= 0无实数根9.ZA的余角为60。


第四章图形的初步认识与三角形、四边形第一节线段、角、相交线和平行线,遵义五年中考命题规律),遵义五年中考真题及模拟)平行线的性质1.(2017遵义中考)如图,△ABC中,E是BC中点,A D是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC =15,则FC的长为( C)A.11 B.12 C.13 D.14,(第1题图)) ,(第2题图))2.(2017遵义中考)把一块等腰直角三角尺和直尺如图放置,如果∠1=30°,则∠2的度数为( D) A.45°B.30°C.20°D.15°3.(2016遵义中考)如图,在平行线a,b之间放置一块直角三角板,三角板的顶点A,B分别在直线a,b 上,则∠1+∠2的值为( A)A.90°B.85°C.80°D.60°(第3题图)(第4题图)4.(2015遵义中考)如图,直线l1∥l2,∠1=62°,则∠2的度数为( D)A.152°B.118°C.28°D.62°5.(2014遵义中考)如图,直线l1∥l2,∠CAB=125°,∠ABD=85°,则∠1+∠2=( A)A.30°B.35°C.36°D.40°(第5题图)(第6题图)6.(2013遵义中考)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( A)A.70°B.80°C.65°D.60°直线与线段7.(2016遵义一中一模)直尺与三角尺按如图所示的方式叠放在一起,在图中所标记的角中,与∠1互余的角有( B)A.2个B.3个C.4个D.6个,中考考点清单)线段与直线1.线段(1)定义:线段的直观形象是拉直的一段线. (2)基本事实:两点之间的所有连线中,线段最短.(3)线段的和与差:如图①,已知两条线段a 和b ,且a>b ,在直线l 上画线段AB =a ,BC =b ,则线段AC 就是线段a 与b 的和,即AC =__a +b__.如图②,在直线l 上画线段AB =a ,在AB 上画线段AD =b ,则线段DB 就是线段a 与b 的差,即DB =a -b.(4)线段的中点:如图③,线段AB 上的一点M ,把线段AB 分成两条线段AM 与MB.如果AM =MB ,那么点M 就叫做线段AB 的中点,此时有__AM__=MB =12AB ,AB =2AM =2MB.2.直线(1)定义:沿线段向两边无限延伸所形成的图形. (2)基本事实:经过两点有一条直线,并且只有一条直线.角及角平分线3.角的分类 (1)分类(2)周角、平角、直角之间的关系和度数 1周角=2平角=4直角=360°, 1平角=2直角=180°,1直角=90°,1°=60′,1′=60″,1′=⎝ ⎛⎭⎪⎫160°,1″=⎝ ⎛⎭⎪⎫160′. 4.角平分线的概念及性质(1)定义:如果一条射线把一个角分成两个相等的角,那么这条射线叫做这个角的角平分线. (2)性质:角平分线上的点到角两边的距离相等. 警示:到角两边距离相等的点在角平分线上. 5.余角、补角、邻补角(1)余角:A .如果两个角的和为__90°__,那么这两个角互为余角;B .同角(等角)的余角相等.(2)补角:A .如果两个角的和为__180°__,那么这两个角互为补角;B .同角(等角)的补角相等.(3)邻补角:A .两个角有一个公共顶点和一条公共边,另一边互为反向延长线的两个角互为邻补角;B .互为邻补角的两个角的和为180°.相交线三线八角(如图)6.同位角有:∠1与__∠5__,∠2与∠6,∠4与∠8,∠3与∠7.7.内错角有:∠2与__∠8__,∠3与∠5.8.同旁内角有:∠3与∠8,∠2与__∠5__.9.对顶角有:∠1与∠3,∠2与__∠4__,∠5与∠7,∠6与__∠8__.垂线及其性质10.定义:两条直线相交所成的四个角中,如果有一个角是直角,我们就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.11.基本事实:经过直线上或直线外一点,有且只有一条直线与已知直线垂直.12.性质:直线外一点与直线上各点连接的所有线段中,垂线段最短.13.点到直线的距离:从直线外一点到这条直线的垂线段长度.14.线段垂直平分线:(1)定理:线段垂直平分线上的点到线段两端的距离__相等__.(2)逆定理:到一条线段的两端点的距离相等的点在线段的垂直平分线上.平行线的判定及性质15.定义:在同一平面内,不相交的两条直线叫做平行线.16.两条平行线之间的距离处处相等.17.性质(1)两直线平行,同位角相等,即∠1=__∠2__.(2)两直线平行,内错角相等,即∠2=__∠3__.(3)两直线平行,同旁内角互补,即∠3+__∠4__=180°.18.判定(1)基本事实:经过已知直线外一点,有且只有一条直线和已知直线平行.(2)同位角相等,两直线平行.(3)内错角相等,两直线平行.(4)同旁内角互补,两直线平行.(5)平行于同一条直线的两条直线平行.命题与定理19.命题:判断一件事情的句子叫做命题,命题由题设、结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,命题常写成“如果……那么……”的形式.20.真命题:如果题设成立,那么结论一定成立的命题叫做真命题.21.假命题:题设成立,不能保证结论一定成立的命题叫做假命题.22.定理:有些命题的正确性是用推理证实的,这样的真命题叫做定理,推理过程叫做证明.【方法点拨】利用平行线性质求角度:先观察要求角与已知角的位置关系,再选择合理的角度进行等量代换,因此需要熟练掌握平行线的性质.另外在解题中要注意平角、直角及三角形内角和、三角形内外角关系等知识的运用.,中考重难点突破)补角、余角的计算【例1】(2018原创)一个角的度数是40°,那么它的余角的补角度数是( )A.130°B.140°C.50°D.90°【解析】若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.依此求出度数.【答案】A1.(2016遵义二中一模)将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( C)A.4个B.3个C.2个D.1个(第1题图)(第2题图)2.(2018原创)如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( D)A.∠1=∠3 B.∠2+∠3=180°C.∠2+∠4<180°D.∠3+∠5=180°平行线的性质【例2】如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )A.85°B.60°C.50°D.35°【解析】过A点作直线c∥b,则c∥a,∵a∥c,∴∠1=∠4=85°,又b∥c,∴∠3=∠5,又∵∠2=35°,∴∠5=85°-35°=50°,∴∠3=50°.【答案】C3.(2016汇川升学模拟)如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数是( B)A.75°B.35°C.40°D.55°,(第3题图)),(第4题图)) 4.(2017重庆中考)如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.解:∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°-72°=108°.∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD-∠ACD=108°-58°=50°.平行线的实际应用【例3】如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点,这时,∠ABC的度数是( )A.120°B.135°C.150°D.160°【解析】首先找准方位角,并从中找出互相平行的直线.【答案】C5.(2016遵义升学样卷)如图,直线a∥b,直角三角形ABC的直角顶点B在直线b上,∠1=36°,则∠2=__126°__ .,(第5题图)) ,(第6题图)) 6.(2017重庆中考)如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE 的度数.解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°.∵EF平分∠AED,∴∠DEF=∠AEF=69°,又∵AB∥CD,∴∠AFE=∠DEF=69°.。
