北邮DSP的matlab作业

1.DFT定义，矩阵形式运算，循环运算 (1)2.fir1 , kaiserord , Kaiser , freqz (2)3.cheb1ord , cheb1 (2)4.系统函数的二阶分解，tf2sos,tf2zp,sort,unique (3)5.零极点形式到直接型的转换 (3)6.阶数估计（表10.2）,hann,fir1，根据定义加窗 (4)7.freqz , real , imag , abs , angle , unwrap , phase (4)8.fir1 , hamming窗 (5)9.直接型转零极点型，tf2zp (6)10.butter,buttord (6)11.部分分式展开（逆），从传输函数计算冲击响应，residuez,impz (7)12.freqz , real , imag , abs , phase , angle , unwrap (7)13.ellipord , ellip , freqz (8)14.fir1 , hann , 分贝转换 (9)15.信号能量计算 (9)16.各IIR阶数估计，buttord , cheb1ord , cheb2ord , ellipord (9)17.square , freqz (10)18.线性卷积，此处用fft实现 (11)19.圆周卷积，要求用基于DFT的方法实现 (11)20.部分分式展开，逆z变换，residuez (12)21.freqz (13)22.信号通过系统的输出，filter (13)23.信号通过系统的输出，filter (13)24.重要提示 (14)1.DFT定义，矩阵形式运算，循环运算2.fir1 , kaiserord , Kaiser , freqz3.cheb1ord , cheb14.系统函数的二阶分解，tf2sos,tf2zp,sort,unique5.零极点形式到直接型的转换6.阶数估计（表10.2）,hann,fir1，根据定义加窗7.freqz , real , imag , abs , angle , unwrap , phase8.fir1 , hamming窗9.直接型转零极点型，tf2zp10.butter,buttord11.部分分式展开（逆），从传输函数计算冲击响应，residuez,impz12.freqz , real , imag , abs , phase , angle , unwrap13.ellipord , ellip , freqz14.fir1 , hann , 分贝转换15.信号能量计算16.各IIR阶数估计，buttord , cheb1ord , cheb2ord , ellipord17.square , freqz18.线性卷积，此处用fft实现19.圆周卷积，要求用基于DFT的方法实现20.部分分式展开，逆z变换，residuez21.freqz22.信号通过系统的输出，filter23.信号通过系统的输出，filter24.重要提示。

学院：电子工程学院
班级：2018211205班
姓名：赵依然
学号：2018212048
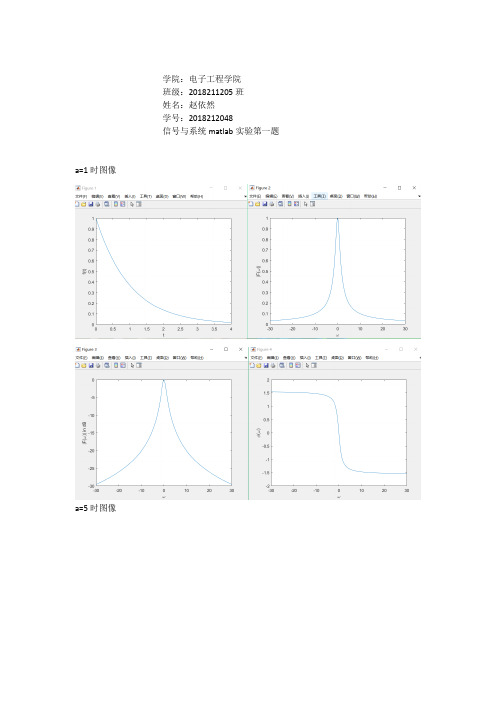
信号与系统matlab实验第一题a=1时图像
a=5时图像
a=10图像
a=20图像
单边指数信号随着a不断增大，发生了如下变化：
f（t）随着a增大而急剧减小，斜率变化很快，趋于0的时间减少。

|F(W)|则变得平缓一些，频域增大。

转换成db也是一样的规律。

而phi（w）则随着变小，随着a增大，曲线变得平缓，下降速度变得缓慢。

总结起来就是，a越小波形下降越慢，高频成分越少低频成分越多频谱越集中，频谱相位越大。

a越大，波形下降越快，高频成份越多，低频成分越少，频谱越分散，频谱相位越小。

2.矩形脉冲信号：
图像如下
代码如下
3.升余弦脉冲信号
图像如下
代码如下
4.三角脉冲信号：
图像如下：
代码如下
比较图像可知：
矩形脉冲信号的带宽为2π，升余弦脉冲信号和三角脉冲信号的带宽为4π。

旁瓣由小到大依次是升余弦脉冲信号、三角脉冲信号、矩形脉冲信号。

实验三：IIR 数字滤波器的设计和实现学院：专业：班级：姓名：学号：班内序号：时间：【实验背景】数字信号处理的另一个重要应用是数字滤波器。

数字滤波器是一个运算过程，将输入数列按既定的要求转换成输出数列。

在数字信号的处理时只需利用数字相加、乘以常数和延时等运算，就可以完全达到传输特性的要求。

数字滤波器分为无限冲激响应（IIR）和有限冲激响应（FIR）两大类。

本实验用IIR 数字滤波器产生双音多频DTMF 拨号信号的产生，演示IIR 数字滤波器在通信系统中的应用。

DTMF 信号是将拨号盘上的0~F 共16 个数字，用音频范围的8 个频率来表示的一种编码方式。

8 个频率分为高频群和低频群两组，分别作为列频和行频。

每个字符的信号由来自列频和行频的两个频率的正弦信号叠加而成。

频率组合方式如下图所示。

【实验要求】根据ITU Q.23 建议，DTMF信号的技术指标是：传送/接收率为每秒10个号码，或每个号码100ms。

每个号码传送过程中，信号存在时间至少45ms，且不多于55ms，100ms的其余时间是静音。

在每个频率点上允许有不超过±1.5%的频率误差。

任何超过给定频率±3.5%的信号，均被认为是无效的，拒绝承认接收。

另外，在最坏的检测条件下，信噪比不得低于15dB。

DTMF 信号的编码: 把您的联系电话号码DTMF 编码生成为一个.wav 文件。

其中关键是不同频率的正弦波的产生，要求采用滤波法生成所要求的DTMF信号。

【实验内容】1.实验代码：phone=input('请输入电话号码:','s');>> sum=length(phone);fs=8000;total_x=[];fH=[1336,1209,1336,1477,1209,1336,1477,1209,1336,1477];fL=[941,697,697,697,770,770,770,852,852,852];for i=1:sumnum=phone(i)-48+1;n=1:400;x=sin(2*pi*n*fL(num)/fs)+sin(2*pi*n*fH(num)/fs);x=[x,zeros(1,400)];total_x=[total_x,x];endaudiowrite('num_sound.wav',total_x,8000)警告: 数据在写入文件期间被裁剪。

设计FIR滤波器作业报告学号：姓名：设计FIR滤波器作业报告本设计主要内容是利用MATLAB验证设计思路并用CCS3.3仿真环境设计一个FIR滤波器，要求滤除给定的叠加正弦波的两个较高频分量。

给定波形函数为：y=sin(2*pi*100*t)+sin(2*pi*250*t)+sin(2*pi*270*t)。

1.设计思路：输入信号是频率为100Hz、250HZ、270Hz的合成正弦等幅信号，由于给定的谐波分量最高为270Hz，根据奈奎斯特准则，采样频率应大于最高频率分量的2倍，即大于2*270，故可以以600Hz的采样频率进行采样，即fs=600Hz。

设计了一个截止频率为200Hz的低通滤波器，目的是通过所设计的低通bartlett滤波器将信号源中频率为200Hz以上的信号滤掉，留下频率为100Hz 的信号，达到滤波的效果。

利用MATLAB设计合适的滤波器实现滤波，然后得到其滤波器系数在CCS的simulator方式下编写滤波程序，调用波形数据，实现滤波，并观看滤波前后的信号波形图、频谱图，观察滤波达到预期效果。

2.设计过程1)在MATLAB中进行算法验证MATLAB语言由于具有数值计算功能、符号计算功能、数据可视化功能、建模仿真可视化功能，使得MATLAB在命题构思、模型建立、仿真研究、假想验证、数据源可视化各环节起着强大的作用。

因此在设计中必须先在MATLAB 语言中设计一个FIR滤波器。

本设计采用的是bartlett窗函数。

下面是在MATLAB 中设计的27阶FIR型bartlett滤波器程序：clear all; %请寄存器clf; %清屏N=256; %清数据点fs=600; %采样频率dt=1/fs; %采样时间间隔for t=1:Nf1=250;f2=100;f3=270;y(t)=(sin(2*pi*f1*t*dt)+sin(2*pi*f2*t*dt)+sin(2*pi*f3*t*dt));%产生合成信号 x(t)=round(10000*y(t)); %为DSP汇编程序做数据转换endfigure(1)plot(y),title('滤波前的波形图像');fp=200fst=250NL=26f1=200;w1=2*pi*f1/fswindow=bartlett(NL+1) %窗函数n=1:NL+1hd=sin(w1*(n-NL/2))./(pi*(n-NL/2));hd(NL/2)=0.67;h=hd.*rot90(window)h1=h*32768;h2=fft(h,N); %将信号做FFT变换pyy=h2.*conj(h2); %做功率谱分析f=(0:(N/2-1));for i=1:N/2-1f(i)=f(i)*fs/N;endfigure(2)plot(f,pyy(1:N/2)),title('滤波器的频谱图像');yy1=filter(h,1,y); %滤波figure(3)plot(yy1),title('滤波后的波形图像');y=fft(y,N);pyy=y.*conj(y);f=(0:(N/2-1));for i=1:N/2-1f(i)=f(i)*fs/N;endfigure(4)subplot(1,2,1),plot(f,pyy(1:N/2)),title('滤波前的波形频谱图像');y=fft(yy1,N);pyy=y.*conj(y);f=(0:(N/2-1));for i=1:N/2-1f(i)=f(i)*fs/N;endsubplot(1,2,2),plot(f,pyy(1:N/2)),title('滤波后的波形频谱图像')其中采样点为256个，采样频率为600Hz，输入信号为100Hz、250Hz、270Hz 的合成信号，设定的截止频率为200Hz，通过FIR滤波器后，期望保留的信号是100Hz的信号，200Hz以上的频率基本被滤掉。

P1．已知两序列[]0.8{[][5]}n x n u n u n =--，[]{1,1,1,1,1}h n =计算两序列的卷积并绘制其波形。

解：for i=1:5x(i)=0.8^(i-1);endh=[1 1 1 1 1];y=conv(x,h)m=[0 1 2 3 4 5 6 7 8];stem(m,y,'filled')P2．已知复指数序列(1.52)[] 1.2j n x n e +=，绘制20点该序列的实部和虚部。

解：(1.52) 1.52 1.5 1.5 1.5[] 1.2 1.2 1.2(cos 2sin 2) 1.2cos 2 1.2sin 2j n n j n n n n x n e e e e n j n e n j e n +===+=+ 所以 1.5 1.5Re([]) 1.2cos 2,Im([]) 1.2sin 2n n x n e n x n e n ==for n=1:20Re(n)=1.2*exp(1.5*(n-1))*cos(2*(n-1));Im(n)=1.2*exp(1.5*(n-1))*sin(2*(n-1));endfor i=1:20x(i)=i-1;endsubplot(2,1,1)stem(x,Re,'filled');lab1='\rightarrowRe(x[n])';text(14,1.2e+12,lab1,'Fontsize',18);subplot(2,1,2)stem(x,Im,'filled');lab2='\rightarrowIm(x[n])';text(14,4e+11,lab2,'Fontsize',18);P3．编写长度为5的中值滤波器程序。

原始未受干扰的序列为：s[n]=3[n(0.5) ]n，加性噪声信号d[n]为随机序列，幅度0.4，分别绘制长度为40的受干扰序列，以及中值滤波器的输出。

Dsp-matlab实验实验一：重叠相加法和重叠保留法的实现设计报告课题名称：学生姓名：班级：班内序号：学号：日期：2015/06/15目录一、实验原理·········································二、Matlab源代码·································三、Matlab运行结果····························四、Matlab结果分析····································五、遇到的难题与解决方法····························参考文献·························································一、实验原理1、算法来源DFT 是连续傅里叶变换在时域和频域上都离散的形式，将时域信号的采样变换为在离散时间傅里叶变换频域的采样。

××××大学实验报告实验名称采样、系统性质及滤波系统频率响应和样本处理算法实现加窗和离散傅氏变换数字滤波器设计陷波器设计课程名称______数字信号处理_______班级学号_______ __________ 姓名_______ ____________开课时间 20 /20 学年，第学期实验一1实验名称: 采样、系统性质及滤波2实验目的和任务，实验内容一、观察采样引起的混叠设模拟信号为)3sin()2sin(4)5cos()(t t t t x πππ⋅+=，t 的单位为毫秒(ms)。

(1)设采样频率为3kHz ，确定与)(t x 混叠的采样重建信号)(t x a 。

(2)画出)(t x 和)(t x a 在)(60ms t ≤≤范围内的连续波形。

（因数字计算机无法真正画出连续波形，可用较密的离散点的连线来近似。

） (3)分别用"" 和""⨯在两信号波形上标记出3kHz 采样点。

两信号波形是否相同？采样后的两序列是否相同？二、判别离散时间系统的时不变性设输入序列为)(n x ，系统)2()(n x n y =实现对)(n x 的抽取。

(1)设500,...,2,1),1002sin()(==n n n x π。

取延迟量D （例如D ＝30）。

记)()(D n x n x D -=，画出)(n x 、)(n x D 的序列波形。

(2)编程求出系统对)(n x 的响应)(n y 以及对)(n x D 的响应)(n y D (3)画出)(D n y -、)(n y D 的波形。

三、利用卷积计算出输入信号通过FIR 滤波器的输出，并观察输出信号的input-on 暂态、input-off 暂态和稳态部分。

1.考虑下面两个滤波器，第一个的单位脉冲响应为⎩⎨⎧≤≤*=其它0140)75.0(25.0n h nn ，另一个的单位脉冲响应为]1,5,10,105,1[51--=，－h ；输入为周期方波，在一个周期内⎩⎨⎧≤≤≤≤=492502401)(x x n x 。

Dsp-matlab实验实验一：重叠相加法和重叠保留法的实现设计报告课题名称：学生姓名：级：班班内序号：学号：2015/06/15 日期：目录一、实验原理·········································二、Matlab源代码·································运行结果Matlab三、····························结果分析Matlab四、····································五、遇到的难题与解决方法····························参考文献·························································一、实验原理1、算法来源DFT 是连续傅里叶变换在时域和频域上都离散的形式，将时域信号的采样变换为在离散时间傅里叶变换频域的采样。

MATLAB DSP实验报告介绍本实验报告将详细介绍在MATLAB环境下进行数字信号处理（DSP）的实验步骤和相关方法。

我们将通过逐步思考的方式，帮助读者理解和学习DSP的基本概念和技术。

实验环境和工具在进行DSP实验之前，我们需要准备以下环境和工具：1.MATLAB软件：确保已安装并配置好MATLAB软件，可以在MATLAB Command窗口中输入命令。

2.信号处理工具包：在MATLAB中，我们可以使用信号处理工具箱（Signal Processing Toolbox）来进行DSP实验和分析。

确保该工具箱已被安装并加载。

实验步骤下面是进行DSP实验的一般步骤：步骤一：加载信号首先，我们需要加载待处理的信号。

这可以通过在MATLAB中使用load命令加载一个音频文件或生成一个模拟信号实现。

例如，我们可以加载一个名为signal.wav的音频文件：load signal.wav步骤二：信号预处理在进行DSP之前，通常需要对信号进行预处理。

这可能包括去噪、滤波、均衡等操作。

例如，我们可以使用滤波器对信号进行降噪：filtered_signal = filter(filter_coefficients, signal);步骤三：信号分析一旦信号经过预处理，我们可以开始进行信号分析。

这可能涉及频域分析、时域分析、谱分析等。

例如，我们可以通过计算信号的快速傅里叶变换（FFT）获得其频谱：spectrum = fft(filtered_signal);步骤四：特征提取在信号分析之后，我们可以根据需要提取信号的特征。

这些特征可能包括幅度、频率、相位等。

例如，我们可以计算信号的能量：energy = sum(abs(filtered_signal).^2);步骤五：信号重构在完成信号分析和特征提取后，我们可以根据需要对信号进行重构。

这可能包括滤波、修复损坏的信号等。

例如，我们可以使用滤波器对信号进行重构：reconstructed_signal = filter(filter_coefficients, filtered_signal);步骤六：结果评估最后，我们需要评估重构后的信号和原始信号之间的差异。

Matlab实验报告学院：信息与通信工程学院班级：201321113学号：2013210381班内序号：18姓名：石雪原实验题目1.实现重叠相加和重叠保留算法一．实验原理重叠相加法和重叠保留法的实质都是以逐段地方式通过循环卷积来完成线性卷积的计算。

将输入序列x (n)进行分段，每段长为N,且N>M(M为有限长因果序列h (n)的长度)，x (n) 逐段与h (n)进行循环卷积，在重叠保留法中需在x (n)序列首部加入长度为M-1的0序列。

在算法中，在获得N个点的输入后，进行N+M-1点循环卷积计算，之后输出N个点。

通过for循环逐段进行循环卷积，使用FFT和IFFT 计算两个有限长序列的N点循环卷积结果。

二．源代码和流程图重叠相加法代码function [Y]=overpl(x,h,N)Lx=length(x); % 序列长度M=length(h); %h (n )长度x=[x,zeros(1,N-1)];t=zeros(1,M-1);Y=zeros(1,Lx+M-1);a=floor(Lx/N);for k=0:aA=x(k*N+1:k*N+N);y1=fft(A,Lx+M-1); % 利用fft 进行运算y2=fft(h,Lx+M-1);y3=y1.*y2;q=ifft(y3,Lx+M-1);Y(k*N+1:k*N+M-1)=q(1:M-1)+t(1:M-1);Y(k*N+M:k*N+N)=q(M:N);t(1:M-1)=q(N+1:N+M-1);endY(1:Lx+M-1);对应流程图图一：每段利用fft和ifft实现循环卷积图二：对X (n)逐段进行循环卷积然后相加得输出线性卷积结果y (n)重叠保留法代码fun cti on [Y]二overlpsav(x,h,N)Lx=le ngth(x);M=le ngth(h);M仁M -1;L=N-M1;h=[h,zeros(1,N-M)];图x=[zeros(1,M1),x,zeros(1,N-1)];a 二floor ((Lx+M1-1)/(L))+1; Y=zeros(1,N); for k=0:a-1 xk=x(k*L+1:k*L+N); b=fft(xk,N); C=fft(h,N); Z=b.*C;Y (k+1,:)=ifft(Z,N); end Y=Y (:,M:N)： Y=( Y(：))'对应流程图装成单列向量再转置成行向量 输出输入数据 x I 各段搭接长 长度及脉冲 —\度M1，有效 响应长度k数据长度L将h 延长 至循环 长度N㈡把x 前面 加上（M- 1）个零各段进 行卷积把 K+1X N 阶输出矩 阵Y 初始 化Y 中各行均去 掉前M-1个样 Z 本，转置后构V成新的Y三.实验结果重叠相加法x=[1,2,3] h二[1,2,3] N=41 5]? 3X] 1 K 12 9 0緒=1 1 10 12 9 0重叠保留法x=[1,2,3,4,5,6,7,8,9,10] h=[1,0,-1] N=4四.结果分析（有关运算量的定量分析结果）有限长因果序列x （n）h （n）的长度分别为N和M直接计算线性卷积y （n），y（n）可视为N个序列的叠加结果，序列长度为M 所以每生成一个序列需完成M次乘法，共需完成MN次乘法运算。