下载文档原格式
1研究目的与问题阐述1.1 基本研究目的(1) 掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。
(2) 熟悉有限元建模、求解及结果分析步骤和方法。
(3) 利用ANSYS软件对梁结构进行有限元计算。
(4) 研究不同泊松比对同一位置应力的影响。
1.2 基本问题提出图1.1 模型示意图如图1.1所示，当EX=3.01e6，F=5000N，悬臂梁杆一端固定，另一端为自由端。
当悬臂梁的泊松比u为：0.2、0.25、0.3、0.35、0.4时，确定同一位置的应力分布，得出分布云图。
二维模型，3*0.09m。
2 软件的介绍与使用2.1 ANSYS 简介ANSYS程序是一个功能强大的灵活的设计分析及优化、融结构、流体、电场、磁场、声场分析于一体的大型通用有限元商用分析软件，可广泛应用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、造船、生物医学、轻工、地矿、水利、日用家电等一般工业及科学研究。
该软件提供了一个不断改进的功能清单，集体包括：结构高度非线性分析、电磁分析、计算流体动力分析、设计优化、接触分析、自适应网格划分、大应变/有限转动工功能一接利用ANSYS参数设计的扩展宏命令功能。
ANSYS由世界上最大的有限元分析软件公司之一的美国ANSYS开发，它能与多数系统下生成的集合数据传入ANSYS,如Pro/Engineer, NASTRAN, Alogor, I－DEAS, AutoCAD等，并通过必要的修补可准确地在该模型上划分网格并求解。
2.2 ANSYS软件的功能介绍ANSYS软件含有多种有限元分析的能力，包括从简单线性静态分析到复杂非线性动态分析。
一个典型的ANSYS分析过程可分为以下三个步骤：创建有限元模型；施加载荷进行求解；查看分析结果；在有限元的分析过程中，程序通常使用以下三个部分：前处理模块，分析求解模块和后处理模块。
前处理模块提供了一个强大的实体建模及网格划分工具，通过这个模块用户可以建立自己想要的工程有限模型。
悬臂梁有限元分析验证XXX-XXX学年第二学期)XXX大学研究生课程论文课程论文题目：悬臂梁有限元分析验证课程名称有限元法课程类别□学位课□非学位课任课教师所在学院学科专业姓名学号提交日期注意事项：1、以上各项由研究生认真填写；2、研究生课程论文应符合一般学术规范，具有一定学术价值，严禁网上下载或抄袭；凡检查或抽查不合格者，一律取消该门课程成绩和学分，并按有关规定追究相关人员责任；3、论文得分由批阅教师填写（见封底），并签字确认；批阅教师应根据作业质量客观、公正的在文后签写批阅意见；4、原则上要求所有课程论文均须用A4纸打印，加装本封面封底，左侧装订；5、课程论文由各学院（部）统一保存，以备查用。
4、卷纸不够写，可另附纸。
摘要：本文通过有限元软件MSC.Patran建立悬臂梁模型，通过对悬臂梁的1D,2D,3D有限元受均布载荷时的应力云图与位移云图作比较，为有限元建模时对梁单元做简化提供验证依据。
关键词：悬臂梁应力位移一提出问题计算矩形截面梁在受均布载荷图1 1D模型应力云图图2 1D模型位移云图结果分析：通过结果云图可以看1D模型应力值在约束点最大值为1.33e7 Pa，最大位移在悬臂梁的自由端其最大值为4.33e-4 m。
计算结果与理论计算结果一致，证明了1D梁单元有限元模型计算的正确性。
2）应力分布由理论计算可得，最大应力为1.33e7Pa，由应力图可得最大应力为1.33e7 Pa，二者基本上相一致；由理论计算，最大挠度为0.423mm，由位移图可得最大桡度为0.433mm，二者基本上相一致。
2D模型分析运用Patran建立有限元模型，划分网格，对其进行约束与加载，并且定义其材料，定义属性，进行分析。
其结果应力云图，与位移云图如下：图4 2D 应力分布云图图5 2D位移云图结果分析：通过结果云图可以看2D模型应力值在约束点最大值为1.13e7 Pa，最大位移在悬臂梁的自由端其最大值为4.34e-4 m。
线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性（材料非线性、几何非线性、接触等），也不考虑惯性及时间相关的材料属性。
在ABAQUS 中，该类问题通常采用静态通用（Static ，General ）分析步或静态线性摄动（Static ，Linear perturbation ）分析步进行分析。
线性静力学问题很容易求解，往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。
这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。
在一般的分析中，应尽量选用精度和效率都较高的二次四边形/ 六面体单元，在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲，使用非协调单元（如CPS4I、C3D8I）的性价比很高。
对于复杂模型，可以采用分割模型的方法划分二次四边形/ 六面体单元；有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/ 四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束，右端自由，结构尺寸如图1-1 所示，求梁受载后的Mises 应力、位移分布。
材料性质：弹性模量 E 2e3 ，泊松比0.3均布载荷：F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法，用户可以任选一种1）在Windows 操作系统中单击“开始” -- “程序” --ABAQUS 6.10 -- ABAQUS/CA。
E（2）在操作系统的DOS窗口中输入命令：abaqus cae 。
启动ABAQUS/CA后E ，在出现的Start Section （开始任务）对话框中选择Create Model Database 。
1.3 创建部件在ABAQUS/CA顶E 部的环境栏中，可以看到模块列表：Module：Part ，这表示当前处在Part （部件）模块，在这个模块中可以定义模型各部分的几何形体。
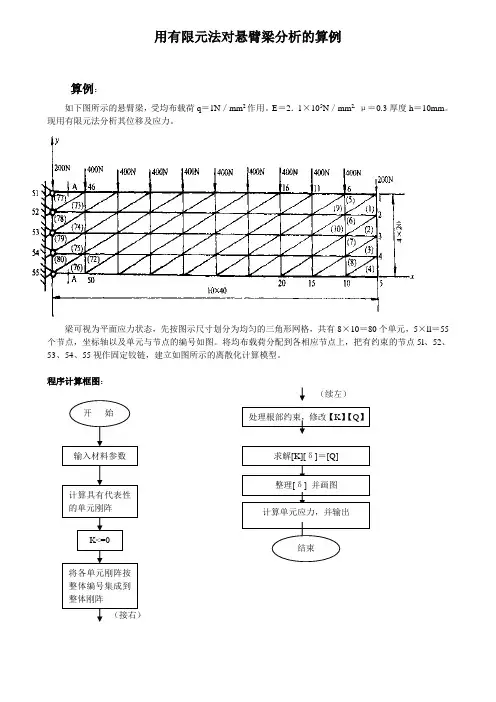
用有限元法对悬臂梁分析的算例算例：如下图所示的悬臂梁，受均布载荷q ＝1N ／mm 2作用。
E ＝2．1×105N ／mm 2, μ＝0.3厚度h ＝10mm 。
现用有限元法分析其位移及应力。
梁可视为平面应力状态，先按图示尺寸划分为均匀的三角形网格，共有8×10＝80个单元，5×ll ＝55个节点，坐标轴以及单元与节点的编号如图。
将均布载荷分配到各相应节点上，把有约束的节点5l 、52、53、54、55视作固定铰链，建立如图所示的离散化计算模型。
程序计算框图：（续左）（接右）开 始 输入材料参数 计算具有代表性的单元刚阵 K<=0 将各单元刚阵按整体编号集成到整体刚阵 处理根部约束，修改【K 】【Q 】 求解[K][δ]＝[Q] 整理[δ] 并画图计算单元应力，并输出结束程序中的函数功能介绍及源代码1. LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2. LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。
每集成一个单元，该函数都将返回2N×2N的整体刚度矩阵K.3. LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm，ym)以及单元位移矢量为u时的单元应力。
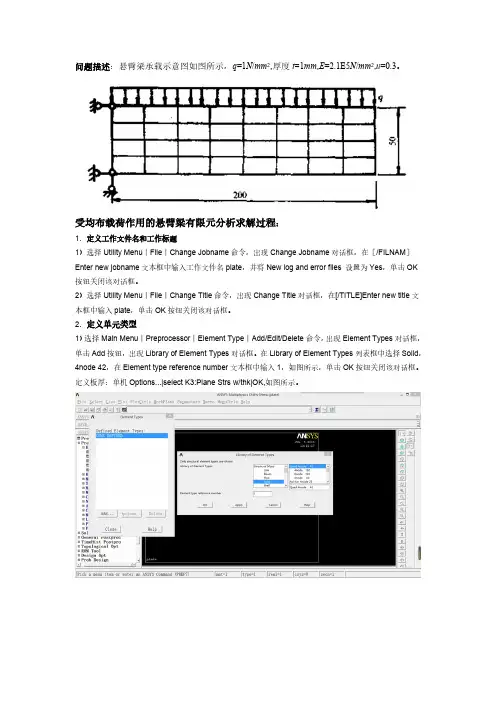
问题描述：悬臂梁承载示意图如图所示，q=1N/mm2,厚度t=1mm,E=2.1E5N/mm2,u=0.3。
受均布载荷作用的悬臂梁有限元分析求解过程：1．定义工作文件名和工作标题1）选择Utility Menu︱File︱Change Jobname命令，出现Change Jobname对话框，在［/FILNAM］Enter new jobname文本框中输入工作文件名plate，并将New log and error files 设置为Yes，单击OK 按钮关闭该对话框。
2）选择Utility Menu︱File︱Change Title命令，出现Change Title对话框，在[/TITLE]Enter new title文本框中输入plate，单击OK按钮关闭该对话框。
2．定义单元类型1）选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令，出现Element Types对话框，单击Add按钮，出现Library of Element Types对话框。
在Library of Element Types列表框中选择Solid，4node 42，在Element type reference number文本框中输入1，如图所示，单击OK按钮关闭该对话框。
定义板厚：单机Options...|select K3:Plane Strs w/thk|OK,如图所示。
3．定义材料性能参数1）选择Main Menu︱Preprocessor︱Material Props︱Material Models命令，出现Define Material Model Behavior对话框。
2）在Material Models Available一栏中依次单击Structural、Linear、Elastic、Isotropic选项（如图3.5所示），出现Linear Isotropic Properties for Material Number 1对话框，在EX文本框中输入2.1E5，在PRXY文本框中输入0.3，如图所示，单击OK按钮关闭该对话框。
abaqus悬臂梁例题
ABAQUS是一种常用的有限元分析软件，用于模拟和分析工程结构的行为。
下面是一个简单的ABAQUS悬臂梁的例题，以便说明如何进行有限元分析：
问题描述：
考虑一个简单的悬臂梁，长度为L，截面为矩形，要分析该梁的挠度和应力分布。
步骤：
1.建立模型：首先，在ABAQUS中建立一个新模型。
定义悬臂梁的几何参数，如长度L 和梁截面的宽度和高度。
2.创建网格：划分悬臂梁的几何形状，创建有限元网格。
可以选择合适的单元类型，如梁单元或壳单元，以模拟结构行为。
3.应用边界条件：定义悬臂梁的支持条件，通常悬臂梁的一端是固定支持，另一端是自由端。
在ABAQUS中，你可以定义这些支持条件。
4.施加载荷：定义悬臂梁所受的载荷，如集中力、分布载荷等。
5.设置材料属性：指定悬臂梁所用的材料属性，如弹性模量、泊松比等。
6.运行分析：运行有限元分析，ABAQUS将计算悬臂梁的挠度和应力分布。
7.分析结果：分析完成后，你可以查看和可视化分析结果，包括挠度云图、应力云图等，以了解悬臂梁的行为。
这只是一个简单的悬臂梁分析示例，ABAQUS提供了广泛的功能来进行复杂结构的有限元分析。
具体的模型参数和步骤可能会因实际情况而有所不同。
你可以根据你的具体问题和需求来调整和扩展这个示例。
需要在软件中具体设置和模拟这个问题，以获得详细的分析结果。
工程地质数值模拟成绩考核——昆明理工大学本科生课程*****学院：国土资源工程学院科系：地科系专业：勘查111学号：************2014年11 月8 日悬臂梁的有限元分析1.问题概述。
悬臂梁为矩形截面的钢梁，长10m宽1m、高2m，不计梁的自重，弹性模量为220GPa，泊松比为0.2，在悬臂端作用一集中荷载P=1200kN。
试分析该悬臂梁的内力和变形情况。
2.启动ANSYS程序。
(1)在【开始】菜单中依次选取【所有程序】/【ANSYS8.0】/【ConfigureANSYSProducts】选项，打开【ANSYS8.0Launcher】对话框。
(2)选中【FileManagement】选项卡，输入目录名：“D:\ANSYSFX\zhang1\Exam01\ANSYSjs”，输入项目名：“Z101Beam”。
(3)单击按钮运行程序，进入ANSYS使用界面。
3.定义材料、实常数和单元类型。
(1)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】（前处理）/【ElementType】/【Add/Edit/Delete】选项，打开单元类型对话框。
单击按钮，打开单元类型库对话框，在右侧两个列表框中分别选取【Beam】选项和【2Delastic3】选项（简称为Beam3单元，以后叙述中记为【Beam】-【2Delastic3】单元，类似的情况记法相同），如图1-16所示。
单击按钮，再单击【ElementType】对话框中的按钮。
图1-16【LibraryofElementTypes】对话框(2)在【ANSYSMainMenu】菜单中依次选取【Preprocessor】/【RealConstants】/【Add/Edit/Delete】选项，打开实常数对话框，如图1-17所示。
单击按钮，打开Beam3实常数对话框，按照提示输入相应的面积、惯性矩和梁高参数，如图1-18所示。
悬臂梁的有限元分析I. 内容综述悬臂梁的有限元分析是结构工程领域中的一个重要课题，它是一种数值计算方法，通过将连续的结构分解成许多小单元，然后对每个单元进行分析，最终得到整个结构的性能指标。
这种方法可以有效地模拟结构的变形和应力分布情况，为设计和优化提供可靠的依据。
在实际应用中，悬臂梁的有限元分析需要考虑多种因素，如材料属性、几何形状、载荷条件等。
因此在进行分析时，需要选择合适的模型和网格尺寸，并对边界条件进行合理设定。
此外由于悬臂梁的结构特点，其在不同位置的受力情况也有所不同，因此需要对各个部位进行分别分析。
悬臂梁的有限元分析是一项复杂而重要的工作，只有通过合理的建模和分析方法，才能得到准确的结果，并为实际工程提供有效的指导。
A. 研究背景和意义悬臂梁作为一种常见的结构形式，广泛应用于建筑、桥梁、机械等领域。
然而在实际应用过程中，由于各种因素的影响，悬臂梁的结构性能可能会发生退化，导致结构的安全性受到威胁。
因此对悬臂梁的有限元分析具有重要的研究意义。
有限元分析是一种基于数学模型的工程分析方法，通过将复杂的结构分解为若干个简单的单元，利用计算机模拟这些单元在受力作用下的变形和应力分布，从而预测结构的响应。
近年来随着计算机技术和数学方法的不断发展，有限元分析在工程领域中的应用越来越广泛，已经成为工程设计和施工的重要工具。
对于悬臂梁这种特殊结构，有限元分析不仅可以帮助我们了解其在不同工况下的性能表现，还可以为优化结构设计、提高结构强度和刚度提供理论依据。
此外通过对悬臂梁的有限元分析，我们还可以更好地了解其在使用过程中可能出现的缺陷和损伤，从而为预防事故、保障人员安全提供技术支持。
悬臂梁的有限元分析研究具有很高的实用价值和理论意义，对于推动工程技术的发展、提高人类生活质量具有重要作用。
B. 研究目的和方法本研究旨在通过有限元分析方法，对悬臂梁进行分析，以探究其在不同荷载下的应力分布情况。
我们将采用ANSYS软件进行模拟计算，并通过对计算结果的分析，得出悬臂梁的最大应力、最小应力以及平均应力等关键指标。
Hans Journal of Civil Engineering 土木工程, 2014, 3, 141-147Published Online September 2014 in Hans. /journal/hjce/10.12677/hjce.2014.35017Finite Element Analysis of Static GeometryNonlinear about Cantilever BeamPei Luo, Jianwei TianNational Engineering Laboratory for Fiber Optic Sensing Technology, Wuhan University of Technology, Wuhan Email: zhaojx_2001@Received: Jul. 12th, 2014; revised: Aug. 10th, 2014; accepted: Aug. 20th, 2014Copyright © 2014 by authors and Hans Publishers Inc.This work is licensed under the Creative Commons Attribution International License (CC BY)./licenses/by/4.0/AbstractThe finite element model of geometry nonlinearity about cantilever has been introduced in this paper. The relation of strain-stress about cantilever has been deduced (in range of linearity).Based on this, using finite element analysis soft, the static geometry nonlinearity of cantilever beam structure has been finitely analyzed. The study finds that the existing strain-stress relation is not linear relation when the cantilever beam structure shows the geometry nonlinearity after receiving large deformation, but is nonlinearity, and that the theoretical derivation must be com-puted by using nonlinear system of equations. But the solution of nonlinear equations can use in-crement means of large distortion question, which is T.L means (Lagrange means).KeywordsCantilever Beam, Concentrating Load, Geometry Nonlinearity, Finite Element Analysis悬臂梁静态几何非线性的有限元分析罗裴，田建伟武汉理工大学光纤传感技术国家工程实验室，武汉Email: zhaojx_2001@收稿日期：2014年7月12日；修回日期：2014年8月10日；录用日期：2014年8月20日摘 要介绍了悬臂梁几何非线性的有限元模型，并对悬臂梁的应力应变关系进行了推导(在线性范围内)，在此基础上，利用有限元分析软件，对悬臂梁结构的静态几何非线性进行了有限元分析，研究发现，当悬臂梁结构在受到大变形而出现几何非线性时，现有的应力应变关系不再呈线性关系，而是呈现非线性，其理论推导必须采用非线性方程组来计算，而非线性方程组的求解可采用大变形问题的增量法——T.L 法(拉格朗日法)。
关键词悬臂梁，集中载荷，几何非线性，有限元分析1. 引言几何非线性问题是不采用小位移假设，从几何上严格分析单元体的尺寸、形状变化，得到非线性的几何运动方程，由此造成基本控制方程的非线性问题。
对于小变形问题的研究已经趋于成熟[1] [2]，而结构在受到大载荷的时候，将出现几何非线性，几何非线性的求解比较复杂，但在日常生活中经常遇到。
引起结构非线性行为的原因很多，主要有以下三种原因[3]：几何非线性、材料非线性、状态非线性。
悬臂梁的几何非线性问题是指悬臂梁在平面内的大位移和大转动问题。
在研究这类问题时，除了要考虑应变-位移的非线性关系外，还要考虑悬臂梁的基本特征是随变形而变化的，所以，平衡方程应建立在变形后的位置上。
若仍用变形前的几何位置来描述，将不能反映梁的真实变形情况。
但是，由于变形后的位置是未知的，这就给处理梁的几何非线性问题带来了一定的复杂性。
有限元分析是用于结构分析的有力工具[4]，它能对结构进行理论上的初步模拟，并得出与实际检测结果接近的理论结果，这些结果对后续的实验起着指导作用，因此，要得到理想的实验数据，必须首先进行有限元分析，根据理论模型，设计实验方案，从而获得理想的实际结果。
本文为了获得悬臂梁结构受到静态集中力的作用而产生非线性现象，采用Analysis2013进行有限元模拟，从而获得悬臂梁的非线性应变分布图，这将为悬臂梁的非线性损伤检测奠定理论基础，对后续的损伤实验起指导性作用。
2. 悬臂梁几何非线性有限元模型当物体产生大变形时，代表所研究的点的微小体元在变形的同时可能产生较大的刚性旋转和刚性平移。
为了度量大变形物体的变形状态，必须更精确地研究物体的变形。
几何非线性问题不仅几何方程不同，而且由于产生大变形，应力和应变需重新定义，本构方程、平衡方程或虚功方程需按重新定义的应力和应变表示。
几何非线性有限元法可以仿照线性弹性有限元法，进行离散化并选取单元位移函数后，按几何方程、本构方程和能量原理，建立以节点位移为基本未知量的非线性有限元方程。
在几何非线性有限元法[3] [5]中，可以按Euler 描述，也可以按Lagrange 描述，一般情况下，Lagrange 描述用于固体力学问题，因此，本文采用Lagrange 描述。
以初始构形为参考构形，将初始构形进行有限单元离散，选用固定不动的直角坐标系。
在大变形情况下，Green 应变E 可分解为线性和非线性两部分之和L N E E E =+ (1)式中，L E 为线性应变，N E 为非线性应变。
其中，e L L E B d = (2)e N N E B d = (3)式中，e d 为单元节点位移矢量，矩阵B L 是Green 应变线性部分与单元节点位移之间的转换矩阵。
将(2)、(3)两式代入(1)式，得()e e L N E B B d Bd =+=(4) 式(4)给出Green 应变和单元节点位移矢量之间的关系，包含非线性项，故Green 应变矢量和单元节点位移矢量之间是非线性关系。
应用虚功原理，将Green 应变式(4)两边同时变分，可得e E B d δδ=⋅ (5)其中，L N B B B =+。
将(5)式代入由Green 应变和Kirchhoff 应力表述的虚功方程，整理得离散系统的平衡方程为()00d 0T V d B S V F ψ⋅=−=∫ (6)式中，F 为有限元离散系统的外力等效节点力。
上式即为有限元系统的位移形式的平衡方程组。
若用矩阵形式表示，则为e e e TK dd F =⋅ (7) e e e e T DL DN SK K K K =++ 式中，e TK 即为单元的切线刚度矩阵，为对称矩阵。
e DL K 是小位移刚度矩阵，e DN K 是由大位移引起的，称为初位移矩阵或大位移矩阵，矩阵e SK 是由于应力状态S 引起的切线刚度，通常称为几何矩阵或初应力矩阵，F e 为单元外部荷载的等效节点力。
有限元非线性方程组的求解过程是一个非常复杂的过程，可采用大变形问题的增量法——拉格朗日法(即T.L 法)来求解，T.L 法是一个复杂的过程，在此不多赘述。
3. 悬臂梁应力-应变关系的理论计算在悬臂梁上粘贴应变片。
h 代表梁的厚度，b 代表应变片所在位置宽度，X 代表应变片中心距离自由力端的距离，L 表示单臂梁自由端到固定端的距离。
悬臂梁的材料为不锈钢，弹性模量在196~216 Gpa 之间，故取弹性模量210Gpa E =。
由材料力学[6]可知：悬臂梁的抗弯截面系数26bh W = (8) 贴应变片位置的弯矩为FLX M FX L == (9) 贴应变片位置的应力为26M FX W bh σ== (10) 式中，F 为悬臂梁的受力，L 为受力点到固定端的距离，b 为梁截面的宽，h 为梁截面的高。
贴应变片位置的应变为E σε=(11)综合上面各式有： 26FX bh Eε= (12) 这就是悬臂梁的应变计算公式，由上式可知，当悬臂梁为等截面梁时，受力位置固定时，悬臂梁的应变只与待计算位置有关，即应变与悬臂梁上各点的位置坐标呈线性关系。
而当悬臂梁呈几何非线性时，这种关系将被打破，应变位置将发生变化，不能再应用这种关系来计算悬臂梁的应变。
要详细了解悬臂梁的应变分布状况，采用有限元软件对悬臂梁进行分析，可以得到悬臂梁的整体应变分布状况。
悬臂梁发生大变形时，其应力应变也将发生大的变化，此时不能再采用前面的计算线性范围内的公式，而应该采用非线性方程来计算应力应变之间的关系，即拉格朗日法。
4. 悬臂梁结构的有限元静态非线性模拟悬臂梁结构是目前最常见的一种结构，并且计算简单，易于分析。
本文针对具体的悬臂梁结构，对悬臂梁在受大载荷情况下的静态非线性特性进行了有限元模拟，待模拟的悬臂梁的基本尺寸如下：弹性模量:210Gpa E =，泊松比：0.3ν=，长：400 mm ，宽：70 mm ，厚：2 mm 。
应用ansys2013进行有限元模拟，图1~4为悬臂梁的非线性静态分析，其临界屈曲载荷为：()32221190222πππ2100.0781012144N 441240.4Bh E EI F D D −××××××====××， 要进行悬臂梁的几何非线性的有限元分析，施加在悬臂梁端的荷载必须大于临界屈曲荷载，才能使悬臂梁呈非线性。
采用有限元分析的悬臂梁的几何非线性所得到的结果如下各图。
