悬臂梁ansys有限元分析求最大挠度

悬臂梁受力分析报告高一博2016.11.13西安理工大学机械与精密仪器工程学院摘要利用ANSYS对悬臂梁进行有限元静力学分析,得到悬臂梁的最大应力和挠度位移。

从而校验结构强度和尺寸定义，从而对结构进行最优化设计修正。

关键词：悬臂梁，变形分析，应力分析目录一.问题描述： (4)二.分析的目的和内容： (4)三.分析方案和有限元建模方法： (4)四.几何模型 (4)五．有限元模型 (4)六．计算结果： (5)七.结果合理性的讨论、分析 (8)八．结论 (8)参考文献 (8)一.问题描述：现有一悬臂梁，长500MM，一端固定，另外一端施加一个竖直向下的集中力200N。

其截面20MMX20MM的矩形，现在要分析该梁的在集中力作用下产生的位移，应力和局部应力。

二.分析的目的和内容：1.观察悬臂梁的变形情况；2.观察分析悬臂梁的应力变化；3.找出其最大变形和最大应力点，分析形成原因；三.分析方案和有限元建模方法：1.使用ANSYS-modeling-create-volumes-block建模，2.对梁进行材料定义，网格划分。

3.一端固定，另外一端施加一个向下的200N的力。

4.后处理中查看梁的应力和变形情况。

四.几何模型500X20X20的梁在在ANSYS中进行绘制.由于结构简单规则，无需简化。

五．有限元模型单元类型：solid brick8node45材料参数：弹性模量2e+11pa,泊松比0.3边界条件：一端固定，一端施加载荷载荷：F=200N划分网格后的悬臂梁模型六．计算结果：变形位移图等效应力图局部应力图七.结果合理性的讨论、分析1.位移分析：在变形位移图上，在约束端位移最小为零，受压端位移最大。

与实际结果一致。

2.应力分析：在应力图上，应力最大处在约束端，而最小的位于受压端，与变形图相对应。

通过材料力学计算可知约束端的所受弯矩最大。

两个结果印证无误。

3.局部应力分析：在局部应力图上，可以看出在固定端上表面存有较大的应力，且为拉应力，受压端直角尖处有最大应力，从形成原因上分析属于尖角处应力集中。

1 研究目的与问题阐述1.1 基本研究目的(1) 掌握ANSYS软件的基本几何形体构造、网格划分、边界条件施加等方法。

(2) 熟悉有限元建模、求解及结果分析步骤和方法。

(3) 利用ANSYS软件对梁结构进行有限元计算。

(4) 研究不同泊松比对同一位置应力的影响。

1.2 基本问题提出图1.1 模型示意图如图1.1所示，当EX=3.01e6，F=5000N，悬臂梁杆一端固定，另一端为自由端。

当悬臂梁的泊松比u为：0.2、0.25、0.3、0.35、0.4时，确定同一位置的应力分布，得出分布云图。

采用二维模型，3*0.09m。

2 软件知识学习2.1 软件的使用与介绍软件介绍：ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。

由世界上最大的有限元分析软件公司之一的美国ANSYS开发，它能与多数CAD软件接口，实现数据的共享和交换，如Pro/Engineer, NASTRAN, Alogor, I－DEAS, AutoCAD等，是现代产品设计中的高级CAE工具之一。

ANSYS有限元软件包是一个多用途的有限元法计算机设计程序，可以用来求解结构、流体、电力、电磁场及碰撞等问题。

因此它可应用于以下工业领域：航空航天、汽车工业、生物医学、桥梁、建筑、电子产品、重型机械、微机电系统、运动器械等。

软件主要包括三个部分：前处理模块，分析计算模块和后处理模块。

前处理模块提供了一个强大的实体建模及网格划分工具，用户可以方便地构造有限元模型；分析计算模块包括结构分析（可进行线性分析、非线性分析和高度非线性分析）、流体动力学分析、电磁场分析、声场分析、压电分析以及多物理场的耦合分析，可模拟多种物理介质的相互作用，具有灵敏度分析及优化分析能力；后处理模块可将计算结果以彩色等值线显示、梯度显示、矢量显示、粒子流迹显示、立体切片显示、透明及半透明显示（可看到结构内部）等图形方式显示出来，也可将计算结果以图表、曲线形式显示或输出。

基于ANSYS和SolidWorks的有限元仿真对比研究作者：耿贺松覃天意李明伟来源：《科学与信息化》2019年第12期摘要结合ANSYS和SolidWorks有限元分析过程，以工字形悬臂梁为优化对象，进行了ANSYS与SolidWorks有限元模拟的对比研究。

首先，利用材料力学知识计算出经典工字悬臂梁的最大应力及挠度理论值。

然后，分别利用ANSYS和SolidWorks软件，对工字悬臂梁模型进行了有限元分析。

最后，将理论值与有限元分析结果进行了比较，总结出两种软件在分析过程中的优缺点，为ANSYS和SolidWorks在有限元模拟和优化中的应用提供参考。

关键词工字悬臂梁；ANSYS；SolidWorks；有限元分析Abstract Combined with the finite element analysis process of ANSYS and SolidWorks， an I-shaped cantilever beam is optimized using ANSYS and SolidWorks for comparative study. First， the theoretical values of the maximum stress and deflection of a classical I-shaped cantilever beam are calculated by material mechanics knowledge. Then， ANSYS and SolidWorks are respectively used to carry out finite element analysis on the I-shaped cantilever beam model. Finally， the theoretical values are compared with the results of finite element analysis. The advantages and disadvantages of the two kinds of software in the analysis process are summarized， so as to provide reference for the application of ANSYS and SolidWorks in the finite element simulation optimization.Key words I-shaped cantilever beam； ANSYS； SolidWorks； Finite element analysis引言结构是工程应用中的一个重要环节，如果结构不合理，可能导致构件的承载力不够或者由于结构过于复杂造成原材料大量浪费[1]，因此需要进行结构优化。

有限元分析及应用报告题目：利用ANSY软件分析带孔悬臂梁姓名：xxx学号：xxx班级：机械xxx学院: 机械学院指导老师：xxx二零一五年一月问题概述图示为一隧道断面，其内受均布水压力q,外受土壤均布压力p；试采用不同单元计算断面内的位移及应力，并分别分析q=0或p=0时的位移和应力分布情况。

（材料为钢，隧道几何尺寸和压力大小自行确定）本例假定内圆半径为1m，外圆半径为2m，外受均布压力p=10000pa ，内受均布压力为q=20000pa 。

问题分析由题目可知，隧道的的长度尺寸远远大于截面尺寸，并且压力在长度方向上均匀分布，因此本问题可以看作为平面应变问题。

由于在一个截面内，压力沿截面四周均匀分布，且截面是对称的圆环，所以可以只取截面1/4进行有限元建模分析，这样不仅简化了建模分析过程，也能保证得到精确的结果。

由以上分析，可以选取单元类型plane42进行有限元分析，在option中选择K3 为plane strain。

三.有限元建模1.设置计算类型由问题分析可知本问题属于平面静应力问题，所以选择preferences 为structure 。

2.单元类型选定选取平面四节点常应变单元plane42,来计算分析隧道截面的位移和应力。

由于此问题为平面应变问题，在设置element type的K3时将其设置为plane strain。

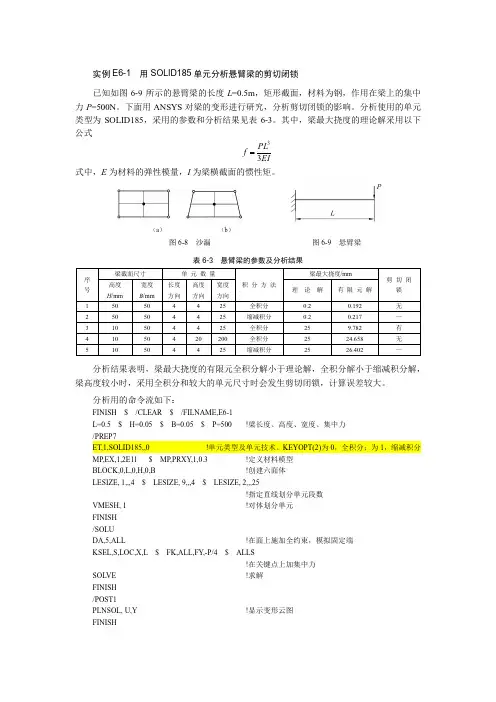
3.材料参数隧道的材料为钢，则其材料参数：弹性模量E=2.1e11，泊松比(T =0.34.几何建模按照题目所给尺寸利用ansys的modeling依次建立keypoint :1(0,0),2(1,0),3(2,0),4(0,2),5(0,1) , create LINES 依次连接keypoint 2、3和4、5即可创建两条直线，使用create article 的By cent & radius 创建两条圆弧。

create AREAS依次选择四条线即建立了所需的1/4截面。

Ansys Workbench是一款广泛应用于工程领域的有限元分析软件，可以用于解决各种结构力学、流体动力学、电磁场等问题。

本文将以Ansys Workbench为例，介绍一个结构力学的例题，并详细讲解解题过程。

1. 问题描述假设有一个悬臂梁，在梁的自由端施加一个集中力，要求计算梁的应力分布和挠度。

2. 建模打开Ansys Workbench软件，新建一个静力学分析项目。

在几何模型中，画出悬臂梁的截面，并确定梁的长度、宽度和厚度。

在材料属性中，选择梁的材料，并输入对应的弹性模量和泊松比。

在约束条件中，将梁的支座固定，模拟悬臂梁的真实工况。

在外部荷载中，施加一个与梁垂直的集中力，确定力的大小和作用位置。

3. 网格划分在建模结束后，需要对悬臂梁进行网格划分。

在Ansys Workbench 中，可以选择合适的网格划分方式和密度，以保证计算结果的准确性和计算效率。

通常情况下，悬臂梁的截面可以采用正交结构网格划分，梁的长度方向可以采用梁单元网格划分。

4. 设置分析类型在网格划分完成后，需要设置分析类型为结构静力学。

在分析类型中，可以选择加载和约束条件，在求解器中，可以选择计算所需的结果类型，如应力、应变、位移等。

5. 求解和结果分析完成以上步骤后，可以提交计算任务进行求解。

Ansys Workbench软件会自动进行计算，并在计算完成后给出计算结果。

在结果分析中，可以查看悬臂梁的应力分布图和挠度图，进一步分析梁的受力情况和变形情况。

6. 参数化分析除了单一工况下的分析，Ansys Workbench还可以进行参数化分析。

用户可以改变材料属性、外部加载、几何尺寸等参数，快速地进行批量计算和结果对比分析，以得到最优的设计方案。

7. 结论通过Ansys Workbench对悬臂梁的结构分析，可以得到悬臂梁在外部加载下的应力分布和挠度情况，为工程设计和优化提供重要参考。

Ansys Workbench还具有丰富的后处理功能，可以绘制出直观的分析结果图，帮助工程师和研究人员更好地理解和使用分析结果。

悬臂梁的受力分析实验目的：学会使用有限元软件做简单的力学分析，加深对材料力学相关内容的理解，了解如何将理论与实践相结合。

实验原理：运用材料力学有关悬臂梁的的理论知识，求出在自由端部受力时，其挠度的大小，并与有限元软件计算相同模型的结果比较 实验步骤： 1，理论分析如下图所示悬臂梁，其端部的抗弯刚度为33EIl ，在其端部施加力F ，可得到其端部挠度为：33Fl EI ，设其是半径为0.05米，长为1米，弹性模量11210E =⨯圆截面钢梁，则其可求出理论挠度值3443Fl ERωπ=，先分别给F 赋值为100kN ，200kN ，300kN ，400kN ，500kN .计算结果如下表：F 100000 200000 300000 400000 500000 ω（m ）0. 033950. 0679060. 1018590. 13581230. 16976542有限元软件（ansys ）计算： （1）有限元模型如下图：模型说明,本模型采用beam188单元，共用11个节点分为10个单元，在最有段施加力为F计算得到端部的挠度如下表所示，F 100000 200000 300000 400000 500000S（端部位移）-0.34079E-01-0.680158E-01-1.020237E-01-1.360136E-01-1.700395E-01得到梁端部在收到力为100kN时Y方向的位移云图：将理论计算结果与ansys分析结果比较如下表：力F（N）100000 200000 300000 400000 500000 理论值0. 03395 0. 067906 0. 101859 0. 1358123 0. 1697654 实验值-0.34079E-01-0.680158E-01-1.020237E-01-1.360136E-01-1.700395E-01相对误差0.37% 0.16% 0.16% 0.15% 0.16%通过比较可得，理论值与软件模拟结果非常接近，在力学的学习中只要能熟练的掌握理论知识，在软件模拟过程中便可做到心中有数，在本实验中理论值是通过材料力学中得一些假设得到的一个解析解，而实验也是用了相同的假设，并将梁离散为十个单元，得到数值解，因此和理论值的误差是不可避免的，通过增加离散单元的个数可以有效的减少误差，但是增大了计算量，因此在实践中，只要选取合适的离散单元数，能够满足实践要求即可，这就需要有更加扎实有限元知识作为指导。