九年级数学中考复习专题之圆的考察：圆周角定理的运用(一)

九年级下册数学圆周角定理一、圆周角定理的定义圆周角定理指的是，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

用数学表达式表示为：在同圆或等圆中，若弧AB与弧CD相等，则AB所对的圆周角∠ACB = CD所对的圆周角∠ADC，且∠ACB = ∠ADC = ∠AOB / 2（其中O为圆心，A、B、C、D为各点）。

二、圆周角定理的证明证明圆周角定理可以采用以下步骤：1. 根据题目给出的条件，作直径上的圆周角。

2. 连接圆心和圆周角的顶点，并将直径平分该角。

3. 由于直径平分该角，所以该角是直角的一半。

4. 由于直角的一半是45度，所以该圆周角等于45度。

5. 根据等腰三角形的性质，我们可以证明圆周角所对的弧等于半圆的弧。

6. 由此可以得出结论，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

三、圆周角定理的应用圆周角定理是解决几何问题的重要工具之一，它可以应用于以下方面：1. 确定圆的中心：通过测量同弧所对的圆周角的大小，可以确定圆的中心。

2. 计算角度：通过圆周角定理，可以计算出圆中任意角度的大小。

3. 证明等腰三角形：利用圆周角定理可以证明等腰三角形的一些性质和判定方法。

4. 解决几何问题：利用圆周角定理可以解决一些与圆有关的几何问题。

四、圆周角定理的推论1. 同弧或等弧所对的圆周角相等；反之，同弧或等弧所对的圆周角相等。

2. 在同圆或等圆中，相等的圆周角所对的弧相等；反之，在同圆或等圆中，相等的弧所对的圆周角相等。

3. 在同圆或等圆中，如果两个圆周角分别是α和β，那么它们所对的弧也满足|α - β| = |⊙o中相等的弧间的比例差|。

这些推论也可以应用于多个等圆的公共点处的情况。

第17课 圆 一⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧辅助线画法：公式：直角三角形内切圆半径三角形内切圆画法：切线长定理：直线与圆的位置关系：圆内接四边形性质：圆内接三角形画法：点与圆的位置关系：圆周角定理：垂径定理：圆中考真题练习1.如图,圆O 的直径AB 垂直于弦CD,垂足是E,∠A=22.50，OC=4,CD 的长为（ ） A.22 B.4 C.24 D.8第1题图 第2题图 第3题图 第4题图2.如图,AB 是⊙O 直径,AC 是⊙O 切线,连接OC 交⊙O 于点D,连接BD,∠C=400．则∠ABD 度数是（ ）A.30°B.25°C.20°D.15° 3.如图,已知⊙O 的直径AB 与弦AC 的夹角为350，过点C 的切线PC 与AB 的延长线交于点P,那么∠P 等于（ ）A.15°B.20°C.25°D.30°4.如图PB 为⊙O 的切线,B 为切点,连结PO 交⊙O 于点A,PA=2,PO=5,则PB 的长度为（ ） A.4 B.10 C.26 D.435.如图,PA ，PB 切⊙O 于A 、B 两点,CD 切⊙O 于点E ，交PA ，PB 于C ，D ．若⊙O 的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是（ ） A.13125 B.512 C.1353 D.1332第5题图 第6题图 第7题图6.如图,小量角器的零度线在大量角器的零度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P 在小量角器上对应的度数为650，那么在大量角器上对应的度数为__________0（只需写出00～900的角度）．7.如图,在⊙O 中，弦CD 垂直于直径AB 于点E,若∠BAD=300，且BE=2,则CD= ．8.如图,A 、B 、C 是⊙O 上的三点,∠AOB=960，则∠ACB= 度．第8题图 第9题图 第`10题图 第11题图9.如图,AB 与⊙O 切于点B,AO=6cm,AB=4cm,则tan ∠A 为10.如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 切⊙O 于点D,连接AD.若∠A=250，则∠C= 度．11.如图,△ABC 为⊙O 内接三角形,AB 为⊙O 直径,点D 在⊙O 上,∠ADC=540，则∠BAC 度数等于 ．12.如图，⊙O 的半径是2，直线l 与⊙O 相交于A 、B 两点，M 、N 是⊙O 上的两个动点，且在直线l 的异侧，若∠AMB=45°，则四边形MANB 面积的最大值是 ．第12题图 第13题图 第14题图 第15题图13.如图,AD 是△ABC 的高,AE 是△ABC 的外接圆⊙O 的直径,且AB=24,AC=5,AD=4,则⊙O 的直径AE= ．14.如图,△ABC 的顶点A 、B 、C 均在⊙O 上,若∠ABC+∠AOC=90°，则∠AOC 的大小是15.如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°，则∠C的度数为16.如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2cm，∠BCD=22°30′，则⊙O的半径为cm．第16题图第17题图第18题图第19题图17.如图,AB、CD是⊙O的两条直径,AE∥CD,BE与CD相交于P点,则OP:AE=.18.如图,AB是直径,AO=2.5,AC=1,CD⊥AB,则CD=_______.19.如图,⊙O是等腰三角形ABC外接圆,AB=AC,D是弧AC中点,∠EAD=114O，则∠CAD在度数=20.如图,设⊙O的半径的为R,且AB=AC=R,则∠BAC=_______.第20题图第21题图第22题图第23题图21.如图,AB为⊙O的弦,∠OAB=75O ,则此弦所对的优弧的圆周角度数为22.如图,在△ABC中,∠C是直角,A=32O18/，以点C为圆心、BC为半径作圆,交AB于点D,交AC于点E,则弧BD的度数是______.23.如图,点O是△ABC的外心,已知∠ACB=110O ,则劣弧AB所对的∠AOB=______度.24.一已知点到圆周上的点的最大距离为m ,最小距离为n .则此圆的半径_____25.有个长、宽分别为8和6的矩形ABCD,现以点A为圆心,若B、C、D至少有一个点在圆内,且至少有一个点在圆外,则⊙A半径r 的范围是________26.在直角坐标系中,⊙O的半径为5厘米,圆心O的坐标为(-1,-4),点P(3,-1)与圆O的位置关系是27.在锐角△ABC中,∠A=50O,若点O为外心,则∠BOC=_____;若点I为内心,则∠BIC=______；若点H为垂心,则∠BHC=________.28.如图,AB是⊙O的直径,C，P是弧AB中点,AB=13,AC=5.求PA的长；29.在图1和图2中,已知OA=OB,AB=24,⊙O的直径为10.（1）如图1,AB与⊙O相切于点C,试求OA的值；（2）如图2,若AB与⊙O相交于D、E两点,且D、E均为AB的三等分点,试求tanA的值．30.如图,半圆的直径AB=10,点C在半圆上,BC=6．(1)求弦AC的长；(2)若P为AB的中点，PE⊥AB交AC于点E,求PE的长．31.已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=12,∠CAD=30°．（1）求证:AD是⊙O的切线；（2）若OD⊥AB,BC=5,求AD的长．32.在△ABC中,∠C=900，以BC上一点O为圆心,以OB为半径的圆交AB•于点M,交BC于点N．（1）求证：BA·BM=BC·BN；（2）如果CM是⊙O的切线,N为OC的中点,当AC=3时,求AB的值．33.如图,AB是⊙O的直径,点E是弧AD上的一点,∠DBC=∠BED．（1）求证：BC是⊙O的切线；（2）已知AD=3,CD=2,求BC的长．第17课圆测试题一日期：月日满分：100分时间：20分钟姓名：得分：1.如图,在⊙O中,弦AB=2a,点C是弧AB的中点,CD⊥AB,CD=b,则⊙O的半径R=______.第1题图第2题图第3题图2.如图,在⊙O中,AO为半径,AB为弦,BC为切线,且OA=AB=BC,则弧BD的度数为；弧DE的度数为_______.3.如图,PA、PB切⊙O于点A、B,BD⊥AP,BD交弧AB于点C,∠CAD=25O ,则∠P的度数为_______.4.如图,ABCD是⊙O1的内接矩形,边AB平行y轴,且AB:BC=3:4,已知⊙O1 的半径为5,圆心O1的坐标是（10,10），矩形四个顶点A、B、C、D的坐标是A______;B______;C______;D_______.第4题图第5题图第6题图5.如图,CD为⊙O的直径,AE切⊙O于点B,DC的延长线交AB于点A,∠DBE=620，则∠A=____度．6.如图,AD是切线,点D是切点,BC是半圆O的直径,AB=BO=2,则AD= ; DC:DB= ；DB= ，DC= ，S△ABD= ．7.如图,在Rt △ABC 中,∠C=90O ,AC=3,BC=5,以点A 为圆心、1为半径作⊙A,又BD 切⊙A 于点D,则切线BD 的长是_______.第7题图 第8题图8.如图,AB 为半圆O 的直径,CB 是半圆O 的切线,B 是切点,AC •交半圆O 于点D,已知CD=1,AD=3，那么cos ∠CAB=________．9.在Rt △ABC 中，∠C=90O ,AC=5,AB=13.(1)以点A 为圆心、4为半径的圆A 与直线BC 的位置关系是_____;(2)以点B 为圆心、以AB 的长为半径的圆B 与直线AC 的位置关系是_____;(3)以点C 为圆心，当半径为______时，圆C 与直线AB 相切。

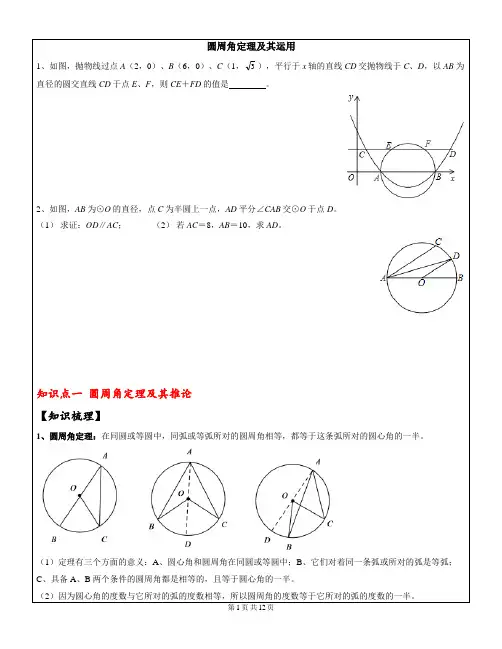
圆周角定理及其运用1、如图，抛物线过点A（2，0）、B（6，0）、C（1，3），平行于x轴的直线CD交抛物线于C、D，以AB为直径的圆交直线CD于点E、F，则CE＋FD的值是。

2、如图，AB为⊙O的直径，点C为半圆上一点，AD平分∠CAB交⊙O于点D。

（1）求证：OD∥AC；（2）若AC＝8，AB＝10，求AD。

知识点一圆周角定理及其推论【知识梳理】1、圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。

（1）定理有三个方面的意义：A、圆心角和圆周角在同圆或等圆中；B、它们对着同一条弧或所对的弧是等弧；C、具备A、B两个条件的圆周角都是相等的，且等于圆心角的一半。

（2）因为圆心角的度数与它所对的弧的度数相等，所以圆周角的度数等于它所对的弧的度数的一半。

（3）定理中的“同弧或等弧”改为“同弦或等弦”结论就不成立。

因为一条弦所对的弧有两段。

2、圆周角定理的推论：推论①：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧是等弧。

推论②：半圆或直径所对的圆周角是直角；圆周角是直角（90°的圆周角）所对的弧是半圆，所对的弦是直径。

推论③：若三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

【例题精讲一】 例1.1、如图，已知A （32，0）、B （0，2），点P 为△AOB 外接圆上的一点，且∠AOP ＝45°，则P 点坐标为 。

（第1题）（第2题）2、如图，点A 、B 、C 在⊙O 上，∠A ＝36°，∠C ＝28°，则∠B ＝（ ） A ．46°B ．72°C ．64°D ．36°3、如图，A 、B 、C 、D 四个点均在⊙O 上，∠AOD ＝70°，AO ∥DC ，则∠B 的度数为 。

（第3 题）（第4 题）4、如图，∠A 是⊙O 的圆周角，则∠A ＋∠OCB ＝ 。

题型全解4 五大性质定理之圆周角定理【知识梳理】1.三个知识点（1）圆周角与圆周角关系：等弧或同弧所对的各个圆周角都相等；即：①∵BĈ=BC ̂，∴∠A=∠D ；②∵AD ̂=AD ̂，∴∠B=∠C ； 注意：不是同弦或等弦，因为一条弦所对的圆周角有两个，相等或互补即：弦BC 所对的圆周角有：∠E 、∠A 、∠D ，其中∠A=∠D ，∠A+∠E=180°（∠D+∠E=180°）（2）圆周角定理与垂径定理综合运用（3）圆周角与直径关系：直径所对的圆周角是90°（或90°的圆周角所对的弦是直径）即：BC 是直径，则∠A=90°；反之也成立：∠A=90°，则BC 是直径；注意：①熟悉两种添辅助线方法：①题中出现直径，常作直径所对的圆周角――直角；②若没有直径的，作直径、延长半径成直径；②拓展：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形D C BA OC B AO 两切线,全等两圆心;连半径证垂直；作垂直证半径321的关系：∠1+∠2=180°；∠2=∠3关系（4）圆内接四边形对角（圆周角）关系：①圆内接四边形的对角的度数和等于180°;②任何一个外角都等于它的内对角; 即：∠C+∠BAD=180°或∠C=∠DAE ；拓展1：如果同一平面内的四个点在同一个圆上，则称这四个点共圆，一般简称为"四点共圆"。

四点共圆有三个性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等;如∠1=∠2;(2)圆内接四边形的对角互补; 如∠DAB+∠DCB=180°;(3)圆内接四边形的外角等于内对角,如∠FBC=∠ADC;(4)△DEC ∽△AEB 、△DEA ∽△CEB;(5) 以上性质逆用,即可判定四点共圆;(6)托勒密定理若ABCD 四点共圆(ABCD 按顺序都在同一个圆上)，那么AB ×DC+BC ×AD=AC ×BD即圆内接四边形中,两组对边的乘积和,会等于两条对角线的乘积.(7)相交弦定理： AE ×CE=BE ×DE;【典型例题】1．如图，A ，B ，C ，D 是⊙O 上的四个点，∠A=60°，∠B=24°，则∠C 的度数为______ED B A O F21ED CB A解析：∠C=∠B=24°̂=CD̂，∠CAD=30°，∠ACD=50°，则∠ADB= ．2．如图，点A，B，C，D在⊙O上，CB解析：∵弧CB=弧CD，∠CAD=30°，∴∠CAD=∠CAB=30°，∴∠DBC=∠DAC=30°，∵∠ACD=50°，∴∠ABD=50°，∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°．3．如图，AB是半圆O的直径，D，E是半圆上任意两点，连结AD，DE，AE与BD相交于点C，要使△ADC与△ABD相似，可以添加一个条件．下列添加的条件其中错误的是（）A. ∠ACD=∠DABB. AD=DEC. AD2=BD•CDD. AD•AB=AC•BD解析：如图，∠ADC=∠ADB，A、∵∠ACD=∠DAB，∴△ADC∽△BDA，故本选项正确；B、∵AD=DE，∴=，∴∠DAE=∠B，∴△ADC∽△BDA，故本选项正确；C、∵AD2=BD•CD，∴AD：BD=CD：AD，∴△ADC∽△BDA，故本选项正确；D、∵AD•AB=AC•BD，∴AD：BD=AC：AB，但∠ADC=∠ADB不是公共角，故本选项错误．故选D．24．直径为10cm的⊙O中，弦AB=5cm，则弦AB所对的圆周角是．解析：连接OA、OB，∵AB=OB=OA，∴∠AOB=60°，∴∠C=30°，∴∠D=180°﹣30°=150°，∴弦AB所对的圆周角是30°或150°．5. 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是____解：由图可知，OA=10，OD=5，在Rt△OAD中，∵OA=10，OD=5，AD=5√3，∴tan∠1=AD/OD=√3，∠1=60°，同理可得∠2=60°，∴∠AOB=∠1+∠2=60°+60°=120°，∴圆周角的度数是60°或120°6．如图，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA，OB，BC，若∠ABC=20°，则∠AOB的度数是________解析：∵∠ABC=20°，∴∠AOC=40°，∵AB是⊙O的弦，OC⊥AB，∴∠AOC=∠BOC=40°，∴∠AOB=80°7．如图，BC是⊙O的弦，OA⊥BC，∠AOB=70°，则∠ADC的度数是_____解析：∵A 、B 、C 、D 是⊙O 上的四点，OA ⊥BC ，∴弧AC=弧AB ，∴∠ADC=12∠AOB （等弧所对的圆周角是圆心角的一半）；又∠AOB=70°，∴∠ADC=35°．8．如图，点A ，B ，C ，D 都在半径为2的⊙O 上，若OA ⊥BC ，∠CDA=30°，则弦BC=____【分析】根据垂径定理得到CH=BH ，=，根据圆周角定理求出∠AOB ，根据正弦的定义求出BH ，计算即可． 解：∵OA ⊥BC ，∴CH=BH ，=，∴∠AOB=2∠CDA=60°，∴BH=OB •sin ∠AOB=√3，∴BC=2BH=2√3，9．如图，⊙O 的半径为5，AB 为弦，点C 为的中点，若∠ABC=30°，则弦AB 的长为___5√3【分析】连接OC 、OA ，利用圆周角定理得出∠AOC=60°，再利用垂径定理得出AB 即可．解：连接OC 、OA ，∵∠ABC=30°，∴∠AOC=60°，∵AB 为弦，点C 为的中点，∴OC ⊥AB ， 在Rt △OAE 中，AE=，∴AB=5√3，10.如图，△ABC 是⊙O 的内接三角形，∠C=30°，⊙O 的半径为5，若点P 是⊙O 上的一点，在△ABP 中，PB=AB ，则PA 的长为_______解析：连接OA 、OB 、OP ，∵∠C=30°，∴∠APB=∠C=30°，∵PB=AB ，∴∠PAB=∠APB=30°∴∠ABP=120°，∵PB=AB ，∴OB ⊥AP ，AD=PD ，∴∠OBP=∠OBA=60°，∵OB=OA ，∴△AOB 是等边三角形，∴AB=OA=5，则Rt △PBD 中，PD=cos30°•PB=√32×5=5√32，∴AP=2PD=5√3，11．如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B的度数是________解：∵OA=OC，∴∠C=∠OAC=32°，∵BC是直径，∴∠B=90°﹣32°=58°12．如图，AB为⊙O的直径，CD是⊙O的弦，∠ADC=35°，则∠CAB的度数为______解：由圆周角定理得，∠ABC=∠ADC=35°，∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB=90°﹣∠ABC=55°，13．如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=3，AB=5，OD⊥BC于点D，则OD的长为解：∵AB是⊙O的直径，∴∠ACB=90°，∴AC==4，∵OD⊥BC，∴BD=CD，而OB=OA，∴OD为△ABC的中位线，∴OD=AC=×4=2．14．如图，⊙A 过点O （0，0），C （√3，0），D （0，1），点B 是x 轴下方⊙A 上的一点，连接BO ，BD ，则∠OBD 的度数是__________解析：连接DC ，∵C （√3，0），D （0，1），∴∠DOC=90°，OD=1，OC=√3，∴∠DCO=30°，∴∠OBD=30°，15．如图，⊙O 的半径为1，△ABC 是⊙O 的内接等边三角形，点D 、E 在圆上，四边形BCDE 为矩形，这个矩形的面积是_______解析：连接BD ，∵∠E=90°，可知BD 是直径，作OM ⊥BC 于点M ，易知∠BOM=∠A=60°，∵OB=1，∴OM=12，BM=√32，∴BC=√3，CD=2OM=1，∴S 矩形BCDE =√316.如图，△ABC 内接于⊙O ，AH ⊥BC 于点H ，若AC=24，AH=18，⊙O 的半径OC=13，则AB=______解析：求线段长，要么针勾股定理，要么相似，由图形及题目条件判断，首先考虑相似，由于求AB ，且知AH 的长，我们选△ABH 跟某个三角形相似，由于△ABH 是直角三角形，所以需构造一个直角三角形，且含AC 为边的直角三角形与△ABH 相似，所以连OA 并延长AO 交⊙O 于点M ，连MC ，由于AM 是直径，∴∠ACM=90°，∵AĈ=AC ̂，∴∠B=∠AMC ，∴△ABH ∽△AMC ，∴AB AM =AH AC ，即AB 26=1824，∴AB=392 M A B C D E OH O A B CMA B C D E O O ED C B A H H O A B C O M C B A17．如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．（1）求证：四边形ABFC是菱形；（2）若AD=7，BE=2，求半圆和菱形ABFC的面积．解析：（1）证明：∵AB是直径，∴∠AEB=90°，∴AE⊥BC，∵AB=AC，∴BE=CE，∵AE=EF，∴四边形ABFC是平行四边形，∵AC=AB，∴四边形ABFC是菱形．（2）设CD=x．连接BD．∵AB是直径，∴∠ADB=∠BDC=90°，∴AB2﹣AD2=CB2﹣CD2，∴（7+x）2﹣72=42﹣x2，解得x=1或﹣8（舍弃）∴AC=8，BD==，∴S菱形ABFC=8．∴S半圆=•π•42=8π．18．如图：四边形ABCD内接于⊙O，E为BC延长线上一点，若∠A=72°，则∠DCE= ．解：∵四边形ABCD是⊙O的内接四边形，∴∠A+∠DCB=180°，又∵∠DCE+∠DCB=180°∴∠DCE=∠A=72°19．如图所示，四边形ABCD为⊙O的内接四边形，∠BCD=120°，则∠BOD=______解：∵四边形ABCD为⊙O的内接四边形，∴∠A=180°﹣∠BCD=60°，由圆周角定理得，∠BOD=2∠A=120°，20．如图，点B，C，D在⊙O上，若∠BCD=130°，则∠BOD的度数是_______解：圆上取一点A，连接AB，AD，∵点A、B，C，D在⊙O上，∠BCD=130°，∴∠BAD=50°，∴∠BOD=100°，21．如图，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC=40°，则∠D的度数为________解析：∵∠BOC=40°，∴∠OBC=70°，∴∠D=180°-70°=110°22. 如图，四边形ABCD 是⊙O 的内接四边形，DP//AC ，交BA 的延长线于P ，求证：AD ·DC=PA ·BC解析：连接BD ，∵DP//AC ，∴∠PDA=∠DAC ，∵∠DAC=∠DBC ，∴∠PDA=∠DBC ，∵四边形ABCD 是圆内接四边形，∴∠DAP=∠DCB ，∴△PAD ∽△DCB ，∴PA ：DC=AD ：BC ，即AD ·DC=PA ·BCD B。

九年级圆周角定理知识点圆周角是在数学几何中的一个重要概念，它与圆形的内角和外角有着密切的关系。

在九年级的几何学学习中，圆周角定理是一个不可或缺的内容。

在本文中，将详细介绍九年级圆周角定理的知识点。

1. 圆周角的定义在一个圆上，连接圆心和圆上两点，所对的角被称为圆周角。

圆周角的尺寸是以弧度为单位进行度量的。

一个完整的圆周角等于360°或2π弧度。

这意味着一个圆周角的度数恰好等于所对弧的弧度数。

2. 圆周角定理圆周角定理是指，在同一个圆中，对应于相同弧的圆周角相等。

换句话说，如果两个圆周角对应于同一个圆上的相同弧，那么这两个角的大小是相等的。

圆周角定理可以用数学表达式来表示：∠AOC = ∠ABC其中∠AOC和∠ABC分别表示对应于相同弧AC的两个圆周角的度数。

3. 圆周角的相关性质除了圆周角定理，还有一些与圆周角相关的性质需要了解。

（1）圆周角定理的逆定理：如果两个角对应于同一个圆上的不同弧，那么这两个角的度数是不等的。

（2）圆周角等于直径角：一个圆上的直径所对应的圆周角恰好等于180°或π弧度。

（3）圆周角的其他性质：圆周角与圆上的弧长有关，根据圆周角的度数可以计算对应的弧长。

4. 圆周角定理的应用圆周角定理是解决各种几何问题的重要工具。

通过应用圆周角定理，我们可以求解关于弧长、角度和半径之间的问题。

例如，可以通过已知弧长计算对应的圆周角，或者通过已知角度计算对应的弧长。

在现实生活中，圆周角定理也有一些实际应用。

例如，在建筑工程中，可以利用圆周角定理来测量圆形表面的角度和长度。

在天文学中，圆周角定理也被广泛用于计算天体的运动轨迹和距离。

总结：本文详细介绍了九年级圆周角定理的知识点。

圆周角的定义和圆周角定理是理解和应用圆周角的基础。

此外，我们还学习了圆周角的其他性质和一些实际应用。

通过掌握这些知识，我们能够更好地理解和解决与圆周角相关的几何问题。

2021年九年级数学中考复习专题之圆的考察：相交弦定理的运用（一）一．选择题1．如图，⨀O的两条弦AB、CD相交于点E，AC和DB的延长线交于点P，下列结论中成立的是（）A．PC•CA＝PB•BD B．CE•AE＝BE•EDC．CE•CD＝BE•BA D．PB•PD＝PC•PA2．如图，在⊙O中，弦AC，BD交于点E，连结AB、CD，在图中的“蝴蝶”形中，若AE＝，AC＝5，BE＝3，则BD的长为（）A．B．C．5 D．3．如图，⊙O的弦AB、CD相交于点P，若AP＝6，BP＝8，CP＝4，则CD长为（）A．16 B．24 C．12 D．不能确定4．如图，正方形ABCD内接于⊙O，点P在劣弧AB上，连接DP，交AC于点Q．若QP＝QO，则的值为（）A．B．C．D．5．如图，矩形ABCD为⊙O的内接四边形，AB＝2，BC＝3，点E为BC上一点，且BE＝1，延长AE交⊙O于点F，则线段AF的长为（）A．B．5 C．+1 D．6．如图，⊙O的弦AB、CD相交于点P，若AP＝3，BP＝4，CP＝2，则CD长为（）A．6 B．12 C．8 D．不能确定7．如图，⊙O的直径AB与弦CD交于点E，AE＝6，BE＝2，CD＝2，则∠AED的度数是（）A．30°B．60°C．45°D．36°8．如图，点P为弦AB上的一点，连接OP，过点P作PC⊥OP，PC交⊙O于C，且⊙O的半径为3．若AP＝4，PB＝1，则OP的长是（）A．2 B．2C．D．9．在⊙O中，弦AB和CD相交于P，且AB⊥CD，如果AP＝4，PB＝4，CP＝2，那么⊙O的直径为（）A．4 B．5 C．8 D．1010．如图，圆中两条弦AC，BD相交于点P．点D是的中点，连结AB，BC，CD，若BP＝，AP＝1，PC＝3．则线段CD的长为（）A．B．2 C．D．二．填空题11．如图，⊙O中，弦AB、CD相交于点P，若AP＝5，BP＝4，CP＝3，则DP为．12．如图，已知⊙O的两条弦AB、CD相交于点E，且E分AB所得线段比为1：3，若AB＝4，DE﹣CE＝2，则CD的长为．13．如图，⊙O的弦AB、CD相交于点E，若AE：DE＝3：5，则AC：BD＝．14．如图，在⊙O中，弦BC，DE交于点P，延长BD，EC交于点A，BC＝10，BP＝2CP，若＝，则DP的长为．15．如图，⊙O的弦AB、CD相交于点E，若CE：BE＝2：3，则AE：DE＝．三．解答题16．如图，弦AB与CD相交于⊙O内一点P，PC＞PD．（1）试说明：△PAC∽△PDB；（2）设PA＝4，PB＝3，CD＝8，求PC、PD的长．17．如图，在⊙O中，弦AD，BC相交于点E，连接OE，已知AD＝BC，AD⊥CB．（1）求证：AB＝CD；（2）如果⊙O的直径为10，DE＝1，求AE的长．18．九年级学生小刚是一个喜欢看书的好学生，他在学习完第二十四章圆后，在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理（圆内的两条相交弦，被交点分成的两条线段长的积相等），非常好奇，仔细阅读原来就是：PA•PB＝PC•PD，小刚很想知道是如何证明的，可已证明部分污损看不清了，只看到辅助线的做法，分别连结AC、BD．聪明的你一定能帮他证出，请在图1中做出辅助线，并写出详细的证明过程．小刚又看到一道课后习题，如图2，AB是⊙O弦，P是AB上一点，AB＝10cm，PA＝4cm，OP＝5cm，求⊙O的半径，愁坏了小刚，乐于助人的你肯定会帮助他，请写出详细的证明过程．19．如图，（1）已知：P为半径为5的⊙O内一点，过P点最短的弦长为8，则OP＝（2）在（1）的条件下，若⊙O内有一异于P点的Q点，过Q点的最短弦长为6，且这两条弦平行，求PQ的长．（3）在（1）的条件下，过P点任作弦MN、AB，试比较PM•PN与PA•PB的大小关系，且写出比较过程．你能用一句话归纳你的发现吗？（4）在（1）的条件下，过P点的弦CD＝，求PC、PD的长．20．请阅读下列材料：圆内的两条相交弦，被交点分成的两条线段长的积相等．即如图1，若弦AB、CD交于点P，则PA•PB＝PC•PD．请你根据以上材料，解决下列问题．已知⊙O的半径为2，P是⊙O内一点，且OP＝1，过点P任作﹣弦AC，过A、C两点分别作⊙O的切线m和n，作PQ⊥m于点Q，PR⊥n于点R．（如图2）（1）若AC恰经过圆心O，请你在图3中画出符合题意的图形，并计算：的值；（2）若OP⊥AC，请你在图4中画出符合题意的图形，并计算：的值；（3）若AC是过点P的任一弦（图2），请你结合（1）（2）的结论，猜想：的值，并给出证明．参考答案一．选择题1．解：∵∠P＝∠P，∠A＝∠D，∴△PAB∽△PDC，∴＝，∴PB•PD＝PC•PA，故选：D．2．解：EC＝AC﹣AE＝，由相交弦定理得，AE•EC＝DE•BE，则DE＝＝，∴BD＝DE+BE＝，故选：B．3．解：∵AP•BP＝CP•DP，∴PD＝，∵AP＝6，BP＝8，CP＝4，∴PD＝12，∴CD＝PC+PD＝12+4＝16．故选：A．4．解：如图，设⊙O的半径为r，QO＝m，则QP＝m，QC＝r+m，QA＝r﹣m．在⊙O中，根据相交弦定理，得QA•QC＝QP•QD．即（r﹣m）（r+m）＝m•QD，所以QD＝．连接DO，由勾股定理，得QD2＝DO2+QO2，即，解得所以，故选：D．5．解：∵四边形ABCD是矩形，∴∠B＝90°，∴AE＝＝＝，∵BC＝3，BE＝1，∴CE＝2，由相交弦定理得：AE•EF＝BE•CE，∴EF＝＝，∴AF＝AE+EF＝；故选：A．6．解：∵AP•BP＝CP•DP，∴PD＝，∵AP＝3，BP＝4，CP＝2，∴PD＝6，∴CD＝PC+PD＝2+6＝8．故选：C．7．解：连接OD，过圆心O作OH⊥CD于点H．∴DH＝CH＝CD（垂径定理）；∵CD＝2，∴DH＝．又∵AE＝6，BE＝2，∴AB＝8，∴OA＝OD＝4（⊙O的半径）；∴OE＝2；∴在Rt△ODH中，OH＝＝＝（勾股定理）；在Rt△OEH中，sin∠OEH＝＝，∴∠OEH＝45°，即∠AED＝45°．8．解：延长CP交圆于一点D，连接OC，∵PC⊥OP，∴PC＝PD，∴PC2＝PA•PB，∵AP＝4，PB＝1，∴PC2＝4×1，∴PC＝2，∴OP＝＝＝．故选：C．9．解：∵AB⊥CD，AP＝PB＝4，∴CD为⊙O的直径，由相交弦定理得，PA•PB＝PC•PD，即2PD＝16，解得，PD＝8，故选：D．10．解：连接OD交AC于H，如图，∵点D是的中点，∴OD⊥AC，AH＝CH＝2，∴PH＝1，∵AP•PC＝BP•PD，∴PD＝＝，在Rt△PDH中，DH＝＝，在Rt△DCH中，CD＝＝．故选：A．二．填空题（共5小题）11．解：由相交弦定理得，PA•PB＝PC•PD，∴5×4＝3×DP，解得，DP＝，故答案为：．12．解：∵E分AB所得线段比为1：3，AB＝4，∴AE＝1，EB＝3，由相交弦定理得，AE•EB＝CE•ED，∴1×3＝CE×（CE+2），解得，CE1＝1，CE2＝﹣3（舍去），则CE＝1，DE＝2，∴CD＝1+3＝4，故答案为：4．13．解：∵弦AB、CD相交于点E，∴∴∠C＝∠B，∠A＝∠D，∴△ACE∽△DBE，∴＝＝，故答案为：3：5．14．解：如图，作CH∥DE交AB于H．设DP＝2a．∵PD∥CH，∴＝＝＝，∴CH＝3a，∵BD：AD＝2：3，∴BD：AD＝BD：BH，∴AD＝BH，∴BD＝AH，∴AH：AD＝2：3，∴CH∥DE，∴＝＝，∴DE＝a，∴PE＝a﹣2a＝a，∵BC＝10，BP：PC＝2：1，∴PB＝，PC＝，∵PB•PC＝PD•PE，∴5a2＝，∴a＝（负根已经舍弃），∴PD＝2a＝．故答案为．15．解：∵⊙O的弦AB、CD相交于点E，∴AE•BE＝CE•DE，∴AE：DE＝CE：BE＝2：3，故答案为：2：3．三．解答题（共5小题）16．（1）证明：由圆周角定理得，∠A＝∠D，∠C＝∠B，∴△PAC∽△PDB；（2）解：由相交弦定理得到，PA•PB＝PC•PD，即3×4＝PC×（8﹣PC），解得，PC＝2或6，则PD＝6或2，∵PC＞PD，∴PC＝6，PD＝2．17．（1）证明：如图，∵AD＝BC，∴＝，∴﹣＝﹣，即＝，∴AB＝CD；（2）如图，过O作OF⊥AD于点F，作OG⊥BC于点G，连接OA、OC．则AF＝FD，BG＝CG．∵AD＝BC，∴AF＝CG．在Rt△AOF与Rt△COG中，，∴Rt△AOF≌Rt△COG（HL），∴OF＝OG，∴四边形OFEG是正方形，∴OF＝EF．设OF＝EF＝x，则AF＝FD＝x+1，在直角△OAF中．由勾股定理得到：x2+（x+1）2＝52，解得x＝5．则AF＝3+1＝4，即AE＝AF+3＝7．18．解：（1）圆的两条弦相交，这两条弦被交点分成的两条线段的积相等．已知，如图1，⊙O的两弦AB、CD相交于E，求证：AP•BP＝CP•DP．证明如下：连结AC，BD，如图1，∵∠C＝∠B，∠A＝∠D，∴△APC∽△DPB，∴AP：DP＝CP：BP，∴AP•BP＝CP•DP；所以两条弦相交，被交点分成的两条线段的积相等．（2）过P作直径CD，如图2，∵AB＝10，PA＝4，OP＝5，∴PB＝10﹣4＝6，PC＝OC+OP＝R+5，PD＝OD﹣OP＝R﹣5，由（1）中结论得，PA•PB＝PC•PD，∴4×6＝（R+5）×（R﹣5），解得R＝7（R＝﹣7舍去）．所以⊙O的半径R＝7cm．19．解：（1）连接OP，过点P作CD⊥OP于点P，连接OD．根据题意，得CD＝8，OD＝5．根据垂径定理，得PD＝4，根据勾股定理，得OP＝3；（2）根据平行线的性质和垂线的性质，知O、P、Q三点共线．根据（1）的求解方法，得OQ＝4，则PQ＝1或7；（3）连接AM、BN．∵∠A＝∠N，∠M＝∠B，∴△APM∽△NPB，∴，即PM•PN＝PA•PB；（4）作直径AB，根据相交弦定理，得PC•PD＝PA•PB＝（5﹣3）（5+3）＝16，又CD＝，设PC＝x，则PD＝﹣x，则有x（﹣x）＝16，解得x＝3或x＝．即PC＝3或，PD＝或3．20．解：（1）AC过圆心O，且m，n分别切⊙O于点A，C，∴AC⊥m于点A，AC⊥n于点C．∵PQ⊥m于点Q，PR⊥n于点R，∴Q与A重合，R与C重合．∵OP＝1，AC＝4，∴PQ＝1，PR＝3，∴+＝1+＝．（2）连接OA，∵OP⊥AC于点P，且OP＝1，OA＝2，∴∠OAP＝30°．∴AP＝．∵OA⊥直线m，PQ⊥直线m，∴OA∥PQ，∠PQA＝90°．∴∠APQ＝∠OAP＝30°．在Rt△AQP中，PQ＝，同理，PR＝，∴．（3）猜想．证明：过点A作直径交⊙O于点E，连接EC，∴∠ECA＝90°．∵AE⊥直线m，PQ⊥直线m，∴AE∥PQ且∠PQA＝90°．∴∠EAC＝∠APQ．∴△AEC∽△PAQ．∴①同理可得：②①+②，得：+＝+∴＝（）＝•＝．过P作直径交⊙O于M，N，根据阅读材料可知：AP•PC＝PM•PN＝3，∴＝．。

中考数学之圆的公式定理整理初中数学学习中，大家首先必须搞懂的就是公式定理，只有先记住了公式，才有可能在运算中活学活用。

下面是小编给大家带来的中考数学复习资料之圆的公式定理，欢迎大家阅读参考，我们一起来看看吧!中考数学复习资料之圆的基本性质与定理1。

点P与圆O的位置关系(设P是一点，则PO是点到圆心的距离)：P在⊙O外，PO>r;P在⊙O上，PO=r;P在⊙O内，PO2。

圆是轴对称图形，其对称轴是任意一条过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

3。

垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

逆定理：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧。

4。

在同圆或等圆中，如果2个圆心角，2个圆周角，2条弧，2条弦中有一组量相等，那么他们所对应的其余各组量都分别相等。

5。

一条弧所对的圆周角等于它所对的圆心角的一半。

6。

直径所对的圆周角是直角。

90度的圆周角所对的弦是直径。

7。

不在同一直线上的3个点确定一个圆。

8。

一个三角形有唯一确定的外接圆和内切圆。

外接圆圆心是三角形各边垂直平分线的交点，到三角形3个顶点距离相等;内切圆的圆心是三角形各内角平分线的交点，到三角形3边距离相等。

9。

直线AB与圆O的位置关系(设OP⊥AB于P，则PO是AB到圆心的距离)：AB与⊙O相离，PO>r;AB与⊙O相切，PO=r;AB与⊙O相交，PO10。

圆的切线垂直于过切点的直径;经过直径的一端，并且垂直于这条直径的直线，是这个圆的切线。

11。

圆与圆的位置关系(设两圆的半径分别为R和r，且R≥r，圆心距为P)：外离P>R+r;外切P=R+r;相交R-r中考数学复习资料之圆的定义1。

平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

2。

圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，小于半圆的弧称为劣弧。

连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。