高等数学-山大全套课件
- 格式:ppt
- 大小:24.26 MB
- 文档页数:435






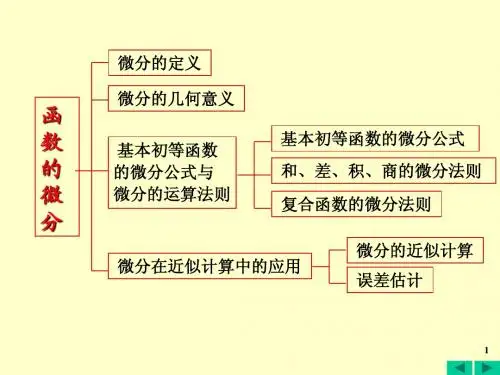

山大内部教材高等数学高等数学(内部教材)第一章:导数与微分一、导数的概念与性质在数学中,导数是描述函数变化率的重要工具。
导数可以通过公式或几何解释来定义。
通过导数,我们可以研究函数的增减性、极值和曲线的凹凸性等性质。
二、导数的计算方法1. 基本导数公式基本导数公式包括常数函数导数、幂函数导数、指数函数导数、对数函数导数、三角函数导数等。
通过这些公式,我们可以计算各种函数的导数。
2. 导数运算法则导数运算法则包括加减法法则、乘法法则、除法法则、复合函数求导法则等。
这些法则可以帮助我们简化导数的计算过程。
三、微分的概念与应用1. 微分的定义微分是导数的一个重要应用,它可以用来描述函数在某一点附近的近似变化量。
微分可以通过导数来计算,并与函数的线性逼近有密切关系。
2. 微分的应用微分在实际问题中有广泛的应用,例如求解极值问题、优化问题、曲线的切线和法线等。
微分还可以用来描述物体的运动、函数的变化趋势等。
第二章:积分与反常积分一、定积分的概念与性质定积分是对函数在一定区间上的积累效应的描述。
定积分可以看作是将曲线下的面积加以量化。
通过定积分,我们可以研究函数的整体变化情况。
二、定积分的计算方法1. 基本积分公式基本积分公式包括幂函数积分、三角函数积分、指数函数积分等。
这些公式可以帮助我们计算各种函数的定积分。
2. 积分运算法则积分运算法则包括线性性质、分部积分法、换元积分法、定积分的可加性等。
这些法则可以简化定积分的计算过程。
三、反常积分的概念与收敛性反常积分是针对无界函数或在某些点不连续的函数的积分概念。
反常积分也具有收敛性和发散性,通过研究函数的性质和变化趋势,可以确定反常积分是否存在。
四、反常积分的计算和应用通过适当的变换和处理,可以将一些常见的反常积分转化为定积分来计算。
反常积分在概率统计、物理学、工程学等领域中有广泛的应用。
第三章:级数与幂级数一、级数的概念与性质级数是由一系列数相加所得到的序列。



高等数学完整全套教学课件一、教学内容本节课的教学内容来自高等数学教材的第五章——多元函数微分学。
本章主要内容包括多元函数的求导法则、隐函数求导、泰勒公式以及多元函数的极值问题。
具体教学内容如下:1. 多元函数的求导法则:主要包括偏导数的定义及其求导法则,如四则法则、链式法则、反函数求导法则等。
2. 隐函数求导:主要讲解如何利用偏导数求解隐函数的导数,包括直接求解和间接求解两种方法。
3. 泰勒公式:介绍泰勒公式的定义及其在多元函数中的应用,重点讲解如何利用泰勒公式展开多元函数。
4. 多元函数的极值问题:包括极值的存在性定理、极值的判定方法以及极值的求解方法。
二、教学目标1. 理解并掌握多元函数的求导法则,能够熟练运用各种法则求解多元函数的导数。
2. 学会隐函数求导的方法,能够独立求解复杂的隐函数导数问题。
3. 掌握泰勒公式的应用,能够利用泰勒公式展开多元函数并进行简化。
4. 理解多元函数极值的概念,学会使用极值判定方法和求解方法解决实际问题。
三、教学难点与重点1. 教学难点:隐函数求导、泰勒公式的应用以及多元函数极值的求解。
2. 教学重点:多元函数的求导法则、隐函数求导、泰勒公式以及多元函数的极值问题。
四、教具与学具准备1. 教具:多媒体教学设备、黑板、粉笔。
2. 学具:笔记本、签字笔、直尺、橡皮。
五、教学过程1. 实践情景引入:以实际问题为例,引入多元函数的求导问题。
2. 讲解多元函数的求导法则:通过示例,讲解四则法则、链式法则、反函数求导法则等。
3. 隐函数求导方法讲解:以具体例子为例,讲解直接求解和间接求解两种方法。
4. 泰勒公式的介绍与应用:讲解泰勒公式的定义及其在多元函数中的应用,通过示例让学生掌握泰勒公式的运用。
5. 多元函数极值问题的讲解:介绍极值的存在性定理、极值的判定方法以及极值的求解方法,并通过实例进行分析。
6. 随堂练习:布置具有代表性的题目,让学生现场解答,检验学习效果。
六、板书设计1. 多元函数的求导法则:四则法则、链式法则、反函数求导法则。