导数与微分重点知识归纳

1、极限的实质是：动而不达导数的实质是：一个有规律商的极限。

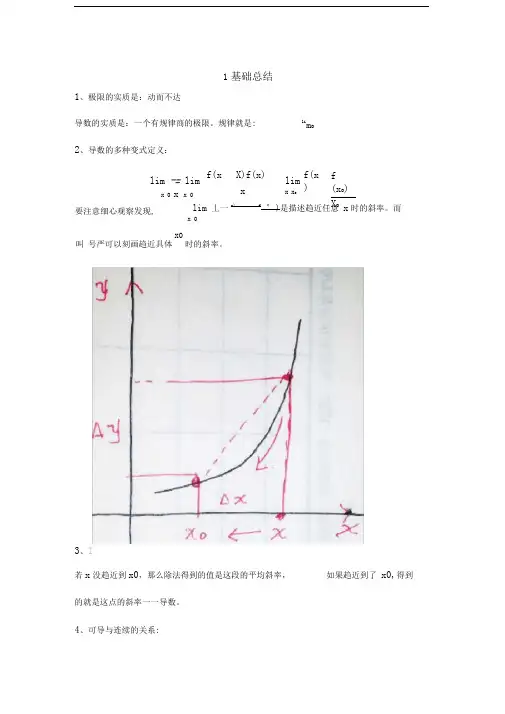
规律就是:2、导数的多种变式定义：lim 丄一x)f°)是描述趋近任意 x 时的斜率。

而x 03、I若x 没趋近到x0，那么除法得到的值是这段的平均斜率， 如果趋近到了 x0,得到的就是这点的斜率一一导数。

4、可导与连续的关系:1基础总结lim -= limx 0 x x 0 f(x X)f(x)xlim x x o f(x )f (x o )X o叫 号严可以刻画趋近具体x0时的斜率。

lim o要注意细心观察发现,导数的实质是定义在某点的左右极限。

既然定义在了某点上，该点自然存在，而 且还得等于左右极限。

因此，可导一定是连续的。

反之，如果连续，不一定可导。

不多说。

同理，如果不连续，肯定某点要么无定义，要么定义点跳跃跑了，肯定 极限有可能存在，但是导数绝不会存在。

同理要注意左右导数的问题。

如果存在左或者右导数，那么在左侧该点一定是存 在的。

如：f(x) x,x 0这个函数，在0点就不存在左导数，只存在右导数。

为什么嫩？看定义:万不要以为导数是一种简单的极限，极限是可以在某点无定义的，而导数却是该 点必须存在! 由此引发了一些容易误判的血案: 例如:A 旦主^謎IC m F 左电鼓 pg 总生戟乞f ( x) f (x)-中的f(x))至u 底是神马。

比如求上图limf(x x) f(x)x 0xlimf(X X)f(0)。

x 0定义里面需要用到f(0)啊！因此，千中 iimf (x)论) x 1x x 0,这个f(x0)千万要等于2/3，而不是1 ！定义解决时候一定要注意问。

X X o由此也可以知道，f (x)2x 3, x 1这个函数是不存在导数的，也不存在左导数,3只存在右导数。

5、反函数的导数与原函数的关系:注意，求反函数时候不要换元。

因为换了元虽然对自身来讲函数形式不变, 与原函数融合运算时候就算是换了一个不是自己反函数的一个函数进行运算 果显然是错误的。

大学微分知识点总结一、导数与微分的概念1. 导数的定义函数y=f(x)在点x0处的导数，定义为：f'(x0) = lim Δx→0 (f(x0+Δx)-f(x0))/Δx如果这个极限存在，就称函数在点x0处可导，导数的值就是这个极限值。

2. 导数的几何意义函数y=f(x)在点x0处的导数f'(x0)，表示函数在这一点的切线的斜率，也就是函数在这一点上的瞬时变化率。

3. 微分的定义函数y=f(x)在点x0处的微分，定义为：dy = f'(x0)dx这个式子表示函数在某一点上微小的变化量dy与自变量的微小变化量dx之间的关系。

4. 微分的几何意义函数y=f(x)在点x0处的微分dy，是函数在这一点处的切线上的微小变化量，它与自变量的微小变化量dx之间存在着近似的线性关系，这个关系即为切线的斜率。

二、导数与微分的运算法则1. 基本导数常数函数的导数为0，幂函数的导数为nx^(n-1)，指数函数的导数为e^x，对数函数的导数为1/x，三角函数和反三角函数的导数等等都是微分学中比较基础的内容。

2. 导数的四则运算函数的和、差、积、商的导数与原函数的导数之间也有着一定的关系。

比如(f+g)' = f' + g'，(f-g)' = f' - g'， (fg)' = f'g + fg'， (f/g)' = (f'g - fg')/g^2。

3. 链式法则如果函数y=u(x)和v(x)都可导，那么复合函数y=u(v(x))的导数可以用链式法则表示：dy/dx = dy/du * du/dx4. 隐函数的求导当一个函数y=f(x)在方程F(x,y)=0中不能显式表示y时，此时的求导需要用到隐函数的求导方法。

5. 参数方程的求导当函数y=f(x)由参数方程x=x(t)，y=y(t)确定时，此时的求导需要用到参数方程的求导方法。

导数与微积分解析与归纳微积分是数学中的一个重要分支，通过导数的概念与运算，可以求解方程、研究变化率、描述曲线等。

本文将对导数的定义、性质以及微积分的应用进行详细的解析和归纳。

一、导数的定义与性质导数是微积分的基础概念之一，它描述了函数在某一点的变化率。

设函数f(x)在点x0处可导，则其导数为f'(x0)，可以按照以下方式进行定义：f'(x0) = lim┬(h→0)⁡〖(f(x_0+h)-f(x_0))/h〗其中，lim表示极限运算，h为自变量的增量。

通过求导数可以得到函数在该点的斜率，进而可以研究曲线的变化情况。

导数具有一些性质，比如线性性、乘法法则、链式法则等。

其中线性性质表明对于函数f(x)和g(x)，以及实数a，有如下等式成立： (af(x))' = af'(x)(f(x)+g(x))' = f'(x)+g'(x)乘法法则以及链式法则提供了求解复杂函数导数的方法，使得微积分的应用更加灵活多样。

二、微积分的应用微积分的应用广泛，涵盖了数学、物理、经济等众多领域。

以下是微积分的一些常见应用：1. 曲线的切线与法线：导数描述了曲线在某一点的斜率，因此通过求导数可以求出曲线在特定点的切线方程。

切线是曲线在该点的最佳近似线性模型，具有重要的几何和物理意义。

2. 极值与最优化：通过求解函数的导数，可以确定函数的极值点。

当导数为0时，函数取得极值，进而可以对函数进行最优化设计，例如求解成本最小、利润最大等问题。

3. 函数的图像和变化：导数可以用来研究函数的图像特征，包括函数的增减性、凹凸性、拐点等。

通过分析导数的符号及变化情况，可以了解函数的整体变化趋势。

4. 积分与面积计算：积分是导数的逆运算，可以通过积分求解曲线下的面积、弧长等。

微积分的基本定理提供了将积分与导数联系起来的方法，为求解复杂问题提供了便利。

总结导数是微积分的核心概念，通过对导数的定义与性质的理解，我们可以更深入地掌握微积分的原理与方法。

导数与微分的总结导数和微分是微积分学中的两个重要概念，也是研究函数变化的基础工具。

本文将从定义、性质、应用等方面对导数和微分进行总结。

一、导数的定义和性质导数是函数在某一点上的变化率，用极限表示形式可以定义为：若函数f(x)在点x0的某个邻域内有定义，当x→x0时，存在有限数L，使得lim (f(x) - f(x0)) / (x - x0) = Lx→x0这个极限L称为函数f(x)在点x0处的导数，记作f'(x0)或dy/dx|_(x=x0)。

导数具有以下性质：1. 导数的存在性：若函数f(x)在点x0的某个邻域内有定义，则f(x)在x0处可导当且仅当上述极限存在。

2. 导数的几何意义：导数表示了函数在某一点的切线斜率。

当函数在某一点可导时，这条切线的斜率就是导数的值。

3. 导函数：若函数f(x)在定义域内的每一点都可导，那么对应的导数函数就是f'(x)，称为原函数f(x)的导函数。

4. 导数的四则运算：导数具有加法、减法、乘法、除法的运算法则，即d(u + v)/dx = du/dx + dv/dx，d(u - v)/dx = du/dx -dv/dx，d(uv)/dx = u(dv/dx) + v(du/dx)，d(u/v)/dx = (v(du/dx) -u(dv/dx))/v²。

二、微分的定义和性质微分是描述函数变化的一种近似方法，它比导数更加具体。

对于函数f(x)，在点x0处进行微分可以表示为：df(x) = f'(x0)dx其中，df(x)称为微分，dx称为自变量的增量。

微分具有以下性质：1. 微分的近似性：微分是函数f(x)在点x0处的变化的近似值，当dx趋近于0时，微分趋近于函数的实际变化值。

2. 微分的几何意义：微分可以理解为函数在某一点上的线性逼近，它是函数值在该点的变化量。

3. 微分与导数的关系：对于可导函数，微分与导数的关系可以表示为df(x) = f'(x0)dx。

全微分知识点笔记总结一、导数与全微分基本概念1. 导数的概念导数是微积分学中非常重要的概念，它描述了一个函数在某一点的变化率。

如果函数y=f(x)在某一点x0处可导，那么它的导数f'(x0)定义为f'(x0)=lim(x→x0) (f(x)-f(x0))/(x-x0)导数可以理解为函数在某一点的斜率，也可以理解为函数在某一点的瞬时变化率。

2. 全微分的概念全微分也是微积分学中的一个重要概念，它描述了函数在某一点的微小变化。

如果函数y=f(x)在某一点x0处可导，那么它的全微分dy可以定义为dy = f'(x0)dx全微分可以理解为函数在某一点微小变化的量，它是函数的局部变化率与自变量的微小变化量的乘积。

二、全微分的计算1. 一元函数的全微分对于一元函数y=f(x)，如果它在某一点x0处可导，那么它的全微分可以通过导数来计算，全微分dy=f'(x0)dx。

这个公式可以准确地描述函数在x0处微小变化的量。

2. 多元函数的全微分对于多元函数z=f(x,y)，如果它在某一点(x0,y0)处可导，那么它的全微分可以通过偏导数来计算。

全微分dz在点(x0,y0)处的计算公式为dz = ∂f/∂x|_(x0,y0)dx + ∂f/∂y|_(x0,y0)dy这个公式可以描述多元函数在某一点微小变化的量，其中∂f/∂x和∂f/∂y分别是函数在各自自变量上的偏导数。

三、全微分的物理意义1. 全微分的物理意义全微分可以用来描述函数在某一点微小增量的变化。

在物理学中，全微分可以用来描述物体在某一点的微小位移、速度、加速度等物理量的变化。

这就是全微分的物理意义。

2. 全微分与微分量的关系在物理学中，微分量描述了一个物体在某一点的微小变化量，而全微分描述了函数在某一点的微小变化量。

它们之间存在着密切的关系，可以相互换算，因此在物理学中也可以用全微分来描述物体的微小变化。

四、全微分的应用1. 全微分在最优化问题中的应用在最优化问题中，全微分可以用来描述函数的微小变化量。

导数微分知识点总结一、微分的定义微分是微积分中的基本概念之一。

在微积分中，微分是用来描述函数在某一点上的变化率的概念。

设函数y=f(x)，若x在x_0处有一个增量Δx，对应的函数值的增量Δy=f(x_0+Δx)-f(x_0)，那么函数f(x)在点x_0处的微分dy=f'(x_0)dx，其中f'(x_0)是函数f(x)在点x_0处的导数。

二、导数的定义导数是微分的数学概念，是用来描述函数在某一点上的变化率的概念。

设函数y=f(x)，在x_0处导数f'(x_0)的定义为：若极限lim_(Δx→0)(f(x_0+Δx)-f(x_0))/Δx存在，那么称该极限为函数f(x)在x_0处的导数，记作f'(x_0)。

导数描述了函数在某一点上的瞬时变化率，也可以用偏导数来描述多元函数的变化率。

三、微分和导数的关系微分和导数是密切相关的概念，它们之间存在着密切的联系。

微分dy=f'(x_0)dx，其中f'(x_0)是函数f(x)在点x_0处的导数，可见微分和导数之间有直接的联系。

微分是导数的一种应用，而导数也可以通过微分来求得。

四、微分和导数的性质1.导数的性质：（1）常数的导数为0: (c)'=0（2）幂函数的导数: (x^n)'=nx^(n-1)（3）和差函数的导数: (f(x)+g(x))'=f'(x)+g'(x)，(f(x)-g(x))'=f'(x)-g'(x)（4）积函数的导数: (f(x)g(x))'=f'(x)g(x)+f(x)g'(x)（5）商函数的导数: (f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/g^2(x)（6）复合函数的导数: 若y=f[g(x)]，则y'=(f[g(x)])'=f'(g(x))g'(x)2.微分的性质：（1）微分的线性性质：若函数y=f(x)和y=g(x)的微分分别为dy=f'(x)dx和dy=g'(x)dx，那么有：d(af(x)+bg(x))=adf(x)+bdg(x)（2）微分的乘法法则：若函数y=f(x)和y=g(x)的微分分别为dy=f'(x)dx和dy=g'(x)dx，那么有：d(f(x)g(x))=f(x)dg(x)+g(x)df(x)五、导数的计算方法1.通过定义求导：根据导数的定义，可以直接求出给定函数的导数。

完整版高数一知识点一、导数与微分高等数学中，导数是一种表示函数变化率的工具。

它是研究函数在某一点上的局部性质和变化趋势的基本概念。

导数可以通过极限的概念进行定义，表示函数在某一点上的瞬时变化率。

导函数的计算方法包括：1. 基本函数的导数公式：常数函数、幂函数、指数函数、对数函数、三角函数等的导数公式。

2. 四则运算法则：求导的四则运算法则包括加法法则、减法法则、乘法法则和除法法则。

3. 复合函数的求导：使用链式法则求解复合函数的导数。

微分是导数的应用之一，用于研究函数的近似变化。

微分的计算方法包括：1. 微分的定义：微分可以通过导数来进行计算，表示函数在某一点上的变化量。

2. 微分的近似计算：使用微分近似计算可以帮助我们在没有具体数值的情况下估计函数的变化。

二、不定积分与定积分不定积分是求解函数原函数的过程，也被称为反导数。

不定积分可以表示函数的面积、函数的平均值等。

计算不定积分的方法包括：1. 基本积分公式：根据一些基本函数的导数公式，可以得到相应的不定积分公式。

2. 积分的线性性质：积分具有线性性质，即函数的线性组合的积分等于各组成函数的积分之和。

3. 特殊函数的积分：对于一些特殊的函数，可以通过一些特殊的方法进行积分。

定积分是求解函数在某一区间上的面积的过程，也被称为积分。

定积分可以表示弧长、质量、体积等物理量。

计算定积分的方法包括：1. 定积分的定义：定积分可以通过分割区间，计算分割点上函数值与区间长度的乘积之和来进行计算。

2. 积分的性质：定积分具有一些性质，例如积分的线性性质、积分的区间可加性等。

3. 牛顿-莱布尼茨公式：牛顿-莱布尼茨公式给出了定积分与不定积分之间的关系。

三、常微分方程常微分方程是研究函数的导数与自变量之间关系的方程。

它是高等数学中一个重要的分支，应用广泛。

常微分方程的求解方法包括：1. 可分离变量法：对于可分离变量的常微分方程，可以通过分离变量并积分的方法进行求解。

高中数学导数与微分知识点总结在高中数学学习中，导数与微分是一个重要的知识点。

导数是微积分的一个基本概念，它研究了函数的变化率。

微分是导数的一种运算方法，它可以帮助我们求得函数的近似值、判别函数的极值以及解决相关实际问题。

本文将对高中数学导数与微分的相关知识点进行总结。

1. 导数的定义与计算方法导数的定义是函数在某一点处的变化率，记作f'(x)或dy/dx。

计算导数有多种方法，常见的有几何定义法、利用基本导数公式求导法、利用导数的性质求导法等。

2. 导数的基本公式高中数学中常用的导数公式有：- 常数函数的导数：若y=c，其中c为常数，则y'=0。

- 幂函数的导数：若y=x^n，其中n为常数，则y'=nx^(n-1)。

- 指数函数的导数：若y=a^x，其中a为常数且a>0且a≠1，则y'=a^x * ln(a)。

- 对数函数的导数：若y=log_a(x)，其中a为常数且a>0且a≠1，则y'=1/(x * ln(a))。

- 三角函数的导数：sin(x)'=cos(x)，cos(x)'=-sin(x)，tan(x)'=sec^2(x)，cot(x)'=-csc^2(x)。

3. 导数的运算法则导数具有一些运算法则，这些法则可以简化导数的计算过程。

常见的导数运算法则有：- 常数倍法则：若f(x)可导，则k * f(x)的导数为k * f'(x)，其中k为常数。

- 和差法则：若f(x)和g(x)都可导，则(f(x) ± g(x))' = f'(x) ± g'(x)。

- 乘积法则：若f(x)和g(x)都可导，则(f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x)。

- 商法则：若f(x)和g(x)都可导且g(x)≠0，则(f(x) / g(x))' = (f'(x) *g(x) - f(x) * g'(x)) / g(x)^2。

导数与微分基础知识导数与微分是微积分学中非常重要的概念，它们可以帮助我们研究函数的变化规律和性质。

在本文中，我们将详细介绍导数与微分的基础知识，包括定义、性质和应用等方面。

一、导数的定义与性质导数的定义是函数变化率的极限值，它的数学表达式可以表示为：\[f'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\]其中，\(f'(x)\)表示函数\(f(x)\)在点\(x\)处的导数。

该定义告诉我们，导数反映了函数在某一点的瞬时变化率。

导数具有一些重要的性质，包括：1. 导数存在性：如果函数在某点可导，则该点处的导数存在。

2. 导数的几何意义：导数等于函数图像在该点切线的斜率。

3. 导数的代数性质：导数的运算可以应用常见的代数法则，如和差、积、商法则等。

二、微分的定义与性质微分是导数的一个重要应用，它可以帮助我们近似计算函数在某一点的值。

微分的基本定义如下：\[df(x)=f'(x)dx\]其中，\(df(x)\)表示函数\(f(x)\)在点\(x\)处的微分，\(dx\)为自变量的微小增量。

微分提供了一个线性近似，使得我们可以用简单的代数方法来计算函数的近似值。

微分也有一些重要的性质：1. 微分与导数的关系：微分可以看作是导数的乘积形式，它们在数值上有相似的近似值。

2. 微分的近似意义：微分可以帮助我们在不知道具体函数表达式的情况下，根据导数的信息对函数进行逼近计算。

三、导数与微分的应用导数与微分在实际问题中有广泛的应用，下面列举了一些常见的例子：1. 切线与法线：导数可以帮助我们确定函数图像在某点的切线斜率，并进而求出切线和法线的方程。

2. 最值问题：导数可以帮助我们确定函数的极值点，进而解决最大值和最小值的求解问题。

3. 函数图像的绘制：通过函数的导数信息，我们可以绘制出函数的大致图像，包括凹凸性、拐点等特征。

高数大一导数和微分知识点在高等数学学科中，导数和微分是非常重要的概念和知识点。

导数用于描述函数在某一点上的变化率，而微分则是导数的一种具体形式。

本文将介绍导数和微分的基本概念、计算方法以及它们在实际问题中的应用。

一、导数的定义和性质导数描述了函数在某一点上的变化率。

函数f(x)在点x=a处的导数可以表示为f'(a)，它的定义如下：f'(a) = lim [f(x) - f(a)] / (x - a) 当 x -> a时导数具有以下一些性质：1. 可导性：如果函数f(x)在点x=a处有导数，那么我们说函数在点x=a处可导。

2. 右导数和左导数：如果函数f(x)在点x=a处的右导数和左导数存在且相等，那么函数在点x=a处可导。

3. 常数导数：常数函数的导数为0。

4. 和差法则：(f+g)'(a) = f'(a) + g'(a)，(f-g)'(a) = f'(a) - g'(a)。

5. 乘法法则：(f·g)'(a) = f'(a)·g(a) + f(a)·g'(a)。

6. 除法法则：(f/g)'(a) = (f'(a)·g(a) - f(a)·g'(a)) / (g(a))^2，其中g(a) ≠ 0。

7. 复合函数的导数：如果y=f(u)和u=g(x)都可导，则复合函数y=f(g(x))也可导，且导数为f'(g(x))·g'(x)。

二、导数的计算方法1. 基本函数的导数：- 常数函数的导数为0。

- 幂函数y=x^n的导数为y'=n·x^(n-1)。

- 三角函数的导数：正弦函数的导数为y'=cos(x)，余弦函数的导数为y'=-sin(x)，正切函数的导数为y'=sec^2(x)。

导数与微分重点知识点总结导数和微分是微积分中的重要概念，对于理解函数的性质和解决实际问题起着至关重要的作用。

本文将对导数与微分的重点知识点进行总结。

一、导数的定义与性质1. 导数的定义：如果函数f(x)在点x处的导数存在，那么导数可以定义为f'(x) = lim(h→0) [f(x+h)-f(x)]/h。

导数表示函数在某一点的瞬时变化率。

2. 导数的几何意义：导数等于函数图像在某点的切线斜率，也可以表示函数图像在该点的切线与x轴正方向夹角的正切值。

3. 导数的性质：导数存在的函数在该点必然连续，导数具有可加性和数乘性，即对于函数f(x)和g(x)，有[f(x)±g(x)]' = f'(x)±g'(x)和[cf(x)]'= cf'(x)。

二、常见函数的导数公式1. 幂函数：对于f(x) = x^n，其中n为实数，导数为f'(x) = nx^(n-1)。

2. 指数函数：对于f(x) = a^x，其中a为正实数且a≠1，导数为f'(x)= a^x·ln a。

3. 对数函数：对于f(x) = logₐx，其中a为正实数且a≠1，导数为f'(x) = 1/(x·ln a)。

4. 三角函数：对于f(x) = sin x，导数为f'(x) = cos x；对于f(x) = cos x，导数为f'(x) = -sin x；对于f(x) = tan x，导数为f'(x) = sec² x。

5. 反三角函数：例如arcsin x的导数为1/√(1-x²)，arccos x的导数为-1/√(1-x²)，arctan x的导数为1/(1+x²)。

三、微分的定义与应用1. 微分的定义：对于函数y = f(x)，若f(x)在某一点x处有定义且可导，那么对应的微分dy为dy = f'(x)dx。

高中数学知识点总结导数与微分导数与微分是高中数学中的重要知识点之一。

它是微积分的基础，也是解决数学问题和建立数学模型的关键工具。

本文将对导数与微分进行深入总结，帮助读者理解和掌握相关概念与技巧。

一、导数的定义与计算方法导数是函数在某一点的变化率。

它描述了函数在该点附近的斜率或切线的斜率。

导数的定义式为：\[f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\]其中，\[f'(x)\]表示函数f(x)在点x处的导数。

根据导数的定义，我们可以得到一些常用的导数计算方法：1. 常数函数的导数为0；2. 幂函数\[f(x) = x^n\]的导数为\[f'(x) = n \cdot x^{n-1}\]；3. 指数函数\[f(x) = a^x\]的导数为\[f'(x) = a^x \cdot \ln a\]；4. 对数函数\[f(x) = \log_a x\]的导数为\[f'(x) = \frac{1}{x \cdot \ln a}\]；5. 三角函数的导数可以通过导数定义或基本导数公式计算。

二、导数的基本性质导数具有一些基本的性质，包括：1. 导数的四则运算：若\[f(x)\]和\[g(x)\]的导数存在，则* \[(f(x)+g(x))' = f'(x) + g'(x)\]* \[(f(x)-g(x))' = f'(x) - g'(x)\]* \[(f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\]* \[(\frac{f(x)}{g(x)})' = \frac{f'(x) \cdot g(x) - f(x) \cdotg'(x)}{[g(x)]^2}\]2. 链式法则：设函数\[y=f(u)\]和\[u=g(x)\]都可导，则\[y=f(u)\]对\[x\]的导数为\[y' = f'(u) \cdot g'(x)\]。

导数与微分知识点导数和微分是高等数学中重要的概念，它们在微积分中具有广泛的应用。

本文将介绍导数与微分的定义、性质以及它们的计算方法。

一、导数的定义与性质在数学中，导数描述了函数在某一点上的变化率。

假设有函数y=f(x)，那么在点x处的导数可以记作f'(x)，其定义如下：f'(x) = lim┬(∆x→0)⁡〖(f(x+∆x)-f(x))/∆x〗①其中，lim表示极限，∆x表示x的增量。

导数衡量了函数在某一点上的瞬时变化率，也可以理解为函数曲线在该点的切线斜率。

导数具有以下几个重要的性质：1. 导数的存在性：函数在某一点上可导的条件是该点的左导数等于右导数，也就是导数的存在需要左右极限相等。

2. 可导性与连续性：若函数在某一点可导，则必定在该点连续；但函数在某一点连续并不意味着可导。

3. 导数与函数的关系：若函数在某一点可导，则该点必定是函数的极值点或拐点；但反之不一定成立。

二、导数的计算方法求导是计算导数的过程，常见的求导法则有以下几种：1. 基本导数法则：常数的导数为0，幂函数的导数等于幂指数乘以常数，指数函数的导数等于函数值乘以自然对数e。

2. 和、差、积、商法则：若函数g(x)和h(x)在点x处可导，则其和、差、积、商的导数分别为其导数的和、差、积、商。

3. 复合函数的导数：若函数h(x)可以表示为f(g(x))，其中f(x)和g(x)都可导，则h(x)的导数等于f'(g(x))乘以g'(x)。

4. 反函数的导数：若函数y=f(x)在区间[a,b]上连续、单调且可导，且导数不为0，则它的反函数x=f⁻¹(y)在对应区间[f(a),f(b)]上也连续、单调可导，且导数为1/f'(f⁻¹(y))。

三、微分的定义与性质微分是导数的一个应用，它可以用来描述函数在某一点上的近似变化量。

函数y=f(x)在点x处的微分可以表示为dy=f'(x)dx。

高中微积分重要知识点总结一、函数与极限1. 函数概念：函数是一种特殊的映射关系，它将一个自变量映射为一个因变量。

2. 函数的性质：奇函数、偶函数、周期函数等。

3. 极限概念：当自变量趋于某一值时，函数的取值趋于一个确定的常数。

4. 极限的性质：唯一性、有界性、保号性等。

5. 极限的计算方法：无穷小替换法、洛必达法则、泰勒展开式等。

二、导数与微分1. 导数的概念：函数在某一点的变化率。

2. 导数的性质：可加性、可积性、伊尔米特公式等。

3. 导数的计算方法：基本导数公式、复合函数求导、隐函数求导、参数方程求导等。

4. 微分的概念：函数值的变化量与自变量的变化量的比值。

5. 微分的性质：可加性、可积性、微分中值定理等。

三、微分中值定理与应用1. 微分中值定理：拉格朗日中值定理、柯西中值定理、罗尔中值定理等。

2. 泰勒公式及应用：泰勒展开式、泰勒公式的应用。

3. 凹凸性与拐点：二阶导数的概念、凹凸性的判定、拐点的判定。

四、不定积分与定积分1. 不定积分：初等函数的不定积分、换元积分法、分部积分法、有理函数的积分、三角函数的积分等。

2. 定积分：黎曼积分的概念、定积分的性质、定积分的计算方法、定积分的应用。

五、微分方程1. 微分方程的基本概念：微分方程的定义、微分方程的分类、微分方程的初值问题等。

2. 微分方程的解法：可分离变量法、齐次微分方程、常数变易法、一阶线性微分方程等。

3. 高阶微分方程：高阶微分方程的基本概念、高阶微分方程的解法、特解与通解等。

六、级数与收敛1. 级数的概念：无穷级数、收敛级数、发散级数、等比级数、调和级数等。

2. 收敛的判定：级数的收敛判定、级数的比较判别法、级数的积分判别法、级数的根值判别法等。

3. 级数的运算：级数的加法、级数的乘法、级数的分解、级数的换序等。

综上所述，高中微积分的重要知识点包括函数与极限、导数与微分、微分中值定理与应用、不定积分与定积分、微分方程以及级数与收敛等内容。

高数基础知识总结与重点概念整理
一、导数与微分
导数：描述函数在某一点附近的变化率，是函数值的极限。

可导性：函数在某点可导，当且仅当该点附近存在一个定义恰当的导数。

微分：一个近似值，表示函数在某点附近的小变化所引起的函数值的大致变化。

二、积分
不定积分：求一个函数的原函数（或反导数），即求函数的不定积分。

定积分：对一个区间上函数的值的总和的量度，即求函数的定积分。

微积分基本定理：定积分可化为不定积分的计算。

三、级数
数列：一个数字序列。

无穷级数：无穷多个数的和，即数列的和。

收敛性：无穷级数趋于一个有限的和的性质称为收敛性。

发散性：无穷级数不收敛的性质称为发散性。

四、多元函数
多元函数：定义在多个变量上的函数。

偏导数：多元函数对一个变量的导数。

方向导数：描述函数在某点处沿某一方向的变化率。

梯度：方向导数的最大值，表示函数在某点处沿梯度方向的增长最快的方向。

五、微分方程
微分方程：包含未知函数的导数或微分的方程。

初值问题：给定初始条件的微分方程问题。

通解与特解：满足微分方程的解称为通解，满足特定初始条件的解称为特解。

高考数学导数与微分知识点精讲在高考数学中，导数与微分是非常重要的知识点，也是许多同学感到头疼的部分。

但别担心，让我们一起来把它弄明白！一、导数的定义导数其实就是函数在某一点的变化率。

我们可以通过函数在某一点的切线斜率来理解它。

比如，对于函数 y ＝ f(x) ，在点 x₀处的导数记为 f'（x₀) ，它的定义式是：f'（x₀) ＝lim(Δx → 0) f(x₀＋Δx) f(x₀) ／Δx简单来说，就是当自变量 x 的变化量Δx 无限趋近于 0 时，函数值的变化量与自变量变化量的比值的极限。

打个比方，假如我们有一个函数描述汽车行驶的路程与时间的关系，那么导数就表示汽车在某一时刻的瞬时速度。

二、常见函数的导数1、常数函数的导数对于常数函数 y ＝ C （C 为常数），其导数为 0 。

因为常数函数的图像是一条水平直线，斜率为 0 。

2、幂函数的导数（1）若 y ＝xⁿ （n 为实数），则 y' ＝nxⁿ⁻¹。

例如，y ＝ x²的导数是 2x ，y ＝ x³的导数是 3x²。

3、指数函数的导数（1）若 y ＝eˣ ，则 y' ＝eˣ 。

（2）若 y ＝aˣ （a ＞ 0 且a ≠ 1），则 y' ＝aˣ ln a 。

4、对数函数的导数（1）若 y ＝ ln x ，则 y' ＝ 1 ／ x 。

（2）若 y ＝logₐ x （a ＞ 0 且a ≠ 1），则 y' ＝ 1 ／（x ln a) 。

5、三角函数的导数（1）若 y ＝ sin x ，则 y' ＝ cos x 。

（2）若 y ＝ cos x ，则 y' ＝ sin x 。

三、导数的运算1、加法与减法法则若 u(x) 和 v(x) 的导数分别为 u'（x) 和 v'（x) ，则（u(x) ± v(x)）＇＝ u'（x) ± v'（x) 。

导数与函数的微分形式关系归纳导数与函数的微分形式关系是微积分中的重要概念之一。

它描述了函数的瞬时变化率与函数自身之间的联系。

在本文中，我们将对导数与函数的微分形式关系进行归纳和总结。

一、导数的定义与意义导数描述了函数在某一点的瞬时变化率。

设函数f(x)在点x=a处可导，则函数f(x)在点x=a处的导数定义为：f'(a) = lim（(f(x)-f(a))/(x-a)）当x→a其中lim代表极限的定义。

简单来说，导数表示了函数在某一点的瞬时增长率或减少率。

导数为正数表示函数在该点上升，为负数表示函数在该点下降，为零表示函数在该点取得极值。

二、导数与函数的微分形式1. 微分形式一：dy = f'(x)dx根据导数的定义，我们可以得出微分形式一：当函数f(x)在某一点x=a处可导时，函数的微分形式为dy = f'(a)dx。

简单来说，函数在某一点的微小变化dy可以用导数与自变量的微小变化dx表示。

2. 微分形式二：dy = f'(x)dx + ε(dx)当函数f(x)在某一点x处两次可导时，函数的微分形式可以进一步推广为：dy = f'(x)dx + ε(dx)，其中ε(dx)为高阶无穷小。

三、导数与函数的微分形式关系导数与函数的微分形式之间存在着紧密的联系。

根据微分形式的定义，我们可以得出以下结论：1. 如果函数f(x)在某一点x=a处可导，则微分形式dy = f'(x)dx成立。

2. 如果微分形式dy = f'(x)dx成立，那么函数f(x)在某一点x处可导。

换言之，导数与函数的微分形式是等价的，它们可以互相转化。

从微分形式可以获得导数的值，而从导数可以获得微分形式的表达式。

四、应用举例下面通过几个具体的例子来说明导数与函数的微分形式关系。

例1：设函数f(x) = x^2，求函数f(x)在点x=2处的导数以及微分形式。

解：首先求导数，由导数的定义可得：f'(2) = lim（(f(x)-f(2))/(x-2)）当x→2代入函数f(x)的表达式，化简得：f'(2) = lim（(x^2-4)/(x-2)）当x→2化简后得：f'(2) = lim（(x+2)）当x→2计算极限得f'(2) = 4因此，函数f(x)在点x=2处的导数为4。

考研数学高数第二章导数与微分的知识点总结来源：文都教育导数与微分是考研数学的基础，占据至关重要的地位。

基本概念、基本公式一定要掌握牢固，常规方法和做题思路要非常熟练。

下面文都考研数学老师给出该章的知识点总结，供广大考生参考。

第一节 导数1．基本概念（1）定义0000000000()()()()()|(|)'()lim lim lim x x x x x x x f x x f x f x f x dy df x y f x dx dx x x x x ==∆→∆→→+∆--∆====∆∆-或 注：可导必连续，连续不一定可导.注:分段函数分界点处的导数一定要用导数的定义求.（2）左、右导数'000000()()()()()lim lim x x x f x x f x f x f x f x x x x ---∆→→+∆--==∆-. 0'000000()()()()()lim lim x x x f x x f x f x f x f x x x x +++∆→→+∆--==∆-. 0'()f x 存在''00()()f x f x -+⇔=.（3）导数的几何应用曲线()y f x =在点00(,())x f x 处的切线方程：000()'()()y f x f x x x -=-.法线方程：0001()()'()y f x x x f x -=--. 2．基本公式（1）'0C = （2）'1()a a x ax -=（3）()'ln x x a a a =（特例()'x x e e =）（4）1(log )'(0,1)ln a x a a x a=>≠ （5）(sin )'cos x x = （6）(cos )'sin x x =-（7）2(tan )'sec x x = （8）2(cot )'csc x x =-（9）(sec )'sec tan x x x = （10）(csc )'csc cot x x x =-（11）21(arcsin )'1x x =- （12）21(arccos )'1x x =--（13）21(arctan )'1x x =+ （14）21(arccot )'1x x=-+ （1522221[ln()]'x x a x a ++=+3．函数的求导法则（1）四则运算的求导法则()'''u v u v ±=± ()'''uv u v uv =+ 2''()'u u v uv v v -= （2）复合函数求导法则--链式法则设(),()y f u u x ϕ==，则(())y f x ϕ=的导数为：[(())]''(())'()f x f x x ϕϕϕ=.例5 求函数21sin x y e =的导数.（3）反函数的求导法则设()y f x =的反函数为()x g y =，两者均可导，且'()0f x ≠，则11'()'()'(())g y f x f g y ==. （4）隐函数求导设函数()y f x =由方程(,)0F x y =所确定，求'y 的方法有两种：直接求导法和公式法'''x yF y F =-. （5）对数求导法：适用于若干因子连乘及幂指函数4．高阶导数二阶以上的导数为高阶导数.常用的高阶求导公式：（1）()()ln (0)x n x n a a a a => 特别地，(n)()x x e e =（2） ()(sin )sin()2n n kx k kx n π=+ （3）()(cos )cos()2n n kx k kx n π=+ （4）()1(1)(1)n n nn x x --+=-+ （5）()()(1)(2)(1)k n k n x k k k k n x -=---+（6）莱布尼茨公式：()()()0()nn k n k k n k uv C u v -==∑，其中(0)(0),u u v v ==第二节 微分1．定义背景：函数的增量()()y f x x f x ∆=+∆-.定义：如果函数的增量y ∆可表示为()y A x o x ∆=∆+∆，其中A 是与x ∆无关的常数，则称函数()y f x =在点0x 可微，并且称A x ∆为x ∆的微分，记作dy ，则dy A x =∆.注：,y dy x dx ∆≠∆=2．可导与可微的关系一元函数()f x 在点0x 可微，微分为dy A x =∆⇔函数()f x 在0x 可导，且0'()A f x =.3．微分的几何意义4．微分的计算（1）基本微分公式'()dy f x dx =.（2）微分运算法则②四则运算法则()d u v du dv ±=± duv vdu udv =+ 2()u vdu udv d v v -= ②一阶微分形式不变若u 为自变量，(),'()'()y f u dy f u u f u du ==∆=；若u 为中间变量，()y f u =，()u x ϕ=，'()'()'()dy f u x dx f u du ϕ==.。

导数与微分一、导数定义函数y=f(x)在点x 0处可导，并把这个极限叫做f （x ）在点x 0处的导数，记作f ’（x 0）或y ’|0x x =或dx dy |0x x =或 dx df|0xx =二、导数的几何意义)三、函数的求导法则=x(f(1x 四、基本初等函数的求导公式五、高阶导数的基本公式函数y=f(x)七、分公式与微分运算法则 ⑴()0d c = ⑵()1d x x dxμμμ-= ⑶()sin cos d x xdx=⑷()cos sin d x xdx=- ⑸()2tan sec d x xdx= ⑹()2cot csc d x xdx=-⑺()sec sec tan d x x xdx=⋅ ⑻()csc csc cot d x x xdx=-⋅⑼()xxd ee dx = ⑽()ln xxd a aadx= ⑾()1ln d x dx x =⑿()1log ln x a d dx x a =⒀()arcsin d x = ⒁()arccos d x = ⒂()21arctan 1d x dx x =+ ⒃()21arc cot 1d x dx x=-+八、微分运算法则 ⑴()d u v du dv±=± ⑵()d cu cdu=⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭九、中值定理： 罗尔定理：内容：如果函数f(x)满足：在闭区间[a,b]上连续；在开区间(a,b)内可导； 在区间端点处的函数值相等，其中a 不等于b ，即f(a)=f(b)， 那么在(a,b)内至少有一点ξ(a<ξ<b)，使得 f'(ξ)=0.拉格朗日中值定理内容：如果函数 f(x) 满足：在闭区间[a,b]上连续；在开区间(a,b)内可导。

那么：在(a,b)内至少有一点ξ(a<ξ<b)，使等式 f(b)-f(a)=f′(ξ)(b -a) 成立。