《多边形的面积》单元知识结构图

第六单元多边形的面积单元解读一、链接课标《义务教育数学课程标准（2022年版）》指出在小学阶段“图形与几何”领域所对应的核心素养侧重于空间观念，几何直观，量感和推理意识。

学生要结合生活情境认识平面图形及特征，会计算图形的周长和面积，并解决一定的实际问题。

多边形的面积是图形与几何领域测量中的重要内容。

通过本单元的教学，要引导学生探索并掌握平行四边形、三角形和梯形的面积公式，会计算组合图形的面积，在观察、实验、猜想、验证等活动中，渗透平移、旋转、转化等数学思想方法，发展合情推理能力，促进学生空间观念的进一步发展、感受几何直观和符号意识的作用，渗透估测意识、策略，了解解决问题方法的多样性，培养学生的应用意识和创新意识。

二、单元目标学生已经在生活中积累了有关图形认识和图形测量的经验，同时已经研究了长方形、正方形、三角形的特征以及长方形、正方形的面积计算。

在研究本单元中，教师应引导学生紧密联系生活实际，从已有的认知基础和生活经验出发，让学生在数、剪、拼、摆等操作活动中，完成对新知的构建。

引导学生利用转化的数学思想，在操作中研究新知是本单元教学的重要环节。

通过实际操作活动，发展学生的空间观念，培养动手操作能力，为接下来研究圆的面积作好铺垫。

根据学情及教材内容制定了教学目标：1.理解并掌握各种图形的面积计算公式。

2.引导学生运用转化的方式来探索规律，认识新旧知识之间的联系。

3.会拼、摆、拆分各种组合图形，并正确计算组合图形的面积。

4.通过实验、操作、拼摆、割补等方法，使学生经历计算公式的推导过程，进一步发展学生的思维。

5.应用面积的计算公式，使学生运用转化的方法解决实际问题，发展学生的空间观念。

沟通知识与生活的联系，激发学生的学习兴趣，培养学生探究意识和创新能力，发展学生的空间观念。

三、单元教学重点、难点：教学重点：掌握平行四边形、三角形和梯形的面积计算公式，并能正确运用。

教学难点：通过探索活动，能够掌握平行四边形、三角形和梯形的面积计算公式推导的过程。

《多边形的面积》单元整体设计解读多边形的面积是几何学中的一个重要概念，是研究多边形性质和解决与多边形相关问题的基础知识。

在初中数学中，多边形的面积通常在七年级上学期或八年级上学期进行学习。

本文将对多边形的面积单元整体设计进行解读。

一、设计目标本单元的设计目标主要有以下几点：1.掌握计算各类多边形的面积的方法。

2.理解面积的概念和计算面积的意义。

3.培养学生观察、分析和解决实际问题的能力。

4.培养学生合作学习和信息技术应用的能力。

二、设计内容本单元的主要内容包括以下几个方面：1.熟悉多边形的概念和分类。

2.掌握计算正方形、长方形和平行四边形的面积公式及应用。

3.掌握计算三角形的面积公式及应用。

4.认识圆和圆的面积计算方法。

5.解决多边形面积计算问题和实际问题。

三、设计步骤1.知识导入：通过图示和实际物体引入多边形面积的概念，并进行讨论。

3.计算三角形的面积：介绍计算三角形的面积公式（底乘以高除以2），并进行实例分析。

5.复习和巩固：进行一些小组练习，包括计算各类多边形的面积和解决实际问题。

6.拓展和应用：进行一些开放性问题，引导学生应用所学知识解决实际生活和数学问题。

7.总结和评价：学生对本单元的学习进行总结，给予评价和反馈。

四、教学方法在本单元的教学中，可以运用多种教学方法，以提高学生的学习效果和兴趣，具体包括：1.讲解法：通过清晰简洁的语言，向学生讲解多边形面积的概念和计算方法。

2.演示法：通过示范具体的计算步骤和实例，让学生能够观察和模仿，提高计算的准确性和效率。

3.合作学习法：组织学生进行小组讨论和合作学习，在解决问题的过程中培养学生的合作与交流能力。

4.情境教学法：设计一些与实际生活相关的问题，让学生在实际情境中应用已学知识解决问题，提高学生的问题解决能力和应用能力。

5.案例分析法：介绍一些实际问题案例，引导学生分析问题和提出解决方法，培养学生的观察和分析能力。

五、评价方式在本单元的评价中，可以采用多种评价方式，综合考察学生的知识掌握程度、思维能力和实际应用能力，具体包括：1.口头回答：通过学生口头回答问题的方式，考察学生对面积概念和计算方法的理解和掌握情况。

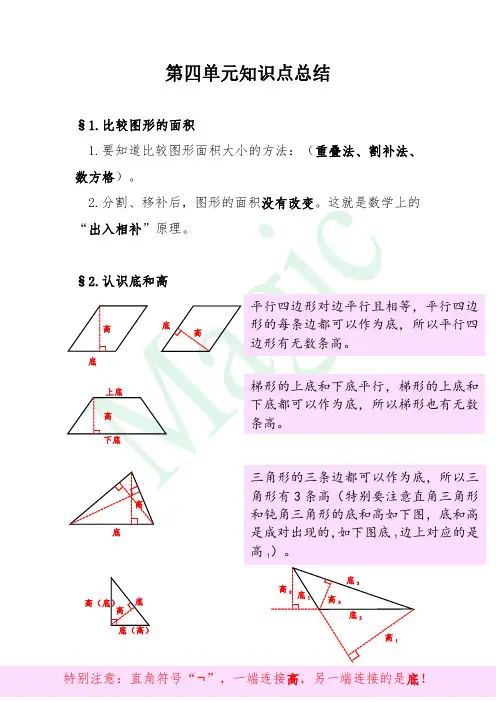
第四单元知识点总结§1.比较图形的面积1.要知道比较图形面积大小的方法：（重叠法、割补法、数方格）。

2.分割、移补后，图形的面积没有改变。

这就是数学上的“出入相补”原理。

§2.认识底和高平行四边形对边平行且相等，平行四边形的每条边都可以作为底，所以平行四边形有无数条高。

底高高底高下底上底梯形的上底和下底平行，梯形的上底和下底都可以作为底，所以梯形也有无数条高。

高底三角形的三条边都可以作为底，所以三角形有3条高（特别要注意直角三角形和钝角三角形的底和高如下图，底和高是成对出现的，如下图底1边上对应的是高1）。

高1底2底3底1高2高3高底底（高）高（底）特别注意：直角符号“¬”，一端连接高，另一端连接的是底！§3.探索活动：平行四边形的面积如果已知平行四边形的面积和高，可以推出底＝S 平÷高；如果已知平行四边形的面积和底，可以推出高＝S 平÷底。

§4.探索活动：三角形的面积方法一：如果已知三角形的面积和高，可以推出底＝2×S △÷高；如果已知三角形的面积和底，可以推出高＝2×S △÷底。

通过割补，平行四边形转化成面积相等的长方形。

长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高，长方形的面积＝长×宽，所以平行四边形的面积＝底×高。

如果用S 表示平行四边形的面积，用a 和h 分别表示平行四边形的底和高，那么，平行四边形的面积公式可以写成：S=ah 用两个完全一样的三角形，可以拼成一个平行四边形，一个三角形的面积是平行四边形面积的一半。

平行四边形的底和高与原三角形的底和高一样，平行四边形的面积＝底×高，所以一个三角形的面积＝底×高÷2。

如果用S 表示三角形的面积，用a 和h 分别表示三角形的底和高，那么，三角形的面积公式可以写成：S=ah÷2。