八年级数学下册各单元知识结构图
- 格式:doc
- 大小:34.50 KB
- 文档页数:2
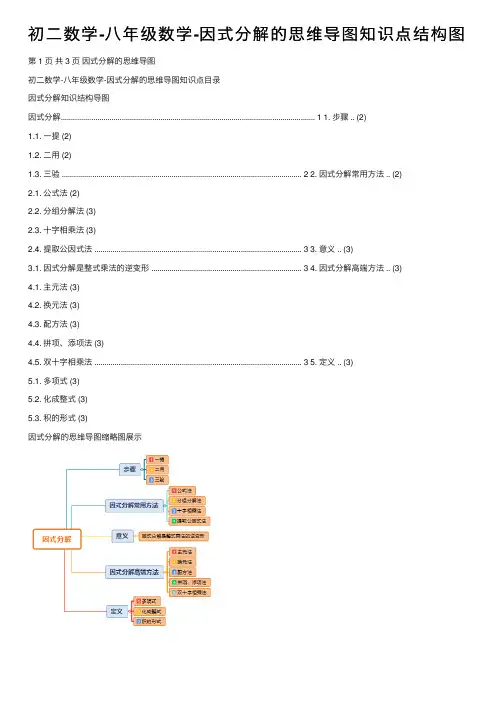


初二数学-八年级数学-因式分解的思维导图知识点结构图因式分解的思维导图初二数学-八年级数学-因式分解的思维导图知识点目录:因式分解知识结构导图因式分解是数学中重要的一部分,它是一种将一个多项式分解成两个或多个多项式的方法。
因式分解可以帮助我们更好地理解和解决各种数学问题。
因式分解的基本概念因式分解的基本概念包括最大公因数、最小公倍数和质因数分解。
最大公因数是指两个或多个整数共有的约数中最大的一个;最小公倍数是指两个或多个整数公有的倍数中最小的一个;质因数分解是将一个正整数分解成质数的乘积。
因式分解的方法因式分解的方法包括提公因式法、分组分解法、差平方公式、和差平方公式和配方法等。
这些方法可以帮助我们更好地进行因式分解,从而解决各种数学问题。
因式分解的应用因式分解在数学中有着广泛的应用,例如解方程、求最大公因数、最小公倍数、约分、通分等。
因式分解还可以帮助我们更好地理解和解决各种数学问题,例如分数的运算、多项式的运算等。
因式分解的思维导图可以帮助我们更好地理解因式分解的基本概念、方法和应用。
通过研究因式分解的思维导图,我们可以更好地掌握因式分解的知识,从而在数学研究中取得更好的成绩。
因式分解是代数学中的一个重要概念,它指的是将一个多项式拆分为若干个乘积的形式。
这个过程可以帮助我们更好地理解多项式的乘法,并且在解决各种数学问题时也非常有用。
在进行因式分解时,一般需要遵循以下三个步骤:1.一提取公因数,将多项式进行因式分解。
2.二用分组分解法、十字相乘法、提取公因式法等常用方法进行因式分解。
3.三验证因式分解是否正确,可以通过乘回去验证。
常用的因式分解方法包括公式法、分组分解法、十字相乘法和提取公因式法等。
这些方法都有其适用的范围和特点,需要根据具体情况进行选择。
因式分解的意义在于,它可以将一个复杂的多项式化简为简单的乘积形式,从而更加方便地进行计算和分析。
同时,因式分解也是整式乘法的逆变形,可以帮助我们更好地理解整式乘法的本质。
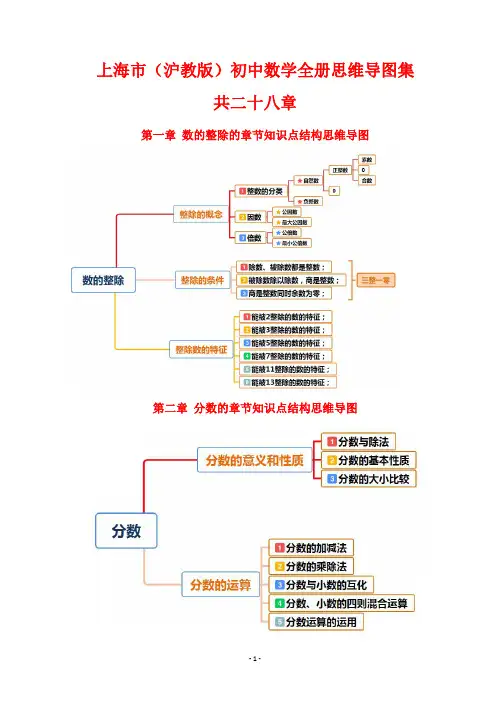
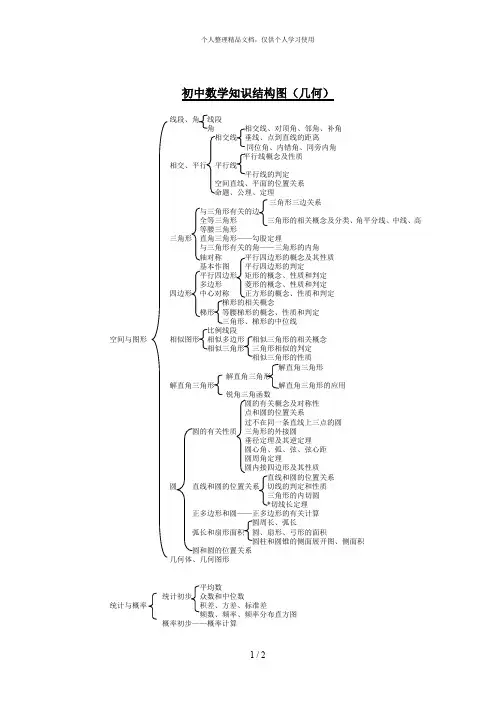
初中数学知识结构图(几何)
线段、角线段
角相交线、对顶角、邻角、补角
相交线垂线、点到直线的距离
同位角、内错角、同旁内角
平行线概念及性质
相交、平行平行线
平行线的判定
空间直线、平面的位置关系
命题、公理、定理
三角形三边关系
与三角形有关的边
全等三角形三角形的相关概念及分类、角平分线、中线、高
等腰三角形
三角形直角三角形——勾股定理
与三角形有关的角——三角形的内角
轴对称平行四边形的概念及其性质
基本作图平行四边形的判定
平行四边形矩形的概念、性质和判定
多边形菱形的概念、性质和判定
四边形中心对称正方形的概念、性质和判定
梯形的相关概念
梯形等腰梯形的概念、性质和判定
三角形、梯形的中位线
比例线段
空间与图形相似图形相似多边形相似三角形的相关概念
相似三角形三角形相似的判定
解直角三角形
解直角三角形
锐角三角函数
圆的有关概念及对称性
点和圆的位置关系
过不在同一条直线上三点的圆
圆的有关性质三角形的外接圆
垂径定理及其逆定理
圆心角、弧、弦、弦心距
圆周角定理
圆内接四边形及其性质
直线和圆的位置关系
圆直线和圆的位置关系切线的判定和性质
三角形的内切圆
*切线长定理
正多边形和圆——正多边形的有关计算
圆周长、弧长
弧长和扇形面积圆、扇形、弓形的面积
圆柱和圆锥的侧面展开图、侧面积
圆和圆的位置关系
几何体、几何图形
平均数
统计初步众数和中位数
统计与概率积差、方差、标准差
频数、频率、频率分布直方图
概率初步——概率计算。
第十六章:解分式方程知识结构图
第十七章:反比例函数知识结构图
第十八章:勾股定理知识结构图
第十九章:四边形知识结构图
归纳
实际应用
现实世界中的
反比例关系
反比例函数
反比例函数的
图象和性质
检验
最简公分母不为
去分母
最简公分母为0
分式方程 a是分式方程的解 整式方程
x = a
目
标
a不是分式方程的解
解整式方程
a2+b2=c
2
互逆定理
归纳
实际问题 (判别直角三角形) 实际问题 (直角三角形边长计算) 勾股定理 勾股定理的逆定理
四边形
梯形
等腰
梯形
直角
梯形
平行四边
矩形 菱
形
正方形
第二十章:数据的分析知识结构图
一个角是直角
两腰相等
梯形
另一组对边不平
一组对边平行
四边形
直角梯形
等腰梯形
一个角是直角 一个角是直角 一组邻边相等 一组邻边相等
两组对边分别平
平行四边形
矩形
菱形
正方形
数据的代表 数据的波动 平均数 中位数 众 数 极差 方差 用样
本
估
计
总
用样本平均数估
计总体平均数
用样本方差估计
总体方差