第三章 曲面立体的阴影
- 格式:pps
- 大小:4.78 MB
- 文档页数:86




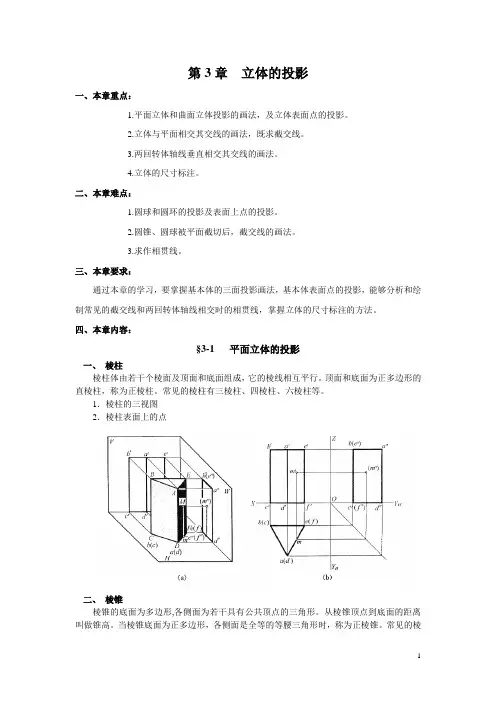
第3章立体的投影一、本章重点:1.平面立体和曲面立体投影的画法,及立体表面点的投影。
2.立体与平面相交其交线的画法,既求截交线。
3.两回转体轴线垂直相交其交线的画法。
4.立体的尺寸标注。
二、本章难点:1.圆球和圆环的投影及表面上点的投影。
2.圆锥、圆球被平面截切后,截交线的画法。
3.求作相贯线。
三、本章要求:通过本章的学习,要掌握基本体的三面投影画法,基本体表面点的投影,能够分析和绘制常见的截交线和两回转体轴线相交时的相贯线,掌握立体的尺寸标注的方法。
四、本章内容:§3-1 平面立体的投影一、棱柱棱柱体由若干个棱面及顶面和底面组成,它的棱线相互平行。
顶面和底面为正多边形的直棱柱,称为正棱柱。
常见的棱柱有三棱柱、四棱柱、六棱柱等。
1.棱柱的三视图2.棱柱表面上的点二、棱锥棱锥的底面为多边形,各侧面为若干具有公共顶点的三角形。
从棱锥顶点到底面的距离叫做锥高。
当棱锥底面为正多边形,各侧面是全等的等腰三角形时,称为正棱锥。
常见的棱锥有三棱锥、四棱锥、六棱锥。
1. 棱锥的三视图2.棱锥表面上的点§3-2曲面立体的投影曲面立体的表面是由一母线绕定轴旋转而成的,故称曲面立体,也称为回转体。
常见的回转体有圆柱、圆锥、圆球和圆环等。
一、圆柱1.圆柱面的形成圆柱面可看作一条直线AB围绕与它平行的轴线OO回转而成。
OO称为回转轴,直线AB称为母线,母线转至任一位置时称为素线。
这种由一条母线绕轴回转而形成的表面称为回转面,由回转面构成的立体称为回转体。
2.圆柱的三视图3.圆柱表面上的点二、圆锥1.圆锥面的形成圆锥面可看作由一条直母线围绕和它相交的轴线回转而成。
2.圆锥的三视图3.圆锥表面上的点三、圆球1.圆球面的形成圆球面可看作一圆(母线),围绕它的直径回转而成。
2.圆球的三视图3.圆球表面上的点四、圆环1.圆环的形成圆环面可看作由一圆母线,绕一与圆平面共面但不通过圆心的轴线回转而成。
图中的回转轴是铅垂线。
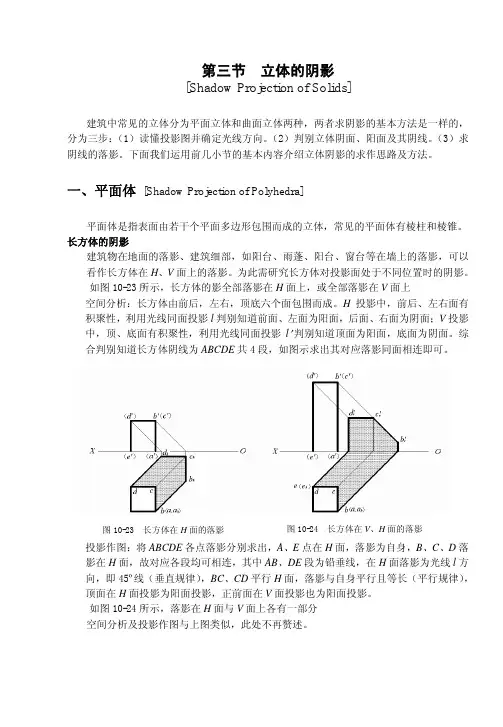
第三节 立体的阴影[Shadow Projection of Solids]建筑中常见的立体分为平面立体和曲面立体两种,两者求阴影的基本方法是一样的,分为三步:(1)读懂投影图并确定光线方向。
(2)判别立体阴面、阳面及其阴线。
(3)求阴线的落影。
下面我们运用前几小节的基本内容介绍立体阴影的求作思路及方法。
一、平面体[Shadow Projection of Polyhedra]平面体是指表面由若干个平面多边形包围而成的立体,常见的平面体有棱柱和棱锥。
长方体的阴影建筑物在地面的落影、建筑细部,如阳台、雨蓬、阳台、窗台等在墙上的落影,可以看作长方体在H、V面上的落影。
为此需研究长方体对投影面处于不同位置时的阴影。
如图10-23所示,长方体的影全部落影在H面上,或全部落影在V面上空间分析:长方体由前后,左右,顶底六个面包围而成。
H投影中,前后、左右面有积聚性,利用光线同面投影l判别知道前面、左面为阳面,后面、右面为阴面;V投影中,顶、底面有积聚性,利用光线同面投影l′判别知道顶面为阳面,底面为阴面。
综合判别知道长方体阴线为ABCDE共4段,如图示求出其对应落影同面相连即可。
图10-23 长方体在H面的落影图10-24 长方体在V、H面的落影投影作图:将ABCDE各点落影分别求出,A、E点在H面,落影为自身,B、C、D落影在H面,故对应各段均可相连,其中AB、DE段为铅垂线,在H面落影为光线l方向,即45º线(垂直规律),BC、CD平行H面,落影与自身平行且等长(平行规律),顶面在H面投影为阳面投影,正前面在V面投影也为阳面投影。
如图10-24所示,落影在H面与V面上各有一部分空间分析及投影作图与上图类似,此处不再赘述。
图10-26 棱锥的阴影切割形体的落影空间分析:图10-25所示的切割形体,参照长方体的阴面、阳面的判别方法,可知底面、右侧面和右前侧面(BCD )为阴面,由于该切割形体紧靠在V 面上,故其阴线为AB 、BC 、CD 、DE 、EF 、FG ,如图10-25(a )。



第3节曲线及曲面立体的阴影圆柱的阴影圆锥的阴影形体在圆柱上的阴影形体在圆锥上的阴影回转体的阴影形体在曲线回转面上的落影圆柱的阴影一、正圆柱阴影的形成二、正圆柱阴影的画法三、圆柱阴面的单面作图法四、垂直圆柱在H面上的落影一、正圆柱阴影的形成半圆阴线阴面素线阴线素线阴线阳面光平面二、正圆柱阴影的画法o o' a'b'o1c'd'c1a1abcd三、圆柱阴面的单面作图法方法(1)方法(2)四、垂直圆柱在H 面上的落影oqc' d' a'b'o 1q 1a 1cdb 1 d 1c 1o' q'圆锥的阴影一、圆锥阴影的形成二、圆锥阴影的画法三、圆锥的阴线及其在V、H面上的落影四、倒立圆锥阴线的作法五、倒立圆锥阴影的作法六、锥面阴线的单面作图法七、圆锥阴线单面作图的证明一、圆锥阴影的形成A S HB二、圆锥阴影的画法a' b' s'hbas h三、圆锥的阴线及其在V 、H 面上的落影s'vas h bx a x ba' b'b' a'abs 0'a 0b 0o 0ob' a'ab s 1' s's o'六、锥面阴线的单面作图法2' 1' a'b'a' b' 2' 1'a1 45ºb45ºa145ºfds's'b145ºfd七、圆锥阴线单面作图的证明1' s' 2'Hbad s hs e§9-10形体在圆柱上的阴影二、内凹半圆柱面的阴影三、方帽柱头的阴影四、方盖盘在内凹半圆柱面上的落影一、圆盖盘在圆柱面上的落影aa' 一、圆盖盘在圆柱面上的落影b' d' d'0 c'0 c'b'0 b b 0 c 0cd d 0 g'f' f'1g'1f 1g 1e'0 e' e'1e e 1 e 0 fg二、内凹半圆柱面的阴影e 0b 0 e'0c'0c' d'dcc 0 b'0ab a' b'三、方帽柱头的阴影 m m110 c 0e 0 e'0 a'vb'v fdc abo a'f'c'd'b'c'0 1'0o'0e' e e'v四、方盖盘在内凹半圆柱面上的落影 1 11102'0 1'0m mb'1o'0 c'1 1'1 o 2 21 a'1 c' d'aba'e' b' c d形体在圆锥上的阴影二、方盖盘在圆锥面上的落影三、在内凹锥面上的落影一、圆盖盘在圆锥面上的落影c'0 s o a'1 a'a a'0 b'0g'go' ≈35°a a' oa 1 a'1 o' a'0 a'10 a 0a 10 d' a d'0o'1 d'1c'0 s o a'a a'0 b'0g' gm' P H mo' ≈35° a a'oa 1 a'1 o' a'0a'10 a 0 a 10 d' ad'0o'1 d'1二、方盖盘在圆锥面上的落影—方法14' 5' 2' 3'a'0f'0 a'10 a'1 d'0 k' a 1 a'b'b o1'k'0二、方盖盘在圆锥面上的落影—方法24' 5' g' 2' 3'a'0f'0 a'10 d'0 k' a'b'a1'k'0三、在内凹锥面上的落影 e's' es 1'01' a ' 3' b' d' 3'0bs'h c101a3 2' 2d 30 20 2'0回转体的阴影一、回转面的阴线二、切锥法切柱法求阴线的实例三、球面的阴影四、用包络线法作回转面阴线的落影一、回转面的阴线1.几种特殊锥面的阴线位置、阴面大小及底角α大小2.切锥面法求回转面阴线的步骤3.回转面阴线的单面作图法−切锥、切柱法1. 几种特殊锥面的阴线位置、阴面大小及底角α大小 α=35° 一条素线与光线重合 1/4锥面为阴面 阴线在右后方 α=35° α=45° α=45° 仅一条素线受光阴线在左前方 3/4锥面为阴面 1/2柱面为阴面 阴线在右后方 阴线在左前方 阴线在左后、右前方 α=90°2. 切锥面法求回转面阴线的步骤相切锥面所求阴点相切纬圆锥面阴线曲线回转面3.回转面阴线的单面作图法---- 切锥、切柱法 s'1e'0 d'0f'0g'0 g'0 k'0 s'5i'0 h'0l'0s'4 s'3a'0s'2 c'0b'0二、切锥法切柱法求阴线的实例1.瓶颈阴线的单面作图(切锥、切柱法)2.鼓面阴线的单面作法3.鼓面阴线的作法4.回转面在V面上的落影1. 瓶颈阴线的单面作图(切锥、切柱法)b'0 e'0 d'0a'1 s'1s'2 s'4 s'3i'0 h'0a'045°45° 45° 45°3' 4'n'0 m'1 2' 1' c'0 l'0 g'0 f'0 j'0 k'0 45°m'02. 鼓面阴线的单面作法s'3b'1 c'0d'0s'1s'2e'0f'0 b'0 g'0 h'0 a'1 a'03. 鼓面阴线的作法c 0d 0f 0g 0h 0a 0b 0b'1 c'0 d'0 e'0f'0 g'0h'0a'1 a'0 b'04. 回转面在V 面上的落影--求法1b'1e'1 h'1d'0e'0 f'0 h'0b'0。