彩虹连通图
- 格式:doc
- 大小:221.00 KB
- 文档页数:9
实验二一步彩虹全息实验一、实验目的1.掌握制作一步彩虹全息图的原理和方法2.制作一张一步彩虹全息图,在白光下观察其重现的像。
二、实验原理彩虹全息是像全息与狭缝技术相结合的产物,可以在白光照明下重现物体的像。
彩虹全息在被摄物和全息干板之间置一狭缝,再现物像时,也再现了狭缝像。
如果用白光照明,眼睛在狭缝像位置观察,可见特定波长光的再现像,而当实现沿垂直于狭缝像方向移动时,再现像也随之按彩虹色序发生变化。
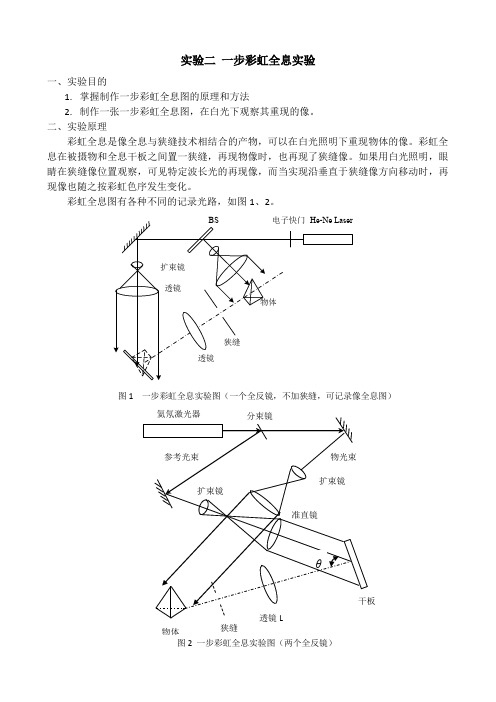
彩虹全息图有各种不同的记录光路,如图1、2。
图1 一步彩虹全息实验图(一个全反镜,不加狭缝,可记录像全息图)三、实验步骤下面是以图2为实验光路图的实验步骤,图1光路图类似。
1、打开激光器,先摆放分束镜、2个全反镜、干板和载物台,使物光和参考光的光程相等(误差不超过2cm)。
注意:物体到干板的距离为45cm(假设成像透镜L的焦距为110mm,物体放在透镜前2倍焦距处,在透镜后2倍焦距处成等大倒立的实像,干板放在实像后1cm处);物光与参考光的夹角θ在30°~60°;参考光光点位于干板中心;参考光与物光的光强比在4:1-8:1之间。
2、将2个准直镜(透镜焦距为190mm和300mm)分别放入物光和参考光光路中,调节透镜位置和高低,使两路光的光斑中心位于干板中央。
3、将2个扩束镜分别放入物光和参考光光路中的透镜前焦点上,使从透镜射出的光为平行光。
4、将物体放置在载物台上,用白屏或白纸观察物体的影子,物体影子应位于平行光斑的中央。
注意:物体躺倒放置;5、将焦距为110mm的透镜放在距物体22cm的地方,将在干板前1cm处可以观察到清晰的物体的像;调节物体的方向,观察物体的像,找反射最强的方向。
6、将狭缝(水平放置)放在物体与透镜之间,且与透镜的距离大于11cm,在干板架后面用毛玻璃寻找狭缝的像,通过狭缝的像观察物体的实像是否完整,若狭缝的像左右不全,可适当加大狭缝宽度或更换更小的物体。
7、曝光、显影、清水、定影、清水。


三类特殊图的(强)彩虹连通数赵燕;柴航【摘要】如果一条路上的任意两条边均染不同颜色,则称这条路是彩虹路.如果在图G的任意两个顶点间都存在一条彩虹路,就称图G是彩虹连通的.对于一个连通图G,保证它是彩虹连通所需的最少颜色数就是G的彩虹连通数,记为rc(G).一条彩虹(u,v)-测地线是指图G中一条长度为d(u,v)的彩虹(u,v)-路,其中d(u,v)表示图G中u,v两点的距离.如果在图G的任意两个顶点间都存在一条彩虹测地线,就称图G是强彩虹连通的.对于一个连通图G,保证它是强彩虹连通所需的最少颜色数就是G的强彩虹连通数,记为src(G).这篇文章主要研究了三类特殊图的(强)彩虹连通数,并得到了它的精确值.【期刊名称】《纯粹数学与应用数学》【年(卷),期】2018(034)003【总页数】7页(P309-315)【关键词】彩虹路;彩虹测地线;彩虹连通;彩虹连通数【作者】赵燕;柴航【作者单位】泰州学院数理学院,江苏泰州 225300;泰州学院数理学院,江苏泰州225300【正文语种】中文【中图分类】O1571 引言本文考虑的图为有限无向简单图.Chartrand等人[1]在2008年首次提出了彩虹连通性的概念.设图G=(V,E)是一个非平凡的连通图,在G上定义一个边染色c:E→{1,2,···,t},t∈N,其中相邻的边可以染相同颜色.如果这条路上的任意两条边均染不同颜色,称图G的一条路是彩虹路.如果在图G的任意两个顶点间都存在一条彩虹路,就称图G是彩虹连通的.对于一个连通图G,保证它是彩虹连通所需的最少颜色数就是G的彩虹连通数,记为rc(G).彩虹连通不仅是一个自然的组合概念,而且在网络中也有着重要的应用.事实上,它的提出起源于政府机构之间的信息安全传递.当人们在机构之间传递信息时,一方面希望所用的密码个数足够得少以便于管理;另一方面,又需要足够多的密码,使得任何两个机构之间至少存在一条信息安全路(路的不同段分配不同密码),以防止入侵者破坏.可以用图来表示这个信息传递网络.如果用边染色表示密码,那么最少的密码个数就是图的彩虹连通数.基于彩虹连通数的概念,Chartrand等人[1]又提出了强彩虹连通数的概念.给定图G 中的两个点u,v,一条彩虹(u,v)-测地线是指图G中一条长度为d(u,v)的彩虹路,其中d(u,v)表示图G中u,v的距离.如果在图G的任意两个顶点间都存在一条彩虹测地线,就称图G是强彩虹连通的.对于一个连通图G,保证它是强彩虹连通所需的最少颜色数就是G的强彩虹连通数,记为src(G).Chakraborty等人[2]证明了给定一个图G,判定rc(G)=2是NP-完全的,特别的,计算一个图的rc(G)是NP-困难的.Chartrand等人[1]得到了一些特殊图类的彩虹连通数.例如,rc(G)=src(G)=1当且仅当G是完全图,rc(G)=src(G)=m当且仅当G为一棵m条边的树,一个顶点数大于3的圈的 (强)彩虹连通数为.注意到,对于任意连通图G,diam(G)≤rc(G)≤src(G)≤m,其中diam(G)表示图G的直径,m表示图G的边数.同时注意到,若H为G的连通生成子图,则rc(G)≤rc(H).更多关于彩虹染色的结果参考文献[3-6].本文研究了两类特殊图的彩虹连通数.首先给出一些定义.2n个点的太阳图是在n 个点的圈图的基础上,每个点处再悬挂一条边.令图G有m个顶点,图H有n个顶点,G和H的日冕(corona)(用G⊙H表示)定义为一个图,取一个G的复制和m个H的复制H1,···,Hm,在G的第i个点和H的第i个复制的每个点均连边.由定义可知,G⊙H有m(1+n)个顶点.对任意两个图G和H显然有G⊙H?H⊙G.接着给出本文需要用到的一些彩虹连通数的结果.引理1.1[7]令n≥2,则扇图(即Pn∨K1)的彩虹连通数为:引理1.2[7]令n≥2,则扇图(即Pn∨K1)的强彩虹连通数为:引理1.3 令n≥3,则太阳图Sn的(强)彩虹连通数为:2 主要结果定理2.1 令G=(Pt1∪Pt2∪···∪Pts)∨K1,其中,2≤ t1≤ t2≤···≤ ts,则证明令其中s=1的情形即引理1.1,因此下设s≥2.首先令s≥3.定义一种染色方式若1≤i≤s,1≤j≤ti,且j为奇数;c(vvti,j)=2,若1≤i≤s,1≤j≤ti,且j为偶数;其余边染3色.易证图中任意两点均有彩虹路连接,因此rc(G)≤3.假设用两种颜色染色,由于并且vt1,i和vt2,j(vt3,k)只有一条2长路,因此得到此时,vt2,j和vt3,k无彩虹路.因此rc(G)=3.当s=2,t2≥4时,仍采用染色方式c1,可以保证图中任意两点均有彩虹路连接,因此rc(G)≤3.假设用两种颜色染色,由于d(vt1,i,vt2,j)=2,并且vt1,i和vt2,j只有一条2长路,因此得到其中1≤j,k≤t2,j̸=k.此时,vt2,1和vt2,t2无彩虹路.因此rc(G)=3.当s=2,t2≤3时,定义一种染色方式c2:E→{1,2}:c(vvt1,1)=c(vvt1,2)=c(vvt1,3)=c(vt1,1vt1,2)=c(vt2,1vt2,2)=1,其余边染2色.易证图中任意两点均有彩虹路连接,因此rc(G)=2.定理2.2 令G=(Pt1∪Pt2∪···∪Pts)∨K1,其中2≤ t1≤ t2≤ ···≤ ts,s≥ 2,则证明令其中s=1的情形即引理1.2,因此下设s≥2.考虑vti,p和vtj,q(i̸=j).由于它们只有一条测地线,为保证vti,p和vtj,q有彩虹测地线,由引理1.2知,如果c(vvti,p)=c(vvti,q),则dPti(vti,pvti,q)≤2.因此另一方面,类似于引理1.2,可以定义一种染色方式保证图中任两点有一条彩虹测地线.因此,定理得证.定理2.3 设n为偶数,令G=Cn⊙K2,则rc(G)=证明令n=2k.设其中1≤i≤n.首先证明rc(G)≤k+3.定义一种染色方式c:E → {1,2,···,k+3}: c(vivi,1)=k+1(1≤ i≤ n), c(vivi,2)=k+2(1 ≤ i≤n),c(vi,1vi,2)=k+3(1≤i≤n), c(vivi+1)=i(1≤i≤k), c(vivi+1)=i−k(k+1≤i≤n).易证图中任意两点均有彩虹路连接,因此得证.下面证明rc(G)≥k+3.反证,假设G使用一种k+2种颜色的边染色方式使得图中任意两点有一条彩虹路连接.首先得到如下的论断:圈中两条同色边只能是相对边.反证,假设为保证vi,1和vj+1,1存在一条彩虹路,d(vivj)=k−1.不妨假设c(v1vn)=c(vk+1vk+2).考虑v1,1(v1,2)和vk+1,1(vk+1,2).易得于是有不妨假设为保证vk+1,1和vk,1,vk+1,1和vk,2均有彩虹路,色k和k+2不能同时出现在vk 悬挂的三角形中. 考虑v1,1和vk,1(vk,2),此时v1,1vk,1-彩虹路只可能走vkvk,1或者vkvk,2vk,1. 如果走vkvk,1,v1,1vk,1必为色k或k+2.如果为色k,为保证v1,1和vk,2有彩虹路,vk,1vk,2染k+2或者vkvk,2染k或k+2,此时vk+1,1和vk,1无彩虹路,矛盾.如果为色k+2,为保证v1,1和vk,2有彩虹路,vk,1vk,2染k或者vkvk,2染k或k+2,此时vk+1,1和vk,1仍无彩虹路,矛盾. 如果走v1,1vk,2vk,1,v1,1vk,2和vk,2vk,1必为色k和k+2,此时vk,2和vk+1,2无彩虹路,矛盾.为保证v1,1和vk+1,1有彩虹路,不妨假设由上述论断知,色k+1在圈中至多出现一次,k+2也至多出现一次.根据色k+1和k+2是否在圈中,分如下三种情形考虑.情形1 色k+1和k+2同时在圈中.此时进一步,只能边vk+1vk+2染色k+1,边vnv1染色k+2.由上述论断知,考虑v1,1和vk,1,如果vkvk,1染色k,为保证v1,1和vk,2有彩虹路,则vk,1vk,2染k+2或者vkvk,2染k或k+2,此时vk,1和vk+1,2无彩虹路,矛盾;如果vkvk,1染色k+2,类似vkvk,1染色k的情形;如果vkvk,1不染色k和k+2,则vkvk,2和vk,2vk,1必为色k和k+2,此时vk,2和vk+1,2无彩虹路,矛盾.情形2 色k+1在圈中,色k+2不在圈中(色k+2在圈中,色k+1不在圈中类似).此时进一步,只能vk+1vk+2染色k+1.由上述论断得类似于情形1,考虑v1,1和vk,1,均会得出矛盾.情形3 色k+1和k+2均不在圈中.由上述论断知,c(vivi+1)=i−k(k+1≤i≤n−1).此时类似于情形1,考虑v1,1和vk,1(vk,2),色k+2或者色k出现在vk悬挂的三角形中两次,或者色k和k+2同时出现在vk悬挂的三角形中,均会得出矛盾.推论2.1 设n≥4为偶数,令G=Cn⊙P3,则rc(G)=证明设其中1≤i≤n.在定理2.3的染色基础上,添加新的染色通过类似定理2.3的讨论,可以得证.定理2.4 设n≥4为偶数,令G=Cn⊙K2,则src(G)=n+1.证明设其中1≤i≤n.首先证明src(G)≤n+1.定义一种染色方式c:E→{1,2,···,n+1},其中易证图中任意两点均有彩虹测地线连接,因此c为强彩虹连通染色.下证用反证方法,假设src(G)≤n.由于推论2.2 设n≥4为偶数,令G=Cn⊙P3,则src(G)=n+1.证明设其中,1≤i≤n.在定理2.4的染色基础上,添加新的染色通过类似定理2.4的讨论,可以得证.参考文献【相关文献】[1]Chartrand G,Johns G,McKeon K,et al.Rainbow connection in graphs[J].Mathematica Bohemica,2008,133:85-98.[2]Chakraborty S,Fischer E,Matsliah A,et al.Hardness and algorithms for rainbow connection[J].Journal of Combinatorial Optimization,2009,21:330-347.[3]Li Xueliang,Li Hengzhe,Sun Yuefang.Rainbow connection number of graphs with diameter 3[J].Discussiones Mathematicae Graph Theory,2017,37:141-154.[4]Li Xueliang,Shi Yongtang,Sun Yuefang.Rainbow connections of graphs:asurvey[J].Graphs and Combinatorics,2013,29:1-38.[5]Li Xueliang,Sun Yuefang.Rainbow Connections of Graphs,Springer Briefs in Mathematics[M].New York:Springer,2012.[6]Li Xueliang,Mao Yaping,Shi Yongtang.The strong rainbow vertex-connection of graphs[J].Utilitas Mathematica,2014,93:213-223.[7]Deng X,Xiang K,Wu B.Polynomial algorithm for sharp upper bound of rainbow connection number of maximal outerplanar graphs[J].Applied Mathematics Letters,2012,25:237-244.。


彩虹的数学物理解释那么彩虹究竟是怎样形成的呢?为什么彩虹的弯的?为什么彩虹看上去是七色的?为什么天空会出现两道彩虹?为什么中午看不到彩虹?1.2 前人的观察及研究据史料记载,早在遥远的殷商时代,我国就出现了有关虹的象形文字。
东汉蔡邕在《月令章句》中这样描述彩虹:“虹见有青赤之色,常依阴云,而昼见于日衙,无云不见,太阴也不见,见辄与日相互,率以日西,见于东方。
”这对彩虹的形成的条件及位置有一定的认识。
唐代孔颖达在《(礼记)注疏》中写道:“若云薄漏日,日照雨滴则虹生”。
沈括的《梦溪笔谈》中有写道,孙彦先云:“虹乃与中日影也,日照雨则有之”。
这解释了彩虹是太阳光在水滴中折射和反射后形成的。
中唐诗人张志和在他的著作——《玄真子》一书中这样描述:“背日喷乎水成霓虹之状”这就是简单的人造彩虹。
亚里士多德是西方第一个试图以科学的眼光观察虹的人,他曾指出:彩虹出现在太阳离地平线较低时,而且彩虹不会出现在夏日的中午;我们可以看到两条颜色相反但形状相似的彩虹,并且外面的那条颜色比较黯淡。
然而亚里士多德并未发现一个现象,那就是两条彩虹带的之间的那片区域较为黯淡。
之后公元约200年的时候,才有亚历山大注意到这个现象,因此后人就将其观察到的这种现象称为“亚历山大暗带”。
此后1307年欧洲人才明白苏格兰上空的双重彩虹是由于太阳光在水珠中产生了折射和反射,这比孙彦先及沈括他们迟了几百年。
法国数学家费马根据他对光的反射的研究得出了“最小时间原理”。
笛卡尔在1637年以充满水的玻璃球充当大水滴来进行实验,得出水对光的折射指数,用数学证明彩虹的主虹和副虹分别是阳光在水珠内经过一个反射和两次反射后再从水珠表面折射出形成的。
他精准地计算出了彩虹的偏向角,但却未能解释彩虹的颜色。
直至牛顿通过三棱镜将太阳光色散之后,通过对电磁波波长的研究指出了彩虹是一道由红色到紫色的连续光谱。
1.3 本文的主要内容在前人研究结果的基础上,本文将从数学物理的角度出发,通过几何光学,包括费马原理、光的反射定律、光的折射定律以及最小偏向角来研究彩虹的形成,包括彩虹在天空出现的位置及其形状、色彩的分布、副虹的存在以及亚历山大暗带的形成。
PPT怎么绘制七色彩虹条形图?
现在小编来介绍一下怎么用PPT绘制七色彩虹(赤、橙、黄、绿、青、蓝、紫)条形图;
打开一个PPT,在工具栏中选择“插入”再选择“文本框”,选择“垂直”,如图;
选择“垂直文本框”在PPT内画出一个文本框来,如图;
选中你画的文本框,在“格式”下面选择“开关填充”,在下面的颜
色里面选择红色,如图;
再依次画出六个条形文本框,把颜色设置成为(橙、黄、绿、青、蓝、紫),具体步骤如上,不再重复,如图;
选中你画的这几个文本框,然后点右键,选择“组合”,如图;
组合好之后现在我们来看一下效果,如图;。
128 实验十六 彩虹全息图的制作实验目的制作彩虹全息图并在白光下观察其再现像。
实验方法第一步:对被照物体制作一个普通的全息图H 1,叫母全息图,见图1。
第二步:将已做好的全息图H 1用R 1*照明再现物体实像,利用此实像作为物(物光),加上参考光R 2及狭缝制作出第二块全息图H 2。
这第二块全息图H 2,具有彩虹的性质,也就是在用R 2*再现时,眼睛放在狭缝位置上可以看到物体的像,若在白光下再现,人眼沿着与狭缝垂直的方向改变观察方向,可看见不同颜色、五彩缤纷的像,如图2所示。
实验光路如图3所示。
实验步骤(制母板步骤省略)1.首先按图3调好光路。
2.放上已作好的母全息图,用R 1*再现原物体实像,可在实像处放一毛玻璃观察。
(这时可挡掉R 2)。
3.挡住物光,调节参考光R 2,使参考光R 2与物光波光强比约为3:1。
(可调连续分束镜或在参考光路中放置衰减镜)。
4.挡住光源,在实像面处放上全息干板,待稳定后进行曝光。
曝光时间,He -Ne 激光器功率40mW ,天津Ⅰ型全息干板为20秒左右,GYT 型干板为90秒左右。
全息干板图1 母全息图图2 第二块全息图1295.经显影、定影和漂白后的干板在白光下观察其再现现象。
注意事项1.狭缝大小和方向的选择:狭缝大小选取由虹全息来说希望越窄越好。
越窄色彩越纯,但太窄物光强太弱,不便观察,也不容易拍照。
至于狭缝方向水平放置与垂直放置均可,只是观察时移动方向不同,依习惯而定。
2.制作彩虹全息图时,参考光与物光光强比约为3:1。
且参考光与物光夹角不宜过大,以免影响衍射效率。
3.观察彩虹全息图的再现像应注意再现条件:白光方向必须是R 1*的方向,再者人眼须刚好置于狭缝原位置。
4.母全息图的制备可参考全息照相实验,为了便于再现实像和制作虹全息图,制作母全息图时物光与参考光的夹角不能太小,例如应在60︒以上,物与干板的距离也应适当选择。
实验原理下面我们稍微定量地讨论基元彩虹全息图的记录与再现。
引言1.1 基本概念在本节中,我们要收集的大部分术语和符号用于此专题。
这里还没有给出,在需要时他们将被定义出来。
所有的图形在这本书中被认为是有限、简单和无向的。
我们也遵循那些不在这里定义的[ 9 ]符号术语。
在这我们分别用V(G)和E(G)表示顶点集,G的边集。
用任何子集(G),用G [X]表示诱导的子图,并且设E[×]的边集为G [X];同样,对E(G)的任意子集为F,让G [F]表示包含在F中的子图。
然后我们表示成,和,这是所有对于y的图的总和。
A 是图G定义的一个集合,作为G的一个完全子图,并且最大集合中不包含任何G的较大的集合。
F对于集合S,|S|为S的势。
一个连通图的边称为桥,它去除将会断开该连通图。
没有桥的图叫做无桥图。
一条有n个顶点的路径表示为n P,其长度为N—1并且用表示。
一个顶点的度是1 那么就叫做悬垂。
我们称G路径长度为悬垂k路径,如果一个末顶点度为1,而所有内顶点度为2。
悬垂1长度的路径就是一个悬垂的势。
我们用表示一个周期的顶点。
对于n≥3,周期为是通过加入一个新的顶点对于每个顶点。
让是一个完全偶图(它的大小可以分别表示成s、t两部分)。
线图G是图(或)其顶点集V(L(G))=E(G)和两个对于相邻顶点当且仅当他它们在G中是相邻。
图G的迭代线图对于图形的线图L(G),被表示成。
一般而言,k-迭代线图是线图。
对于一个相交图集,其顶点可以映射到集,所以有图中的两个顶点之间的边当且仅当对应的两个集合有一个非空交。
区间图是一个实线区间图的相交图。
圆弧图是圆弧形的一个相交图。
一个独立的三个顶点的x、y、z图G一个星状的三重(AT),如果每一对中的顶点,有一个路径不包含任何相邻的第三路径。
有自动测试系统的图形称为无图[25]。
图G如果存在权函数,一个阈值图:V(G)→R和真正的常数,那么要两个顶点 u,v∈V(G)相邻只有满足w(u)+w(v)≥t。
二部图G(A,B)称为链图,如果一个顶点可以令为那么。
让为一个组,并让a为的元素。
我们使用(a)表示a生成的循环子群。
元素的数目(a)称为a的顺序,用a表示。
一对元素a和b如果,那么它就是一个交换群。
果每一对元素是交换的那么它就是一个阿贝尔群。
凯利图对于S来说就是顶点集相邻的两个顶点的x和y的如果,其中是逆封闭。
一个 k-正规图G ,v是严格的正规图,并表示为如果有λ和μ,每两个相邻顶点的整数λ共同的相邻点,每两个不相邻顶点有μ共用的相邻点。
设G是一个连通图。
G中两个顶点u和v 之间的距离由d(u、v)表示,是他们之间的最短路径的长度。
偏心距对于一个顶点v是G的半径为。
一个顶点v和一个集合之间的距离为。
k步打开临近的一个集合为。
一组称为k步支配集G如果所有G的顶点距离最多k步。
此外,如果D诱导一个连接子图G,则称为连接k 步支配集G。
G集合的最小连通k步主导的基数称为它的连接k步控制数,由表示出来。
我们称这个集合为一个二步强支配集k[55],如果每个顶点,至少有k个邻点不占主导地位,占据优势。
一个支配集D在G中被称为双向控制集,如果它的每个垂饰顶点的都包含在D中。
此外,如果G[D]连接,我们称D连接为双向控制集。
一个(连接)两步支配集D中的顶点图G称为(连接)双向两步支配集,如果(1)每个顶点包括D和(2)中的每个顶点在至少有两个临点在里。
注意,如果δ(G)≥2,然后在G中每(连接)支配集是一个(连接)双向控制集。
设F图的是G的一个子图。
在G中耳型是一个非平凡路径, F,其目的是在F里,但其内部没有顶点。
一个嵌套序列图的序列为,我们可以得到。
一个2-连通图G的耳朵分解是一个嵌套序列在2-连接的子图里:(1)是一个周期;(2),其中是里的一个耳朵,1≤i≤k;(3)。
如果在H中每一对顶点之间的距离是一样的,那么G中的H图称为等距。
在G里最大等长周期可被表示。
如果它不包含周期长度大于3的图,就叫做弦图。
在G里的chordality图是一个包含最大周期的长度。
请注意,每等长周期性都是封闭的,因此在G是最大的 chordality。
对于k≤α(G),我们使用来表示最小度数的总和,接管所有的在G中的独立集合的顶点,其中在G中α(G)是的最大独立集元素的数量。
1.2动机和事例连接是最基本的图论的话题之一,无论在组合和算法的理念。
许多优雅和强大的结论是图论连接的结果。
还有很多方面要加强连接的概念,例如要求的哈密尔顿性,k连接,实行直径范围,要求边缘不相交的生成树的存在,等等。
一种有趣的方法来定量加强连接要求,彩虹连接,首次引入查特兰等。
[15]在2006年,重申如下:这个新概念来自资源联合部之间的信息政府机构。
美国国土安全署的创建在2003年回应中发现的弱点机密的安全传输在2001年9月11日之后,恐怖袭击的信息,Ericksen [38] 下列意见:这些致命攻击的一个意外后果实现执法和情报机构无法沟通彼此通过正常渠道从无线电系统数据库。
利用技术是独立的en ti tie和禁止共享访问,意义那不可能人员和爱格ts之间交叉检查信息不同的组织。
而信息需要保护,因为它涉及国家安全,还必须允许访问相应的缔约方之间的过程。
这通过分配之间的信息传输路径可以解决两个问题可能有其他机构中介的机构,同时要求大高昂的数字密码和防火墙入侵者,然而小足以管理(即,足以让每对一个或多个路径机构没有密码重复)。
一个直接的问题是:是什么密码或防火墙需要的最低数量,允许一个或多个安全沿每个路径的每两个机构之间的路径的密码是不同的?这种情况的图论模型。
我们是一个非平凡连接图上进行边缘的coloring c:E(G)→{1,2,···,n},n∈n,定义在哪里相邻边可能是彩色的相同路径如果没有两个边是彩虹这是颜色相同的。
如果每一个边缘色图G彩虹连接由彩虹路径连接两个不同的顶点。
下边缘色彩 G彩虹连接的称为彩虹色。
显然,如果一个图是彩虹连接,它必须连接。
相反,每个连接图一个微不足道的边缘色彩,使其连接的彩虹,即通过色彩边缘用不同的颜色。
因此,我们定义彩虹连接的连接graph G,具体由钢筋混凝土(G)所需的最小颜色数的顺序使七彩虹连接[15]。
彩虹的色彩使用(G)颜色称为最小的彩虹色。
所以上面提到的问题可以建模利用计算彩虹连接数的值。
显然,彩虹连接数可以视为一种新的色指数。
对基本主题的介绍,我们的读者参考。
11[19]。
读者一项调查也可以看到[81]除了关于彩虹色彩的自然组合措施cl的安全传输的应用愚弄机构之间的信息,彩虹连接数也可以是出于其有趣的解释在网络领域[12]。
假设G代表的网络(例如一个细胞网络)。
我们希望在管道的任何两个顶点之间路由消息要求每个链接上的顶点之间的路由(即每个边缘路径)分配一个不同的渠道(如,不同的频率)。
显然,我们希望不同渠道的数量降至最低,我们利用我们的网络。
这个数字正是钢筋混凝土(G)。
让c彩虹连通图的着色G。
任何两个顶点 v G彩虹u−v测地在G是一个彩虹u−v路径长度d(u、v)。
一图G强烈如果存在一个彩虹,彩虹连接u−v测地线每对不同的顶点的u和v G。
在这种情况下,着色c调用 G强的彩虹色。
同样,我们定义强彩虹连接。
实例:fig1.1彩虹3着色和强大彩虹4色彼得森图fig1.2 A graph G (G)=(G)=4人数连接图G,具体由型钢(G),作为最小的数所需的颜色,以便使连接克强彩虹[15]。
注意,这个数字也被称为彩虹直径数[12]。
强大的彩虹着色G usin gsrc(G)称为最小强彩虹的颜色着色克。
显然,我们直径(G)≤(G)≤(G)≤美元,where diam(G)表示G和m直径的大小of G。
为了说明这些新的概念,作者[15]考虑彼得森图P图。
1.1、凡彩虹还显示3色。
(P)≤3。
另一方面,if和v P 两个不相邻顶点,end (u、v)=2,所以u−v路径的长度至少是2。
因此,在使用的任何彩虹色彩至少有两种颜色,所以(P)≥2。
如果P有彩虹2-coloring c,然后存在颜色相同的两个相邻边G c,说e=紫外线和f=下能够安装颜色相同。
因为恰好有一个u−路径长度的2,没有彩虹−在P的路径,这是一个矛盾。
因此,(P)=3。
从钢筋混凝土后(P)=3,因此,(P)≥3。
此外,由于色彼得森图索引是已知的4,有3色c P的边缘结果在两个相邻边紫外和 being分配相同的颜色。
由于u、v、w 是唯一−w测地在P色素c不是一个强大的彩虹色。
由于4色的边缘,P图所示。
1.1是一个强大的彩虹着色,然后钢混凝土(P)=4 作为另一个例子,他们认为graph G图。
1.2a,其中彩虹 4着色of G还显示。
事实上,G和c是最小的彩虹色(G)=4,我们现在验证。
由于直径(G)≥3,因此,(G)≥3。
假设相反,(G)=3。
然后存在G彩虹3色,因为每个u−v路径在G length3,至少有一个three u−v路径是彩虹u−v 路径,说你,u1,v1,v是彩虹u−v路径。
我们可假设(uu1)=1,(u1v1)=2,和(v1v)=3。
(见图。
1.2b。
)G如果x和y是两个顶点,使d(x,y)=2,那么到底包含一个x−y路径长度的2,而其他所有x−y路径长度的4或更多。
这意味着任何两个相邻边可以是彩色的相同。
因此,我们可以假设,不失一般性that(uu2)=2 and (uu3)=3。
(见图。
1.2b。
){(vv2)、(vv3)}={1,2}。
如果(vv2)=1 and (vv3)=2,那么(u2v2)=3 and (u3v3)=1。
在这种情况下,没有彩虹u1−G v3路径。
在另一方面,如果(vv2)=2和(vv3)=1,那么(u2v2)∈{1,3}和(u3v3)=2。
如果Cu2v2)=1,则没有彩虹u2 G −v3path ;而如果(u2v2)=3,有no rain bow u2−v1 G 路径,矛盾。
因此,作为声称,(G)=4。
Since4=(G)≤(G)图的图G 。
1.2、彩虹色of G 图4。
1.2a 还是强彩虹4色,然后钢骨混凝土(G)=4。
1.4 彩虹点连通,彩虹连通度,彩虹索引如我们所见,上述彩虹连通数包括点着色.是Krivelevich 和Yuster[55]首先介绍一种新的参数与定义在点着色图上的彩虹连通数一致.若点着色图G 任一不相邻的两点通过一个路径连通,该路径的中间点着色不同,那么该图是彩虹点连通的.在G 是点连通下的点着色称为彩虹点着色.连通图G 的彩虹点连通数,记为)(G rvc ,是为了让G 满足彩虹点连通所必需的色数中最小的数.类似的,定义最小彩虹点着色.显而易见,我们总是有2)(-≤n G rvc (除了一个图)和0)(=G rvc 当且仅当G 是完全图.注意一个未着色图也被视为0色点找着色图.很明显,1)()(-≥G diam G rvc 等式满足的条件是G 的直径为1或2.注意某些图G 中)(G rvc 可能比)(G rv 小很多.例如,当1)(1,1-=-n K rv n 时1)(1,1=-n K rvc .某些图G 中)(G rvc 可能比)(G rv 大很多.例如去n 点不相邻的三角,并且通过标记每个三角上的一点,将这些标记点补成完全图.该图有n 个割点,而且n G rvc ≥)(.实际上,通过对割点分别着不同的颜色有n G rvc =)(.另一方面,不难理解,4)(≤G rv ,对n K 的边进行着色,不如说着色1,并且每个三角的边着色2,3,4.在彩虹着色,我们只需要找到一个彩虹连接连点的路.所以另一个自然概括如下:在某些边着色图中,任一连点间的彩虹路的数至少是一个大于 1 的整数.一个众所周知的理论Merger[83]证明了在每个κ连通图G 满足1≥κ,对任一两个不相连的点u 和v,有k 个中间不相连的v u -路连接着,整数k 满足κ≤≤k 1.彩虹着色类似的,若至少有k 条中间不相连的彩虹路v u -连接着不相连的点u 和v,我们称边着色为k 彩虹着色.Chartrand et al.[16]定义G 的彩虹k 连通)(G rv 为最小整数j,以至于有j 边彩虹k 色着色.彩虹k 色用)(G rc k 色.通过定义,)(G rc k 是)(G rv 的一般式,而且)()(1G rv G rc =是G 的彩虹连通数.给图G 的边着不同色,我们知道G 的任一两点通过k 条内部不相交的彩虹路相连,并且)(G rc k 中κ≤≤k 1,所以良定义的.此外,)()(G rc G rc j k ≤,κ≤≤≤j k 1.注意这种新的定义彩虹k 连通计算色数,这与计算内部(边)不相交的连通(边连通)数不同.因此,我们称之为彩虹k 连通数.Chartrand et al.[18]介绍了一种更一般的彩虹连通数.令G 是序列n 的边着色非平凡连通图.若G 中树T 中没有着相同的颜色,那么T 为彩虹树.令k 为固定整数n k ≤≤2,若对于G中k 点的子集S,图G 中存在一个彩虹树连接着S中的点,我们称G的边着色为k 彩虹着色.G 的k 彩虹索引)(G rx k 是G中k 彩虹着色必需的最小着色数.k 彩虹着色用)(G rx k 色称为最小的k 彩虹着色.因此,)(2G rx 是彩虹连通数)(G rc .紧接着,对于每个序列为n 的非平凡连通图G,有)()()(32G rx G rx G rx n ≤≤≤ .下面是一个简单但是有用的研究.假设G 连接着两条边uv e =和xy f =.那么f e G --蕴含三个分支)31(≤≤i G i .其中有两个分支包含u,v,x 和y 中的一个.第三分支包含两点,比如说)(),(21G V x G V u ∈∈和)(,3G V y v ∈,若S 是包含u 和x 的k 点的子集,那么每条包含S 的树一定也包含e 和f.这给了我们边着色图到k 彩虹图的必要条件.观察1.4.1([18])令G 是顺序n 的连通图,包含两个桥e 和f.对任一整数k n k ≤≤2,G 的每一个e 到f 的k 彩虹着色一定着不同的颜色.从观察1.4.1,我们知道若G 在某些边着色下是彩虹连通的,那么两个桥包含不同的颜色,这个观察在后面的证明中多次运用.下面是一个直接推论:观察 1.4.2([90])令G 为一个3≥n 点连通图,有)(1G n 吊边.那么,)(G rc )}(),(max{1G n G diam .。