第4章 不完全信息动态博弈
- 格式:ppt
- 大小:223.50 KB
- 文档页数:44

第四章参考答案2、火车站和机场餐饮商业服务的顾客往往都是一次性的,回头客、常客比较少,这些经济交易具有一次性博弈的特征,它们的价格总是较高而质量又会差一些,顾客也会尽量不在这些地方购买商品和消费。
在一般商业区和居民区的餐饮商业服务则回头客和常客较多,有明显的重复博弈特征,在居民区购买商品和消费的老顾客一般能得到比较公平、优惠的价格,还能得到较好的服务,甚至有些还可以信用消费(赊账),因此消费者一般会比较放心地消费。
这就是现实生活中重复博弈和一次性博弈效率不同的典型例子之一。
3、从研究对象和问题特征看,有限次重复博弈研究的主要是有明确结束时间的(合作、竞争等)关系,无限次重复博弈研究的主要是没有明确结果时间,或者较长期的关系。
从分析方法的角度,动态博弈和重复博弈分析中常用的逆推归纳法在无限次16重复博弈中无法直接运用,因为没有最后一次重复。
因此无限次重复博弈分析的主要方法是构造法,即根据特定效率意义等构造了博弈完美纳什均衡。
此外,也可以运用某些技巧解决问题,如教材中利用三阶段讨价还价博弈分析无限阶段讨价还价博弈的技巧。
从博弈的结果看,无限次重复博弈的效率往往高于有限次重复博弈,有些在有限次重复博弈中无法实现的效率较高的结果,在无限次重复博弈中有可能实现。
例如囚徒的困境型博弈的无限次重复博弈和有限次重复博弈就体现了这种差别。
两类重复博弈民间定理的差异也说明了这一点。
最后,在重复次数不多的有限次重复博弈中不一定要考虑得益贴现问题,在我限次重复博弈问题中这是必须考虑的。
上述区别在理论方面最主要的启发是重视有限次和无限次重复博弈的区别,区分研究这两类博弈问题是非常重要的,在实践方面的主要启发是促进和保持经济关系的长期稳定性,对于提高社会经济效率等常常有非常重要的意义。
6、用画线法容易找出该博弈的两个纯策略纳什均衡(T,L)和(M,R)。
这两个纳什均衡的得益都帕累托劣于(B,S)。
一次性博弈中效率较高的(B,S)不可能实现。

不完全信息动态斯塔克尔伯格博弈模型下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!不完全信息动态斯塔克尔伯格博弈模型1. 引言斯塔克尔伯格博弈模型是一种常见的非合作博弈模型,它描述了市场上的领导者和追随者之间的相互作用。





企业间合作与竞争的博弈模型第一章引言企业间的合作与竞争是经济活动中常见的一类现象。
企业间合作,可以加强企业之间的联系,形成企业协同效应,提高企业的竞争力,实现共同利益。
而企业间竞争则是企业之间为争夺市场份额和利润而采取的一种行为,它可以促进市场生态的发展和优化。
因此,如何在企业间进行合作与竞争,是当前企业经营和发展面临的重要问题。
本文将从博弈论的角度探讨企业间合作与竞争的博弈模型。
第二章合作的博弈模型企业间的合作,可以通过博弈论模型进行研究。
博弈论是对决策制定者行为和决策的影响进行定量研究的一种数学方法。
下面以纳什博弈为例,解析企业间合作的博弈模型。
2.1 纳什博弈纳什博弈是一种非合作博弈模型,是博弈论中最著名的博弈模型之一。
该博弈模型是基于每个人都做出最优决策的假设,并考虑到其他参与者也会做出最优决策的可能性。
在纳什博弈中,每个人通过考虑其他人可能的行为来选择自己的行为,以达到自己的最优收益。
2.2 合作的纳什均衡在企业间的合作中,纳什博弈中的合作是比较常见的行为。
当多个企业在选择是否进行合作时,会考虑到其他企业是否也会进行合作。
如果有多个企业都选择进行合作,则可以形成一个纳什均衡。
在这种情况下,每个企业对于合作的决策是最优的,因为每个企业的利益可以得到最大化。
2.3 合作的追求问题然而,在企业间的合作中,每个企业都追求自身利益的最大化。
因此,在企业合作时,存在任一企业追求自身利益的情况下,合作可能会被打破。
此时,合作方可能会受到不利的影响,从而导致合作的失败。
企业间的合作可以利用纳什博弈模型进行分析,以确定最佳的合作策略。
第三章竞争的博弈模型企业间的竞争可以通过博弈论模型进行分析。
下面以重复的囚徒困境博弈为例,解析企业间竞争的博弈模型。
3.1 重复的囚徒困境博弈重复的囚徒困境博弈是一种重复博弈模型,也是博弈论中最常见的博弈模型之一。
在重复囚徒困境博弈中,两个企业面临决定是否采取合作或竞争的问题。
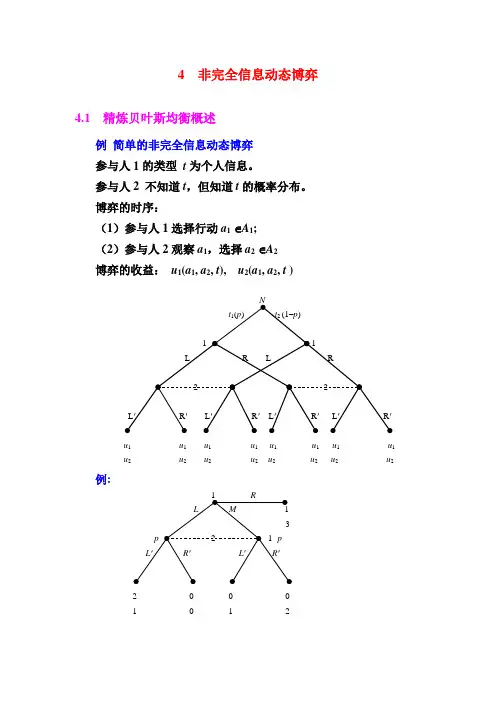
4 非完全信息动态博弈4.1 精炼贝叶斯均衡概述例简单的非完全信息动态博弈参与人1的类型t为个人信息。
参与人2 不知道t,但知道t的概率分布。
博弈的时序:(1)参与人1选择行动a1∈A1;(2)参与人2观察a1,选择a2∈A2博弈的收益:u1(a1, a2, t), u2(a1, a2, t )u1u1u1u1 u1u1u1u1u2u2u2u2 u2u2u2u2例:1 RL M 13p 2 1- pL'R'L'R'2 0 0 01 0 1 2标准式表示参与人 2L'R'L2,10,0参与人 1 M0, 20,1R1, 31, 3纯战略纳什均衡: (L,L'), (R,R')均为子博弈精炼纳什均衡(无子博弈)。
但是(R, R')不可信。
排除不可信的纳什均衡:要求1 参与人必须有一个推断(belief).要求2 参与者的战略必须满足序贯理性(sequentially rational).定义: 处于均衡路径上(on the equilibrium path)的信息集: 在均衡战略下,博弈以正的概率到达该集.要求3 在处于均衡路径上的信息集上, 推断由贝叶斯法则和参与人的均衡战略决定。
例要求3的说明参与人1的类型空间:{ t1,t2,t3,t4 }行动空间:A= { L,R}推断p i: 观察到L后,参与人1的类型是t i的概率。
推断q i: 观察到R后,参与人1的类型是t i的概率。
p1 + p2 + p3 + p4 = 1q1 + q2 + q3 + q4= 1N如果参与人1的战略: t 1选 L ,t 2选 L , t 3选R ,t 4 选R 。
参与人2对p i 与 q i 的推断:p 1 = 3.02.02.0+= 0.4, p 2 = 3.02.03.0+= 0.6, p 3 = 0, p 4 =0; q 1 = 0, q 2= 0, q 3 =3.02.02.0+= 0.4, q 4= 3.02.03.0+= 0.6,例 3个参与人的博弈。



《经济博弈论》复习题及参考答案一、名词解释1、混合战略纳什均衡如果在博弈的利益表中,无法找到任何一方都可以接受(不一定利益最大化)的方案,也就是没有哪一种组合是在给定对手策略下没有动机改变自己策略的情况。
这时博弈没有纯策略均衡,需要一个“概率表”指导博弈结果。
在博弈G={S1,S2……Sn;U1,U2……Un}中第i个博弈方策略空间为Si={Si1……Sik}则博弈方以概率分布Pi=(Pi……Pik)随机在k个可选策略中选的的策略称为一个混合策略纳什均衡。
2、子博弈精炼纳什均衡对于扩展式博弈的策略组合S*=(S1*,…,Si*,…,Sn*) ,如果它是原博弈的纳什均衡;它在每一个子博弈上也都构成纳什均衡,则它是一个子博弈精炼纳什均衡。
子博弈精练纳什均衡所要求的是参与人应该是序惯理性的。
对于有限完美信息博弈,逆向归纳法是求解子博弈精炼纳什均衡的最简便的方法。
3、完全信息动态博弈完全信息动态博弈,是指博弈中信息是完全的,即双方都掌握参与者对他参与人的战略空间和战略组合下的支付函数有完全的了解,但行动是有先后顺序的,后动者可以观察到前者的行动,了解前者行动的所有信息。
4、不完全信息动态博弈指在动态博弈中,行动有先后次序,博弈的每一参与人知道其他参与人的有哪几种类型以及各种类型出现的概率,即知道“自然”参与人的不同类型与相应选择之间的关系,但是,参与人并不知道其他的参与人具体属于哪一种类型。
由于行动有先后顺序,后行动者可以通过观察先行动者的行为,获得有关先行动者的信息,从而证实或修正自己对先行动者的行动。
5、完全信息静态博弈完全信息静态博弈指的是信息对于博弈双方来说是完全公开的情况下,双方在博弈中所决定的决策是同时的或者不同时但在对方做决策前不为对方所知的。
6、囚徒困境囚徒困境是博弈论的非零和博弈中具代表性的例子,反映个人最佳选择并非团体最佳选择。
虽然困境本身只属模型性质,但现实中的价格竞争、环境保护等方面,也会频繁出现类似情况。