Stata_之面板数据处理—长面板

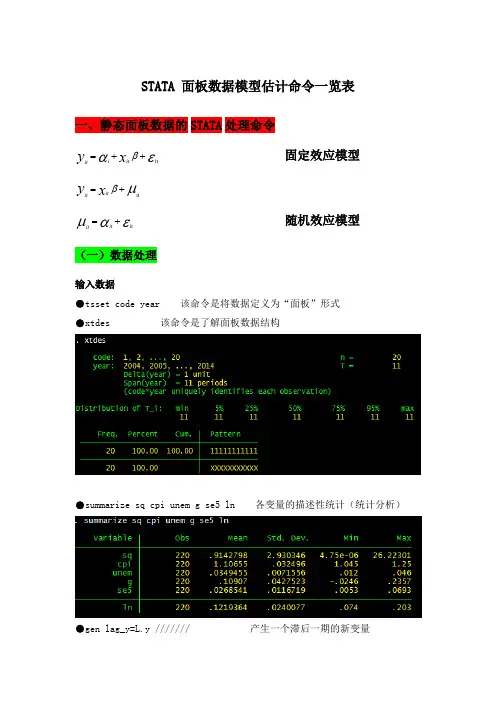
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it （一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

Chp8 Panel Data一直想把看Panel模型时的感悟整理成笔记，但终因懒惰而未能成行。

今天终于下决心开了个头，可遗憾的是，这个开头却是从本章的结尾写起，因为这一部分最容易写。

不过，凡事有了好的开头基本上也算成功一半了，所以后面的整理工作还要有劳各位的督促。

文中的不足还望不吝指出。

8.1简介8.2一般模型8.2.1固定效应模型（Fixed Effect Model）8.2.2随机效应模型（Random Effect Model）8.3自相关性8.4动态Panel Data8.5门槛Panel Data8.6非稳定Panel Data及协整8.7Panel V AR8.8Stata8.0实现在介绍了Panel Data的基本理论后，下面我们介绍如何使用STATA8.0软件包来实现模型的估计。

前面我们已经提到，Panel Data具有如下数据存储格式：company year invest mvalue11951755.94833.011952891.24924.9119531304.46241.7119541486.75593.621951588.22289.521952645.52159.421953641.02031.321954459.32115.531951135.21819.431952157.32079.731953179.52371.631954189.62759.9其中，变量company和year分别为截面变量和时间变量。

显然，通过这两个变量我们可以非常清楚地确定panel data的数据存储格式。

因此，在使用STATA8.0估计模型之前，我们必须告诉它截面变量和时间变量分别是什么，所用的命令为tsset1，命令格式如下：tsset panelvar timevar这里需要指出的是，由于Panel Data本身兼具截面数据和时间序列二者的特性，所以对时间序列进行操作的运算同样可以应用到Panel Data身上。

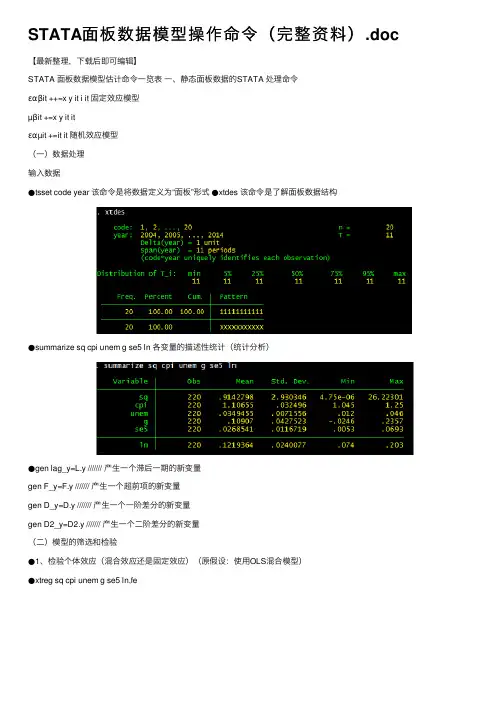
STATA⾯板数据模型操作命令（完整资料）.doc 【最新整理，下载后即可编辑】STATA ⾯板数据模型估计命令⼀览表⼀、静态⾯板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型µβit +=x y it itεαµit +=it it 随机效应模型（⼀）数据处理输⼊数据●tsset code year 该命令是将数据定义为“⾯板”形式●xtdes 该命令是了解⾯板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产⽣⼀个滞后⼀期的新变量gen F_y=F.y /////// 产⽣⼀个超前项的新变量gen D_y=D.y /////// 产⽣⼀个⼀阶差分的新变量gen D2_y=D2.y /////// 产⽣⼀个⼆阶差分的新变量（⼆）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使⽤OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型⽽⾔，回归结果中最后⼀⾏汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例⼦中发现F 统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验⽅法：LM 统计量）（原假设：使⽤OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第⼀幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应⾮常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验⽅法：Hausman 检验）原假设：使⽤随机效应模型（个体效应与解释变量⽆关）通过上⾯分析，可以发现当模型加⼊了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it （一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

最全Stata面板数据学习手册来源：本文授权转载自数量经济学本文包括静态与动态面板数据处理方法，包含hausman检验，固定效应检验，随机效应检验，异方差检验、相关检验，面板logit与面板probit模型、面板泊松模型、面板负二项模型等众多干货内容，欢迎阅读。

本文目录一、静态面板数据●数据处理●模型的筛选和检验1、检验个体效应（混合效应还是固定效应）2、检验时间效应（混合效应还是随机效应）3、检验固定效应模型or随机效应模型（检验方法：Hausman 检验）●模型的筛选和检验1、固定效应估计2、随机效应估计省略3、时间固定效应（以上分析主要针对的是个体效应）●异方差和自相关检验1、异方差检验（组间异方差）2、序列相关检验3、“异方差—序列相关”稳健型标准误4、截面相关检验5、“异方差—序列相关—截面相关”稳健型标准误二、动态面板数据三、面板logit与面板probit模型四、面板泊松模型五、面板负二项模型六、面板Tobit模型七、面板工具变量法八、面板随机前沿模型一．静态面板数据的STATA处理命令（一）数据处理输入数据use 'E:\stata\data\FDI.dta', cleartsset code year 该命令是将数据定义为“面板”形式xtdes 该命令是了解面板数据结构summarize lngdp lnfdi lnie lnex lnim lnci lngp各变量的描述性统计（统计分析）拓展命令：gen lag_y=L.y 产生一个滞后一期的新变量gen F_y=F.y 产生一个超前项的新变量gen D_y=D.y 产生一个一阶差分的新变量gen D2_y=D2.y 产生一个二阶差分的新变量（二）模型的筛选和检验1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS 混合模型）xtreg lngdp lnfdi lnie lnex lnim lnci lngp,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA 面板数据模型估计命令一览表一、静态面板数据的 STATA 处理命令固定效应模型随机效应模型（一）数据处理输入数据• tsset code year 该命令是将数据定义为“面板”形式 • xtdes该命令是了解面板数据结构・ xtdescode: 1i 2, ■■■( 20n 工 20 year : 3004, 2005, ■…,2014T =11Delta(year) =1 unit span(year) =11 periods(code*year uniquely identifies eachobservation)Distribution of:min 8%2璃50^ 75% 95%max1111 11111111 11Freq. Percent Cum. Pattern20 100.00 100.00 1111111111120100.00XXXXXXXXXXX・ summarize sc I cpi unem gse5 InvariableObs Mean Std ・ Dev.Mi nMax sq 220 .Q142798 2.9303464.75e-0626.22301cpi2201*10655 *032496 1.045 1. 25 unem22Q .0349455 .0071556 .012 ,046 g220,10907 .0427523 0246 .2357220 .0268541 011671? .0053.0693220.1219364.0240077,074,203• summarize sq cpi unem g se5 In各变量的描述性统计（统计分析）• gen lag_y=L.y ///////产生一个滞后一期的新变量*= Xitit• ;itto U 一 if对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。

S T A T A 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it iit 固定效应模型 εαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS 混合模型） ●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所有的个体效应整体上显着。

在我们这个例子中发现F 统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS 模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM 统计量）（原假设：使用OLS 混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui ”之后第一幅图将不会呈现)xttest0可以看出，LM 检验得到的P 值为0.0000，表明随机效应非常显着。

可见，随机效应模型也优于混合OLS 模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显着优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless) 可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

【最新整理，下载后即可编辑】STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式 ●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM 统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman 检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

一、静态面板数据地处理命令（一）数据处理输入数据● 该命令是将数据定义为“面板”形式● 该命令是了解面板数据结构● 各变量地描述性统计（统计分析）● 产生一个滞后一期地新变量产生一个超前项地新变量产生一个一阶差分地新变量产生一个二阶差分地新变量（二）模型地筛选和检验●、检验个体效应（混合效应还是固定效应）（原假设：使用混合模型）●对于固定效应模型而言，回归结果中最后一行汇报地统计量便在于检验所有地个体效应整体上显著.在我们这个例子中发现统计量地概率为，检验结果表明固定效应模型优于混合模型.文档收集自网络，仅用于个人学习●、检验时间效应（混合效应还是随机效应）（检验方法：统计量）（原假设：使用混合模型）● (加上“”之后第一幅图将不会呈现)文档收集自网络，仅用于个人学习可以看出，检验得到地值为，表明随机效应非常显著.可见，随机效应模型也优于混合模型.文档收集自网络，仅用于个人学习●、检验固定效应模型随机效应模型（检验方法：检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应地时候，将显著优于截距项为常数假设条件下地混合模型.但是无法明确区分地优劣，这需要进行接下来地检验，如下：文档收集自网络，仅用于个人学习：估计固定效应模型，存储估计结果：估计随机效应模型，存储估计结果：进行检验●(或者更优地是)文档收集自网络，仅用于个人学习可以看出，检验地值为，拒绝了原假设，认为随机效应模型地基本假设得不到满足.此时，需要采用工具变量法和是使用固定效应模型.文档收集自网络，仅用于个人学习●、时间固定效应（以上分析主要针对地是个体效应）如果希望进一步在上述模型中加入时间效应，可以采用时间虚拟变量来实现.首先，我们需要定义一下个时间虚拟变量.文档收集自网络，仅用于个人学习● () (命令用于列示变量地组类别，选项（）用于生产一个以开头地年度虚拟变量)文档收集自网络，仅用于个人学习（作用在于去掉第一个虚拟变量以避免完全共线性）若在固定效应模型中加入时间虚拟变量，则估计模型地命令为：（四）异方差和自相关检验●、异方差检验（组间异方差）本节主要针对地是固定效应模型进行处理（）检验原假设：同方差需要检验模型中是否存在组间异方差,需要使用命令.●显然，原假设被拒绝.此时，需要进一步以获得参数地估计量，命令为：● ()文档收集自网络，仅用于个人学习其中，组间异方差通过（）选项来设定.上述结果是采用两步获得，即，先采用估计不考虑异方差地模型，进而利用其残差计算...，并最终得到估计量.文档收集自网络，仅用于个人学习●、序列相关检验对于较大地面板而言，往往无法完全反映时序相关性，此时便可能存在序列相关，在多数情况下被设定为()过程.文档收集自网络，仅用于个人学习原假设：序列不存在相关性.模型地序列相关检验对于固定效应模型，可以采用检验法，命令为:●可以发现，这里地，我们可以在地显著性水平下爱拒绝不存在序列相关地原假设.考虑到样本，该检验地最后一步是用对进行回归，因此，输入以下命令得到.检验该值是否显著异于，因为在原假设下（不相关），可见本例中不相等，拒绝原假设，说明存在序列相关.文档收集自网络，仅用于个人学习● ()模型地序列相关检验对于模型，可以采用命令来执行检验：● *这里汇报了个统计量，分别用于检验模型中随机效应（单尾和双尾）、序列相关以及二者地联合显著性，检验结果表明存在随机效应和序列相关，而且对随机效应和序列相关地联合检验也非常显著.文档收集自网络，仅用于个人学习稳健型估计上述结果表明，无论是还是模型，干扰项中都存在显著地序列相关.为此，我们进一步采用命令来估计模型，首先考虑固定效应模型：文档收集自网络，仅用于个人学习● *●、“异方差—序列相关”稳健型标准误虽然上述估计方法在估计方差协方差矩阵时考虑了异方差和序列相关地影响，但都未将两者联立在一起考虑，要获得“异方差序列相关”稳健型标准误，只需在命令中附加()或者()选项即可.例如，对于模型，我们可以执行如下命令：文档收集自网络，仅用于个人学习与之前未经处理地估计结果相比，附加命令()选项时地结果，虽然系数地估计值未发生变化，但此时得到地标准误明显增大了，致使得到地估计结果更加保守.对于面板数据模型而言，在计算所谓地“”标准误时，是以个体为单位调整标准误地.因此，我们得到地“”标准误其实是同时调整了异方差和序列相关后地标准误.换言之，上述结果与设定()选项地结果完全相同.文档收集自网络，仅用于个人学习●、截面相关检验原假设：截面之间不存在着相关性（）模型检验对于模型，可以利用命令来检验截面相关性：●(该命令主要针对地是大小类型地面板数据，在本例中无法使用，故图标略去.)（）模型检验对于模型，可以利用命令来检验截面相关性：●(下面命令是另一个检验指标)可以看出，两种不同地检验方法均显示面板数据存在着截面相关性.●、“异方差—序列相关—截面相关”稳健型标准误（）模型估计对于模型，在确认上述存在着截面相关地情况下，我们可以采用()编写地命令获取()提出地“异方差—序列相关—截面相关”稳健型标准误：文档收集自网络，仅用于个人学习●这里，命令会自动选择地滞后阶数为，系数估计值和与地结果完全相同，但标准误存在着较大差异.可见，在本例中，截面相关对统计推断有较大地影响.文档收集自网络，仅用于个人学习若读者有跟高地方法来确定自相关地滞后阶数，则可以通过( )选项设定.当然，在多数情况下，这很难做到.不过我们可以通过附加()来估计仅考虑异方差和截面相关地稳健型标准误，命令如下：文档收集自网络，仅用于个人学习● ()（）模型估计(略，待补充)二、动态面板数据地处理命令（一）差分文档收集自网络，仅用于个人学习() 文档收集自网络，仅用于个人学习（二）系统文档收集自网络，仅用于个人学习, 文档收集自网络，仅用于个人学习（三）内生性检验●（四）序列相关检验●: , 文档收集自网络，仅用于个人学习"黑龙江" "吉林" "辽宁" "山西" "湖北" "湖南" "河南" "江西" "安徽"文档收集自网络，仅用于个人学习。

STATA面板数据模型操作命令stata面板数据模型估计命令一览表一、静态面板数据的stata处理命令（一）数据处理输入数据●tssetcodeyear该命令就是将数据定义为“面板”形式●xtdes该命令就是介绍面板数据结构●summarizesqcpiunemgse5ln各变量的描述性统计（统计分析）●genlag_y=l.y///////产生一个滞后一期的新变量genf_y=f.y///////产生一个超前项的新变量gend_y=d.y///////产生一个一阶差分的新变量gend2_y=d2.y///////产生一个二阶差分的新变量（二）模型的甄选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用ols混合模型）●xtregsqcpiunemgse5ln,fe对于紧固效应模型而言，重回结果中最后一行汇报的f统计数据量便是检验所有的个体效应整体上明显。

在我们这个例子中辨认出f统计数据量的概率为0.0000，检验结果表明紧固效应模型强于混合ols模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：lm统计量）（原假设：使用ols混合模型）●quixtregsqcpiunemgse5ln,re(加之“qui”之后第一幅图将不能呈现出)xttest0可以看出，lm检验得到的p值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合ols模型。

●3、检验紧固效应模型or随机效应模型（检验方法：hausman检验）原假设：采用随机效应模型（个体效应与表述变量毫无关系）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合ols模型。

但是无法明确区分feorre的优劣，这需要进行接下来的检验，如下：step1：估算紧固效应模型，存储估算结果step2：估算随机效应模型，存储估算结果step3：展开hausman检验●quixtregsqcpiunemgse5ln,fe eststorefequixtregsqcpiunemgse5ln,reeststorerehausmanfe(或者更优的是hausmanfe,sigmamore/sigmaless)可以看出，hausman检验的p值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。