stata面板数据操作示例
- 格式:pdf
- 大小:365.71 KB
- 文档页数:33
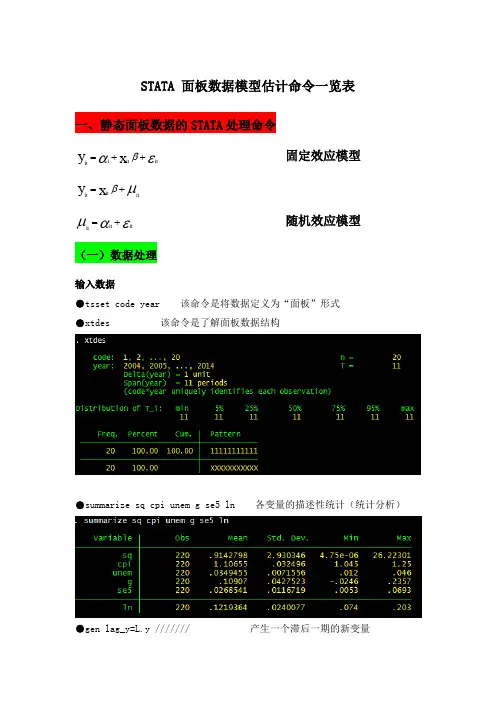
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
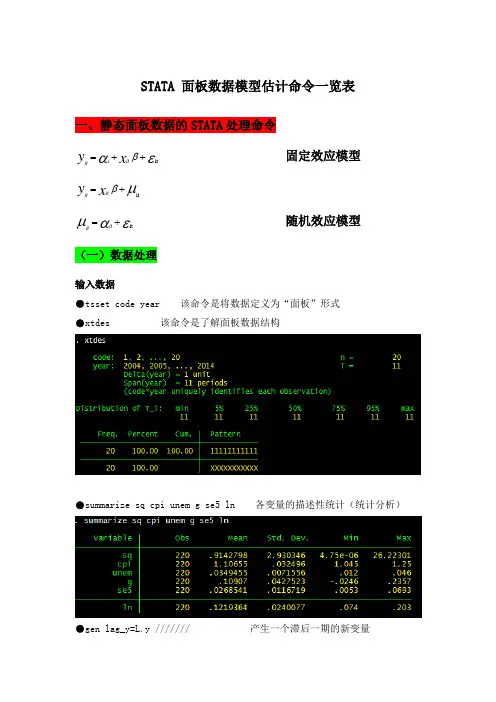
STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
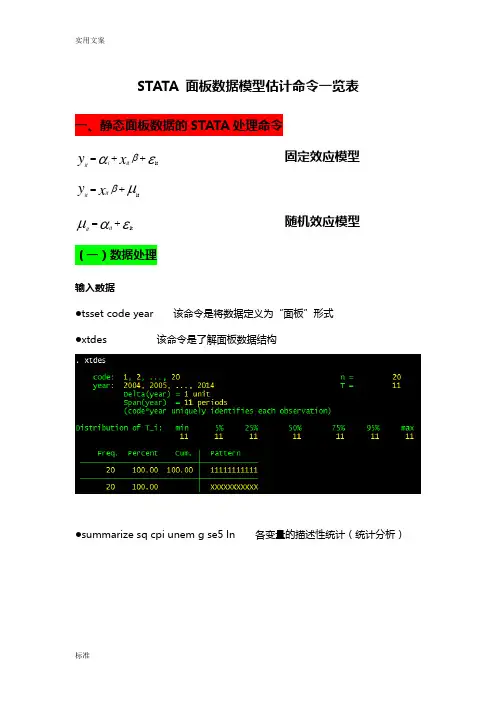
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=xy itiit固定效应模型μβit +=xy ititεαμit+=itit随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式 ●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it iit 固定效应模型 εαμit +=it it 随机效应模型一数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计统计分析 ●gen lag_y=αi αi αi εit ~e it ~1-t e i ,8858.0~=θ5.0-~=θ验:是否存在门槛效应混合面板:reg is lfr lfr2 hc open psra tp gr,vcecluster sf固定效应、随机效应模型xtreg is lfr lfr2 hc open psra tp gr,feest store fextreg is lfr lfr2 hc open psra tp gr,reest store rehausman fe两步系统GMM 模型xtdpdsys rlt plf1 nai efd op ew ig ,lags1 maxldep2 twostep artests2 注:rlt 为被解释变量,“plf1 nai efd op ew ig ”为解释变量和控制变量; maxldep2表示使用被解释变量的两个滞后值为工具变量;pre 表示以某一个变量为前定解释变量;endogenous 表示以某一个变量为内生解释变量; 自相关检验:estat abond萨甘检验:estat sargan差分GMM模型Xtabond rlt plf1 nai efd op ew ig ,lags1 twostep artests2内生:该解释变量的取值是一定程度上由模型决定的;内生变量将违背解释变量与误差项不相关的经典假设,因而内生性问题是计量模型的大敌,可能造成系数估计值的非一致性和偏误;外生:该解释变量的取值是完全由模型以外的因素决定的;外生解释变量与误差项完全无关,不论是当期,还是滞后期;前定:该解释变量的取值与当期误差项无关,但可能与滞后期误差项相关;。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA处理命令(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless) 可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。

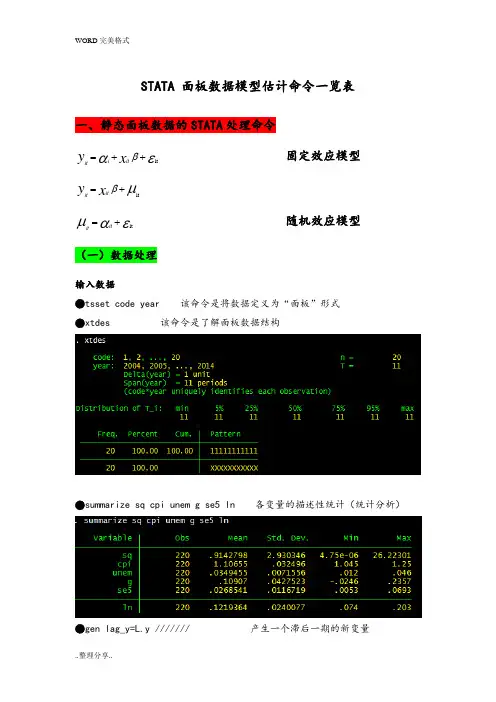
STATA 面板数据模型估计命令一览表一、静态面板数据的 STATA 处理命令固定效应模型随机效应模型(一)数据处理输入数据• tsset code year 该命令是将数据定义为“面板”形式 • xtdes该命令是了解面板数据结构・ xtdescode: 1i 2, ■■■( 20n 工 20 year : 3004, 2005, ■…,2014T =11Delta(year) =1 unit span(year) =11 periods(code*year uniquely identifies eachobservation)Distribution of:min 8%2璃50^ 75% 95%max1111 11111111 11Freq. Percent Cum. Pattern20 100.00 100.00 1111111111120100.00XXXXXXXXXXX・ summarize sc I cpi unem gse5 InvariableObs Mean Std ・ Dev.Mi nMax sq 220 .Q142798 2.9303464.75e-0626.22301cpi2201*10655 *032496 1.045 1. 25 unem22Q .0349455 .0071556 .012 ,046 g220,10907 .0427523 0246 .2357220 .0268541 011671? .0053.0693220.1219364.0240077,074,203• summarize sq cpi unem g se5 In各变量的描述性统计(统计分析)• gen lag_y=L.y ///////产生一个滞后一期的新变量*= Xitit• ;itto U 一 if对于固定效应模型而言,回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。
【原创】5分钟搞定Stata面板数据分析简易教程ver2.0作者:张达5分钟搞定Stata面板数据分析简易教程步骤一:导入数据原始表如下,数据请以时间(1998 ,1999,2000, 2001 ??)为横轴,样本名(北京,天津,河北??) 为纵轴1 裁*■■別1A I11 ■u 9K ILEXxl-V,j si aoLL B-iic190 ..1( HJ曲1 1g力«r4 々■l* Mfl 1KM J| JgRi MM3icm*w II7QQ-HQ Siq<XM3 7>D tuff 1'C4 3 4 IftJV-mi KH>loogi liW(0M 3M9WH jaii I MOKai W w ■齐itmxm fill OTI MiltaiK ■5W»U|JTXE HH sia心«9 f Id 叼m in a*ft I*■JtaC如M~4 気HiA|$A rm inoo IM? livra.wvtatr1IJMj X#*4>t1|筑・BF7 ■«|!N I9*V1IRV gw1W1VJ I-J H itW Ml «稠申审砂y li>M l>R Mdw VIM e> mu IM HM 內)944w 命■ n I L BII i mi 靜Ml hw w3K:1ST? *7^ FJE inm ifini uni4 5w 心HtJ TW JTfl 9MI*HAS■ilJto KO >4*461/M31 <141*11诃却4LJt 4ktt VM匸F<MO 4dN,■M I!Wi・】•\ 4 ■R- 呵鬥1皑用MA■J广*»i g Ml* <KM11*K=« 1 31 1MM I“tlM韓!1fi >w g ivt E4M laM■ii T PD w im W i.JV 1P w L*l 1tiZF MM7 <1 H1! liyi将中文地名替换为数字。

STATA面板数据模型操作命令讲解面板数据模型主要用于分析在一段时间内,多个个体上观察到的数据。
在面板数据模型中,个体可以是个人、家庭、公司等。
面板数据模型的分析主要包括汇总统计、描述性统计、回归分析等。
下面是一些STATA中常用的面板数据分析命令的介绍和使用说明:1. xtset命令:该命令用于设置数据集的面板数据特征。
在使用面板数据模型之前,需要先将数据集设置为面板数据。
使用xtset命令可以指定面板数据集的个体维度和时间维度。
示例:xtset id year该命令将数据集按照id(个体)和year(时间)进行分类。
2. xtsummary命令:该命令用于生成面板数据的汇总统计信息,包括平均值、标准差、最小值、最大值等。
示例:xtsummary var1 var2该命令将变量var1和var2的汇总统计信息显示出来。
3. xtreg命令:该命令用于进行固定效应模型(Fixed Effects Model)的估计,其中个体效应被视为固定参数,时间效应被视为随机参数。
示例:xtreg y x1 x2, fe该命令将变量y对x1和x2进行固定效应模型估计。
4. xtfe命令:该命令用于进行固定效应模型的估计,并提供了更多的选项和功能。
示例:xtfe y x1 x2, vce(robust)该命令将变量y对x1和x2进行固定效应模型估计,并使用鲁棒标准误。
5. xtlogit命令:该命令用于进行面板Logistic回归分析,适用于因变量为二分类变量的情况。
示例:xtlogit y x1 x2, re该命令将变量y对x1和x2进行面板Logistic回归分析,并进行随机效应的估计。
6. areg命令:该命令用于进行差别法(Difference-in-Differences)模型的估计,适用于时间和个体差异的面板数据分析。
上述命令只是STATA中一部分常用的面板数据模型操作命令。
在实际应用中,根据具体的研究需求和数据特征,还可以使用其他面板数据模型命令进行分析,如xtlogit、xtprobit等。

面板模型的Stata命令及实例面板数据的设定xtset panelvar timevar设定面板数据的Stata 命令为:告诉Stata 你的数据为面板数据面板(个体)变量取值须为整数且不重复时间变量假如“panelvar ”是字符串,可用encode country, gen(cntry)转换为数字型变量面板数据的设定xtset panelvar timevar设定面板数据的Stata 命令为:面板数据的设定面板数据统计特性的Stata 命令:xtdes 显示面板数据的结构,是否为平衡面板。
xtsum xtline varname显示组内、组间与整体的统计指标。
对每位个体分别显示该变量的时间序列图;如希望将所有个体的时间序列图叠放在一起,可加上选择项overlay。
“种植业产值对数”(ltvfo,1980 年不变价格)案例以数据集lin_1992.dta为例,取自Lin(1992) 发表在美国经济评论上,对家庭联产承包责任制与中国农业增长的经典研究。
该省际面板包含中国28个省1970-1987年有关种植业的数据。
被解释变量解释变量耕地面积对数(ltlan,千亩),种植业劳动力(ltwlab),机械动力与畜力对数(ltpow,千马力),化肥使用量对数(ltfer,千吨),截止年底采用家庭联产承包制的生产队比重(hrs),农村消费者价格与农村工业投入品价格之比的一阶滞后(mipric1,1950 年=100),超额收购价格与农村工业投入品价格之比(giprice,1950 年=100),复种指数(mci,播种面积除以耕地面积),非粮食作物占播种面积比重(ngca),时间趋势(t),province(省),year(年)。
案例设定province与year为面板(个体)变量及时间变量:1use lin_1992.dta,clearxtset province year面板数据的设定案例显示数据集中以上变量的统计特征,进行描述性统计xtsum ltvfo ltlan ltwlab ltpow ltfer hrs mipric1 giprice mci ngca不同省的种植业产值均随时间而增长,但变化趋势与时机不尽相同。
STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
STATA⾯板数据模型操作命令讲解STATA ⾯板数据模型估计命令⼀览表⼀、静态⾯板数据的STATA 处理命令εαβit ++=xy itiit固定效应模型µβit +=xy ititεαµit+=itit随机效应模型(⼀)数据处理输⼊数据●tsset code year 该命令是将数据定义为“⾯板”形式●xtdes 该命令是了解⾯板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产⽣⼀个滞后⼀期的新变量gen F_y=F.y /////// 产⽣⼀个超前项的新变量gen D_y=D.y /////// 产⽣⼀个⼀阶差分的新变量gen D2_y=D2.y /////// 产⽣⼀个⼆阶差分的新变量(⼆)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使⽤OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型⽽⾔,回归结果中最后⼀⾏汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例⼦中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验⽅法:LM统计量)(原假设:使⽤OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第⼀幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应⾮常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验⽅法:Hausman检验)原假设:使⽤随机效应模型(个体效应与解释变量⽆关)通过上⾯分析,可以发现当模型加⼊了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是⽆法明确区分FE or RE的优劣,这需要进⾏接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进⾏Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满⾜。
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令εαβit ++=x y it iit 固定效应模型 εαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析) ●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS 混合模型) ●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F 统计量便在于检验所有的个体效应整体上显着。
在我们这个例子中发现F 统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS 模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM 统计量)(原假设:使用OLS 混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui ”之后第一幅图将不会呈现) xttest0可以看出,LM 检验得到的P 值为0.0000,表明随机效应非常显着。
可见,随机效应模型也优于混合OLS 模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显着优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless) 可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
STATA面板数据模型操作命令讲解STATA是一种常用的统计分析软件,可以用于面板数据模型的操作。
面板数据模型是一种用来分析涉及多个单位和多个时间点的数据的统计模型,其主要特点是能够考虑单位间和时间间的相关性。
在STATA中,可以使用一系列命令来进行面板数据模型的操作,包括数据导入、数据清洗、模型估计和结果展示等。
下面将详细介绍STATA中面板数据模型操作的常用命令。
首先,要进行面板数据模型的操作,首先需要将数据导入到STATA中。
STATA支持多种数据格式的导入,包括Excel、CSV和数据库等。
常用的导入命令包括:1. use命令:用于导入STATA格式的数据文件。
例如:use data.dta2. import命令:用于导入其他格式的数据文件。
例如:import excel data.xlsx, firstrow导入数据后,接下来需要进行数据清洗和变量定义。
可以使用一系列命令对数据进行操作,例如生成新变量、删除缺失值和标识变量等。
常用的数据清洗命令包括:1. generate命令:用于生成新变量。
例如:generate log_y = log(y)2. drop命令:用于删除变量。
例如:drop x3. replace命令:用于替换变量值。
例如:replace y = 0 if y < 0数据清洗完成后,就可以开始估计面板数据模型。
常用的估计命令包括固定效应模型(Fixed Effects Model)和随机效应模型(Random Effects Model)。
下面分别介绍这两种模型的估计命令。
1.固定效应模型的估计命令:xtreg y x1 x2, fe其中,xtreg表示面板数据的回归命令,y为因变量,x1和x2为自变量,fe为固定效应模型的选项。
2.随机效应模型的估计命令:xtreg y x1 x2, re其中,re表示随机效应模型的选项。
除了固定效应模型和随机效应模型,STATA还支持其他面板数据模型的估计方法,如差分估计(Difference-in-Differences)、合成控制法(Synthetic Control Method)等。
STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
STATA面板数据模型操作命令STATA是一个强大的统计分析软件,可以进行各种数据操作和模型建立。
对于面板数据,即具有时间序列和跨个体的数据,STATA提供了多种命令来进行数据的操作和模型的拟合。
以下是一些常用的STATA面板数据模型操作命令:1. xtset命令:用于设置数据集的面板结构,将数据按个体和时间次序排序。
例如,xtset country year可以将数据按照国家和年份排序。
2. xtreg命令:用于拟合面板数据的固定效应模型。
例如,xtreg y x1 x2, fe可以拟合一个包含固定效应的面板数据模型,其中y为因变量,x1和x2为解释变量。
3. xtfe命令:用于估计固定效应模型的固定效应,即个体固定效应模型。
例如,xtfe y x1 x2可以计算出个体固定效应。
4. xtgls命令:用于估计面板数据的一般化最小二乘回归模型。
例如,xtgls y x1 x2可以拟合一个包含一般固定效应的面板数据模型。
5. xtmixed命令:用于估计混合效应模型,即个体和时间固定效应模型。
例如,xtmixed y x1 x2 , country:, var(can)可以在个体和时间固定效应下估计一个模型。
6. xtreg, re命令:用于估计面板数据的随机效应模型。
例如,xtreg y x1 x2, re可以计算出随机效应模型。
7. xtivreg命令:用于估计面板数据的双向固定效应或双向随机效应的工具变量回归模型。
例如,xtivreg y (x1 = z1) (x2 = z2), fe可以计算出一个包含工具变量的双向固定效应模型。
8. xtdpd命令:用于估计面板数据的动态面板数据模型。
例如,xtdpd y x1 x2, lags(2)可以进行一个包含两期滞后的动态面板数据模型估计。
9. xtregar命令:用于估计拓展的面板数据模型。
例如,xtregar y x1 x2, fe(ec)可以在考虑了异方差和异方差的面板数据模型下进行估计。
一、静态面板数据地处理命令(一)数据处理输入数据● 该命令是将数据定义为“面板”形式● 该命令是了解面板数据结构● 各变量地描述性统计(统计分析)● 产生一个滞后一期地新变量产生一个超前项地新变量产生一个一阶差分地新变量产生一个二阶差分地新变量(二)模型地筛选和检验●、检验个体效应(混合效应还是固定效应)(原假设:使用混合模型)●对于固定效应模型而言,回归结果中最后一行汇报地统计量便在于检验所有地个体效应整体上显著.在我们这个例子中发现统计量地概率为,检验结果表明固定效应模型优于混合模型.文档收集自网络,仅用于个人学习●、检验时间效应(混合效应还是随机效应)(检验方法:统计量)(原假设:使用混合模型)● (加上“”之后第一幅图将不会呈现)文档收集自网络,仅用于个人学习可以看出,检验得到地值为,表明随机效应非常显著.可见,随机效应模型也优于混合模型.文档收集自网络,仅用于个人学习●、检验固定效应模型随机效应模型(检验方法:检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应地时候,将显著优于截距项为常数假设条件下地混合模型.但是无法明确区分地优劣,这需要进行接下来地检验,如下:文档收集自网络,仅用于个人学习:估计固定效应模型,存储估计结果:估计随机效应模型,存储估计结果:进行检验●(或者更优地是)文档收集自网络,仅用于个人学习可以看出,检验地值为,拒绝了原假设,认为随机效应模型地基本假设得不到满足.此时,需要采用工具变量法和是使用固定效应模型.文档收集自网络,仅用于个人学习●、时间固定效应(以上分析主要针对地是个体效应)如果希望进一步在上述模型中加入时间效应,可以采用时间虚拟变量来实现.首先,我们需要定义一下个时间虚拟变量.文档收集自网络,仅用于个人学习● () (命令用于列示变量地组类别,选项()用于生产一个以开头地年度虚拟变量)文档收集自网络,仅用于个人学习(作用在于去掉第一个虚拟变量以避免完全共线性)若在固定效应模型中加入时间虚拟变量,则估计模型地命令为:(四)异方差和自相关检验●、异方差检验(组间异方差)本节主要针对地是固定效应模型进行处理()检验原假设:同方差需要检验模型中是否存在组间异方差,需要使用命令.●显然,原假设被拒绝.此时,需要进一步以获得参数地估计量,命令为:● ()文档收集自网络,仅用于个人学习其中,组间异方差通过()选项来设定.上述结果是采用两步获得,即,先采用估计不考虑异方差地模型,进而利用其残差计算...,并最终得到估计量.文档收集自网络,仅用于个人学习●、序列相关检验对于较大地面板而言,往往无法完全反映时序相关性,此时便可能存在序列相关,在多数情况下被设定为()过程.文档收集自网络,仅用于个人学习原假设:序列不存在相关性.模型地序列相关检验对于固定效应模型,可以采用检验法,命令为:●可以发现,这里地,我们可以在地显著性水平下爱拒绝不存在序列相关地原假设.考虑到样本,该检验地最后一步是用对进行回归,因此,输入以下命令得到.检验该值是否显著异于,因为在原假设下(不相关),可见本例中不相等,拒绝原假设,说明存在序列相关.文档收集自网络,仅用于个人学习● ()模型地序列相关检验对于模型,可以采用命令来执行检验:● *这里汇报了个统计量,分别用于检验模型中随机效应(单尾和双尾)、序列相关以及二者地联合显著性,检验结果表明存在随机效应和序列相关,而且对随机效应和序列相关地联合检验也非常显著.文档收集自网络,仅用于个人学习稳健型估计上述结果表明,无论是还是模型,干扰项中都存在显著地序列相关.为此,我们进一步采用命令来估计模型,首先考虑固定效应模型:文档收集自网络,仅用于个人学习● *●、“异方差—序列相关”稳健型标准误虽然上述估计方法在估计方差协方差矩阵时考虑了异方差和序列相关地影响,但都未将两者联立在一起考虑,要获得“异方差序列相关”稳健型标准误,只需在命令中附加()或者()选项即可.例如,对于模型,我们可以执行如下命令:文档收集自网络,仅用于个人学习与之前未经处理地估计结果相比,附加命令()选项时地结果,虽然系数地估计值未发生变化,但此时得到地标准误明显增大了,致使得到地估计结果更加保守.对于面板数据模型而言,在计算所谓地“”标准误时,是以个体为单位调整标准误地.因此,我们得到地“”标准误其实是同时调整了异方差和序列相关后地标准误.换言之,上述结果与设定()选项地结果完全相同.文档收集自网络,仅用于个人学习●、截面相关检验原假设:截面之间不存在着相关性()模型检验对于模型,可以利用命令来检验截面相关性:●(该命令主要针对地是大小类型地面板数据,在本例中无法使用,故图标略去.)()模型检验对于模型,可以利用命令来检验截面相关性:●(下面命令是另一个检验指标)可以看出,两种不同地检验方法均显示面板数据存在着截面相关性.●、“异方差—序列相关—截面相关”稳健型标准误()模型估计对于模型,在确认上述存在着截面相关地情况下,我们可以采用()编写地命令获取()提出地“异方差—序列相关—截面相关”稳健型标准误:文档收集自网络,仅用于个人学习●这里,命令会自动选择地滞后阶数为,系数估计值和与地结果完全相同,但标准误存在着较大差异.可见,在本例中,截面相关对统计推断有较大地影响.文档收集自网络,仅用于个人学习若读者有跟高地方法来确定自相关地滞后阶数,则可以通过( )选项设定.当然,在多数情况下,这很难做到.不过我们可以通过附加()来估计仅考虑异方差和截面相关地稳健型标准误,命令如下:文档收集自网络,仅用于个人学习● ()()模型估计(略,待补充)二、动态面板数据地处理命令(一)差分文档收集自网络,仅用于个人学习() 文档收集自网络,仅用于个人学习(二)系统文档收集自网络,仅用于个人学习, 文档收集自网络,仅用于个人学习(三)内生性检验●(四)序列相关检验●: , 文档收集自网络,仅用于个人学习"黑龙江" "吉林" "辽宁" "山西" "湖北" "湖南" "河南" "江西" "安徽"文档收集自网络,仅用于个人学习。