三年级奥数面积问题

完整版)三年级奥数面积计算在三年级的奥数课程中，我们研究了求解正方形和长方形面积的公式。

具体而言，正方形的面积可以表示为a×a（其中a为边长），长方形的面积可以表示为a×b（其中a为长，b为宽）。

通过这两个公式，我们可以计算出各种直角多边形的面积。

对于一些无法直接求解面积的图形，我们可以通过将其分割或切割成若干个正方形或长方形，再计算各块面积的和或差，得出整个图形的面积。

例如，对于下图中的图形，我们无法直接求解其面积。

但是，我们可以将其分割成三个长方形，或者添补成一个大长方形和两个小长方形，然后计算各个长方形的面积之和或差，得出整个图形的面积。

这种“分割”和“添补”的方法是计算直角多边形面积的基本方法。

练题中给出了几个图形，我们可以运用上述方法，将其分割或添补成若干个长方形，计算各个长方形的面积之和或差，求解出图形的面积。

例如，对于一个长50米、宽25米的标准游泳池，四周铺设了宽2米的白瓷地砖。

我们可以将阴影部分分割成四个长方形，计算各个长方形的面积之和，得出白瓷地砖的面积为316平方米。

1、将边长为40米的正方形运动场扩建为长60米、宽50米的长方形运动场，面积增加了900平方米，周长增加了80米。

2、一块长方形的玻璃，从长边截去宽为20厘米的一块后，剩下的玻璃正好是一个正方形，其周长为160厘米。

原来长方形玻璃的周长为200厘米，面积为480平方厘米。

3、一个机器零件如图所示，中间是一个边长为6厘米的大正方形，每边正中向外凸出一个边长为2厘米的小正方形。

1)这个机器零件的周长为28厘米。

2)这个机器零件的面积为32平方厘米。

4、一块长16米、宽8米的菜地中间留了宽2米的路，将菜地平均分成四块，每一块地的面积为24平方米。

5、北京某四合院子正好是一个边长为10米的正方形，在院子中央修建了一条宽2米的“十字形”甬路。

这条“十字形”甬路的面积为36平方米。

6、如图所示，有四个正方形，其中图①的边长为32厘米，图②的边长为16厘米，图③的边长为8厘米，图④的边长为4厘米。

三年级巧求面积题型摘要：一、三年级奥数巧求面积概述二、长方形面积的巧求方法三、正方形面积的巧求方法四、其他多边形面积的巧求方法五、实际应用举例正文：一、三年级奥数巧求面积概述三年级奥数中的面积问题，主要涉及到长方形、正方形以及其他多边形的面积求解。

在这些题型中，巧妙地运用分割、组合等方法，可以简化计算过程，提高解题效率。

二、长方形面积的巧求方法当我们遇到求长方形面积的题目时，可以运用分割和组合的方法。

例如，给定两个长方形，长和宽分别为a、b和c、d，我们可以将它们分割成若干个正方形或长方形，然后计算这些小正方形或长方形的面积之和，从而得到原长方形的面积。

三、正方形面积的巧求方法正方形的面积公式为a，其中a为边长。

求解正方形面积的问题时，可以直接给出边长a，或者通过已知条件间接求出边长a。

例如，已知正方形的周长c，可以通过公式a=c/4求得边长a。

四、其他多边形面积的巧求方法对于其他多边形，我们可以将它们分割成若干个三角形或矩形，然后计算这些三角形的面积之和，从而得到原多边形的面积。

在计算过程中，可以运用海伦公式（用于求解三角形面积）和矩形面积公式等。

五、实际应用举例下面我们通过一个实际例子来演示如何运用这些方法求解面积问题。

已知两个长方形，长和宽分别为1025厘米和1628厘米，原来每个长方形的面积是8540平方厘米。

我们可以将这两个长方形拼接成一个新长方形，周长增加的是2个长。

求这个新长方形的面积。

解：首先计算新长方形的长和宽。

由于周长增加的是2个长，所以新长方形的长为1628+1025=2653厘米。

新长方形的宽为1025厘米。

然后，根据长方形面积公式计算新长方形的面积：2653 × 1025 = 2733375平方厘米。

综上所述，通过巧妙地运用分割、组合等方法，我们可以轻松地求解三年级奥数中的面积问题。

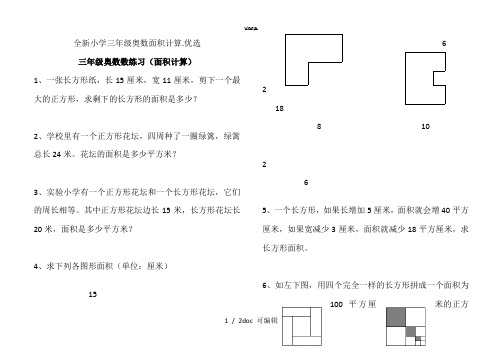
全新小学三年级奥数面积计算.优选三年级奥数数练习（面积计算）1、一张长方形纸，长15厘米，宽11厘米，剪下一个最大的正方形，求剩下的长方形的面积是多少？2、学校里有一个正方形花坛，四周种了一圈绿篱，绿篱总长24米。

花坛的面积是多少平方米？3、实验小学有一个正方形花坛和一个长方形花坛，它们的周长相等。

其中正方形花坛边长15米，长方形花坛长20米，面积是多少平方米？4、求下列各图形面积（单位：厘米）1562188 10265、一个长方形，如果长增加5厘米，面积就会增40平方厘米，如果宽减少3厘米，面积就减少18平方厘米，求长方形面积。

6、如左下图，用四个完全一样的长方形拼成一个面积为100平方厘米的正方1 / 2doc 可编辑形，如果每个长方形的宽是3厘米，求每个长方形的面积。

7、如右上图，大正方形的面积是128平方厘米，求三个阴影小正方形面积的和。

8、如左下图，4个完全一样的长方形和一个小正方形拼成了一个大正方形，求长方形的周长是多少？7厘米9、右上图是一个工厂新建的“工”字形厂房，求厂房的周长和面积。

10、正方形花坛周围有一圈宽2米的小路，小路的面积是136平方米，求花坛的面积。

附加题：一个长方形的木板，如果长减少5分米，宽减少2分米，那么它的面积就减少66平方分米，这时剩下的部分恰好是一个正方形，求原来长方形面积。

最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改感谢您使用本店文档您的满意是我们的永恒的追求！（本句可删）------------------------------------------------------------------------------------------------------------2 / 2doc 可编辑。

题目：三年级奥数题，求阴影部分面积1.题目描述：一个三角形的三条边分别为3cm，4cm和5cm。

在这个三角形的底边上截取一个4cm的线段，使得这个线段成为这个三角形的底边。

将截取的线段向三角形的内部平移，使得这个线段的一端与这个三角形的斜边垂直相交，另一端与斜边上的一个点相交，这个点的到三角形的顶点的距离为3cm。

求平移后的线段与三角形的相交部分的面积。

2.解题思路：利用三角形的三条边和切线定理可得出这个三角形的高，然后根据相似三角形性质可得出截取线段后的两个小三角形的相似关系。

最后利用相似三角形的面积性质求得所需的阴影部分面积。

3.具体步骤：步骤一：计算三角形的面积三角形的三条边分别为3cm，4cm和5cm，根据切线定理可得这个三角形的高h。

令a=3，b=4，c=5，p=(a+b+c)/2，则三角形的面积S=√[p(p-a)(p-b)(p-c)]步骤二：求平移后的线段与三角形的相交部分的面积设截取的线段为AB，平移后的线段为CD，D是在斜边上的一个点，CD的长度为x。

根据相似三角形性质可得出AB与CD的相似关系，即AB/CD=BC/AC=3/x。

设BD=y，则CD=3-y，根据勾股定理可得出AC的长度为√(16-y^2)。

则平移后的线段与三角形的相交部分的面积为阴影部分的面积等于1/2*3*(3-y)4.具体计算过程：步骤一的计算过程略步骤二：由AB/CD=BC/AC=3/x可得出CD=4x/3。

由BD=y，CD=3-y可得出y+3-y=4x/3，即x=3/4。

则阴影部分的面积为1/2*3*(3-3/4)=9/8 cm²。

5.答案确认：平移后的线段与三角形的相交部分的面积为9/8 cm²。

6.总结：通过计算可得出，平移后的线段与三角形的相交部分的面积为9/8平方厘米。

通过以上步骤的详细计算，我们可以得到平移后的线段与三角形的相交部分的面积为9/8平方厘米。

这道题目考察的是对基本几何知识和面积计算方法的理解与应用，在解题过程中需要注意细节，化繁为简，深入浅出，灵活运用所学知识，才能得出正确的结果。

面积问题三年级奥数练习题面积问题-三年级奥数练习题在数学学习中，面积问题是一个非常常见的内容。

通过解决面积问题，孩子们可以培养空间想象力、解决实际问题的能力，并为将来学习更高级的数学打下基础。

本文将介绍一些适合三年级学生练习的面积问题，帮助他们提高解决问题的能力。

问题一：小明画了一个正方形花坛，花坛的边长是4米。

请问花坛的面积是多少平方米？解答：一个正方形的面积可以通过边长的平方来计算。

根据题目，花坛的边长是4米，所以可以计算出花坛的面积为4 * 4 = 16平方米。

问题二：小红正在做一个手工项目，她使用了一个长方形的纸片，长是8厘米，宽是3厘米。

请问这个纸片的面积是多少平方厘米？解答：一个长方形的面积可以通过长度乘以宽度来计算。

根据题目，纸片的长度是8厘米，宽度是3厘米，所以可以计算出纸片的面积为8 * 3 = 24平方厘米。

问题三：小李正在准备午餐，他准备切一个圆形的蛋糕。

蛋糕直径是10厘米，请问这个蛋糕的面积是多少平方厘米？解答：一个圆形的面积可以通过半径的平方乘以π来计算。

根据题目，蛋糕的直径是10厘米，所以半径是直径的一半，即5厘米。

因此，蛋糕的面积为5 * 5 * π = 25π平方厘米，其中π约等于3.14。

问题四：小华正在铺一个矩形花坛，长是6米，宽是2米。

他想知道铺上花坛需要多少土地？请计算出这个矩形花坛的面积。

解答：一个矩形的面积可以通过长度乘以宽度来计算。

根据题目，花坛的长度是6米，宽度是2米，所以可以计算出花坛的面积为6 * 2 = 12平方米。

问题五：小明要铺设一个三角形的草坪，底边长是8米，高是5米。

请问这个三角形的面积是多少平方米？解答：一个三角形的面积可以通过底边乘以高的一半来计算。

根据题目，底边长是8米，高是5米，所以可以计算出三角形的面积为(8 * 5) / 2 = 20平方米。

通过以上的练习题，我们可以看到，计算面积问题可以通过不同的公式来解决，取决于形状的不同。

三年级奥数专题-面积计算专题简析：我们已经学会了计算长方形、正方形的面积,知道长方形的面积=长×宽,正方形的面积=边长×边长.利用这些知识我们能解决许多有关面积的问题.在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧.因此,敏锐的观察力和灵活的思维在解题中十分重要.例题1 把一张长为4米,宽为3米的长方形木板,剪成一个面积最大的正方形.这个正方形木板的面积是多少平方米？思路导航：要使剪成的正方形面积最大,就要使它的边长最长（如图）,那么只能选原来的长方形宽为边长,即正方形的边长是3米.4米3米正方形的面积：3×3=9米.练习一1,把一张长6厘米,宽4厘米的长方形纸剪成一个面积最大的正方形,这张正方形纸的面积是多少平方厘米？2,把一块长2米、宽6分米的长方形铁板切割成一个面积最大的正方形,这个正方形铁板的面积是多少？3,将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形,那么剪下的另一个小长方形的面积是多少？例题2 学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20米.花坛的面积是多少平方米？思路导航：要求正方形花坛的面积,必须知道花坛的边长是多少.根据绿篱总长是20米,可求出花坛的边长为20÷4=5米,所以花坛的面积是：5×5=25平方米.练习二1,一个正方形的周长为36厘米,那么这个正方形的面积是多少平方厘米？2,运动场有一个正方形的游泳池,在游泳池四周粘上瓷砖,瓷砖总长400米,求游泳池的面积是多少平方米.3,在公园里有两个花圃,它们的周长相等.其中长方形花圃长40米,宽20米,求另一个正方形花圃的面积.例题3 求下面图形的面积.（单位：厘米）思路导航：这个图形无法直接求出它的面积,我们可以画一条辅助线,将这个图形分割成两个长方形.如下图：从图上可以看出,左边长方形的长为4厘米,宽为2厘米,面积为4×2=8平方厘米；右边长方形的长为3厘米,宽为1厘米,面积为3×1=3平方厘米.所以,这个图形的面积为：8＋3=11平方厘米.想一想：这道题还可以怎样画辅助线,分割后求面积呢？练 习 三计算下面图形的面积.（单位：厘米）13241324(1)15203040例题4 有两个相同的长方形,长是8厘米,宽是3厘米.如果把它们按下图叠放,这个图形的面积是多少？思路导航：如果两个长方形没有叠放,那么它们的面积就是8×3×2=48平方厘米,现在两个长方形重叠了一部分,重叠部分是个边长3厘米的正方形,面积是3×3=9平方厘米,因此,这个图形的面积是48－9=39平方厘米.练 习 四1,两张边长8厘米的正方形纸,一部分叠在一起放在桌上（如下图）,桌面被盖住的面积是多少？(2)31122(3)11125142,求下图中阴影部分的面积.（单位：分米）3,一个长方形与一个正方形部分重合（如下图）,求没有重合的阴影部分面积相差多少？（单位：厘米）例题5 一个长方形若长增加2厘米,面积就增加10平方厘米,若宽减少3厘米,面积就减少18平方厘米.求原来长方形的面积.从图上可以看出,长增加2厘米,面积就增加10平方厘米,说明原来长方形88844832厘米的宽是10÷2=5厘为；宽减少3厘米,面积就减少18平方厘米,说明原来长方形的长是18÷3=6厘米.所以,原来长方形的面积是：6×5=30平方厘米.练习五1,一个长方形,若长减少5厘米,面积就减少50平方厘米,若宽增加7厘米,面积就增加28平方厘米.原来长方形的面积是多少平方厘米？2,一个正方形若边长都增加4厘米,面积就增加56平方厘米.原来正方形的面积是多少平方厘米？3,一个长方形,若宽增加6分米就是一个正方形,面积就增加了66平方分米,求原来长方形的面积.。

三年级奥数：巧求面积专项练习小学数学三年级下册竞赛试题及答案人教版巧算面积计算长方形、正方形的面积，知道长方形的面积=长×宽，正方形的面积=边长×边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例如，对左下图，我们无法直接求出它的面积，但是通过将它分割成几块，其中每一块都是正方形或长方形(见右下图)，分别计算出各块面积再求和，就得出整个图形的面积。

认识面积：1、请你用笔描出下面图形的周长，用画出下面图形的面积。

2、根据刚才画的图我们知道周长是指一周的长度，面积是指一个面的大小。

3、边长是（）的正方形，面积是1平方厘米；边长是（）的正方形，面积是1平方分米；面积单位都是边长是（）的正方形，面积是1平方米；带“平方”的。

以前我们学习的长度单位有：厘米、分米、米、千米。

面积单位换算：相邻两个单位之间的进率是100。

4、1平方分米=（）平方厘米1平方米=（）平方分米1分米=（）厘米1米=（）厘米1米=（）分米5、填上合适的单位名称。

我们教室的面积大约是50（），操场面积大约3600（）数学书的封面大约是2（），数学书的封面大约是200（）方桌面的面积大约是64（），连云港到南京的距离大约是321（）教室门的高度大约是2（），教室门的高度大约是200（）橡皮的长度大约是5()，语文书的厚度大约是1（）文具盒表面的面积大约是4（），教室里黑板的面积大约是4（）一栋楼房的占地面积大约200（）,我的身高大约140（）一枚5分的硬币大约重1（）电脑键盘长5分米、宽2分米，它的面积是（），在键盘四周贴一条花边，花边的总长是（）。

6、求下面图形的周长、面积我发现这两个图形的周长（），（）的面积比较大。

我发现这两个图形的面积（），（）的周长小。

三年级面积奥数应用题及答案一、填空（每空一分，共30分）1、物体的表面或( )的大小，就是它们的面积。

常用的面积单位有平方米、( ) 和( )。

[填空题] *_________________________________2、长方形的面积=( )×( )正方形的面积＝( )×( )正方形的周长＝（）×（） [填空题] *_________________________________3、长方形的长是16厘米，宽是12厘米，它的周长是( )厘米，面积是( )平方厘米。

[填空题] *_________________________________4、正方形的边长是8分米，它的面积是（），周长是（ ) [填空题] *_________________________________5、一个长方形的面积是40平方米，长是8分米，宽是（）分米 [填空题] *_________________________________6、长方形的长是12米，宽是长的一半，这个长方形的周长是( )，面积是( )。

[填空题] *_________________________________7、在括号里填上合适的单位：一枚邮票的面积是4（） [填空题] *_________________________________黑板约长4（） [填空题] *_________________________________数学书厚约1（） [填空题] *_________________________________教室地面的面积约50（） [填空题] *_________________________________小红家的房屋面积大约是123（） [填空题] * _________________________________一张课桌高6（） [填空题] *_________________________________8、在括号里填上合适的数：30分米=（）米 [填空题] *_________________________________4000平方厘米=（）平方分米 [填空题] *_________________________________2米2厘米=（）厘米 [填空题] *_________________________________65平方分米=（）平方厘米 [填空题] *_________________________________1600平方分米=（）平方米 [填空题] *_________________________________200厘米=（）分米=（）米 [填空题] *_________________________________3平方米=（）平方分米 [填空题] *_________________________________二、判断下面各题，对的打“√”，错的打“×”。

面积是物体占据的平面区域的大小。

在三年级的奥数中，面积计算是一个重要的概念，学生们需要学会使用适当的公式和方法来计算不同形状物体的面积。

下面我将介绍几种常见的面积计算方法。

1.长方形的面积计算：长方形的面积可以通过将长和宽相乘来计算。

假设长方形的长为L，宽为W，则其面积为A=L×W。

学生们可以通过将长方形划分为单位格子的方式，来直观地理解这个公式。

例如，一块长方形土地可以划分为10个乘以10个的格子，那么它的面积就是100个格子。

2.正方形的面积计算：正方形是一种特殊的长方形，其特点是四边长度相等。

正方形的面积可以通过边长的平方来计算。

假设正方形的边长为A，则其面积为A×A=A²。

学生们可以通过划分正方形为单位格子的方式，来理解这个公式。

例如，一块正方形地板可以划分为5个乘以5个的格子，那么它的面积就是25个格子。

3.三角形的面积计算：三角形是一个有三个边的图形。

三角形的面积可以通过底边长度和高的乘积再除以2来计算。

假设三角形的底边为B，高为H，则其面积为A=(B×H)/2、学生们可以通过画一条底边和相应的高，然后划分为单位格子的方式来理解这个公式。

例如，如果一块三角形地面的底边长度为8个单位，高为4个单位，那么它的面积就是(8×4)/2=16个单位。

4.圆形的面积计算：除了上述常见的图形，还有一些其他形状，如梯形、长方体等，它们的面积计算方法略有不同。

在这里，我只介绍了一些基本的概念和计算方法。

在三年级奥数的学习中，学生们还会遇到更多的面积计算问题，需要将这些概念和方法灵活运用。

因此，通过多做练习，加深对面积计算的理解，是非常重要的。

在实际生活中，面积计算常常用于解决实际问题，比如测量房屋面积、购买地毯时计算需要的面积等等。

因此，掌握面积计算的方法不仅对奥数学习有帮助，也对实际生活有实用价值。

希望同学们能够通过不断学习和练习，掌握面积计算的技巧，为今后的学习和生活打下坚实的基础。

三年级面积奥数题思维训练题一、基础题型。

1. 一个长方形的长是8厘米，宽是5厘米，这个长方形的面积是多少平方厘米？- 解析：长方形的面积 = 长×宽，所以这个长方形的面积是8×5 = 40平方厘米。

2. 正方形的边长是6分米，它的面积是多少平方分米？- 解析：正方形的面积 = 边长×边长，所以这个正方形的面积是6×6=36平方分米。

3. 一个长方形花坛长12米，宽8米，这个花坛的面积是多少平方米？如果每平方米能种3株花，这个花坛一共能种多少株花？- 解析：- 长方形花坛面积 = 长×宽=12×8 = 96平方米。

- 每平方米种3株花，一共能种96×3 = 288株花。

4. 有一块正方形手帕，边长为15厘米，它的面积是多少平方厘米？- 解析：正方形面积 = 边长×边长，所以手帕面积为15×15 = 225平方厘米。

5. 一个长方形的长增加3厘米，宽不变，面积增加18平方厘米，原来长方形的宽是多少厘米？- 解析：长增加3厘米，宽不变，增加的面积就是增加的长乘以原来的宽。

所以原来的宽=18÷3 = 6厘米。

二、组合图形面积。

6. 如图，一个大长方形由两个小长方形组成，左边小长方形长8厘米，宽3厘米，右边小长方形长5厘米，宽3厘米，求大长方形的面积。

- 解析：- 大长方形的长是8 + 5=13厘米，宽是3厘米。

- 面积 = 长×宽=13×3 = 39平方厘米。

7. 有一个组合图形，由一个正方形和一个长方形组成。

正方形边长为4分米，长方形长6分米，宽4分米，求组合图形的面积。

- 解析：- 正方形面积=4×4 = 16平方分米。

- 长方形面积=6×4 = 24平方分米。

- 组合图形面积=16+24 = 40平方分米。

8. 如下图，一个长方形被分成了一个正方形和一个小长方形。