江苏省扬中市第二高级中学2019届高三周末练习数学试题(01.12)

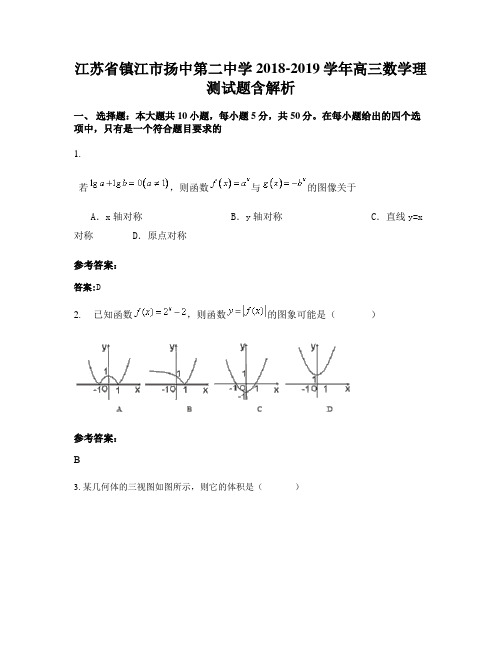
江苏省镇江市扬中第二中学2018-2019学年高三数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1.若，则函数与的图像关于A．x轴对称 B．y轴对称 C．直线y=x 对称 D．原点对称参考答案：答案:D2. 已知函数，则函数的图象可能是（）参考答案：B3. 某几何体的三视图如图所示，则它的体积是（）A． B． C． D．参考答案：A由三视图可知，该组合体下面是边长为2的正方体，上面是底边边长为2，侧高为2的四棱锥。

四棱锥的高为，四棱锥的体积为，所以组合体的体积为，答案选 A.4. 已知a>0且a≠1，若函数f（x）= loga（ax2 –x）在[3，4]是增函数，则a的取值范围是（）A．（1，+∞） B． C． D．参考答案：A略5. 已知是首项为1的等比数列，是的前n项和，且，则数列的前5项和为（）A．或5 B．或5 C． D．参考答案：C6. 若x，y满足，则的取值范围是（）A．（﹣∞，﹣4]∪[3，+∞）B．（﹣∞，﹣2]∪[﹣1，+∞）C．[﹣2，﹣1] D．[﹣4，3]参考答案：A【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用z的几何意义结合直线的斜率公式进行求解即可．【解答】解：作出不等式组对应的平面区域，的几何意义是区域内的点到定点（3，4）的斜率由图象知z大于等于PA的斜率，z小于等于PB的斜率，∵A（2，1），B（4，0），∴=≥3；则=≤﹣4，即，（﹣∞，﹣4]∪[3，+∞）．故选：A．【点评】本题主要考查线性规划的应用，利用直线斜率的几何意义以及数形结合是解决本题的关键．7. 已知实数m，n，若m≥0，n≥0，且m+n=1，则+的最小值为（）A．B．C．D．参考答案：A【考点】利用导数研究函数的极值；基本不等式．【专题】导数的综合应用．【分析】由m≥0，n≥0，且m+n=1，可得n=1﹣m，（0≤m≤1）．代入+，再利用导数研究其单调性极值即可．【解答】解：∵m≥0，n≥0，且m+n=1，∴n=1﹣m，（0≤m≤1）．∴f（m）=+==．则f′（m）=，令f′（m）=0，0≤m≤1，解得m=．当时，f′（m）＜0；当时，f′（m）＞0．∴当m=时，f（m）取得极小值即最小值， ==．故选：A．【点评】本题考查了利用导数研究函数的单调性极值与最值，属于中档题．8. 如图为某几何体的三视图，则该几何体的外接球的表面积为（）A．B．27πC．27πD．参考答案：B【考点】由三视图求面积、体积．【分析】由已知中的三视图，可得该几何体是以俯视图为底面的四棱锥，其外接球等同于棱长为3的正方体的外接球，从而求得答案．【解答】解：由已知中的三视图，可得该几何体是以俯视图为底面的四棱锥，其底面是边长为3的正方形，且高为3，其外接球等同于棱长为3的正方体的外接球，所以外接球半径R满足：2R==，所以外接球的表面积为S=4πR2=27π．故选：B．9. 已知双曲线C：﹣=1（a＞0，b＞0）的左焦点为F，第二象限的点M在双曲线C的渐近线上，且|OM|=a，若直线MF的斜率为，则双曲线C的渐近线方程为（）A．y=±x B．y=±2x C．y=±3x D．y=±4x参考答案：A【考点】KC：双曲线的简单性质．【分析】求出双曲线的渐近线方程，运用同角的三角函数关系式，求得M的坐标，再由直线的斜率公式，化简可得a，b的关系，即可得到所求渐近线方程．【解答】解：双曲线C：﹣=1的渐近线方程为y=±x，由|OM|=a，即有M（﹣acos∠MOF，asin∠MOF），即为tan∠MOF=，sin2∠MOF+cos2∠MOF=1，解得cos∠MOF==，sin∠MOF=，可得M（﹣，），设F（﹣c，0），由直线MF的斜率为，可得=，化简可得c2=2a2，b2=c2﹣a2=a2，即有双曲线的渐近线方程为y=±x，即为y=±x．故选：A．【点评】本题考查双曲线的方程和性质，主要是渐近线方程的求法，考查直线的斜率公式的运用，考查化简整理的运算能力，属于中档题．10. 设，，则“”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件参考答案：B【分析】根据充分条件和必要条件的定义结合表达式的性质进行判断即可．【详解】解：若a＝0，b＝1，满足a＜b，但（a﹣b）a2＜0不成立，若“（a﹣b）a2＜0，则a＜b且a≠0，则a＜b成立，故“a＜b”是“（a﹣b）a2＜0”的必要不充分条件，故选B．【点睛】本题主要考查充分条件和必要条件的判断，根据不等式的关系进行判断即可．二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数满足，且的导函数，则的解集为____________(原创)参考答案：略12. （几何证明选讲选做题）如图，是半径为的⊙的直径，是弦，，的延长线交于点，，则 .参考答案：由割线定理知，，，得13. 直线l的参数方程是（其中t为参数），若原点O为极点，x正半轴为极轴，圆C的极坐标方程为ρ=2cos（θ+），过直线上的点向圆引切线，则切线长的最小值是．参考答案：2考点：直线的参数方程；简单曲线的极坐标方程．专题：直线与圆．分析：将圆的极坐标方程和直线l的参数方程转化为普通方程，利用点到直线的距离公式求出圆心到直线l的距离，要使切线长最小，必须直线l上的点到圆心的距离最小，此最小值即为圆心到直线的距离d，求出d，由勾股定理可求切线长的最小值．解答：解：∵圆C的极坐标方程为ρ=2cos（θ+），∴ρ2=ρcosθ﹣ρsinθ，∴x2+y2=x﹣y，即（x﹣）2+（y+）2=1，∴圆C是以M（，﹣）为圆心，1为半径的圆…2分化直线l的参数方程（t为参数）为普通方程：x﹣y+4=0，…4分∵圆心M（，﹣）到直线l的距离为d==5，…6分要使切线长最小，必须直线l上的点到圆心的距离最小，此最小值即为圆心M（，﹣）到直线的距离d，由勾股定理求得切线长的最小值为==2．故答案为：2．点评：本题考查圆的极坐标方程，直线的参数方程、直线与圆的位置关系，考查运算求解能力，考查数形结合思想、化归与转化思想，属于中档题．14. 不等式的解集是.参考答案：当时，，即；当时，，；所以原不等式解集是。

高三数学周末练习（01.12）1．若复数2(1)(1)z x x i =-+-为纯虚数，则实数x 的值为 ．2．集合{|lg 0}M x x =>,2{|4}N x x =≤,则M N = ．3．在圆x 2+y 2=4所围成的区域内随机取一个点P (x ，y )，则| x |+| y | ≤ 2的概率为 ． 4．已知4cos 5α=-且(,)2παπ∈，则tan()4πα+= ． 5．已知定义域为R 的函数121()2xx f x a+-+=+是奇函数，则a = ．6．右图是一个算法的流程图，则输出S 的值是 ． 7．在ABC ∆中，已知4AB AC ⋅=，12AB BC ⋅=-，则AB ＝ ．8．在样本的频率分布直方图中，共有9个小长方形，若第一个长方形的面积为0.02，前五个与后五个长方形的 面积分别成等差数列且公差是互为相反数，若样本容量 为1600，则中间一组（即第五组）的频数为 ．9．已知B 为双曲线22221(0,0)x y a b a b-=>>的左准线与x 轴的交点，点(0,)A b ，若满足2AP AB =的点P 在双曲线上，则该双曲线的离心率为 ．10．函数x x x f cos sin )(+=的图象向左平移)0(>m m 个单位后，与x x y sin cos -=的图象重合，则实数m 的最小值为 .11．已知等比数列{}n a 为递增数列,且251021,2()5n n n a a a a a ++=+=,则数列的通项公式n a = ．12．将一个长宽分别是,(0)a b b a <<的铁皮的四角切去相同的正方形，然后折成一个无盖的长方体的盒子，若这个长方体的外接球的体积存在最小值，则ab的取值范围是 ．样本数据频率组距开始结束是否100k ≥3s s k←+1,0k s ←←S输出2k k ←+13．在平面直角坐标系xOy 中，抛物线y 2＝2x 的焦点为F ． 设M 是抛物线上的动点，则MOMF的最大值为 ． 14．设等差数列{}n a 的前n 项和为n S ，若对任意的等差数列{}n a 及任意的正整数n 都有不等式22212n n S a a nλ+≥成立，则实数λ的最大值为 ．15．已知函数231()2cos ,22f x x x x R =--∈（1）求函数()f x 的最小值和最小正周期；（2）设ABC ∆的内角A 、B 、C 的对边分别为a ，b ，c ，且3c =，()0f C =，若sin 2sin B A =，求a ，b 的值．16．如图，在四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，侧棱PA PD ⊥，底面ABCD 是直角梯形，其中//BC AD ，090BAD ∠=，3AD BC =，O 是AD 上一点．(1)若//CD PBO 平面，试确定点O 的位置； (2)求证:PAB PCD ⊥平面平面．17．如图，一载着重危病人的火车从O 地出发，沿射OPDCBA第16题NA Cα北线OA 行驶，其中1tan 3α=,在距离O 地a 5（a 为正数）公里北偏东β角的N 处住有一位医学专家，其中3sin 5β=,现有110指挥部紧急征调离O 地正东p 公里的B 处的救护车赶往N 处载上医学专家全速追赶乘有重危病人的火车，并在C 处相遇，经测算当两车行驶的路线与OB 围成的三角形OBC 面积S 最小时，抢救最及时. （1）求S 关于p 的函数关系；（2）当p 为何值时，抢救最及时.18．已知圆C 方程为x 2＋y 2－8mx －(6m ＋2)y ＋6m ＋1＝0(m ∈R ，m ≠0)，椭圆中心在原点，焦点在x 轴上．(1) 证明圆C 恒过一定点M ，并求此定点M 的坐标；(2) 判断直线4x ＋3y －3＝0与圆C 的位置关系，并证明你的结论；(3) 当m ＝2时，圆C 与椭圆的左准线相切，且椭圆过(1)中的点M ，求此时椭圆方程；在x 轴上是否存在两定点A 、B ，使得对椭圆上任意一点Q (异于长轴端点)，直线QA 、QB 的斜率之积为定值？若存在，求出A 、B 坐标；若不存在，请说明理由．19．已知数列{a n }的首项a 1＝35，a n ＋1＝3a n2a n ＋1，n ＝1,2，….(1) 求证：数列⎩⎨⎧⎭⎬⎫1a n －1为等比数列；(2) 记S n ＝1a 1＋1a 2＋…＋1a n，若S n ＜100，求最大的正整数n ；(3) 是否存在互不相等的正整数m 、s 、n ，使m 、s 、n 成等差数列，且a m －1、a s －1、a n －1成等比数列？如果存在，请给出证明；如果不存在，请说明理由．答案1．-1； 2．(1,2]； 3．2π； 4．17； 5．2； 6．7500；7．4； 8．360；92； 10．2π； 11．2n；12．)45,1(； 132314．1515． 解：（1）31cos 21()2sin(2)1226x f x x x π+=--=--，…………3分则()f x 的最小值是－2， …………5分最小正周期是22T ππ==； …………7分（2）()sin(2)106f C C π=--=，则sin(2)16C π-=，0C π<< 022C π∴<< 112666C πππ∴-<-<，262C ππ∴-=，3C π∴=， …………10分sin 2sin B A =，由正弦定理，得12a b =，① …………11分由余弦定理，得2222cos 3c a b ab π=+-，即223a b ab +-=， ②由①②解得1,2a b ==． …………14分16．（1） …………7分 （2）……14分17．解：（1）以O 为原点，正北方向为y 轴建立直角坐标系，……… 2分则x y l OA 3:= .设00N x y （，），有05sin 3x a a β==,05cos 4y a a β==, (3,4)N a a ∴.又0B p （，），∴直线BC 的方程为：)(34p x pa ay --=.……… 6分 由⎪⎩⎪⎨⎧--==)(343p x p a a y xy 得C 的纵坐标)35(5312a p a p ap y c >-=，∴2165||,()2353c ap S OB y p a p a ∆=⋅=>-.……… 10分（2）由（1）得22625353ap ap S p a p a ==--,令5(0)3t p a t =->∴222510402[]933a a S a t a t =++≥， ∴当且仅当,9252ta t =即53a t =,此时103a p =时，上式取等号，……… 13分 ∴当103ap =公里时，抢救最及时. ……… 14分 18．(1) 证明：圆C 的方程可化为(x 2＋y 2－2y ＋1)－m (8x ＋6y －6)＝0，(2分) 由⎩⎪⎨⎪⎧ x 2＋y 2－2y ＋1＝0，8x ＋6y －6＝0，解得⎩⎪⎨⎪⎧x ＝0，y ＝1，(4分) 所以圆C 过定点M (0,1)．(5分)(2) 解：直线4x ＋3y －3＝0与 圆C 相切．证明如下． 圆C 的方程可化为(x －4m )2＋[y －(3m ＋1)]2＝25m 2，(6分)圆心到直线l 的距离为d ＝|4·4m ＋3·(3m ＋1)－3|42＋32＝25|m |5＝5|m |＝r ，(9分)所以直线与圆C 相切．(10分)(3) 解：当m ＝2时，圆C 方程为(x －8)2＋(y －7)2＝100，圆心为(8,7)，半径为10，与直线x ＝(8－10)，即x ＝－2相切，B NA OCα东北所以椭圆的左准线为x ＝－2.(11分) 又椭圆过点M (0,1)，则b ＝1，所以⎩⎪⎨⎪⎧a 2c ＝2，b ＝1⇒⎩⎨⎧a ＝2，b ＝1⇒椭圆方程为x 22＋y 2＝1.(12分)在椭圆上任取一点Q (x ，y )(y ≠0)，设定点A (s,0)，B (t,0)，则k QA ·k QB ＝y x －s ·yx －t ＝1－x 22(x －s )(x －t )＝k 对x ∈(－2，2)恒成立，(13分)所以－12x 2＋1＝kx 2－k (s ＋t )x ＋kst 对x ∈(－2，2)恒成立．所以⎩⎪⎨⎪⎧k ＝－12，k (s ＋t )＝0，kst ＝1⇒⎩⎪⎨⎪⎧k ＝－12，s ＝2，t ＝－2或⎩⎪⎨⎪⎧k ＝－12，s ＝－2，t ＝ 2.(14分)故A (－2，0)，B (2，0)或者A (2，0)，B (－2，0)．(15分)19．(1) 证明：∵ 1a n ＋1＝23＋13a n ，∴ 1a n ＋1－1＝33a n －13，(2分)且∵ 1a 1－1≠0，∴ 1a n －1≠0(n ∈N *)，(3分)∴ 数列⎩⎨⎧⎭⎬⎫1a n －1为等比数列．(4分)(2) 解：由(1)可求得1a n －1＝23×⎝⎛⎭⎫13n －1，∴ 1a n＝2×⎝⎛⎭⎫13n ＋1.(5分) S n ＝1a 1＋1a 2＋…＋1a n ＝n ＋2(13＋132＋…＋13n )＝n ＋2·13－13n ＋11－13＝n ＋1－13n ，(7分)若S n ＜100，则n ＋1－13n ＜100，∴ n max ＝99.(9分)(3) 解：假设存在，则m ＋n ＝2s ，(a m －1)·(a n －1)＝(a s －1)2.(10分)∵ a n ＝3n 3n ＋2，∴ (3n 3n ＋2－1)·(3m 3m ＋2－1)＝(3s3s ＋2－1)2.(12分)化简得：3m ＋3n ＝2·3s，(13分)∵ 3m ＋3n ≥2·3m ＋n ＝2·3s ，当且仅当m ＝n 时等号成立．(15分) 又m 、n 、s 互不相等，∴ 不存在．(16分)。

高三数学练习(12.16)1.设集合{}{}25,log (3),,(,)R A a B a b a b =+=∈，若{}1A B =I ，则A B =U ．2.若实数x 满足对任意正数0>a ，均有12->x a ，则x 的取值范围是 ． 3.已知函数)2lg()(2--=x x x f ，若().,a b m ∀∈+∞，都有[()()]()0f a f b a b -->，则实数m 最小值是 ．4.已知不等式1x m -<成立的充分不必要条件是1132x <<，则m 的取值范 ． 5.设函数()f x 在定义域R 恒有()()0f x f x -+=，当0x ≤时，1()14xf x a =++，则(1)f = ．6. 若直线2(2)10a a x y +-+=的倾斜角为钝角，则实数a 的取值范围是 . 7.等比数列{n a }的前n 项和为n S ,已知123,2,3S S S 成等差数列，则等比数列{n a }的公比为 .8.函数),,0)(sin(R x x A y ∈<>+=πϕωϕω的部分图象如图所示，则函数表达式为 ．9. 过点P （1,1）的直线，将圆形区域{（x ，y ）|x 2+y 2≤4}分两部分，使这两部分的面积之差最大，则该直线的方程为10.函数2()f x ax bx c =++，其中0a <，对x R ∀∈，恒有()(4)f x f x =-，若22(13)(1)f x f x x -<+-，则x 的取值范围是 ．11. 已知{n a }是等比数列，2512,4a a ==，则12()n n S a a a n N *=+++∈L 的取值范围是 . 12.已知函数x x x f 231)(3+=，对任意的]33[，-∈t ，0)()2(<+-x f tx f 恒成立，则x 的取值范围是 ．13. 在平面直角坐标系中，设直线:20l kx y -=与圆C ：224x y +=相交于A 、B 两点，.OM OA OB =+u u u u r u u u r u u u r若点M 在圆C 上，则实数k = .14.（普通班做） 设函数2()ln f x x x ax =++.若()f x 在其定义域内为增函数，则a 的取值范围为 ；14.（重点班做） 对于函数()y f x =，若存在区间[,]a b ，当[,]x a b ∈时的值域为[,]ka kb (0)k >，则称()y f x =为k 倍值函数．若()ln f x x x =+是k 倍值函数，则实数k 的取值范围是 ．15.设ABC ∆的内角A ，B ，C 的对边长分别为a ，b ，c ，且.212ac b = ⑴求证：43cos ≥B ；⑵若1cos )cos(=+-B C A ，求角B 的大小.16.已知m R ∈, 2 (1, )a x m =-+u u r ，1 (1, )b m x =+u u r ， (, )x c m x m=-+u r.（Ⅰ）当1m =-时，求使不等式 1a c ⋅<u u r u r成立的x 的取值范围；（Ⅱ）求使不等式 0a b ⋅>u u r u u r成立的x 的取值范围.17. 已知﹛n a ﹜是以a 为首项，q 为公比的等比数列，n S 为它的前n 项和(1)当134,,S S S 成等差数列时，求q 的值；(2)当m S ，n S ，k S 成等差数列时，求证：对任意自然数i k i n i m a a a i +++,,,也成等差数列。

江苏扬中第二高级中学2019高三练习限时练习（1-7）-数学1、 设集合{}Rx x x x A ∈+≤-=,112)2(2，那么集合*⋂NA 中有 个元素。

2、假设()35cos =+απ且⎪⎭⎫⎝⎛∈ππα，2，那么()απ-2sin =__________3、正项等比数列{}na 的前n 项和为n S ，假设137a S =，那么等比数列{}na 的公比等于_____ 4、 函数2()f x x x=-，假设2(1)(2)f m f --<，那么实数m 的取值范围是 、5、 直线1l ：32+=x y ，直线2l 与直线1l 关于直线x y -=对称，那么直线2l 的斜率为_______6、 函数x be ax x f +=)(图象上在点)2,1(-P 处的切线与直线x y 3-=平行，那么函数)(x f 的解析式为_____7、 等差数列{}n a 的前n 项和为()21,n S a n a =++某三角形三边之比为234::a a a ，那么该三角形最大角为 ____8、 直线0132=+++y x 与圆032-22=-+x y x 交于N M ,两点，那么弦MN 的垂直平分线方程为__________9、 在锐角ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且满足(2)cos cos a c B b C -=、 〔1〕求角B 的大小；〔2〕设(sin ,1),(3,cos 2)m A n A ==，试m n ⋅求的取值范围、限时训练〔01〕参考答案1.72.23- 3.2 4. (1,1)- 5. 0.5 6. 12.50.5x y x e +=-- 7. 120 8.3x-2y-3=0 9、〔1〕60B =， 〔2〕17(2,]8高三数学复习限时训练〔02〕1、假设复数2(3)(,()z a a i a R =--+∈=2、假设双曲线12222=-b y a x 的两个焦点到一条准线的距离之比为3：2,那么双曲线的离心率是___________ 3、点A 、B 、C345，那么AB CA CA BC BC AB ⋅+⋅+⋅的值是____.4、ABC ∆的三内角A ，B ，C 所对边长分别是c b a ,,，设向量),sin ,(C b a +=)sin sin ,3(A B c a -+=，假设n m //，那么角B 的大小为_____________5、：}2|1||{<-=x x A ，}11|{+<<-=m x x B ,假设B x ∈成立的一个充分不必要条件是A x ∈ ，那么实数m 的取值范围6、过点()0,4-作直线与圆0204222=--++y x y x 交于A 、B 两点，假设AB=8，那么直线的方程为______7、||1a =，||2b =，()a a b ⊥+，那么a 与b 夹角的度数为 .8、假设]2,0[πθ∈，且54sin =θ，那么2tanθ=9、向量a = (1，1)，向量b 与向量a 的夹角为34π，且a ·b = －1.〔1〕求向量b ；〔2〕假设向量b 与q =〔1，0〕的夹角为2π，向量p =2(cos ,2cos )2C A ，其中A ，C 为△ABC 的内角，且A + C =23π，求|b + p |的最小值.限时训练〔02〕参考答案1、5 3、 25- 4、π65 5、),2(+∞ 6.、 020125=++y x 或4-=x7、23π 8、21 9、〔1〕b =(－1,0)或b =(－1,0).；〔2〕22高三数学复习限时训练〔03〕1、函数x x y 22-=的定义域为{}3,2,1,0，那么其值域为_____2、设复数1212,()z i z x i x =-=+∈R ，假设12z z ⋅为实数，那么x = 、3、{}n a 为等差数列，且74321,0a a a -=-=,那么公差d ＝ 4、有四个游戏盘，将它们水平放稳后，在上面扔一颗玻璃小球，假设小球落在阴影部分，那么可中奖，小明要想增加中奖机会，应选择的游戏盘的序号 那么实数c 的取值范围是 6、1tan 2a =，那么sin cos a a =7、过定点P (1,2)的直线在x y 轴与轴正半轴上的截距分别为a b 、,那么422a b +的最小值为.8、设等比数列{}n a 中，前n 项和为n S ,38S =，67S =,那么789a a a ++=.9、函数()ln f x x ax =-()a ∈R . (Ⅰ)求函数()f x 的单调区间；(Ⅱ)当a >0时，求函数()f x 在[1,2]上最小值.限时训练〔03〕参考答案1.{}0,1,3- 2.21- 3.－124.〔1〕5.121021<≤≤<-c c 或 6.527.328.819、(Ⅰ)1()f x a x '=-(0x >),①当a ≤0时，1()f x ax'=->0， 故函数()f x 增函数，即函数()f x 的单调增区间为(0,)+∞、②当0a >时，令1()0f x a x'=-=，可得1x a=,当10x a <<时，1()0ax f x x -'=>；当1x a >时，1()0ax f x x-'=<， 故函数()f x 的单调递增区间为1(0,]a ,单调减区间是1[,)a+∞.(Ⅱ)①当11a≤,即1a ≥时,函数()f x 在区间[1,2]上是减函数,∴()f x 的最小值是(2)ln 22f a =-. ②当12a≥，即12a ≤时，函数()f x 在区间[1,2]上是增函数，∴()f x 的最小值是(1)f a =-. ③当112a <<，即112a <<时，函数()f x 在1[1,]a 上是增函数，在1[,2]a是减函数、 又(2)(1)ln 2f f a -=-，∴当1ln 22a <<时,最小值是(1)f a =-；当ln 21a ≤<时,最小值为(2)ln 22f a =-.综上可知,当0ln 2a <<时,函数()f x 的最小值是min ()f x a =；当ln 2a ≥时，函数()f x 的最小值是min()ln 2f x =.高三数学复习限时训练〔04〕1、=︒+︒-︒570sin 2135cos 315sin 。

江苏省扬中市第二高级中学2021-2022第一学期高三数学周练3姓名一、选择题．请把答案直接填涂在答题卡相应位置上．．．．．．．．． 1．复数(1)2(z i i i -=为虚数单位〕，那么z =〔C 〕 A ．1i + B ．1i - C ．1i -+D ．1i --2．假设从甲、乙、丙、丁4人中选出3名代表参加学校会议，那么甲被选中的概率为〔 D 〕A ．14B ．13C ．12D ．343．函数2()ln 1f x x x=-+的零点所在的大致区间是 〔D 〕A ．(2,)e B.(1,2)C ．(,3)e D ．(3,)+∞4．以下函数中，既是奇函数又在区间(﹣1，1)上是增函数的是〔 B 〕 A ．1y x=B ．tan y x =C ．sin y x =-D ．cos y x = 5．菱形ABCD 的边长为4，∠ABC ＝60°，E 是BC 的中点，DF 2AF =-，那么AE BF ⋅＝〔 D 〕 A ．24 B ．﹣7 C ．﹣10 D ．﹣12 6．?周髀算经?是中国古代重要的数学著作，其记载的“日月历法〞曰：“阴阳之数，日月之法，十九岁为一章， 四章为一部，部七十六岁，二十部为一遂，遂千百五二十岁，生数皆终，万物复苏，天以更元作纪历〞，某老年公寓住有20位老人，他们的年龄〔都为正整数〕之和恰好为一遂，其中年长者己是奔百之龄〔年龄介于90至100〕，其余19人的年龄依次相差一岁，那么年长者的年龄为〔 B 〕 A ．94 B ．95 C ．96 D ．987．定义在R 上的函数()y f x =的导函数为()f x '，满足()()f x f x '>，且(0)2f =，那么不等式．()2xf x e >的解集为〔A 〕A ．(,0)-∞B ．(0,)+∞C ．(,2)-∞D ．(2,)+∞8．函数22,0()ln(1),0x x x f x x x ⎧-+≤=⎨+>⎩假设|()|f x ax ≥，那么a 的取值范围是〔D 〕A ．(,0]-∞B ．(,1]-∞C ．[2,1]-D ．[2,0]- 二、多项选择题：〔每题给出的四个选项中，不止一项为哪一项符合题目要求的，请把正确的所有选项填涂在答题卡相应的位置上〕9．0x y >>，以下不等式成立的是 〔BCD 〕A ．ln 1243ln x x +≥B ．23331x x x ++≥+C ．11x y y x +>+D ．44y y x x +<+10．如图，在三棱锥C －ABD 中，△ABD 与△CBD 是全等的等腰直角三角形，O 为斜边BD 的中点，AB ＝4，二面角A －BD －C 的大小为60°，以下结论正确的选项是〔ABC 〕A. AC ⊥BDB. △AOC 为正三角形C. 四面体A-BCD 外接球的外表积为32πD. cos ∠ADC= 3411．函数()sin()(0,0,)2f x A x A πωϕωϕ=+>><的局部图象如下图，将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象，那么以下说法正确的选项是〔 BD 〕 A ．函数()g x 为奇函数 B ．函数()g x 的最小正周期πODCBAC ．函数()g x 的图象的对称轴为直线()6x kx k Z π=+∈D ．函数()g x 的单调递增区间为5[,]()1212k k k Z ππππ-++∈ 12．关于函数()e xf x ax =-，x ∈R 〔其中e 为自然对数的底数〕，以下说法正确的选项是〔 AC 〕A ．当a ＝1时，函数()y f x =在(-∞，0)上单调递增B ．当a ＝0时，不等式()ln 3f x x -≥在(0，+∞)上恒成立C ．对任意a ＜0，函数()y f x =在(-∞，0)上一定存在零点D ．存在a ＞0，使得函数()y f x =有唯一极小值三、填空题．请把答案直接填写在答题卡相应位置上．．．．．．．．． 13．tan 2α=，那么cos 22πα⎛⎫+= ⎪⎝⎭__ 45-___．14．等比数列{}n a 的公比为2，前n 项和为n S ，那么42S a ＝152．15．函数()f x 定义域为R ，对于任意的x 有(4)3()f x f x +=，当[2,2]x ∈-时，11(),[2,0]()lg ,(0,2]x x f x ex +⎧-∈-⎪=⎨⎪⎩，那么(4)f =3e -；(2,6]x ∈时，2()4f x t t ≥-恒成立，那么t 的取值范围是[1,3].〔此题第一空2分，第二空3分〕16．实数α，β满足3e e αα=，4(ln 1)e ββ-=〔其中e 是自然对数的底数〕，那么αβ＝4e ．四、解答题．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17．集合{}220A xx x =-->∣，集合{}22(25)50,B x x k x k k R =+++<∈∣ 〔1〕求集合B ；〔2〕假设“x B ∈〞是“x A ∈〞的充分不必要条件，求实数k 的取值范围．17．解：〔1〕根据题意，{}{}22(25)5025)()0B xx k x k x x x k =+++<=++<∣∣(， 当52k >时，有，52k -<-那么5(,)2B k =--， 当52k =时，有，52k -=-那么B =∅，当52k <时，有，52k ->-那么5(,)2B k =--；〔2〕根据题意，(,1)(2,)B =-∞-⋃+∞，假设“x B ∈〞是“x A ∈〞的充分不必要条件， 那么B A ⊆，当52k >时，有，52k -<-那么5(,)2B k =--，满足B A ⊆，当52k =时，有，52k -=-那么B =∅，满足B A ⊆，当52k <时，有，52k ->-那么5(,)2B k =--，假设B A ⊆，那么必有1,1k k -≤-∴≥，综上所述，实数k 的取值范围是 1.k ≥18．函数2()sin 22cos (0)66f x a x x a ππ⎛⎫⎛⎫=--+> ⎪ ⎪⎝⎭⎝⎭，且满足_________．〔1〕求函数()f x 的解析式及最小正周期；〔2〕假设关于x 的方程()1f x =在区间[0,]m 上有两个不同解，求实数m 的取值范围．从①()f x 的最大值为1，②()f x 的图像与直线3y =-的两个相邻点的距离等于π③()f x 的图像过点,06π⎛⎫⎪⎝⎭这三个条件中选择一个，补充在上面问题中并解答． 〔注：如果选择多个条件分别解答，按第一个解答计分．〕 18．解：〔I 〕函数2()sin 22cos 66f x a x x ππ⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭sin 2cos 2163a x x ππ⎛⎫⎛⎫=--+- ⎪ ⎪⎝⎭⎝⎭〔2〕假设满足①()f x 的最大值为1，那么12a +=，解得1a =，所以()2sin 216f x x π⎛⎫=-- ⎪⎝⎭； ()f x 的最小正周期为22T ππ==； 令()1f x =，得sin 216x π⎛⎫-= ⎪⎝⎭，解得2262x k πππ-=+，k Z ∈；即3x k ππ=+，k Z ∈；假设关于x 的方程()1f x =在区间[0,]m 上有两个不同解，那么3x π=或43π； 所以实数m 的取值范围是47,33ππ⎡⎫⎪⎢⎣⎭．假设满足②()f x 的图象与直线3y =-的两个相邻交点的距离等于π， 且()f x 的最小正周期为22T ππ==，所以(1)13a -+-=-，解得1a =； 以下解法均相同．假设满足③()f x 的图象过点,06π⎛⎫⎪⎝⎭，那么(1)sin 1066f a ππ⎛⎫=+-= ⎪⎝⎭，解得1a =；以下解法均相同．19．在①35a =，2526a a b +=；②22b =，3433a a b +=；③39S =，4528a a b +=，这三个条件中任选一个，补充在下面问题中，假设并解答．等差数列{}n a 的公差为d (d ＞1)，前n 项和为n S ，等比数列{}n b 的公比为q ，且1a ＝1b ，d ＝q ，．〔1〕求数列{}n a ，{}n b 的通项公式； 〔2〕记nn na cb =，求数列{}n c 的前n 项和n T ． 注：如果选择多个条件分别解答，按第一个解答计分． 19．解：方案一：选条件①〔1〕325211561a a a b a b d q d ====>，＋，，，11125256a d a d a d +=⎧∴⎨+=⎩解得112a d =⎧⎨=⎩或1256512a d ⎧=⎪⎪⎨⎪=⎪⎩〔舍去〕112b q =⎧∴⎨=⎩〔2〕n nn a c b =11211(21)()22n n n n c n ---∴==-⨯ 方案二：选条件②〔1〕2343112,3,,,1b a a b a b d q d =+===>12112253a d a d a d =⎧∴⎨+=⎩112256a d a d d =⎧∴⎨+=⎩解得112a d =⎧⎨=⎩或112a d =-⎧⎨=-⎩〔舍去〕112b q =⎧∴⎨=⎩ 〔2〕n nn a c b =11211(21)()22n n n n c n ---∴==-⨯ 方案三：选条件③1113278a d a d a d +=⎧∴⎨+=⎩解得112a d =⎧⎨=⎩或121838a d ⎧=⎪⎪⎨⎪=⎪⎩〔舍去〕112b q =⎧⎨=⎩ 〔2〕nn na cb =【点睛】此题考查等差等比数列综合应用，掌握乘公比错位相减求和的题型特点，属于较易题目。

江苏扬中第二高级中学2019高三上9月综合练习-数学数学(9.22)【一】填空题：本大题共14小题，每题5分，共70分、 1、设全集Z U =，集合}211{，，-=A ，}11{，-=B ，那么集合）（B C A u 为、 2.假设(2)a i i b i -=-，其中,a b R ∈，i 是虚数单位，复数a bi +=、3.某棉纺厂为了解一批棉花的质量，从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标)，所得数据均在区间[5,40]中，其频率分布直方图如下图，那么在抽测的100根棉花纤维中，有根的长度小于20mm.4.设22,1,()1,log (1),1x a a x f x f x x ⎧≤⎪==⎨->⎪⎩且那么((2))f f =、5.执行如下图的程序框图，那么输出的S=、第3题图第5题图6.幂函数()f x k x α=⋅的图象过点1,2⎛ ⎝，那么k α+=、7、角θ的顶点为坐标原点，始边为x 轴非负半轴，假设P (4，y)是角θ终边上一点，且sinθ＝－255，那么y ＝________.8.假设样本12,n a a a ⋅⋅⋅的方差为3，那么样本1231,31,31na a a ++⋅⋅⋅+的方差为、9.从长度为2，3，4，5的四条线段中任意取出三条，以这三条线段为边能够构成三角形的概率为、10.假设函数f (x )=x 2+ax ，x ∈[1，3]是单调函数，那么实数a 的取值范围是_____11.cos ⎝ ⎛⎭⎪⎫－17π4－sin ⎝ ⎛⎭⎪⎫－17π4的值是 12.tan α＝2.那么4sin 2α－3sin αcos α－5cos 2α.＝13.角α终边上一点P (－4,3)，那么cos ⎝ ⎛⎭⎪⎫π2＋αsin －π－αcos ⎝ ⎛⎭⎪⎫11π2－αsin ⎝ ⎛⎭⎪⎫9π2＋α的值为________、14、函数32()2,()log ,()x f x x g x x x h x x x =+=+=+零点依次为,,a b c ，那么,,a b c 的大小关系为.【二】解答题：15.〔本小题总分值18分〕α是第三象限角，且)23cos()sin()cos()sin()23sin()2cos()sin()(απαππαπααπαπαπα---------=f 〔1〕化简)(αf ；〔2〕假设51)23cos(=-πα，求)(αf 的值；〔3〕假设01860-=α，求)(αf 的值。

高三数学周末练习（）1．若复数2(1)(1)z x x i =-+-为纯虚数，则实数x 的值为 ．2．集合{|lg 0}M x x =>,2{|4}N x x =≤,则M N = ．3．在圆22=4所围成的区域内随机取一个点4cos 5α=-(,)2παπ∈tan()4πα+=121()2x x f x a+-+=+ABC ∆4AB AC ⋅=12AB BC ⋅=-22221(0,0)x y a b a b -=>>(0,)A b 2AP AB =xx x f cos sin )(+=)0(>m m x x y sin cos -={}n a 251021,2()5n n n aa a a a ++=+=n a =,(0)a b b a <<22212n n S a a nλ+≥231()sin 2cos ,22f x x x x R=--∈ABC∆3c =()0f C =sin 2sin B A =P ABCD-PAD ⊥ABCD PA PD ⊥ABCD //BC AD 090BAD ∠=3AD BC =//CD PBO平面PAB PCD ⊥平面平面1tan 3α=3sin 5β=－6m ＋2＋6m ＋1＝0m ∈R ，m ≠0，椭圆中心在原点，焦点在轴上．1 证明圆C 恒过一定点M ，并求此定点M 的坐标；2 判断直线4＋3－3＝0与圆C 的位置关系，并证明你的结论；3 当m ＝2时，圆C 与椭圆的左准线相切，且椭圆过1中的点M ，求此时椭圆方程；在轴上是否存在两定点A 、B ，使得对椭圆上任意一点Q 异于长轴端点，直线QA 、QB 的斜率之积为定值若存在，求出A 、B 坐标；若不存在，请说明理由．19．已知数列{a n }的首项a 1＝错误!，a n ＋1＝错误!，n ＝1,2，… 1 求证：数列错误!为等比数列；2 记S n ＝错误!＋错误!＋…＋错误!，若S n ＜100，求最大的正整数n ；样本数据频率组距开始结束是否100k ≥3s s k←+1,0k s ←←S输出2k k ←+O PCBA第16题BNA OCα东北第17题3 是否存在互不相等的正整数m 、、n ，使m 、、n 成等差数列，且a m －1、a －1、a n －1成等比数列如果存在，请给出证明；如果不存在，请说明理由． 答案1．-1； 2．(1,2]； 3．2π； 4．； 5．2； 6．7500；7．4； 8．360；9．； 10．2π； 11．；12．)45,1(； 13 14．1515． 解：（1）1cos 21()2sin(2)1226x f x x x π+=--=--，…………3分则的最小值是－2， …………5分最小正周期是22T ππ==； …………7分（2）()sin(2)106f C C π=--=，则sin(2)16C π-=，0C π<< 022C π∴<< 112666C πππ∴-<-<，262C ππ∴-=，3C π∴=， …………10分sin 2sin B A =，由正弦定理，得12a b =，① …………11分由余弦定理，得2222cos 3c a b ab π=+-，即223a b ab +-=， ②由①②解得1,2a b ==． …………14分 16．（1） …………7分 （2）……14分 17．解：（1）以为原点，正北方向为轴建立直角坐标系，……… 2分则x y l O A 3:= 设00N x y （，），有05sin 3x a a β==, 05cos 4y a a β==, (3,4)N a a ∴又0B p （，），∴直线的方程为：)(34p x pa a y --=……… 6分由⎪⎩⎪⎨⎧--==)(343p x p a a y xy 得的纵坐标)35(5312a p a p ap y c >-=，∴2165||,()2353c ap S OB y p a p a ∆=⋅=>-……… 10分（2）由（1）得22625353ap ap S p a p a==--,令5(0)3t p a t =->∴222510402[]933a a S a t a t =++≥， ∴当且仅当,9252ta t =即53a t =,此时103a p =时，上式取等号，……… 13分 ∴当103ap =公里时，抢救最及时 ……… 14分 18．1 证明：圆C 的方程可化为2＋2－2＋1－m 8＋6－6＝0，2分 由错误!解得错误!4分所以圆C 过定点M 0,1．5分2 解：直线4＋3－3＝0与 圆C 相切．证明如下．圆C 的方程可化为－4m 2＋[－3m ＋1]2＝25m 2，6分圆心到直线的距离为d ＝错误!＝错误!＝5|m |＝r ，9分 所以直线与圆C 相切．10分3 解：当m ＝2时，圆C 方程为－82＋－72＝100，圆心为8,7，半径为10，与直线＝8－10，即＝－2相切， 所以椭圆的左准线为＝－211分 又椭圆过点M 0,1，则b ＝1，所以错误!⇒错误!⇒椭圆方程为错误!＋2＝112分 在椭圆上任取一点Q ，≠0，设定点A,0，Bt,0，则QA ·QB ＝错误!·错误!＝错误!＝对∈－错误!，错误!恒成立，13分所以－错误!2＋1＝2－＋t ＋t 对∈－错误!，错误!恒成立． 所以错误!⇒错误!或错误!14分故A －错误!，0，B 错误!，0或者A 错误!，0，B －错误!，0．15分19．1 证明：∵ 错误!＝错误!＋错误!，∴ 错误!－1＝错误!－错误!，2分且∵ 错误!－1≠0，∴ 错误!－1≠0n ∈N *，3分 ∴ 数列错误!为等比数列．4分2 解：由1可求得错误!－1＝错误!×错误!n－1，∴错误!＝2×错误!n＋15分S n＝错误!＋错误!＋…＋错误!＝n＋2错误!＋错误!＋…＋错误!＝n＋2·错误!＝n＋1－错误!，7分若S n＜100，则n＋1－错误!＜100，∴n ma＝999分3 解：假设存在，则m＋n＝2，a m－1·a n－1＝a－1210分∵a n＝错误!，∴错误!－1·错误!－1＝错误!－1212分化简得：3m＋3n＝2·3，13分∵ 3m＋3n≥2·错误!＝2·3，当且仅当m＝n时等号成立．15分又m、n、互不相等，∴不存在．16分。

高三数学周末练习（10.20）一．填空题1．已知全集}5,4,3,2,1{=U ，集合2{|320}A x x x =-+=，{|2}B x x a a A ==∈，，则集合=⋃)(B A C U __________________。

2．用分层抽样的方法从某高中学校学生中抽取一个容量为55的样本参加问卷调查，其中高一年级、高二年级分别抽取10人、25人。

若该校高三年级共有学生400人，则该校高一和高二年级的学生总数为人。

3．若1524z z z i ⋅+=+（i 为虚数单位），则复数z =__________4．右图是一个算法流程图，则执行该算法后输出的s =______。

5．函数2()lg(31)f x x =+的定义域是______________。

6．袋中装有大小相同且形状一样的四个球,四个球上分别标 有“2”、“3”、“4”、“6”这四个数，现从中随机选取三个球,则 所选的三个球上的数恰好能构成一个等差数列的概率是_____。

7．已知4cos 5α=-且(,)2παπ∈，则tan(4πα+=8．如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =， 则四棱锥11A BB D D -的体积为_______________cm 3。

9．已知2παπ<<,3sin 22cos αα=,则cos()απ-=__________.10．函数5()sin 2sincos 2cos66f x x x ππ=⋅-⋅在,22ππ⎡⎤-⎢⎥⎣⎦上的单调递增区间为 . 11．已知函数)1,0(1)1(log )(≠>+-=a a x x f a 的图像恒过点A ,若点A 在直线0mx y n -+=上，则42m n +的最小值为___________________________。

12．已知a ，b 为正实数，函数xbx ax x f 2)(3++=在[]1,0上的最大值为4，则)(x f 在DABC 11D1A 1B[]0,1-上的最小值为 .13．设P 是函数(1)y x x =+图象上异于原点的动点，且该图象在点P 处的切线的倾斜角为θ，则θ的取值范围是 .14．已知角ϕ的终边经过点(1,2)P -，函数()sin()(0)f x x ωϕω=+>图象的相邻两条对称轴之间的距离等于3π，则()12f π= .。

扬中市第二高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1．求值：=（ ）A ．tan 38° B． C． D．﹣2． 已知f （x ）=x 3﹣3x+m ，在区间[0，2]上任取三个数a ，b ，c ，均存在以f （a ），f （b ），f （c ）为边长的三角形，则m 的取值范围是（ ）A ．m ＞2B ．m ＞4C ．m ＞6D ．m ＞83． 如图，棱长为的正方体1111D ABC A B C D -中，,E F 是侧面对角线11,BC AD 上一点，若 1BED F 是菱形，则其在底面ABCD 上投影的四边形面积（ ） A ．12 B ．34C. D4． 设变量x ，y满足约束条件，则目标函数z=4x+2y 的最大值为（ ）A ．12B ．10C ．8D ．25． 下列命题正确的是（ ）A ．已知实数,a b ，则“a b >”是“22a b >”的必要不充分条件B ．“存在0x R ∈，使得2010x -<”的否定是“对任意x R ∈，均有210x ->” C ．函数131()()2xf x x =-的零点在区间11(,)32内D ．设,m n 是两条直线，,αβ是空间中两个平面，若,m n αβ⊂⊂，m n ⊥则αβ⊥6． 棱锥被平行于底面的平面所截，当截面分别平分棱锥的侧棱、侧面积、体积时，相应截面面积 为1S 、2S 、3S ，则（ ）A ．123S S S <<B ．123S S S >>C ．213S S S <<D ．213S S S >> 7． 将函数y=cosx 的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），再向右平移个单位，所得函数图象的一条对称轴方程是（ ） A ．x=π B．C．D．8． S n 是等差数列{a n }的前n 项和，若3a 8－2a 7＝4，则下列结论正确的是（ ） A ．S 18＝72 B ．S 19＝76 C ．S 20＝80D ．S 21＝849． 不等式x （x ﹣1）＜2的解集是（ ）A ．{x|﹣2＜x ＜1}B ．{x|﹣1＜x ＜2}C ．{x|x ＞1或x ＜﹣2}D ．{x|x ＞2或x ＜﹣1}10．阅读如图所示的程序框图，运行相应的程序．若该程序运行后输出的结果不大于20，则输入的整数i 的最大值为（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A．3 B．4 C．5 D．611．已知等比数列{a n}的第5项是二项式（x+）4展开式的常数项，则a3•a7（）A．5 B．18 C．24 D．36N ，则输出的S的值是（）12．在下面程序框图中，输入44A．251B．253C．255D．260【命题意图】本题考查阅读程序框图，理解程序框图的功能，本质是把正整数除以4后按余数分类.二、填空题13．（﹣）5的展开式的常数项为 （用数字作答）．14．在极坐标系中，O 是极点，设点A ，B 的极坐标分别是（2，），（3，），则O 点到直线AB． 15．设,则的最小值为16．已知tan()3αβ+=，tan()24πα+=，那么tan β= .17．一个椭圆的长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 ．18．平面向量，满足|2﹣|=1，|﹣2|=1，则的取值范围 ．三、解答题19．在直角坐标系xOy 中，曲线C 1的参数方程为C 1：为参数），曲线C 2：=1．（Ⅰ）在以O为极点，x轴的正半轴为极轴的极坐标系中，求C1，C2的极坐标方程；（Ⅱ）射线θ=（ρ≥0）与C1的异于极点的交点为A，与C2的交点为B，求|AB|．20．在直角坐标系xOy中，圆C的参数方程（φ为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．（Ⅰ）求圆C的极坐标方程；（Ⅱ）直线l的极坐标方程是ρ（sinθ+）=3，射线OM：θ=与圆C的交点为O，P，与直线l的交点为Q，求线段PQ的长．21．如图所示，已知在四边形ABCD中，AD⊥CD，AD=5，AB=7，BD=8，∠BCD=135°．（1）求∠BDA的大小（2）求BC的长．22．在平面直角坐标系XOY中，圆C：（x﹣a）2+y2=a2，圆心为C，圆C与直线l1：y=﹣x的一个交点的横坐标为2．（1）求圆C的标准方程；（2）直线l2与l1垂直，且与圆C交于不同两点A、B，若S△ABC=2，求直线l2的方程．23．已知函数上为增函数，且θ∈（0，π），，m∈R．（1）求θ的值；（2）当m=0时，求函数f（x）的单调区间和极值；（3）若在上至少存在一个x0，使得f（x0）＞g（x0）成立，求m的取值范围．24．函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜）的部分图象如图所示（Ⅰ）求函数f（x）的解析式（Ⅱ）在△ABC中，角A，B，C所对的边分别是a，b，c，其中a＜c，f（A）=，且a=，b=，求△ABC的面积．扬中市第二高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案） 一、选择题1． 【答案】C【解析】解： =tan （49°+11°）=tan60°=，故选：C ．【点评】本题主要考查两角和的正切公式的应用，属于基础题．2． 【答案】C 【解析】解：由f ′（x ）=3x 2﹣3=3（x+1）（x ﹣1）=0得到x 1=1，x 2=﹣1（舍去）∵函数的定义域为[0，2]∴函数在（0，1）上f ′（x ）＜0，（1，2）上f ′（x ）＞0， ∴函数f （x ）在区间（0，1）单调递减，在区间（1，2）单调递增，则f （x ）min =f （1）=m ﹣2，f （x ）max =f （2）=m+2，f （0）=m由题意知，f （1）=m ﹣2＞0 ①； f （1）+f （1）＞f （2），即﹣4+2m ＞2+m ②由①②得到m ＞6为所求．故选C 【点评】本题以函数为载体，考查构成三角形的条件，解题的关键是求出函数在区间[0，2]上的最小值与最大值3． 【答案】B 【解析】试题分析：在棱长为的正方体1111D ABC A B C D -中，11BC AD ==AF x =x =解得x =，即菱形1BED F =，则1BED F 在底面ABCD 上的投影四边形是底边为34，高为的平行四边形，其面积为34，故选B. 考点：平面图形的投影及其作法. 4． 【答案】B【解析】解：本题主要考查目标函数最值的求法，属于容易题，做出可行域，由图可知，当目标函数过直线y=1与x+y=3的交点（2，1）时，z 取得最大值10．5． 【答案】C 【解析】考点：1.不等式性质；2.命题的否定；3.异面垂直；4.零点；5.充要条件．【方法点睛】本题主要考查不等式性质，命题的否定，异面垂直，零点，充要条件.充要条件的判定一般有①定义法:先分清条件和结论（分清哪个是条件,哪个是结论），然后找推导关系（判断,p q q p ⇒⇒的真假），最后下结论（根据推导关系及定义下结论）. ②等价转化法:条件和结论带有否定性词语的命题,常转化为其逆否命题来判断. 6． 【答案】A 【解析】考点：棱锥的结构特征． 7． 【答案】B【解析】解：将函数y=cosx 的图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到y=cos x ，再向右平移个单位得到y=cos[（x ）]，由（x ）=k π，得x =2k π，即+2k π，k ∈Z ，当k=0时，，即函数的一条对称轴为，故选：B【点评】本题主要考查三角函数的对称轴的求解，利用三角函数的图象关系求出函数的解析式是解决本题的关键．8． 【答案】【解析】选B.∵3a 8－2a 7＝4， ∴3（a 1＋7d ）－2（a 1＋6d ）＝4，即a 1＋9d ＝4，S 18＝18a 1＋18×17d 2＝18（a 1＋172d ）不恒为常数．S 19＝19a 1＋19×18d2＝19（a 1＋9d ）＝76，同理S 20，S 21均不恒为常数，故选B. 9． 【答案】B【解析】解：∵x （x ﹣1）＜2，∴x 2﹣x ﹣2＜0，即（x ﹣2）（x+1）＜0， ∴﹣1＜x ＜2，即不等式的解集为{x|﹣1＜x ＜2}． 故选：B10．【答案】B【解析】解：模拟执行程序框图，可得 s=0，n=0满足条件n ＜i ，s=2，n=1 满足条件n ＜i ，s=5，n=2 满足条件n ＜i ，s=10，n=3 满足条件n ＜i ，s=19，n=4 满足条件n ＜i ，s=36，n=5所以，若该程序运行后输出的结果不大于20，则输入的整数i 的最大值为4， 有n=4时，不满足条件n ＜i ，退出循环，输出s 的值为19． 故选：B ．【点评】本题主要考查了循环结构的程序框图，属于基础题．11．【答案】D【解析】解：二项式（x+）4展开式的通项公式为T r+1=•x 4﹣2r ，令4﹣2r=0，解得r=2，∴展开式的常数项为6=a 5，∴a 3a 7=a 52=36，故选：D ．【点评】本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．12．【答案】B二、填空题13．【答案】 ﹣10【解析】解：由于（﹣）5展开式的通项公式为T r+1=•（﹣1）r•，令15﹣5r=0，解得r=3，故展开式的常数项是﹣10， 故答案为：﹣10．【点评】本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．14．【答案】．【解析】解：根据点A ，B 的极坐标分别是（2，），（3，），可得A 、B 的直角坐标分别是（3，）、（﹣，），故AB的斜率为﹣，故直线AB 的方程为 y﹣=﹣（x ﹣3），即x+3y ﹣12=0，所以O 点到直线AB的距离是=，故答案为：．【点评】本题主要考查把点的极坐标化为直角坐标的方法，点到直线的距离公式的应用，属于基础题．15．【答案】9【解析】由柯西不等式可知16．【答案】43【解析】试题分析：由1tan tan()241tan πααα++==-得1tan 3α=， tan tan[()]βαβα=+-tan()tan 1tan()tan αβααβα+-=++13433133-==+⨯． 考点：两角和与差的正切公式．17．【答案】．【解析】解：由题意可得，2a，2b，2c成等差数列∴2b=a+c∴4b2=a2+2ac+c2①∵b2=a2﹣c2②①②联立可得，5c2+2ac﹣3a2=0∵∴5e2+2e﹣3=0∵0＜e＜1∴故答案为：【点评】本题主要考查了椭圆的性质的应用，解题中要椭圆离心率的取值范围的应用，属于中档试题18．【答案】[，1]．【解析】解：设两个向量的夹角为θ，因为|2﹣|=1，|﹣2|=1，所以，，所以，=所以5=1，所以，所以5a2﹣1∈[]，[，1]，所以；故答案为：[，1]．【点评】本题考查了向量的模的平方与向量的平方相等的运用以及通过向量的数量积定义，求向量数量积的范围．三、解答题19．【答案】【解析】解：（Ⅰ）曲线为参数）可化为普通方程：（x﹣1）2+y2=1，由可得曲线C1的极坐标方程为ρ=2cosθ，曲线C2的极坐标方程为ρ2（1+sin2θ）=2．（Ⅱ）射线与曲线C1的交点A的极径为，射线与曲线C2的交点B的极径满足，解得，所以．20．【答案】【解析】解：（I）圆C的参数方程（φ为参数）．消去参数可得：（x﹣1）2+y2=1．把x=ρcosθ，y=ρsinθ代入化简得：ρ=2cosθ，即为此圆的极坐标方程．（II）如图所示，由直线l的极坐标方程是ρ（sinθ+）=3，射线OM：θ=．可得普通方程：直线l，射线OM．联立，解得，即Q．联立，解得或．∴P．∴|PQ|==2．【点评】本题考查了极坐标化为普通方程、曲线交点与方程联立得到的方程组的解的关系、两点间的距离公式等基础知识与基本方法，属于中档题．21．【答案】【解析】（本题满分为12分）解：（1）在△ABC中，AD=5，AB=7，BD=8，由余弦定理得…=…∴∠BDA=60°…（2）∵AD⊥CD，∴∠BDC=30°…在△ABC中，由正弦定理得，…∴．…22．【答案】【解析】解：（1）由圆C与直线l1：y=﹣x的一个交点的横坐标为2，可知交点坐标为（2，﹣2），∴（2﹣a）2+（﹣2）2=a2，解得：a=2，所以圆的标准方程为：（x﹣2）2+y2=4，（2）由（1）可知圆C的圆心C的坐标为（2，0）由直线l2与直线l1垂直，直线l1：y=﹣x可设直线l2：y=x+m，则圆心C到AB的距离d=，|AB|=2=2所以S△ABC=|AB|•d=•2•=2令t=（m+2）2，化简可得﹣2t2+16t﹣32=﹣2（t﹣4）2=0，解得t=（m+2）2=4，所以m=0，或m=﹣4∴直线l2的方程为y=x或y=x﹣4．23．【答案】【解析】解：（1）∵函数上为增函数，∴g′（x）=﹣+≥0在，mx﹣≤0，﹣2lnx﹣＜0，∴在上不存在一个x0，使得f（x0）＞g（x0）成立．②当m＞0时，F′（x）=m+﹣=，∵x∈，∴2e﹣2x≥0，mx2+m＞0，∴F′（x）＞0在恒成立．故F（x）在上单调递增，F（x）max=F（e）=me﹣﹣4，只要me﹣﹣4＞0，解得m＞．故m的取值范围是（，+∞）【点评】本题考查利用导数求闭区间上函数的最值，考查运算求解能力，推理论证能力；考查化归与转化思想．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答．24．【答案】【解析】解：（Ⅰ）∵由图象可知，T=4（﹣）=π，∴ω==2，又x=时，2×+φ=+2kπ，得φ=2kπ﹣，（k∈Z）又∵|φ|＜，∴φ=﹣，∴f（x）=sin（2x﹣）…6分（Ⅱ）由f（A）=，可得sin（2A﹣）=，∵a＜c，∴A为锐角，∴2A﹣∈（﹣，），∴2A﹣=，得A=，由余弦定理可得：a2=b2+c2﹣2bccosA，可得：7=3+c2﹣2，即：c2﹣3c﹣4=0，∵c＞0，∴解得c=4．∴△ABC的面积S=bcsinA==…12分【点评】本题主要考查了余弦定理，三角形面积公式，由y=Asin（ωx+φ）的部分图象确定其解析式等知识的应用，属于基本知识的考查．。