下载文档原格式
解：第一步——离散对于一维杆问题，我们先离散成单元，对每个单元作如下计算[][][][][]00,,,,00)(22,,,,2222222=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-∂∂⎥⎦⎤⎢⎣⎡⇒=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-∂∂⎥⎦⎤⎢⎣⎡⇒=-∂∂∂∂-∂∂⇒=-∂∂=-∂∂⎰⎰⎰⎰⎰⎰⎰⎰ΓΓΓdx x N N u u K x u N N dx x N N u u dx u u N N N N u u x uN N u u dx ux dx xu x u x u u dx ux dx x u u dx x x u u j i x x j i j i j i x x ji j i j i j i x x ji j i j i xx x x x x x x x x j i jijij i j i j ij i jiδδδδδδδδδδδδ其中杆被平均离散为e 个单元（有限元不一定要均分），于是有node=e+1个结点，每个单元长度len=1/e,于是第n 个单元的左端点坐标len n x i )1(-=，右端点坐标nlen x j =；第二步——刚度矩阵线性插值有每个单元)()(j j ej j j ei x x e lenx x N x x e lenx x N -=-=-=-=⇒⎥⎦⎤⎢⎣⎡-=e e B e⇒⎥⎦⎤⎢⎣⎡--===⎰e e e e len B B dx B B K T e e T e e xx e j i 对于整体叠加⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=e e e e e K 00020 （K 为一个node×node 阶矩阵） 程序用for 循环给K 赋值K=zeros(node,node); K1=zeros(node,node); for n=1:(node-1);K1(n:n+1,n:n+1)=[e,-e;-e,e]; K=K1+K;K1=zeros(node,node);End第三步——力矩阵体积力由第一步公式[]02=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-∂∂⎥⎦⎤⎢⎣⎡⎰Γdx x N N u u K x uN N j i x x j i j i j i其中第三项为体积力dxx N N F j i x x j i 21⎥⎦⎤⎢⎣⎡=⎰用matlab 中int （）函数对积分进行计算并用for 函数进行循环且赋值，其中)()(j j ej j j ei x x e lenx x N x x e len x x N -=-=-=-=，nlenx lenn x j i =-=)1(程序如下Syms x; F1=zeros(1,node);F11=zeros(1,node); G=zeros(1,2); for n=1:e;B=[(xj(n)*x^2-x^3)/len,(x^3-xi(n)*x^2)/len]; G=int(B,x,xi(n),xj(n)); G=double(G);F11(1,n:n+1)=[G(1,1),G(1,2)]; F1=F11+F1;F11=zeros(1,node); End边界力由第一步中公式[]02=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-∂∂⎥⎦⎤⎢⎣⎡⎰Γdx x N Nu u K x uN N j i x x j i j i j i 其中第一项ijx x j i x x j i j i xuN N xu N N x u N N F ==Γ∂∂⎥⎦⎤⎢⎣⎡-∂∂⎥⎦⎤⎢⎣⎡=∂∂⎥⎦⎤⎢⎣⎡=2为边界力因为u （0）处约束力未知为C ，u （1）处边界条件11=∂∂=x xu各单元之间的边界力叠加的时候均抵消，所以边界力矩阵最终为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=102 C F第四步——解方程由上面我们可以得到方程02121=-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-F u u u K F n ,代入位移边界条件01=u先对方程进行置一处理，令F=F2-F1且的第一项置0，刚度矩阵变换成⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=e e K 00020001方程变换为Kd=F ， 求逆⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==-n u u F K d 21第五步——作图用到两个作图函数plot 、ezplot 分别做原函数图和折线图 折线图程序如下x=0:len:1; y=zeros(1,node);for n=1:node;y(1,n)=X(1,n); endplot(x,y,'r');hold on; （hold on 可将两图画在一个坐标下）原函数图程序如下ezplot('(1/12)*x^4+2/3*x',[0,1]);附：程序clearformat longfirst_time=cputime;e=10; %单元数node=e+1; %结点数len=1/e; %单元长度xi=0:len:(1-len); %单元左端点坐标xj=len:len:1; %单元右端点坐标K=zeros(node,node); %刚度矩阵（由于是线性插值）K1=zeros(node,node);for n=1:(node-1);K1(n:n+1,n:n+1)=[e,-e;-e,e];K=K1+K;K1=zeros(node,node);endsyms x; %F1力矩阵F1=zeros(1,node);F11=zeros(1,node);G=zeros(1,2);for n=1:e;B=[(xj(n)*x^2-x^3)/len,(x^3-xi(n)*x^2)/len];G=int(B,x,xi(n),xj(n));G=double(G);F11(1,n:n+1)=[G(1,1),G(1,2)];F1=F11+F1;F11=zeros(1,node);endF2=zeros(1,node); %F2力矩阵F2(1,node)=1;K(2,1)=0; %刚度矩阵置一K(1,2)=0;K(1,1)=1;F=F2-F1; %求合力矩阵F(1,1)=0;X=F*inv(K); %求结点位移Xx=0:len:1; %画折线图y=zeros(1,node);for n=1:node;y(1,n)=X(1,n);endplot(x,y,'r');hold on;ezplot('(1/12)*x^4+2/3*x',[0,1]); %画原函数图以10个单元为例，图数据。
有限元等参数单元有限元分析是一种工程数值分析方法，广泛用于结构力学、固体力学等领域。
在有限元分析中，将结构或物体离散为许多小单元，每个小单元称为参数单元。
本文将介绍有限元等参数单元的概念和应用。
在有限元分析中，参数单元是对结构或物体进行离散化的基本单元。
它是通过数学建模技术将连续域问题转化为离散模型的重要工具。
参数单元可以是一维、二维或三维的。
在一维情况下，常见的参数单元有杆单元和梁单元等。
在二维情况下，常见的参数单元有三角形单元和四边形单元等。
在三维情况下，常见的参数单元有四面体单元和六面体单元等。
在有限元分析中，参数单元的选择要根据具体问题的性质来确定。
一般来说，参数单元的几何形状应能较好地适应结构或物体的形状。
对于复杂结构或物体，可以使用不同形状的参数单元进行组合，以更好地描述结构的几何特征。
在参数单元中，需要定义材料性质、几何性质和加载条件等参数。
材料性质包括弹性模量、泊松比、密度等。
几何性质包括长度、面积、体积等。
加载条件包括外力、边界条件等。
这些参数可以通过实验测量或根据经验来确定。
在有限元分析中，参数单元的刚度、质量和荷载等可以通过这些参数来计算。
有限元分析的基本思想是，将结构或物体分解为多个参数单元，并将其转化为一个或多个代数方程组。
通过求解这个方程组，可以得到结构或物体的应力、应变、位移等信息。
有限元方法可以有效地分析复杂结构的性能和行为，并为工程设计和优化提供依据。
总之，有限元等参数单元是在有限元分析中对结构或物体进行离散化的基本单元。
它是将连续域问题转化为离散模型的重要工具。
参数单元的选择要根据具体问题的性质来确定，并通过定义材料性质、几何性质和加载条件等参数来描述结构的特征。
有限元分析是一种用于求解结构或物体应力、应变、位移等信息的数值分析方法，可以为工程设计和优化提供依据。
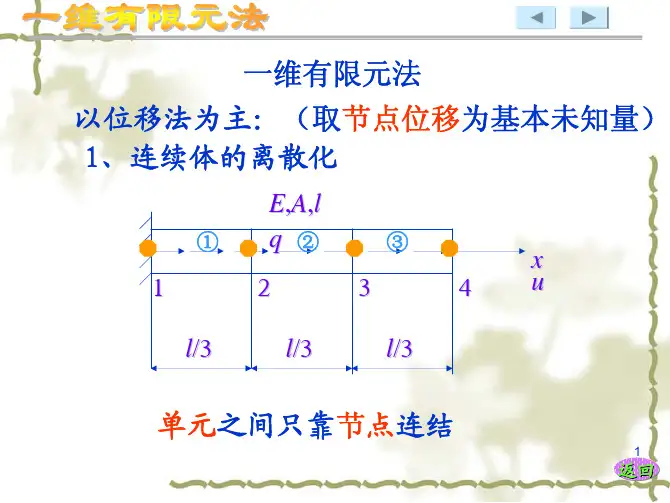
一维问题的有限元方法一、问题的离散化有限元方法是一种将连续问题离散化的数值计算方法。
在一维问题中，我们将连续的物理系统或结构离散化为一系列的单元，每个单元由节点连接。
离散化过程是为了将连续的物理问题转化为可以数值求解的形式。
二、单元划分与节点设置在离散化过程中，我们需要将连续的物理系统划分为一系列的单元。
每个单元由节点连接，节点是单元之间的连接点。
节点的设置需要考虑问题的特性和计算的精度要求。
三、插值函数与形函数插值函数用于描述节点之间的函数关系，形函数用于描述节点处的函数值。
插值函数和形函数的选择需要根据问题的特性和计算的精度要求来确定。
常用的插值函数有线性插值、二次插值等。
四、有限元方程的建立根据问题的特性和边界条件，我们可以建立有限元方程。
有限元方程是描述节点处的函数值和节点之间的函数关系的关系式。
在建立有限元方程时，需要考虑物理方程、边界条件等因素。
五、有限元方程的求解有限元方程的求解可以采用多种方法，如直接法、迭代法等。
直接法适用于小型问题，迭代法适用于大型问题。
在求解过程中，需要注意收敛性和误差分析。
六、收敛性与误差分析收敛性是指迭代法在迭代过程中是否能收敛到正确解，误差分析是指求解结果与真实解之间的误差大小和分布情况。
对于不收敛或误差较大的情况，需要进行相应的调整和处理。
七、边界条件的处理边界条件是描述物理系统在边界上的行为，对于有限元方法来说，需要正确处理边界条件。
常用的处理方法有强加边界条件、引入罚函数等。
八、自适应网格加密技术自适应网格加密技术是一种根据求解过程中的误差分布情况自动加密网格的方法。
该技术可以提高计算的精度和效率，适用于复杂问题和多物理场耦合问题。
九、多物理场耦合有限元方法多物理场耦合问题是指多个物理场之间相互作用的问题，如力学、流体、电磁等。
多物理场耦合有限元方法需要考虑多个物理场的相互作用和耦合效应，建立相应的有限元方程进行求解。
