第一章简支梁有限元结构静力分析

第二章简支梁有限元结构静力分析（实体单元）前言本文利用ANSYS软件中SOLID45实体单元建立简支梁有限元模型，对其进行静力分析与模态分析，来比较建模时不同约束方位的选择所带来的不同结果，以便了解和认识ANSYS 用于分析计算结果的方法。

2.1实体单元SOLID45介绍2.1.1SOLID45单元的几何描述：SOLID45单元用于构造三维实体结构。

单元通过八个节点来定义，每个节点有三个沿着XYZ方向平移的自由度UX、UY、UZ。

单元具有塑性，蠕变，膨胀，应力强化，大变形和大应变等能力。

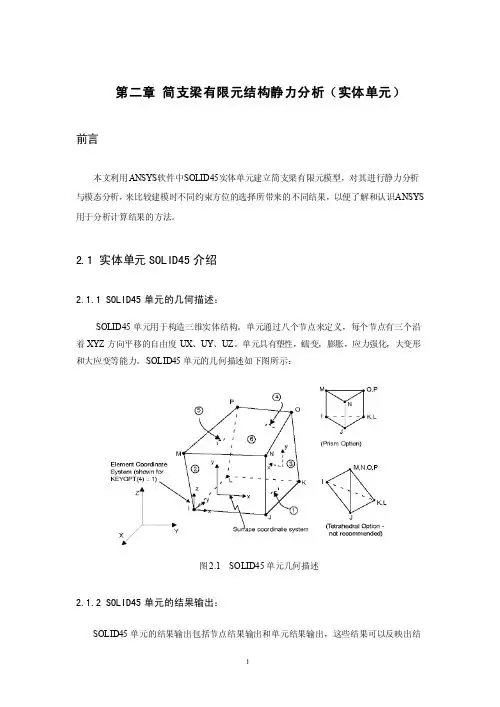
SOLID45单元的几何描述如下图所示：图2.1SOLID45单元几何描述2.1.2SOLID45单元的结果输出：SOLID45单元的结果输出包括节点结果输出和单元结果输出，这些结果可以反映出结构整体以及局部的应力、应变、内力等参量，详细输出结果见下表：表2.1SOLID45单元的结果输出项名称定义S:X,Y,Z,XY,YZ,XZ应力S;1,2,3主应力S:INT应力强度S:EQV等效MISES应力EPEL:X,Y,Z,XY,YZ,XZ弹性应变EPEL:1,2,3主弹性应变EPEL:EQV等效弹性应变EPTH:X,Y,Z,XY,YZ,XZ平均热应变EPTH:EQV等效热应变EPPL:X,Y,Z,XY,YZ,XZ平均塑性应变EPPL:EQV等效塑性应变EPCR:X,Y,Z,XY,YZ,XZ平均蠕变应变EPCR:EQV等效蠕变应变EPSW:平均膨胀应变NL:EPEQ平均等效塑性应变NL:SRAT屈服表面上的迹应力和应力之比NL:SEPL从应力-应变曲线平均等效mises应力NL:HPRES静水压力FACE表面lableAREA表面面积TEMP表面平均温度EPEL表面弹性应变(X,Y,XY)PRESS表面压力S(X,Y,XY)表面应力(X轴平行于定义该表面的前面两个结点连接) S(1,2,3)表面主应力SINT表面应力强度SEQV表面等效mises应力LOCI:X,Y,Z积分点位置2.1.3SOLID45单元的参数设置：SOLID45单元可定义正交各向异性材料：即该单元属性允许材料的物理性能和力学性能在不同方向上具有不同的数值。

有限元结构静力学分析有限元结构静力学分析的基本原理是将结构分割为离散的小单元，通过对这些小单元的力学行为进行数学建模来研究整个结构的行为。

通常情况下，结构被离散为多个三角形或四边形单元，每个单元内的力学行为可通过有限元模型进行模拟。

有限元方法基于结构的力学行为方程，通过数值计算的方式求解出结构的位移、应力等物理量。

1.生成有限元离散网格：将结构几何分割为小单元，构成有限元离散网格。

通常受到计算资源和准确性的限制，根据具体情况选择单元尺寸和分割密度。

2.建立有限元模型：对每个单元进行力学行为的建模，包括约束、边界条件等。

通常使用线性弹性模型，即假设结构为弹性体，在小变形范围内满足胡克定律。

3.求解结构位移：根据结构的边界条件和受力情况，求解结构的位移。

位移是结构分析的基本结果，可通过求解结构的刚度矩阵和载荷向量来获得。

4.计算应力和变形：根据结构的位移，计算结构中各个单元的应力和变形。

应力和变形是结构分析的重要结果，可用于评估结构的安全性和合理性。

5.分析结果的后处理：对求解得到的位移、应力和变形等结果进行后处理，如绘制位移云图、应力云图等，以便更直观地了解结构的行为。

在实际应用中，有限元结构静力学分析需要注意以下几个方面：1.模型准确性：选择合适的有限元模型和求解方法以保证结果的准确性。

选择适当的单元尺寸和分割密度，根据具体情况对模型进行验证和校正。

2.材料特性：结构的力学性质受到材料特性的影响，如弹性模量、泊松比等。

确保材料特性的准确性和可靠性，以获得可靠的力学分析结果。

3.界面和边界条件：结构的界面和边界条件对分析结果有重要影响。

需要仔细设定和模拟各个界面和边界条件，以反映实际工况和受力情况。

4.结构非线性问题：有限元结构静力学分析通常假设结构在小变形范围内满足胡克定律。

对于存在非线性行为的结构，如大位移、屈曲等，需要采用相应的非线性分析方法。

总而言之，有限元结构静力学分析是一种重要的结构力学分析方法，通过离散化和数值计算的方式求解结构的力学性质。

有限元静力分析范文有限元静力分析（finite element static analysis）是一种广泛应用于工程领域的数值分析方法，用于计算和预测结构的受力情况和变形，并支持优化设计和工程决策。

通过将结构分割成离散的小元素，在每个小元素上建立数学模型和方程，可以近似地描述结构的力学行为。

本文将介绍有限元静力分析的基本原理、步骤，以及其在工程中的应用和局限性。

有限元静力分析的基本原理是将结构离散化为有限个小元素，并在每个小元素上建立力学模型。

这些小元素通常是简单形状，如点、线、面或体。

然后，通过基于物理原理和数学模型推导出的方程组来求解各个小元素的受力和变形情况。

最终，通过组合求解得到整个结构的受力和变形情况。

有限元静力分析的步骤包括：几何建模、网格划分、边界条件的施加、材料特性的定义、力学模型的建立、方程的推导和求解等。

首先，需要根据实际情况进行结构的几何建模，即将结构转化为几何模型。

然后，将几何模型划分为离散的小元素，形成有限元网格。

接下来，需要根据受力情况和边界条件来为结构定义边界条件。

同时，还需要给材料赋予相应的物理特性，如弹性模量、密度等。

然后，在每个小元素上建立合适的数学模型，如杆元、壳元、体元等。

根据弹性力学原理和平衡方程，可以推导出每个小元素的力学方程。

最后，通过求解这些方程，可以获得整个结构的受力和变形情况。

有限元静力分析在工程中有广泛的应用。

首先，它可以用于评估结构的受力性能和安全性。

通过分析结构在不同载荷下的受力情况，可以了解结构的承载能力和强度。

其次，有限元静力分析还可以用于优化设计。

通过改变结构的几何形状、材料选择或边界条件，可以比较不同设计方案的效果，找到最优设计方案。

此外，有限元静力分析还可以用于模拟结构在不同工况下的受力和变形情况，为工程决策提供依据。

然而，有限元静力分析也有一些局限性。

首先，它是基于一些假设和简化条件的数值方法，其结果可能不完全准确。

其次，有限元静力分析是一个计算密集型的过程，需要较强的计算能力和资源支持。

桥梁结构的静力与动力分析方法引言：桥梁作为人类最重要的交通工程之一，承载着人们的出行需求，具有重要的经济、社会和文化意义。

而桥梁的设计与施工过程中，静力与动力分析方法的运用则至关重要。

本文将探讨桥梁结构静力与动力分析方法的原理、优势以及具体应用。

一、静力分析方法静力方法是桥梁设计中最基本的分析方法，根据结构静力学原理，通过求解结构内力和变形，确定桥梁的受力状态。

静力分析方法适用于比较简单的桥梁结构系统，如简支梁、悬链线以及简单连续梁等。

其基本思想是将桥梁结构看作刚体，根据平衡条件和支座约束关系，推导出结构的力学方程，并求解得到内力和变形。

静力分析方法具有计算简便、结果准确等优点，部分结构仍然可以应用于工程实践中。

二、有限元法有限元法是一种现代化的计算方法，广泛应用于桥梁结构的静力与动力分析中。

有限元法将复杂结构离散为许多小单元，通过有限元单元的力学方程及其边界条件，建立整个结构的力学模型，进而进行计算与分析。

有限元法不再依赖于结构的简单性，适用于各种复杂的桥梁结构形式。

当桥梁结构形状、材料特性和荷载情况变得复杂时，有限元法具有更高的计算准确性和精度。

三、斯坦福大桥案例为了探究静力与动力分析方法在实践中的应用，我们以美国斯坦福大桥为例。

斯坦福大桥是一座具有代表性的悬索桥，采用了大跨度和高塔楼的设计方案。

在桥梁设计中，斯坦福大桥不仅需要考虑自重和行车荷载，还需要考虑地震和风荷载等动力因素。

此时，传统的静力分析方法已经无法满足工程要求。

因此，斯坦福大桥设计团队采用了有限元法来进行静力和动力分析。

首先，通过建立桥梁的有限元模型，考虑结构的刚度、材料特性以及荷载情况，得到结构的内力和变形情况。

接下来，引入地震和风荷载等动力因素，通过时程分析和频率分析等方法，分析结构在不同荷载作用下的响应特性，确保桥梁的安全性和稳定性。

四、结构健康监测除了设计阶段的分析方法，静力与动力分析方法还广泛应用于桥梁的健康监测领域。

目录一前言目前，在工程领域中应用最广泛的数值模拟方法是有限单元法, 它不但可以解决固体力学及结构分析方面的问题, 而且应用于传热学、流体力学、电磁学等领域, 其计算结果已成为各类工业产品设计和性能分析的可靠依据, 广泛应用于航空航天、机械制造、建筑设计、石油化工等领域。

有限元分析(Finite Element Analysis,FEA)是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。

利用简单而又相互作用的元素，即单元，就可以用有限数量的未知量去逼近无限未知量的真实系统。

有限元方法是一种应用十分广泛的数值分析方法，也是工程科学的重要工具，其重要性仅次于数学。

复杂的工程问题需要借助计算机得到满足一定精度要求的数值结果。

本次课设所采用的是CAE软件的ANSYS命令，它是目前国际上应用最广泛的有限元软件。

通过本次现代设计方法课程设计，学习有限元分析方法及ANSYS命令，了解并掌握利用CAE软件的ANSYS命令进行连杆，珩架，梁等的力学分析，将理论与实际工作结合，并最终达到能够独立对梁，杆等进行有限元内力分析。

本设计的研究对象是一简支梁。

二物理模型教程3：平面梁结构的内力计算问题阐述有一简支梁结构如图所示，其中，M=10KN.M，q=2KN/m，F=2KN。

对该梁进行分析，画出弯矩图和剪力图。

用材料力学计算所得剪力和弯矩图如下：剪力图：弯矩图：有限元计算说明将梁划分为16个单元，17个节点，用BEAM3来建立单元，进行静力学分析交互式的求解过程1．创建节点1.1 创建梁的各个节点1．Main Menu：Preprocessor→Modeling→Create→Node→In Active CS。

2．在创建节点窗口内，在NODE后的编辑框内输入节点号1，并在X，Y，Z后的编辑框内输入0，0，0作为节点1的坐标值。

3．按下该窗口内的Apply按钮。

4．输入节点号17，并在X，Y，Z后的编辑框内输入8，0，0作为节点17的坐标值。

第一章绪论LI引言随着现代社会的进展，经济的提高和科技的进步，我们我国的土木工程建设项目正处于新的高潮期，重大的工程结构，如超大跨桥梁、超高层建筑、大型场馆和大型水利工程等正在不断建成，桥梁工程的进展如今更是突飞猛进。

梁是由支座支撑的主要承受弯矩和剪力的构件。

在机械，建筑等工程中存在大量受弯曲的杆件，例如起重机大梁，火车轮轴等，主要承受的外力以横向力为主。

社会的飞速进展给人们带来了诸多的便利，同时，也使我们我国的建筑土木行业得到了空前的进展，在建筑结构中，不管从它的承载力还是构造等，梁的地位显得尤为重要，由于在建筑结构中，梁是最具有典型特征的元素，它以多种形态展现在人们面前，以线性受力体系为主要的特征。

1. 2国内外梁受力分析讨论的现状20世纪以来，世界各地也相继兴建了很多以斜拉桥、悬索桥为主的大跨桥粱结构。

斜拉桥的主跨也从当时的100米左右进展到了现在的上千米。

90年月到现在，仅我们我国建筑的主跨在400米以上的斜拉桥也已有几十座。

现在世界上跨度超过IOOO米的悬索桥则更是不计其数。

由于这些大跨桥梁不仅可以满意更大流量的交通要求，并且造型轻快美观。

一般都是作为城市交通运输的重要枢纽工程和标志性建筑，投资特别巨大，对国民经济持续、稳定的进展有着特别重要的作用，这些结构假如一旦发生损坏，就会造成特别重大的人员伤亡和经济损失，并且也会产生极坏的社会影响，桥梁损坏造成的严峻损失也将是难以估量的。

桥梁在长期运营过程中也不行避开的会受到环境和有害化学物质的侵蚀，并要承受车辆，风暴、地震、破坏、爆炸、疲惫等因素的作用，这些因素使桥梁的自身性能不断退化，从而导致结构的各部分在没有达到设计年限就发生不同程度的损伤和劣化。

其中，循环荷载作用下的疲惫损伤累积和有损结构在动力荷载作用下的裂纹失稳扩展是造成很多桥梁发生灾难性事故的主要缘由，据美国土木工程协会(ASCE)统计斟，80%〜90%钢结构的破坏与疲惫损伤有关。

第一章简支梁有限元结构静力分析0 前言本文利用ANSYS软件中BEAM系列单元建立简支梁有限元模型，对其进行静力分析与模态分析，来比较建模时不同单元类型的选择和网格划分精细程度不同所带来的不同结果，以便了解和认识ANSYS对于分析结果准确性的影响。

1.1 梁单元介绍梁是工程结构中最为常用的结构形式之一。

ANSYS 程序中提供了多种二维和三维的梁单元，分别具有不同的特性，是一类轴向拉压、弯曲、扭转单元，用以模拟各类结构中的平面以及空间的梁构件。

常用的梁单元中 BEAM3、BEAM 23 和 BEAM 54 为二维梁单元，BEAM 4、BEAM 24、BEAM344、BEAM188 和 BEAM189 为三维梁单元。

下文将简单介绍常用的梁单元 BEAM3、BEAM4、BEAM44、BEAM188 以及 BEAM189。

1.1.1 BEAM3单元：图 1.1 Beam3 单元几何图形BEAM3 是具有拉伸、压缩和弯曲的单轴2-D 弹性梁单元。

上图给出了单元的几何图形、节点位置及坐标系统。

单元由两个节点、横截面面积、横截面惯性矩、截面高度及材料属性定义。

初始应变通过Δ/L 给定，Δ为单元长度 L（由 I，J 节点坐标算得）与 0 应变单元长度之差。

该单元在每个节点处有三个自由度，可以进行忽略环箍效应的轴对称分析，例如模拟螺栓和槽钢等。

在轴对称分析中，单元的面积和惯性矩必须给出360°范围内的值。

剪切变形量SHERAR 是可选的，如给SHERAR 赋值为0则表示忽略剪切变形，当然剪切模量（GXY）只有在考虑剪切变形时才起作用。

同时可以运用实常数中的 ADDMAS 命令为单位长度梁单元施加附加质量。

1.1.2 BEAM4单元：图 1.2 Beam4 单元几何图形BEAM4 是具有拉伸、压缩、扭转和弯曲的单轴 3-D 弹性梁单元。

关于本单元的几何模型，节点座标及座标系统详见上图。

该单元在每个节点处有六个自由度。

目录一、前言-------------------------------------二、物理模型--------------------------------三、有限元模型------------------------------四、计算结果与分析------------------------五、结论--------------------------------------六、优化设计及结果分析------------------七、致谢----------------------------------------八、参考文献----------------------------------一前言目前，在工程领域中应用最广泛的数值模拟方法是有限单元法, 它不但可以解决固体力学及结构分析方面的问题, 而且应用于传热学、流体力学、电磁学等领域, 其计算结果已成为各类工业产品设计和性能分析的可靠依据, 广泛应用于航空航天、机械制造、建筑设计、石油化工等领域。

有限元分析(Finite Element Analysis,FEA)是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。

利用简单而又相互作用的元素，即单元，就可以用有限数量的未知量去逼近无限未知量的真实系统。

有限元方法是一种应用十分广泛的数值分析方法，也是工程科学的重要工具，其重要性仅次于数学。

复杂的工程问题需要借助计算机得到满足一定精度要求的数值结果。

本次课设所采用的是CAE软件的ANSYS命令，它是目前国际上应用最广泛的有限元软件。

通过本次现代设计方法课程设计，学习有限元分析方法及ANSYS命令，了解并掌握利用CAE软件的ANSYS命令进行连杆，珩架，梁等的力学分析，将理论与实际工作结合，并最终达到能够独立对梁，杆等进行有限元内力分析。

本设计的研究对象是一简支梁。

二物理模型教程3：平面梁结构的内力计算问题阐述有一简支梁结构如图所示，其中，M=10KN.M，q=2KN/m，F=2KN。