大学物理4-4定轴转动的动能定理

刚体绕定轴转动的动能定理1. 引言刚体是指其内部各点之间的相对位置关系在运动过程中不会发生改变的物体。

刚体绕定轴转动是指刚体在固定轴线上做圆周运动的情况。

动能定理是物理学中的一条重要定理，描述了物体运动过程中动能的变化与外力做功之间的关系。

本文将对刚体绕定轴转动的动能定理进行全面详细、完整且深入的阐述。

2. 刚体绕定轴转动在刚体绕定轴转动的情况下，我们需要考虑刚体的转动惯量和角速度等因素。

转动惯量是描述刚体对转动运动抵抗程度的物理量，通常用符号I表示。

角速度是描述刚体旋转快慢程度的物理量，通常用符号ω表示。

根据牛顿第二定律和角动量守恒定律，我们可以得到刚体绕定轴转动时的基本方程：τ=Iα其中，τ表示作用于刚体上产生转矩（力矩）大小，α表示角加速度。

刚体绕定轴转动的运动规律与作用在刚体上的转矩和转动惯量有关。

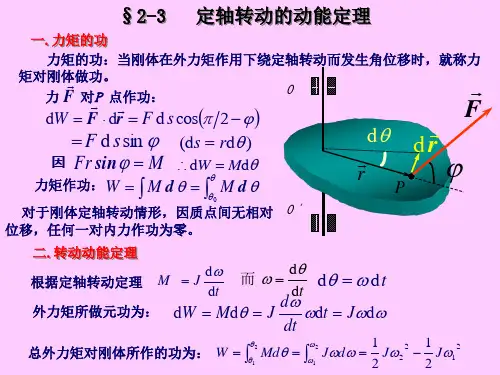
3. 动能定理的推导根据刚体绕定轴转动的基本方程，我们可以推导出刚体绕定轴转动的动能定理。

我们来考虑刚体上某一质点的动能T。

由于刚体上各质点都在绕着同一个轴旋转，因此它们具有相同的角速度ω。

设某一质点到轴心的距离为r，则该质点具有的线速度v为v=rω。

该质点的动能T′可以表示为：T′=12mv2=12m(rω)2=12mr2ω2其中，m表示质点的质量。

由于刚体是由众多质点组成的，因此整个刚体的动能T 可以表示为所有质点动能之和：T=∑Tni=1′i其中，n表示刚体上质点的总数。

根据牛顿第二定律和角动量守恒定律，我们知道刚体绕定轴转动时转动惯量I和角加速度α之间存在关系τ=Iα。

将该关系代入动能的表达式中，得到：T=12Iω2其中，ω表示整个刚体的角速度。

刚体绕定轴转动的动能可以表示为12Iω2。

这就是刚体绕定轴转动的动能定理。

4. 动能定理的物理意义刚体绕定轴转动的动能定理描述了刚体在转动过程中动能的变化与外力做功之间的关系。

根据动能定理，我们可以得出以下物理结论：1.外力对刚体做功会改变刚体的动能。

转动动能定理转动动能定理引言：在物理学中，旋转运动是一种非常重要的运动形式。

它广泛应用于机械、电子、化学等领域。

而转动动能定理则是研究旋转运动的重要定理之一。

一、定义1.1 转动惯量在物理学中，物体的转动惯量是描述物体对于旋转运动的惯性大小的物理量。

它表示了一个物体对于绕某个轴旋转时所表现出来的抵抗力大小。

1.2 角速度角速度是指一个物体绕某个轴线旋转时单位时间内所经过的角度。

它通常用符号ω表示，单位是弧度每秒（rad/s）。

1.3 转动角加速度转动角加速度是指一个物体绕某个轴线旋转时单位时间内角速度变化量，通常用符号α表示，单位是弧度每秒平方（rad/s²）。

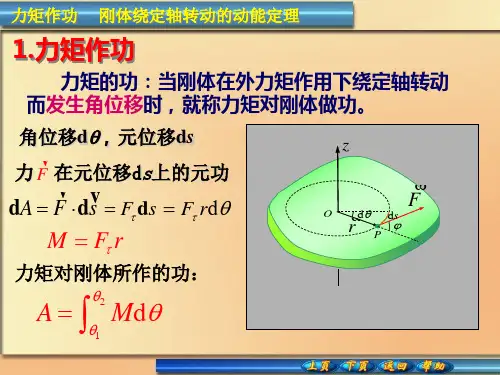
二、公式推导2.1 转动运动定律在刚体绕固定轴线做匀加速直线运动时，其加速度a与作用力F之间有如下关系：F=ma同样，在刚体绕固定轴线做匀加速圆周运动时，其加速度a与作用力F 之间也有如下关系：F=ma但是，由于旋转运动涉及到角度的概念，因此在刚体绕固定轴线做匀加速圆周运动时，我们需要引入一个新的物理量——转动惯量。

2.2 转动惯量的定义当一个物体绕某个轴线旋转时，它所表现出来的抵抗力大小与以下三个因素有关：1）物体质量的大小；2）轴线距离物体质心的远近；3）物体形状和密度分布情况。

因此，我们可以定义一个新的物理量——转动惯量I来描述这种抵抗力大小。

具体而言，当一个质量为m、距离轴线为r、转动惯量为I的物体绕某个轴线旋转时，它所表现出来的抵抗力大小可以表示为：τ=Iα其中τ表示物体所受到的扭矩（或者说力矩），α表示物体绕轴线旋转时所表现出来的角加速度。

2.3 转动动能定理在刚体绕固定轴线做匀加速圆周运动时，其机械能守恒，即E=K+U=常数其中E表示机械能，K表示动能，U表示势能。

我们可以将刚体的机械能分解为平动动能和转动动能两部分：E=Kp+Kr+U其中Kp表示平动动能，Kr表示转动动能。

根据定义可知，Kp=½mv²Kr=½Iω²因此，E=½mv²+½Iω²+U我们将上式两边同时对时间求导数，得到：dE/dt=mvdv/dt+Iωdω/dt+dU/dt由于匀加速圆周运动中v、ω和r之间有如下关系：v=rω因此，dv/dt=r dω/dt代入上式可得：dE/dt=mvr dω/dt+I dω/dt+dU/dt根据牛顿第二定律可以得到：F=mvr dω/dt=τ因此，dE/dt=τdθ/dt+dU/dθ dθ/dt=d(τθ)/dt+dU/dθ dθ/dt=d(τθ)/dt+dU/dt=dWext/dt其中Wext表示外力所做的功。

转动动能定理引言转动动能定理是物理学中的一个重要定理，它描述了刚体绕固定轴旋转时转动动能的变化规律。

本文将对转动动能定理进行全面、详细、完整和深入的探讨。

转动动能定理的定义转动动能定理是指刚体绕固定轴旋转时，刚体的转动动能(简称为转动动能)随着时间的变化而改变的规律。

转动动能可以通过以下公式计算得到：ΔK=12Iω2其中，ΔK表示转动动能的变化量，I表示物体的转动惯量，ω表示物体的角速度。

转动动能定理的推导转动动能定理的推导过程如下：1.假设刚体在t1时刻的转动动能为K1，在t2时刻的转动动能为K2。

2.刚体在t1时刻的角速度为ω1，在t2时刻的角速度为ω2。

3.转动动能的变化量可以表示为ΔK=K2−K1。

4.根据定义可以得到K1=12I1ω12，K2=12I2ω22，其中I1和I2分别表示t1和t2时刻刚体的转动惯量。

5.将K1和K2代入ΔK=K2−K1中，得到ΔK=12I2ω22−12I1ω12。

6.化简上式，得到ΔK=12(I2ω22−I1ω12)。

7.根据角动量守恒定理，可以得到I1ω1=I2ω2。

8.将I1ω1代入上式，得到ΔK=12I1ω1(I2ω2I1ω1−1)=12I1ω1(I2I1−1)=12Iω2，其中I=I1。

因此，转动动能定理可以推导得到ΔK=12Iω2。

转动动能定理的应用转动动能定理在物体的转动运动中有广泛的应用。

下面介绍几个应用实例：应用实例1：旋转物体的动能变化当一个物体绕固定轴旋转时，它的转动动能会随着角速度的变化而改变。

转动动能定理可以帮助我们计算物体在不同角速度下的转动动能变化量，从而对物体的旋转运动进行分析。

应用实例2：转子动能的转换转动动能定理可以用来研究转子动能的转换。

例如，发电机中的转子通过机械能转换成电能，由于转子的转动惯量不变，转动动能定理可以帮助我们计算转子在转动过程中的动能转换效率。

应用实例3：转动惯量的测量转动动能定理可以通过测量物体的角速度和转动动能的变化量，间接计算出物体的转动惯量。