当前位置：文档之家 › 自动控制原理(胡寿松_)第四章根轨迹法ppt

自动控制原理(胡寿松_)第四章根轨迹法ppt

  • 格式：ppt
  • 大小：3.84 MB
  • 文档页数：81

下载文档原格式

  / 81

合集下载

自动控制原理胡寿松 第4章

自动控制原理胡寿松 第4章

s 令s a＝s z1 s z2 s p1 s p2
代入标准形式：
s zm
s pn
nm
s a
K *
(n m) s a (2l 1)
(2l 1) s a (l 0,1, 2,..., n m 1) ( n m)
(s z )
i 1 n i
m
K
*
sm
(s p )
j 1 j
1
sm
zm z1 z2 (1 )(1 ) (1 ) s s s pm p1 p2 (1 )(1 ) (1 )( s pm 1 ) s s s 1 * 0( K * ) K
180 2l 1 a 60,180,300(60) nm
渐近线与实轴的交点坐标为：
a
p z
i 1 i j 1
n
m
j
nm

0 (1) (2) 0 1 30
• （4）实轴上的根轨迹： • 在s平面实轴上[0，-1]和[-，-2]线段上存在根轨 迹。
渐近线与实轴正方向夹角：
( 2l 1) a nm
l 0,1,2,, n m 1
规则5: 实轴上的根轨迹
在实轴上任取一点，若在其右侧的开环实极点与开环实零点 的总数为奇数，则该点所在线段构成实轴上的根轨迹 j
z1 p2 z2
(s z1 ) (s z2 ) (s p1 ) (s p2 ) (2l 1)
规则4:根轨迹的渐近线
s a
n j 1 m
nm
snm (n m) a snm1

自动控制原理第四章根轨迹课件

自动控制原理第四章根轨迹课件

幅值条件
s z
i 1
Hale Waihona Puke mi s p
j 1
n

j
1 Kg
Kg=0
(s p ) 0
j 1 j
n
根轨迹起始于开环极点
Kg=∞
(s z ) 0
i 1 i
m
根轨迹终止于开环零点
根轨迹分支数 • n阶系统的根轨迹有n条分支
s z
i 1
m
i
s p
j 1
jω
-p3
ⅹ
j4
K1 G( s) H ( s) s( s 4)( s 2 4s 20)
规则1、2、3、4 根轨迹对称于实轴， 有四条根轨迹分支，分别起 始于极点0,－4和－2±j4，终止 于无限远零点。 实轴上0~－4区段为根轨迹. 相角条件 -p3、-p4的连接线为 根轨迹
-p2
s1 z1 ( z1 p1 )(z1 p2 )
s2 z1 ( z1 p1 )( z1 p2 )
7.根轨迹的出射角和入射角(1)

出射角：根轨迹离开复数极点处的切线方向与实轴 正方向的夹角 入射角：而进入开环复数零点处的切线方向与实轴 正方向的夹角
7.根轨迹的出射角和入射角(2)
i 1 i 1
每对共轭复数极点所提供的相角 之和为360°； s1右边所有位于实轴上的每一个极 点或零点所提供的相角为180°；
ⅹ ⅹ
-p3 s2
-p4
jω
-θ -z1
○
ⅹ
-p2 s1
ⅹ
-p1
σ
s1左边所有位于实轴上的每一个极
点或零点所提供的相角为0°。

自动控制原理课件 第四章根轨迹分析法

自动控制原理课件 第四章根轨迹分析法

G k(s)
, 例 4 6 s1 s 0 P ' ) 0.3333 (s 0 s(s 1)(s 2)
2
Kg
P(s 0 )
已 求 : P(s) 3s 6s 2, P(-1) -1 0,P(0) 2 0,故 实 轴 [ 1,0]段 必 有 分 离 点 . 另 在 [ 1,0]区 段 : P (s) 6s 6 0,
§4-2 绘制根轨迹的基本法则 (一、二、三、四)
CASE.SCUT
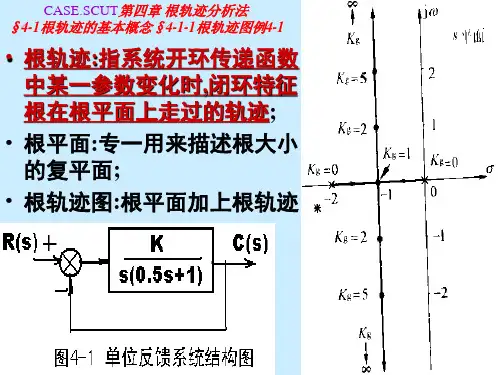
五.实轴上的根轨迹:实轴根轨迹区 θ 180 (2k 1) , 段其右方实数极点个数、实数零 nm n m 点个数总和应为奇数； ( p j ) ( zi ) 六.根轨迹的渐近线: j 1 i 1 当n＞m,Kg→∞时,有n-m条根轨迹 σ a nm 分支沿着与正实轴夾角θ, 截距为式中k 0,1,2, ,n m 1 σa的一组渐近线趋于无穷远处：
2.幅值条件 求K g
: s 2的K g
(s p )
j
n
(s z )
i i1
j1 m
s 2 p1 s 2 p 2 0.5 j 0 0.5 j 1 1.118 1.118 1.25
利用MATLAB进行控制 系统分析 四绘制根轨迹图 例4-27.exp412140.m num=1;den=[1 5 8 6 0];
s平面上满足相角条件 方程的一切点, 都是 对应不同K g 值的闭环特征根, 即根轨迹, 所以 相角条件是确定根轨迹的充要条件。
•
CASE.SCUT §4-1-4幅值条件方程和相角条件方程的应用 例4-2,例4-3
1.相角条件 求根轨迹

自动控制原理简明版第4章根轨迹法课件35页PPT

自动控制原理简明版第4章根轨迹法课件35页PPT

令 dK 1 0
ds
s2 2s2 K1 s2 s24s20
求得 s10.58(舍6去)
s23.414
7
(2)
m
1
n
1
i1 szi j1 spi
因为
P (s ) Q (s ) P (s ) Q (s ) 0
即
P(s) Q(s) P(s) Q(s)
d
d
[lnP(s)] [ln Q(s)]Βιβλιοθήκη dsIm a倾角。
s1
pa
在根轨迹曲线上取试验点s1，与
复极点-pa的距离为 。 当 0时，可近似地 认为s1在切线上，切线
3 p3
1 z1
1
0 p1
Re
的倾角就等于复极点的
p2
出射角。
2
1 (a 1 9 0 3 ) 1 ( 8 2 k 0 1 )
所以 a 的出射角:
a18 (2 0 k1)1(190 3)
d[G1(s)H1(s)]0 或
ds
d[G(s)H(s)]0 ds
以上分析没有考虑 K1 0 (且为实数)的约束条件，所以只有满 足 K1 0的这些解，才是真正的分离点（或会合点）。
2
例: 设系统
R(s)
K1(s 2) s2 2s 2
C(s)
试求该系统根轨迹在实轴上的会合点。
解：系统的开环传递函数：
9
Im
复杂情况用试探法。
在-2-3之间存在一个分离点。
3
2 1
0 Re
1 1 1 1 s1 s s2 s3
s2.4
1 ? 1 1 1
2 .412 .4 2 .42 2 .43
0.715 1.247

自动控制原理第四章 根轨迹法PPT

自动控制原理第四章 根轨迹法PPT

第二节 绘制根轨迹的基本方法
四、根轨迹的渐近线
趋于无穷远处的根轨迹的渐近线 由下式确定 渐近线与实轴的夹角： +(2k+1)π K= 0,1,2,3 θ= n-m 渐近线与实轴的交点： σ=
pj zi ∑ ∑ i =1 j=1 n-m
n m
第二节 绘制根轨迹的基本方法
例 已知系统的开环传递函数，试确定 系统的根轨迹图。 Kr G(s)H(s)= s(s+1)(s+2) 渐近线与实轴的夹角 : jω 解： 1）开环零、极点： +(2k+1)π O+ O p =-3 p =0 p =-2 + 180 60 = , θ= 1 3 2 3 p2 60 p p3 2 ）实轴上的根轨迹段： 渐近线与实轴的交点 : 0 1 -1 -2 p ~ p1~p-1-2 3 -1 = σ= 2 3 n-m= 3 3 4）根轨迹的渐近线： ）系统的根轨迹
‫ב‬-
‫ב‬
‫ב‬
‫ב‬
第二节 绘制根轨迹的基本方法
2） <T (1)开环零、极点分布 1 1 p1=0 p2=T z1= (2) 实轴上根轨迹段 p1~p2 z1~-∞ ‫ב‬ ‫ב‬
jω
z1
1 ‫ב‬p2 1 -T p
1 0
(3)系统的根轨迹
p1和p2为根轨迹 的起点 Z1和-∞为根轨迹 的终点
第二节 绘制根轨迹的基本方法
五、根轨迹的分离点和会合点
闭环特征方程的根在 S 平面上的重合 闭环特征方程式： K B ( s)+A(s)=0 r 注意：只有位于根轨迹上的重根才是 点称为根轨迹的分离点或会合点。 重根必须同时满足以下两式 分离点或会合点。 一般将根轨迹 KrB'(s)+A'(s)=0 KrB(s)+ A(s)=0 若不在根轨迹上的分离点或会 离开实轴进入复平面的点称为分离点 即 A'(s) 合点应该舍去。 dB ( s ) dA ( s ) 离开复平面进入实轴的点称为会合点 Kr =K + =0 B'(s) ds ds r 设系统的开环传递函数为 解上式得 Kr B(s) G H((s A (s)B' s)= )=A' A((s s))B(s)

《自动控制原理》 胡寿松 自动控制原理简明教程(专业教学)

《自动控制原理》 胡寿松 自动控制原理简明教程(专业教学)

i 1
j1, j x
= 180 + 1 + 2 + 3 1 2 3
=180 + 56.5 + 19 + 59 技1术0教8育.5 37 90 = 79 23
n
m
zx 180 (zx p j ) (zx zi )
j 1
i1,i x
=180 117 90 + 153 + 63.5 + 119 + 121 =149.5
1）劳斯判据法 应用劳斯判据求出系统处于稳定边界的临界值K’， 由K’值求出相应的ω值。
2）代数法 把 s j 代入特征方程 1 G( j)H ( j) 0
1 1 1 0 d 0 d 1 d 5
3d 2 + 12d + 5 = 0
d1 = 0.472 d2 = 3.53(不在根轨迹上，
舍去，也可代入幅值方程看Kg>0否？) 分 离点上根轨迹的分离角为±90°。
d1 = 0.472
d 180 / k
如果方程的阶次高时，可用试技探术教法育 确定分离点。
j1, ji
p j zi
j 1
;
k 0, 1, 2,
z1
(p1－z1) ( p1－p2 )
( p1－p3 )
p3
0
p2
Im
A
a
s1
pa
3 p3
1 z1
1
0 p1
Re
p2 2
p1 180 (2k 1) ( p1 z1)
(( p1 p2 ) ( p1 p3))
例：起始角 技a 术教育180 (2k 1) 1 (1 2 232)
实轴上的交点 n

自动控制原理第四章根轨迹法(管理PPT)


根轨迹法的优化建议
结合其他方法
将根轨迹法与其他分析方 法（如频率响应法）相结 合，以获得更全面的系统 性能分析。
ቤተ መጻሕፍቲ ባይዱ开发软件工具
开发专门用于根轨迹分析 的软件工具，以提高分析 的效率和准确性。
加强实践应用
在实际工程中加强根轨迹 法的应用，通过实践不断 优化和完善该方法。
05
CATALOGUE
根轨迹法与其他控制方法的比较
根轨迹分析的实例
假设一个开环传递函数为 G(s)H(s) = (s+1)(s+2)/(s^2+2s+5)，对其进行 根轨迹分析。
分析根轨迹图，确定系统的稳定性、 动态性能和系统参数的影响。
根据开环传递函数，绘制出根轨迹图 ，并标注出系统的极点和零点。
根据根轨迹图进行系统设计和优化， 例如调整开环传递函数的增益参数， 以改善系统的性能。
对于非线性系统，根轨迹法可能无法给出准确的描述和分析。
04
CATALOGUE
根轨迹法的改进与优化
根轨迹法的局限性与挑战
参数敏感性
根轨迹法对系统参数的微小变化非常敏感，可能导致根轨迹的剧 烈变化，影响系统的稳定性。
无法处理非线性系统
根轨迹法主要适用于线性系统，对于非线性系统的分析存在局限性 。
计算复杂度较高
和设计。
对于具有特定性能指标要求的系统，如 快速响应、低超调量等，可以根据系统 特性和性能要求选择适合的控制方法，
如状态反馈控制器等。
06
CATALOGUE
根轨迹法的实际应用案例
根轨迹法在工业控制系统中的应用
根轨迹法在工业控制系统中广泛应用于系统的分析和设计。通过绘制根轨迹图，可以直观地 了解系统性能的变化，如稳定性、响应速度和超调量等。

自动控制原理(胡寿松版)课件

自动控制原理(胡寿松版) 课件
自动控制原理是关于自动化生产中的传感器及控制器的课程。系统性、专业 性、实用性是其特点。学好自动控制原理，掌握自动化生产的核心技术，是 提高现代工业水平的重要途径之一。
什么是自动控制原理？
定义
自动控制原理是指用传感器将被控对象（如温 度、压力等）转换为电信号，再由控制电路进 行比较，控制执行机构输出控制量，以在实现 目标的同时，对被控对象进行自动调节的一种 学科。
2
基于控制方式分类
例如PID、ON/OFF等。
3
基于功能分类
例如开关型、调节型等。
控制系统的数学模型
模型
数学模型是用数学语言来描述控制系统的行为 规律所构建的数学关系式。
应用
控制系统的数学模型是系统分析、系统设计及 系统性能评价的重要依据。
总结及提问
总结
自控原理是自动控制专业中的一门基础课。 通过这门课的学习，我们不仅可以掌握自动 控制的核心技术，还能不断提高工业的自动 化水平。
自动控制系统的特点
1 自动性
实现机器的智能程度，减少人工干预，提高工作效率。
2 高精度
自动控制系统的控制对象精度要求很高，智能程度决定系统控制精度。
3 高可靠性
自动控制系统由多个组件组成，如一单个组件出现问题不会对系统的正常工作产生影响。
自动控制系统的分类
1
基于传感器类别分类
例如压力、温度、流量等。
提问
有没有什么实例可以更好地解释基于控制方 式的自动控制系统的分类？
应用
自动控制原理的应用非常广泛，例如在汽车制 造、机床、钢铁、化工等工业中都有着非常重 要的地位。
自动控制系统的基本组成
传感器
将被控对象的信息（如温度、压力等）转 化为电信号。

自动控制原理_胡寿松_第四章ppt


f
l
(s zi ) (s z j )
G(s)H(s) K*
i 1 q
j 1 h
(s pi ) (s pj )
i 1
j 1
K*

K
* G
K
* H
称为开环系统根轨迹增益。
14
3. 闭环零、极点与 开环零、极点之间的关系
对于有 m 个开环零点和 n 个开环极点的系统， 必有 f+l=m 和 q+h=n 。则 ：
bm1s bm an1s an
当 K * , s 时有 G(s)H(s) 近似为：
K* G(s)H(s) snm (a1 b1)snm1
32
由根轨迹方程： G(s)H(s) 1 得：
snm (1 a1 b1 ) K *
或
s(1
2
第四章 线性系统的根轨迹法
4-1 根轨迹法的基本概念
1948年，W·R·伊凡思在他的一篇论文 “控制系统的图解分析”中提出了在复平面上 由系统的开环传递函数求取闭环特征根的方法， 这就是根轨迹法。当开环增益或其它参数改变 时，其全部数值对应的闭环极点均可在根轨迹 图上简便地确定，因此在工程实践中得到了广 泛的应用。
i 1
j 1
nm
31
证明：渐近线可以理解为|s|很大时的根轨迹，故其 必对称于实轴。
m
由于：G(s)H(s) K*
j 1 n
(s (s
zj) pi )

K*
sm sn
b1sm1 a1sn1

i 1
n
式中： a1 pi i 1
m
b1 z j j 1

自动控制原理课件第四章根轨迹法ppt

2013-8-11 自动控制原理 16
nm s
Kg
sz
i
在实际系统通常是 n m ，则还有 (n m) 条根轨迹终止于s平 面的无穷远处，这意味着在无穷远处有 (n m) 个无限远（无穷） 零点。
Kg 0
nm
Kg 0
nm
0
Kg
有两个无穷远处的终点
_
K s ( s 1)
C(s)
特征根：S
s sK 0
1, 2

1 1 4K 2
K:0 ~ ∞
1 2
．．．．．．
K
0 0
1 8
1 4

0.5 j
s1
0.146 0.5 0.5 j 0.5
．．．．．．
s2 1 0.854 0.5 0.5 j 0.5
第4章 根轨迹法
4.1 根轨迹法的概念 4.2 根轨迹方程 4.3 常规根轨迹及其绘制 4.4 广义根轨迹及其绘制 4.5 按根轨迹分析控制系统 4.6 用MATLAB绘制根轨迹

2013-8-11
自动控制原理
1
4.1
根轨迹法的概念
R(s)
根轨迹的概念
K ( s) 2 闭环传递函数： s sK 特征方程： 2
2013-8-11
自动控制原理
18
规则2：根轨迹的分支数、连续性和对称性
根轨迹的分支数即根轨迹的条数。既然根轨迹是描述闭环 系统特征方程的根（即闭环极点）在S平面上的分布，那么，根 轨迹的分支数就应等于系统特征方程的阶数。 根轨迹方程： ( s p ) K ( s z ) 0 系统开环根轨迹增益(实变量）与复变量s有一一对应的关 系，当 K g 由零到无穷大连续变化时，描述系统特征方程根的复 变量s在平面上的变化也是连续的，因此，根轨迹是n条连续的 曲线。 由于实际的物理系统的参数都是实数，若它的特征方程有复 数根，一定是对称于实轴的共轭复根，因此，根轨迹总是对称 于实轴的。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

m
G(s)H(s)
Kg
M(s) N(s)
Kg (s zi )
i 1 n
(s pj)
成零极点 表达式
j 1
式中Kg为系统的根迹增益， zi 为系统的开环零点，pj为系统的开
环极点。上述方程又可写为：
m
(s zi )
i 1
1
n
(s pj )
Kg
j1
“-”号，对应负反馈， “+”号对应正反馈。 由于满足上式的任何s都是系统的闭环极点，所以当系统的结构 参数，如Kg在某一范围内连续变化时，由上式制约的s在s平面上描
上式说明Kg= 0时，闭环特征方程的根就是开环极点。
将特征方程改写为：
1 n
m
Kg
(s pj ) (s zi ) 0
j 1
i 1
当 Kg 时，有
s = zi
( i =1, 2, … , m)
所以根轨迹必终止于开环零点。
在实际系统中，开环传函中 m n ，有m 条根轨迹终 点为开环零点处，另有nm条根轨迹的终点将在无穷远处， 可以认为有nm 个无穷远处的开环零点。
点，称为根轨迹的分离点(会合点)。
Kg=0 p1
j
j1
Kg A
Kg z1
0
p2 Kg=0
分离点的性质：
1）分离点是系统闭环重根； 2）由于根轨迹是对称的，所以分离点或位于实轴上， 或以共轭形式成对出现在复平面上； 3）实轴上相邻两个开环零（极）点之间（其中之一可 为无穷零（极）点）若为根轨迹，则必有一个分离点；
Gs Kg
s(s 2)
s1,2 1 1 K g
闭环特征根s1，s2是Kg函数， 随着Kg的改变而变化。
(1) Kg= 0：s1 = 0,s2 = 2,是根迹的起点(开环极点),用“”表
示。
(2) 0
<
Kg<
1
：s1
，s2
均是
j
Kg
负实数。 Kg s1 ，s2 。
s1从坐标原点开始沿负实轴 向左移动； s2从（2，j0） 点开始沿负实轴向右移动。
法则3 根轨迹的条数
n阶系统，其闭环特征方程有n个根。当Kg 从0连续
变化时，n个根将绘出有n条轨迹分支。因此根轨迹的条 数或分支数等于其闭环特征根的个数，即系统的阶数。
K j
K= 0
K= 0
0
K Kg
j Kg
0
Kg
j
0
j
0
j
-21
j
1
0
法则4 根轨迹的起点和终点
根轨迹起始于系统开环极点， 终止于系统开环零点。
（3）各分支的终点(Kg )或为开环零点处或为无限点；
（4）重根点，称为分离点或汇合点。
根轨迹与系统性能
j
Kg
1. 稳定性 当Kg从0 时，图中
的根轨迹不会越过虚轴进入
Kg= 0
2
Kg=1 Kg= 0
1 0
s右半平面，因此二阶系统
对所有的Kg值都是稳定的。
Kg
如果高阶系统的根轨迹 有可能进入s 右半平面，此 时根迹与虚轴交点处的Kg 值， 成为临界开环增益。
定义：当系统开环传递函数中某一参数从0时， 闭环系统特征根在s 平面上的变化轨迹，就称作系统根 轨迹。一般取开环传递系数（根轨迹增益Kg）作为可 变参数。
举例说明：已知系统的结构图，分析0 < K < ，闭环特 征根在s平面上的移动路径及其特征。
R(s)
+﹣
K
C(s)
s(0.5s+1)
解：系统的开环传递函数为
]0 N(s)
法二：公式法
设分离点的坐标为 d，则d 满足如下公式：
m 1
n1
i1 d zi j1 d p j
牢记！
式中，z i 、p j 是系统的有限开环零点和开环极点。
证明：根轨迹在s 平面上相遇，说明闭环特征方程有重根出现，
设s = d 处为分离点。
D(s) 0且 dD(s) 0 ds
的Kg值时，才使用幅值条件。
下面看看怎样按上式表示的幅值条件和幅角条件绘制
系统的闭环根轨迹图。
j
已知负反馈系统开环零极点 分布如图示。
2 p2
在s平面找一点s1 ，
1
画出各开环零、极点到 z1
s1
1
p1 0
s1点的向量。
3
检验s1是否满足幅角条件： p3
(s1 z1) [(s1 p1) + (s1 p2) + (s1 p3)]
n
m
(s p j ) K g (s zi ) 0
j 1
i 1
d n
dm
ds
(s
j1
pj ) K g ds
(s zi ) 0
i 1
d n
(s ds j1
n
pj)
dm
ds i1
m
(s zi )
(s pj ) (s zi )
j 1
i 1
(lnV ) V V
n
m
第四章 根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制系统根轨迹的基本法则 §4-3 控制系统的根轨迹分析方法
学习指导与小结
4-1 根轨迹法的基本概念 4.1.1 根轨迹
反馈控制系统的性质取决于闭环传递函数。只要求解
出闭环系统的特征根，系统响应的变化规律就知道了。但
是对于3阶以上的系统求根比较困难。如果系统中有一个可
d ln (s pj ) d ln (s zi )
j 1
i 1
ds
ds
m
1
n
1
i1 s zi j1 s p j
n d ln(s p j ) m d ln(s zi )
j 1
ds
i 1
研究下图所示反馈控制系统的一般结构。
R(s)
+±
C(s) G(s)
H(s)
系统的闭环传递函数为
(s)
C(s) R(s)
1
G(s) G(s)H(s)
该系统的闭环特征方程为: D(s) = 1 ± G(s)H(s) = 0 或 G(s)H(s) = ±1
若将系统的开环传递函数G(s)H(s)写成如下形式： 一定要写
Kg= 0
2
Kg=1 Kg= 0
1 0
(3) Kg= 1： s1 = s2 = 1，重根。
(4) Kg >1： s1,2 1 j K g 1
Kg
根据2阶系统根轨迹的特点，可以推得n阶系统，会有如下的 结论：
（1）n阶系统有n个根，根轨迹有n条分支 ；
（2）每条分支的起点 (Kg= 0)位于开环极点处；
2
其右边开环实数零、极点
个数之和为奇数，则该区 域必是根轨迹。
“奇是偶不是”
1 =0
z1
s1
证明：设零、极点分
布如图示：
p3
在实轴上取一测试点s1 。
p2
1
p1 0
3
由图可见，复数共轭极点到实轴s1 点的向量幅角和为 2，复数共轭零点如此。因此在确定实轴上的根轨迹时，
可以不考虑复数零、极点的影响。
s1 点左边开环实数零、极点到s1 点的向量幅角均为零， 也不影响实轴上根轨迹的幅角条件。
法则5 根轨迹的渐近线
根据法则4，当开环传递函数中m < n 时，将有n m 条
根轨迹分支沿着与实轴夹角为a ，交点为a 的一组渐近
线趋于无穷远处，且有：
a
(2k 1)
nm
(k = 0,1, … , n m 1)
n
m
pj zi
a
j1
i 1
nm
法则6 实轴上的根轨迹分布
j
实轴上的某一区域，若
j
0
4）在一个开环零点和一个开环极点之间若有根轨迹，该段无 分离点或分离点成对出现。
分离点上，根轨迹的切线与正实轴的夹角称为根轨迹的分离角，
用下式计算： d 180 / k k为分离点处根轨迹的分支数。
确定分离点位置的方法（均需验证）：
法一：重根法（极值法）
dD(s) d
M(s)
ds
ds [1 K g
实轴上的交点 n
m
a
pj zi
j 1
i 1
nm
0 1 5 2 30
G(s)H(s)
Kg
s(s 1)( s 5)
j
三条渐近线与正实轴上间的夹角：
a
2k 1
3
，， 5
3
3
k 0，1，2
60
-2
0
实轴上的根轨迹分布在(0，1)和 (5， )的实轴段上。
法则7 根轨迹分离点和会合点 两条或两条以上的根轨迹在s平面上相遇后立即分开的
根轨迹上Kg= 0的点为起点，Kg时的点为终点。
m
证明：
G( s) H ( s)
Kg
M(s) N(s)
Kg (s zi )
i s) = 0
n
m
(s p j ) K g (s zi ) 0
j 1
i 1
当 Kg= 0 时，有
s = pj
( j =1, 2, … , n)
系统为过阻尼系统，单位阶跃响应为非周期过程。
当 Kg = 1时，闭环两 个实极点重合，系统为临 界阻尼系统，单位阶跃响 应为非周期过程。
当Kg > 1时，闭环极 点为一对共轭复数极点， 系统为欠阻尼系统，单位 阶跃响应为阻尼振荡过程。
Kg= 0
2
j
Kg
Kg=1 Kg= 0