07应力状态习题

《金属塑性变形理论》前言前言《金属塑性变形理论》是关于金属塑性加工学科的基础理论课，也是金属材料工程、材料成型及控制工程专业大学本科生的主干课程。

《金属塑性变形理论》总学时为80，内容上分为两部分，即“塑性加工力学”（44学时）和“塑性加工金属学”（36学时）。

为使学生能够学好本课，以奠定扎实的理论基础，提高分析问题和解决问题的能力，编者集20余年的教学经验特编制本习题集，一方面作为学生在学习本课程时的辅导材料，供课下消化课堂内容时使用，另一方面也可供任课教师在授课时参考，此外对报考研究生的学生还具有指导复习的作用。

本“习题集”在编写时，充分考虑了学科内容的系统性、学生学习的连贯性以及与教材顺序的一致性。

该“习题集”中具有前后关联的一个个题目，带有由浅入深的启发性，能够引导学生将所学的知识不断深化。

教师也可根据教学进程从中选题，作为课外作业指导学生进行练习。

所有这些都会有助于学生理解和消化课堂上所学习的内容，从而提高课下的学习效率。

编者2005年10月第一部分：塑性加工力学第一章 应力状态分析1． 金属塑性加工中的外力有哪几种？其意义如何？2． 为什么应力分量的表达需用双下标？每个下标都表示何物理意义？ 3． 已知应力状态如图1-1所示，写出应力分量，并以张量形式表示。

4． 已知应力状态的六个分量7-=x σ，4-=xy τ，0=y σ，4=yz τ，8-=zx τ，15-=z σ(MPa)，画出应力状态图，写出应力张量。

5． 作出单向拉伸、单向压缩、三向等值压缩、平面应力、平面应变、纯剪切应力状态的应力Mehr 圆。

6． 已知应力状态如图1-2所示，当斜面法线方向与三个坐标轴夹角余弦31===n m l 时，求该斜面上的全应力S 、全应力在坐标轴上的分量x S 、y S 、z S 及斜面上的法线应力n σ和切应力n τ。

7． 将下列应力状态用单元体表示。

（1）⎪⎪⎪⎭⎫ ⎝⎛---=6040504050705070100σT N/mm 2 （用直角坐标系）（2）图1-1图1-2⎪⎪⎪⎭⎫ ⎝⎛-=2007090701000900120σT N/mm 2 （用柱面坐标系）8． 单元体上各面所作用的应力分量如图1-3所示。

应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示，则三者间的关系为（ ）。

A ．完全等价B ．完全不等价C ．图(b )、图(c )等价D ．图(a )、图(c )等价题1图2. 已知应力情况如图所示，则图示斜截面上的应力为（ ）。

（应力单位为 MPa)。

A ．70-=ασ，30-=ατB ．0=ασ，30=ατC ．70-=ασ，30=ατD ．0=ασ，30-=ατ3. 在纯剪切应力状态中，其余任意两相互垂直截面上的 正应力，必定是（ ）。

A ．均为正值B ．一为正值一为负值C ．均为负值 题2图D ．均为零值4. 单元体的应力状态如图所示，由x 轴至1σ方向的夹角为（ ）。

A ．︒5.13 B ．︒-5.76 C ．︒5.76 D ．︒-5.13题4图 题5图5. 单元体的应力状态如图所示，则主应力1σ、2σ分别为（ ）。

(应力单位MPa). -33-A ．901=σ，102-=σB ．1001=σ，102-=σC ．901=σ，02=σD ．1001=σ，02=σ 6. 如图6所示单元体最大剪应力m ax τ为（ ）。

A ．100 MPaB ．50 MPaC ．25 MPaD ．0题6图 题7图7. 单元体如图所示，关于其主应力有下列四种答案，正确的是（ ）。

A ．1σ＞2σ，03=σ B ．3σ＜2σ＜0，03=σ01=σ C ．1σ＞0，2σ= 0，3σ＜0，1σ＜3σ D ．1σ＞0，2σ= 0，3σ＜0，1σ＞3σ8. 已知应力圆如图7-22所示，图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力，则与应力圆所对应的单元体为( )。

A ．图(a )B ．图(b )C ．图(c )D ．图(d )题8图9. 在图示四种应力状态中，其应力圆具有相同的圆心和相同的半径是（ ）。

-34-题9图A ．图(a )、图(d )B ．图(b )、图(c )C ．图(a )、图(b )、图(c ) 、图(d )D ．图(a )、图(d )、图(b )、图(c )10. 如图所示，较大体积的钢块上开有一贯穿的槽，槽内嵌入一铝质立方体，铝块受到均布压力P 作用，假设钢块不变形，铝块处于（ ）。

第6章 应力状态分析一、选择题1、对于图示各点应力状态，属于单向应力状态的是（A ）。

（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点 。

2、在平面应力状态下，对于任意两斜截面上的正应力αβσσ=成立的充分必要条件，有下列四种答案，正确答案是（ B ）。

（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。

3、已知单元体AB 、BC 面上只作用有切应力τ，现关于AC 面上应力有下列四种答案，正确答案是（ C ）。

（A ）AC AC /2,0ττσ==； （B）AC AC /2,/2ττσ=； （C）AC AC /2,/2ττσ==；（D）AC AC /2,/2ττσ=-。

4、矩形截面简支梁受力如图（a ）所示，横截面上各点的应力状态如图（b ）所示。

关于它们的正确性，现有四种答案，正确答案是（ D ）。

（A ）点1、2的应力状态是正确的；（B ）点2、3的应力状态是正确的； （C ）点3、4的应力状态是正确的；（D ）点1、5的应力状态是正确的。

5、对于图示三种应力状态（a ）、（b ）、（c ）之间的关系，有下列四种答案，正确答案是（ D ）。

（A ）三种应力状态均相同；（B ）三种应力状态均不同； （C ）（b ）和（c ）相同； （D ）（a ）和（c ）相同；6、关于图示主应力单元体的最大切应力作用面有下列四种答案，正确答案是（ B ）。

解答：max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围，有下列四种答案，正确答案是（ C ）。

（A ）脆性材料；（B ）塑性材料；（C ）材料为各向同性，且处于线弹性范围内；（D ）任何材料； 8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适用于（ C ）。

（A ）任何材料在任何变形阶级； （B ）各向同性材料在任何变形阶级； （C ）各向同性材料应力在比例极限范围内；（D ）任何材料在弹性变形范围内。

材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的力。

2-2图示矩形截面杆，横截面上正应力沿截面高度线性分布，截面顶边各点处的正应力均为MPa100max=σ，底边各点处的正应力均为零。

杆件横截面上存在何种力分量，并确定其大小〔C 点为截面形心〕。

2-3 试指出图示各单元体表示哪种应力状态。

2-4 应力状态如下图〔应力单位为MPa〕，试用解析法计算图中指定截面的应力。

2-5 试作应力圆来确定习题2-4图中指定截面的应力。

2-6应力状态如下图〔应力单位为MPa 〕，试用解析法求：〔1〕主应力及主方向；〔2〕主切应力及主切平面；〔3〕最大切应力。

2-7 应力状态如习题2-6图所示，试作应力圆来确定：〔1〕主应力及主方向； 〔2〕主切应力及主切平面；〔3〕最大切应力。

2-8构件某点处的应力状态为两种应力状态的叠加结果，试求叠加后所得 应力状态的主应力、主切应力。

2-9图示双向拉应力状态，σσσ==y x 。

试证明任一斜截面上的正应力均等于σ，而切应力为零。

2-10K 点处为二向应力状态，过K 点两个截面上的应力如下图〔应力单位为MPa 〕。

试分别用解析法与图解法确定该点的主应力。

2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。

试确定未知的应力分量y y x xy '''σττ、、的大小与方向。

2-12 图示受力板件，试证明尖角A 处各截面的正应力与切应力均为零。

2-13应力状态如下图〔单位为MPa 〕，试求其主应力及第一、第二、第三不变量321I I I 、、。

2-14应力状态如下图〔单位为MPa 〕，试画三向应力圆，并求主应力、最大正应力与最大切应力。

第3章3-1某点的位移分量u = A ， v = Bx +Cy +Dz ， w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。

A 、B 、C 、D 、E 、F 、G 、I 、J 、K 均为常数，求该点处的应变分量。

应力状态和强度理论一、判断题1.若单元体某一截面上的剪应力为零，则该截面称为主平面。

（）2.主平面上的剪应力称为主应力。

（）3.当单元体上只有一个主应力不为零时，称作二向应力状态。

（）5.图2所示单元体最大剪应力为25Mpa。

（）6.图3所示单元体为单向应力状态。

（）图2图3图47. 向应力状态如图4所示，其最大主应力σ1=3σ（）。

8. 任一单元体，在最大正应力作用面上，剪应力为零。

（）9. 主应力是指剪力为零的截面上的正应力。

（）10.力圆上任一点的横坐标值对应单元体某一截面上的正应力。

（）二、选择题1.图1所示应力圆对应的单元体为图（）。

图 5三、选择题1.若一点的应力状态为平面应力状态，那么该点的主应力不可能为：（）。

A 、σ1> 0 σ2=σ3=0 B、σ1> 0 σ2 =0 σ3 < 0C、σ1>σ2>0 σ3=0D、σ1>σ2>σ3>0２.已知单元体各面上的应力如图，则其主平面方位为（）。

A、B、C、D、四、填空题１.图示为一平面应力状态的单元体及其应力圆，试在应力圆上表示０－１，０－２，０－３平面的位置。

图 62.试验表明，材料受力后的破坏主要有两种形式，一种是，是由于或所引起；另一种是，是由于所引起的。

3.一单元体如图所示，则单元体的主应力为__________ ，为__________ ，为__________ ，最大主应力与x 轴的夹角为__________ 。

五、简单计算1.单元体上的应力如图7所示，试求其它应力和最大剪应力。

2.图8所示单元体，试求图示斜截面上的正应力和剪应力。

图7图8 3.试求图示单元体o斜截面应力。

已知：。

图 9。

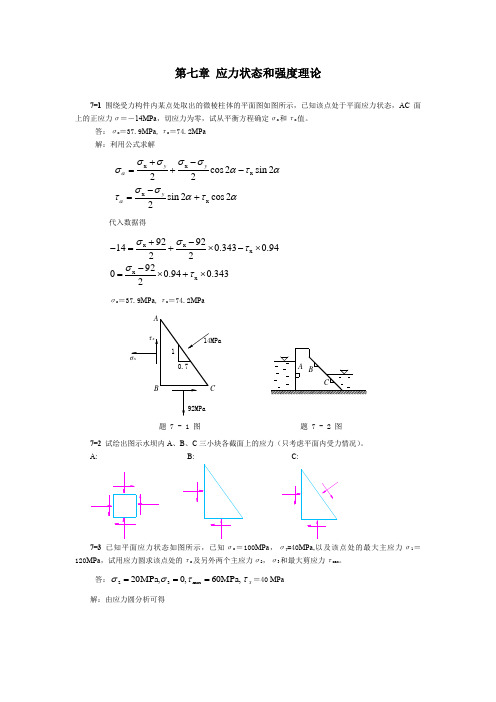
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。

绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。

b = 60 mm ，h = 100 mm 。

解题分析： 从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。

则各点处的应力状态如图示。

2、 梁截面惯性矩为 点微体上既有正应力又有切应力。

解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z1点处弯曲正应力（压应力）MPa 100Pa 10100m 10500m1050m N 101064833−=×=×××⋅×==−−zI My σ 1点为单向压缩受力状态，所以 021==σσ，MPa 1003−=σ 2点为纯剪切应力状态， MPa 30Pa 1030m10100602N 1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa 303−=σ 3点为一般平面应力状态弯曲正应力MPa 50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−zI My σ 弯曲切应力F S =120 kN题图1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−z z bI S F τ MPa 6.8MPa 6.58Pa)105.22()2Pa 1050(2Pa 1050)2(22626622min max −=×+×±×=+−±+=xy x y x τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。

第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。

(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管内的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大内力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件内任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说法正确的是（ B ）。

图1-23（题19）图1-24（题20）解：由题意得知塑性区一点在与x轴交成θ角的一个平面上的切应力为为最大切应力此可以判断该平面为主剪平面，又由于切应力方向为逆时针，因此切应力为负，图1-25θτθσσos2c K Ksin2xy y =-=-32xy y x 210-1.13125-I ⨯==γεε0I 3=即：0101.13125-101.0-32-23=⨯⨯-εεε 解方程得主应变：0,0.029-0.039,321===εεε由：3-3-1000002900039n m l 100000532.5032.515⨯⎪⎪⎪⎭⎫ ⎝⎛=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⨯⎪⎪⎪⎭⎫ ⎝⎛得： 1m l 39m 5.32l 1522=+=+ 解这个方程得：m 1=0.5575, m 2=5.16。

由于m 2=5.16＞1，与方向余弦规定不符，因此，m 1=0.5575才是正确解。

由此得：l=0.689。

即ε1=-0.039时，方向余弦为：l=0.689，m=0.5575，n=0。

同理可求：ε2=0.029时，方向余弦为：l=0.8025，m=0.5966，n=0。

图4-16 (题15))()532493=++=σ两端封闭的细长薄壁管平均直径为r，平均壁厚为l，承受内压力管材各向同性，试计算切向、轴向及径向应变增量比及应变比。

=0.2 Y =0.2×746ε0.20=129.9MPa max，图6-11（题2）解：从变形区内取一单元体作受力分析。

单元体的高度为平板间的高度，长度为一个单位。

假定是主应力且均匀分布，当沿x 轴坐标有相应的变化量就可用微分d σx 来表示。

y 方向上的压应力用的方向同金属质点流动方向相反，设每侧槽壁所受的压力p ，如图所示。

列出单元体的微分平衡方程：02)(=-+dx f h d y x x σσσ 02=⋅⋅+dx f y σ。

图6-12（题3）解：圆柱压缩为轴对称问题，采用柱座标。

一、单项选择题：1．除零应力外，过受力杆件的任一点，其主平面（ ）。

A ．只有三个； B. 不多于三个；C ．至少有三个； D. 可能有三个。

2．广义胡克定律适用的范围是（ ）。

A ．在小变形范围内； B. 在屈服极限范围内；C ．在比例极限范围内； D. 在强度极限范围内。

3．图示某危险点的应力状态，其主应力1σ和最大切应力max τ为（ ）。

A ．120MPa ，30 MPa ； Ｂ．130 MPa, 80 MPa ；Ｃ．150MPa ，60 MPa ； Ｄ．140 MPa,, 80MPa 。

4．按照第三强度理论，如图所示应力状态的相当应力是为（ ）MPa 。

A ．100； Ｂ．80； Ｃ．60； Ｄ．120。

5．以下结论中（ ）是正确的。

A ．第一、二强度理论主要用于塑性材料；Ｂ．第三、四强度理论主要用于脆性材料；Ｃ．第一强度理论主要用于单向应力状态；Ｄ．第四强度理论可用于塑性材料的应力状态。

6．某处的应力单元如图所示，则该处最大的正应力为（ ）MPa 。

A ． 14；B ． 114；C ． 140D ． 50。

7．图示两危险点应力状态，其中τσ=，按第四强度理论比较危险程度，则（ ）。

A. a 点较危险B. 两者危险程度相同C. b 点较危险D ． 判断题3图题4图题6图 题7图二、填空题1．图示单元体为平面应力状态，则其主应力之和为 ，主应力之差为 。

2．图示单元体各应力值均为30MPa ，它处于 向应力状态。

当 E =200GPa ，ν=0.3，则2ε= 。

三、计算题已知应力状态如图所示，图中应力单位皆为MPa 。

试求：（1）主应力大小，主平面位置；（2）在单元体上绘出主平面位置及主应力方向；（3）最大剪应力。

题1图题2图答案及解题思路：一、单项选择题：1．A ； 2．C ； 3．B ； 4．A ； 5．D ； 6．B ； 7．B 。

二、填空题：1．y x σσσσ+=+21， 222122x y x τσσσσ+-=+）（2．单，5109-⨯三、计算题：解： （1）主应力因为：203020==-=x y x τσσ，，所以： ）（MPa 273732520250230222222min max -=±=+⎪⎭⎫ ⎝⎛±=+⎪⎪⎭⎫ ⎝⎛-±+=x y x y x τσσσσσ （2）主平面位置33.1954302020222tan 00=∴=--⨯-=--=ασσταy x x（3）最大剪应力 MPa 322min max max =-=σστmin。