当前位置：文档之家 › 第八章 材料力学习题解

第八章 材料力学习题解

  • 格式：pdf
  • 大小：129.30 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

《材料力学》第八章课后习题参考答案

《材料力学》第八章课后习题参考答案

解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析， 明确各力的大小和方向，以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题，可以画出 相应的示意图或变形图，帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式，能够 准确应用公式进行计算和分析。
检查结果
在解题完成后，要对结果进行检查和 验证，确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题，明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件，选用相应的公式 进行计算。
注意单位换算
在计算过程中，要注意各物理量的单位换算， 确保计算结果的准确性。
检查答案合理性
得出答案后，要检查其是否符合实际情况和 物理规律，避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合，如弯曲与扭转 的组合、拉伸与压缩的组合等，需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构，需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ，需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ，需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。

《材料力学》课程讲解课件第八章组合变形

《材料力学》课程讲解课件第八章组合变形

强度条件（简单应力状态）——
max
对有棱角的截面，最大的正应力发生在棱角点处，且处于单向应力状态。
max
N A
M zmax Wz
M ymax Wy
x
对于无棱角的截面如何进行强度计算——
1、确定中性轴的位置；
y
F z
M z F ey M y F ez
ez F ey z
y
zk yk z
y
x
1、荷载的分解
F
Fy F cos
Fz F sin
z
2、任意横截面任意点的“σ”
x
F
y
（1）内力： M z (x) Fy x F cos x
M y (x) Fz x F sin x
（2）应力：
Mz k
M z yk Iz
My k
M y zk Iy
（应力的 “＋”、“－” 由变形判断）
F
1， 首先将斜弯曲分解
为两个平面弯曲的叠加 Fy F cos
z
L2
L2
Fz F sin
z
2， 确定两个平面弯曲的最大弯矩
y
Mz
Fy L 4
M
y
Fz L 4
3， 计算最大正应力并校核强度
max
My Wy
Mz Wz
217.8MPa
查表： Wy 692.2cm3
4， 讨论 0
y
Wz 70.758cm3
的直径为d3，用第四强度理论设计的直径为d4，则d3 ___＝__ d4。
（填“＞”、“＜”或“＝”）
因受拉弯组合变形的杆件，危险点上只有正应力，而无切应力，
r3 1 3 2 4 2
r4

周建方版材料力学习题解答[第八章9]分析

周建方版材料力学习题解答[第八章9]分析

8-49现用某种黄铜材料制成的标准圆柱形试件做拉伸试验。

已知临近破坏时，颈缩中心部位的主应力比值为113321::::=σσσ；并已知这种材料当最大拉应力达到770MPa 时发生脆性断裂，最大切应力达到313MPa 时发生塑性破坏。

若对塑性破坏采用第三强度理论，试问现在试件将发生何种形式的破坏？并给出破坏时各主应力之值。

解： 令主应力分别为：σσ31=，σσσ==32脆性断裂时，由第一强度理论=1r σσσ31==770MPa所以，塑性破坏时，由第三强度理论 所以故，试件将发生脆性断裂。

破坏时MPa 7701=σ，MPa 25732==σσ8-50 钢制圆柱形薄壁压力容器（参见图8-13），其平均直径mm d 800=，壁厚mm 4=δ，材料的M P a ][120=σ，试根据强度理论确定容器的许可内压p 。

解：在压力容器壁上取一单元体，其应力状态为二向应力状态。

p pd 504'==δσ ，p pd1002"==δσ 其三个主应力为p 100"1==σσ， p 50'2==σσ，03=σ据第三强度理论所以 ，MPa p 2.13≤，许可内压MPa p 2.13= 据第四强度理论所以，MPa p 39.14≤，许可内压MPa p 39.14=8-51 空心薄壁钢球，其平均内径mm d 200=，承受内压MPa p 15=，钢的MPa ][160=σ。

试根据第三强度理论确定钢球的壁厚δ。

解：钢球上任一点应力状态如图示 其三个主应力为：σσσ==21，03=σ而 MPa MPa d p R R p δδδδππσ4342.0152222=⨯=⋅=⋅⋅=据第三强度理论 所以 mm m 69.41069.41601433=⨯=⨯≥-δ 8-52 图8-77所示两端封闭的铸铁圆筒，其直径mm d 100=，壁厚mm 10=δ，承受内压MPa p 5=，且在两端受压力kN F 100=和外扭矩m kN T ⋅=3作用，材料的许用拉应力MPa ][40=+σ，许用压应力MPa ][160=-σ，泊松比250.=ν，试用莫尔强度理论校核其强度。

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

课
后 答
案
网
解：由挠度表查得：
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m，取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状，并说明需要分几段 建立微分方程，积分常数有几个，确定积分常数的条件是什么？（不要求详细解答）
习题 8－3 图
后 答
案
网
习题 8－4 图
课
习题 8－4a 解图
解： (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
（静力学与材料力学）
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
（教师用书）
−3 9 4
(
.k hd
解：由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8－9 图
8
aw .
)

材料力学：第八章-应力应变状态分析

材料力学：第八章-应力应变状态分析
斜截面: // z 轴； 方位用 a 表示；应力为 sa , ta
正负符号规定:
切应力 t － 使微体沿顺时针 旋转为正 方位角 a － 以 x 轴为始边、逆时针旋转 为正
斜截面应力公式推导 设α斜截面面积为dA, 则eb侧面和bf 底面面积分别为dAcosα, dAsinα
由于tx 与 ty 数值相等，同时
sa+90 ,ta+90
E
sa+90 ,ta+90
结论: 所画圆确为所求应力圆
应力圆的绘制与应用3
应力圆的绘制
已知 sx , tx , sy ,
画相应应力圆
t
先确定D, E两点位置, 过此二点画圆即为应力圆
Ds x ,t x , E s y ,t y
t
C OE
s 2 , 0
s 1 , 0
应力圆绘制 作D, E连线中垂线,与x轴相交即为应力圆圆心
tb sb
t
sa
O
C
ta
D
sa ,ta
t
s
E
sb ,tb
O
D
sa ,ta
C
s
E
sb ,tb
由|DC|=|CE|,可得sC值:
sC
s
2 β
+
t
2 β
s
2 α
+
t
2 α
2 sα sβ
点、面对应关系
转向相同, 转角加倍 互垂截面, 对应同一直径两端
应变状态
构件内一点处沿所有方位的应变总况或集合, 称为该点处的 应变状态
研究方法
环绕研究点切取微体, 因微体边长趋于零, 微体趋于所研究 的点, 故通常通过微体, 研究一点处的应力与应变状态

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析
1．绘出梁的剪力图和弯矩图；
2．确定梁内横截面上的最大拉应力和最大压应力；
3．确定梁内横截面上的最大切应力；
4．画出横截面上的切应力流。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
1．图（a）：
kN
， kN
剪力与弯矩图如图（b）、（c）；
2．形心C位置
MPa
MPa
3． m3
MPa
4．切应力流如图（e）。
（A）下移且绕点O转动；
（B）下移且绕点C转动；
（C）下移且绕z轴转动；
（D）下移且绕 轴转动。
知识点：弯曲中心、薄壁截面梁产生平面弯曲的加载条件
难度：一般
解答：
正确答案是D。
8－19试判断下列图示的切应力流方向哪一个是正确的。
知识点：横向弯曲时梁横截面上的切应力流、弯曲切应力分析方法
难度：难
解答：
（A）细长梁、横截面保持平面；
（B）弯曲正应力公式成立，切应力沿截面宽度均匀分布；
（C）切应力沿截面宽度均匀分布，横截面保持平面；
（D）弹性范围加载，横截面保持平面。
知识点：弯曲时梁横截面上切应力分析
难度：易
解答：
正确答案是B。
公式 推导时应用了局部截面的正应力合成的轴力，该正应力 则要求弯曲正应力公式成立；另外推导时在 时，应用了 沿截面宽度均匀分布假设。
难度：难
解答：
正确答案是D。
8－21简支梁受力与截面尺寸如图所示。试求N－N截面上a、b两点的铅垂方向的切应力以及腹板与翼缘交界处点c的水平切应力。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
FQ = 120kN，形心C位置。

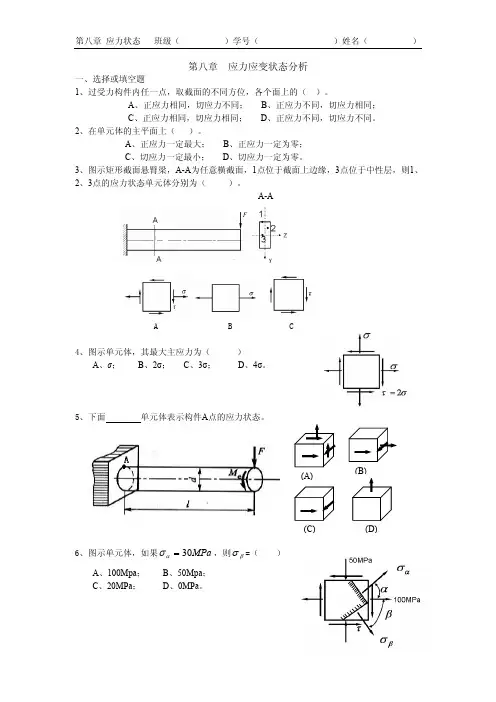
材料力学作业(8-11)

第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点，取截面的不同方位，各个面上的（ ）。

A 、正应力相同，切应力不同；B 、正应力不同，切应力相同；C 、正应力相同，切应力相同；D 、正应力不同，切应力不同。

2、在单元体的主平面上（ ）。

A 、正应力一定最大；B 、正应力一定为零；C 、切应力一定最小；D 、切应力一定为零。

3、图示矩形截面悬臂梁，A-A 为任意横截面，1点位于截面上边缘，3点位于中性层，则1、2、3点的应力状态单元体分别为（ ）。

A-AA B C4、图示单元体，其最大主应力为（ ）A 、σ；B 、2σ；C 、3σ；D 、4σ。

5、下面 单元体表示构件A 点的应力状态。

6、图示单元体，如果MPa 30=ασ，则βσ=（ ） A 、100Mpa ； B 、50Mpa ； C 、20MPa ； D 、0MPa 。

(C)7、图示单元体应力状态，沿x 方向的线应变εx 可表示为（ ）A 、Eyσ； B 、)(1y x E μσσ−；C 、)(1x y E μσσ− ；D 、Gτ。

8、图示应力圆对应于单元体( )。

9、已知单元体及应力圆如图所示，σ1所在主平面的法线方向为( )。

A 、n 1；B 、 n 2；C 、n 3；D 、n4。

二、计算题1、已知应力状态如图所示，试用解析法计算图中指定截面上的正应力和切应力。

2、试画图示应力状态的三向应力圆，并求主应力、最大正应力和最大切应力。

3、边长为20mm的钢立方块置于刚性模中，在顶面受力F=14kN作用。

已知材料的泊松比为0.3，求立方体各个面上的正应力。

4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m，Q=120 kN。

试绘出截面上1、2、3、4各点的应力状态单元体，并求其主应力。

第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下，水管中的水会受冻而结冰。

根据低温下水管和冰所受力情况可知（ ）。

A 、冰先破裂而水管完好；B 、水管先破裂而冰完好；C 、冰与水管同时破裂；D 、不一定何者先破裂。

材料力学_第八章截面核心


''' Mzy Iz
z
(yF , zF)
F A
Myz Iy
M z y I z
y
max
F A
Mz Wz
My Wy
min
F A
Mz Wz
My Wy
中性轴任意点（y0，z0）满足：
F Mz y0 M yz0 0
A Iz
Iy
中性轴方程 az
ay 中性轴 z
F A
FyF y0 Aiz2
FzF z0
组合变形的分析方法：在小变形和线弹性情况下，可先 分别计算每一种基本变形情况下的应力和变形，然后采 用叠加原理计算所有载荷对弹性体系所引起的总应力和 总变形。
F
Ft
Ft
z
l/2 l/2
y
II、偏心拉(压) (拉：F 0 ; 压: F 0)
xF
xF
z
My
y
z y
Mz
F
My
MZ
' F
A
'' Myz Iy
a
2. 确定形心主惯性轴，并求形心主惯性矩 z
4a 6a
由于z轴为对称轴，且y、z轴的交 点过形心，故图c中y轴和z轴的为形 心主惯性轴。
* C
y
形心主惯性矩Iy为
4a
Iy
a(4a)3 [
12
(a
4a) (2a)2]
4a(2a)3 [
12
(4a
(c)
2a) a2 ]
32a4
Iz

4a(a)3 12
2a(4a)3 12
11a4
3. 计算横截面上的内力
将F力向形心C简化，可得杆的内力分别为 FN=F，My=F·2a， Mz=F·2a

材料力学第八章-弯曲变形

q0 B x 等价 MA A EI f q0 B
L
A
L
解：建立静定基 确定超静定次数 用反力代替多余约束 得新结构 —— 静定基
或
q0
A
B L RB
32
q0 A L B RB
几何方程——变形协调方程
f B f Bq f BRB 0
物理方程
=
A B RB q0 A B
qL RB L f Bq ; f BRB 8EI 3EI
A A 铰连接
P
C D
C
D
B
A点：f A 0, A 0
B点： f B左 f B右
C点： f C左 f C右 C左 C右
D点：f D 0
21
边界条件、连续条件应用举例
P
弯矩图分二段，
共积分常数 需4个边界条件 和连续条件
A B
C
(+)
A点： A 0 B点： f B左 f B右 , C点：f C 0
解：载荷分解如图
=
P A B
查梁的简单载荷变形表，
得到变形
Pa PA 4 EI
q B
2
Pa f PC 6 EI
3
+
A
qa qA 3EI
3
5qL f qC 24 EI24
4
P
A
C a a
q B
Pa PA 4 EI
qa 3 qA 3EI
2
Pa 3 f PC 6 EI
Differential Equation of beam deformation 1 M ( x) 已知曲率为 EI z x
M>0

材料力学- 8组合变形

l/2 l/2
D
A P
C
d
B
Q
l/2
D
l/2
解：
B
A P
mA
C
Q Q 1 mC QD 2 A M C
Ql/4
B
（1）受力分析与计算简 图：将载荷Q向轮心平移 （2）内力分析，画出弯 矩图和扭矩图；找出危险 面和危险点：危险面在中 点C处 （3）代公式：求最大安 全载荷Q
d
T
QD/2
r3
设计中常采用的简便方法：
因为偏心距较大，弯曲应力 是主要的，故先考虑按弯曲强 度条件 设计截面尺寸
M Wz 6000 6 35 10 d 3 32
解得立柱的近似直径 取d=12.5cm,再代 入偏心拉伸的强 度条件校核
d 0.12 m
15000 6000 3.14 0.1252 3.14 0.1253 4 32 32.4 106 32.4MPa 35MPa
M 2 T2 [ ] Wz
l/2
D
l/2
Ql Q M 0.8 0.2Q 4 4
B
A P
mA
C
d
T
Q Q 1 mC QD 2 A M C
Ql/4
QD Q 0.36 0.18Q 2 2
r3
B
M 2 T2 [ ] Wz
Wz
ቤተ መጻሕፍቲ ባይዱ 3
32
T
QD/2
（1）计算内力
将立柱假想地截开，取上段为 研究对象，由平衡条件，求出 立柱的轴力和弯矩分别为
F
N
FN P 15000 N M Pe 15000 0.4 6000N m
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(c)解：由题图所示应力状态可知，
由此可得指定斜截面上的正应力和切应力分别为
σα = [
10 − 20 10 + 20 + cos(−120 o ) − 15sin(−120 o )]MPa = 0.490MPa 2 2 10 + 20 τα = [ sin(−120 o ) + 15cos(−120 o )]MPa = −20.5MPa 2
(a) (b) (c)
= 350 × 10 −6
将式(a)和(b)的结果代入式(c)，得
γ xy = (550 − 700) × 10 −6 = −150 × 10 −6
(d)
将以上所得结果(a),(b)和(d)代入平面应变状态任意方位的正应变公式，计算 ε135o 应有的 测量值，
ε135o =
1 1 (450 + 100) × 10 −6 + (450 − 100) × 10 −6 cos270 o 2 2 1 − × (−150 × 10 −6 )sin270 o = 200 × 10 −6 2
题 8-15 图 解：依据平面应变状态任意方位的正应变公式，有
ε 0o = ε 90o = ε 45o =
εx + ε y 2 εx + ε y 2 εx + ε y 2
+ − −
εx − ε y 2 εx − ε y 2 γ xy 2
= ε x = 450 × 10 −6 = ε y = 100 × 10 −6
由于式中 α 为任意值，故原命题得证。
8-7
已知某点 A 处截面 AB 与 AC 的应力如图所示 （应力单位为 M方位。
题 8-7 图 解：根据题图所给的已知应力，可画出应力圆来，如图 8-7 所示。
图 8-7 从所画的应力圆上可以量得两个主应力，它们是：
由此可得指定斜截面上的正应力和切应力分别为
σα = (
− 30 + 10 − 30 − 10 + cos45 o − 20sin45 o )MPa = −38.3MPa 2 2 − 30 − 10 τα = ( sin45 o + 20cos45o )MPa = 0 2 σ x = 10MPa，σ y = −20MPa，τ x = 15MPa，α = −60 o
应力的大小及方位。
题 8-9 图 解：由题图可知，指定截面的剪力、弯矩分别为
| M | = Fa = 20 ×1kN ⋅ m = 20kN ⋅ m Fs = F = 20kN，
微体 A,B,C 的应力图依次示如图 8-9 (a),(b)和(c)。
图 8-9 对于应力图(a)，其正应力为
|M | 6 × 20 × 10 3 N σA = = = 6.00 × 10 7 Pa = 60.0MPa 2 2 Wz 0.050 × 0.200 m
第八章 应力、应变状态分析
题号 页码 8-2 .........................................................................................................................................................1 8-3 .........................................................................................................................................................2 8-6 .........................................................................................................................................................2 8-7 .........................................................................................................................................................3 8-9 .........................................................................................................................................................4 8-12 .......................................................................................................................................................5 8-15 .......................................................................................................................................................6 8-16 .......................................................................................................................................................7 8-20 .......................................................................................................................................................8 8-21 .......................................................................................................................................................8 8-23 .......................................................................................................................................................9 8-24 .......................................................................................................................................................9
由
tanα 0 = −
得 σ 1 的方位角为
τx 2.25 =− = −0.07458 σ x − σ min 30.0 + 0.1678
α 0 = −4.27 o
对于应力图(c)，其切应力为
τC =
3Fs 3 × 20 × 10 3 N = = 3.00 × 10 6 Pa = 3.00MPa 2 2 A 2 × 0.050 × 0.200m σ 1 = 3.00MPa，σ 2 = 0，σ 3 = −3.00MPa
σ 1 = 84.7 MPa，σ 2 = 20.0 MPa，σ 3 = −4.72 MPa
8-15
在构件表面某点 O 处，沿 00，450，900 与 1350 方位粘贴四个应变片，并测得相
0 0 0 0
应正应变依次为ε = 450×10-6，ε45 = 350×10-6，ε = 100×10-6 与ε = 100×10-6 ，试判断 0 90 135 上述测试结果是否可靠。
σ 1 = 69.7MPa，σ 2 = 9.9MPa
由于是平面应力状态，故知
3
σ3 = 0
从该应力圆上还可以量得 σ1 的方位角为
α 0 = −23.7 o
式中负号表示从 AB 面的外法线沿顺时针方向旋转。
8-9
图示悬臂梁，承受载荷 F = 20kN 作用，试绘微体 A，B 与 C 的应力图，并确定主
σα = (
30 + 10 + 20sin 90 o )MPa = 40.0MPa 2 30 − 10 τα = ( sin 90 o )MPa = 10.0MPa 2
(b)解：由题图所示应力状态可知，
1
σ x = −30MPa，σ y = 10MPa，τ x = 20MPa，α = 22.5 o
5
σx − σy 2 σ max σ x + σ y 2 ± ( ) + τx = σ min 2 2 =[ 84.7 60 + 20 60 − 20 2 ± ( ) + 40 2 ] MPa = MPa 2 2 − 4.72
将此二极值应力与 σ z 一同排序，得三个主应力依次为
由此可知，主应力各为
σ1 = 60.0MPa, σ 2 = σ 3 = 0
σ 1 的方位角为
α0 = 0o
对于应力图(b),其正应力和切应力分别为
σB = τB =
| M | | y B | 12 × 20 × 10 3 × 0.050 N = = 3.00 × 10 7 Pa = 30.0MPa 3 2 Iz 0.050 × 0.200 m Fs S z (ω) 12 × 20 × 10 3 × 0.050 × 0.050 × 0.075 N = 2.25 × 10 6 Pa = 2.25MPa = I zb 0.050 × 0.200 3 × 0.050m 2