部分课外平面几何定理证明

平面几何定理及其证明梅涅劳斯定理1 .梅涅劳斯定理及其证明 定理：一条直线与 ABC 的三边AB BC CA 所在直线分别交于点 D E 、F ,且D E 、F 均证明：如图，过点C 作AB 的平行线，交EF 于点G. 因为 CG // AB ，所以 CG CF --------------------- （ 1）AD FA因为 CG // AB ，所以 EC （ 2） DB BEC F ，即得 AD C FEC FA DB EC FA2.梅涅劳斯定理的逆定理及其证明定理：在 ABC 的边AB BC 上各有一点 D E ,在边 AC 的延长线上有一点 F ,若二、 塞瓦定理3 .塞瓦定理及其证明定理：在ABC 内一点P,该点与ABC 的三个顶点相连所在的 三条直线分别交 ABCE 边AB BC CA 于点D E 、F ,且D E 、F 三点均不是 ABC不是ABC 的顶点，则有AD BECF 1DB EC由（1）宁（2） DB可得兀AD BE CF DB EC FA1，那么，D E 、F 三点共线.证明：设直线EF 交AB 于点D ，则据梅涅劳斯定理有AD /BE CF 丽EC FA因为AD Bl CF DB EC FA1，所以有誥段AB 上，所以点D 与D 重合.即得D鴿.由于点D D 都在线 E 、F 三点共线.证明：运用面积比可得 ADDB S ADP S BDPS ADC S BDC根据等比定理有S ADP S ADCSADC S ADP S APCSSBDPBDCSBDCSBDPS的顶点，则有AD BE CF “1 DB EC FA .所以AD S A PC .同理可得BE SDB S BPCAPB, CFEC S APC FA SBPCS APB三式相乘得竺吏 DB EC CF i FA 4.塞瓦定理的逆定理及其证明 定理：在 ABC 三边AB BC CA 上各有一点 H 1，那么直线CD AE BF 三线共点. DE 、F ,且 D E 、 F 均不是 ABC 的顶点,AD BE若 DB EC证明：设直线AE 与直线BF 交于点P,直线CP 交AB 于点D ,则 据塞瓦定理有 AD Z DBBE EC CA1 -1,所以有 段AB 上，所以点D 与D 重合.即得 因为竺 DB EC CF FA AD DB D DDB •由于点D D 都在线 E 、F 三点共线.三、西姆松定理 5.西姆松定理及其证明 定理：从 ABC 外接圆上任意一点 F ,则D E 、F 三点共线. 证明：如图示，连接PC ,连接EF P 向BC CA AB 或其延长线引垂线, 垂足分别为DE、交BC 于点D ，连接P D• 因为PE 因为A 、 所以， 共圆. 所以， 即 PD BC 由于过点 F D E 、 四、 6 AE,PF AF,所以A 、F 、P 、E 四点共圆，可得B 、P 、C 四点共圆，所以 FEP = BCP 即 DEP = CDP + CEP = 180°。

高中平面几何定理汇总及证明1.共边比例定理有公共边AB的两个三角形的顶点分别是P、Q,AB与PQ的连线交于点M,则有以下比例式成立：△ PAB的面积：△ QAB的面积＝PM：QM.证明：分如下四种情况,分别作三角形高,由相似三角形可证S△PAB=S△PAM-S△PMB=S△PAM/S△PMB-1×S△PMB=AM/BM-1×S△PMB等高底共线,面积比=底长比同理,S△QAB=AM/BM-1×S△QMB所以,S△PAB/S△QAB=S△PMB/S△QMB=PM/QM等高底共线,面积比=底长比定理得证特殊情况：当PB∥AQ时,易知△PAB与△QAB的高相等,从而S△PAB=S△QAB,反之,S△PAB=S△QAB,则PB∥AQ;2.正弦定理在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍”,即a/sinA = b/sinB =c/sinC = 2r=Rr为外接圆半径,R为直径证明：现将△ABC,做其外接圆,设圆心为O;我们考虑∠C及其对边AB;设AB长度为c;若∠C为直角,则AB就是⊙O的直径,即c= 2r;∵特殊角正弦函数值∴若∠C为锐角或钝角,过B作直径BC`交⊙O于C`,连接C'A,显然BC'= 2r=R; 若∠C为锐角,则C'与C落于AB的同侧,此时∠C'=∠C同弧所对的圆周角相等∴在Rt△ABC'中有若∠C为钝角,则C'与C落于AB的异侧,BC的对边为a,此时∠C'=∠A,亦可推出;考虑同一个三角形内的三个角及三条边,同理,分别列式可得;3.分角定理在△ABC中,D是边BC上异于B,C或其延长线上的一点,连结AD,则有BD/CD=sin∠BAD/sin∠CADAB/AC;证明：S△ABD/S△ACD=BD/CD………… 1.1S△ABD/S△ACD=1/2×AB×AD×sin∠BAD/1/2 ×AC×AD×sin∠CAD= sin∠BAD/sin∠CAD ×AB/AC…………1.2由1.1式和1.2式得BD/CD=sin∠BAD/sin∠CAD ×AB/A C4.张角定理在△ABC中,D是BC上的一点,连结AD;那么;证明：设∠1=∠BAD,∠2=∠CAD由分角定理,S△ABD/S△ABC=BD/BC=AD/ACsin∠1/sin∠BAC→ BD/BCsin∠BAC/AD=sin∠1/AC 1.1S△ACD/S△ABC=CD/BC=AD/ABsin∠2/sin∠BAC→ CD/BCsin∠BAC/AD=sin∠2/AB 1.21.1式+1.2式即得 sin∠1/AC+sin∠2/AB=sin∠BAC/AD5.帕普斯定理直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD交于G,AF,DC交于I,BF,EC交于H,则G,I,H共线;6.蝴蝶定理设S为圆内弦AB的中点,过S作弦CF和DE;设CF和DE各相交AB于点M和N,则S 是MN的中点;证明：过O作OL⊥ED,OT⊥CF,垂足为L、T,连接ON,OM,OS,SL,ST,易明△ESD∽△CSF∴ES/CS=ED/FC根据垂径定理得：LD=ED/2,FT=FC/2∴ES/CS=EL/CT又∵∠E=∠C∴△ESL∽△CST∴∠SLN=∠STM∵S是AB的中点所以OS⊥AB∴∠OSN=∠OLN=90°∴O,S,N,L四点共圆,一中同长同理,O,T,M,S四点共圆∴∠STM=∠SOM,∠SLN=∠SON∴∠SON=∠SOM∵OS⊥AB∴MS=NS7.西姆松定理过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线;此线常称为西姆松线;证明：若L、M、N三点共线,连结BP,CP,则因PL⊥BC,PM⊥AC,PN⊥AB,有B、L、P、N和P、M、C、L分别四点共圆,有∠NBP = ∠NLP = ∠MLP= ∠MCP.故A、B、P、C四点共圆;若A、P、B、C四点共圆,则∠NBP= ∠MCP;因PL⊥BC,PM⊥AC,PN⊥AB,有B、L、P、N和P、M、C、L四点共圆,有∠NBP = ∠NLP= ∠MCP= ∠MLP.故L、M、N三点共线;西姆松逆定理：若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上;证明：PM⊥AC,PN⊥AB ,所以A,M,N,P共圆8.清宫定理设P、Q为△ABC的外接圆上异于A、B、C的两点,P关于三边BC、CA、AB的对称点分别是U、V、W,且QU、QV、QW分别交三边BC、CA、AB或其延长线于D、E、F,则D、E、F在同一直线上.证明：A、B、P、C四点共圆,因此∠PCE=∠ABP点P和V关于CA对称所以∠PCV=2∠PCE又因为P和W关于AB对称,所以∠PBW=2∠ABP从这三个式子,有∠PCV=∠PBW另一方面,因为∠PCQ和∠PBQ都是弦PQ所对的圆周角,所以∠PCQ=∠PBQ两式相加,有∠PCV+∠PCQ=∠PBW+∠PBQ即∠QCV=∠QBW即△QCV和△QBW有一个顶角相等,因此但是,,所以同理,于是根据梅涅劳斯定理的逆定理,D、E、F三点在同一直线上;9.密克定理三圆定理：设三个圆C1, C2, C3交于一点O,而M, N, P分别是C1 和C2, C2和C3, C3和C1的另一交点;设A为C1的点,直线MA交C2于B,直线PA交C3于C;那么B, N, C这三点共线;逆定理：如果是三角形,M, N, P三点分别在边AB, BC, CA上,那么△AMP、△BMN、△CPN 的外接圆交于一点O;完全四线形定理如果ABCDEF是完全四线形,那么三角形的外接圆交于一点O,称为密克点;四圆定理设C1, C2,C3, C4为四个圆,A1和B1是C1和C2的交点,A2和B2是C2 和C3的交点,A3和B3是C3和C4的交点,A4和B4是C1和C4的交点;那么A1, A2, A3, A4四点共圆当且仅当B1, B2, B3, B4四点共圆;证明：在△ABC的BC,AC,AB边上分别取点W,M,N,对AMN,△BWN和△CWM分别作其外接圆,则这三个外接圆共点;该定理的证明很简单,利用“圆内接四边形对角和为180度”及其逆定理;现在已知U是和的公共点;连接UM和UN,∵四边形BNUW和四边形CMUW分别是和的内接四边形,∴∠UWB+∠UNB=∠UNB+∠UNA=180度∴∠UWB=∠UNA;同理∠UWB+∠UWC=∠UWC+∠UMC=180度∴∠UWB=∠UMC;∵∠UMC+∠UMA=180度∴∠UNA+∠UMA=180度,这正说明四边形ANUM是一个圆内接四边形,而该圆必是,U必在上;10.婆罗摩笈多定理圆内接四边形ABCD的对角线AC⊥BD,垂足为M;EF⊥BC,且M在EF上;那么F是A D 的中点;证明：∵AC⊥BD,ME⊥BC∴∠CBD=∠CME∵∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF∵∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,即F是AD中点逆定理：若圆内接四边形的对角线相互垂直,则一边中点与对角线交点的连线垂直于对边;证明：∵MA⊥MD,F是AD中点∴AF=MF∴∠CAD=∠AMF∵∠CAD=∠CBD,∠AMF=∠CME∴∠CBD=∠CME∵∠CME+∠BME=∠BMC=90°∴∠CBD+∠BME=90°∴EF⊥BC11.托勒密定理圆内接四边形中,两条对角线的乘积两对角线所包矩形的面积等于两组对边乘积之和一组对边所包矩形的面积与另一组对边所包矩形的面积之和．圆内接四边形ABCD,求证：AC·BD=AB·CD+AD·BC．证明：过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP．得AC：BC=AD：BP,AC·BP=AD·BC ①;又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP．得AC：CD=AB：DP,AC·DP=AB·CD ②;①+②得ACBP+DP=AB·CD+AD·BC．即AC·BD=AB·CD+AD·BC．12.梅涅劳斯定理当直线交三边所在直线于点时,;证明：过点C作CP∥DF交AB于P,则两式相乘得梅涅劳斯逆定理：若有三点F、D、E分别在边三角形的三边AB、BC、CA或其延长线上,且满足AF/FB×BD/DC×CE/EA=1,则F、D、E三点共线;证明：先假设E、F、D三点不共线,直线DE与AB交于P;由梅涅劳斯定理的定理证明如利用平行线分线段成比例的证明方法得：AP/PBBD/DCCE/EA=1;∵ AF/FBBD/DCCE/EA=1;∴ AP/PB=AF/FB ；∴ AP+PB/PB=AF+FB/FB ；∴ AB/PB=AB/FB ；∴ PB=FB；即P与F重合;∴ D、E、F三点共线;13.塞瓦定理在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则BD/DC×CE/EA×AF/FB=1;∵△ADC被直线BOE所截,∴CB/BDDO/OAAE/EC=1①∵△ABD被直线COF所截,∴BC/CDDO/OAAF/FB=1②②/①约分得：DB/CD×CE/EA×AF/FB=114.圆幂定理相交弦定理：如图Ⅰ,AB、CD为圆O的两条任意弦;相交于点P,连接AD、BC,由于∠B与∠D同为弧AC所对的圆周角,因此由圆周角定理知：∠B=∠D,同理∠A=∠C,所以;所以有：,即：;割线定理：如图Ⅱ,连接AD、BC;可知∠B=∠D,又因为∠P为公共角,所以有,同上证得;切割线定理：如图Ⅲ,连接AC、AD;∠PAC为切线PA与弦AC组成的弦切角,因此有∠PBC=∠D,又因为∠P为公共角,所以有,易证图Ⅳ,PA、PC均为切线,则∠PAO=∠PCO=90°,在直角三角形中：OC=OA=R,PO为公共边,因此;所以PA=PC,所以;综上可知,是普遍成立的;弦切角定理：弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数;点对圆的幂P点对圆O的幂定义为点P在圆O内→P对圆O的幂为负数；点P在圆O外→P对圆O的幂为正数；点P在圆O上→P对圆O的幂为0;三角形五心：内心：三角形三条内角平分线的交点外心：三角形三条边的垂直平分线中垂线的相交点重心：三角形三边中线的交点垂心：三角形的三条高线的交点旁心：三角形的旁切圆与三角形的一边和其他两边的延长线相切的圆的圆心九点圆心：三角形三边的中点,三高的垂足和三个欧拉点〔连结三角形各顶点与垂心所得三线段的中点〕九点共圆的圆心15.根心定理三个两两不同心的圆,形成三条根轴,则必有下列三种情况之一：1 三根轴两两平行；2 三根轴完全重合；3 三根轴两两相交,此时三根轴必汇于一点,该点称为三圆的根心;平面上任意三个圆,若这三个圆圆心不共线,则三条根轴相交于一点,这个点叫它们的根心；若三圆圆心共线,则三条根轴互相平行;根轴定义：A与B的根轴L1：到A与B的切线相等的点;B与C的根轴L2：到B与C的切线相等的点;证明设A、B、C三个圆,圆心不重合也不共线;考察L1与L2的交点P;因为P在L1上,所以：P到A的切线距离=P到B的切线距离;因为P在L2上,所以：P到B的切线距离=P到C的切线距离;所以：P到A的切线距离=P到B的切线距离=P到C的切线距离;也就是：P到A的切线距离=P到C的切线距离;所以：P在A与C的根轴上; 所以：三个根轴交于一点;16.鸡爪定理设△ABC的内心为I,∠A内的旁心为J,AI的延长线交三角形外接圆于K,则KI=KJ=KB=KC;证明：由内心和旁心的定义可知∠IBC=∠ABC/2,∠JBC=180°-∠ABC/2∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ同理,∠ICJ=90°∵∠IBJ+∠ICJ=180°∴IBJC四点共圆,且IJ为圆的直径∵AK平分∠BAC∴KB=KC相等的圆周角所对的弦相等又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB∴KB=KI由直角三角形斜边中线定理逆定理可知K是IJ的中点∴KB=KI=KJ=KC逆定理：设△ABC中∠BAC的平分线交△ABC的外接圆于K;在AK及延长线上截取KI=KB=KJ,其中I在△ABC的内部,J在△ABC的外部;则I是△ABC的内心,J是△ABC 的旁心;证明：利用同一法可轻松证明该定理的逆定理;取△ABC的内心I'和旁心J’,根据定理有KB=KC=KI'=KJ'又∵KB=KI=KJ∴I和I'重合,J和J’重合即I和J分别是内心和旁心17.费尔巴哈定理三角形的九点圆与其内切圆以及三个旁切圆相切设△ABC的内心为I,九点圆的圆心为V;三边中点分别为L,M,N,内切圆与三边的切点分别是P,Q,R,三边上的垂足分别为D,E,F;不妨设AB>AC;假设⊙I与⊙V相切于点T,那么LT与⊙I相交,设另一个交点为S;过点S作⊙I的切线,分别交AB和BC于V,U,连接AU;又作两圆的公切线TX,使其与边AB位于LT的同侧;由假设知∠XTL=∠LDT而TX和SV都是⊙I的切线,且与弦ST所夹的圆弧相同,于是∠XTL=∠VST因此∠LDT=∠VST则∠UDT+∠UST=180°这就是说,S,T,D,U共圆;而这等价于：LU×LD=LS×LT又LP²=LS×LT故有LP²=LU×LD另一方面,T是公共的切点,自然在⊙V上,因此 L,D,T,N共圆,进而有∠LTD=∠LND由已导出的S,T,D,U共圆,得∠LTD=∠STD=180°-∠SUD=∠VUB=∠AVU-∠B而∠LND=∠NLB-∠NDB=∠ACB-∠NBD=∠C-∠B这里用了LN∥AC,以及直角三角形斜边上中线等于斜边的一半所以,就得到∠AVU=∠C注意到AV,AC,CU,UV均与⊙I相切,于是有∠AIR=∠AIQ∠UIS=∠UIP∠RIS=∠QIS三式相加,即知∠AIU=180°也即是说,A,I,U三点共线;另外,AV=AC,这可由△AIV≌△AIC得到;这说明,公切点T可如下得到：连接AI,并延长交BC于点U,过点U作⊙I的切线,切点为S,交AB于V,最后连接LS,其延长线与⊙I的交点即是所谓的公切点T;连接CV,与AU交于点K,则K是VC的中点;前面已得到：LP²=LU×LD而2LP=BL+LP-CL-LP=BP-CP=BR-CQ=BR+AR-CQ+AQ=AB-AC=AB-AV=BV即 LP=BV然而LK是△CBV的中位线于是 LK=BV因之 LP=LK故LK²=LU×LD由于以上推导均可逆转,因此我们只需证明：LK²=LU×LD;往证之这等价于：LK与圆KUD相切于是只需证：∠LKU=∠KDU再注意到 LK∥ABLK是△CBV的中位线,即有∠LKU=∠BAU又AU是角平分线,于是∠LKU=∠CAU=∠CAK于是又只需证：∠CAK=∠KDU即证：∠CAK+∠CDK=180°这即是证：A,C,D,K四点共圆由于 AK⊥KC易得,AD⊥DC所以 A,C,D,K确实共圆;这就证明了⊙I与⊙V内切;旁切圆的情形是类似的;证毕另略证：OI2=R2-2RrIH2=2r2-2Rr'OH2=R2-4Rr'其中r‘是垂心H的垂足三角形的内切圆半径,R、r是三角形ABC外接圆和内切圆半径FI2=1/2OI2+IH2-1/4OH2=1/2R-r2FI=1/2R-r这就证明了九点圆与内切圆内切九点圆半径为外接圆半径一半;F是九点圆圆心,I为内心18.莫利定理将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一个交点,则这样的三个交点可以构成一个正三角形证明：设△ABC中,AQ,AR,BR,BP,CP,CQ为各角的三等分线,三边长为a,b,c,三内角为3α,3β,3γ,则α+β+γ=60°;在△ABC中,由正弦定理,得AF=csinβ/sinα+β;不失一般性,△ABC外接圆直径为1,则由正弦定理,知c=sin3γ,所以AF=sin3γsinβ/sin60°-γ= sinβsinγ3-4sin²γ/1/2√3cosγ-sinγ= 2sinβsinγ√3cosγ+sinγ= 4sinβsinγsin60°+γ.同理,AE=4sinβsinγsin60°+β∴AF:AE=4sinβsinγsin60°+γ：4sinβsinγsin60°+β=sin60°+γ:sin60°+β=sin∠AEF:sin∠AFE∴∠AEF=60°+γ,∠AFE=60°+β.同理得,∠CED=60°+α∠FED=180°-CED-AEF-α-γ=180°-60°-α-60°+α=60°∴△FED为正三角形19.拿破仑定理若以任意三角形的各边为底边向形外作底角为60°的等腰三角形,则它们的中心构成一个等边三角形;在△ABC的各边上向外各作等边△ABF,等边△ACD,等边△BCE;。

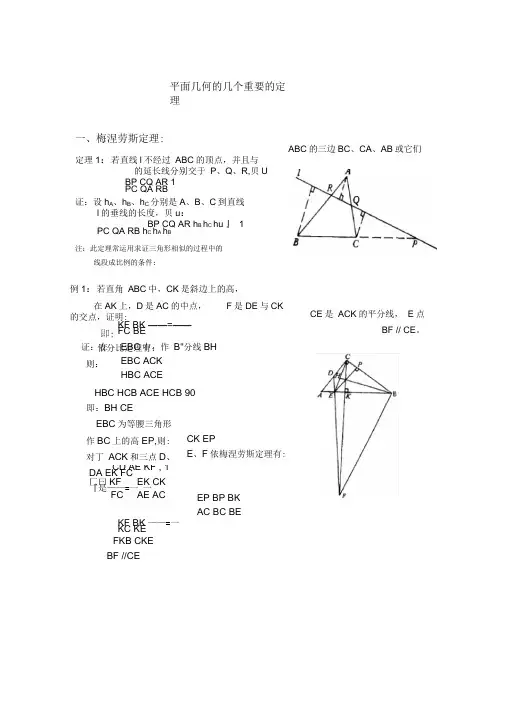
平面几何的几个重要的定理一、梅涅劳斯定理:定理1：若直线l 不经过 ABC 的顶点，并且与的延长线分别交于 P 、Q 、R,贝U BP CQ AR 1 PC QA RB证：设h A 、h B 、h C 分别是A 、B 、C 到直线l 的垂线的长度，贝u ：BP CQ AR h B h C hu 』 1PC QA RB h C h A h B注：此定理常运用求证三角形相似的过程中的线段成比例的条件;例1：若直角 ABC 中，CK 是斜边上的高， 在AK 上，D 是AC 的中点， F 是DE 与CK的交点，证明:KF BK ——=—— FC BE KF BK ——=一 KC KE FKB CKE BF //CECE 是 ACK 的平分线， E 点BF // CE 。

证：在 则：EBC 中，作 B"分线BH EBC ACK HBC ACEHBC HCB ACE HCB 90即：BH CEEBC 为等腰三角形作BC 上的高EP,则:对丁 ACK 和三点D 、 CK EPE 、F 依梅涅劳斯定理有:CD AE KF , 1 DA EK FC匚曰KF EK CK 『是——=一 一FC AE ACEP BP BK AC BC BE依分比定理有: ABC 的三边BC 、CA 、AB 或它们【练习1从点K 引四条直线，另两条直 -一 一 、…AC和 A 1、B 1、C 1、D 1,试证： ------- 1 1 1BC线分别交这四条直线丁 A 、B 、C 、DAD BD定理2：设P 、Q 、R 分别是 ABC 的三边 BC 、CA 、AB 上或它们的延长线上的 P 、Q 、R 三点中，位于 ABC 边上的点的个数为 0或2,这时若 既 PC 三点，并且 CQ AR QA RB 1, 求证：P 、Q 、R 三点共线; 证：设直线PQ 与直线AB 交丁 R ', 丁是由定理 BP CQ AR _ __ ' PC QA R B乂 BP CQ AR PC QA RB 由丁在同一直线上的 _ ' ____ AR AR1,则：^―=—— R B RB P 、Q 、R '三点中，位丁 ABC 边上的点的个数也为 0或2,因此R 与R '或者同在AB 线段上，或者同在 AB 的延长线上； 若R 与R '同在AB 线段上，则R 与R '必定重合，不然的话， 设AR AR ', AR AR BR BR 这时AB AR AB AR ',即BR BR ',丁是可得 _ ____ ' 这与AR =竺 矛盾 BR BR 类似地可证得当 R 与R '同在AB 的延长线上时,综上可得：P 、Q 、R 三点共线； 注：此定理常用于证明三点共线的问题，且常需要多次使用 R 与R '也重合再相乘;例2点P 位丁 ABC 的外接圆上；A 1、B 1、C 1是从点P 向BC 、CA 、AB 引的垂线的垂足, 证明点A 1、B 1、 BA 1BP cos PBC CA 1 CP cos PCB CB 1 CP cos PCA AB 1 AP cos PAC AC 1AP cos PABBC 1 PB cos PBAC i 共线; 证：易得: 将上面三条式子相乘， 且 PAC PBC , PAB PCB , 十曰 BA 1 CB 1 AC 1可得 一111= 1 ,CA 1 AB 1 BC 1依梅涅劳斯定理可知 A 1、B 1、C 1三点共线;PCA PBA 180A 1C 1 A 1D 1B 1C ； :BD【练习2设不等腰 ABC 的内切圆在三边 BC 、CA 、AB 上的切点分别为 D 、E 、F,则EF 与BC , FD 与CA , DE与AB 的交点 X 、Y 、Z 在同一条 直线上；【练习&已知直线 AA i, BB i, CC i 相交于O,直线AB 和A 1B 1的交点为C 2,直线 BC 与B 1C 1的交点是 A 2,直 线AC 与A i C i 的交点是B 2,试证：A 2、B 2、C 2三点共线;【练习M 在一条直线上取点 E 、C 、A,在另一条上取点 B 、F 、D,记直线AB 和ED , CD 和AF ,CD 和AF , EF 和BC 的交点依次为 L 、M 、N,证明：L 、M 、N 共线练习i 的证明练习2的证明乂 AE AF 代人上式可得：BXXC FB =—— CE CY DC AZ EA同理口」彳寸： — —YA AFZB BD将上面三条式子相乘可 得：乳CY J i XC YA ZB 乂 X 、Y 、Z 都不在 ABC 的边上，由定理 2可得X 、Y 、 证： ABC 被直线XFE 所截，由定理 Z 三点共线 证：若AD // A i D^,结论显然成立;若AD 与A i D i 相交与点 AD LD LD BD LD 〔 A i K A i D i AK BK BQ B i K LDi L,则把梅涅劳斯定理分 LC AK A 。

目录一、平面几何定理 (2)1、三角形 (2)（1）、重心 (2)（2）、垂心 (5)（3）、内心 (10)（4）、外心 (16)（5）、基本定理及其它性质 (23)○1、正弦定理 (23)○2、余弦定理 (23)○3、正切定理 (23)○4、半角定理 (24)○5、面积公式 (24)○6、三角函数 (24)2、圆 (25)垂径定理、圆周定理、切线长定理、弦切角定理、相交弦定理、割线定理、切割线定理3、重要的几何定理（1）、托勒密定理 (26)（2）、塞瓦定理 (27)（3）、梅涅劳斯定理 (28)（4）、斯特瓦尔特定理 (29)（5）、张角定理 (29)二、反演变换 (29)三、数形结合 (33)一、平面几何定理1、三角形（1）三角形的重心三角形的中线是接三角形顶点和它的对边中点的线段。

每个三角形都有三条中线，它们都在三角形的内部 [1]。

在三角形中，三条中线的交点是三角形的重心。

三角形的三条中线交于一点，这点位于各中线的三分之二处。

3/4。

这样就构成了由中线组成的三角形，两个三角形共同的元素为○7.重心和三角形3个顶点组成的3个三角形面积相等。

证明：S△AMB= S△BMC= S△CMA△AMB和△BMC以BM为底边，分别以AD、CE为高，易知AD＝CE∴S△AMB= S△BMC同理S△BMC= S△CMA○8.重心到三角形3个顶点距离的平方和最小。

证明（物理法）由平方和联想到转动惯量I＝mr2(其中m是其质量，r 是质点和转轴的垂直距离),根据转动惯量平行轴定理，可知质元绕过形心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。

而对于密度相同的平面来说，形心与重心重合，所以重心到三角形3个顶点距离的平方和最小。

证明（代数法）建立直角坐标系,为了方便,三角形的A顶点作为坐标原点（0,0）,AB边在X轴上,B点坐标（b,0）好算,然后设出C点的坐标(m,n)；再设三角形内的任意一点为（x,y）(x2+y2)+[(x-b)2+y2]+[(x-m)2+(y-n)2]=3x2+3y2-2bx-2mx-2ny+b2+m2+n2=3x2-2(b+m)x+3y2-2ny+b2+m2+n2=3[x-(b+m)/3]2+3(y-n/3)2+ b2+m2+n2-(b+m)2/3-n2/3 只有当2个平方项全等于0时，才最小。

定义：通过构造新的图形或对象来证明定理的方法 特点：直观、易于理解，能够将复杂问题转化为简单问题 应用：在平面几何中广泛应用于证明各种定理和性质 示例：通过构造辅助线来证明三角形的一些性质和定理
定义：通过代 数运算和逻辑 推理来证明平 面几何定理的
方法
特点：基于代 数方程和不等 式的推导，可 以证明一些较 为抽象和复杂
欧几里得几何定理 非欧几里得几何定理 解析几何定理 射影几何定理
计算机图形学：用于生成二 维图形和动画
物理学：用于描述物体运动 轨迹和力的作用
航空航天：用于设计和分析 飞行器的结构和性能
建筑学：用于设计和分析建 筑物的结构和稳定性
平行线性质： 平行线之间的
距离相等
角平分线性质： 角平分线将一 个角分为两个
计算机图形学中的应用：平面几何定理在计算机图形学中也有着重要的应用，例如在绘制二维图形、三维 模型等方面，需要利用平面几何定理进行计算和推导。
经济学中的应用：在经济学中，平面几何定理也被广泛应用，例如在分析市场供需关系、预测商品价格走 势等方面，需要利用平面几何定理进行数据分析和模型构建。
生物学中的应用：在生物学中，平面几何定理也被应用于一些领域，例如生态学中研究生物种群分 布、行为学中研究动物运动轨迹等方面，需要利用平面几何定理进行数据分析和模型构建。
的几何定理、三 角形的余弦定
理等
实例：通过代 数方法证明勾 股定理的过程
欧几里得几何定理：公元前300年左右，欧几里得在《几何原本》中提出了平面几何 的基本定理，奠定了平面几何的基础。
非欧几里得几何定理：19世纪，高斯、黎曼等数学家提出了非欧几里得几何，突破 了欧几里得几何的限制，进一步推广了平面几何定理。
定理在计算机图形学 中的应用：在制作动 画、游戏等计算机图 形学领域中，平面几 何定理被广泛应用。

高中数学的归纳平面几何基本定理与证明总结在高中数学中，平面几何是一个非常重要的分支，它研究了平面内各种图形之间的关系和性质。

而在学习平面几何时，归纳法是一个常用的证明方法。

本文将对高中数学中的归纳平面几何基本定理与证明进行总结。

一、线段中点定理线段中点定理是平面几何中的基本定理之一，它指出：在一条线段的中点上，可以作一条平行于这条线段的直线。

换句话说，如果在线段AB的中点M上作一条直线l，那么l与AB平行。

证明：连接AM、BM。

由于M是线段AB的中点，所以AM=BM，且由中点连线定理可知，AM∥BM。

根据平行线的性质可知，l∥AB。

二、角平分线定理角平分线定理是另一个重要的平面几何定理，它指出：一条角的平分线将这个角分成两个相等的小角。

证明：设∠AOB为一锐角，其中OC是∠AOB的平分线。

要证明∠AOC=∠BOC，我们可以利用三角形AOB和COA的相似性来进行证明。

由于OC是∠AOB的平分线，所以∠AOC=∠BOC。

又因为∠AOB是个锐角，所以∠COA也是个锐角，故∆COA和∆AOB是相似三角形。

根据相似三角形的性质可知，AO/CO=BO/CO，即AO=BO。

因此，∠AOC=∠BOC。

三、垂直平分线定理垂直平分线定理也是平面几何中的重要定理，它指出：一条线段的垂直平分线上所有点到线段的两个端点的距离相等。

证明：设线段AB上的垂直平分线为l，垂直平分线上的一点为M。

要证明AM=BM，我们可以利用三角形AMO和BMO的全等性来进行证明。

由于l是线段AB的垂直平分线，所以AM=BM，且∠AMO=∠BMO=90°。

又因为OM是l的一部分，所以MO=MO，自反性成立。

故∆AMO和∆BMO是全等三角形。

根据全等三角形的定义，可知AM=BM。

四、角的外角定理角的外角定理指出：一个三角形的外角等于它的两个不相邻内角的和。

证明：设三角形ABC的三个内角分别为∠A、∠B和∠C，对于∠A，其外角为∠D。

我们可以利用∆ABC和∆ACD的相似性来进行证明。

平面几何 定理及其证明一、 梅涅劳斯定理1．梅涅劳斯定理及其证明定理：一条直线和∆ABC 的三边AB 、BC 、CA 所在直线分别交于点D 、E 、F ，且D 、E 、F 均不是∆ABC 的顶点，则有．证明：如图，过点C 作AB 的平行线，交EF 于点G ． 因为CG // AB ，所以 ————（1） 因为CG // AB ，所以 ————（2）由（1）÷（2）可得，即得． 2．梅涅劳斯定理的逆定理及其证明 定理：在∆ABC 的边AB 、BC 上各有一点D 、E ，在边AC 的延长线上有一点F ，若，那么，D 、E 、F 三点共线． 证明：设直线EF 交AB 于点D /，则据梅涅劳斯定理有．因为 ，所以有．由于点D 、D /都在线段AB 上，所以点D 和D /重合．即得D 、E 、F 三点共线．二、 塞瓦定理3．塞瓦定理及其证明定理：在∆ABC 内一点P ，该点和∆ABC 的三个顶点相连所在的三条直线分别交∆ABC 三边AB 、BC 、CA 于点D 、E 、F ，且D 、E 、F 三点均不是∆ABC 的顶点，则有．证明：运用面积比可得．根据等比定理有 ADC ADC ADP APCADP BDP BDC BDC BDP BPCS S S S S S S S S S ∆∆∆∆∆∆∆∆∆∆-===-， 所以．同理可得，． 三式相乘得．4．塞瓦定理的逆定理及其证明定理：在∆ABC 三边AB 、BC 、CA 上各有一点D 、E 、F ，且D 、E 、F 均不是∆ABC 的顶点，若，那么直线CD 、AE 、BF 三线共点．证明：设直线AE 和直线BF 交于点P ，直线CP 交AB 于点D /，则据塞瓦定理有．因为 ，所以有．由于点D 、D /都在线段AB 上，所以点D 和D /重合．即得D 、E 、F 三点共线． 三、 西姆松定理5．西姆松定理及其证明 定理：从∆ABC 外接圆上任意一点P 向BC 、CA 、AB 或其延长线引垂线，垂足分别为D 、E 、F ，则D 、E 、F 三点共线．ABCDEFPA B C DEFD / A B CD E F G证明：如图示，连接PC ，连接 EF 交BC 于点D /，连接PD /．因为PE ⊥AE ，PF ⊥AF ，所以A 、F 、P 、E 四点共圆，可得∠FAE =∠FEP ．因为A 、B 、P 、C 四点共圆，所以∠BAC =∠BCP ，即∠FAE =∠BCP ． 所以，∠FEP =∠BCP ，即∠D /EP =∠D /CP ，可得C 、D /、P 、E 四点共圆．所以，∠CD /P +∠CEP = 1800。

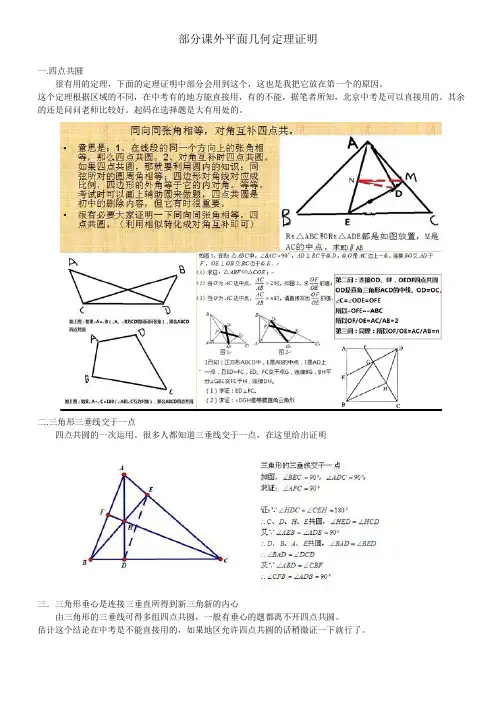
部分课外平面几何定理证明一.四点共圆很有用的定理，下面的定理证明中部分会用到这个，这也是我把它放在第一个的原因。

这个定理根据区域的不同，在中考有的地方能直接用，有的不能，据笔者所知，北京中考是可以直接用的。

其余的还是问问老师比较好。

起码在选择题是大有用处的。

二.三角形三垂线交于一点四点共圆的一次运用。

很多人都知道三垂线交于一点，在这里给出证明三．三角形垂心是连接三垂直所得到新三角新的内心由三角形的三垂线可得多组四点共圆，一般有垂心的题都离不开四点共圆。

估计这个结论在中考是不能直接用的，如果地区允许四点共圆的话稍微证一下就行了。

四．圆幂定理（在这里只是一部分）·为割线定理、切割线定理于相交弦定理的总称。

这个应该是很多地方都允许用的，如果不能用的话也是稍微证一下就行了。

五．射影定理（欧几里得定理）什么也不说了，初中几何里应该是比较常用的。

目测考试随便用六．三角形切线长公式·已知三角形三边长可求内切圆切点到顶点距离可能是做的题比较少吧，很少见有这样的中考题。

推导也是很简单的。

七．广勾股定理估计中考允许用的地方不多，除非你那允许“引理”这货八．弦切角定理很简单，估计每个地方都允许的。

就算不把它当定理，自己也能发现这个结论九．燕尾定理（共边比例定理）面积法思想，出现中点时可以用来证线段相等（例如下一个，重心），另外用于比例也是挺好使的。

中考的时候，直接用的话估计老师会认为你跳跃度太大，考虑的时候想到这个，证明的时候用面积法就行了。

十．海伦公式已知三角形三边可求其面积，可用余弦定理和正弦求面积公式推导，但余弦定理是高中知识（在后面会放出来）所以不用在这里。

另外公式里带根号，若三边中有根号的配凑一下应该可以开根。

这里是海伦公式的一个探讨，推广至n边形面积。

在第五页有海伦公式的各种变形，其中变形⑤的个边带有平方，可以解决边长带根号的问题，缺点是过于冗繁。

吧友可以根据自己的情况进行探讨。

中考嘛，一直不是很喜欢，过多的限制，不能发挥自己的能力。

Gerrald 加油坚持住Gerrald 加油坚持住Gerrald 加油坚持住莫利定理：将任意三角形的各角三等分，则每两个角的相邻三等分线的交点构成一个正三角形。

設△ABC中的∠B,∠C的两条三等分角线分別交于P, D两个点（图1），按照莫利定理，D是莫莱三角形的一個頂点，当然D就是△BPC的內心，因為BD, CD正好是∠CBP, ∠BCP的角平分线。

莫利三角形的另两个頂点E, F应该分別落在CP和BP上，因此我们产生了一个念头，如果能夠在CP, BP上找到E, F这两个点，使△DEF是个正三角形，再证AE、AF正好是∠BAC的三等分线就行了为此，先把DP连起來，在CP, BP上分別取两点E, F使∠EDP＝∠FDP＝30°,于是就得到一个三角形△DEF。

为什么它是一个正三角形呢？因为D是△BPC的內心，所以DP是∠BPC的角平分线，即∠DPE＝∠DPF，由作图知∠EDP＝∠FDP＝30°,在△DPE和△DPF中，DP是公共边，而夹此边的两角又是对应相等的，所以△DPE≌△DPF。

于是DE＝DF,即△DEF是个等腰三角形，它的腰是DE 和DF，而它的頂角又是60°，所以它当然是个正三角形。

接下來，我们的目标就是希望能证明△DEF真的是莫利三角形，亦即AE, AF 的确会三等分∠BAC。

如图2所示，在AB, AC上各取一点G,H,使得BG＝BD, CH＝CD，把G、F、E、H各点依次连起來，根据△BFD≌△BFG，△CED≌△CEH，我们就得到GF ＝FD＝FE＝ED＝EH。

下面，如果能夠证明G,F,E,H，A五点共圆，則定理的证明就完成了，因为∠GAF,∠FAE,∠EAH这三个圆周角所对的弦GF, FE, EH都等長，因而这三个圆周角也就都相等了。

为了证明G,H,E,F，A共圓，必须证明∠FGE＝∠FHE＝∠A/3。

看图2，首先我们注意到△GFE是个等腰三角形，∠GFE是它的顶角，如果这个角能求出來，其底角∠FGE也就能求出来了。

【认识平面几何的61个著名定理，自行画出图形来学习，★部分要求证明出来】★1、勾股定理（毕达哥拉斯定理）★2、射影定理（欧几里得定理）★3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线和两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

★6、三角形各边的垂直平分线交于一点。

★7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC 的外心为O ，垂心为H ，从O 向BC 边引垂线，设垂足不L ，则AH=2OL9、三角形的外心，垂心，重心在同一条直线上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中心、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上12、库立奇大上定理：（圆内接四边形的九点圆） 圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

★13、（内心）三角形的三条内角平分线交于一点，内切圆的半径公式： ()()()s c s b s a s r ---=，s 为三角形周长的一半★14、（旁心）三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理：（巴布斯定理）设三角形ABC的边BC的中点为P，则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理：P将三角形ABC的边BC分成m和n两段，则有n×AB2+m×AC2=BC×（AP2+mn）17、波罗摩及多定理：圆内接四边形ABCD的对角线互相垂直时，连接AB中点M和对角线交点E 的直线垂直于CD18、阿波罗尼斯定理：到两定点A、B的距离之比为定比m:n（值不为1）的点P，位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上★19、托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC×BD★20、以任意三角形ABC的边BC、CA、AB为底边，分别向外作底角都是30度的等腰△BDC、△CEA、△AFB，则△DEF是正三角形，21、爱尔可斯定理1：若△ABC和△DEF都是正三角形，则由线段AD、BE、CF的重心构成的三角形也是正三角形。

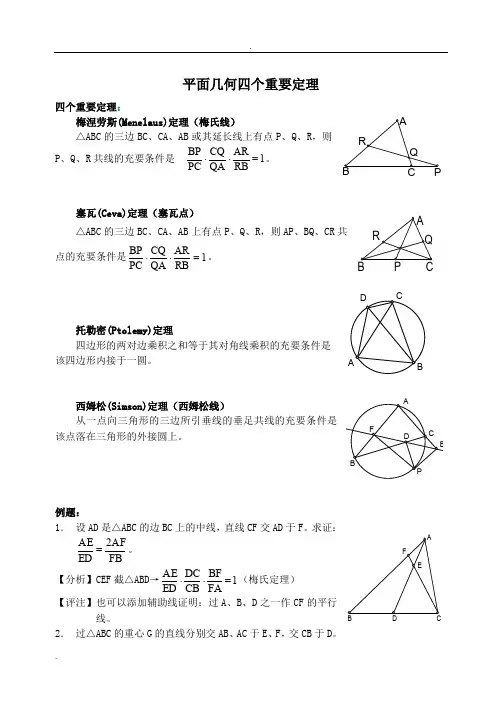
.平面几何四个重要定理四个重要定理：梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是 1RBARQA CQ PC BP =⋅⋅。

塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1RBAR QA CQ PC BP =⋅⋅。

托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。

西姆松(Simson)定理（西姆松线）该点落在三角形的外接圆上。

例题：1． 设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F。

求证：FBAF2ED AE =。

【分析】CEF 截△ABD →1FABF CB DC ED AE =⋅⋅（梅氏定理）【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。

2． 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。

DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅（梅氏定理）DGF 截△ACM →1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1 【评注】梅氏定理3． D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EA CEFB AF DC BD ，AD 、BE 、CF 交成△LMN 。

求S △LMN 。

【分析】【评注】梅氏定理4． 以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。

求证：AE 、BF 、CG 相交于一点。

【分析】【评注】塞瓦定理5． 已知△ABC 中，∠B=2∠C 。

求证：AC 2=AB 2+AB ·BC 。

【分析】过A 作BC 的平行线交△ABC 的外接圆于D ，连结BD 。

初中数学平面几何证明知识点总结平面几何作为初中数学的重要内容之一，是建立在基础几何概念和定理的基础上的。

在这篇文章中，我们将对初中数学平面几何证明的知识点进行总结和分析，帮助同学们更好地掌握这一部分知识。

一、平行线定理与证明1. 平行线的基本定义平行线是指在同一个平面内永不相交的两条直线。

平行线具有以下性质：- 平行线上的任意两点与另一条直线上的任意一点连线所得的角相等。

- 在同一个直线上，如果有一条线与另一直线平行，则与这两条线相交的直线也平行于它们。

2. 同位角定理和内错角定理平行线切割任意一对平行线时，所得的同位角相等，同位角的证明主要基于同位角定理。

同位角定理的表述如下：如果两条直线被一组平行线所截，那么从任意一条直线上截下的相应角和从另一直线上截下的相应角相等。

内错角定理亦是平行线定理的重要内容之一。

当一组平行线被一条截线切割时，截线分别与这两条平行线所夹的错角相等。

二、三角形的证明1. 三角形中的角度和定理三角形的内角和是180度，这是初中数学中的基本概念之一。

三角形的角度和定理有以下几种形式：- 三角形内角和等于180度；- 三角形的外角等于与之不相邻的两个内角之和。

2. 等腰三角形的性质和证明等腰三角形是指两条边长度相等的三角形。

等腰三角形具有以下性质和定理：- 等腰三角形的底角相等；- 等腰三角形的等腰边上的角是锐角；- 等腰三角形的等腰边上的角平分底角。

3. 相似三角形的性质和证明相似三角形是指具有相同形状但不同尺寸的三角形。

相似三角形具有以下性质和定理：- 相似三角形的对应角相等；- 相似三角形的对应边成比例；- 相似三角形的高比等于对应边长的比。

三、四边形的证明1. 平行四边形的性质和证明平行四边形是指具有两对平行边的四边形。

平行四边形具有以下性质和定理：- 相邻角互补；- 对角相等；- 对边成比例。

2. 矩形、菱形和正方形的性质和证明矩形、菱形和正方形是特殊的平行四边形。

．
证明：如图，过点C作AB的平行线，交EF于点G．
因为CG // AB，所以 ————（1）
因为CG // AB，所以 ————（2）
由（1）÷（2）可得 ，即得 ．
注：添加的辅助线CG是证明的关键“桥梁”，两次运用相似比得出两个比例等式，再拆去“桥梁”（CG）使得命题顺利获证．
4．梅涅劳斯定理的逆定理及其证明
由于 DAE = BAM，所以 DAM = BAE，即 DAC = BAE。而 ABD = ACD，即 ABE = ACD，所以 ABE∽ ACD．即得
，即 ————（2）
由（1）+（2）得
．
所以AB·CD + BC·AD = AC·BD．
注：巧妙构造三角形，运用三角形之间的相似推得结论．这里的构造具有特点，不容易想到，需要认真分析题目并不断尝试．
三、托勒密定理
5．托勒密定理及其证明
定理：凸四边形ABCD是某圆的内接四边形，则有
AB·CD + BC·AD = AC·BD．
证明：设点M是对角线AC与BD的交点，在线段BD上找一点，使得 DAE = BAM．
因为 ADB= ACB，即 ADE = ACB，所以 ADE∽ ACB，即得
，即 ————（1）
五、欧拉定理
9．欧拉定理及其证明
定理：设ΔABC的重心、外心、垂心分别用字母G、O、H表示．则有G、O、H三点共线（欧拉线），且满足 ．
证明（向量法）：连BO并延长交圆O于点D。连接CD、AD、HC，设E为边BC的中点，连接OE和OC．则
———①
因为CD⊥BC，AH⊥BC，所以AH // CD．同理CH // DA．
另外，待定系数法在其中扮演了非常重要的角色，需注意掌握其用法．

所以
AD DB
三式相乘得
SADP SBDP

SAPC SBPC
AD DB

BE EC
SADC SBDC


CF FA
．同理可得
BE EC

CF FA


1．

SADP SBDP
SADC SADP SBDC SBDP
1．
注：在运用三角形的面积比时，要把握住两个三角形是
的延长线上有一点
那么，D、E、F 三点共线．
证明：设直线 EF 交 AB 于点
D/，则据梅涅劳斯定理有
F，若
AD DB
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气，线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

平面几何的性质平行四边形的性质及其证明平面几何的性质——平行四边形的性质及其证明平行四边形是平面几何中的一种特殊形状，具有独特的性质和特点。

本文将介绍平行四边形的性质以及相关的证明。

一、平行四边形的定义及性质平行四边形是指四边形的对边两两平行，即其中任意两条边都是平行的四边形。

在平行四边形中，存在以下性质：1. 对角线互相平分平行四边形的对角线互相平分。

证明如下：设平行四边形ABCD的对角线AC和BD相交于点O。

由于平行四边形的两组对边平行，因此∠BAD=∠BCD、∠ABD=∠ACD。

再结合共同顶点A和共线的点B、D，根据三角形内角和定理可得：∠BAD+∠ABD+∠ACD=180°。

又因为∠BAD=∠BCD，代入上述等式，得到2∠BAD+∠BAD=180°，即3∠BAD=180°，所以∠BAD=∠BCD=60°。

同理可证，∠ABC=∠ADC=120°。

因此，以点O为圆心，OB为半径的圆可以过点D，以点O为圆心，OD为半径的圆可以过点B，这说明对角线AC和BD互相平分。

2. 对边相等平行四边形的对边相等。

证明如下：由于平行四边形的两组对边平行，可以得到以下等式：AB ∥ CD，AD ∥ BC。

根据平行线与横切线定理可知，任意一条横切线AB与平行线CD之间的交角等于对边AD与平行线BC之间的交角。

因为平行线CD与AD之间的交角等于∠ADC，平行线BC与AB之间的交角等于∠ABC，根据前述证明可得∠ADC=∠ABC=120°。

再结合对角线互相平分的性质，可以推导出∠ACD=∠ABD=60°。

根据三角形的全等条件，可以得到△ADC≌△ABC，因此AD=BC，AB=CD，即平行四边形的对边相等。

3. 对角线长度关系平行四边形的对角线长度关系。

证明如下：设平行四边形ABCD的对角线AC和BD相交于点O。

根据三角形内角和定理可得∠ADC+∠ACD+∠ADC=180°。

平面几何的几个重要的定理一、梅涅劳斯定理：1=⋅⋅=⋅⋅BAA C CBC B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度，则：到直线、、分别是、、证：设注：此定理常运用求证三角形相似的过程中的线段成比例的条件；。

的交点，证明：与是的中点，是上，在点的平分线，是是斜边上的高，中，：若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠∆11PC BP R Q PAB CA BC ABC ABC l 1=⋅⋅RBARQA CQ ，则、、的延长线分别交于或它们、、的三边的顶点，并且与不经过：若直线定理∆∆CE//BF CKEFKB KEBK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FCKFEK AE DA CD F E D ACK EPCK EP BC EBC CEBH 90HCB ACE HCB HBC ACEHBC ACKEBC BHB EBC ∴≅∴=====⋅⋅=∴⊥︒=∠+∠=∠+∠∠=∠∠=∠∠∆∆∆∆∆＝依分比定理有：＝即：＝于是依梅涅劳斯定理有：、、和三点对于，则：上的高作为等腰三角形即：则：的平分线中，作在证：111111111111D B D A :C B C A BD AD :BC AC D C B A DC B A K 1=，试证：、、、和、、、线分别交这四条直线于引四条直线，另两条直】从点【练习注：此定理常用于证明三点共线的问题，且常需要多次使用 再相乘；共线；、、证明点引的垂线的垂足，、、向是从点、、的外接圆上；位于点例111111C B A AB CA BC P C B A ABC P .2∆三点共线；、、综上可得：也重合与的延长线上时，同在与类似地可证得当矛盾＝这与于是可得即这时设必定重合，不然的话，与线段上，则同在与若的延长线上；线段上，或者同在或者同在与因此，或边上的点的个数也为三点中，位于、、由于在同一直线上的＝，则：又得：，于是由定理交于与直线证：设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RBAR B R AR 1RB AR QA CQ 1BR AR QA CQ 1R AB PQ ''''''''''''''''''><-<->=⋅⋅=⋅⋅∆PC BP PC BP 三点共线；、、求证：，，这时若或边上的点的个数为三点中，位于、、三点，并且上或它们的延长线上的、、的三边分别是、、：设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RBARQA CQ =⋅⋅∆∆ C BA1A 1B 1C 三点共线；、、依梅涅劳斯定理可知，＝可得且将上面三条式子相乘，证：易得：111111111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBAcos PB PABcos AP BC AC PAC cos AP PCAcos CP AB CB ,PCBcos CP PBCcos BP CA BA ⋅⋅︒=∠+∠∠=∠∠=∠∠⋅∠⋅-=∠⋅∠⋅-=∠⋅∠⋅-=直线上；在同一条、、的交点与，与，与，则、、上的切点分别为、、的内切圆在三边】设不等腰【练习Z Y X AB DE CA FD BC EF F E D AB CA BC ABC 2∆三点共线；、、，试证：的交点是与线，直的交点是与，直线的交点为和，直线相交于，，】已知直线【练习222211*********C B A B C A AC A C B BC C B A AB O CC BB AA 311111111111111111111111111111111111111D B D A :C B C A BD AD :BC AC 1C BD B D A C A BD BC AC AD 1LD D B K B BK BD LD 1BKKB C B LC LC BC 1LC C A K A AK AC LC 1AK KA D A LD LD AD BLB AL A L D A AD D A //AD 1==⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅即：得：将上面四条式子相乘可可得：和别用于，则把梅涅劳斯定理分相交与点与若，结论显然成立；证：若的证明练习∆∆共线、、，证明：、、的交点依次为和，和，和，和，记直线、、，在另一条上取点、、】在一条直线上取点【练习N M L N M L BC EF AF CD AF CD ED AB D F B A C E 4三点共线、、可得的边上，由定理都不在、、又得：将上面三条式子相乘可＝＝同理可得：＝代人上式可得：又可得：所截，由定理被直线证：的证明练习Z Y X 2ABC Z Y X 1ZBAZYA CY XC BX BDEAZB AZ AF DC YA CY CEFBXC BX AF AE 1FBAFEA CE XC BX 1XFE ABC 2∆∆ =⋅⋅==⋅⋅共线由梅涅劳斯定理可知可得：将上面的三条式子相乘应用梅涅劳斯定理有：，和，和，和们边上的点：对所得的三角形和在它的交点，和，和，和分别是直线、、证：设的证明练习222222222221111221111221111211211211111111222C ,B ,A 1BA CA CB AB AC BC 1CB AB OC CC AA OA 1BA CA OB BB CC OC 1AC BC BB OB OA AA )B ,C A (OAC ),A ,C B (OBC ),C ,B A (OAB B A AB C A AC C B BC C B A 3=⋅⋅=⋅⋅=⋅⋅=⋅⋅平面几何的几个重要定理――――塞瓦定理 塞瓦定理：1:=⋅⋅∆RBARQA CQ PC BP CR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点，则、、的分别是、、设共线点得：将上面五条式子相乘可，则有点涅劳斯定理于五组三元，应用梅，对、、的交点分别为和，和，和证：记直线的证明练习N ,M ,L ,1VNUNUM WM WL VL 1UFVFWD UD VB WB 1UE VE WC UC VA WA 1WB VB UC WC VN UN 1YM WM VF UF WA VA 1UD WD WL VL VE UE )F ,D ,B (),E ,C ,A (),N ,C ,B (),F ,M ,A (),E ,D ,L (UVW W V U CD AB AB EF CD EF 4∴=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅∆MQRACPB；相交于一点点、、重合，故必与上，所以都在线段和因为＝于是：，由塞瓦定理有：，于交，且直线相交于与，设再证充分性：若＝以上三式相乘，得：同理：，则：相交于点、、证：先证必要性：设’’‘’‘’‘M CR BQ AP R R AB R R RB ARB R AR BR AR QA CQ PC BP R AB CM M BQ AP RB AR QA CQ PC BP RB ARQA CQ PC BP S S RB AR S S QA CQ S S S S S S PC BP M CR BQ AP BCMACMABMBCMACM ABMCMP BMP ACP ABP 111=⋅⋅=⋅⋅⋅⋅=====∆∆∆∆∆∆∆∆∆∆交于一点；：证明：三角形的中线例1交于一点；成立，即而显然有：我们只须证明，，，的中线证明：记ABC AB CBC A BA B C AC A B CB C A BA B C AC AB CBC A BA B C AC CC BB AA ABC ∆∴=⋅⋅====⋅⋅∆1,,1111111111111111111111分线交于一点；】证明：三角形的角平【练习1 高交于一点；】证明：锐角三角形的【练习2ABCP P BM AN N M BC AC L L AB C ABC ⊥∠∆，证明：的交点是和，设和足分别是的垂线，垂和作边，从于的平分线交于中，角：在锐角例2CB A1A 1B 1C CBA1A 1B 1CABCP P AN BM CK BLBCAC AL BLBCAC AL BLBCNB BK BKC BNL ACALAK AM AKC AML NBBKAK AM CNMC AKBK NB CN MC AM AN BM CK P AN BM CK ABCK ⊥∴∴=⋅=⋅=⇒∆≅∆=⇒∆≅∆=⋅==⋅⋅⊥点三线共点，且为、、理可知：依三角形的角平分线定即要证即要证明：又即要证：三线共点，依塞瓦定理、、要证点，三线共点，且为、、下证证：作1111FDA EDA ANAM BF BD AF CE CD AE FBAFEA CE DC BD P CF BE AD BFBDAFAN CE CD AE AM BF AF BD AN CE AE CD AM BDFANF CDE AME BC MN BCAD ∠=∠∴=∴⋅=⋅∴=⋅⋅⋅=⋅===∴∆≅∆∆≅∆⊥1,,,//，根据塞瓦定理可得：共点于、、于是，可得，故三线共点；、、，证明：，且、、外有三点】已知【练习CR BN AM BCM ACN ABR CBM CAN BAR R N M ABC γβα=∠=∠=∠=∠=∠=∠∆,,3K LNM CBAFDAEDA F E AB AC CP BP AD P BC D ABC AD ∠∠∆＝，则和交于、分别与、上任一点，是边上，若在的高，且是设例.3ANAM FDA EDA N M DF DE AD A =∠=∠可以转化为证明，。

平⾯⼏何基本定理（共线、共点问题）⼏何重要定理⼀【基础知识】梅涅劳斯定理设直线DEF 交ABC 三边,,BC CA AB 所在直线于,,D E F ，若,,D E F 三点共线，则1AE CD BF EC DB FA= 证明⼀过C 作DF 平⾏线交AB 于P则AE AF EC FP =，CD PFDB FB=，两式相乘得AE CD AF EC DB BF = ，即1AE CD BF EC DB FA= 证明⼆由正弦定理，sin sin CD CEDCE CDE∠=∠ sin sin BF BDF BD BFD ∠=∠，sin sin AE AFEAF AEF∠=∠三式相乘即得1AE CD BF EC DB FA = 证明三由于CD CDF DB BDF = ，BF BDFFA ADF= ， AE AEF AED AEF AED ADFEC CEF CED CEF CED CDF+====+ ，三式相乘即得1AE CD BF EC DB FA= 梅涅劳斯定理的逆定理设,,D E F 分别是ABC 的边,,BC CA AB 或其延长线上的点，且有奇数个点在边的延长线上，1AE CD BF EC DB FA= ，则,,D E F 三点共线塞⽡定理设,,D E F 分别是ABC 的边,,BC CA AB 或其延长线上的点，若,,AD BE CF 三线平⾏或共点，则1AE CD BF EC DB FA= 这⾥只给出三线共点时的证明证明⼀过A 作BC 平⾏线交,BE CF 于,M N于是有AE AM EC BC =，CD ANDP AP= PD AP DB AM =，BF BC= 四式相乘即得1AE CD BF EC DB FA=证明⼆对截线CPF 以及ABD 应⽤梅涅劳斯定理有1AP DC BF PD CB FA= ，对截线BPE 以及ACD 应⽤梅涅劳斯定理有1AP DB CE PD BC EA= ，两式相除即得1AE CD BF EC DB FA= 证明三由合⽐定理AE ABE APE ABE APE ABPEC BCE PCE BCE PCE BCP-====- ，同理有CD ACP DB ABP = ，BF BCP FA ACP = ，三式相乘即得1AE CD BFEC DB FA= 注点P 常称为赛⽡点塞⽡定理的逆定理设,,D E F 分别是ABC 的边,,BC CA AB 或其延长线上的点，且有偶数个点在边的延长线上，1AE CD BFEC DB FA= ，则,,AD BE CF 三线平⾏或共点⾓元形式的塞⽡定理设,,D E F 分别是ABC 的边,,BC CA AB 或其延长线上的点，且有偶数个点在边的延长线上，则三直线,,AD BE CF 平⾏或共点的充要条件是sin sin sin 1sin sin sin BAD ACF CBEDAC FCB EBA∠∠∠=∠∠∠证明由于sin sin BD ABD AB BADDC ACD AC DAC∠==∠，同理sin sin AF AC ACF FB BC FCB ∠=∠，sin sin CE BC CBEEA AB EBA∠=∠，三式相乘，再运⽤塞⽡定理及其逆定理，知结论成⽴【典型例题】例1在四边形ABCD 中，,,ABD BCD ABC 的⾯积⽐是3：4：1，点,M N 分别在,A C B D 上，满⾜::AM AC CN CD ，并且,,B M N 共线，求证：M 与N 分别是AC 和BD 的中点（1983年全国⾼中数学联赛）证明设(01)AC AM CN==<<，AC 交BD 于E ∵ABD ：BCD ：ABC =3：4：1∴17BE BD =，37AE AC = 37371771AM AE r EM AM AE r AC AC AM MC AC AM r r AC----====---- 对CDE 以及截线BMN 应⽤梅涅劳斯定理：1CN DB EMND BE MC= 即77311177r r r r -=-- ，化简整理，得2610r r --=，解得12r = 故M 与N 分别是AC 和BD 的中点例2在ABC 中，AM 是中线，G 在AM 上且2AG GM =，过G 的直线分别交线段,AB AC 于,E F ，交直线BC 于D ，求证：1B E C FE AF A+=证明对,ABM ACM 以及截线DEGF 应⽤两次梅涅劳斯定理：1AE BD MG EB DM GA = 1AF CD MG FC DM GA= ∵2AG GM = ∴2BD BE DM EA =……① 2CD CFDM FA=……②⽽2BD CD DM BM DM CM DM +=-++= ∴①+②即得1BE CFEA FA+=例3在平⾏四边形ABCD中，,E F分别是,AF ED交于G，AB CD上的点，,AD BC于,L M，求证：BF CE交于H，直线GH分别交,, Array DL BM证明设直线GH 分别交,CD AB 于,I J 对ECD 以及截线GHI 应⽤梅涅劳斯定理：1EG DI CH GD IC HE= ……①对FAB 以及截线HGJ 应⽤梅涅劳斯定理：1AG FH BJGF HB JA= ……②由于//AB CD ，于是,EG AG CH FH GD GF HE HB ==，结合①②有DI BJIC JA = 即CD CI AB AJCI AJ++=，于是CI AJ = ⼜BM BJ AB AJ CD CI DI DLCM CI CI AJ AJ AL++===== 结合AD BC =，所以DL BM =说明多次应⽤梅涅劳斯定理时要有对称的思想例 4 过ABC的三个顶点,,A B C作它的外接圆的切线，分别和直线P Q R三点共线P Q R，求证：,,,,BC CA AB交于,,证明由梅涅劳斯定理及其逆定理，知 ,,P Q R 三点共线1BP CQ AR PC QA RB= ⽽∵AP 是圆的切线∴BPA APC ∽从⽽22BP BPA AB PC APC AC == 同理22CQ BC QA AB=，22AR AC RB BC = 所以1BP CQ ARPC QA RB= ，故,,P Q R 三点共线说明证明点共线问题常⽤梅涅劳斯定理的逆定理例5 圆内接六边形ABCDEF中，三组对边AB与DE，BC与EF，CD 与FA分别交于,,P Q R三点共线（帕斯卡定理）P Q R，求证：,,N证明设直线,,BC AF DE 交得KMN ，对KMN 以及截线,,PAB QEF RDC 应⽤梅涅劳斯定理：1NB KP MA BK PM AN= ……① 1NQ KE MF QK EM FN= ……② 1NC KD MR CK DM RN= ……③另⼀⽅⾯，KC KB KD KE = ……④ME MD MF MA = ……⑤NB NC NA NF = ……⑥①×②×③结合④⑤⑥得：1KP MR NQPM RN QK= 由梅涅劳斯定理的逆定理知,,P Q R 三点共线说明把题⽬中的圆换成任意⼆次曲线（圆，椭圆，双曲线，抛物线），结论仍然成⽴例6 设,,D E F 分别是ABC 的边,,BC CA AB 或其延长线上的点，且有奇数个点在延长线上，则,,D E F 共线当且仅当sin sin sin 1sin sin sin ABE CAD BCFEBC DAB FCA∠∠∠=∠∠∠（第⼀⾓元形式的梅涅劳斯定理）证明由梅涅劳斯定理及其逆定理：,,D E F 共线1AE CD BF EC DB FA= ⽽sin sin AE ABE AB ABEEC BCE BC EBC ∠==∠ sin sin CD CDA AC CADDB DAB AB DAB ∠==∠ sin sin BF BCF BC BCFFA ACF AC FCA ∠==∠∴sin sin sin 11sin sin sin AE CD BF ABE CAD BCF EC DB FA EBC DAB FCA∠∠∠=?=∠∠∠例7凸四边形ABCD对⾓线交于点J，点,,,AB BC CD DASW X T分别在,,,上，点P在AC上，点,Q R在BD上，且点,,,S P R X四点W Q P T四点共线，点,,,共线，若,=BQ RD WQ PT==，求证：SP RX证明设,,,BQ a QJ b JR c RD d ====，则a d = 对PQJ 以及截线BWC 应⽤梅涅劳斯定理：1PW QB JCWQ BJ CP= ……①对PQJ 以及截线ATD 应⽤梅涅劳斯定理：1PT QD JA TQ DJ AP= ……②由于,WQ PT WP TQ ==，①×②得：1JA JC a b c d AP CP a b c d++=++ ……③对PRJ 以及截线ASB 应⽤梅涅劳斯定理：1PS RB JA SR BJ AP = ……④对PRJ 以及截线CXD 应⽤梅涅劳斯定理：1PX RD JCXR DJ CP= ……⑤④×⑤得：JA JC d a b c SR XR AP CP c d a b SP XP++=++ ……⑥由于a d =，⽐较③，⑥式，得：1SR XRSP XP=设,,SP x PR y RX z ===，代⼊，知x z =，即SP RX =说明有时在⼀条直线上的线段过多时，可分别设其长度为,,a b c 等，⽤代数⽅法解决例8 在ABC 中，,D E 是边,AC AB 上的点，,BD CE 交于P ，延长AP 交BC于M ，求证：M 是BC 中点当且仅当//DE BC证明对ABC 以及点P 应⽤塞⽡定理：1AD CM BEDC MB EA= 于是//AD AEBM CM DE BC DC EB=?=? 说明当,D E 分别在,AC AB 延长线上时，也有此结论，请读者⾃⾏证明例9 凸四边形ABCD 中AC 交BD 于Q ，BA 延长线交CD 延长线于P ，BC 延长线交AD 延长线于F ，PQ 延长线交BC 于E ，求证：BF BEFC EC=证明对PBC 以及点Q 应⽤塞⽡定理得：1BE CD PA EC DP AB= 对PBC 以及截线ADF 应⽤梅涅劳斯定理得：1BF CD PA FC DP AB= ⽐较两式即得BF BEFC EC=B例10在四边形ABCD中，对⾓线AC平分BAD∠，在CD上取⼀点E，BE 与AC相交于F，延长DF交BC于G，求证：GAC EAC∠=∠（1999年全国⾼中数学联赛）B证明连接BD 交AC 于H 对BCD 以及点F 应⽤塞⽡定理：1CG BH DEGB HD EC= 由⾓平分线定理得BH ABHD AD= 于是1CG AB DEGB AD EC= ……①过C 作AB 的平⾏线交AG 延长线于I 过C 作AD 的平⾏线交AE 延长线于J 则,CG CI DE ADGB AB EC CJ== 代⼊①中得CI CJ =⼜180180ACI BAC DAC ACJ ∠=?-∠=?-∠=∠因此ACI ACJ ? ，从⽽GAC EAC ∠=∠。