当前位置：文档之家 › 07 粘性流体动力学基础

07 粘性流体动力学基础

  • 格式：doc
  • 大小：1.17 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

粘性流体动力学基础

粘性流体动力学基础
第七章 粘性流体动力学基础
我们知道，任何流体都是有粘性的。现在也发现，有些流体在极 低的温度条件下会出现超流现象（如同超导一样），此时流体的粘性 为零。但我们不去关注这些物理现象，把我们的注意力集中在通常时 间空间和工程条件的规定的范围内，所以可以有上述的结论。
在第四章（积分方程）和第五章（微分方程）基本方程的推导过 程中，我们尽量避免限制条件的引入，以使所建立的数学模型具有广 泛的适用性。但在应用时却又无一例外的加上了理想流体的限制，粘 性仿佛成了使人望而生畏的东西。那么人们为什么会谈粘色变，他肯 定会对流动过程产生影响，那么这种影响又是什么。怎样建立描述粘 性流体流动过程的封闭方程组，以及在流动过程中的合理简化方程并 获得解，等等。这些将使我们在这一章要开始接触的问题。当然，粘 性流动工程问题的解决，我们更多的还是依赖于经验，而80年代以 后迅速发展的计算流体动力学也为我们提供了有力的武器。
一、圆柱绕流
利用流场叠加法，均直流+偶极子，求得理想流体作圆柱绕流的 流场，流谱左右和上下对称。当Re很小时，这时惯性力相对粘性力 很小，可忽略惯性力。可得到粘性流场的精确解，如图。从流谱图 上看，两者非常接近。两个极限情况图画是很相似的，但在细节上 还是有不同的。1，速度分布如图。2，压力分布的左右不对称。
沿程损失： 局部损失： 则总损失：
λ：沿程阻力系数 ζ：局部阻力系数
第二节 层流与湍流
人们从实践中认识到，流动过程存在两种完全不同的状态，称之 为层流状态和湍流状态，湍流也叫紊流，100多年前（1883年）,雷诺 的著名实验对这两种状态能作出最好的说明，即通过一个染色液线 对圆管内的流动进行观察。
第一节 流动的粘性效应
在理想流体的假设下，我们通过求解位势流动的拉普拉斯方程组 可以得到一些流动图画。由于流体都是有粘性的，所以我们在实验条 件下的到的，总是粘性流体流动的真实图画，那么两者之间有什么区 别，粘性又会产生怎么样的影响呢？下面我们通过几个典型流场来讨 论这一问题，以建立初步的认识。

粘性流体动力学基础

粘性流体动力学基础
于是有：
v vvx dy v dy vx (v vx )dy
2 0 0 2 x 0
因此可得：







0
vx vx (1 ) dy v v
物理意义：
边界层内损失的动量相当于厚度为
的理想流体动量。
几个厚度比较：

dv 1 p x p y p z f dt x y z
上式即为粘性流体运动应力形式的动量方程。
( v) 0 t 未知量10个： u, v, w, , pxx , p yy , pzz , pxy , pxz , p yz
y 0时vx ( x,0) 0与v y ( x,0) 0 y 时vx ( x, y ) v ( x)
在推导边界层方程时曾得到过下述结论，即
u u 2u u v 与 x y y 2
是同数量级的。所以推出：

x
v
可见，边界层厚度 与流体的运动粘度 以及边界层所 在位置的坐标x的平方根成正比，和势流的速度的平方根成反比。 即流体越粘稠，势流速度越小，边界层越厚。并且边界层的厚度 随x的增大而不断加厚。
而与粘性系数
及管长
成反比。
4.阻力及阻力系数（层流） u p t r 剪应力分布: r 2l
p a 管壁剪应力： t 0 2l
2 t 0 u m
1 8
摩擦阻力：
F t 0 2al a 2 p
第二节 边界层基本概念
边界层定义：在被绕流物体表面上的一层厚度很小且其中的 流动具有很大法向速度梯度和旋度的流动区域称做边界层。 在边界层中呈现有较强的粘性作用，并形成对流动的阻力。

《工程流体力学》第七章 粘性流体动力学

《工程流体力学》第七章 粘性流体动力学

x方向 ： 1)表面力：作用在左右两面上力的合力：
作用在上下两面上力的合力：
作用在前后两面上力的合力：
作用在整个六面体上表面力沿x轴方向的合力：
2) x方向质量力 ： 单位质量流体受到的质量力分量：X;
六面体受到的质量力： Xrdxdydz
牛顿第二定律：
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式：
应力：各向同性
运动粘性流体：存在法向、切向表面力 应力：各向异性
流体中：任一点c ：绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz：定义c上的应力
需要2个下标表示：9个应力分量
第1个下标i：应力作用方向 第2个下标j：作用面方向
第七章 粘性流体动力学
运动粘性流体与理想流体的差别： 1. 粘性切应力：存在 2. 物面上流体速度：为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力： 1.质量力：与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法：和理想流体相同
2. 表面力： 静止和运动理想流体：仅存在指向作用面法向表面力
由于外部无粘流：受到分离流的排挤 明显改变：其中压强分布 实际计算：用实测物面压力分布计算分离点前附面层流动 附面层分离：使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生：是工程上一个重要问 题
边界层分离后：形成尾涡区 尾涡区压强：基本上等于分离点压强 压强：上下对称 若将压强在圆柱面上积分：则得压差阻力
流体在y+l层时均速度：

第六章粘性流体动力学基础

第六章粘性流体动力学基础

第六章 粘性流体动力学基础实际流体都是有粘性的，只有当粘性力与惯性力相比很小时，才能忽略粘性力而采用“理想流体”这个简单的理想模型。

支配粘性流体运动的方程比理想流体的基本方程复杂得多，因此粘性流体动力学问题的求解比理想流体动力学问题更加复杂、困难。

本章的目的在于介绍粘性流体动力学的一些基本知识。

§1 雷诺数（Re ）——粘性对于流动的影响的大小的度量粘性流体运动方程为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=z y x Dt D z y x p p p f V ρ1 在x 方向的投影为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+∂∂z p y p x p f z u w y u v x u u t u zx yx xx x ρ1 这里以xu u ∂∂作为惯性力的代表； y p yx ∂∂ρ1作为粘性力项的代表，其大小为⎪⎪⎭⎫ ⎝⎛∂∂∂∂y u y μρ1。

下面以圆球的粘性流体绕流为例，来估算作用在单位质量流体上的惯性力和粘性力的量阶：（插圆球绕流图）L 为所研究问题的特征长度；∞V 为特征速度；∞ρ为特征密度；∞μ为特征粘性系数。

u 的量阶为∞V ；x u ∂∂的量阶为L V ∞； 22yu ∂∂的量阶为L V 2∞， 则： 作用在单位质量流体上的惯性力的量阶为：LV 2∞ 作用在单位质量流体上的粘性力的量阶为：2L V ∞∞∞ρμ 粘性力惯性力～22L V L V ∞∞∞∞ρμ＝∞∞v L V ＝∞Re Re 称为雷诺数（Reynolds 数），它的物理意义是作用在流体上的惯性力与粘性力的比值的度量。

Re 数是粘性流体动力学中最重要的无量纲参数，它在粘性流体动力学中所占地位与无粘气体动力学的M 数相当。

在不同Re 数范围内的粘性流体运动可以有完全不同的性质，下面以圆柱绕流为例看不同Re 数范围内的圆柱绕流运动。

（插圆柱绕流图）总之：Re 增加，粘性影响变弱，当Re 》1时，对于某些问题，如无分离绕流物体的升力问题，可忽略粘性影响，采用“理想流体”模型。

流体力学第7章黏性流体动力学

流体力学第7章黏性流体动力学
影响因素
影响层流向湍流过渡的因素包括流体的物理性质（如黏度、密度等）、流动通道的几何形 状、流动速度以及外部扰动等。这些因素共同作用，决定了层流向湍流过渡的条件和过程 。
04
管道内黏性流体流动规律 探讨
管道内充分发展层流流动规律
速度分布
在管道截面上，黏性流体的速度分布呈现抛物线形，最大速度出 现在管道中心，沿径向逐渐减小至管壁处为零。
生成。漩涡会不断从流体中吸收能量并逐渐扩大，对物体产生阻力和升
力作用。
03
尾迹形成
随着漩涡的脱落和扩散，流体会在物体后方形成一个尾迹区。尾迹中的
流动速度较低，压力较高，对物体的阻力和升力产生影响。
黏性流体绕运动物体流动现象描述
边界层变化
当黏性流体绕过运动物体时，由于相对速度的变化，物体表面的边界层会发生变化。在顺流方向，边界层厚度逐渐增 加；在逆流方向，边界层厚度逐渐减小。
05
黏性流体绕物体流动现象 研究
黏性流体绕静止物体流动现象描述
01
流动分离
当黏性流体绕过静止物体时，由于黏性作用，流体会在物体表面形成一
层附面层。随着流体向下游流动，附面层厚度逐渐增加，流动速度逐渐
减小，直至流动分离发生。
02
漩涡生成
在流动分离后，流体会在物体后方形成一个低压区，导致流体中的漩涡
流量与压力降关系
层流流动时，管道内流量与压力降成正比，符合泊肃叶定律。
ห้องสมุดไป่ตู้流动稳定性
层流流动相对稳定，不易受到扰动影响。
管道内充分发展湍流流动规律
速度分布
湍流流动时，速度分布在管道截面上呈现不规则变化，存在涡旋和 脉动。
流量与压力降关系
湍流流动时，管道内流量与压力降的关系不再符合泊肃叶定律，而 是呈现更为复杂的非线性关系。

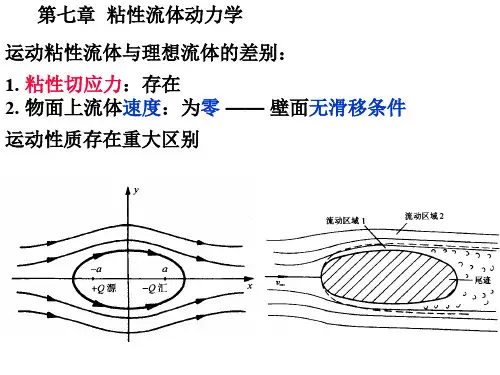
《工程流体力学》第七章 粘性流体动力学

《工程流体力学》第七章 粘性流体动力学
附面层厚度d：从外边界到物面的垂直距离
2.附面层位移厚度d*: 设物面P点附面层厚度d ，在垂直于纸面方向取单位宽度，
则该处通过附面层的质量流量：
通过同一面积理想流体流量：
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面，
使两块阴影处面积相同：
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动，整个流场分为三个区域：
1)附面层： 流速：由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向：速度梯度很大
即使流体粘性系数小：粘性应力仍可达到一定数值
由于速度梯度很大： 使得通过附面层物体 涡旋强度很大，流体 是有旋的
2)尾迹流： 附面层内流体：离开物体流入下游，在物体后形成尾迹流
各物理量都是统计平均值， \ 瞬时物理量＝平均物理量＋脉动物理量， 对整个方程进行时间平均的运算。
一、常用时均运算关系式：
时均运算规律：
推论：脉动量对空间坐标各阶导数的时均值=0。
二、连续方程：对二维流动，瞬态运动连续方程 进行时均运算：
\ 可压缩紊流运动连续方程：
进行时均运算： 上两式相减：
\ 附加法向应力
法向应力： l： 比例系数，与体积变化率有关
三个法向应力平均值的负值：为粘性流体在该点压强
最后得表面应力与变形率之间的关系：
第二节 粘性流体运动的基本方程
一、连续方程：
粘性流体运动：服从质量守恒定律 连续方程：不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程： 粘性流体中：微元六面体 微元六面体中心：c
三、雷诺方程： 二维不可压缩粘性流，不考虑质量力，N-S为：
对上式进行时均运算：

粘性流体动力学基础

粘性流体动力学基础
⎩
= τ xz
=
μ ( ∂vz
∂x
+
∂vx ) ∂z
=
2με zx
五、法向应力与变形速度的关系
在理想流体中，同一点各个方向的法向应力（压强）与作用的方位无
关而且相等，即： pxx = pyy = pzz = p 但在粘性流体中，流体微团除了发生角变形（角变形引起切应力）,同时
发生直线变形，使微团产生拉伸或压缩。
方程。 N-S 方程表示了质量力、表面力、粘性力、惯性力的平衡关系（∑ Fv = m av ）。
一、实际流体中的应力 在讨论理想流体（平衡流体）时，作用在流体微团表面上的力只有一
个与表面垂直的压应力，这个压应力称为理想流体的动压强（= 平衡流体 的静压强）。其特性为：1）方向沿作用面的内法线方向，2）大小与作用 面的方位无关。
对于实际流体，由于具有粘性，不仅在表面应力中存在切向应力，而 且在法线方向上也不再具有理想流体中的与方位无关的性质。
在实际流体中，一点处的三个方向的应力由于切应力的存在，不再 垂直于作用面，而与作用面斜交，即具有某一方向，应写成，
pvx ， pv y ， pvz 对任一面积，设作用在其上任一点的表面应力为 pv ，如图所示， pv 分解 为：
第七章 粘性流体动力学基础
实际流体都是有粘性的,粘性流体运动中不可避免地存在阻力、衰减 和扩散现象，运动时总是伴随着内摩擦和传热过程，发生能量损耗。
对于每一个具体的流动问题来讲，粘性所起的作用不一定相同。对于 某些问题，例如求解流体作用于被绕流物体上的升力、表面波的运动等， 粘性的作用并不是占支配地位，因而可以应用非粘性流体力学（理想流体 动力学）理论，可以获得较满意的结果。而对另一些问题，例如求解运动 流体中的粘性阻力、旋涡的扩散，以及能量的传递等，粘性的作用已占主 导地位，若忽略粘性的存在，将导致完全不符合实际的结果。

粘性流体动力学基础

粘性流体动力学基础

建立边界层方程，求解边界层内的速度分布和粘性摩擦力。
紊流概述，雷诺方程及雷诺应力，紊流的时均速度分布与 粘性切应力。
1
第七章 粘性流体动力学基础
§7—1 粘性流体运动的纳维—斯托克斯方程 §7—2 简单边界条件下纳维—斯托克斯方程的精确解 §7—3 边界层的概念 §7—4 边界层方程组及边界条件 §7—5 平板层流边界层的精确解 §7—6 边界层动量积分关系式 §7—7 平板边界层计算 §7—8 边界层分离及减阻 §7—9 紊流概述 §7—10 雷诺方程及雷诺应力 §7—11 紊流的半经验理论 §7—12 紊流模式理论
18
dvx vx 1 2 f x p v 2 dt x 3 x 1 v y vx vz vx y x y z x z 1 p fx vx v x 3 x 1 p dvx 同理可得Y和Z方向 fx vx v dt x 3 x 的运动微分方程： dv y 1 p 2 fy v y v , v v y 3 y dt dvz 1 p fz vz v z 3 z dt
惯性力:
dvx dxdydz dt
p zx
p zx dz z
pxx
p yx p yx y dy
根据牛顿第二定律:
Fx dm ax
可得到X方向的运动方程:
o x
z
y
p yx
pzx
pxx pxx dx x
8
可得到X方向的运动方程:
dvx pxx p yx pzx dxdydz fx dxdydz dt x y z

第七章 粘性流体动力学基础(2)

第七章 粘性流体动力学基础(2)

A n , B m , 则有： 4、如果 r , A B mn A B
r 为 m，n 中之较小者。
12
量级分析： v 2v v 2v x x x x v , , , , 1、 x 的量级： x2 y y2 x


y
0
vx vx 1 dy 0 1 dy v v
（7-28）
式（7-28）的积分上限为无穷，在实 际计算中，通常取为边界层名义厚 度 。在定常流中，边界层内的 vx
v
总是小于 v 且两者方向保持一致，则 可直接推出定常层流边界层的位移厚 度 总小于边界层厚度 。
(f)
18
vx v y 0 x y vx vx 2vx 1 p vy v x x y
(f)
上式中（3）式表明边界层内压力的法向梯度近似为零， 压力只是X的函数，即压力穿过边界层保持不变。因此，




0
vx vx 1 dy v v
（7-29）
7
第四节 边界层方程组及边界条件
基本假设： 1、边界层厚度 是一个小量； 2、边界层内粘性力与惯性力同阶； 3、边界层内的压力分布等于边界层外部势流的压力分布， 即压力穿过边界层是不变的。 较物体的特征长度L小得多，
13
v 2v v 2v y y y y , , , , 2、 vy 的量级： 2 y x2 y x
由连续方程得：
v v y x 1 y x
y
v y
从而有：
0
v y dy y y
v 2v v 2v 1 y y y y , , 1, 2 2 x x y y

粘性流体动力学基础

粘性流体动力学基础

（10.8 a ）
同理可以得出y，z方向的合力
dFy p ( xy ) ( yy ) ( zy ) dv y x y z dFz p ( xz ) ( yz ) ( zz ) dv z x y z
dF dF p dv surf dv viscous
(kT )dxdydz Q k
(10.25)
粘性应力做功率等于粘性应力分量、相应的速度分量和相应 的面积三项的乘积，见图10.3 ，与x轴垂直的左侧面上粘性应 力做功率为
w dydz 其中 w (V V V ) (10.26) W v.LF x x x xx y xy z xz
10.1微分形式的动量方程（N-S） 10.2微分形式的能量方程 10.3 初始条件和边界条件
10.4 雷诺方程和雷诺应力
10.5附面层基本知识
10.6附面层微分方程
10.7附面层积分方程
10.1微分形式的动量方程（N-S）
图10.1动量方程推导用图
与第八章分析质量守恒方法类似，我们可以针对微元控制体图 10.1,列出动量方程
dt
Vx Vz zx zt
y z 3 x x 2Vy 2Vy 2Vy p 2 2 ( V) （10.18 b） = Ry 2 y y z 3 y x 2Vz 2Vz 2Vz p ( V) （10.18 c） = Rz 2 2 2 z y z 3 z x
图10.3分析粘性应力做功率
与上述分析质量流量、动量流量和热流量完全相同可以得出， 在与x轴垂直的两个面上粘性应力的做功率为

7第七章粘性流体动力学基础

7第七章粘性流体动力学基础
1、应力与变形速率成线性关系。
2、应力与变形速率的关系在流体中各向同性。
3、在静止流体中，切应力为零，正应力的数值为静压力p。
在建立应力—变形速率关系之前，我们还要澄清一个概念，前 P 面已将应力张量分解为： D pm ，其中pm为平均正应力，尚不是热 力学平衡意义上的压力p，严格说来，这两者之间不一定相等。我们 定义pm - p为平均压力偏量，其目的是为了将来能应用假设3。 在建立应力—变形速率关系时，我们分两步走：第一步，建立偏 应力张量D与变形速率张量E之间的关系；第二步，建立平均压力偏 量pm - p与变形速率E之间的关系，这里可以设想，pm和p不会直接与 E发生关系。
其中：
φ表示的是粘性力所做的功，它的物理意义是单位质量流体在单位时 间内，由于粘性摩擦而耗散的机械能，这部分能量完全转变成了热能 的形式，故φ又称耗散函数，可以证明φ永远大于零。 由焓的定义： ，经整理后能量方程还可以写成：
四、粘性流体动力学方程组的封闭性
一、圆柱绕流
利用流场叠加法，均直流+偶极子，求得理想流体作圆柱绕流的 流场，流谱左右和上下对称。当Re很小时，这时惯性力相对粘性力 很小，可忽略惯性力。可得到粘性流场的精确解，如图。从流谱图 上看，两者非常接近。两个极限情况图画是很相似的，但在细节上 还是有不同的。1，速度分布如图。2，压力分布的左右不对称。
三、管内流动
1、充分发展段的速度分布 2、进口段的附面层发展。 层流 L≈120D 湍流 L≈50D 3、弯管段的二次流动 4、缓变流和急变流，流动损失。 已知真实流体流动过程的伯努利方程为：
其中， pl12 、 hl12 分别代表流体从１点流到２点时，损失的总压力和总 水头。在缓变流中是沿程损失，急变流中是局部损失。

第七章粘性流体动力学基础

第七章粘性流体动力学基础

第七章粘性流体动⼒学基础第七章粘性流体动⼒学基础实际流体都具有粘性，⽽在研究粘性较⼩的流体的某些流动现象时，可将有粘性的实际流体近似地按⽆粘性的理想流体处理。

例如，粘性⼩的流体在⼤雷诺数情况下，其流速和压强分布等均与理想流体理论⼗分接近。

但在研究粘性⼩的流体的另⼀些问题时，与实际情况不符，如按照理想流体理论得到绕流物体的阻⼒为零。

产⽣⽭盾的主要原因是未考虑实际流体所具有的粘性对流动的影响。

本章，⾸先建⽴具有粘性的实际流体运动微分⽅程，并介绍该⽅程的在特定条件下的求解。

由于固体边界对流体与固体的相互作⽤有重要的影响，本章后⾯主要介绍边界层的⼀些基本概念、基本原理和基本的分析⽅法。

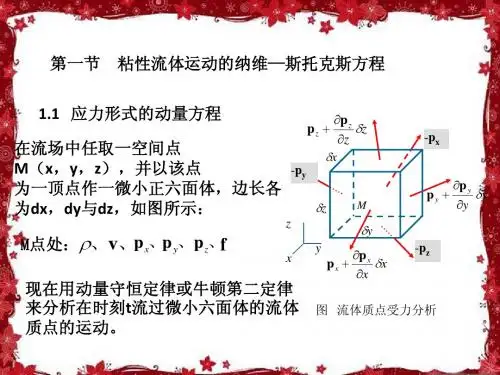
§7.1 纳维—斯托克斯⽅程7.1.1 粘性流体的应⼒实际流体具有粘性，运动时会产⽣切应⼒，它的⼒学性质不同于理想流体，在作⽤⾯上的表⾯应⼒既有压应⼒，也有切应⼒。

在流场中任取⼀点M ，过该点作⼀垂直于z 轴的⽔平⾯，如图7-1 所⽰。

过M 点作⽤于⽔平⾯上的表⾯应⼒p n 在x 、y 、z 轴上的分量为⼀个垂直于⽔平⾯的压应⼒p zz 和两个与⽔平⾯相切的切应⼒τzx 、τzy 。

压应⼒和切应⼒的下标中第⼀个字母表⽰作⽤⾯的法线⽅向，第⼆个字母表⽰应⼒的作⽤⽅向。

显然，通过M 点在三个相互垂直的作⽤⾯上的表⾯应⼒共有九个分量，其中三个是压应⼒p xx 、p yy 、p zz ，六个是切应⼒τxy 、τxz 、τyx 、τyz 、τzx 、τzy ，将应⼒分量写成矩阵形式：图7-1 作⽤于⽔平⾯的表⾯应⼒ττττττzz zyzxyz yy yxxz xy xx p p p (7-1) 九个应⼒分量中，由于τxy =τyx 、τyz =τzy 、τzx =τxz ，粘性流体中任意⼀点的应⼒分量只有6个独⽴分量，即τxy 、τyz 、τzx 、p xx 、p yy 、p zz 。

7.1.2 应⼒形式的运动⽅程在粘性流体的流场中，取⼀以点M 为中⼼的微元直⾓六⾯体，其边长分别为dx 、dy 、 dz 。

粘性流体动力学基础

粘性流体动力学基础

1 p 2 uy z C1 z C2 2 y
利用边界条件 u y
z 0
0和u y
z
U 可以确定出积分常数
1 p C1 , C2 0 2 y U
整理得
dvx 1 p xx yx zx fx ( ) x y z dt
3-4 纳维-斯托克斯方程式
dv y
同样可得
1 yx p yy yz dt x y z dv z 1 zx zy p zz fz dt x y z fy
p xx p 2 p yy p 2 p p 2 zz
v x x v y y v z z
二、本构方程
定义： 确定应力与变形速度关系的方程叫做本构方程。
为建立牛顿流体的本构方程，斯托克斯 Stokes 提出如 下假设： （1）小变形，即应力与变形速度成线性；
dv y dv dvx dvz a i j k dt dt dt dt
dxdydz
应力的第一个下标 i 表示应力作用面的法线方向；第二个下 标 j 表示应力的方向。当 i j 时 Fij 代表法向应力，否则代表切 应力 。将它们标注在包含A点在内的三个微元表面上，则如图 7—1所示，这里假定外界对微元这三个表面的法向应力都沿坐标 的正向，切向应力都沿坐标的负向。
由牛顿第二定律
F ma
微元六面体x向的运动方程为： dv x p xx dxdydz f x dxdydz p xx dydz ( p xx dx)dydz dt x yx yx dxdz ( yx dy )dxdz y
zx zx dxdy ( zx dz )dxdy z

07粘性流体动力学基础

07粘性流体动力学基础

07粘性流体动力学基础第七章粘性流体动力学基础第一节粘性流体运动的基本方程采用流体力学微元体平衡分析方法可以推导出粘性流体运动的基本方程组，该方法可参考本书的第二章和第三章。

本节将直接由两大守恒定律(质量守恒定律和动量守恒定律)来建立控制流体运动的基本方程组。

首先需要给出空间某点物理量的随体时间导数表达式、雷诺输运方程以及本构关系。

一、随体导数描述流体运动规律有拉格朗日和欧拉两种基本方法。

拉格朗日法着眼于确定的流体质点,观察它的位置随时间的变化规律。

欧拉法着眼于从空间坐标去研究流体流动，它的描述对象是流场。

随体导数的物理意义是：将流体质点物理量q的拉格朗日变化率以欧拉导数的形式表示出来。

随体时间导数的数学表达式为：四V'、q (7-1)dt ft式中右边第一项代表由时间的变化所引起的变化率，也就是由于场的时间不定性所造成的变化率，叫做当地导数。

第二项代表假定时间不变时，流体质点在流场中的位置变化所引起的变化率。

这是由于场的不均匀性造成的，叫做迁移导数。

二、雷诺输运方程雷诺输运方程描述了积分形式的拉格朗日法和欧拉法的时间导数的变换关系。

设封闭系统在t时刻占有体积Q (t )，如图7-1所示。

其中关于物理量q的总量的随体时间导数有图7-1封闭系统输运示意图d ；:aqd半崇」qV ndS （7-2）d L】t <="">其中s（t沪封闭体积的曲面，n为曲面的法向向量。

上式表明：封闭系统中，某物理量总和的随体导数等于该瞬间与该系统重合的控制域中该物理量总和的当地时间导数（非定常效应）和通过控制面流出的该物理量的流量（对流效应）之和，此即为流体的雷诺输运方程。

用广义的高斯公式将面积分转换成体积分，上式也可以写成§qd” =彳"qV 心（7-3）dt“t：i 二F M三、连续方程连续性方程反映了流体在运动过程中必须满足质量守恒定律。

其中拉格朗日法的研究对象是流体中一个确定质量的流体物质团（称为封闭系统），随着流体的运动，封闭系统的表面的位置会不断随时间而变化，但没有流体穿过它的边界。

《高等流体力学》第7章 粘性流体力学基础

《高等流体力学》第7章 粘性流体力学基础

1 v2 ∂v + ∇ + Ω × v= f + ∇ ⋅ P ∂t ρ 2
2 P = − pδ + τ = − p + µ∇ ⋅ v δ + 2 µε 3
v2 1 1 ∂v 1 2 + ∇ + Ω × v= f − ∇p − ∇( µ∇ ⋅ v ) + ∇ ⋅ (2 µε ) ∂t ρ ρ 3 ρ 2
对初始条件的极度敏感性目前只解决了低维系统中的几种转捩方式而湍流场是时间与空间的函数对于每一空间点可看成一维混沌所以湍流是无穷维混沌现有的低维系统理论只能对湍流作定性描述说明湍流是ns方程内在特性的表现从理论上证明了ns方程对湍流的适用性
第七章 粘性流体力学基础
主 讲：刘全忠 单 位：能源科学与工程学院 流体机械及工程研究所 Email：liuquanzhong@
Lamb型方程变为
对上式两边取旋度，得到
整理后得到
这是最一般的涡量输运方程。该式清楚地表明：流 体的粘性、非正压性和质量力无势，是破坏旋涡守 恒的根源。在这三者中，最常见的是粘性作用。
1 2 1 ∂Ω 1 + ∇ × (Ω × v ) = ∇ × f − ∇ × ( ∇p ) − ∇ × ∇( µ∇ ⋅ v ) + ∇ × ∇ ⋅ (2 µε ) ρ ∂t ρ 3 ρ
λδ ijδ kl + µ (δ ik δ jl + δ ilδ jk ) ε kl τ ij = Cijkl ε kl = = λδ ij ε kk + µ ( ε ij + ε ji = ) λδ ijε kk + 2µε ij

流体力学第7章 黏性流体动力学_OK

流体力学第7章 黏性流体动力学_OK
任何一个物理量B的量纲都可用3个基本量纲的幂次形
式来表示：
dim B M L T
1
16
工程流体力学
上式称为量纲公式，物理量B的性质由量纲幂次, , 决 定：一般来讲当 0， 0 时，B为几何量；当 0， 0， 0 时，B为运动学量；当 0， 0， 0 时，B为动力学量。
f 1,2,3 n4
这个方程式是真正的描述客观物理过程的方程式，它 不受单位制的影响。
1
25
工程流体力学
【例7.6】求有压管流压强降损失表达式。
【解】 管流的压强降损失p 和流体的性质（密度 、运 动粘度）、管道条件（管长l、直径d、壁面粗糙高度 ks） 以及流动情况（流速V）有关。即
p F(,,l,d,ks,V )
线（即x轴）处速度为最大，即
y0 处
umax
1
2
dp dx
H2
其它处
y2
u
umax
1
H
2
由此表明，黏性流动流态层流的一大特征是速度分布呈 抛物线分布。
1
11
工程流体力学
【例7.3】试证明：在不可压缩恒定均匀管流中，过流断 面上动压强按静压强规律分布。
【解】 如图7.3所示，建
立坐标系，过流断面为
所谓 定理是指，原来物理量之间的复杂函数关系
可以用这些无量纲数之间的关系式来表示。即
f (1,2, ,n4 )
对于不可压缩流体运动，通常选取速度v、密度 和 物体的特征长度l为3个基本量。
在应用 定理时，一般有以下几个步骤：
（1）根据对物理现象的深入分析，列举影响物理现象
的n个物理量。
1
24
物理量B
属性 dim B

粘性流体动力性基础资料

粘性流体动力性基础资料

第4章 粘性流体动力学基础4.1、流体的粘性及其对流动的影响 4.2、雷诺实验、层流与湍流 4.3、粘性流体的应力状态4.4、广义牛顿内摩擦定理（本构关系）4.5、粘性流体运动方程---Navier-Stokes 方程 4.6、流动相似及相似准则*工程中遇到的问题大多是粘性流体运动问题，实际的粘性流体运动现象远比理想流复杂，从而控制粘性流体运动的基本方程及其求解也相对复杂 以下两章的任务是：• 介绍粘性流体运动的基本概念、流动现象和流动特征 • 建立控制粘性流体运动的基本方程• 得到解决粘性流体运动问题的基本思路、方法和途径4.1、流体的粘性及其对流动的影响• 流体的粘滞性是指，流体在运动状态下抵抗剪切变形能力。

• 流体的剪切变形是指流体质点之间出现相对运动。

因此流体的粘滞性是指抵抗流体质点之间的相对运动能力。

• 在静止状态下，流体不能承受剪力。

但是在运动状态下，流体可以承受剪力，而且对于不同种流体所承受剪力大小是不同的。

粘性流体抵抗剪切变形的能力，可通过流层间的剪切力表现出来（这个剪切力称为内摩擦力）。

粘性流体在流动过程中必然要克服内摩擦力做功，因此流体粘滞性是流体发生机械能损失的根源。

牛顿的内摩擦定律（Newton ，1686年） F=µAU/h流层之间的内摩擦力与接触面上的压力无关。

设 τ 表示单位面积上的内摩擦力（粘性切应力），则hUA F μτ==µ-----流体的动力粘性系数（单位：Ns/m2=Pa.s ）ν =µ/ρ---流体的运动粘性系数（单位：m2/s ）ν水= 1.139⨯10-6 (m2/s) ν空气= 1.461⨯10-5 (m2/s)一般流层速度分布不是直线，如图所示。

dydu μτ= du/dy ---- 表示单位高度流层的速度增量，称为速度梯度速度梯度 du/dy 物理上也表示流体质点剪切变形速度或角变形率。

如图所示：dydu dt d dudt dy d ==θθ流体切应力与速度梯度的一般关系为：ndy du B A ⎪⎪⎭⎫⎝⎛+=τ1 . τ =τ0+µdu/dy ，binghan 流体，泥浆、血浆、牙膏等2 . τ =µ（du/dy ）0.5 ，伪塑性流体，尼龙、橡胶、油漆等3 . τ =µdu/dy ，牛顿流体，水、空气、汽油、酒精等4 . τ =µ(du/dy)2，胀塑性流体，生面团、浓淀粉糊等5 . τ＝0，µ＝0，理想流体，无粘流体。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 粘性流体动力学基础第一节 粘性流体运动的基本方程采用流体力学微元体平衡分析方法可以推导出粘性流体运动的基本方程组，该方法可参考本书的第二章和第三章。

本节将直接由两大守恒定律（质量守恒定律和动量守恒定律）来建立控制流体运动的基本方程组。

首先需要给出空间某点物理量的随体时间导数表达式、雷诺输运方程以及本构关系。

一、随体导数描述流体运动规律有拉格朗日和欧拉两种基本方法。

拉格朗日法着眼于确定的流体质点，观察它的位置随时间的变化规律。

欧拉法着眼于从空间坐标去研究流体流动，它的描述对象是流场。

随体导数的物理意义是：将流体质点物理量q 的拉格朗日变化率以欧拉导数的形式表示出来。

随体时间导数的数学表达式为：()q V t q dt dq ∇⋅+= ∂∂ (7-1)式中右边第一项代表由时间的变化所引起的变化率，也就是由于场的时间不定性所造成的变化率，叫做当地导数。

第二项代表假定时间不变时，流体质点在流场中的位置变化所引起的变化率。

这是由于场的不均匀性造成的，叫做迁移导数。

二、雷诺输运方程雷诺输运方程描述了积分形式的拉格朗日法和欧拉法的时间导数的变换关系。

设封闭系统在t 时刻占有体积()t Ω，如图7-1所示。

其中关于物理量q 的总量的随体时间导数有图7-1 封闭系统输运示意图()()()⎰⎰⎰⎰⎰⎰⎰⎰⋅+Ω=ΩΩΩt S t t dS n V q d t q d q dt d ∂∂ (7-2) 其中()t S 为封闭体积的曲面，n 为曲面的法向向量。

上式表明：封闭系统中，某物理量总和的随体导数等于该瞬间与该系统重合的控制域中该物理量总和的当地时间导数（非定常效应）和通过控制面流出的该物理量的流量（对流效应）之和，此即为流体的雷诺输运方程。

用广义的高斯公式将面积分转换成体积分，上式也可以写成()()()Ω∂∂ΩΩΩd V q t q d q dt d t t ⎰⎰⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡⋅∇+= (7-3)三、连续方程连续性方程反映了流体在运动过程中必须满足质量守恒定律。

其中拉格朗日法的研究对象是流体中一个确定质量的流体物质团（称为封闭系统），随着流体的运动，封闭系统的表面的位置会不断随时间而变化，但没有流体穿过它的边界。

质量守恒定律可表述为：封闭系统内流体的质量在流体运动的过程中不发生变化。

而欧拉法的研究对象则是流场空间中一个固定的区域（称为控制域），控制域表面的位置不随时间而变化，由于流体的运动，控制域的表面通常会有流体通过。

质量守恒定律可表述为：控制域内流体质量随时间的增加与流体经控制体表面流入的质量相等。

在式(7-3)中令ρ=q ，可得连续方程()()0=⎥⎦⎤⎢⎣⎡⋅∇+⎰⎰⎰Ωρ∂∂ρΩd V t t (7-4)考虑到积分体积的任意性并假定被积函数连续，上式可以写成()∂ρ∂ρt V +∇⋅= 0 (7-5)这是基于欧拉观点的微分形式的连续方程。

它表明控制体中流体质量在单位时间内的增加来自流体质量经控制体表面的流入速率。

将随体时间导数表达式代入上式，便得到基于拉格朗日观点的微分形式的连续方程。

10ρρd dtV +∇⋅= (7-6) 对于不可压缩流动，恒有d dt ρ/=0成立，此时连续方程简化为 ∇⋅= V 0 (7-7)连续方程仅反映了流体的运动学特性，与流体的本构关系无关。

动量方程反映了流体的动力学特性，因此需要先介绍本构方程。

四、 本构方程本构方程反应了应力和应变率之间存在的制约关系，这是建立流体动力学方程的基础。

真实流体的力学性质是很复杂的，不同种类的流体可能表现出完全不同的力学特性，即便是同一种流体在不同的外部条件下，比如温度不同时，力学特性也会有很大的差异。

因此要建立一个普适的本构方程几乎是不可能的。

Stokes 提出了适用于牛顿流体的如下三条假设：（1）流体是各向同性的，也就是说流体的物理性质与方向无关，只是坐标位置的函数；（2）应力张量ij σ是应变率张量ij e 的线性函数，与旋度无关。

（3）静止流体中，切应力为零，正应力的值为流体的静压。

根据以上假设，考虑到应力张量和应变率张量的对称性，由张量理论便可以推导出应力和应变率间的关系如下：ij ij kk ij ij e e p μδλδσ2++-= (7-8)其中μ为动力粘性系数，λ为第二粘度。

静压p 是一个热力学状态参数()p p T =ρ,。

在热力学平衡态下，它总是等于三个相互垂直方向上正应力的平均值(力学压强)。

在流体力学研究的问题中，有相当一部分是接近平衡态的非平衡体系，这时p 与一点处的平均压强p 是有一定的差别的。

将上式的下标缩并后两边除以-3后得到p p e p e kk kk B kk =-=-+⎛⎝ ⎫⎭⎪=-1323σλμμ (7-9)图7-2 应力张量示意图其中μλμB =+23 (7-10)称为体积粘性系数。

这表明热力学平衡压强或静水压强p 与力学压强p 相差kk B e μ。

式（7-8）也可写成：()⎪⎭⎫ ⎝⎛-++-=ij kk ij ij kk B ij e e e p δμδμσ312 (7-11) 对于单原子气体p ＝p ，μB ＝0。

对于多原子牛顿流体，根据Stokes 假设，通常满足体积粘性系数μB 为零的条件，不必区分力学压强p 与热力学压强p ，本构方程简化为⎪⎭⎫ ⎝⎛-+-=ij kk ij ij ij e e p δμδσ312 (7-12)其中只含有动力粘性系数，该本构关系样适用于静止流体、理想流体（σδij ij p =-）。

五、动量方程动量方程在物理上反映了流体在流动过程中满足的动量守恒定律。

基于拉格朗日观点，动量守恒定律可叙述为：封闭系统内流体动量随时间的变化率等于作用在该系统上所有外力之和。

其数学表达式可以写成⎰⎰⎰⎰⎰⎰⎰⎰⋅+=S dS n d f d V dt d σΩρΩρΩΩ (7-13)在雷诺输运方程中（7-3）式中，令V q ρ=并代入上式，可得到基于欧拉观点的积分形式的动量方程()()⎰⎰⎰⎰⎰⎰⎰⎰⋅+=⎥⎦⎤⎢⎣⎡∇+S dS n d f d V V V t σΩρΩρρ∂∂ΩΩ (7-14)利用广义高斯公式将上式中的面积分项改写成体积分，考虑到积分体积的任意性并假定被积函数连续，则有()∂ρ∂ρρσ() V t VV f +∇⋅=+∇⋅ (7-15)这是基于欧拉观点的微分形式的动量方程。

以连续方程（7-5）代入上式，得到动量方程的另一种常见的形式()∂∂ρσ V t V V f +⋅∇=+∇⋅1 (7-16)将牛顿流体的本构方程式（7-12）代入式（7-16）后，得到牛顿流体的动量方程（或称为Navier-Stokes 方程）()()∂∂ρνν V t V V p V V f +⋅∇=-∇+∇+∇∇⋅+1132 (7-17)式中2∇即为Laplace 算子，ν为运动粘滞系数。

在不可压缩流动中，有()∂∂ρν V t V V p V f +⋅∇=-∇+∇+12 (7-18)对于理想流体的假设，则可简化简化为欧拉方程()∂∂ρ V t V V p f +⋅∇=-∇+1 (7-19)第二节 边界层的概念由于N S —方程的非线性特征，使得问题的求解非常困难。

在许多情况下，需要根据流动的特点对方程进行不同程度的简化。

在低雷诺数流动中，由于粘性力远大于惯性力的特点，Stokes 近似将N S —方程的惯性力项略去，使基本方程得以线化，得到了具有一定精度的小球阻力公式。

在Oseen 近似中，在方程中保留了线化的惯性力项，使小球绕流的远场特性得到了改善。

大雷诺数流动的情况相反，惯性力项远大于粘性力项。

作为近似将粘性力项略去后，N S —方程化为无粘流体的欧拉方程。

若使用与它相匹配的无粘流的可滑移边界条件，对固体的绕流问题会出现零阻力的非物理解（达朗贝尔佯谬）；若使用无滑移的粘性固壁条件会导致数学模型在边界条件上的过约束。

为了解决大雷诺数情况下欧拉方程和粘性边界条件间的矛盾，普朗特（1904）引入了边界层的概念。

对绕流问题，他认为在固壁附近的很薄的一层区域内，沿固壁切向的速度由外部势流的值迅速下降为零，以满足粘性流体的固壁边界条件。

如图7-3所示，边界层形成的原因也可通过从涡旋传输的观点来解释。

流动中的任何固体边界层都相当于连续分布的涡源，它不断的在流动中产生涡旋。

紧靠表面附近的涡旋，一方面向外扩散，另一方面随着流体向下游流动。

涡旋扩散的速度取决于流体的粘性系数，粘度越大，扩散得越快，而涡旋向下游流动的速度取决于来流速度。

当雷诺数足够大时，平板表面附近的涡旋向下游流动的速度比向垂直于流动方向的速度大得多，以致包含这些涡旋的流动仅仅限于贴近表面的一个向下游伸展的薄层，这个薄层就是边界层。

在边界层内，流动是有旋的；而边界层以外的流动则可视为无旋的。

目前边界层理论已成为近代流体力学的重要基石，它澄清了大雷诺数流动问题中粘性对流动的影响。

在许多情况下，大雷诺数与湍流相互关联，本章将分节讨论低速层流边界层和湍流边界层。

边界层理论基于大雷诺数流动的近似，首先需在近似中保留部分粘性项而建立Prandtl 边界层方程。

为了说明边界层的基本特征，本章将先引出描述边界层的数学方程式，接着讨论一个最典型的边界层流动（平板边界层），然后再介绍边界层分离现象。

图7-3 边界层内的涡旋和速度分布示意图第三节 边界层的微分方程式由粘性流体力学的基本方程，采用量级分析方法和普朗特展开方法都可以推导出边界层的微分方程式。

本节将介绍第一种方法。

考虑大雷诺数的二维绕流问题，假定固壁是平直的(平板或楔)。

设y 轴与壁面垂直，x 轴与壁面平行且指向下游，坐标原点和顶点重合，如图7-3所示。

连续性方程和动量方程的两个投影分别为0=∂+∂y v x v y x ∂∂ (7-20a)⎪⎪⎭⎫ ⎝⎛∂+∂+∂-=∂+∂+∂22221y v x v x p y v v x v v t v x x x y x x x ∂∂ν∂ρ∂∂∂ (7-20b)⎪⎪⎭⎫ ⎝⎛∂+∂+-=∂+∂+∂22221y v x v y p y v v x v v t v y y y y y x y ∂∂ν∂∂ρ∂∂∂ (7-20c)当雷诺数Re 远大于1时，在边界层内x 方向和y 方向的物理量具有不同的数量级。

设板长为L 、无穷远来流速度为U ，边界层厚度为δ（当横截面上速度恢复到99％时的厚度）、边界层外缘的y 向速度分量为V 。

且有1Re 1~~<<L U V δ。

取L 、U 分别为x 方向的特征长度与特征速度； δ、V 分别为y 方向的特征长度与特征速度。

∞p 为远前方来流的静压，则将L x x =*， δy y =*，U v v x x =*， V v v yy =* L tU t =*， ∞=p p p * 代入式(7-20)中并将各项的量级标注如下：0****=∂∂+∂∂y v V x v L U y x δ1 1 (7-21a)⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂∞2**2222**2**2********Re 1y v L x v x p U p y v v L U V x v v t v x x x y x x x δρδ 1 1 1 Re 1（1 Re ） (7-21b)⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∞2**22**22**2********Re Re 1Re 1y v x v y p U p y v v x v v t v y y y y y x y ρ Re1 2Re 1（1 Re ） (7-21c)当Re>>1时，在式（7-21）中略去高阶小量，并恢复为有量纲的形式可得0=∂+∂y v x v y x ∂∂ (7-22a)221y v x p y v v x v v t v x x y x x x ∂ν∂ρ∂∂∂∂+∂-=∂+∂+∂ (7-22b)0=y p ∂∂ (7-22c)式(7-22c)表明边界层内压力的法向梯度近似为零，只是x 的函数，它可由外部势流区的压力分布来描述。