第七章不可压缩流体动力学基础

重庆大学2022年城市建设与环境学院《流体力学》考研大纲第一章绪论：表面张力不考。

流体的内摩擦阻力计算题要考。

第二章流体静力学：浮体，潜体不考，本章的一些证明不考(如压强公式的证明)第三章*（重点章）一元流体动力学：1、考试重点章节，动量方程为重点。

2、水头线不考，气体部分的总压线和全压线不考。

气体能量方程（供暖，供热，供燃气，通风及空调工程考）。

3、恒定平面势流问题：关于应力和应变率的关系不考，关于微团的流动只需了解，需知道液体微团运动的意义，恒定平面势流中势流的叠加不考，流函数，势函数的关系重点(必考)。

4、不可压缩流体运动微分方程:方程的意义要会写，紊流的基本方程，要知道平均值，切应力如何产生要知道。

第四章流动阻力的能量损失：1、只考普朗特假设，粗糙雷诺数，层流底层厚度，局部阻碍相互干扰要了解比较透彻。

水击不考。

2、切应力计算公式(层流圆管切应力τ)需了解，紊流运动中了解概念，普朗特假设不考。

3、绕流阻力:什么叫绕流阻力，如何产生的？边界层分离的概念要考。

第五章孔口，管嘴，管路闸孔：计算一般不考(非重点，但需了解)1、孔口，管嘴环状管网，闸孔不考，但枝状管网，串，并联要考。

2、管网的水力计算:环状管网的水力计算不考，枝状管网需了解。

3、堰流、闸孔出流不考，水击不考。

4、气孔射流(稳定射流)计算不考，概念要考（如什么叫质量流速）。

第六章射流与扩散：重点掌握射流特征，其余不考。

1、射流计算不考（市政工程，供暖，供热，供燃气，通风及空调工程不用看射流，其他专业要了解它的概念）。

扩散不用看。

第七章不可压缩流体动力基础：1、微团运动不考，但微团的运动分为平动和转动和变形运动要记牢。

应力表示的运动方程不考，应力不考，应变率不考第八章绕流，平面势流*（重点章）：涡流运动的性质不考。

掌握判断势流的叠加，流函数和势函数必考计算题。

差分法不考。

第九章气体动力基础（除供暖，供热，供燃气，通风及空调工程，其他专业不用看）：等温管路不考，绝热管路不考，只考可压缩气体方程。

流体动力学基础流体动力学是研究流体的运动规律和性质的科学，它是流体力学的分支之一，广泛应用于航空、航天、水力、能源等领域。

本文将介绍流体动力学的基础概念、基本方程以及常用方法。

一、流体动力学的基本概念1. 流体力学与流体静力学的区别流体力学研究流体在运动中的行为，包括流体的流动速度、压力、密度等参数的分布规律；而流体静力学则研究流体在静止状态下的平衡规律，主要关注流体的静压力和浮力等性质。

2. 流体的本构关系流体的本构关系描述了流体的应力与变形速率之间的关系。

常见的本构关系有牛顿黏性流体、非牛顿流体以及理想流体等。

3. 流体的运动描述流体的运动可以通过流体速度场来描述，流体速度场是空间中的矢量函数，它描述了流体的速度分布。

流体速度场的描述可以使用欧拉描述方法或者拉格朗日描述方法。

二、流体动力学的基本方程1. 连续性方程连续性方程描述了质量守恒的原理，即单位时间内通过某一截面的质量是恒定的。

对于稳定流动的不可压缩流体来说，连续性方程可表示为流体密度与速度之积在空间中的量级是恒定的。

2. 动量方程动量方程是描述质点运动定律的基本方程，对流体来说，动量方程体现了运动流体的动力学行为。

对于稳定流动的不可压缩流体来说，动量方程可表示为流体的密度乘以速度与压力梯度的叠加等于外力的结果。

3. 能量方程能量方程描述了热力学系统的能量守恒原则，对于流体来说，能量方程考虑了流体的流动对能量转移的影响，以及热源、做功所导致的能量变化。

三、流体动力学的常用方法1. 数值模拟方法数值模拟是流体动力学研究的重要工具，通过在计算机上建立流体动力学方程的数值解，可以模拟复杂流动现象，如湍流、多相流等。

2. 实验方法实验方法是流体动力学研究的另一重要手段，通过搭建实验平台，测量流体的压力、速度等参数，从而验证理论和数值模拟结果的准确性。

3. 理论分析方法理论分析方法是流体动力学研究中的基础，通过建立假设和推导数学表达式，可以得到流体动力学问题的解析解，为实验和数值模拟提供参考。

831流体力学考试内容范围
第一章绪论
质量力，表面力，流体的主要力学性质，流体的力学模型。

第二章流体静力学
流体静压强及分布规律，压强的量度单位，液柱测压计，作用于平面及曲面的液体压力，流体平衡微分方程，液体的相对平衡。

第三章一元流体动力学基础
流线和迹线，一元流动连续性方程，恒定元流、总流能量方程，过流断面的压强分布，能量方程的应用，总水头线和测压管水头线，恒定气流能量方程，总压线和全压线，恒定流动量方程。

第四章流动阻力和能量损失
沿程损失和能量损失，层流与紊流、雷诺数，尼古拉兹实验，非圆管的沿程损失，减小阻力的措施。

第五章孔口管嘴管路流动
孔口自由及淹没出流，管嘴出流，简单管路及串、并联，有压管中的水击。

第六章气体射流
无限空间淹没紊流射流的特征，圆断面射流的运动分析，温差或浓差射流，有限空间射流。

第七章不可压缩流体动力学基础
流体微团运动的分析，有旋流动，不可压缩流体连续性微分方程，以应力表示的粘性流体运动微分方程式，纳维—斯托克斯方程，理想流体运动微分方程及积分，流体运动的定解条件。

第八章绕流运动
无旋流动，平面无旋流动，势流叠加，绕流运动及附面层基本概念，附面层动量方程，曲面附面层的分离现象与卡门涡街，绕流阻力与升力。

第九章一元气体动力学基础
理想气体一元恒定流动的运动方程，音速、滞止参数、马赫数，气体一元恒定流动的连续性方程，等温与绝热管路中的流动。

第十章相似性原理和因次分析。

第一章，绪论1、质量力：质量力是作用在流体的每一个质点上的力。

其单位是牛顿，N。

单位质量力：没在流体中M点附近取质量为d m的微团，其体积为d v，作用于该微团的质量力为dF，则称极限lim(dv→M)dF/dm=f，为作用于M点的单位质量的质量力，简称单位质量力。

其单位是N/kg。

2、表面力：表面力是作用在所考虑的或大或小得流体系统（或称分离体）表面上的力。

3、容重：密度ρ和重力加速度g的乘积ρg称容重，用符号γ表示。

4、动力黏度μ：它表示单位速度梯度作用下的切应力，反映了黏滞性的动力性质。

其单位为N/（㎡·s），以符号Pa·s表示。

运动黏度ν：是单位速度梯度作用下的切应力对单位体积质量作用产生的阻力加速度。

国际单位制单位㎡/s。

动力黏度μ与运动黏度ν的关系：μ=ν·ρ。

5、表面张力：由于分子间的吸引力，在液体的自由表面上能够承受的极其微小的张力称为表面张力。

毛细管现象：由于表面张力的作用，如果把两端开口的玻璃细管竖立在液体中，液体就会在细管中上升或下降h高度的现象称为毛细管现象。

6、流体的三个力学模型：①“连续介质”模型；②无黏性流体模型；③不可压缩流体模型。

（P12，还需看看书，了解什么是以上三种模型！）。

第二章、流体静力学1、流体静压强的两个特性：①其方向必然是沿着作用面的内法线方向；②其大小只与位置有关，与方向无关。

2、a流体静压强的基本方程式：①P=Po+rh，式中P指液体内某点的压强，Pa(N/㎡)；Po指液面气体压强，Pa(N/㎡)；r指液体的容重，N/m³；h指某点在液面下的深度，m；②Z+P/r=C（常数），式中Z指某点位置相对于基准面的高度，称位置水头；P/r指某点在压强作用下沿测压管所能上升的高度，称压强水头。

两水头中的压强P必须采用相对压强表示。

b流体静压强的分布规律的适用条件：只适用于静止、同种、连续液体。

3、静止均质流体的水平面是等压面；静止非均质流体（各种密度不完全相同的流体——非均质流体）的水平面是等压面，等密度和等温面。

不可压缩流体名词解释
不可压缩流体是指在流动过程中，其体积或密度不发生显著变化的流体。

这类流体在平衡状态下，任何微小变化（如温度或压力的变化），都不会影响其深度、形状或体积等物理性质。

在工程和科学领域，不可压缩流体通常用来描述流体动力学中的一类理想化现象。

例如，一般假设在低速流动中，气体可以视为不可压缩的。

然而，当速度接近或超过音速时，气体的压缩效应就变得重要起来。

不可压缩流体的概念非常重要，因为在许多实际问题中，流体的性质足够接近不可压缩的性质，可以忽略其小的压缩性，从而简化对流体动力学进行的研究和计算。

例如，在研究和设计飞机、船舶、管道、水轮机等的流体力学问题时，常常
假设工作介质为不可压缩流体，以便于使用更简单的方程进行分析。

不可压缩流体理论在流体力学中占据重要位置。

流体运动的基本规律——质量守恒定律、动量守恒定律、能量守恒定律在不可压缩流体中的表现形式，成为流体力学的基础方程。

这些基础方程是研究流体运动最重要的工具，也是解决实际流
体力学问题的基础。

在模拟和解析实际问题时，不可压缩流体假设为工程师和科研人员提供了实用的工具。

这些工具不仅帮助他们理解和解决复杂的流体动力学问题，而且帮助他
们设计和优化了许多工程系统，例如管道输送系统、液压系统、制冷系统等等。

然而，需要注意的是，不可压缩流体模型只是一个理想化的模型，它不一定能完全描述所有类型的流体动力学现象。

例如，对于高速流、音速流或者强烈震动和振动的流，压缩效应可能不能忽略，需要使用其他更复杂的模型来描述其物理行为。

因此，使用不可压缩流体模型时，必须清楚它的适用范围和局限性，以避免误导设计和决策。

热工与流体力学基础第二版知识点《热工与流体力学基础》第二版是一本涵盖热工学和流体力学基础知识的教材。

下面是该教材的主要知识点总结。

第一章：热力学基础1.热力学基本概念：系统、过程、状态、平衡等。

2.热力学第一定律：能量守恒原理，包括内能、功和热量的转化。

3.理想气体的状态方程和理想气体的内能、焓、比热容等基本性质。

4.热力学第二定律：热量无法自流体温度较低的物体传递到温度较高的物体，熵增原理。

5.热力学过程：等温过程、绝热过程、等焓过程、等熵过程等。

第二章：热力学第二定律1.热力学第二定律的表述：克劳修斯表述、开尔文表述、普朗克表述等。

2.热力学可逆性：可逆过程和不可逆过程的区别。

3.温度原理：第二定律的另一个表述。

4.卡诺循环：理想热机的最高效率，热量机和制冷机的理论效率等。

5.热力学状态函数：焓、熵等。

第三章：气体物性1.理想气体状态方程：理想气体的状态方程、气体的通用状态方程等。

2.实际气体的物性：气体的压缩因子、物态方程等。

3.混合气体：混合气体的压力、物态方程等。

4.湿空气的物性：湿空气的物态方程，空气的相对湿度等。

第四章：热力学循环1.热力学循环的基本概念：容器、工质、制冷剂等。

2.理想循环：卡诺循环、斯特林循环、布雷顿循环等。

3. 实际循环：由理想循环引出的实际循环，如Otto循环、Diesel 循环等。

4.循环效率：循环效率的计算和提高方法等。

第五章：流体力学基础1.流体力学的基本概念：流体、运动、静压力、动压力等。

2.流体的物理性质：密度、体积模量、表面张力等。

3. 流体静力学：流体的静力学平衡方程、静压力、Pascal定律等。

4.流体流动的描述：速度场、流线、流管、速度势等。

第六章：定常流动1.流体的连续性方程：质量守恒定律。

2.流体的动量方程：动量守恒定律，流体的动力学压强等。

3. 流体的能量方程：能量守恒定律，Bernoulli方程等。

4.流动的稳定性：雷诺数、层流和湍流等。

不可压缩流体动力学基础1．已知平面流场的速度分布为xy x u x+=2，y xy u y 522+=。

求在点（1，-1）处流体微团的线变形速度，角变形速度和旋转角速度。

解：（1）线变形速度：y x xu x x +=∂∂=2θ 54+=∂∂=xy y u yy θ 角变形速度：()x y y u x u x y z +=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=222121ε 旋转角速度：()x y x u x u x y z -=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=222121ω 将点（1，-1）代入可得流体微团的1=x θ，1=y θ；23/z =ε；21/z =ω2．已知有旋流动的速度场为322+=y u x，x z u y 32+=，y x u z 32+=。

试求旋转角速度，角变形速度和涡线方程。

解：旋转角速度：2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=z u y u y z x ω 2121=⎪⎭⎫ ⎝⎛∂∂-∂∂=x u z u z x y ω 2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=y u x u x yz ω 角变形速度：2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=z u y u y z x ε 2521=⎪⎭⎫ ⎝⎛∂∂-∂∂=x u z u z x y ε 2521=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=y u x u x y z ε 由z y x dz dy dx ωωω==积分得涡线的方程为：1c x y +=，2c x z +=3．已知有旋流动的速度场为22z y c u x+=，0=y u ，0=z u ，式中c 为常数，试求流场的涡量及涡线方程。

解：流场的涡量为： 0=∂∂-∂∂=zu y u y z x Ω 22z y cz xu z u z x y +=∂∂-∂∂=Ω 22z y cy y u x u x yz +-=∂∂-∂∂=Ω旋转角速度分别为：0=x ω222zy czy +=ω 222z y cyz +-=ω 则涡线的方程为：c dz dy z y +=⎰⎰ωω 即c y dz z dy +-=⎰⎰可得涡线的方程为：c c y =+22 4．求沿封闭曲线2 22b y x =+,0=z 的速度环量。

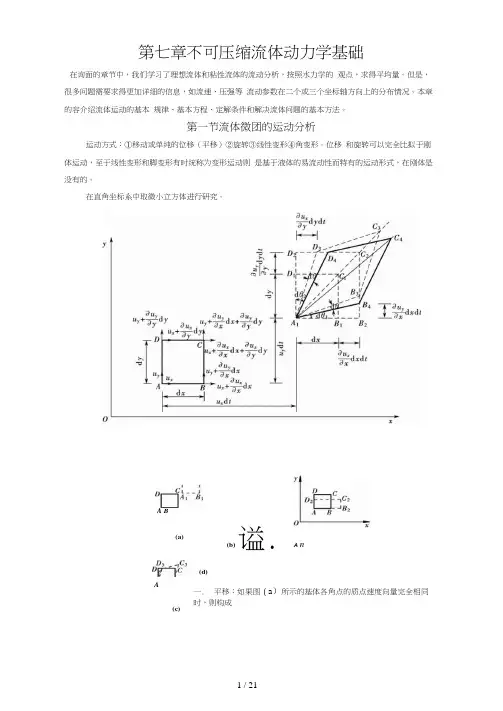
第七章不可压缩流体动力学基础在询面的章节中，我们学习了理想流体和粘性流体的流动分析，按照水力学的 观点，求得平均量。

但是，很多问题需要求得更加详细的信息，如流速、压强等 流动参数在二个或三个坐标轴方向上的分布情况。

本章的容介绍流体运动的基本 规律、基本方程、定解条件和解决流体问题的基本方法。

第一节流体微团的运动分析运动方式：①移动或单纯的位移（平移）②旋转③线性变形④角变形。

位移 和旋转可以完全比拟于刚体运动，至于线性变形和脚变形有时统称为变形运动则 是基于液体的易流动性而特有的运动形式，在刚体是没有的。

在直角坐标系中取微小立方体进行研究。

(b)谥.A n(d)一. 平移：如果图（a ）所示的基体各角点的质点速度向量完全相同时，则构成(c)A B(a)A了液体基体的单纯位移，其移动速度为心、®、“,。

基体在运动中可能沿直线也 可能沿曲线运动，但其方位与形状都和原来一样（立方基体各边的长度保持不 变）。

二、 线变形：从图（b ）中可以看出，由于沿y 轴的速度分量，B 点和C 点都比 A 点和D 点大了竺如 而比就代表〃y = l 时液体基体运动时，在单位时间沿勿dyy 轴方向的伸长率。

du x °"、. du : dxdydz三、 角变形（角变形速度）—BIA ■ dp -------------------------------- Jda-0 = dp + 00 =J"些+些k dz. dx四、旋转（旋转角速度）1O = —0 =—21勿du vdx—dx角变形:血 A那么，代入欧拉加速度表达式，得：du r du Tdu r八 八5=说=古叫 云+"卑+"0+-叭巴加、6仇 du Ya v = ----- = — + u v ---------- + U.0, +ii t a ）. -iLCoydt dt dy “'2 …加.du diL q 。

（完整版）流体力学选择题精选题库《流体力学》选择题库第一章绪论1．与牛顿内摩擦定律有关的因素是：A、压强、速度和粘度；B、流体的粘度、切应力与角变形率；C、切应力、温度、粘度和速度；D、压强、粘度和角变形。

2．在研究流体运动时，按照是否考虑流体的粘性，可将流体分为：A、牛顿流体及非牛顿流体；B、可压缩流体与不可压缩流体；C、均质流体与非均质流体；D、理想流体与实际流体。

3．下面四种有关流体的质量和重量的说法，正确而严格的说法是。

A、流体的质量和重量不随位置而变化；B、流体的质量和重量随位置而变化；C、流体的质量随位置变化，而重量不变；D、流体的质量不随位置变化，而重量随位置变化。

4．流体是一种物质。

A、不断膨胀直到充满容器的；B、实际上是不可压缩的；C、不能承受剪切力的；D、在任一剪切力的作用下不能保持静止的。

5．流体的切应力。

A、当流体处于静止状态时不会产生；B、当流体处于静止状态时，由于内聚力，可以产生；C、仅仅取决于分子的动量交换；D、仅仅取决于内聚力。

6．A、静止液体的动力粘度为0；B、静止液体的运动粘度为0；C、静止液体受到的切应力为0；D、静止液体受到的压应力为0。

7．理想液体的特征是A、粘度为常数B、无粘性C、不可压缩D、符合RT=。

pρ8．水力学中，单位质量力是指作用在单位_____液体上的质量力。

A、面积B、体积C、质量D、重量9．单位质量力的量纲是A、L*T-2B、M*L2*TC、M*L*T(-2)D、L(-1)*T10.单位体积液体的重量称为液体的______，其单位。

A、容重N/m2B、容重N/M3C、密度kg/m3D、密度N/m311.不同的液体其粘滞性_____，同一种液体的粘滞性具有随温度______而降低的特性。

A、相同降低B、相同升高C、不同降低D、不同升高12.液体黏度随温度的升高而____，气体黏度随温度的升高而_____。

B、增大，减小；C、减小，不变；D、减小，减小13.运动粘滞系数的量纲是：A、L/T2B、L/T3C、L2/TD、L3/T14.动力粘滞系数的单位是：A、N*s/mB、N*s/m2C、m2/sD、m/s15.下列说法正确的是：A、液体不能承受拉力，也不能承受压力。