第三章 连续梁的矩阵位移法

第9章矩阵位移法9.1 概述前面介绍的力法、位移法和渐近法都是传统的解算超静定结构的方法，它们是建立在手算基础上的。

随着基本未知量数目的增加，其计算工作极为冗繁和困难。

而计算机的问世及其广泛应用，为结构计算提供了有效工具。

矩阵位移法就是以计算机为运算工具的一种新的结构分析方法，它完全可以代替人来完成大型复杂结构的计算问题。

矩阵位移法是以位移法为理论基础，结构分析的全部过程中运用了线性代数中的矩阵理论。

引入矩阵运算的目的就是使计算过程程序化，便于把结构分析的过程用算法语言编成计算程序，实现计算机自动化处理。

目前，应用矩阵位移法编制的结构分析软件，已在结构设计中得到了广泛的应用。

矩阵位移法又称为杆件有限元法。

它的主要解题思路是：首先将结构离散成为有限个独立的单元，进行单元分析，建立单元杆端力与单元杆端位移之间的关系式——单元刚度方程；然后利用结构的变形连续条件和平衡条件将各单元组合成整体，建立结点力与结点位移之间的关系式——结构刚度方程，这一过程称为整体分析；最后求得结构的位移和内力。

矩阵位移法就是在一分一合，先拆后搭的过程中，把复杂结构计算问题转化为简单的单元分析和集合问题。

本章主要讨论杆系结构的单元刚度矩阵及其在单元局部坐标系与结构整体坐标系间的变换、结构刚度矩阵的形成、荷载及边界条件处理等内容。

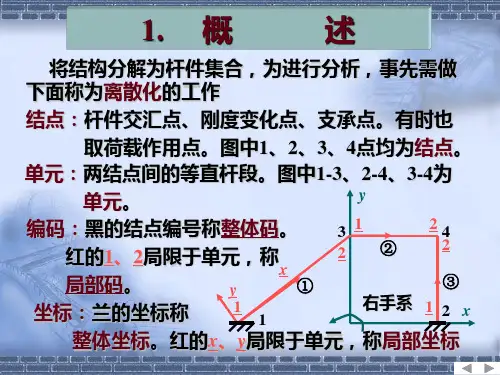
9.2 单元分析9.2.1 结构离散化结构离散化是指把结构分离成有限个独立杆件(单元)，由单元的组合体代替原结构(图9.1)。

一般单元为等截面直杆，杆系结构中每根杆件可以作为一个或几个单元。

单元的联接点称为结点。

对于等截面直杆所组成的杆系结构，只要确定了一个结构的所有结点，则它的各个单元也就随之确定了。

根据杆件联接的方式，可以将构造结点，如转折点、汇交点、支承点和截面的突变点取为结点。

在有些情况下，非构造点，如集中力作用点，也可作为结点处理。

离散化的结构用数字进行描述，即对各结点和单元进行编号。

通常用①,②,…表示单元编号，用1,2,…表示结点编号。

矩阵位移法解法步骤解：1）、单元及结点位移分量统一编码单元及结点位移分量编码、整体坐标系如图所示，局部坐标系横轴正向在各单元上标出。

注：编结点位移分量总码时，后处理法和先处理法有区别：采用后处理法编码时暂不考虑边界条件对支座处位移分量的限制，皆视为一般情形处理；采用先处理法时，对已知为零的位移分量总是以零编码。

对于连接于铰结点的杆端编码时，线位移采用同码，而角位移异码。

2）、形成局部坐标中单元刚度矩阵 k e：首先，计算各单元杆件的几何特征：⋯ ⋯各单元的单元刚度矩阵如下：单元①： ⋯ ⋯3）、形成整体坐标中单元刚度矩阵：（计算公式： k e = T T ke T ） 整体坐标系中的各单元刚度矩阵转换如下：单元①： ⋯ ⋯4）、集成整体刚度矩阵 K （单元集成法或直接刚度法）：首先，由各单元的局部码与总码的对应关系写出各单元的定位向量如下：λ e = ⋯ ⋯ T其次，将各单元刚度矩阵 k e 按其定位向量 λ e 在整体刚度矩阵 K 中定位并累加 得整体刚度矩阵如下：K =(⋯ ⋯)5）、计算综合等效结点荷载向量 F P ：①、计算局部坐标系中各杆件单元的固端力向量：F P e =(F N1F ，F Q1F ，M 1F ，F N2F ，F Q2F ，M 2F )T ②、转换整体坐标系中各杆件单元的固端力向量：{F P }e =(F x1F ，F y1F ，M 1F ，F x2F ，F y2F ，M 2F )T ③、将各杆件单元的固端力反其指向，并按其定位向量 λ e 在综合等效结点荷载向量 F P 定位并累加，得综合等效结点荷载向量如下：F P = ⋯ ⋯ T6）、计入边界条件条件，写出刚度方程并解之：刚度方程： K Δ = F P采用后处理法时，对已知为零的结点位移，在整体刚度矩阵 K 中将其所对应行列的主元素记为1，其余都变为零，然后写出刚度方程，解之。

采用先处理法时，由于在进行位移分量编码时已考虑边界条件，因而无须再计入，只写出刚度方程求解即可。

矩阵位移法——连续梁的结构刚度矩阵import numpy as npfrom math import sqrt, sin, cos, acosnp.set_printoptions(precision=3)np.set_printoptions(suppress=True) # 将科学数组转化为浮点数EI = 1 # 为了⽅便计算，设EI=1# n = input("请输⼊位移数量：")n = 3ElemNode = np.array([[0, 1], [1, 2], [2, 3]]) # 组成单元的两结点编号NodeForce = np.array([[-60], [50], [30]]) # 作⽤在结点上的⼒，单位N·mEi = [0.75, 1.5, 1]ki = np.array([[4 * EI, 2 * EI],[2 * EI, 4 * EI]]) # 单元刚度矩阵*LNodeCoord = np.array([[0, 0], [6, 0], [14, 0], [20, 0]]) # 结点整体坐标NodeX = NodeCoord[:, 0] # 结点x坐标NodeY = NodeCoord[:, 1] # 结点y坐标def k_i(i):"""整体坐标系下单元刚度矩阵,i为单元编号:param i:结点编号:return: 整体坐标系下单元刚度矩阵，由于连续梁不⽤坐标变换，所以k = ke"""NodeIndex = ElemNode[i, :]#print(NodeIndex)Node1_locx = NodeX[NodeIndex[0]]Node1_locy = NodeY[NodeIndex[0]]Node2_locx = NodeX[NodeIndex[1]]Node2_locy = NodeY[NodeIndex[1]]Len = sqrt((Node1_locx - Node2_locx) ** 2 + (Node1_locy - Node2_locy) ** 2)# print("len = %d " % (Len))return ki * Ei[i] / Len # 假设为⽔平def TransMatrix(angle):#坐标转换矩阵Treturn np.array([[ cos(angle), sin(angle) , 0, 0 , 0 ],[-sin(angle), cos(angle), 0, 0 , 0 ],[ 0 , 0 , 1, 0 , 0 ],[ 0 , 0 , 0, cos(angle), sin(angle)],[ 0 , 0 , 0, -sin(angle), cos(angle)],[ 0 , 0 , 0, 0 , 1 ],])# 对上述单元刚度矩阵的各元素，按照其⾏码和列码直接送⼊结构刚度矩阵，进⾏”对号⼊座“NumberOfNodeFreeDof = 3K = np.zeros((NumberOfNodeFreeDof, NumberOfNodeFreeDof))for i in range(0, n):kii = k_i(i)# print(kii)for j in range(0, 2):for k in range(0, 2):if i + j - 1 < 0 or i + k - 1 < 0:continueK[i + j - 1, i + k - 1] += kii[j, k]# print(K)print("结构刚度矩阵K = ")print(K)print('-' * 20)K_1 = np.linalg.inv(K) # 求K矩阵的逆print('K的逆 = ')print(K_1)print('-' * 20)NodeDis = np.matmul(K_1, NodeForce) # = K-1*FNodeDisplacement = np.zeros((1,n+1))for i in range(0, n):NodeIndex = NodeDis[i,:]NodeDisplacement[0,i+1] = NodeIndex[0]print(NodeDisplacement)for i in range(0,n):kii = k_i(i)M1 = kii[0,0]*NodeDisplacement[0,i]+kii[0,1]*NodeDisplacement[0,i+1]M2 = kii[1, 0] * NodeDisplacement[0, i] + kii[1, 1] * NodeDisplacement[0, i + 1]print("在%d号杆件上，左端弯矩为M = %.3f, 右端弯矩为M = %.3f" % (i,M1,M2))。

结力大作业报告连续梁的矩阵位移计算水工812008010226彭慧民2010-10-30结力大作业报告1、问题描述通过矩阵位移法计算连续梁的杆端弯矩，画出弯矩图。

报告通过用matlab编程序，实现了连续梁杆端弯矩的计算机计算，并且输出弯矩图。

2、知识介绍矩阵位移法的要点是先将结构整体拆开，分解成若干个单元，然后再将这些单元通过定位向量集合成整体，包括单元分析和集合成整体两部分。

单元分析中，要建立单元刚度方程，形成单元刚度矩阵；整体分析中，要将单元集合成整体，由单元刚度矩阵按照刚度集成规则形成整体刚度矩阵，建立整体结构的位移法方程，从而求出解答。

计算连续梁的杆端弯矩的步骤如下：➢将连续梁的结点和位移进行编号，写出定位向量；➢对应于连续梁的单元刚度矩阵是4224EI EIl lEI EIl l⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭，根据连续梁上的实际情况，分别写出每一段的单元刚度矩阵；➢根据定位向量，写出整体刚度矩阵；➢根据外加荷载，求等效结点荷载；➢解方程组，求位移；➢根据单元刚度矩阵和定位向量，求出杆端弯矩；➢画出弯矩图。

3、程序代码>> L=[4,6,8];%定义梁长度的数组，L(1)=4M,L(2)=6M,L(3)=8M>> EI=[1,1.5,2];%定义梁刚度，EI（1）=EI，EI（2）=1.5EI，EI（3）=2EI>> P=[40,50,80];%定义跨中荷载的大小，P（1）=40，P（2）=50，P（3）=80 >> q=[15,30,20];%定义跨上的连续荷载大小，q(1)=15,q(2)=30,q(3)=20>> n=5;>> rEI=[EI(1),EI(3),EI(1),EI(1),EI(2)];>> rL=[L(1),L(2),L(3),L(2),L(1)];>> ri=[rEI(1)/rL(1),rEI(2)/rL(2),rEI(3)/rL(3),rEI(4)/rL(4),rEI(5)/rL(5)];>> %下面是固端荷载>> outerP=[0,P(3),0,P(2),0];>> outerQ=[q(2),0,q(2),0,0];>> direct=zeros(n,2);>> for i=1:ndirect(i,1)=i-1;direct(i,2)=i;end %输入定位向量和连续梁的数据>> element=zeros(2*n,2);for i=1:nelement(2*i-1,1)=4*ri(i);element(2*i-1,2)=2*ri(i);element(2*i,1)=2*ri(i);element(2*i,2)=4*ri(i);end %单元刚度矩阵>> structure=zeros(n,n);for i=1:(n-1)structure(i,i)= structure(i,i)+element(2*i,2)+element(2*i+1,1);structure(i,i+1)= structure(i,i+1)+element(2*i+1,2);end>> structure(n,n)= structure(n,n)+element(2*n,2);>> %这是整体刚度矩阵>> for i=2:nstructure(i,i-1)=structure(i-1,i);end>> %得到对称的整体刚度矩阵>> %下面是结点固端荷载P=zeros(1,n);for i=1:(n-1)P(i)=P(i)+(1/8)*outerP(i)*rL(i)+(1/12)*outerQ(i)*rL(i)*rL(i)-(1/8)*outerP(i+1)*rL(i+1)-(1/12)*outerQ( i+1)*rL(i+1)*rL(i+1);end>> P(n)=P(n)+(1/8)*outerP(n)*rL(n)+(1/12)*outerQ(n)*rL(n)*rL(n);>> P=-P;>> P=P';>> %下面解方程组，求位移向量>> X=structure\P;>> %下面求杆端弯矩>> F=zeros(2*n,1);>>F(1:2)=element(1:2,:)*[0,X(1,1)]'+[-(1/8)*outerP(1)*rL(1),(1/8)*outerP(1)*rL(1)]'+[-(1/12)*outerQ( 1)*rL(1)*rL(1),(1/12)*outerQ(1)*rL(1)*rL(1)]';>> for i=2:nF((2*i-1):(2*i))=element((2*i-1):(2*i),:)*X((i-1):i)+[-(1/8)*outerP(i)*rL(i),(1/8)*outerP(i)*rL(i)]'+[-(1/ 12)*outerQ(i)*rL(i)*rL(i),(1/12)*outerQ(i)*rL(i)*rL(i)]';end>> %下面开始画弯矩图>> line=zeros(1,2*n+1);>> for i=2:(2*n+1)line(i)=line(i-1)+(1/2)*rL(floor(i/2));end>> torque=zeros(1,2*n+1);>> torque(1)=-F(1);>> torque(2*n+1)=-F(2*n);>> for i=1:(n-1)torque(2*i+1)=F(2*i);end>> for i=1:ntorque(2*i)=(1/2)*(torque(2*i-1)+torque(2*i+1))-(1/8)*outerQ(i)*rL(i)*rL(i)-(1/4)*outerP(i)*rL(i); end>> plot(line,torque,'r*');>> hold on, z=0*line;plot(line,z),hold off;程序说明：➢可以改变输入的n值，相应地改变输入的连续梁各跨的长度、EI、i，可以改变相应向量的维数，但是维数必须等于每次输入的n；➢输入好数据之后，将以上代码粘贴到matlab里面，就可以输出弯矩图了，输出的弯矩图是散点图，可以自己根据实际作用的外加荷载，将散点连接起来。

矩阵位移法过程嘿，朋友们！今天咱就来好好唠唠矩阵位移法这个神奇的玩意儿。

你想想啊，矩阵位移法就像是搭积木，一块一块地把整个结构给拼凑起来。

只不过这积木有点特别，是用数字和公式搭成的。

咱先说说这第一步，得确定结构的节点和单元吧。

这就好比是给要盖的房子先确定好柱子和梁的位置。

每个节点就像是一个关键点，单元呢就是连接这些关键点的部件。

然后呢，咱要给这些节点和单元编上号，就跟给小朋友分学号似的，可不能乱了套。

接下来，就得建立这些节点和单元的关系啦。

这就像是给每个积木块找到它该放的位置，它们之间的连接呀、力的传递呀，都得搞清楚。

这可不是个简单事儿，但咱得耐着性子慢慢来。

然后呢，咱要根据这些关系列出矩阵。

哎呀呀，这矩阵可就像个大表格，里面装满了各种数字和符号。

别被它吓着，其实它就是把那些复杂的关系用一种整齐的方式表现出来。

再说说这计算过程，就跟解谜题似的。

你得一步步地去推导、去计算，找到那个正确的答案。

有时候可能会遇到一些难题，就像走在路上碰到了一块大石头，但咱可不能退缩，得想法子把它挪开或者绕过去。

还有啊，这矩阵位移法还得考虑各种边界条件呢。

就好像盖房子得考虑地基稳不稳呀，周围环境怎么样呀。

这些边界条件可不能马虎，要不然整个结构可就不牢固啦。

咱在实际运用的时候，可得细心再细心。

一个小数字算错了，可能整个结果就全错啦。

这就跟下棋一样，一步错步步错。

总之呢，矩阵位移法虽然有点复杂，但它可是结构分析的得力助手呢！只要咱认真学，多练习，就一定能掌握它。

别害怕困难，别嫌麻烦，等你真正搞懂了它，你就会发现它的神奇之处啦！就像打开了一扇通往新世界的大门，让你看到结构背后的奥秘。

所以呀，加油吧朋友们，和矩阵位移法这个小伙伴好好相处，让它为我们的工程建设出一份力！原创不易，请尊重原创，谢谢!。