北师大版八年级上册第二章实数小结与复习
- 格式:ppt
- 大小:945.63 KB
- 文档页数:18
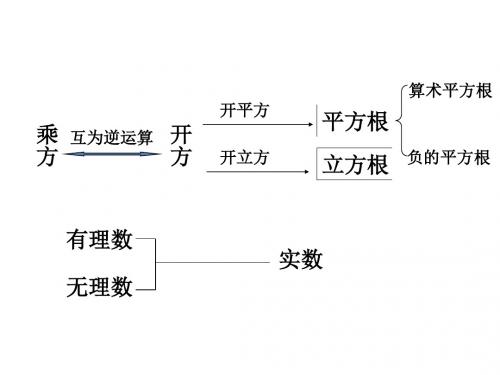

第二章:实数本章的知识网络结构:知识梳理一.数的开方主要知识点:【1】平方根:如果一个数x 的平方等于a ,那么,这个数x 就叫做a 的平方根;也即,当)0(2≥=a a x 时,我们称x 是a 的平方根,记做:)0(≥±=a a x 。
因此:4.当a=0时,它的平方根只有一个,也就是0本身;4.当a >0时,也就是a 为正数时,它有两个平方根,且它们是互为相反数,通常记做:a x ±=。
4.当a <0时,也即a 为负数时,它不存在平方根。
例1.(1) 的平方是64,所以64的平方根是 ;(2) 的平方根是它本身。
(3)若x 的平方根是±2,则x= ;16的平方根是(4)当x 时,x 23-有意义。
(5)一个正数的平方根分别是m 和m-4,则m 的值是多少?这个正数是多少?【算术平方根】:(1)如果一个正数x 的平方等于a ,即a x =2,那么,这个正数x 就叫做a 的算术平方根,记为:“a ”,读作,“根号a”,其中,a 称为被开方数。
特别规定:0的算术平方根仍然为0。
(2)算术平方根的性质:具有双重非负性,即:)0(0≥≥a a 。
(3)算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。
因此,算术平方根只有一个值,并且是非负数,它只表示为:a ;而平方根具有两个互为相反数的值,表示为:a ±。
例2.(1)下列说法正确的是 ( )A .1的立方根是1±;B .24±=;(C )、81的平方根是3±; (D )、0没有平方根;(2)下列各式正确的是( )A 、981±=B 、14.314.3-=-ππC 、3927-=-D 、235=- (3)2)3(-的算术平方根是 。
(4)若x x -+有意义,则=+1x ___________。
(5)已知△ABC 的三边分别是,,,c b a 且b a ,满足0)4(32=-+-b a ,求c 的取值范围。



八年级数学 第二章复习(1) 【复习回顾】 知识点一:实数包括: 和 。
有理数: 和 统称有理数;无理数: 叫无理数。
三种形式: . 知识点二:1.二次根式:一般的,我们把形如 (a )的式子叫做二次根式。
2.( )2= (a≥0); 2a a= 。
3.积的算术平方根的性质: ,公式 。
二次根式的乘法法则: ,公式 。
4.商的算术平方根的性质: ,公式 。
二次根式的除法法则: ,公式 。
课前练习:1.一个正数有 个平方根,他们互为 ;0 的平方根为 ;负数 。
一个数有 个立方根;正数的立方根是 ;负数的立方根是 。
0的立方根是 。
平方根等于它本身的数是 ;立方根等于它本身的数是 。
2.—27 的立方根为______;16 的平方根为______,3.求3π-= ,62-= 。
4.比较大小:【课堂学习内容】 例题1.把下列数分别填入相应的集合内:722,0,38-,2π,3.14,925-,•74.2,33, 372015.1,4.0,0-)(π,2-21)(。
有理数集合: 。
无理数集合: 。
负数集合: 。
非负整数集合: 。
分数集合: 。
练习:1.把下列各数分别填入相应的集合内:32-,41,7,π,25-,2,3205-,38-,94,0.3737737773 0无理数集合: 。
整数集合: 。
分数集合: 。
例题23 1.5O 52133-O(1) 818-18+ (2) 361-24÷)( (3)2716133⨯练习2:(1)2(232.校园里有旗杆高11米,如果想要在旗杆顶部点A 与地面一固定点B 之间拉一根直的铁丝,小强已测量固定点B 到旗杆底部C 的距离是8米,小军已准备好一根长12.3米,你认为这一次长度够用吗?课堂检测:1.81的算术平方根是( )A .9 B.-9 C. ±9 D. 32. 下列说法正确的是( )A. 有理数只是有限小数B. 无理数是无限小数C. 无限小数是无理数D. 是分数3.-27 的立方根为______,16 的平方根为______,4.若一个正数的平方根是2a +1和3a +6,则a=____,这个正数是 ;5、(1)18212-2⨯)( (2) 32712-327-12⨯A CB6.已知实数a 、b 在数轴上的位置如图.化简:.上交作业1. 下列说法正确的是( )A.064.0-的立方根是0.4B.9-的平方根是3±C.16的立方根是316D.0.01的立方根是0.0000012.10的小数部分可以表示为 .3.64______38______.4. ①1(6215)362 ②246+③6.观察下列各式及其验证过程:222233=+验证:()3322222222233213-+===+- ()3323333333388318-+===+-(1)按照上述两个等式及其验证过程的基本思路,猜想4415(2)针对上述各式反映的规律,写出用n (n 为任意自然数,且n≥2)表示的等式,并证明它成立.20162015767-6•=。

“ 64; ; 0.0004; (-25)2;11.北师大版八年级数学上册第二章实数知识点和习题北师大版八年级数学上册第二章实数知识点及习题实数知识点知识点一、【平方根】如果一个数 x 的平方等于 a ,那么,这个数 x 就叫做 a 的平方根;也即,当 x 2 = a(a ≥ 0) 时,我们称 x 是 a 的平方根,记做: x = ± a (a ≥ 0) 。
因此:1、当 a=0 时,它的平方根只有一个,也就是 0 本身;2、当 a >0 时,也就是 a 为正数时,它有两个平方根,且它们是互为相反数,通常记做: x = ± a 。
3、当 a <0 时,也即 a 为负数时,它不存在平方根。
例 1.(1)的平方是 64,所以 64 的平方根是 ;(2)的平方根是它本身。
(3)若 x 的平方根是±2,则 x= ; 16 的平方根是(4)当 x时, 3-2 x 有意义。
(5)一个正数的平方根分别是 m 和 m-4,则 m 的值是多少?这个正数是多少?知识点二、【算术平方根】:1、如果一个正数 x 的平方等于 a ,即 x 2 = a ,那么,这个正数x 就叫做 a 的算术平方根,记为:“ a ”,读作, 根号 a”,其中,a 称为被开方数。
特别规定:0 的算术平方根仍然为 0。
2、算术平方根的性质:具有双重非负性,即: a ≥ 0(a ≥ 0) 。
3、算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。
因此,算术平方根只有一个值,并且是非负数,它只表示为: a ;而平方根具有两个互为相反数的值,表示为:±a 。
例 2.(1)下列说法正确的是( )A .1 的立方根是 ± 1 ;B . 4 = ±2 ; (C )、 81 的平方根是 ± 3 ;( D )、0 没有平方根;(2)下列各式正确的是()A 、 81 = ±9B 、 3.14 - π = π - 3.14C 、 - 27 = -9 3D 、 5 - 3 =(3) (-3) 2 的算术平方根是。
北师大版八年级上册第二章《实数复习》说课稿一. 教材分析北师大版八年级上册第二章《实数复习》是学生在学习了实数相关概念和性质后的一次复习。
本节课的主要内容是回顾和巩固有理数、无理数和实数的概念,以及它们的性质和运算。
教材通过例题和练习题的形式,帮助学生理解和掌握实数的运算规则,提高解决问题的能力。
二. 学情分析学生在进入八年级之前,已经学习了有理数和无理数的基本概念和性质,对实数有一定的了解。
但在实际应用中,部分学生可能对实数的理解和运算还存在一定的困难。
因此,在复习实数时,需要帮助学生巩固基础知识,提高运算能力,并培养解决问题的能力。
三. 说教学目标1.知识与技能:通过复习,使学生掌握实数的概念和性质,能够熟练进行实数的运算。
2.过程与方法:通过自主学习和合作交流,培养学生发现问题、分析问题和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识,提高学生的自我学习能力。
四. 说教学重难点1.教学重点:实数的概念、性质和运算规则。
2.教学难点:实数运算的灵活应用,以及解决实际问题。
五. 说教学方法与手段本节课采用自主学习、合作交流和教师引导相结合的教学方法。
利用多媒体课件和黑板,帮助学生直观地理解和掌握实数的运算规则。
同时,通过小组讨论和例题讲解,引导学生主动参与学习,提高解决问题的能力。
六. 说教学过程1.导入:通过复习有理数和无理数的概念,引出实数的概念,激发学生的学习兴趣。
2.新课导入:讲解实数的性质和运算规则,通过例题和练习题,让学生理解和掌握实数的运算方法。
3.课堂练习:设计一些有关实数运算的练习题,让学生独立完成,巩固所学知识。
4.小组讨论:引导学生分组讨论实际问题,培养学生解决问题的能力。
5.总结:对本节课的主要内容进行总结,强调实数运算的注意事项。
6.布置作业:布置一些有关实数运算的练习题,让学生课后巩固所学知识。
七. 说板书设计板书设计主要包括实数的概念、性质和运算规则。
第二章:实数知识梳理【无理数】1.定义:无穷不循小数的小数叫做无理数;注:它必足“无穷”以及“不循” 两个条件。
2.常有无理数的几种种类:( 1)特别意的数,如:周率以及含有的一些数,如:2-, 3等;( 2)特别构的数(看似循而不循):如: 2.010010 001 000 01⋯(两个 1 之挨次多 1 个0)等。
(3)无理数与有理数的和差果都是无理数。
如:2-是无理数( 4)无理数乘或除以一个不0 的有理数果是无理数。
如 2 ,( 5)开方开不尽的数,如:2,5,39等;当要注意的是:根号的数不必定是无理数,如:9 等;无理数也不必定根号,如:)3.有理数与无理数的差别:(1)有理数指的是有限小数和无穷循小数,而无理数是无穷不循小数;( 2)全部的有理数都能写成分数的形式(整数能够当作是分母 1 的分数),而无理数不可以写成分数形式。
例:( 1)以下各数:① 3.141 、② 0.33333 ⋯⋯、③57 、④π、⑤2.25、⑥2、⑦ 0.3030003000003 ⋯⋯3(相两个 3 之 0 的个数逐次增添 2)、此中是有理数的有____;是无理数的有___。
(填序号)( 2)有五个数 :0.125125⋯ ,0.1010010001 ⋯ ,-, 4, 32此中无理数有 ()个【算平方根】:1. 定义:假如一个正数x 的平方等于 a,即x2 a ,那么,个正数x 就叫做 a 的算平方根,:“ a ”,作,“根号a”,此中,a称被开方数。
比如32=9,那么9 的算平方根是3,即9 3。
特地, 0 的算平方根是0,即0 0 ,数没有算平方根2. 算术平方根拥有两重非负性:(1)若a存心,被开方数 a 是非数。
( 2)算平方根自己是非数。
3.算术平方根与平方根的关系:算平方根是平方根中正的一个,它与它的相反数共同组成了平方根。
所以,算平方根只有一个,而且是非数,它只表示:a;而平方根拥有两个互相反数的,表示: a 。
实数2 a a 知识点一、【平方根】假如一个数 x 的平方等于 a,那么,这个数 x 就叫做 a 的平方根;也即,当( 0)x 时,我们称 x 是 a 的平方根,记做:x a(a 0)。
所以:1、当 a=0 时,它的平方根只有一个,也就是 0 自己;2 、当 a>0 时,也就是 a 为正数时,它有两个平方根,且它们是互为相反数,往常记做:x a 。
3 、当 a<0 时,也即 a 为负数时,它不存在平方根。
例 1.〔1〕的平方是 64 ,所以 64 的平方根是;〔2 〕的平方根是它自己。
〔3 〕假定x 的平方根是± 2,那么 x= ;16 的平方根是〔4 〕当 x 时,3-2x 存心义。
〔5 〕一个正数的平方根分别是 m 和 m-4 ,那么 m 的值是多少?这个正数是多少?知识点二、【算术平方根】:2 1、假如一个正数 x 的平方等于 a,即x a ,那么,这个正数 x 就叫做 a 的算术平方根,记为:“a 〞,读作,“根号 a〞,此中, a 称为被开方数。
特别规定: 0 的算术平方根仍旧为 0 。
2、算术平方根的性质:拥有两重非负性,即:a 0(a 0) 。
3、算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同组成了平方根。
所以,算术平方根只有一个值,而且是非负数,它只表示为:a ;而平方根拥有两个互为相反数的值,表示为:a 。
例 2.〔1〕以下说法正确的选项是〔〕A .1 的立方根是1;B.4 2 ;〔C〕、81 的平方根是3;〔 D〕、0 没有平方根;〔2〕以下各式正确的选项是〔〕A 、81 9 B、3.14 3. 14 C、27 9 3 D、5 3 2〔3〕 2( 3) 的算术平方根是。
〔4〕假定x x 存心义,那么x 1 ___________ 。
2〔5〕△ABC 的三边分别是a, b, c, 且a,b 知足a 3 (b 4) 0,求 c 的取值范围。