aV
V
.
.
.
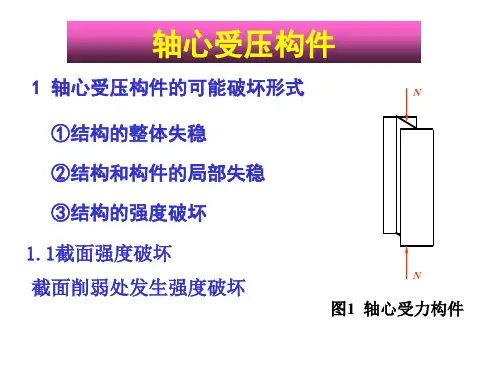
弯曲中心
形心 产生扭矩:Va
扭矩=0
具有双对称轴的截面,弯曲中心与形心重合;单 对称轴和无对称轴截面,弯曲中心与形心不重合.
弯曲产生的截面剪力不通过弯曲中心 〔通过形心〕产生的扭矩.可以认为这是 轴心压力因弯曲变形对杆件截面产生外 扭矩.
• 对于理想压杆,欧拉弯曲失稳临界力、欧 拉弯曲失稳临界力
Ncr
弯曲屈曲——屈曲模态为弯曲变形
计算临界力的基本假设:
▲ 杆件是理想直的,两端铰支; ▲ 轴心压力作用在两端,且为保向力; ▲ 屈曲变形属于小变形,平截面假设 成立,忽略杆 件长度的变化; ▲ 屈曲后的挠曲线〔屈曲模态〕可用正弦曲线描述. 目标:求弯曲屈曲临界荷载Nb,cr、临界应力b, cr [弹性临界荷载]
〔8〕1950年以后的试验证明:切线模量理论 值接近于试验值,并略微偏低是试验值的下限;双 模量理论值是试验值的上限.用切线模量理论于工 程是偏于安全的.最后被工程所接受.
这段历史说明:一个科学的认识过程是一个不 断深化、不断完善的过程;只有坚持真理、修 正错误才能逐渐达到科学的境界;实践是检验 真理的标准在科学发展史上早已是无争准则.
3.2 实际轴心受压构件的整体稳定
3.1节中讨论的轴心受压构件是一种理想情况.那时, 曾指出构件的特点有:作用在构件上的荷载是轴心压 力或轴心拉力;构件理想地直;构件无初应力. 这些理想化情形在实际工程中是不存在的.
Euler公式从提出到为轴心加载试验证实花了约 100年时间.说明轴心加载的不易;
〔2〕Considere认为切线模量理论有 误,提出双模量理论概念. 〔3〕Engesser认同Considere意见的正确 性,并于1895年导出了双模量.