虚功原理
- 格式:ppt
- 大小:427.50 KB
- 文档页数:31

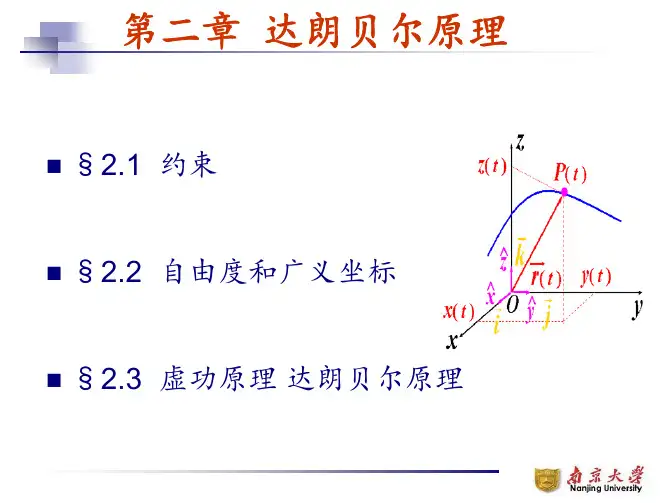


虚功原理的内容及应用条件1. 虚功原理的概念虚功原理是力学中的基本原理之一,它根据体系处于平衡状态时的平衡条件,从而推导出力学中的一些重要定理。
根据虚功原理,一个约束系统在平衡位置上的任意虚位移所做的虚功等于零。
虚功原理是可以应用在各个领域的一个重要原理,包括物理学、工程学等。
2. 虚功原理的条件虚功原理适用于满足以下条件的体系: - 约束体系:虚功原理主要应用于约束体系,即约束在某些条件下运动的物体体系。
- 平衡位置:虚功原理适用于约束体系处于某个平衡位置的情况。
- 虚位移:虚功原理建立在虚位移的基础上,即物体在平衡位置上的任意虚位移。
3. 虚功原理的应用虚功原理在力学中有广泛的应用,以下是几个常见的应用领域:3.1 静力学应用在静力学中,虚功原理可以应用于分析力的平衡和支持结构的设计等问题。
通过建立平衡方程和应用虚功原理,可以推导出约束体系的平衡条件和约束反力等。
3.2 动力学应用在动力学中,虚功原理可以用于分析非平衡状态下的物体运动。
通过应用虚功原理,可以推导出物体受力和加速度之间的关系,并得到物体的运动方程。
3.3 物体变形分析虚功原理还可以应用于物体的变形分析。
通过对物体进行虚位移,利用虚功原理和弹性力学理论,可以计算物体在受力作用下的变形情况。
3.4 热力学应用在热力学中,虚功原理可以应用于分析热力学平衡和传热等问题。
通过应用虚功原理,可以推导出热平衡条件和传热方程等。
3.5 其他应用领域除了上述应用领域外,虚功原理还可以应用于弹性体的弹性力学分析、流体力学中的动量守恒和能量守恒等问题。
4. 总结虚功原理是力学中的一个重要原理,它可以应用于各个领域的问题。
虚功原理适用于约束体系处于平衡位置的情况,并建立在虚位移的基础上。
通过应用虚功原理,可以推导出约束体系的平衡条件、力学关系和变形情况等。
虚功原理的应用广泛,包括静力学、动力学、热力学等领域。
了解虚功原理的内容及应用条件,对于深入理解力学和应用力学原理具有重要意义。



虚功原理
在物理学中,虚功原理是一个重要的概念,它在力学、电磁学等领域有着广泛的应用。
虚功原理是基于能量守恒和力学平衡的原理,通过考虑系统内部各部分之间的相互作用,从而得出系统达到平衡的条件。
1. 虚功原理的基本概念
在力学中,虚功原理可以简单地表述为:在一个平衡的力学系统中,作用在系统内所有部分的外力所作的虚功之和为零。
这意味着系统内各个部分之间的相互作用满足一个使得整个系统保持平衡的条件。
2. 虚功原理在力学中的应用
在力学中,虚功原理可以应用于弹簧系统、摩擦力系统等各种力学问题的分析中。
通过将系统分解为各个部分,并考虑各部分之间的相互作用,可以利用虚功原理来求解系统的平衡条件和运动规律。
3. 虚功原理在电磁学中的应用
在电磁学中,虚功原理同样具有重要的作用。
在电磁场中,电荷之间的相互作用可以通过虚功原理来描述,从而推导出麦克斯韦方程组等电磁学的基本规律。
4. 虚功原理的应用举例
以简单的弹簧振子系统为例,可以通过虚功原理来推导出系统的振动方程,并进一步分析系统的动力学行为。
类似地,可以将虚功原理应用于其他复杂系统的分析中,从而揭示系统的运动规律和平衡条件。
5. 结语
虚功原理作为力学和电磁学中的重要原理之一,对于系统的分析和理解具有重要意义。
通过应用虚功原理,可以更深入地理解自然界中的各种物理现象,为科学研究和工程应用提供有力的理论支持。
在今后的研究和应用中,虚功原理必将继续发挥重要作用,推动科学技术的发展和进步。

虚功原理概念
虚功原理是力学中的重要概念,主要运用于静力学和弹性力学的问题中。
该原理是通过比较系统在实际情况下的受力和在虚位移情况下的受力之间的差异,来推导出力学问题的解析解。
虚功原理的基本思想是,如果一个力系统处于平衡状态,则在任意虚位移下,系统所受到的合力必然为零。
这意味着在虚位移下,系统没有做任何实际的功。
因此,可以根据虚功原理来解决平衡问题。
虚功原理的应用主要涉及到两个方面:平衡条件和变形计算。
在平衡条件中,通过比较系统在实际情况下的受力和在虚位移情况下的受力,可以得出力的平衡条件。
在变形计算中,可以通过比较系统在实际变形和虚位移情况下的变形能量,来计算系统的位移和应变。
虚功原理的使用需要考虑以下几个要点:
1. 虚位移应满足几何约束条件,即虚位移必须满足系统的边界条件和约束条件。
2. 虚功原理可以应用于单个物体或整个力系统,这取决于具体的力学问题。
3. 虚功原理可以推广到三维空间中的力学问题,并且可以应用于弹性体和非弹性体。
4. 虚功原理还可以推广到动力学问题,即考虑物体的运动和加速度。
总之,虚功原理是力学中非常重要的概念,可以用于平衡条件
和变形计算。
通过应用虚功原理,可以简化力学问题的分析,得到解析解。

力学系统的虚功原理与最小能量原理力学是研究物体运动和力的学科,虚功原理和最小能量原理是力学中的两个重要概念。
虚功原理是指在平衡状态下,外力对于系统所做的虚功为零;最小能量原理则是指在运动过程中,系统的能量达到最小值。
本文将介绍力学系统的虚功原理与最小能量原理,并探讨其在实际问题中的应用。
一、虚功原理虚功原理是力学中的一个重要原理,它描述了力学系统在平衡状态下外力对系统所做的虚功为零。
虚功原理的基本思想是,当系统处于平衡状态时,任何微小的虚位移所做的功都是虚功,而这些虚功的总和为零。
虚功原理的应用十分广泛。
例如,在静力学中,我们可以利用虚功原理来求解物体的平衡条件。
在弹性力学中,虚功原理可以用来推导物体的弹性形变和应力分布。
在动力学中,虚功原理可以用来推导物体的运动方程。
二、最小能量原理最小能量原理是力学中的另一个重要原理,它描述了力学系统在运动过程中系统的能量达到最小值。
最小能量原理的基本思想是,系统在运动过程中,会通过各种力的作用进行能量的转化,而系统的能量会趋向于最小。
最小能量原理的应用也非常广泛。
例如,在弹性力学中,我们可以利用最小能量原理来求解物体的弹性形变和应力分布。
在动力学中,最小能量原理可以用来推导物体的运动方程。
此外,在流体力学中,最小能量原理可以用来推导流体的运动方程和流速分布。
三、虚功原理与最小能量原理的联系虚功原理和最小能量原理在某种程度上是相互关联的。
虚功原理描述了系统在平衡状态下外力对系统所做的虚功为零,而最小能量原理描述了系统在运动过程中系统的能量达到最小值。
虚功原理可以看作是最小能量原理的一种特殊情况,即在平衡状态下系统的能量已经达到最小值。
虚功原理和最小能量原理的联系在实际问题中具有重要意义。
通过应用虚功原理和最小能量原理,我们可以求解物体的平衡条件、弹性形变、应力分布、运动方程等问题。
这些原理为我们研究力学系统提供了重要的理论工具。
总结起来,虚功原理和最小能量原理是力学中的两个重要概念。
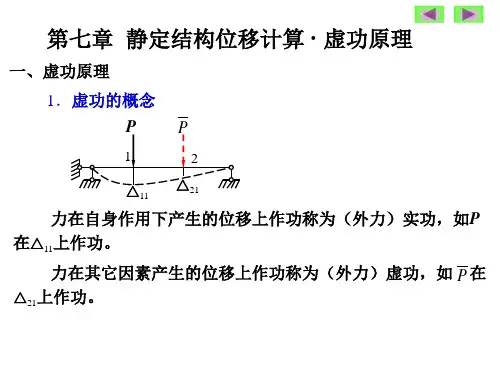

结构力学虚功原理
结构力学虚功原理是指在静力学分析中,结构平衡的条件可以通过能量守恒原理来表示。
根据虚功原理,结构在任何形变状态下,受力系统所作的虚功等于外界对结构所做的虚功。
虚功是指由于结构内部力引起的位移所做的功。
根据虚功原理,结构的平衡可以通过计算结构内部力引起的位移所做的功来判断。
具体而言,可以通过计算结构每个构件上的受力与位移的乘积,然后将它们求和,得到结构内部力所作的总虚功。
如果结构处于平衡状态,则结构受力与位移之积的总和为零。
虚功原理的应用非常广泛。
它可以用于计算结构的位移、应力、应变等重要参数。
例如,在弹性力学中,可以利用虚功原理求解结构的位移和应力分布。
在塑性力学中,虚功原理可以用来分析结构在超过弹性极限后的变形情况。
此外,虚功原理还可以用于分析非线性和非弹性结构的行为。
通过应用虚功原理,可以对结构进行静态分析和设计。
静态分析可以确定结构在受力条件下的平衡状态,进而计算各个构件的受力和位移。
静态设计可以根据结构的受力和位移要求,确定结构的尺寸和材料,以满足结构的强度和刚度要求。
总之,结构力学虚功原理为结构分析和设计提供了重要的理论基础。
通过虚功原理,可以建立结构平衡的数学模型,计算结构的位移、应力和应变等关键参数,为工程实践提供了可靠的理论支持和设计方法。
虚功原理有限元虚功原理是力学中的一个基本原理,它是运用能量守恒原理和虚位移原理进行问题求解的一种方法。
虚功原理的应用十分广泛,特别是在有限元方法中,它是解答复杂结构力学问题的一种常用手段。
虚功原理的基本原理是:在刚体或弹性体的力学问题中,力系对于结构的作用机理可以使用能量方法来描述,即外力对物体所做的功等于内力弹性势能的变化。
在有限元方法中,虚功原理的应用可以被概括为以下几个步骤:1. 确定系统的弹性势能表达式:根据材料力学性质和结构几何形状,建立并表达出结构的弹性势能。
2. 设定虚位移场:在结构的静力平衡方程中,引入一组满足边界条件的虚位移场,并将结构的位移表示为真实位移与虚位移的叠加。
虚位移场是一个理想化的假设,它用于引导计算的进行。
3. 计算虚功:将虚位移场代入弹性势能表达式中,得到每个单元的虚功。
4. 构造系统的刚度方程:根据虚功原理,对每一个虚位移方向进行变分,得到相应的虚功。
将这些虚功累加起来,并考虑结构边界条件和约束条件,得到整个系统的刚度方程。
5. 解刚度方程:使用适当的数值方法(如矩阵求解方法)求解刚度方程组,得到结构的位移响应。
6. 计算应力和应变分布:利用位移响应,通过一定的插值方法,计算出结构各点的应力和应变分布。
有限元方法利用虚功原理的优点在于,它可以解决复杂结构的力学问题,并且可以处理非线性材料、大变形和大变位等情况。
虚功原理的运用使得有限元方法成为求解工程结构问题的一种强大工具。
需要注意的是,在使用虚功原理时,应注意选择合适的虚位移场,并保证其满足结构的边界条件和约束条件;同时,还需要进行适当的数值技巧处理,如选择合适的数值积分方法和数值求解方法,以提高计算的精确性和效率。
总结来说,虚功原理是有限元方法求解问题的基础,它通过能量守恒原理和虚位移原理,将原问题转化为求解刚度方程的问题,从而得到结构的位移响应和应力应变分布。
虚功原理在结构力学中的应用是十分重要和广泛的,它为工程问题的解答提供了有效的途径。
动力学分析中的虚功原理和实功原理动力学是物理学中研究物体运动规律的一个重要分支。
在动力学分析中,虚功原理和实功原理是两个基本概念,它们在解决力学问题中起着重要的作用。
本文将探讨虚功原理和实功原理的定义、应用以及它们之间的关系。
一、虚功原理虚功原理是指在力学系统中,虚位移所做的功为零。
虚功原理是通过对力学系统的平衡条件进行推导得到的。
在虚功原理中,虚位移是指系统中各个质点发生的微小位移,该位移并不是真实的物体运动,而是为了推导问题方便而引入的。
虚功原理的应用广泛,特别是在静力学和弹性力学问题中。
例如,当我们研究一个物体受力平衡时,可以通过虚功原理来推导出物体所受的各个力的关系。
虚功原理还可以用于分析弹性体的变形和应力分布等问题。
二、实功原理实功原理是指在力学系统中,实位移所做的功等于外力对系统所做的功。
实功原理是基于能量守恒的原理推导出来的。
在实功原理中,实位移是指物体真实的位移,是由外力所引起的。
实功原理的应用也非常广泛。
例如,当我们研究一个物体在重力作用下的运动时,可以通过实功原理来计算物体所做的功。
实功原理还可以用于分析机械能的转化和损失等问题。
三、虚功原理与实功原理的关系虚功原理和实功原理在物理学中是相辅相成的。
虚功原理通过平衡条件来推导力学问题,而实功原理通过能量守恒来解决力学问题。
虚功原理和实功原理之间的关系可以通过以下几个方面来说明:1. 虚功原理是实功原理的基础。
虚功原理是通过对力学系统的平衡条件进行推导得到的,而实功原理是基于能量守恒的原理推导出来的。
虚功原理提供了实功原理所需要的平衡条件。
2. 虚功原理和实功原理可以相互验证。
在解决力学问题时,可以通过虚功原理和实功原理相互验证结果的正确性。
如果虚功原理和实功原理得到的结果相符,那么我们可以认为所得到的结论是正确的。
3. 虚功原理和实功原理可以相互补充。
在一些复杂的力学问题中,虚功原理和实功原理可以相互补充,帮助我们更好地理解和解决问题。
力学中的虚功原理力学是物理学的一个重要分支,研究物体的运动和力的作用。
在力学的研究中,虚功原理是一个基本概念,它在解决力学问题时起着重要的作用。
本文将介绍力学中的虚功原理,并探讨其应用。
1. 虚功的概念和定义虚功是力学中的一个重要概念,它用于描述一个力对物体的作用所做的功,但物体实际上并未发生位移。
虚功可以通过以下公式计算:虚功 = 力 ×虚位移其中,力是作用在物体上的力,虚位移是物体在力的作用下所产生的虚拟位移。
虚位移是一个想象出来的位移,用于计算力对物体的作用所做的功。
虚功是一个标量,它的单位是焦耳(J)。
2. 虚功原理的表述虚功原理是力学中的一个基本原理,它描述了一个力对物体的作用所做的虚功等于零。
换句话说,当物体处于平衡状态时,力对物体的作用所做的虚功总和等于零。
虚功原理可以通过以下公式表述:Σ虚功 = 0其中,Σ虚功表示所有力对物体的作用所做的虚功的总和。
根据虚功原理,当物体处于平衡状态时,所有作用在物体上的力对物体所做的虚功总和为零。
3. 虚功原理的应用虚功原理在力学中有广泛的应用,以下是一些常见的应用场景:3.1 弹簧的伸缩虚功原理可以用于分析弹簧的伸缩问题。
当一个物体施加一个力使弹簧伸长或缩短时,虚功原理可以帮助我们计算弹簧对物体所做的虚功。
根据虚功原理,弹簧对物体所做的虚功等于零,即力与虚位移的乘积为零。
通过这个原理,我们可以求解弹簧的伸长或缩短距离。
3.2 斜面上的物体虚功原理还可以应用于斜面上的物体。
当一个物体沿着斜面上升或下降时,虚功原理可以帮助我们计算斜面对物体所做的虚功。
根据虚功原理,斜面对物体所做的虚功等于零。
通过这个原理,我们可以求解物体在斜面上的运动状态。
3.3 摩擦力的分析虚功原理还可以用于分析摩擦力的作用。
当一个物体在受到摩擦力的作用下运动时,虚功原理可以帮助我们计算摩擦力对物体所做的虚功。
根据虚功原理,摩擦力对物体所做的虚功等于零。
通过这个原理,我们可以求解物体在摩擦力作用下的运动状态。