多元统计分析习题分为三部分思考题验证题和论文题
- 格式:doc
- 大小:62.00 KB
- 文档页数:5

《多元统计分析》思考题答案记得老师课堂上说过考试内容不会超出这九道思考题,如下九道题题目中有错误的或不清楚的地方,欢迎大家指出、更改、补充。
1、 简述信度分析答题提示:要答可靠度概念,可靠度度量,克朗巴哈α系数、拆半系数、单项与总体相关系数、稀释相关系数等(至少要答四个系数,至少要给出两个指标的公式)答:信度(Reliability )即可靠性,它是指采用同样的方法对同一对象重复测量时所得结果的一致性程度。
信度指标多以相关系数表示,大致可分为三类:稳定系数(跨时间的一致性),等值系数(跨形式的一致性)和内在一致性系数(跨项目的一致性)。
信度分析的方法主要有以下四种:1)、重测信度法这一方法是用同样的问卷对同一组被调查者间隔一定时间重复施测,计算两次施测结果的相关系数。
重测信度属于稳定系数。
重测信度法特别适用于事实式问卷,如果没有突发事件导致被调查者的态度、意见突变,这种方法也适用于态度、意见式问卷。
由于重测信度法需要对同一样本试测两次,被调查者容易受到各种事件、活动和他人的影响,而且间隔时间长短也有一定限制,因此在实施中有一定困难。
2)、复本信度法复本信度法是让同一组被调查者一次填答两份问卷复本,计算两个复本的相关系数。
复本信度属于等值系数。
复本信度法要求两个复本除表述方式不同外,在内容、格式、难度和对应题项的提问方向等方面要完全一致,而在实际调查中,很难使调查问卷达到这种要求,因此采用这种方法者较少。
3)、折半信度法折半信度法是将调查项目分为两半,计算两半得分的相关系数,进而估计整个量表的信度。
折半信度属于内在一致性系数,测量的是两半题项得分间的一致性。
这种方法一般不适用于事实式问卷(如年龄与性别无法相比),常用于态度、意见式问卷的信度分析。
在问卷调查中,态度测量最常见的形式是5级李克特(Likert )量表。
进行折半信度分析时,如果量表中含有反意题项,应先将反意题项的得分作逆向处理,以保证各题项得分方向的一致性,然后将全部题项按奇偶或前后分为尽可能相等的两半,计算二者的相关系数。

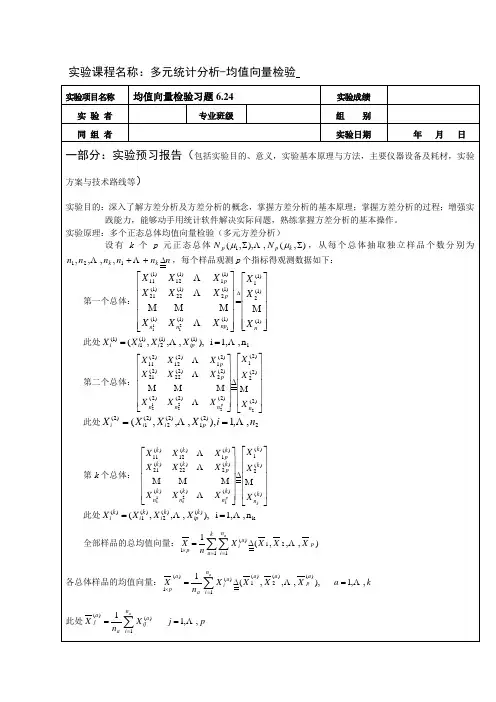
2009学年第2学期 考试科目:多元统计分析 考试类型:(闭卷) 考试时间:100 分钟学号 姓名 年级专业一、填空题(5×6=30)22121212121~(,),(,),(,),,1X N X x x x x x x ρμμμμσρ⎛⎫∑==∑=⎪⎝⎭+-1、设其中则Cov(,)=____.10312~(,),1,,10,()()_________i i i i X N i W X X μμμ='∑=--∑、设则=服从。
()1234433,492,3216___________________X x x x R -⎛⎫ ⎪'==-- ⎪ ⎪-⎝⎭=∑、设随机向量且协方差矩阵则它的相关矩阵4、__________, __________,________________。
215,1,,16(,),(,)15[4()][4()]~___________i p p X i N X A N T X A X μμμμ-=∑∑'=--、设是来自多元正态总体和分别为正态总体的样本均值和样本离差矩阵,则。
二、计算题(5×11=50)(),123设X=x x x 的相关系数矩阵通过因子分析分解为211X h =的共性方差111X σ=的方差21X g =1公因子f 对的贡献121330.93400.1280.9340.4170.8351100.4170.8940.02700.8940.44730.8350.4470.1032013R ⎛⎫- ⎪⎛⎫⎛⎫ ⎪-⎛⎫ ⎪ ⎪⎪=-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎪⎝⎭12332313116421(,,)~(,),(1,0,2),441,2142X x x x N x x x x x μμ-⎛⎫⎪'=∑=-∑=-- ⎪ ⎪-⎝⎭-⎛⎫+ ⎪⎝⎭、设其中试判断与是否独立?11262(90,58,16),82.0 4.310714.62108.946460.2,(5)( 115.6924)14.6210 3.17237.14.5X S μ--'=-⎛⎫ ⎪==-- ⎪ ⎪⎝⎭0、对某地区农村的名周岁男婴的身高、胸围、上半臂围进行测量,得相关数据如下,根据以往资料,该地区城市2周岁男婴的这三个指标的均值现欲在多元正态性的假定下检验该地区农村男婴是否与城市男婴有相同的均值。

多元统计分析考试内容最后成绩作业50% 考试50% 他们班这样 不知咱们班什么情况 估计也差不多 考试一共八道题 分三大类(卷面值100分 最后折合成50分) 一 计算题 (每题12分)1 计算性的判别分析题 主要用Fisher 判别法 要掌握公式的方法原理2 聚类分析题 主要应用两种聚类法:系统聚类法和模糊聚类法题中会给出距离或相关系数矩阵直接计算 老师强调要看清题意 不要做无用功! 3如何将非线性函数形式用线性回归的方法将其线性化 写出其过程 可能不涉及计算 二 简答(简答哦 不要长篇大论免得后面的题没时间做 主要作概略性总结即可)在这一部分中主要有三道题(分值分别10 10 12)老师没有具体给出三道题的题目 只是举了些例子 回答问题的主要思路是:统计分析方法的基本思想,基本原理与应用,在应用中要注意的问题 个别要回答与其他方法的对比 举的主要例子有(个人以为前两个比较重要):1 回归分析模型:回归方程的基本假定,涉及到回归分析方程系数为何作显著性检验 统计性的依据是什么(方差分析) 给出一个回归分析方程如何作显著性检验2 判别分析:判别分析的优良性 两方面考虑:(1)组与组之间的差别是否显著有无必要作判别分析 (2)误判率下面的几个例子 主要也是按上面的思路回答 因子分析 聚类分析(不会四种方法一块考,会选其中某个或某两个) 主成分分析的基本思想 可以做什么应用及在应用中要选几个主成分 对应分析的基本思想 三 发挥题(每题16分)这个部分老师会给出问题的背景及所问的问题,个人结合自己所学的几种分析方法 选择适合的作分析 没有标准答案,只要能自圆其说即可 注意:第一步一定要先指出自己所用的分析方法 老师没有说具体会考什么题只是说不会考很专业的 自由发挥 简单提到一个例子就是教学评价的问题 也没有说用什么方法 他说不同的人会采用不同的方法 一道题不会只有一种解决方法.题量大,做不完1 计算题1.1 计算性的判别分析题 主要用Fisher 判别法 要掌握公式的方法原理处理概率分布未知的判别问题中的最著名的方法。
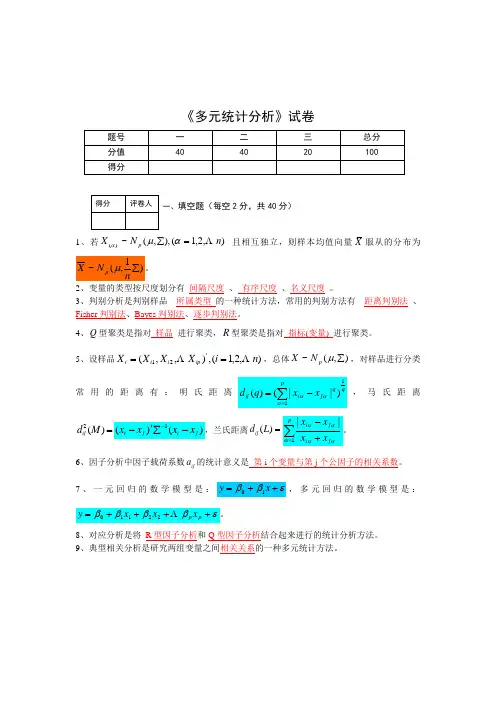
《多元统计分析》试卷1、若),2,1(),,(~)(n N X p =∑αμα 且相互独立,则样本均值向量X 服从的分布为2、变量的类型按尺度划分有_间隔尺度_、_有序尺度_、名义尺度_。
3、判别分析是判别样品 所属类型 的一种统计方法,常用的判别方法有__距离判别法_、Fisher 判别法、Bayes 判别法、逐步判别法。
4、Q 型聚类是指对_样品_进行聚类,R 型聚类是指对_指标(变量)_进行聚类。
5、设样品),2,1(,),,('21n i X X X X ip i i i ==,总体),(~∑μp N X ,对样品进行分类常用的距离有:明氏距离,马氏距离2()ijd M =)()(1j i j i x x x x -∑'--,兰氏距离()ij d L =6、因子分析中因子载荷系数ij a 的统计意义是_第i 个变量与第j 个公因子的相关系数。
7、一元回归的数学模型是:εββ++=x y 10,多元回归的数学模型是:εββββ++++=p p x x x y 22110。
8、对应分析是将 R 型因子分析和Q 型因子分析结合起来进行的统计分析方法。
9、典型相关分析是研究两组变量之间相关关系的一种多元统计方法。
一、填空题(每空2分,共40分)1、设三维随机向量),(~3∑μN X ,其中⎪⎪⎪⎭⎫ ⎝⎛=∑200031014,问1X 与2X 是否独立?),(21'X X 和3X 是否独立?为什么?解: 因为1),cov(21=X X ,所以1X 与2X 不独立。
把协差矩阵写成分块矩阵⎪⎪⎭⎫⎝⎛∑∑∑∑=∑22211211,),(21'X X 的协差矩阵为11∑因为12321),),cov((∑='X X X ,而012=∑,所以),(21'X X 和3X 是不相关的,而正态分布不相关与相互独立是等价的,所以),(21'X X 和3X 是独立的。

《多元统计分析》试卷1、若),2,1(),,(~)(n N X p =∑αμα 且相互独立,则样本均值向量X 服从的分布为2、变量的类型按尺度划分有_间隔尺度_、_有序尺度_、名义尺度_。
3、判别分析是判别样品 所属类型 的一种统计方法,常用的判别方法有__距离判别法_、Fisher 判别法、Bayes 判别法、逐步判别法。
4、Q 型聚类是指对_样品_进行聚类,R 型聚类是指对_指标(变量)_进行聚类。
5、设样品),2,1(,),,('21n i X X X X ip i i i ==,总体),(~∑μp N X ,对样品进行分类常用的距离有:明氏距离,马氏距离2()ijd M =)()(1j i j i x x x x -∑'--,兰氏距离()ij d L =6、因子分析中因子载荷系数ij a 的统计意义是_第i 个变量与第j 个公因子的相关系数。
7、一元回归的数学模型是:εββ++=x y 10,多元回归的数学模型是:εββββ++++=p p x x x y 22110。
8、对应分析是将 R 型因子分析和Q 型因子分析结合起来进行的统计分析方法。
9、典型相关分析是研究两组变量之间相关关系的一种多元统计方法。
一、填空题(每空2分,共40分)1、设三维随机向量),(~3∑μN X ,其中⎪⎪⎪⎭⎫ ⎝⎛=∑200031014,问1X 与2X 是否独立?),(21'X X 和3X 是否独立?为什么?解: 因为1),cov(21=X X ,所以1X 与2X 不独立。
把协差矩阵写成分块矩阵⎪⎪⎭⎫⎝⎛∑∑∑∑=∑22211211,),(21'X X 的协差矩阵为11∑因为12321),),cov((∑='X X X ,而012=∑,所以),(21'X X 和3X 是不相关的,而正态分布不相关与相互独立是等价的,所以),(21'X X 和3X 是独立的。


一、什么是多元统计分析❖多元统计分析是运用数理统计的方法来研究多变量(多指标)问题的理论和方法,是一元统计学的推广。
❖多元统计分析是研究多个随机变量之间相互依赖关系以及内在统计规律的一门统计学科。
二、多元统计分析的内容和方法❖1、简化数据结构(降维问题)将具有错综复杂关系的多个变量综合成数量较少且互不相关的变量,使研究问题得到简化但损失的信息又不太多。
(1)主成分分析(2)因子分析(3)对应分析等❖2、分类与判别(归类问题)对所考察的变量按相似程度进行分类。
(1)聚类分析:根据分析样本的各研究变量,将性质相似的样本归为一类的方法。
(2)判别分析:判别样本应属何种类型的统计方法。
例5:根据信息基础设施的发展状况,对世界20个国家和地区进行分类。
考察指标有6个:1、X1:每千居民拥有固定电话数目2、X2:每千人拥有移动电话数目3、X3:高峰时期每三分钟国际电话的成本4、X4:每千人拥有电脑的数目5、X5:每千人中电脑使用率6、X6:每千人中开通互联网的人数❖3、变量间的相互联系一是:分析一个或几个变量的变化是否依赖另一些变量的变化。
(回归分析)二是:两组变量间的相互关系(典型相关分析)❖4、多元数据的统计推断点估计参数估计区间估计统 u检验计参数 t检验推 F检验断假设相关与回归检验卡方检验非参秩和检验秩相关检验❖1、假设检验的基本原理小概率事件原理❖ 小概率思想是指小概率事件(P<0.01或P<0.05等)在一次试验中基本上不会发生。
反证法思想是先提出假设(检验假设H0),再用适当的统计方法确定假设成立的可能性大小,如可能性小,则认为假设不成立;反之,则认为假设成立。
❖ 2、假设检验的步骤 (1)提出一个原假设和备择假设❖ 例如:要对妇女的平均身高进行检验,可以先假设妇女身高的均值等于 160 cm (u=160cm )。
这种原假设也称为零假设( null hypothesis ),记为 H 0 。

多元统计分析重点宿舍版第一讲:多元统计方法及应用;多元统计方法分类(按变量、模型、因变量等) 多元统计分析应用选择题:①数据或结构性简化运用的方法有:多元回归分析,聚类分析,主成分分析,因子分析 ②分类和组合运用的方法有:判别分析,聚类分析,主成分分析 ③变量之间的相关关系运用的方法有:多元回归,主成分分析,因子分析, ④预测与决策运用的方法有:多元回归,判别分析,聚类分析 ⑤横贯数据:{因果模型(因变量数):多元回归,判别分析相依模型(变量测度):因子分析,聚类分析多元统计分析方法选择题:①多元统计方法的分类:1)按测量数据的来源分为:横贯数据(同一时间不同案例的观测数据),纵观数据(同样案例在不同时间的多次观测数据) 2)按变量的测度等级(数据类型)分为:类别(非测量型)变量,数值型(测量型)变量3)按分析模型的属性分为:因果模型,相依模型 4)按模型中因变量的数量分为:单因变量模型,多因变量模型,多层因果模型第二讲:计算均值、协差阵、相关阵;相互独立性第三讲:主成分定义、应用及基本思想,主成分性质,主成分分析步骤主成分定义:何谓主成分分析 就是将原来的多个指标(变量)线性组合成几个新的相互无关的综合指标(主成分),并使新的综合指标尽可能多地反映原来的指标信息。
主成分分析的应用 :(1)数据的压缩、结构的简化;(2)样品的综合评价,排序主成分分析概述——思想:①(1)把给定的一组变量X1,X2,…XP ,通过线性变换,转换为一组不相关的变量Y1,Y2,…YP 。
(2)在这种变换中,保持变量的总方差(X1,X2,…Xp 的方差之和)不变,同时,使Y1具有最大方差,称为第一主成分;Y2具有次大方差,称为第二主成分。
依次类推,原来有P 个变量,就可以转换出P 个主成分(3)在实际应用中,为了简化问题,通常找能够反映原来P 个变量的绝大部分方差的q (q<p )个主成分。
主成分性质:1)性质1:主成分的协方差矩阵是对角阵:(2)性质2:主成分的总方差等于原始变量的总方差(3)性质3:主成分Yk 与原始变量Xi 的相关系数为:ρ(YK,Xi )=√λ√σiitki,并称之为因子负荷量(或因子载荷量)。

第1章 多元正态分布1、在数据处理时,为什么通常要进行标准化处理?数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是0-1标准化和Z 标准化。
2、欧氏距离与马氏距离的优缺点是什么?欧氏距离也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m 维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。
当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待,这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点:夸大了变化微小的变量的作用。
受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
3、当变量X1和X2方向上的变差相等,且与互相独立时,采用欧氏距离与统计距离是否一致?统计距离区别于欧式距离,此距离要依赖样本的方差和协方差,能够体现各变量在变差大小上的不同,以及优势存在的相关性,还要求距离与各变量所用的单位无关。
如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。

一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为 Q型聚类和 R型聚类。
4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。
5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。
6、若()(,), Px N αμα∑=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。
二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
2、简述相应分析的基本思想。
相应分析,是指对两个定性变量的多种水平进行分析。
设有两组因素A和B,其中因素A包含r个水平,因素B包含c个水平。
对这两组因素作随机抽样调查,得到一个rc的二维列联表,记为。
要寻求列联表列因素A和行因素B的基本分析特征和最优列联表示。
相应分析即是通过列联表的转换,使得因素 A 和因素B具有对等性,从而用相同的因子轴同时描述两个因素各个水平的情况。
把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上,从而得到因素A、B的联系。
3、简述费希尔判别法的基本思想。
从k个总体中抽取具有p个指标的样品观测数据,借助方差分析的思想构造一个线性判别函数系数:确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
将新样品的p 个指标值代入线性判别函数式中求出 值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。
多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法,它通过同时考虑多个变量之间的关系,帮助研究者更全面地理解和解释现象。
在本文中,我将分享一些多元统计分析的习题和答案,希望能够帮助读者更好地掌握这一方法。
习题一:相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。
你收集了100个学生的数据,学习成绩用分数表示,学习时间用小时表示。
以下是你的数据:学习成绩(X):75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间(Y):5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数,并解释其含义。
答案一:首先,我们需要计算学习成绩和学习时间之间的协方差和标准差。
根据公式,协方差可以通过以下公式计算:协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中,X和Y分别表示学习成绩和学习时间,X平均和Y平均表示它们的平均值,n表示样本数量。
标准差可以通过以下公式计算:标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式,我们可以得出学习成绩和学习时间之间的协方差为-22.5,标准差分别为18.03和2.87。
然后,我们可以通过以下公式计算相关系数:相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式,我们可以得出相关系数为-0.93。
由于相关系数接近于-1,可以得出结论:学习成绩和学习时间之间存在强烈的负相关关系,即学习时间越长,学习成绩越低。
习题二:多元线性回归假设你正在研究一个人的身高(X1)、体重(X2)和年龄(X3)对其收入(Y)的影响。
你收集了50个人的数据,以下是你的数据:身高(X1):160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重(X2):50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄(X3):20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入(Y):5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析,建立一个预测人的收入的模型,并解释模型的结果。
《多元统计分析思考题》第1章回归分析1、回归分析是怎样的一种统计方法,用来解决什么问题?回归分析是统计学的一个重要分支,它基于观测数据建立变量之间的某种依赖关系,分析数据的内在规律,并可用于预报、控制等方面。
当自变量的个数大于1时称为多元回归,当因变量个数大于1时称为多重回归。
2、线性回归模型中线性关系指的是什么变量之间的关系?自变量与因变量之间一定是线性关系形式才能做线性回归吗?为什么?线性关系指的是自变量和因变量之间的关系。
多重线性回归中要求前提条件是线性——自变量和因变量之间的关系是线性的、独立性——各观测值之间是独立的、正态性——指自变量取不同值时,因变量服从正态分布、方差齐性——指自变量取不同值时,因变量的方差相同3、实际应用中,如何设定回归方程的形式?(P36)①假设方程的线性关系为:,其中是未知参数,是不可观测的随机误差且服从正态分布②估计未知参数,需要进行n次独立观测,得到n组样本数据4、多元线性回归理论模型中,每个系数(偏回归系数)的含义是什么?称为(偏)回归系数,随机因变量对各个自变量的回归系数,表示各自变量对随机变量的影响程度。
5、经验回归模型中,参数是如何确定的?有哪些评判参数估计的统计标准?最小二乘估计两有哪些统计性质(P37)?要想获得理想的参数估计值,需要注意一些什么问题?称为经验回归方程,这里是的最小二乘估计。
评判参数估计的统计标准有无偏性、有效性、一致性。
想要获得理想的参数估计值,需要尽量分散的取自变量,另外,样本数据个数n越大Var()越小。
6、理论回归模型中的随机误差项的实际意义是什么?为什么要在回归模型中加入随机误差项?建立回归模型时,对随机误差项作了哪些假定?这些假定的实际意义是什么?随机误差又称为偶然误差(accidental error)。
由于测试过程中诸多因素随机作用而形成的具有抵偿性的误差。
它是不可避免的,可以设法将其减少,但又不能完全消除。
随机误差具有统计性,在多次重复测量中,绝对值相同的正、负误差出现的机会大致相同,大误差出现的机会比小误差出现的机会少。
《多元统计分析》思考题答案记得老师课堂上说过考试内容不会超出这九道思考题,如下九道题题目中有错误的或不清楚的地方,欢迎大家指出、更改、补充。
1、 简述信度分析答题提示:要答可靠度概念,可靠度度量,克朗巴哈α系数、拆半系数、单项与总体相关系数、稀释相关系数等(至少要答四个系数,至少要给出两个指标的公式)答:信度(Reliability )即可靠性,它是指采用同样的方法对同一对象重复测量时所得结果的一致性程度。
信度指标多以相关系数表示,大致可分为三类:稳定系数(跨时间的一致性),等值系数(跨形式的一致性)和内在一致性系数(跨项目的一致性)。
信度分析的方法主要有以下四种:1)、重测信度法这一方法是用同样的问卷对同一组被调查者间隔一定时间重复施测,计算两次施测结果的相关系数。
重测信度属于稳定系数。
重测信度法特别适用于事实式问卷,如果没有突发事件导致被调查者的态度、意见突变,这种方法也适用于态度、意见式问卷。
由于重测信度法需要对同一样本试测两次,被调查者容易受到各种事件、活动和他人的影响,而且间隔时间长短也有一定限制,因此在实施中有一定困难。
2)、复本信度法复本信度法是让同一组被调查者一次填答两份问卷复本,计算两个复本的相关系数。
复本信度属于等值系数。
复本信度法要求两个复本除表述方式不同外,在内容、格式、难度和对应题项的提问方向等方面要完全一致,而在实际调查中,很难使调查问卷达到这种要求,因此采用这种方法者较少。
3)、折半信度法折半信度法是将调查项目分为两半,计算两半得分的相关系数,进而估计整个量表的信度。
折半信度属于内在一致性系数,测量的是两半题项得分间的一致性。
这种方法一般不适用于事实式问卷(如年龄与性别无法相比),常用于态度、意见式问卷的信度分析。
在问卷调查中,态度测量最常见的形式是5级李克特(Likert )量表。
进行折半信度分析时,如果量表中含有反意题项,应先将反意题项的得分作逆向处理,以保证各题项得分方向的一致性,然后将全部题项按奇偶或前后分为尽可能相等的两半,计算二者的相关系数。
一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为 Q型聚类和R型聚类。
4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。
5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。
6、若()(,), Px N αμα∑=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。
二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
2、简述相应分析的基本思想。
相应分析,是指对两个定性变量的多种水平进行分析。
设有两组因素A和B,其中因素A包含r个水平,因素B包含c个水平。
对这两组因素作随机抽样调查,得到一个rc的二维列联表,记为。
要寻求列联表列因素A和行因素B 的基本分析特征和最优列联表示。
相应分析即是通过列联表的转换,使得因素A 和因素B具有对等性,从而用相同的因子轴同时描述两个因素各个水平的情况。
把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上,从而得到因素A 、B 的联系。
3、简述费希尔判别法的基本思想。
从k 个总体中抽取具有p 个指标的样品观测数据,借助方差分析的思想构造一个线性判别函数 系数:确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
将新样品的p 个指标值代入线性判别函数式中求出 值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。
多元统计分析课后练习答案第1章多元正态分布1、在数据处理时,为什么通常要进行标准化处理?数据的标准化就是将数据按比例翻转,并使之掉入一个大的特定区间。
在某些比较和评价的指标处置中经常可以使用,除去数据的单位管制,将其转变为无量纲的纯数值,易于相同单位或量级的指标能展开比较和平均值。
其中最典型的就是0-1标准化和z标准化。
2、欧氏距离与马氏距离的优缺点是什么?欧氏距离也表示欧几里得度量、欧几里得度量,就是一个通常使用的距离定义,它就是在m维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。
当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待,这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点:误导了变化微小的变量的促进作用。
受到协方差矩阵不稳定的影响,马氏距离并不总是能够成功排序出来。
3、当变量x1和x2方向上的变差相等,且与互相独立时,采用欧氏距离与统计距离是否一致?统计数据距离区别于欧式距离,此距离必须倚赖样本的方差和协方差,能彰显各变量在变差大小上的相同,以及优势存有的相关性,还建议距离与各变量所用的单位毫无关系。
一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为 Q型聚类和 R型聚类。
4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。
5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。
6、若()(,), Px N αμα∑:=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。
二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
2、简述相应分析的基本思想。
相应分析,是指对两个定性变量的多种水平进行分析。
设有两组因素A和B,其中因素A包含r个水平,因素B包含c个水平。
对这两组因素作随机抽样调查,得到一个rc的二维列联表,记为。
要寻求列联表列因素A和行因素B的基本分析特征和最优列联表示。
相应分析即是通过列联表的转换,使得因素 A 和因素B具有对等性,从而用相同的因子轴同时描述两个因素各个水平的情况。
把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上,从而得到因素A、B的联系。
3、简述费希尔判别法的基本思想。
从k个总体中抽取具有p个指标的样品观测数据,借助方差分析的思想构造一个线性判别函数系数:确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
将新样品的p 个指标值代入线性判别函数式中求出 值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。
《多元统计分析》习题分为三部分:思考题、验证题和论文题
思考题
第一章绪论
1﹑什么是多元统计分析?
2﹑多元统计分析能解决哪些类型的实际问题?
第二章聚类分析
1﹑简述系统聚类法的基本思路。
2﹑写出样品间相关系数公式。
3﹑常用的距离及相似系数有哪些?它们各有什么特点?
4﹑利用谱系图分类应注意哪些问题?
5﹑在SAS和SPSS中如何实现系统聚类分析?
第三章判别分析
1﹑简述距离判别法的基本思路,图示其几何意义。
2﹑判别分析与聚类分析有何异同?
3﹑简述贝叶斯判别的基本思路。
4﹑简述费歇判别的基本思路。
5﹑简述逐步判别法的基本思想。
6﹑在SAS和SPSS软件中如何实现判别分析?
第四章主成分分析
1﹑主成分分析的几何意义是什么?
2﹑主成分分析的主要作用有那些?
3﹑什么是贡献率和累计贡献率,其意义何在?
4﹑为什么说贡献率和累计贡献率能反映主成分中所包含的原始变量的信息?
5﹑为什么要用标准化数据去估计V的特征向量与特征值?
6﹑证明:对于标准化数据有S=R。
7﹑主成分分析在SAS和SPSS中如何实现?
第五章因子分析
1﹑因子得分模型与主成分分析模型有何不同?
2﹑因子载荷阵的统计意义是什么?
3﹑方差旋转的目的是什么?
4﹑因子分析有何作用?
5﹑因子模型与回归模型有何不同?
6﹑在SAS和SPSS中如何实现因子分析?
第六章对应分析
1﹑简述对应分析的基本思想。
2﹑简述对应分析的基本原理。
3﹑简述因子分析中Q型与R 型的对应关系。
4﹑对应分析如何在SAS和SPSS中实现?
第七章典型相关分析
1﹑典型相关分析适合分析何种类型的数据?
2﹑简述典型相关分析的基本思想。
3﹑典型变量有哪些性质?
4﹑典型相关系数和典型变量有何意义?
5﹑典型相关分析有何作用?
6 ﹑在SAS和SPSS中如何实现典型相关分析?
验证题
第二章聚类分析
1、为了更深入了解我国人口的文化程度,现利用1990年全国人口普查数据对全国30个省、直辖市、自治区进行聚类分析。
分析选用了三个指标:(1)大学以上文化程度的人口占全部人口的比例(DXBZ);(2)初中文化程度的人都占全部人口的比例(CZBZ);(3)文盲半文盲人口占全部人口的比例(WMBZ),分别用来反映较高、中等、较低文化程度人口的状况。
计算样品之间的相似系数,使用最长距离法、重心法和Ward法,将上机结果按样品号画出聚类图,并根据聚类图将30个样品分为四类。
2、根据信息基础设施的发展状况,对世界20个国家和地区进行分类。
只要采用6个指标:(1)Call—每千人拥有电话线数,(2)movecall—每千户居民蜂窝移动电话数,(3)fee—高峰时期每三分钟国际电话的成本,(4)Computer—每千人拥有的计算机数,(5)mips—每千人中计算机功率(每秒百万指令),(6)net—每千人互联网络户主数。
计算样本之间的距离采用欧式距离,用最长距离法、重心法、离差平方和法进行计算。
3、按照城乡居民消费水平,对我国30个省市自治区分类。
第三章 判别分析
1、从1995年世界各国人文发展指数的排序中,选取高发展水平、中等发展水平的国家各五个作为两组样本,另选四个国家作为待判样品做距离判别分析。
2、对全国30个省市自治区1994年影响各地区经济增长差异的制度变量:1x —经济增长率(%)、
—非国有化水平(%)、3x —开放度(%)、4x —市场化程
度(%)作判别分析。
3、为了解全国各地职工生活费用上涨水平,对29个省市自治区九项指标作判别分析。
第四章 主成分分析
1、对全国30个省市自治区经济发展基本情况的八项指标作主成分分析。
2、对30个省市自治区工业企业经济效益作综合评价。
3、对我国城市居民生活费支出作主成分分析。
第五章 因子分析
1、利用1995年的数据对我国社会发展状况进行综合考察。
2、对我国30个省市自治区的农业生产情况作因子分析。
从农业生产条件和生产结果济效益出发,选取六项指标分别为:1X —乡村劳动力人口(万人),2X —人均经营耕地面积(亩),3X —户均生产性固定资产原值(元),4X —家庭基本纯收入(元),5X —人均农业总产值(千元/人),6X —增加值占总产值比重(%)。
3、对1979-1988年中国人民银行资金来源的10项指标作因子分析。
第六章 对应分析
1、用对应分析研究我国部分省份的农村居民家庭人均消费支出结构。
选取7个变量:1X —食品支出比重,2X —衣着支出比重,3X —居住支出比重,4X —家庭设备及服务支出比重,5X —医疗保健支出比重,6X —交通和通讯支出比重,7X —文教娱乐、用品及服务支出比重。
样品为10个:山西、内蒙古、辽宁、吉林、黑龙江、海南、四川、贵州、甘肃、青海。
2、对全国31个省市自治区按各种经济类型资产占总资产比重(%),利用1997年数据作对应分析。
选取6个变量:1X —国有经济/总资产,2X —集体经济/总资产,3X —联营经济/总资产,4X —股份制经济/总资产,5X —外商投资经济/总资产,6X —港澳台经济/总资产
3、用对应分析研究1991年全国各地区独立核算工业企业的经济效益情况。
第七章 典型相关分析
1、对某高中一年级男生38人进行体力测试(共有七项指标)及运动能力测试(共有五项指标),试对两组指标作典型相关分析。
体力测试指标:1X —反复横向跳(次),2X —纵跳(cm),3X —背力(kg),4X —握力(kg),5X —台阶试验(指数),6X —立定体前屈(cm),7X —俯卧上体后仰(cm)。
运动能力测试的指标为:8X —50米跑(秒),9X —跳远(cm),10X —投球(m),11X —引体向上(次),12X —耐力跑(秒)。
2、全国30个省市自治区农村居民收入和支出的典型相关分析。
反映农村居民收入的变量取4个:1X —劳动者报酬(元),2X —家庭经营收入(元),3X —转移性收入(元),4X —财产性收入(元)。
反映农村居民生活费支出的变量取8个:5X —食品支出(元), 6X —衣着支出(元),7X —居住支出(元),8X —家庭设备及服务支出(元),9X —医疗保健支出(元),10X —交通和通讯支出(元),11X —文教、娱乐用品及服务支出(元),12X —其它商品及服务支出(元)。
3、社会经济综合发展水平与邮电发展状况的典型相关分析。
论 文 题
通过论文题,可以让学生掌握如何在图书馆查阅数据,录入数据,并根据论文要求对数据进行预处理,使学生了解各分析方法适合解决的问题类型,能够运用所学的多元统计分析方法解决实际数据分析问题。
1、自拟题目,论文中的数据处理方法至少选用对应分析、典型相关分析中的一种。
2、自拟题目,论文中的数据处理方法至少选用主成分分析、因子分析中的一种。
3、自拟题目,论文中的数据处理方法至少选用聚类分析、判别分析中的一种。