(完整word版)实用多元统计分析相关习题
- 格式:doc
- 大小:212.00 KB
- 文档页数:8

复习题原文:答案:4.2 试述判别分析的实质。
4.3 简述距离判别法的基本思想和方法。
4.4 简述贝叶斯判别法的基本思想和方法。
4.5 简述费希尔判别法的基本思想和方法。
4.6 试析距离判别法、贝叶斯判别法和费希尔判别法的异同。
4.2 试述判别分析的实质。
答:判别分析就是希望利用已经测得的变量数据,找出一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别的样本点尽可能地区别开来。
设R1,R2,…,Rk是p维空间R p的k个子集,如果它们互不相交,且它们的和集为R p,则称R1,R2⋯R p为R p的一个划分。
判别分析问题实质上就是在某种意义上,以最优的性质对p维空间R p构造一个“划分”,这个“划分”就构成了一个判别规则。
4.3 简述距离判别法的基本思想和方法。
答:距离判别问题分为①两个总体的距离判别问题和②多个总体的判别问题。
其基本思想都是分别计算样本与各个总体的距离(马氏距离),将距离近的判别为一类。
①两个总体的距离判别问题设有协方差矩阵∑相等的两个总体G1和G2,其均值分别是μ1和μ2,对于一个新的样品X,要判断它来自哪个总体。
计算新样品X到两个总体的马氏距离D2(X,G1)和D2(X,G2),则X∈G1,D2(X,G1)≤ D2(X,G2)X ∈G 2 ,D 2(X ,G 1)> D 2(X ,G 2, 具体分析,2212(,)(,)D G D G -X X111122111111111222*********()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ11211212112122()()()2()22()2()---''=-++-'+⎛⎫=--- ⎪⎝⎭''=--=--X ΣμμμμΣμμμμX ΣμμX μααX μ 记()()W '=-X αX μ 则判别规则为X ∈G 1 ,W(X)≥0 X ∈G 2 ,W(X)<0②多个总体的判别问题。

2009学年第2学期 考试科目:多元统计分析 考试类型:(闭卷) 考试时间:100 分钟学号 姓名 年级专业一、填空题(5×6=30)22121212121~(,),(,),(,),,1X N X x x x x x x ρμμμμσρ⎛⎫∑==∑=⎪⎝⎭+-1、设其中则Cov(,)=____.10312~(,),1,,10,()()_________i i i i X N i W X X μμμ='∑=--∑、设则=服从。
()1234433,492,3216___________________X x x x R -⎛⎫ ⎪'==-- ⎪ ⎪-⎝⎭=∑、设随机向量且协方差矩阵则它的相关矩阵4、__________, __________,________________。
215,1,,16(,),(,)15[4()][4()]~___________i p p X i N X A N T X A X μμμμ-=∑∑'=--、设是来自多元正态总体和分别为正态总体的样本均值和样本离差矩阵,则。
二、计算题(5×11=50)(),123设X=x x x 的相关系数矩阵通过因子分析分解为211X h =的共性方差111X σ=的方差21X g =1公因子f 对的贡献121330.93400.1280.9340.4170.8351100.4170.8940.02700.8940.44730.8350.4470.1032013R ⎛⎫- ⎪⎛⎫⎛⎫ ⎪-⎛⎫ ⎪ ⎪⎪=-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎪⎝⎭12332313116421(,,)~(,),(1,0,2),441,2142X x x x N x x x x x μμ-⎛⎫⎪'=∑=-∑=-- ⎪ ⎪-⎝⎭-⎛⎫+ ⎪⎝⎭、设其中试判断与是否独立?11262(90,58,16),82.0 4.310714.62108.946460.2,(5)( 115.6924)14.6210 3.17237.14.5X S μ--'=-⎛⎫ ⎪==-- ⎪ ⎪⎝⎭0、对某地区农村的名周岁男婴的身高、胸围、上半臂围进行测量,得相关数据如下,根据以往资料,该地区城市2周岁男婴的这三个指标的均值现欲在多元正态性的假定下检验该地区农村男婴是否与城市男婴有相同的均值。

主成分分析6.1 试述主成分分析的基本思想。
答:我们处理的问题多是多指标变量问题,由于多个变量之间往往存在着一定程度的相关性,人们希望能通过线性组合的方式从这些指标中尽可能快的提取信息。
当第一个组合不能提取止。
这就是主成分分析的基本思想。
6.2 主成分分析的作用体现在何处?答:一般说来,在主成分分析适用的场合,用较少的主成分就可以得到较多的信息量。
以各个主成分为分量,就得到一个更低维的随机向量;主成分分析的作用就是在降低数据“维数”6.3 简述主成分分析中累积贡献率的具体含义。
答:主成分分析把p 个原始变量12,,,p X X X 的总方差()tr Σ分解成了p 个相互独立的变量p 个主成分的,忽略一些带有较小方差的主成分将不会给总方差带来太大的影响。
这里我们()m p <个主成分,则称11pmm kkk k ψλλ===∑∑ 为主成分1,,m Y Y 的累计贡献率,累计贡献率表明1,,m Y Y 综合12,,,p X X X 的能力。
通常取m ,使得累计贡献率达到一个较高的百分数(如85%以上)。
答:这个说法是正确的。
即原变量方差之和等于新的变量的方差之和6.5 试述根据协差阵进行主成分分析和根据相关阵进行主成分分析的区别。
答:从相关阵求得的主成分与协差阵求得的主成分一般情况是不相同的。
从协方差矩阵出发的,其结果受变量单位的影响。
主成分倾向于多归纳方差大的变量的信息,对于方差小的变量就可能体现得不够,也存在“大数吃小数”的问题。
实际表明,这种差异有时很大。
我6.6 已知X =()’的协差阵为 试进行主成分分析。
解:=0计算得当时,同理,计算得时,易知相互正交单位化向量得,,综上所述,第一主成分为第二主成分为第三主成分为6.7 设X=()’的协方差阵(p为, 0<p<1证明:为最大特征根,其对应的主成分为。
证明:==,为最大特征根当时,=所以,6.8利用主成分分析法,综合评价六个工业行业的经济效益指标。

《多元统计分析》习题分为三部分:思考题、验证题和论文题思考题第一章绪论1﹑什么是多元统计分析?2﹑多元统计分析能解决哪些类型的实际问题?第二章聚类分析1﹑简述系统聚类法的基本思路。
2﹑写出样品间相关系数公式。
3﹑常用的距离及相似系数有哪些?它们各有什么特点?4﹑利用谱系图分类应注意哪些问题?5﹑在SAS和SPSS中如何实现系统聚类分析?第三章判别分析1﹑简述距离判别法的基本思路,图示其几何意义。
2﹑判别分析与聚类分析有何异同?3﹑简述贝叶斯判别的基本思路。
4﹑简述费歇判别的基本思路。
5﹑简述逐步判别法的基本思想。
6﹑在SAS和SPSS软件中如何实现判别分析?第四章主成分分析1﹑主成分分析的几何意义是什么?2﹑主成分分析的主要作用有那些?3﹑什么是贡献率和累计贡献率,其意义何在?4﹑为什么说贡献率和累计贡献率能反映主成分中所包含的原始变量的信息?5﹑为什么要用标准化数据去估计V的特征向量与特征值?6﹑证明:对于标准化数据有S=R。
7﹑主成分分析在SAS和SPSS中如何实现?第五章因子分析1﹑因子得分模型与主成分分析模型有何不同?2﹑因子载荷阵的统计意义是什么?3﹑方差旋转的目的是什么?4﹑因子分析有何作用?5﹑因子模型与回归模型有何不同?6﹑在SAS和SPSS中如何实现因子分析?第六章对应分析1﹑简述对应分析的基本思想。
2﹑简述对应分析的基本原理。
3﹑简述因子分析中Q型与R 型的对应关系。
4﹑对应分析如何在SAS和SPSS中实现?第七章典型相关分析1﹑典型相关分析适合分析何种类型的数据?2﹑简述典型相关分析的基本思想。
3﹑典型变量有哪些性质?4﹑典型相关系数和典型变量有何意义?5﹑典型相关分析有何作用?6 ﹑在SAS和SPSS中如何实现典型相关分析?验证题第二章聚类分析1、为了更深入了解我国人口的文化程度,现利用1990年全国人口普查数据对全国30个省、直辖市、自治区进行聚类分析。
分析选用了三个指标:(1)大学以上文化程度的人口占全部人口的比例(DXBZ);(2)初中文化程度的人都占全部人口的比例(CZBZ);(3)文盲半文盲人口占全部人口的比例(WMBZ),分别用来反映较高、中等、较低文化程度人口的状况。
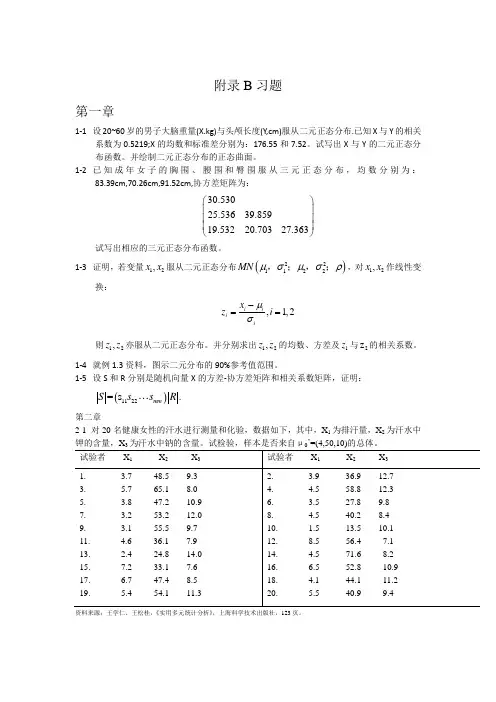

22121212121~(,),(,),(,),,1X N X x x x x x x ρμμμμσρ⎛⎫∑==∑=⎪⎝⎭+-1、设其中则Cov(,)=____.10312~(,),1,,10,()()_________i i i i X N i W X X μμμ='∑=--∑L 、设则=服从。
()1234433,492,3216___________________X x x x R -⎛⎫ ⎪'==-- ⎪ ⎪-⎝⎭=∑、设随机向量且协方差矩阵则它的相关矩阵4、__________, __________,________________。
215,1,,16(,),(,)15[4()][4()]~___________i p p X i N X A N T X A X μμμμ-=∑∑'=--L 、设是来自多元正态总体和分别为正态总体的样本均值和样本离差矩阵,则。
12332313116421(,,)~(,),(1,0,2),441,2142X x x x N x x x x x μμ-⎛⎫⎪'=∑=-∑=-- ⎪ ⎪-⎝⎭-⎛⎫+ ⎪⎝⎭、设其中试判断与是否独立?(),123设X=x x x 的相关系数矩阵通过因子分析分解为211X h =的共性方差111X σ=的方差21X g =1公因子f 对的贡献121330.93400.1280.9340.4170.8351100.4170.8940.02700.8940.44730.8350.4470.1032013R ⎛⎫- ⎪⎛⎫⎛⎫⎪-⎛⎫ ⎪ ⎪⎪=-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎪⎝⎭11262(90,58,16),82.0 4.310714.62108.946460.2,(5)( 115.6924)14.6210 3.17237.14.5X S μ--'=-⎛⎫ ⎪==-- ⎪ ⎪⎝⎭0、对某地区农村的名周岁男婴的身高、胸围、上半臂围进行测量,得相关数据如下,根据以往资料,该地区城市2周岁男婴的这三个指标的均值现欲在多元正态性的假定下检验该地区农村男婴是否与城市男婴有相同的均值。

复习题原文:答案:4.2 试述判别分析的实质。
4.3 简述距离判别法的基本思想和方法。
4.4 简述贝叶斯判别法的基本思想和方法。
4.5 简述费希尔判别法的基本思想和方法。
4.6 试析距离判别法、贝叶斯判别法和费希尔判别法的异同。
4.2 试述判别分析的实质。
答:判别分析就是希望利用已经测得的变量数据,找出一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别的样本点尽可能地区别开来。
设R1,R2,…,Rk是p维空间R p的k个子集,如果它们互不相交,且它们的和集为R p,则称R1,R2⋯R p为R p的一个划分。
判别分析问题实质上就是在某种意义上,以最优的性质对p维空间R p构造一个“划分”,这个“划分”就构成了一个判别规则。
4.3 简述距离判别法的基本思想和方法。
答:距离判别问题分为①两个总体的距离判别问题和②多个总体的判别问题。
其基本思想都是分别计算样本与各个总体的距离(马氏距离),将距离近的判别为一类。
①两个总体的距离判别问题设有协方差矩阵∑相等的两个总体G1和G2,其均值分别是μ1和μ2,对于一个新的样品X,要判断它来自哪个总体。
计算新样品X到两个总体的马氏距离D2(X,G1)和D2(X,G2),则X∈G1,D2(X,G1)≤ D2(X,G2)X ∈G 2 ,D 2(X ,G 1)> D 2(X ,G 2, 具体分析,2212(,)(,)D G D G -X X111122111111111222*********()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ11211212112122()()()2()22()2()---''=-++-'+⎛⎫=--- ⎪⎝⎭''=--=--X ΣμμμμΣμμμμX ΣμμX μααX μ 记()()W '=-X αX μ 则判别规则为X ∈G 1 ,W(X)≥0 X ∈G 2 ,W(X)<0②多个总体的判别问题。

多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法,它通过同时考虑多个变量之间的关系,帮助研究者更全面地理解和解释现象。
在本文中,我将分享一些多元统计分析的习题和答案,希望能够帮助读者更好地掌握这一方法。
习题一:相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。
你收集了100个学生的数据,学习成绩用分数表示,学习时间用小时表示。
以下是你的数据:学习成绩(X):75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间(Y):5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数,并解释其含义。
答案一:首先,我们需要计算学习成绩和学习时间之间的协方差和标准差。
根据公式,协方差可以通过以下公式计算:协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中,X和Y分别表示学习成绩和学习时间,X平均和Y平均表示它们的平均值,n表示样本数量。
标准差可以通过以下公式计算:标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式,我们可以得出学习成绩和学习时间之间的协方差为-22.5,标准差分别为18.03和2.87。
然后,我们可以通过以下公式计算相关系数:相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式,我们可以得出相关系数为-0.93。
由于相关系数接近于-1,可以得出结论:学习成绩和学习时间之间存在强烈的负相关关系,即学习时间越长,学习成绩越低。
习题二:多元线性回归假设你正在研究一个人的身高(X1)、体重(X2)和年龄(X3)对其收入(Y)的影响。
你收集了50个人的数据,以下是你的数据:身高(X1):160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重(X2):50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄(X3):20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入(Y):5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析,建立一个预测人的收入的模型,并解释模型的结果。

练习题一、填空题1.人们通过各种实践,发现变量之间的相互关系可以分成(相关)和(不相关)两种类型。
多元统计中常用的统计量有:样本均值、样本方差、样本协方差和样本相关系数。
2.总离差平方和可以分解为(回归离差平方和)和(剩余离差平方和)两个部分,其中(回归离差平方和)在总离差平方和中所占比重越大,则线性回归效果越显著。
3.回归方程显著性检验时通常采用的统计量是(S R/p)/[S E/(n-p-1)]。
4.偏相关系数是指多元回归分析中,(当其他变量固定时,给定的两个变量之间的)的相关系数。
5.Spss中回归方程的建模方法有(一元线性回归、多元线性回归、岭回归、多对多线性回归)等。
6.主成分分析是通过适当的变量替换,使新变量成为原变量的(线性组合),并寻求(降维)的一种方法。
7.主成分分析的基本思想是(设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来替代原来的指标)。
8.主成分表达式的系数向量是(相关系数矩阵)的特征向量。
9.样本主成分的总方差等于(1)。
10.在经济指标综合评价中,应用主成分分析法,则评价函数中的权数为(方差贡献度)。
主成分的协方差矩阵为(对称)矩阵。
主成分表达式的系数向量是(相关矩阵特征值)的特征向量。
11.SPSS中主成分分析采用(analyze—data reduction—facyor)命令过程。
12.因子分析是把每个原始变量分解为两部分因素,一部分是(公共因子),另一部分为(特殊因子)。
13.变量共同度是指因子载荷矩阵中(第i行元素的平方和)。
14.公共因子方差与特殊因子方差之和为(1)。
15.聚类分析是建立一种分类方法,它将一批样品或变量按照它们在性质上的(亲疏程度)进行科学的分类。
16.Q型聚类法是按(样品)进行聚类,R型聚类法是按(变量)进行聚类。
17.Q型聚类统计量是(距离),而R型聚类统计量通常采用(相关系数)。
18.六种Q型聚类方法分别为(最长距离法)、(最短距离法)、(中间距离法)、(类平均法)、(重心法)、(离差平方和法)。

多元统计分析多元统计分析习题集(⼀)⼀、填空题1.若()(,),(1,2,,)p X N n αµα∑= 且相互独⽴,则样本均值向量X 服从的分布是____________________。
2.变量的类型按尺度划分为___________、____________、_____________。
3.判别分析是判别样品_____________的⼀种⽅法,常⽤的判别⽅法有_____________、_____________、_____________、_____________。
4.Q 型聚类是指对_____________进⾏聚类,R 型聚类指对_____________进⾏聚类。
5.设样品12(,,,),(1,2,,)i i i ip X X X X i n '== ,总体(,)p X N µ∑ ,对样品进⾏分类常⽤的距离有____________________、____________________、____________________。
6.因⼦分析中因⼦载荷系数ij a 的统计意义是_________________________________。
7.主成分分析中的因⼦负荷ij a 的统计意义是________________________________。
8.对应分析是将__________________和__________________结合起来进⾏的统计分析⽅法。
9.典型相关分析是研究__________________________的⼀种多元统计分析⽅法。
⼆、计算题 1.设3(,)X N µ∑ ,其中410130002?? ?∑= ? ??,问1X 与2X 是否独⽴?12(,)X X '与3X 是否独⽴?为什么?2.设抽了5个样品,每个样品只测了⼀个指标,它们分别是1,2,4.5,6,8。
若样品间采⽤绝对值距离,试⽤最长距离法对其进⾏分类,要求给出聚类图。
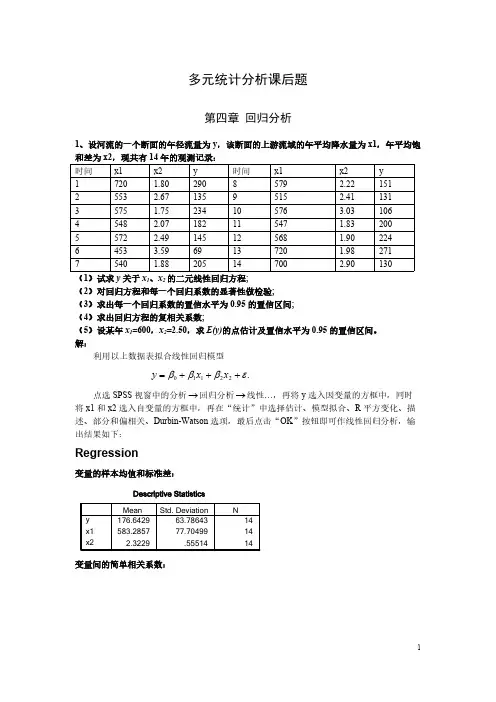
多元统计分析课后题第四章 回归分析1、设河流的一个断面的年径流量为y ,该断面的上游流域的年平均降水量为x1,年平均饱和差为x2,现共有14年的观测记录:时间x1x2y 时间x1x2y17201.8029085792.221512553 2.6713595152.411313575 1.75234105763.031064548 2.07182115471.832005572 2.49145125681.902246453 3.5969137201.982717540 1.88205147002.90130(1)试求y 关于x 1、x 2的二元线性回归方程;(2)对回归方程和每一个回归系数的显著性做检验;(3)求出每一个回归系数的置信水平为0.95的置信区间;(4)求出回归方程的复相关系数;(5)设某年x 1=600,x 2=2.50,求E(y)的点估计及置信水平为0.95的置信区间。
解:利用以上数据表拟合线性回归模型.22110εβββ+++=x x y 点选SPSS 视窗中的分析回归分析线性…,再将y 选入因变量的方框中,同时→→将x1和x2选入自变量的方框中,再在“统计”中选择估计、模型拟合、R 平方变化、描述、部分和偏相关、Durbin-Watson 选项,最后点击“OK ”按钮即可作线性回归分析,输出结果如下:Regression变量的样本均值和标准差:变量间的简单相关系数:这里给出了回归方程的样本决定系数和P值以及DW值:下面的框图是方差分析表,从中可以看出,y关于x1和x2的线性回归方程通过了显著性检验,均方残差为554.963,F统计量值为42.155,P值为0.000,回归方程在0.000的统计意义上是显著的。
上面的框图给出了非标准化和标准化的回归方程,以及回归系数的t 统计量检验结果。
从中我们可以看出,非标准化的回归方程为:(1)21x 647.87292.0875.209-+=x y(2)回归系数、均通过了显著性检验。
1 、设 X ~ N2 ( ,), 其中 X( x1 , x 2 ),( 1 ,212 ),,1则 Cov( x1x 2 , x1x 2 )=____.102、设X i ~N 3 (,), i 1, L,10,则 W =( X i)( X i)i 1服从_________。
4433、设随机向量X x1x2x3, 且协方差矩阵 4 9 2 ,3 2 16则它的相关矩阵R___________________4、设 X= x1x2x3,的相关系数矩阵通过因子分析分解为112330.93400.1280.4171R100.4170.9340.83530.8940.8940.027 0.83500.4472010.4470.10332__________,__________,X1的共性方差 h1X1的方差11公因子 f 1对 X的贡献 g12________________。
5、设 X i , i 1,L ,16 是来自多元正态总体N p (, ), X 和 A分别为正态总体N p ( ,)的样本均值和样本离差矩阵 , 则T 215[4( X)] A 1[4( X)] ~ ___________。
1642、设( x1 , x2 , x3) ~ N3(, ),其中(1,0, 2) ,44 1 ,1X214试判断 x12 x3与x2x3是否独立?x12、对某地区农村的 6 名 2 周岁男婴的身高、胸围、上半臂围进行测量,得相关数据如下 , 根据以往资料 , 该地区城市 2周岁男婴的这三个指标的均值0(90,58,16), 现欲在多元正态性的假定下检验该地区农村男婴是否与城市男婴有相同的均值。
82.0 4.310714.62108.9464其中 X60.2 ,(5 S ) 1( 115.6924)114.6210 3.17237. 376014.58.946437.376035.5936 (0.01,F 0.01 (3, 2)99.2, F 0.01 (3,3)29.5,F0.01 (3, 4)16.7)、设已知有两正态总体G与 G,且12,24,1211,3126219而其先验概率分别为q1q20.5,误判的代价C (2 1)4;e ,C(1 2)e试用判别法确定样本X 3属于哪一个总体?Bayes514、设X( X1 , X2 , X3 , X4 )T,协方差阵1~ N (0, ),0111(1)试从Σ出发求 X 的第一总体主成分;(2)试问当取多大时才能使第一主成分的贡献率达95%以上。
1 、设 X ~ N2 ( ,), 其中 X( x1 , x 2 ),( 1 ,212 ),,1则 Cov( x1x 2 , x1x 2 )=____.102、设X i ~N 3 (,), i 1, L,10,则 W =( X i)( X i)i 1服从_________。
4433、设随机向量X x1x2x3, 且协方差矩阵 4 9 2 ,3 2 16则它的相关矩阵R___________________4、设 X= x1x2x3,的相关系数矩阵通过因子分析分解为112330.93400.1280.4171R100.4170.9340.83530.8940.8940.027 0.83500.4472010.4470.10332__________,__________,X1的共性方差 h1X1的方差11公因子 f 1对 X的贡献 g12________________。
5、设 X i , i 1,L ,16 是来自多元正态总体N p (, ), X 和 A分别为正态总体N p ( ,)的样本均值和样本离差矩阵 , 则T 215[4( X)] A 1[4( X)] ~ ___________。
1642、设( x1 , x2 , x3) ~ N3(, ),其中(1,0, 2) ,44 1 ,1X214试判断 x12 x3与x2x3是否独立?x12、对某地区农村的 6 名 2 周岁男婴的身高、胸围、上半臂围进行测量,得相关数据如下 , 根据以往资料 , 该地区城市 2周岁男婴的这三个指标的均值0(90,58,16), 现欲在多元正态性的假定下检验该地区农村男婴是否与城市男婴有相同的均值。
82.0 4.310714.62108.9464其中 X60.2 ,(5 S ) 1( 115.6924)114.6210 3.17237. 376014.58.946437.376035.5936 (0.01,F 0.01 (3, 2)99.2, F 0.01 (3,3)29.5,F0.01 (3, 4)16.7)、设已知有两正态总体G与 G,且12,24,1211,3126219而其先验概率分别为q1q20.5,误判的代价C (2 1)4;e ,C(1 2)e试用判别法确定样本X 3属于哪一个总体?Bayes514、设X( X1 , X2 , X3 , X4 )T,协方差阵1~ N (0, ),0111(1)试从Σ出发求 X 的第一总体主成分;(2)试问当取多大时才能使第一主成分的贡献率达95%以上。
多元统计复习题答案一、单项选择题1. 多元统计分析中,用于描述多个变量之间关系的统计方法是()。
A. 相关分析B. 聚类分析C. 因子分析D. 主成分分析答案:C2. 以下哪个不是多元统计分析中常用的降维方法?()A. 主成分分析B. 因子分析C. 聚类分析D. 典型相关分析答案:C3. 在多元统计分析中,用于识别数据集中的异常值或离群点的统计方法是()。
A. 马氏距离B. 箱线图C. 相关系数D. 卡方检验答案:B二、多项选择题1. 多元统计分析中,以下哪些方法可以用来进行变量选择?()A. 逐步回归B. 岭回归C. 偏最小二乘回归D. 主成分分析答案:A|B|C2. 多元统计分析中,以下哪些方法可以用来进行数据的分类?()A. 判别分析B. 聚类分析C. 因子分析D. 典型相关分析答案:A|B三、判断题1. 多元统计分析中的因子分析可以用于变量的降维。
(对)2. 多元统计分析中的主成分分析和因子分析是完全相同的方法。
(错)3. 多元统计分析中的聚类分析可以用于识别数据集中的异常值。
(错)四、简答题1. 简述多元统计分析中主成分分析(PCA)的主要步骤。
答:主成分分析的主要步骤包括:数据标准化、计算协方差矩阵、求解特征值和特征向量、选择主成分、构造主成分得分。
2. 描述多元统计分析中判别分析的应用场景。
答:判别分析在多元统计分析中主要应用于根据已有的分类变量来预测新样本的分类,例如在医学诊断、市场细分、信用评分等领域。
五、计算题1. 给定一组数据,计算其主成分得分。
答:首先需要对数据进行标准化处理,然后计算协方差矩阵,接着求解特征值和特征向量,最后根据特征值的大小选择前几个主成分,并计算对应的得分。
2. 利用判别分析对一组数据进行分类,并给出分类结果。
答:首先需要确定分类的依据,然后计算各类别的判别函数,接着对新样本进行判别分析,最后根据判别得分将样本分类到相应的类别中。
多元统计分析期末试题Word版一、填空题(20分)1、若),2,1(),,(~)(n N X p =∑αμα 且相互独立,则样本均值向量X2、变量的类型按尺度划分有_间隔尺度_、_有序尺度_、名义尺度_。
3、判别分析是判别样品所属类型的一种统计方法,常用的判别方法有__距离判别法_、Fisher 判别法、Bayes 判别法、逐步判别法。
4、Q 型聚类是指对_样品_进行聚类,R 型聚类是指对_指标(变量)_进行聚类。
5、设样品),2,1(,),,('21n i X X X X ip i i i ==,总体),(~∑μp N X ,对样品进行分类常用的距离有:明氏距离,马氏距离2()ijd M =)()(1j i j i x x x x -∑'--,兰氏距离()ij d L=6、因子分析中因子载荷系数ij a 的统计意义是_第i 个变量与第j 个公因子的相关系数。
7、一元回归的数学模型是:εββ++=x y 10,多元回归的数学模型是:εββββ++++=p p x x x y 22110。
8、对应分析是将R 型因子分析和Q 型因子分析结合起来进行的统计分析方法。
9、典型相关分析是研究两组变量之间相关关系的一种多元统计方法。
二、计算题(60分)1、设三维随机向量),(~3∑μN X ,其中=∑200031014,问1X 与2X 是否独立?),(21'X X 和3X 是否独立?为什么?解:因为1),cov(21=X X ,所以1X 与2X 不独立。
把协差矩阵写成分块矩阵∑∑∑∑=∑22211211,),(21'X X 的协差矩阵为11∑因为12321),),cov((∑='X X X ,而012=∑,所以),(21'X X 和3X 是不相关的,而正态分布不相关与相互独立是等价的,所以),(21'X X 和3X 是独立的。
2、设抽了五个样品,每个样品只测了一个指标,它们分别是1 ,2 ,4.5 ,6 ,8。
第1章 多元正态分布1、在数据处理时,为什么通常要进行标准化处理?数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。
在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。
其中最典型的就是0-1标准化和Z 标准化。
2、欧氏距离与马氏距离的优缺点是什么?欧氏距离也称欧几里得度量、欧几里得度量,是一个通常采用的距离定义,它是在m 维空间中两个点之间的真实距离。
在二维和三维空间中的欧氏距离的就是两点之间的距离。
缺点:就大部分统计问题而言,欧氏距离是不能令人满意的。
每个坐标对欧氏距离的贡献是同等的。
当坐标表示测量值时,它们往往带有大小不等的随机波动,在这种情况下,合理的方法是对坐标加权,使变化较大的坐标比变化较小的坐标有较小的权系数,这就产生了各种距离。
当各个分量为不同性质的量时,“距离”的大小与指标的单位有关。
它将样品的不同属性之间的差别等同看待,这一点有时不能满足实际要求。
没有考虑到总体变异对距离远近的影响。
马氏距离表示数据的协方差距离。
为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。
优点:它不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关。
由标准化数据和中心化数据计算出的二点之间的马氏距离相同。
马氏距离还可以排除变量之间的相关性的干扰。
缺点:夸大了变化微小的变量的作用。
受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
3、当变量X1和X2方向上的变差相等,且与互相独立时,采用欧氏距离与统计距离是否一致?统计距离区别于欧式距离,此距离要依赖样本的方差和协方差,能够体现各变量在变差大小上的不同,以及优势存在的相关性,还要求距离与各变量所用的单位无关。
如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。
(完整版)多元统计分析试题及答案试题:1. 试解释多元统计分析的含义及其与单变量和双变量统计分析的区别。
2. 简述卡方检验方法及适用场景。
3. 请解释回归分析中的回归系数及其p值的含义及作用,简单说明如何进行回归模型的选择和评估。
4. 试解释主成分分析的原理及目的,如何进行主成分分析及如何解释因子载荷矩阵。
5. 请列举和简要解释聚类分析和判别分析的适用场景,并说明两种方法的区别。
答案:1. 多元统计分析是一种将多个变量进行综合分析的方法。
与单变量和双变量统计分析不同的是,多元统计分析可以处理多个自变量和因变量的组合关系,从而探究它们之间的综合关系。
该方法通常适用于探究多种变量在某个问题中的关系、探究影响某一结果变量的因素、探究各个变量相互作用的影响等。
2. 卡方检验是根据样本数据与期望值的差异来判断观察值与理论预期是否相符,以此来验证假设是否成立的方法。
它通常用于对某个现象进行分类的相关度检验。
适用场景包括:样本的数量大于等于40,且至少有一个期望值小于5;变量为分类变量,且分类类别数不超过10个。
卡方检验的原理是将观察值和期望值进行比较,并计算卡方值,然后根据卡方值与自由度的乘积查找p值,从而得出结论。
3. 回归系数是回归方程中自变量与因变量之间的关系,在线性回归中,回归系数表示每一个自变量单位变化与因变量单位变化的关系。
p值是评估回归系数是否具有显著性的指标。
回归模型的选择有两种方法:一种是逐步回归分析,根据不同的准则进行多个回归模型的比较,选择最优的模型;另一种是正则化回归,通过加入惩罚项来保证回归模型具有良好的泛化性能。
回归模型的评估有多种方法,包括:残差分析、R方值、方差齐性检验、变量的共线性检验等。
4. 主成分分析是一种将多维数据降维处理的方法,它的目的是通过数据的变换,将多个变量转化为一些综合指标,这些指标是原始变量的线性组合。
主成分分析的步骤包括:数据标准化、计算协方差矩阵或相关系数矩阵、计算特征值和特征向量、选取主成分。
练习题一、填空题1.人们通过各种实践,发现变量之间的相互关系可以分成(相关)和(不相关)两种类型。
多元统计中常用的统计量有:样本均值、样本方差、样本协方差和样本相关系数。
2.总离差平方和可以分解为(回归离差平方和)和(剩余离差平方和)两个部分,其中(回归离差平方和)在总离差平方和中所占比重越大,则线性回归效果越显著。
3.回归方程显著性检验时通常采用的统计量是(S R/p)/[S E/(n-p-1)]。
4.偏相关系数是指多元回归分析中,(当其他变量固定时,给定的两个变量之间的)的相关系数。
5.Spss中回归方程的建模方法有(一元线性回归、多元线性回归、岭回归、多对多线性回归)等。
6.主成分分析是通过适当的变量替换,使新变量成为原变量的(线性组合),并寻求(降维)的一种方法。
7.主成分分析的基本思想是(设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来替代原来的指标)。
8.主成分表达式的系数向量是(相关系数矩阵)的特征向量。
9.样本主成分的总方差等于(1)。
10.在经济指标综合评价中,应用主成分分析法,则评价函数中的权数为(方差贡献度)。
主成分的协方差矩阵为(对称)矩阵。
主成分表达式的系数向量是(相关矩阵特征值)的特征向量。
11.SPSS中主成分分析采用(analyze—data reduction—facyor)命令过程。
12.因子分析是把每个原始变量分解为两部分因素,一部分是(公共因子),另一部分为(特殊因子)。
13.变量共同度是指因子载荷矩阵中(第i行元素的平方和)。
14.公共因子方差与特殊因子方差之和为(1)。
15.聚类分析是建立一种分类方法,它将一批样品或变量按照它们在性质上的(亲疏程度)进行科学的分类。
16.Q型聚类法是按(样品)进行聚类,R型聚类法是按(变量)进行聚类。
17.Q型聚类统计量是(距离),而R型聚类统计量通常采用(相关系数)。
18.六种Q型聚类方法分别为(最长距离法)、(最短距离法)、(中间距离法)、(类平均法)、(重心法)、(离差平方和法)。
19.快速聚类在SPSS中由(k-均值聚类(analyze—classify—k means cluster))过程实现。
20.判别分析是要解决在研究对象已(已分成若干类)的情况下,确定新的观测数据属于已知类别中哪一类的多元统计方法。
21.用判别分析方法处理问题时,通常以(判别函数)作为衡量新样本点与各已知组别接近程度的指标。
22.进行判别分析时,通常指定一种判别规则,用来判定新样本的归属,常见的判别准则有(Fisher准则)、(贝叶斯准则)。
23.类内样本点接近,类间样本点疏远的性质,可以通过(类与类之间的距离)与(类内样本的距离)的大小差异表现出来,而两者的比值能把不同的类区别开来。
这个比值越大,说明类与类间的差异越(类与类之间的距离越大),分类效果越(好)。
24.Fisher判别法就是要找一个由p个变量组成的(线性判别函数),使得各自组内点的(离差)尽可能接近,而不同组间点的尽可能疏远。
二、简答题1、简述复相关系数与偏相关系数。
答:复相关系数:又叫多重相关系数。
复相关是指因变量与多个自变量之间的相关关系。
例如,某种商品的需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。
偏相关系数:又叫部分相关系数。
部分相关系数反映校正其它变量后某一变量与另一变量的相关关系。
偏相关系数是指多元回归分析中,当其他变量固定后,给定的两个变量之间的的相关系数。
偏相关系数的假设检验等同于偏回归系数的t 检验。
复相关系数的假设检验等同于回归方程的方差分析。
2、简述逐步回归分析方法的具体实施步骤。
答:逐步回归过程如下:1)自变量的剔除;2)重新进行少一个自变量的多元线性回归分析; 3)重新进行多一个自变量的多元线性回归分析;4)重新进行上述步骤,直至无法再删除和再引入自变量为止。
3、提取样本主成分的原则。
答:主成分个数提取原则为主成分对应的特征值大于1的前m 个主成分。
特征值在某种程度上可以被看成是表示主成分影响力度大小的指标,如果特征值小于1,说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大,因此,一般可以用特征值大于1作为纳入标准。
4、简述系统聚类法的基本思想及主要步骤。
答:系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中。
系统聚类过程是:假设总共有n 个样品(或变量),第一步将每个样品(或变量)独自聚成一类,共有n 类;第二步根据所确定的样品(或变量)“距离”公式,把距离较近的两个样品(或变量)聚合为一类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类;第三步将“距离”最近的两个类进一步聚成一类,共聚成n 2类;……,以上步骤一直进行下去,最后将所有的样品(或变量)全聚成一类,也简称聚集法。
还有与以上方法相反的称分解法。
5、简述快速聚类(k —均值聚类)的基本思想及主要步骤。
答:基本思想:1.一个样品分配给最近中心(均值)的类中,将所有样品分成k 个初始类。
2.通过欧式距离将每个样品划入离中心最近的类中,并对得到样品或失去样品的类重新计算中心坐标。
3.重复步骤2,直到所有样品都不能再分配时为止。
6、判别分析的分类。
答:判别分析是多元统计分析中用于判别样本所属类型的一种统计分析方法。
判别分析按判别的组数来分,有两组判别分析和多组判别分析;按区分不同总体所用的数学模型来分,有线性判别和非线性判别;按判别对所处理的变量方法不同,有逐步判别、序贯判别等;按判别准则不同,有距离判别、贝叶斯判别(Bayes )、费歇(Fisher )判别等。
7、简述Fisher 判别规则及具体判别步骤。
答:Fisher 判别法的基本思想:从多个总体(类)抽取一定的样本,借助方差分析的思想,建立p 个指标的线性判别函数,把待判样品代入线性判别函数,然后与临界值比较,就可判样品属于哪个类。
Fisher 判别法的具体算法步骤:由Fisher 线性判别式()M M S 211*-=-ωω求解向量ω*的步骤:① 把来自两类ωω21训练样本集X 分成ω1和ω2两个子集X1和X2。
② 由2,1,1i =∑=∈I X n M X x ik k i ,计算M i 。
③ 由()()Ti k i k X x ik M x M X S ∑--=∈i 计算各类的类内离散度矩阵S i ,i=1,2。
④ 计算类内总离散度矩阵S S S 21+=ω。
⑤ 计算S ω的逆矩阵S 1-ω。
⑥ 由()M M S 211*-=-ωω求解ω*。
三、计算题1.现收集了92组合金钢中的碳含量x 及强度y ,且求得:03.29415126.263019.07989.45,1255.0=====yy xy xx L L L y x(1)求y 关于x 的一元线性回归方程; (2)求y 与x 的相关系数;(3)列出对方程作显著性检验的方差分析表;(4)在x=0.1时,求yˆ的点估计。
2. 某地区通过一个样本容量为722的调查数据得到劳动力受教育年数的一个回归方程为10.360.0940.1310.210i i i i edu sibs medu fedu =-++ 20.214R =式中,edu 为劳动力受教育年数,sibs 为劳动力家庭中兄弟姐妹的个数,medu 与fedu 分别为母亲与父亲受到教育的年数。
问 (1)若m e d u与fedu 保持不变,为了使预测的受教育水平减少一年,需要sibs 增加多少?(2)请对medu 的系数给予适当的解释。
(3)如果两个劳动力都没有兄弟姐妹,但其中一个的父母受教育的年数均为12年,另一个的父母受教育的年数均为16年,则两人受教育的年数预期相差多少年3(2)2R和2R?(3)检验假设:解释变量总体上对Y有无影响。
你用什么假设检验?为什么?4.在一项研究中,测量了376只鸡的骨骼,并利用相关系数矩阵进行主成分分析,见(2)对于y4,y5,y6的方差很小这一点,你怎样对实际情况作出推断。
解:5.在一项对杨树的性状的研究中,测定了20株杨树树叶,每个叶片测定了四个变量:叶长(x1),2/3处宽(x2),1/3处宽(x3),1/2处宽(x4)。
这四个变量的相关系数矩阵的特征根和标准正交特征向量分别为:)7930.0,5513.0,2519.0,0612.0(007.0)1624.0,5589.0,7733.0,2516.0(049.0)0824.0,2695.0,0984.0,9544.0(024.1)5814.0,5577.0,5735.0,1485.0(920.244332211--='=--='=-='=---='=U U U U λλλλ写出四个主成分,计算它们的贡献率。
解:各自的主成分为:Z1=0.1485X 1-0.5735X 2-0.5577X 3-0.5814X 4 Z2=0.9544X 1-0.0984X 2+0.2695X 3+0.0824X 4 Z3=0.2516X 1+0.7733X 2-0.5589X 3-0.1624X 4 Z4=-0.0612X 1+0.2519X 2+0.5513X 3-0.7930X 4 则各自的贡献率为:W1=2.920/(2.920+1.024+0.049+0.007)=0.73 W2=1.024/(2.920+1.024+0.049+0.007)=0.256 W2=0.049/(2.920+1.024+0.049+0.007)=0.01225 W2=0.007/(2.920+1.024+0.049+0.007)=0.001756.对纽约股票市场上的五种股票的周回升率x1,x2,x3,x4,x5进行了主成分分析,其中x1,x2,x3分别表示三个化学工业公司的股票回升率,x4,x5表示两个石油公司的股票回升率,主成分分析是从相关系数矩阵出发进行的,前两个特征根和对应的标准正交特征向量为:)582.0,526.0,260.0,509.0,240.0(809.0)421.0,421.0,470.0,457.0,464.0(857.22211--='=='=U U λλ(1) 计算这两个主成分的方差贡献率。
解:各自的主成分为:Z1=0.464X 1+0.457X 2+0.470X 3+0.421X 4+0.421X 5 Z2=0.240X 1+0.509X 2+0.260X 3-0.526X 4-0.582X 5 则各自的贡献率为:W1=2.587/(2.587+0.809)=0.762 W2=0.809/(2.587+0.809)=0.238(2) 能否对这两个主成分的意义作一个合理的解释,并给两个主成分命名。