基于MATLAB的FM调制实现

目录摘要 (II)1课程设计的任务与说明 (1)2 FM信号的MATLAB仿真设计方案制定 (2)3 FM信号的MATLAB仿真设计方案的设计 (3)3.1调制过程 (3)3.2解调过程 (4)3.3噪声 (4)4 FM信号调制解调模型的建立与分析 (5)4.1 调制模型的建立与分析 (5)4.1.1 FM调制模型 (5)4.1.2 调制过程分析 (5)4.1.3 调制程序 (6)4.1.4 FM调制仿真波形图 (7)4.2 解调模型的建立与分析 (10)4.2.1 FM解调模型 (10)4.2.2 解调过程分析 (11)4.2.3 解调程序 (12)4.2.4 FM解调仿真波形图 (13)4.3 高斯白噪声信道特性及FM系统抗噪声性能分析 (16)5.心得体会 (21)6.参考文献 (22)附录 (23)摘要调制在通信系统中的作用至关重要。

通过调制，不仅可以进行频谱搬移，把调制信号的频谱搬移到所希望的位置上，从而将调制信号转换成适合于传播的已调信号，而且它对系统的传输有效性和传输的可靠性有着很大的影响，调制方式往往决定了一个通信系统的性能。

FM信号的调制属于频谱的非线性搬移，它的解调也有相干和非相干解调两种方式。

本次课程设计使用的仿真软件为MATLAB，利用MATLAB集成环境下的M文件，编写程序来实现FM信号的仿真分析，并分别绘制出基带信号、载波信号、已调信号的时域波形和频域波形；再进一步分别绘制出对已调信号叠加噪声后信号、同步解调前信号和解调后基带信号的时域波形；最后绘出FM基带信号调制和解调系统后的输入输出信噪比的关系，并通过与理论结果波形对比来分析该仿真调制与解调过程的正确性及噪声对FM信号解调的影响，完成对FM调制和解调以及对叠加噪声后解调结果的观察和分析。

关键词: FM 调制与解调 MATLAB 噪声AbstractModulation in a communication system has extremely important role. Through the modulation, not only can frequency shift, the modulation signal spectrum is moved to want, thus will position modulation signal is converted into suitable for transmission of the signal, and it has attune to the transmission effectiveness and reliability of transferring having very big effect, modulation method often determines a communication system performance. FM signals modulation of nonlinear shift, belong to the spectrum of its demodulation also have coherent and incoherent demodulation in two ways.This course is designed to use simulation software for MATLAB, use of MATLAB integration environment of M files, write a program to realize FM signals of the simulation analysis, and draw the baseband signal respectively, carrier signal, already adjustable signal and the time domain waveform frequency domain waveform; Further respectively to map out already adjustable signal after adding noise signal, synchronous demodulation signal demodulation before and after baseband signal temporal profile, Finally draw FM baseband signal modulation and demodulation system after the input/output SNR, and the relationship with the theoretical results wave contrast to analyze the simulation modulation and demodulation process accuracy and noise on FM signal demodulation of the influence,then finish to FM modulation and demodulation of adding noise and after the observation and analysis results demodulation.Keywords ：FM Modulation and Demodulation MATLAB noise1课程设计的任务与说明FM在通信系统中的使用非常广泛。

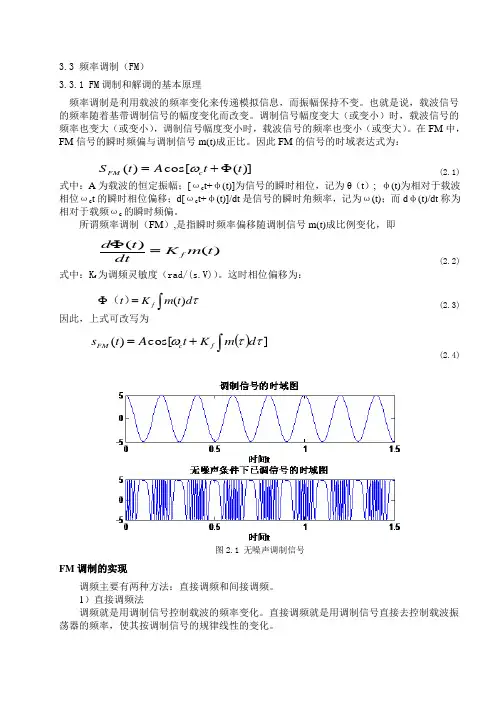
3.3 频率调制（FM ）3.3.1 FM 调制和解调的基本原理频率调制是利用载波的频率变化来传递模拟信息，而振幅保持不变。

也就是说，载波信号的频率随着基带调制信号的幅度变化而改变。

调制信号幅度变大（或变小）时，载波信号的频率也变大（或变小），调制信号幅度变小时，载波信号的频率也变小（或变大）。

在FM 中，FM 信号的瞬时频偏与调制信号m(t)成正比。

因此FM 的信号的时域表达式为：(2.1)式中：A 为载波的恒定振幅；[ωc t+φ(t)]为信号的瞬时相位，记为θ（t ）; φ(t)为相对于载波相位ωc t 的瞬时相位偏移；d[ωc t+φ(t)]/dt 是信号的瞬时角频率，记为ω(t)；而d φ(t)/dt 称为相对于载频ωc 的瞬时频偏。

所谓频率调制（FM ）,是指瞬时频率偏移随调制信号m(t)成比例变化，即(2.2)式中：K f 为调频灵敏度（rad/(s.V)）。

这时相位偏移为：(2.3)因此，上式可改写为(2.4)图2.1 无噪声调制信号FM 调制的实现调频主要有两种方法：直接调频和间接调频。

1）直接调频法调频就是用调制信号控制载波的频率变化。

直接调频就是用调制信号直接去控制载波振荡器的频率，使其按调制信号的规律线性的变化。

()]cos[)(⎰+=ττωd m K t A t s f c FM )()(t m K dt t d f =Φ⎰=Φτd t m K t f )(）（)](cos[)(t t A t S c FM Φ+=ω可以由外部电压控制震荡频率的振荡器叫做压控振荡器器。

每个压控振荡器自身就是一个FM 调制器，因为它的振荡频率正比于输入控制电压，即(2.9) 若用调制信号作控制电压信号，就能产生FM 波。

若被控制的振荡器是LC 振荡器，则只需控制振荡回路的某个电抗元件（L 或C ) ，使其参数随调制信号变化。

目前常用的电抗元件是变容二极管。

用变容二极管实现直接调频，由于电路简单，性能良好，已成为目前最广泛采用的调频电路之一。

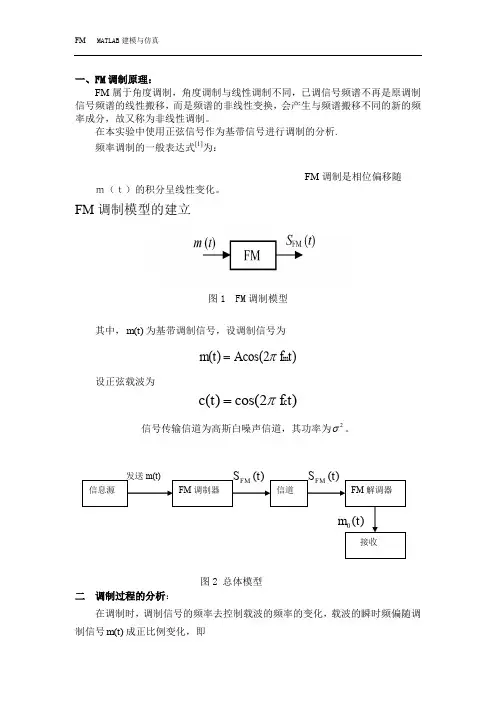
一、FM调制原理：FM属于角度调制，角度调制与线性调制不同，已调信号频谱不再是原调制信号频谱的线性搬移，而是频谱的非线性变换，会产生与频谱搬移不同的新的频率成分，故又称为非线性调制。

在本实验中使用正弦信号作为基带信号进行调制的分析.频率调制的一般表达式[1]为：FM调制是相位偏移随ｍ（ｔ）的积分呈线性变化。

FM调制模型的建立图1 FM调制模型其中，为基带调制信号，设调制信号为设正弦载波为信号传输信道为高斯白噪声信道，其功率为。

图2 总体模型二调制过程的分析：在调制时，调制信号的频率去控制载波的频率的变化，载波的瞬时频偏随调制信号成正比例变化，即式中，为调频灵敏度（）。

这时相位偏移为则可得到调频信号为FM调制1. 对FM调制信号的频谱分析clear allts=0.00125; %信号抽样时间间隔t=0:ts:10-ts; %时间向量am=10;fs=1/ts; %抽样频率df=fs/length(t); %fft的频率分辨率msg=am*cos(2*pi*10*[0:0.01:0.99]);msg1=msg'*ones(1,fs/10); %扩展成取样信号形式msg2=reshape(msg1.',1,length(t));Pm=fft(msg2); %求消息信号的频谱f=-fs/2:df:fs/2-df;subplot(3,1,1)plot(t,fft(abs(Pm)))title('消息信号频谱')m=fft(msg,1024); %对msg进行傅利叶变换N=(0:length(m)-1)*fs/length(m)-fs/2;subplot(3,1,2)plot(N,abs(m)); %调制信号频谱图title('调制信号频谱')int_msg(1)=0; %消息信号积分for ii=1:length(t)-1int_msg(ii+1)=int_msg(ii)+msg2(ii)*ts;endkf=50;fc=250; %载波频率Sfm=am*cos(2*pi*fc*t+2*pi*kf*int_msg); %调频信号Pfm=fft(Sfm)/fs; % FM信号频谱subplot(3,1,3);plot(f,fftshift(abs(Pfm))) % 画出已调信号频谱title('FM信号频谱')Pc=sum(abs(Sfm).^2)/length(Sfm) %已调信号功率Ps=sum(abs(msg2).^2)/length(msg2) %消息信号功率fm=50;betaf=kf*max(msg)/fm % 调制指数W=2*(betaf+1)*fm % 调制信号带宽用FFT函数进行傅利叶变换，进行傅立叶变化便分别得到调制信号与调制之后的FM信号的频谱图如下：图2-5通过频谱图的对照比较我们可以看出FM调制并不是使原正弦信号的频谱在原来位置上通过移动得到调制波形，调制后的波形与调制前的完全不同，这证明FM 调制并不是线性的，而是非线性的。

基于MATLAB的模拟信号频率调制与解调分析信号频率调制（FM）是一种将信息信号调制到载频波形上以便在传输过程中保持信号质量的技术。

本文将基于MATLAB对信号频率调制与解调进行分析与模拟。

首先，我们需要生成一个调制信号。

以正弦信号为例，通过改变该信号的频率来模拟调制信号。

我们可以使用MATLAB的信号处理工具箱中的`fmmod(`函数来实现这一点。

以下是一个示例代码：```matlabt = 0:1/fs:1; % 时间向量fc = 2000; % 载频频率fm = 100; % 调制信号频率m = sin(2*pi*fm*t); % 调制信号modulatedSignal = fmmod(m, fc, fs); % 使用fmmod进行调频调制subplot(2,1,1);plot(t, m);title('调制信号');xlabel('时间');ylabel('振幅');subplot(2,1,2);title('调制后信号');xlabel('时间');ylabel('振幅');```上述代码中，我们定义了采样频率、时间向量、载频频率和调制信号频率，并生成了调制信号。

然后，我们使用`fmmod(`函数将调制信号调制到载频波形上。

最后，我们用两个子图分别显示调制信号和调制后信号。

接下来，我们将对调制后的信号进行解调以还原原始信号。

我们可以使用MATLAB的信号处理工具箱中的`fmdemod(`函数。

以下是一个示例代码：```matlabdemodulatedSignal = fmdemod(modulatedSignal, fc, fs); % 使用fmdemod进行解调subplot(2,1,1);plot(t, modulatedSignal);title('调制后信号');xlabel('时间');ylabel('振幅');subplot(2,1,2);title('解调后信号');xlabel('时间');ylabel('振幅');```上述代码中，我们使用`fmdemod(`函数对调制后的信号进行解调。

MATLAB实现FM调制摘要：FM属于角度调制，角度调制与线性调制不同，已调信号频谱不再是原调制信号频谱的线性搬移，而是频谱的非线性变换，会产生与频谱搬移不同的新的频率成分，故又称为非线性调制。

FM调制又称为频率调制，与幅度调制相比，角度调制的最突出的优势在于其较高的抗噪声性能，但获得这种优势的代价是角度调制占用比幅度调制信号更宽的带宽。

调制在通信系统中有十分重要的作用，通过调制不仅可以进行频谱搬移，把调制信号的频谱搬移到所希望的位置上，从而将调制信号转换成适合于传播的已调信号，而且它对系统的传输有效性和传输的可靠性有着很大的影响，调制方式往往决定了一个通信系统的性能。

本课程设计主要基于MATLAB集成环境编写程序实现FM 调制与解调过程，并分别绘制出调制信号、已调信号和解调信号的时域及频域波形。

1FM 调制被调信号()0sin 100()0else⎧≤⎪=⎨⎪⎩c t t t m t00.1t =，载波()()cos 2c c t ft π=，其中250c f Hz =，偏移常量100kf =。

1. 绘制()m t 的时域、频域曲线；2. 令()x t 表示调频信号，求()x t 的表达式，绘制()x t 的时域、频域曲线；3. 绘制解调信号的时域、频域曲线。

二、课程设计目的1.熟悉MATLAB 的使用方法，其中包括了解简单函数、了解原理和掌握操作方法；2.加深对FM 信号调制原理的理解；3.增强在通信原理仿真方面的动手能力与自学能力；4.完成FM 调制仿真之后，再遇到类似的问题时，学会对所面对的问题进行系统的分析，并能从多个方面进行比较。

三、实验原理角度调制信号的一般表达式为()cos[()]m c s t A t t ωϕ=+式中：A 为载波的恒定振幅；[()]c t t ωϕ+为信号的瞬时相位，记为()t θ；()t ϕ为相对于载波相位c t ω的瞬时相位偏移；d[()]/dt c t t ωϕ+是信号的瞬时角频率，记为(t)ω；而d ()/dt t ϕ称为相对于载频c ω的瞬时频偏。

基于matlab的fm系统调制与解调的仿真课程设计课程设计题目：基于MATLAB的FM系统调制与解调的仿真一、设计任务与要求1.设计并实现一个简单的FM（调频）调制和解调系统。

2.使用MATLAB进行仿真，分析系统的性能。

3.对比和分析FM调制和解调前后的信号特性。

二、系统总体方案1.系统组成：本设计包括调制器和解调器两部分。

调制器将低频信号调制到高频载波上，解调器则将已调制的信号还原为原始的低频信号。

2.调制方式：采用线性FM调制方式，即将低频信号直接控制高频载波的频率变化。

3.解调方式：采用相干解调，通过与本地载波信号相乘后进行低通滤波，以恢复原始信号。

三、调制器设计1.实现方式：使用MATLAB中的modulate函数进行FM调制。

2.参数设置：选择合适的载波频率、调制信号频率以及调制指数。

3.仿真分析：观察调制后的频谱变化，并分析其特性。

四、解调器设计1.实现方式：使用MATLAB中的demodulate函数进行FM解调。

2.参数设置：选择与调制器相同的载波频率、低通滤波器参数等。

3.仿真分析：观察解调后的频谱变化，并与原始信号进行对比。

五、系统性能分析1.信噪比（SNR）分析：通过改变输入信号的信噪比，观察解调后的输出性能，绘制信噪比与误码率（BER）的关系曲线。

2.调制指数对性能的影响：通过改变调制指数，观察输出信号的性能变化，并分析其影响。

3.动态范围分析：分析系统在不同输入信号幅度下的输出性能，绘制动态范围曲线。

六、实验数据与结果分析1.实验数据收集：根据设计的系统方案进行仿真实验，记录实验数据。

2.结果分析：根据实验数据，分析系统的性能指标，并与理论值进行对比。

总结实验结果，提出改进意见和建议。

七、结论与展望1.结论：通过仿真实验，验证了基于MATLAB的FM系统调制与解调的可行性。

实验结果表明，设计的系统具有良好的性能，能够实现低频信号的FM调制和解调。

通过对比和分析，得出了一些有益的结论，为进一步研究提供了基础。

一、FM 调制原理：FM 属于角度调制，角度调制与线性调制不同，已调信号频谱不再是原调制信号频谱的线性搬移，而是频谱的非线性变换，会产生与频谱搬移不同的新的频率成分，故又称为非线性调制。

在本实验中使用正弦信号作为基带信号进行调制的分析.频率调制的一般表达式[1]为：FM 调制是相位偏移随ｍ（ｔ）的积分呈线性变化。

FM 调制模型的建立图1 FM 调制模型其中，()m t 为基带调制信号，设调制信号为()cos(2)m m t A f t π=设正弦载波为()cos(2)c c t f t π=信号传输信道为高斯白噪声信道，其功率为2σ。

图2 总体模型二 调制过程的分析：在调制时，调制信号的频率去控制载波的频率的变化，载波的瞬时频偏随调制信号()m t 成正比例变化，即()()f d t K m t dtϕ=式中，f K 为调频灵敏度（()rad s V ∙）。

这时相位偏移为()()f t K m d ϕττ=⎰则可得到调频信号为()cos ()FM c f s t A t K m d ωττ⎡⎤=+⎣⎦⎰ FM 调制1. 对FM 调制信号的频谱分析clear allts=0.00125; %信号抽样时间间隔 t=0:ts:10-ts; %时间向量 am=10;fs=1/ts; %抽样频率df=fs/length(t); %fft 的频率分辨率 msg=am*cos(2*pi*10*[0:0.01:0.99]);msg1=msg'*ones(1,fs/10); %扩展成取样信号形式 msg2=reshape(msg1.',1,length(t));Pm=fft(msg2); %求消息信号的频谱 f=-fs/2:df:fs/2-df; subplot(3,1,1)plot(t,fft(abs(Pm))) title('消息信号频谱')m=fft(msg,1024); %对msg 进行傅利叶变换 N=(0:length(m)-1)*fs/length(m)-fs/2; subplot(3,1,2)plot(N,abs(m)); %调制信号频谱图 title('调制信号频谱')int_msg(1)=0; %消息信号积分 for ii=1:length(t)-1int_msg(ii+1)=int_msg(ii)+msg2(ii)*ts; endkf=50;fc=250; %载波频率 Sfm=am*cos(2*pi*fc*t+2*pi*kf*int_msg); %调频信号Pfm=fft(Sfm)/fs; % FM 信号频谱 subplot(3,1,3);plot(f,fftshift(abs(Pfm))) % 画出已调信号频谱 title('FM 信号频谱')Pc=sum(abs(Sfm).^2)/length(Sfm) %已调信号功率 Ps=sum(abs(msg2).^2)/length(msg2) %消息信号功率fm=50;betaf=kf*max(msg)/fm % 调制指数W=2*(betaf+1)*fm % 调制信号带宽用FFT 函数进行傅利叶变换，进行傅立叶变化便分别得到调制信号与调制之后的FM 信号的频谱图如下：012345678910-225消息信号频谱-500-400-300-200-1001002003004005000200400600调制信号频谱-500-400-300-200-10001002003004005000510FM 信号频谱图2-5通过频谱图的对照比较我们可以看出FM 调制并不是使原正弦信号的频谱在原来位置上通过移动得到调制波形，调制后的波形与调制前的完全不同，这证明FM 调制并不是线性的，而是非线性的。

基于Matlab 调制与解调的实现一．实验目的1.熟悉Matlab 的使用2.掌握幅度调制、角度调制及FSK 调制的基本原理3.掌握解调的基本原理，并实现解调二．实验原理，仿真及结果分析 AM 调制与解调1.标准AM 波调制与解调的原理调制信号是只来来自信源的调制信号（基带信号），这些信号可以是模拟的，亦可以是数字的。

为首调制的高频振荡信号可称为载波，它可以是正弦波，亦可以是非正弦波(如周期性脉冲序列)。

载波由高频信号源直接产生即可，然后经过高频功率放大器进行放大，作为调幅波的载波，调制信号由低频信号源直接产生，二者经过乘法器后即可产生双边带的调幅波。

设载波信号的表达式为t c ωcos ，调制信号的表达式为t A t m m m ωcos )(= ，则调幅信号的表达式为t t m A t s c AM ωcos )]([)(0+=标准调幅波示意图从高频已调信号中恢复出调制信号的过程称为解调，又称为检波。

对于振幅调制信号，解调就是从它的幅度变化上提取调制信号的过程。

解调是调制的逆过程。

)(t m )(t可利用乘积型同步检波器实现振幅的解调，让已调信号与本地恢复载波信号相乘并通过低通滤波可获得解调信号。

2．matlab仿真% ======================载波信号===========================t=-1:0.00001:1;A0=10; %载波信号振幅f=6000; %载波信号频率w0=f*pi;Uc=A0*cos(w0*t); %载波信号figure(1);subplot(2,1,1);plot(t,Uc);title('载频信号波形');axis([0,0.01,-15,15]);subplot(2,1,2);Y1=fft(Uc); %对载波信号进行傅里叶变换plot(abs(Y1));title('载波信号频谱');axis([5800,6200,0,1000000]);% ======================调制信号============================== t=-1:0.00001:1;A1=5; %调制信号振幅f=6000; %载波信号频率w0=f*pi;mes=A1*cos(0.001*w0*t); %调制信号subplot(2,1,1);plot(t,mes);xlabel('t'),title('调制信号');subplot(2,1,2);Y2=fft(mes); % 对调制信号进行傅里叶变换plot(abs(Y2));title('调制信号频谱');axis([198000,202000,0,1000000]);% =======================AM已调信号=========================t=-1:0.00001:1;A0=10; %载波信号振幅A1=5; %调制信号振幅A2=3; %已调信号振幅f=3000; %载波信号频率w0=2*f*pi;m=0.15; %调制度mes=A1*cos(0.001*w0*t); %消调制信号Uam=A2*(1+m*mes).*cos((w0).*t); %AM 已调信号subplot(2,1,1);plot(t,Uam);grid on;title('AM调制信号波形');subplot(2,1,2);Y3=fft(Uam); % 对AM已调信号进行傅里叶变换plot(abs(Y3)),grid;title('AM调制信号频谱');axis([5950,6050,0,500000]);%=========================FIR低通滤波器=======================Ft=2000; %采样频率fpts=[100 120]; %通带边界频率fp=100Hz，阻带截止频率fs=120Hzmag=[1 0];dev=[0.01 0.05]; %通带波动1%，阻带波动5%[n21,wn21,beta,ftype]=kaiserord(fpts,mag,dev,Ft);%kaiserord估计采用凯塞窗设计的FIR滤波器的参数b21=fir1(n21,wn21,Kaiser(n21+1,beta)); %由fir1设计滤波器[h,w]=freqz(b21,1); %得到频率响应plot(w/pi,abs(h));grid ontitle('FIR低通滤波器');%=========================AM信号解调=======================t=-1:0.00001:1;A0=10; %载波信号振幅A1=5; %调制信号振幅A2=3; %已调信号振幅f=3000; %载波信号频率w0=2*f*pi;m=0.15; %调制度k=0.5 ; %DSB 前面的系数mes=A1*cos(0.001*w0*t); %调制信号Uam=A2*(1+m*mes).*cos((w0).*t); %AM 已调信号Dam=Uam.*cos(w0*t); %对AM调制信号进行解调subplot(4,2,1);plot(t,Dam);title('滤波前AM解调信号波形');subplot(4,2,2);axis([187960,188040,0,200000]);Y5=fft(Dam); % 对AM解调信号进行傅里叶变换plot(abs(Y5)),grid;title('滤波前AM解调信号频谱');subplot(4,2,3);plot(t,z21);title('滤波后的AM解调信号波形');T5=fft(z21); %求AM信号的频谱subplot(4,2,4);plot(abs(T5));title('滤波后的AM解调信号频谱');axis([198000,202000,0,100000]);角度调制与解调角度调制是频率调制和相位调制的总称。

目录第1章前言1第2章AM，FM,PM调制原理22。

1 AM调制原理22。

2 FM调制原理22。

3 PM调制原理3第3章几种调制方式的比较错误!未定义书签。

3。

1 PM与FM的比较43。

2 几种不同的模拟调制方式53.3 几种模拟调制的性能比较53。

4 几种模拟调制的特点及应用6第4章AM,FM,PM的调制仿真错误!未定义书签。

4。

1 AM的调制仿真64.1。

1理想状态下的AM调制仿真64。

1。

2含噪声情况下的AM调制仿真64.2 FM的调制仿真74。

21理想状态下的FM调制仿真74.22含噪声情况下的FM调制仿真74.3 PM的调制仿真7心得体会错误!未定义书签。

参考文献错误!未定义书签。

附录错误!未定义书签。

AM、FM、PM、实现及性能比较第1章前言通信系统是为了有效可靠的传输信息，信息由信源发出,以语言、图像、数据为媒体,通过电(光)信号将信息传输，由信宿接收.通信系统又可分为数字通信与模拟通信。

基于课程设计的要求，下面简要介绍模拟通信系统。

信源是模拟信号，信道中传输的也是模拟信号的系统为模拟通信.模拟通信系统的模型如图1所示。

图1 模拟通信系统模型调制器：使信号与信道相匹配，便于频分复用等.发滤波器：滤除调制器输出的无用信号。

收滤波器：滤除信号频带以外的噪声，一般设N(t）为高斯白噪声,则Ni(t）为窄带白噪声。

第2章AM，FM，PM调制原理2.1 AM调制原理幅度调制是用调制信号去控制高频正弦载波的幅度，使其按调制信号的规律变化的过程.幅度调制器的一般模型如图2。

1.1所示。

图2。

1 幅度调制模型在图2。

1中，若假设滤波器为全通网络（H（）＝1)，调制信号叠加直流后再与载波相乘，则输出的信号就是常规双边带（AM)调幅.AM调制器模型如图2。

2所示：图2.2 AM调制模型AM信号波形的包络与输入基带信号成正比,故用包络检波的方法很容易恢复原始调制信号. 但为了保证包络检波时不发生失真，必须满足,否则将出现过调幅现象而带来失真。