数字信号处理吴镇扬第一章答案

故系统是线性系统。
第 1 章 时域离散信号和时域离散系统
n
（7） y(n)= x(m) 令输入为m0
x(n－n0)
输出为
n
y′(n)= =0[DD)]x(m-n0)
m0
nn0
y(n－n0)= x(m)≠y′(n) m0
故系统是时变系统。 由于
n
T［ax1(n)+bx2(n)］=
［ax1(m)+bx2(m)
第 1 章 时域离散信号和时域离散系统
解：
x(n)=δ(n+4)+2δ(n+2)－δ(n+1)+2δ(n)+δ(n－1)
+2δ(n－2)+4δ(n－3)+0.5δ(n－4)+2δ(n－6)
2． 给定信号：
2n+5
－4≤n≤－1
(x(n)= 6 0
0≤n≤4 其它
(1) 画出x(n)序列的波形， 标上各序列值；
（2） y(n)=x(n)+x(n+1)
n n0
（3） y(n)= x(k) k nn0
（4） y(n)=x(n－n0) （5） y(n)=ex(n)
第 1 章 时域离散信号和时域离散系统
解：（1）只要N≥1， 该系统就是因果系统， 因为输出 只与n时刻的和n时刻以前的输入有关。
如果|x(n)|≤M， 则|y(n)|≤M， （2） 该系统是非因果系统， 因为n时间的输出还和n时间以 后（（n+1）时间）的输入有关。如果|x(n)|≤M, 则 |y(n)|≤|x(n)|+|x(n+1)|≤2M,
第 1 章 时域离散信号和时域离散系统 题2解图（四）

k = n0
∑
n
x[ k ]
（B） T {x[n]} =
∑
x[k ]
（C） T {x[ n]} = 0.5
x[ n ]
（D） T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ，输出为 y[n] ，满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ，则系统是（A） （A）线性的 （B）时不变的 （C）因果的 （D）稳定的 解：
（a） T { x[ n ]} = h[ n] + x[ n ], （c） T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ，单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 ， n < 0 ， 则 y[3] = 0.5 。 解： y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解： （a）
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞

所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
（2）解：
该系统不是线性系统；
该系统是时不变系统。
（3）解：
令 ，则
而
该系统是线性系统时不变系统。
注：
令 ，则
而
该系统是线性时不变系统。
（4）解：
该系统是线性系统时不变系统。
（5）解：
该系统是线性系统时变系统。
1.14解：
(1)
(2)
(3)
1.16
（1）解：因果、稳定。
(2)当n0<0时，系统非因果,不稳定。
（2）解：
所求序列为双边序列，采用留数法求解。
当n>=1时，围线C内只有一个极点 ，
则：
当n<1时，围线外只有一个极点 ，利用辅助留数定理，则：
因此
（4）解：
1.12
(1)解：定理：
（3）解：直接法
帕氏定理：
1.13
(1)解：
该系统不是线性系统；
该系统是时不变系统。
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。
2.（1）解：由题意可知
则周期为：
（2）解：由题意可知
则
则所求周期N为： 和 的最小公倍数，即为：56

jw0 n
u (n)] e jw0n z n
n 0
1 1 (e jw0 z 1 )
(1) 解：令 y (n) RN (n)
由题意可知，所求序列等效为 x (n 1) y (n) y (n) 。
Z [ y (n)] z n
n 0
N 1
1 zN z N 1 , 1 z 1 z N 1 ( z 1)
1
A B 1 2 1 1 1 1 z 1 2z 1 z 1 2 z 1 B 1 | 1 2 1 z 1 z 1 2
1 | 1 1 1 2 z 1 z 1
x(n) u (n) 2 2 n u ( n 1) u (n) 2 n 1u ( n 1)
n0
若n0 0时，收敛域为：0 z ;
(2) 解： Z [0.5 u (n)]
n
若n0 0 时，收敛域为： z 0 z 0.5
0.5
n 0

n
z n
1
1 , 1 0.5 z 1
n
(3) 解： Z [ 0.5 u ( n 1)]
n
n
j j 1 1 (3) X (e 2 ) X ( e 2 ) 2 2 j
(2) e
j n0
X (e j ) （移位特性）


2
数字信号处理习题指导

G ( z ) ZT [ x (2n)] G( z)
n
g ( n )e

jwn
令n' 2n, 则
n ' 取偶数
( z 5) z n |z 0.5 (1 0.5 z)

傅立叶系数
提示：与理想采样信号的频谱进行比较。上述过程是物理采样后的频谱。
1.6解：
(1) （性质1）
(2) （性质4）
(3)
(4)1.7（1）Fra bibliotek：(2)解：
(3)解：
(4)解：
（5）解:
1.8 (1)解：令
由题意可知，所求序列等效为 。
而
故：
（2）解：
因为：
所以,
1.10 (1)解：
，为双边序列
本小题采用部分分式法求逆Z变换，可以使用“留数法”…..
所以
（3）解：
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解：
1.19
（1）解：
无论 还是 ，右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考：1、为何讨论当 时的情况；2、为何不用讨论 的情况
解答过程如下：
（2）解：
右边序列的围线C内包含 一个极点。故
当 时
因此，
思考：1、为何只讨论当 时的情况
(3) 当n0＞0时，该系统是因果系统；当n0＜0时，该系统是非因果系统；系统稳定。
（4）因果、稳定。
（5）因果、稳定。
（6）因果、稳定。
（7）因果，但由于 。
（8） 在 时刻有值，故非因果。由于 的值都在 的时刻内，那么 ，故系统稳定。
1.17解：由图可知：
所以
（1）解：
（2）解：
通解
特解
带入方程得：
（3）解：
当 时，右边序列的围线C内包含 两个极点。故
因此
第1章
1.解：由题意可知
则周期为： 其中 为整数，且满足使N为最小整数。

解：
2 i 14i i 3 , N min 14 (1) N 0 3 / 7 3 (2) i 7, j 4, N min 56 2 j 2 j 14 j N2 0 / 7 2 i 8i N1 0 / 4 2 i
0
20
40
60 n
80
100
120
1 3 绘出如下序列的波形。 1.3
(1) x(n) 3 (n 3) 2 (n 1) 4 (n 1) 2 (n 2) (2) x(n) 0.5n R5 (n)
解 (1)
3
2
1
0 x(n n) -1 -2 2 -3 -4 -4
因此，T[.]为线性系统；
T x( n n1 ) nx ( n n1 ) T x( n n1 ) y ( n n1 ) y ( n n1 ) ( n n1 ) x ( n n1 )
因此 T[.]为时变系统。 因此， 为时变系统
1 16 确定下列系统的因果性与稳定性。 1.16
(2) 收敛区域为|z|>a，即圆|z|=a的外部。
1 0.8 0.6 0.4 Imagina ary Part 0.2 0 -0.2 -0.4 -0.6 -0.8 -1 -1 -0.5 0 Real Part 0.5 1 1.5
j 1 1 2 e a c 1 2 a cos a 1 j (3) H (e ) j 2 e a d a 1 2a cos a
2 i
3 x(n) cos n 4 7
1 0.8 0.6 04 0.4 0.2 x(n) 0 -0.2 -0.4 -0 0.6 6 -0.8 -1

1-2习题1-2图所示为一个理想采样—恢复系统，采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。

解：(1)根据余弦函数傅里叶变换知：)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ，)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。

又根据抽样后频谱公式：∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(，得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以，)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示（2）)(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到，)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ，故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理，)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=（3）由题（2）可知，无失真，有失真。

原因是根据采样定理，采样频率满足信号)(1t x a 的采样率，而不满足)(2t x a 的，发生了频谱混叠。

1-3判断下列序列是否为周期序列，对周期序列确定其周期。

（1）()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭（2）()8n j x n eπ⎛⎫- ⎪⎝⎭=（3）()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解：（1）85πω=，5162=ωπ为有理数，是周期序列，.16=N （2）πωπω162,81==，为无理数，是非周期序列； （3）382,43==ωππω，为有理数，是周期序列，8=N 。

－m≤3， 或写成n－3≤m≤n， 这样y(n)的非零区间要求m同时满足下
面两个不等式：
0≤m≤3
m－3≤m≤n
上面公式表明m的取值和n的取值有关， 需要将n作分段的假设。 按 照上式， 当n变化时， m应该按下式取值：
第九页，共105页。
max{0, n－3}≤m≤min{3, n}
当0≤n≤3时， 下限应该是0， 上限应该是n； 当4≤n≤6时， 下限应该是
y(n)=
n 1 y(n) 7 n
0
0≤n≤3
4≤n≤6
其它
第十一页，共105页。
在封闭式求解过程中， 有时候决定求和的上下限有些麻烦， 可借助于 非零值区间的示意图确定求和限。 在该例题中， 非零值区间的示意图如图
1.2.1所示。 在图1.2.1(b)中， 当n<0时， 图形向左移动， 图形不可能 和图1.2.1(a)的图形有重叠部分， 因此y(n)=0。 当图形向右移动时， 0≤n≤3， 图形如图1.2.1(c)所示， 对照图1.2.1(a)， 重叠部分的上下限自 然是0≤m≤n。 当图形再向右移动时， 4≤n≤6， 如图1.2.1(d)所示， 重 叠部分的上下限是n－3≤m≤3。 当图形再向右移动时, 7≤n， 图形不可能和
(1) x(n) Acos 3 πn A是常数
第二十二页，共105页。
图1.3.2
第二十三页，共105页。
［例1.3.5］已知x1(n)=δ(n)+3δ(n－1)+2δ(n－2)，x2(n)=u(n)－u(n－3)，
试求信号x(n)， 它满足x(n)=x1(n)*x2(n), 并画出x(n)的波形。
解： 这是一个简单的计算线性卷积的题目。
x(n)=x1(n)*x2(n) =［δ(n)+3δ(n－1)+2δ(n－2)］*［u(n)－u(n－3)

1.2 (5) y(n) x(n)*h(n) [ (n) (n 3)]*0.8u(n 1)
0.8u(n 1) 0.8u(n 4) {0,0.8,0.8,0.8,0, }
sin( n)
1.4 (5) x(n)
7
n
非周期序列
（7）sin(3 n) cos(15n)
aT [ x1(n)] bT [ x2 (n)]
为线性系统
T[x(n)]g(n)x(n) T[x(nm)]g(n)x(nm)
y(n)T[x(n)]g(n)x(n), y(nm)g(nm)x(nm)T[x(nm)]
为移变系统
1.7 (1) T[x(n)] g(n)x(n) 系统的输出仅取决于n时刻的输入x(n)和g(n)，
为因果系统 设 x(n) M ，T[x(n)] g(n)x(n) g(n) x(n)
若 g(n) N ,则系统为稳定系统，否则为不稳定系统
1.7 (5) T[x(n)] nx(n)
T[x1(n)] nx1(n)
T[x2(n)] nx2(n)
T[ax1(n)bx2 (n)]n[ax1(n)bx 2(n)]
x2(n) y2(n) x2(n)
ax1(n) bx2(n) y(n) ax1(n) bx2(n)
ay1(n) by2(n)
为线性系统
T[x(n)]x(n) T[x(nm)]x((nm))x(nm)
y(nm) x((nm)) x(n m)T [ x(n m)]
anx1(n)bnx2 (n)aT [ x1(n)]bT [ x2 (n)]] 系统为线性系统。
T[x(n m)] nx(n m)
y(n)T[x(n)]nx(n), y(n-m)(nm)x(nm)T[x(nm)]

由于 x2 (n) x1 (n 1) ，而且 y2 (n) y1(n 1) 故当 y(-1)=0时，系统具有移不变性。
(c)设 x3 (n) (n) (n 1) 则 y3 (n) a y3 (n 1) x3 (n) 且 y3 (1) 0
根据 y3 (n) a y3 (n 1) x3 (n) ，当 n ≥ 0 时有
3 ( a ) x( n) A cos( n ) 7 8 (c ) x ( n ) e
j( n ) 6
;
13 (b) x( n) A sin n 3
π π 解 (a) 2 2 14 为有理数 3 π 3 ω
0
7
故 x(n)是周期的，周期 N=14


x(m)h(n m)
x(m) : m n0
h(n m) : n N 1 m n
① 当 n n0时， y(n) 0 ② 当 n0 n n0 N 1 时，
n n
n n y(n) x(m)h(n m) mn0 nm n 0 mn0 mn0 mn0
(b)设 x2 (n) (n 1) ，则 y2 (n) a y2 (n 1) x2 (n) 且 y2 (0) 0
根据 y2 (n) a y2 (n 1) x2 (n) ，当 n > 0 时有
y2 (1) a y2 (0) x2 (1) 1 ,
……
y2 (2) a y2 (1) x2 (2) a
y3 (1) a y3 (0) x3 (1) 1 , y3 (2) a y3 (1) x3 (2) a y3 (3) a y3 (2) x3 (3) a 2 , , y3 (n) a y3 (n 1) x3 (n) a n1

第 1 章 时域离散信号和时域离散系统
解线性卷积也可用Z变换法， 以及离散傅里叶变换求解， 这是后面几章的内容。 下面通过例题说明。
设x(n)=R4(n), h(n)=R4(n)， 求y(n)=x(n)*h(n) 该题是两个短序列的线性卷积， 可以用图解法（列表法） 或者解析法求解。 表1.2.1给出了图解法（列表法）， 用公 式可表示为
第 1 章 时域离散信号和时域离散系统
1.1.1
（1） 信号： 模拟信号、 时域离散信号、 数字信号三 者之间的区别； 常用的时域离散信号； 如何判断信号是周期 性的， 其周期如何计算等。
（2） 系统： 什么是系统的线性、 时不变性以及因果 性、 稳定性； 线性、 时不变系统输入和输出之 间的关系； 求解线性卷积的图解法（列表法）、 解析法， 以及用MATLAB工具箱函数求解； 线性常系数差分方程的递
%程序exp134.m %调用conv实现5 xn=0.5*ones(1， 15)； xn(4)=1； xn(6)=1； xn(10)=1； hn=ones(1， 5)； yn=conv(hn， xn)；
第 1 章 时域离散信号和时域离散系统
% n=0： length(yn)－1； subplot(2， 1， 1)； stem(n， yn， ′.′) xlabel(′n′)； ylabel(′y(n)′) 程序运行结果如图1.3.2所示。 由图形可以看出， 5项滑 动平均滤波器对输入波形起平滑滤波作用， 将信号的第4、 8、 12、 16的序列值平滑去掉。
第 1 章 时域离散信号和时域离散系统 图1.3.2
第 1 章 时域离散信号和时域离散系统
［例1.3.5］已知x1(n)=δ(n)+3δ(n－1)+2δ(n－2)，x2(n)=u(n) －u(n－3)， 试求信号x(n)， 它满足x(n)=x1(n)*x2(n), 并画出 x(n)的波形。

•pp 35： 1.11 (3)
判断系统
yn
n
xm
是否为线性系统?时不变系统
m
解：线性性判断 令x(n)=ax1(n)+bx2(n)
n
n
yn xm ax1 m bx2 m
m
m
n
n
n
n
ax1m bx2 m a x1m b x2 m
y(n) 4 (n 1) 4 (n 1) (n 3) 2 (n 5) (n 7)
•pp 35： 1.12 (3)
利用卷积性质
y(n) x1(n) x2 (n)
(n) 2 (n 2) (n 4)2 (n 1) (n 3)
(n) 2 (n 2) (n 4) 2 (n 1) 2(n()n21) (n42()n1)(n24)(n 5(n) 3)
• 解：
a nu n

1
1 aZ
1
,
Z a

n
a nu n

Z

d 1
1 aZ
1

,
dZ

Z

1 1 aZ 1
2

d
1 aZ dZ
1
,

Z

1 1 aZ 1
2



a
d
Z 1 dZ
,

Z
1 1 aZ 1
2



a

Z
2

,

2013-10-22 3
2. 时不变系统
如果
T[x（n）]=y（n），
则 T[x（n-n0）]=y（n-n0） （ n0为任意整数）,即系统的特性不随 时间而变化。 线性时不变系统简称为：LTI
2013-10-22 4
3. 线性时不变系统
线性时不变系统——既满足迭加原理又具有时不变性的系统。线性时不 变系统可以用单位脉冲响应来表示。 我们知道，任一序列都可表示成各延时单位脉冲序列的加权和
2013-10-22
22
5． 差分方程——描述系统输入输出之间的运算关系 一个线性的连续时间系统总可以用线性微分方程来 表达。而对于离散时间系统，由于其变量n是离散整型 变量，故只能用差分方程来反映其输入输出序列之间 的运算关系。 其N阶线性常系数差分方程的一般形式：
y(n) ai x(n i) bi y(n i)
n
， 稳定、因果系统 25
②输入相同，但初始条件改为 n〉0，y（n）=0 将上述差分方程 y(n) 1.5 x(n) 1 y(n 1) 2 改写成 y（n-1）=2[ y（n）-1.5x（n）] 此时 y（0）=2[ y（1）-1.5x(1) ]=0
1 y(1) 2 y(0) 1.5x(0) 1.5 2 2 1 y(2) 2 y(1) 1.5x(1) 1.5 2
0
1
2
3
4
5
6
7
8
9
n
x(k)
h(2-k)
n=2
-5 -4 -3 -2
2013-10-22
-1 0
1
2
3
4
10
n
y(n) 对 h（-k）移位得 h（n-k）

中 训
) 心
k = 2 X ( ); 2
⎧1, 0 ≤ n ≤ 4 x(n) = ⎨ ⎩0,5 ≤ n ≤ 9
⎧1, 0 ≤ n ≤ 4 y ( n) = ⎨ ⎩ −1,5 ≤ n ≤ 9
用作图表示 x ( n ), 解答:
y ( n ) 及 f ( n) = x ( n) ∗ y ( n)
⎧1, 2,3, 4,5,3,1, −1, −3, −5, −4, −3, −2, −1, n = 0,1,..13 f ( n) = ⎨ ⎩0, 其它
数字信号处理习题 第一章 1-4
今对三个正弦信号
xa1 (t ) = cos 2π t , xa 2 (t ) = − cos 6π t , xa 3 (t ) = cos10π t 进行理想采
样,采样频率为 Ω s
= 8π
,求着三个采样输出序列,比较其结果.画出 xa1 (t ), xa 2 (t ), xa 3 (t ) 的波形及采
培 信 通
中 训
−1 −1
,式中 a 为实数
) 心
（3） 通过 z 平面上作图，可以发现，极点 a 在单位圆内的实轴上，零点 1/a 在单位圆外的实轴上， 它们各自到单位圆上任一点的矢量长度可由余弦定理求取，分别为
零点矢量长度= a
+ 1 − 2a -1cos(ω ) =
1 a
a 2 + 1 − 2acos(ω )
解答:
(3) y (n) =
m =−∞
∑ x ( m)
n
(1)T [ax1 (n) + bx2 (n)] = 2[ax1 (n) + bx2 (n)] + 5 = a[2 x1 (n) + 5] + b[2 x2 (n) + 5] − 5a − 5b + 5

【最新整理，下载后即可编辑】习题一 (离散信号与系统)1.1周期序列，最小周期长度为5。

1.2 (1) 周期序列，最小周期长度为14。

(2) 周期序列，最小周期长度为56。

1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统；该系统是时不变系统。

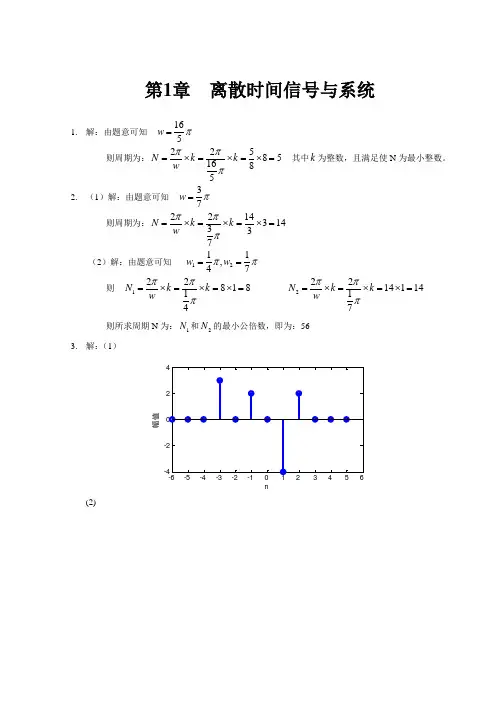
第一章1-2)(n x 如图所示，求以下序列。

（b ）)2(+n x （g ）)1(+-n x （f ）)2(n x解：原序列)3(3)2(2)1()(-+-+-=n n n n x δδδ（b ）)32(3)22(2)12()2(-++-++-+=+n n n n x δδδ )1(3)(2)1(-+++=n n n δδδ（g ）)31(3)21(2)11()1(-+-+-+-+-+-=+-n n n n x δδδ )2(3)1(2)(--+--+-=n n n δδδ )2(3)1(2)(++++=n n n δδδ（f ）)32(3)22(2)12()2(-+-+-=n n n n x δδδ舍去n 2不为整数的部分，得 )1(2)2(-=n n xδ1-8求卷积（a ）)()()(1N n u n u n x --= )()(2n nu n x =∑∞-∞=-=*k k nxk x n x n x )()()()(2121解：（1）10-≤≤N n2)1(2)1()1()()()(021nn n n n n k n n x n x nk +=+-+=-=*∑= （2）N n ≥222)1()()()(2121NN Nn N N Nn k n n x n x N k +-=--=-=*∑-=（d ）)()21()(7n u n x n = )10()()(8--=n u n u n x∑∞-∞=-=*k k nx k xn x n x )()()()(8787解：（1）90≤≤n])21(1[2)21()()()1(0)(87+=--==*∑n nk k n n x n x（2）10≥nn n k k n n x n x )21()21()21()()()10(90)(87-==*-=-∑1- 11设有如下差分方程确定的系统)()2()1(2)(n x n y n y n y =-+-+ 0≥n当0<n 时，0)(=n y（a ） 计算)()(n n x δ=时的)(n y 在5,4,3,2,1=n 点的值。

另解上式做Z变换
Y ( Z ) 2Y ( Z ) Z 通解： H ( Z )
1
2Y ( Z ) Z 1 Z
2
X (Z )
1 2Z
k
y [ k ] 2 y [ k 1] 1 y [ k 2 ] k ] x[ 2
h [ k ] (1 k )( 1) u [ k ]
是否 (1) 线性 (2) 因果 (3) 时不变 (4) 稳定
y[ k ] a
l 5

5
x(k l )
a 0
解：
(1)
T {ax1 [ k ] bx2 [ k ]} a+
l 5

5
(ax1[k-l ] bx2 [ k-l ])
5 l 5
aT { x1 [ k ]} bT { x 2 [ k ]} 2a+ (ax1[k-l ] bx2 [ k-l ])
r 2 r 1 0 r1 , 2 1
2
通解： h [ k ] c 1 ( 1) c 2 k ( 1)
k
k
初始条件：
h [ 0 ] 2 h [ 1] h [ 2 ] d [ 0 ] h [ 0 ] 1
y [ k ] 2 y [ k 1] y [ k 2 ] x [ k ]
1 x[ n ] 2x[ n 1] 3 x[ n 2 ] [ n 3] 4x

k 0
{4,11,20,30,20,[ k ] 2 y [ k 1] y [ k 2 ] x [ k ]
解
h [ k ] 2 h [ k 1] h [ k 2 ] d [ k ]