5.幂律流体流动规律

《工程流体力学》※<学习目的和要求> 本课程的目的是通过各种教学环节，使学生掌握流体力学的基本知识、原理和计算方法，包括流体的基本性质，流体平衡及运动的基本规律，简单的管路计算。

能运用基本理论分析和解决实际问题，并掌握基本的实验技能，为从事专业工作、科研和其他专业课的学习打好基础。

本课程要求学生首先具备较好的数学、物理和力学基础，需先修课程应包括高等数学、大学物理学、线性代数、工程力学等；其次，强调学生认真做好预习、听课、复习、作业四环节内容。

本课程教学过程中要求教师侧重于流体力学的基本知识、原理和计算方法讲解，同时还应注意结合实验和工程实际问题，进行流体力学分析问题、解决问题思维方式和能力的全面培养。

做到：1）认真备课①熟悉教学大纲，再三研究教材，查阅资料，认真备课；②了解学生的基本情况，便于因材施教。

2）教法多样、学法研究为进一步提高教学水平，培养学生素质和能力，采取的措施：①从教学方法上，从实际出发适当地采用课堂讨论、质疑、自学、“一比一教学法”、“单元教学法”等多种不同形式教学方法, 丰富了教学活动。

②从传授学法上，帮助学生知道如何学习，引导学生有效地使用教材和相应的参考书；指导学生听课要有针对性；教会学生善于系统整理，使知识系统化，培养学生善于概括归纳的逻辑思维能力；对促进学生的多向创造性思维有着不可抵估的作用。

3）教书育人传授知识的同时，结合学生思想动态、流体实例进行教书育人。

重视学生平时表现，督促学生时时努力，避免出现“平时不努力，考试搞突击”不良现象，有利于学生知识的有效积累和能力的全面提高。

4）做好课后工作①认真批改作业，要求自己全批；②安排定期答疑同时，进行不定期随时答疑；③和学生们多交流，了解实际情况，对学习基础差、学习目的不明进行多帮助。

※<内容提要>（一）流体的基本概念和物理性质1．流体的概念2．连续介质假设3．流体的物理性质4．作用在流体上的力5．常用单位制简介（二）流体静力学1．流体静压强及其特性2．流体平衡微分方程式3．流体静力学基本方程及其应用4．相对平衡5．流体作用在平面上的总压力6．流体作用在曲面上的总压力7．浮体与潜体的稳定性（三）流体运动与动力学基础1．研究流体运动的两种方法2．流体运动的基本概念3．连续性方程4．欧拉运动微分方程5．伯努利方程及其应用6．拉格朗日方程及其意义7．稳定流动量方程及应用（四）液流阻力与水头损失1．液流阻力产生的原因及分类2．流体的两种流动状态3．相似原理和因次分析4．圆管层流流动5．圆管紊流流动6．紊流沿程水头损失的分析及计算7．局部水头损失分析及计算（五）压力管路的水力计算1．简单长管的水力计算2．复杂管路的水力计算3．孔口与管嘴泄流4．水击现象及水击压力的计算5．习题课（六）非牛顿流体运动基础1．非牛顿流体及其流变方程2．非牛顿流体运动的研究方法3．塑性流体的流动规律4．幂律流体的流动规律5．判别非牛顿流体流动的Z值方法6．非牛顿流体的物理参数测定《工程流体力学》教学大纲英文名称：Engineering Fluid Mechanics课程编码：0222114学分：4.0 参考学时：64 实验学时：8 上机学时：适用专业：油气储运B、F大纲执笔人：周晓君系（教研室）主任：孙宝江※ 一、课程目标本课程是油气储运专业的一门重要技术基础课，它的任务是通过各种教学环节，使学生掌握流体平衡和运动的一般规律及其相关的基本概念、基本理论、基本计算方法和基本实验技能，培养学生应用基本理论和方法来分析和解决实际问题的能力，为后续专业知识的学习、从事专业工作和科学研究打下理论基础。

《幂律流体在Kenics型静态混合器流动特性分析》一、引言随着化工行业的持续发展，流体力学逐渐成为了工程科学的重要领域。

作为该领域中的一个关键应用，Kenics型静态混合器在各种复杂流体混合中表现出其独特的效果。

其中，幂律流体作为非牛顿流体的一种，因其具有特殊的流动行为，对Kenics型静态混合器的流动特性具有深远影响。

本文旨在深入探讨幂律流体在Kenics型静态混合器中的流动特性，分析其流变行为与混合效果。

二、幂律流体的基本特性幂律流体是一种非牛顿流体，其流动行为不同于传统的牛顿流体。

幂律流体的剪切应力与剪切率之间存在幂律关系，这种关系决定了其流动行为的复杂性和非线性特征。

这种非线性特征使得幂律流体在流动过程中表现出独特的流变行为，如剪切变稀或剪切增稠等。

三、Kenics型静态混合器的结构与工作原理Kenics型静态混合器是一种广泛应用于化工、制药等行业的混合设备。

其结构特点是由一系列弯曲的叶片组成，这些叶片在混合器内部形成复杂的流道。

当流体通过这些流道时，由于流道的弯曲和叶片的阻碍，流体会受到不断的剪切和拉伸作用，从而达到混合的效果。

四、幂律流体在Kenics型静态混合器中的流动特性分析在Kenics型静态混合器中，幂律流体的流动特性受到多种因素的影响。

首先，流体的幂律指数将直接影响其流动行为。

幂律指数较小的流体往往表现出剪切增稠的特性，而幂律指数较大的流体则可能表现出剪切变稀的特性。

这些不同的流动行为将影响流体在混合器中的分布和混合效果。

其次，混合器的结构参数如叶片的形状、弯曲程度以及流道的尺寸等也会对流体的流动特性产生影响。

这些结构参数将决定流体在混合器中的流动路径和剪切强度，从而影响混合效果。

五、实验方法与结果分析为了更深入地了解幂律流体在Kenics型静态混合器中的流动特性，我们进行了系列实验。

通过改变流体的幂律指数、混合器的结构参数以及操作条件（如流量、压力等），我们观察了流体在混合器中的流动行为和混合效果。

幂律流体流变特性的研究
按照指数幂律流体流变特性的研究，这里对该领域的相关内容进行综述。

一、定义
指数幂律流体流变特性是指流体在静态下的流变特性，它描述的是指数幂律流体的流动性能。

指数幂律流体是指以一定的指数幂表示的流体，像是由弹性颗粒，流体分子和/或悬浮物以一定的指数分布在一个空间里。

二、流变特性
指数幂律流体在施加外力下，其流变特性是特殊的。

它可以由在施加荷重后，在其表面上产生曲率变化，以及由此形成的拉力(ten-sion)和凝结力(compressive force)表现出来。

三、流变模型
指数幂律流体的拉伸特性可以通过示意曲线表示，其特征在于拉伸程度及其速度定义了一种指数幂律的流体变形模型，即Vauhier–Newton-Stokes方程式(VNST Model)。

VNST方程的几何意义可以用二维和三维的拉伸示意曲线来表示，其解析解可以给出拉伸示意曲线上近似定义点的位置，即可以作为拉伸特性模型的特征时间参数。

四、量变形研究
通过精细的实验研究，发现指数幂律流体在施加外力后可以显示出量
变形的特点。

因此，在研究过程中需要充分考虑量变形，进行精细实验研究来判断量变形程度，进而得出拉伸曲线的拟合结果以及施加外力对量变形的影响因素。

五、结论
按照指数幂律流体流变特性的研究，它的拉伸特性可以通过示意曲线表示，由此可以得出拉伸曲线的拟合结果。

此外，通过精细的实验研究，也可以得出量变形的特点，从而可以更深入地认识指数幂律流体的流变特性。

幂律流体在环形通道中的流动规律0 前言在许多工程领域中经常会遇到非牛顿流体在环空中流动的情况，例如在石油工程中泥浆或钻井液在钻杆和套管间的流动，类似的例子在化学工程、生物食品工业和摩擦润滑中都会经常遇到。

按照非牛顿流体的分类，许多情况下都可将其看成是幂律流体。

幂律流体在这样的环空中的流动规律直接关系到具体工艺过程的效率、成本和质量。

因此研究幂律流体在环空中的流动规律有着非常重要的工程实际意义。

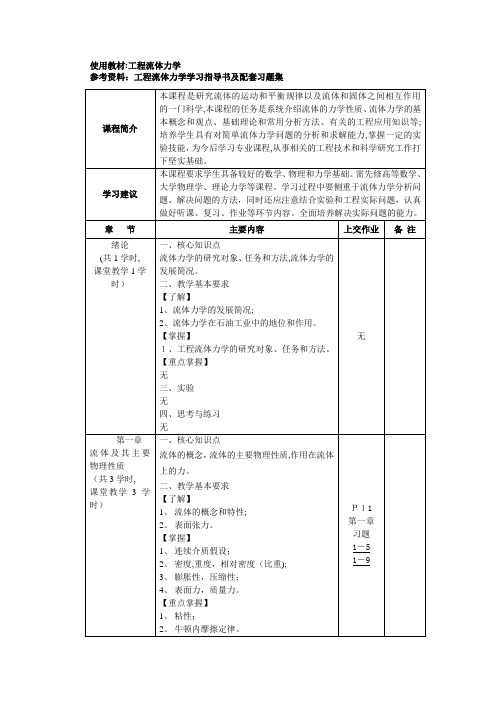
1 运动方程及求解假设不可压缩的幂律流体在如图1所示的同心环空中作轴向稳定等温的层流流动，R i为环形空间内径，R o 为环形空间外径，R λ为环形空间内最大速度所对应的半径。

图1 环空的几何结构这样幂律流体在环形空间的速度为：0==θu u r ()r u u z = (1)同时其偏应力张量为:0==θθz r T T ()γτ =rz T (2)式中()drr du =γ为剪切速率。

这样运动方程可以简化为：()01=--∂∂g dzdp rT r r rz ρ （3） 引入有效压力*p ：gz p p ρ+=*（4）（3）式可以简化为：()01=-∂∂*dzdp rT r r rz （5） 定解条件为：0==i R r u 0==o R r u （6） 0==λR r drdu （7）将（5）式对r 积分，得到：rc dz dp r T rz 02+=* （8）根据（7）式，在λR r =处，剪切速率0=γ ，剪切应力也应为零，故由（8）式解得：dzdp R c *-=220λ （9）将（9）式代到（8）式有：⎪⎪⎭⎫ ⎝⎛-=*r R r dz dp T rz 221λ（10） （1）当λR r R i ≤≤时，0≥drdu，0≥rz T ，幂律流体的本构方程为： nrz dr du K T ⎪⎭⎫⎝⎛= （11）由（10）、（11）式可得：nr R r dz dp K dr du 1221⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=*λ （12） 将上式从i R 到r 积分并利用定解条件（6），可得λR r R i ≤≤时的速度分布：dr r R r dz dp K u nr R i 1221⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=*λ （13） （2）当o R r R ≤≤λ时，0≤drdu，0≤rz T ，幂律流体的本构方程为： nrz dr du K T ⎪⎭⎫⎝⎛--= （14）由（10）、（11）式可得：nr r R dz dp K dr du1221⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=*λ （15）将上式从r 到o R 积分并利用定解条件（6），可得o R r R ≤≤λ时的速度分布：dr r rR dz dp K u nR ro 1221⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=*λ（16） （13）式和（16）式即为幂律流体在环空中的速度分布。

g 0(3)P P gz(4)幕律流体在环形通道中的流动规律0前言在许多工程领域中经常会遇到非牛顿流体在环空中流动的情况，例如在石油工程中泥浆或钻井液在钻杆和套管间的流动， 类似的例子在化学工程、生物食品工业和摩擦润滑中都会 经常遇到。

按照非牛顿流体的分类， 许多情况下都可将其看成是幕律流体。

幕律流体在这样的环空中的流动规律直接关系到具体工艺过程的效率、 成本和质量。

因此研究幕律流体在环空中的流动规律有着非常重要的工程实际意义。

1运动方程及求解为环形空间内径，R 0为环形空间外径, 皿为环形空间内最大速度所对应的半径。

图1环空的几何结构这样幕律流体在环形空间的速度为：T rT z 0 T rz式中詈为剪切速率。

这样运动方程可以简化为:引入有效压力p :假设不可压缩的幕律流体在如图 1所示的同心环空中作轴向稳定等温的层流流动, E LRoU r u 0 U z u r同时其偏应力张量为：(1)rT rzdpdz(14)(15)dudpR 2 dr2K dz r（3 ）式可以简化为:1 rrT rz rdp0 dz(5)定解条件为：u r R iiur R o(6)dur R 0(7)dr将（5）式对 r 积分，得到：「rzr dp Cc_(8)2 dzr根据（7）式，在r R 处，剪切速率 0,剪切应力也应为零，故由（8）式解得:2 dz将（9）式代到（8）式有:ndu dr由（10）、（ 11）式可得:du dr由（10）、（ 11）式可得:(9)T r zR 2dz(10)pl..(1)当 R r R 时，dUT rz，幕律流体的本构方程为:T rz(11)du dr1 dp 2K dzR 2(12)将上式从R i 到r 积分并利用定解条件6)，可得R r R 时的速度分布: R i1 dp2K dzR 21ndr(13)(2)当 R r R o 时,dudr T rz幕律流体的本构方程为:T rz(16)(22)(23)将上式从r 到R o 积分并利用定解条件（6），可得R r R o 时的速度分布:Ro 1 dp u r2K dz（13）式和（16）式即为幕律流体在环空中的速度分布。