衔接方程与根系关系1

进门测试建议5min1、设1x 、2x 是关于x 的方程02=++q px x 的两根，1x +1、2x +1是关于x 的方程的两根，则p 、q 的值分别等于 ．2、方程019972=++px x 恰有两个正整数根1x 、2x ，则)1)(1(21++x x p的值是 ．．3、如果方程0)2)(1(2=+--m x x x 的三根可以作为一个三角形的三边之长，那么实数m 的取值范围是 ．4、已知α、β是方程012=--x x 的两个根，则βα34+的值为 ．5、已知关于x 的方程01)32(22=++--k x k x ． （1）当k 为何值时，此方程有实数根；（2） 若此方程的两个实数根1x 、2x 满足：312=+x x ，求k 的值． 解：1、-1，-3；2、21-；3、143≤<m ；4、5；5、(1)512k ≤；(2) 0．课堂导入建议10min数形结合数与形是数学中的两个最古老，也是最基本的研究对象，它们在一定条件下可以相互转化。

中学数学研究的对象可分为数和形两大部分，数与形是有联系的，这个联系称之为数形结合，或形数结合。

作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，0∆>⎧0∆>⎧大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a【例题精讲】例1. 已知方程()2210x m x m -++=有两个不等正实根，求实数m 的取值范围．【解析】由()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩⇒ ()218010m m m m ⎧+->⎪>-⎨⎪>⎩ ⇒ 3223220m m m ⎧<->+⎪⎨>⎪⎩或 ⇒ 0322m <<-或322m >+即为所求的范围．例2. 若方程05)2(2=-+-+m x m x 的根满足下列条件，分别求出实数m 的取值范围．（1）方程两实根均为正数；（2）方程有一正根一负根．【解析】讨论二次方程根的分布，应在二次方程存在实根的条件下进行．代数方法与图象法是研究二次方程根的分布问题的主要方法． 解1 （1）由题意，得.45244050)2(0)5(4)2(00022121-≤⇒⎪⎩⎪⎨⎧<<≥-≤⇒⎪⎩⎪⎨⎧>->--≥---⇒⎪⎩⎪⎨⎧>>+≥∆m m m m m m m m m x x x x 或所以，当4-≤m 时，原方程两实根均为正数；（2）由题意，得.5050021>⇒<-⇒⎩⎨⎧<≥∆m m x x所以，当5>m 时，原方程有一正根一负根．解2 二次函数m x m x y -+-+=5)2(2的图象是开口向上的抛物线．（1）如图，由题意，得4052)2(4)2(022050)2(020)0(22-≤⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-+--->-->-⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≤->->m m m m m m a b f a b f 。

2021-2022新高一 初高中衔接辅导课程 （解析版） 衔接教材06 根与系数的关系（韦达定理）知识点讲解1.一元二次方程的根我们知道，对于一元二次方程ax 2＋bx ＋c ＝0（a ≠0），用配方法可以将其变形为2224()24b b acx a a -+= ①因为a ≠0，所以，4a 2＞0．于是（1）当b 2－4ac ＞0时，方程①的右端是一个正数，因此，原方程有两个不相等的实数根x 1，2＝2b a-±；（2）当b 2－4ac ＝0时，方程①的右端为零，因此，原方程有两个等的实数根x 1＝x 2＝－2b a； （3）当b 2－4ac ＜0时，方程①的右端是一个负数，而方程①的左边2()2b x a+一定大于或等于零，因此，原方程没有实数根．由此可知，一元二次方程ax 2＋bx ＋c ＝0（a ≠0）的根的情况可以由b 2－4ac 来判定，我们把b 2－4ac 叫做一元二次方程ax 2＋bx ＋c ＝0（a ≠0）的根的判别式，通常用符号“Δ”来表示． 综上所述，对于一元二次方程ax 2＋bx ＋c ＝0（a ≠0），有（1）当Δ＞0时，方程有两个不相等的实数根x 1，2（2）当Δ＝0时，方程有两个相等的实数根x 1＝x 2＝－2ba；（3）当Δ＜0时，方程没有实数根．2.一元二次方程的根与系数的关系若一元二次方程ax 2＋bx ＋c ＝0（a ≠0）有两个实数根1x =，2x =，则有1222b b b bx x a a-+--+=+==-；221222(4)444b b ac ac c x x a a a--====． 所以，一元二次方程的根与系数之间存在下列关系：如果ax 2＋bx ＋c ＝0（a ≠0）的两根分别是x 1，x 2，那么x 1＋x 2＝b a -，x 1·x 2＝ca．这一关系也被称为韦达定理．特别地，对于二次项系数为1的一元二次方程x 2＋px ＋q ＝0，若x 1，x 2是其两根，由韦达定理可知x 1＋x 2＝－p ，x 1·x 2＝q ，即p ＝－(x 1＋x 2)，q ＝x 1·x 2，所以，方程x 2＋px ＋q ＝0可化为 x 2－(x 1＋x 2)x ＋x 1·x 2＝0，由于x 1，x 2是一元二次方程x 2＋px ＋q ＝0的两根，所以，x 1，x 2也是一元二次方程x 2－(x 1＋x 2)x ＋x 1·x 2＝0．因此有以两个数x 1，x 2为根的一元二次方程（二次项系数为1）是x 2－(x 1＋x 2)x ＋x 1·x 2＝0．3. 一元二次方程的两根之差的绝对值是一个重要的量，今后我们经常会遇到求这一个量的问题，为了解题简便，我们可以探讨出其一般规律：设x 1和x 2分别是一元二次方程ax 2＋bx ＋c ＝0（a ≠0），则1x =，2x =，∴| x 1－x 2|=||||a a ==． 于是有下面的结论：若x 1和x 2分别是一元二次方程ax 2＋bx ＋c ＝0（a ≠0），则| x 1－x 2|＝||a （其中Δ＝b 2－4ac ）． 今后，在求一元二次方程的两根之差的绝对值时，可以直接利用上面的结论．经典例题解析例1 判定下列关于x 的方程的根的情况（其中a 为常数），如果方程有实数根，写出方程的实数根．（1）x 2－3x ＋3＝0； （2）x 2－ax －1＝0； （3） x 2－ax ＋(a －1)＝0； （4）x 2－2x ＋a ＝0． 解：（1）∵Δ＝32－4×1×3＝－3＜0，∴方程没有实数根． （2）该方程的根的判别式Δ＝a 2－4×1×(－1)＝a 2＋4＞0，所以方程一定有两个不等的实数根1x =， 2x = （3）由于该方程的根的判别式为Δ＝a 2－4×1×(a －1)＝a 2－4a ＋4＝(a －2)2，所以，①当a ＝2时，Δ＝0，所以方程有两个相等的实数根 x 1＝x 2＝1；②当a ≠2时，Δ＞0， 所以方程有两个不相等的实数根 x 1＝1，x 2＝a －1．（3）由于该方程的根的判别式为Δ＝22－4×1×a ＝4－4a ＝4(1－a )，所以①当Δ＞0，即4(1－a ) ＞0，即a ＜1时，方程有两个不相等的实数根11x = 21x = ②当Δ＝0，即a ＝1时，方程有两个相等的实数根 x 1＝x 2＝1； ③当Δ＜0，即a ＞1时，方程没有实数根．说明：在第3，4小题中，方程的根的判别式的符号随着a 的取值的变化而变化，于是，在解题过程中，需要对a 的取值情况进行讨论，这一方法叫做分类讨论．分类讨论这一思想方法是高中数学中一个非常重要的方法，在今后的解题中会经常地运用这一方法来解决问题．例2 已知方程2560x kx +-=的一个根是2，求它的另一个根及k 的值．分析：由于已知了方程的一个根，可以直接将这一根代入，求出k 的值，再由方程解出另一个根．但由于我们学习了韦达定理，又可以利用韦达定理来解题，即由于已知了方程的一个根及方程的二次项系数和常数项，于是可以利用两根之积求出方程的另一个根，再由两根之和求出k 的值． 解法一：∵2是方程的一个根，∴5×22＋k ×2－6＝0，∴k ＝－7．所以，方程就为5x 2－7x －6＝0，解得x 1＝2，x 2＝－35． 所以，方程的另一个根为－35，k 的值为－7． 解法二：设方程的另一个根为x 1，则 2x 1＝－65，∴x 1＝－35．由 （－35）＋2＝－5k ，得 k ＝－7．所以，方程的另一个根为－35，k 的值为－7． 例3 已知关于x 的方程x 2＋2(m －2)x ＋m 2＋4＝0有两个实数根，并且这两个实数根的平方和比两个根的积大21，求m 的值．分析： 本题可以利用韦达定理，由实数根的平方和比两个根的积大21得到关于m 的方程，从而解得m 的值．但在解题中需要特别注意的是，由于所给的方程有两个实数根，因此，其根的判别式应大于零． 解：设x 1，x 2是方程的两根，由韦达定理，得 x 1＋x 2＝－2(m －2)，x 1·x 2＝m 2＋4．∵x 12＋x 22－x 1·x 2＝21， ∴(x 1＋x 2)2－3 x 1·x 2＝21，即 [－2(m －2)]2－3(m 2＋4)＝21，化简，得 m 2－16m －17＝0， 解得 m ＝－1，或m ＝17．当m ＝－1时，方程为x 2＋6x ＋5＝0，Δ＞0，满足题意； 当m ＝17时，方程为x 2＋30x ＋293＝0，Δ＝302－4×1×293＜0，不合题意，舍去．综上，m ＝17． 说明：（1）在本题的解题过程中，也可以先研究满足方程有两个实数根所对应的m 的范围，然后再由“两个实数根的平方和比两个根的积大21”求出m 的值，取满足条件的m 的值即可。

根系关系及应用题题型一：根与系数关系一元二次方程的根与系数的关系（韦达定理）若21,x x 是关于x 的一元二次方程)0(02≠=++a c bx ax 的两个根，则方程的两个根21,x x 和系数c b a ,,有如下关系：ac x x a b x x =⋅-=+2121,. 【例1】 不解方程，求下列方程两根的积与和．⑴25100x x --= ⑵22710x x ++= ⑶23125x x -=+ ⑷()137x x x -=+【例2】 已知关于x 的一元二次方程22(21)0x m x m +-+=有两个实数根1x 和2x ．⑴求实数m 的取值范围；⑵当22120x x -=时，求m 的值．【例3】 已知一元二次方程2(1)230m x mx m +++-=有两个不相等的实数根，并且这两个根又不互为相反数. ⑴ 求m 的取值范围；⑵ 当m 在取值范围内取最小偶数时，方程的两根为12,x x ，求2123(14)x x -的值.【探究对象】根系关系的进一步应用 【探究方式】在做含参一元二次方程根系关系的问题时，先考虑二次项系数不为0→再判断∆→然后根据题意看是否有两根的特殊关系（如例3，已知中强调两根不互为相反数，则根据根系关系能够得出0m ≠）．在这里主要探讨一下根的正负性问题： 利用根与系数的关系，我们可以不直接求方程2++=0ax bx c 的根，而知其根的正、负性． 在2=40b ac ∆-≥的条件下，我们有如下结论：①当<0c a时，方程的两根必一正一负．若0ba -≥，则此方程的正根不小于负根的绝对值；若<0ba-，则此方程的正根小于负根的绝对值．①当>0c a时，方程的两根同正或同负．若>0b a -，则此方程的两根均为正根；若<0b a -，则此方程的两根均为负根．【探究1】已知关于x 的一元二次方程x 2－2ax +a 2－9=0 （1）a 为何值时，方程有两个正根？（2）a 为何值时，方程有一正根、一负根？【探究2】已知关于x 的一元二次方程（m +2）x 2+2mx +232m -=0． （1）若方程有两个不相等的实数根，求m 的取值范围；（2）若 362m <<，试判断方程两个实数根的符号，并证明你的结论．【探究3】已知方程22430x x k -+-=，k 为实数且k ≠0，证明：此方程有两个实数根，其中一根大于1，另一根小于1．题型二：一元二次方程的应用题列一元二次方程解应用题的时候，要注意检验得到的根是否符合题意．【引例】 ⑴某汽车销售公司2019年盈利1500万元， 2020年盈利2160万元，且从2019年到2020年，每年盈利的年增长率相同．设每年盈利的年增长率为x ，根据题意，下面所列方程正确的是（ ）．A ．()2150012160x += B ．2150015002160x x += C ．215002160x = D ．()()215001150012160x x +++=⑵某种商品原价是120元，经两次降价后的价格是100元，求平均每次降价的百分率．设平均每次降价的百分率为x ，可列方程为 ． （3）某厂一月份生产产品50台，计划二、三月份共生产产品120台，设 二、三月份平均每月增长率为x ，根据题意，可列出方程为（ ） A ．50（1+x ）2=60 B ．50（1+x ）2=120C ．50+50（1+x ）+50（1+x ）2=120D ．50（1+x ）+50（1+x ）2=120【例4】 某商品进价为40元的衬衫按50元售出时.每月能卖500件.这种衬衫每涨价1元，其销售量减少10件.如果商场计划每月赚8000元利润.售价应定为多少?练习1.某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。

第三讲 一元二次方程的判别式及根系关系（一） 一元二次方程根的判别式的定义：运用配方法解一元二次方程过程中得到222424b b ac x a a -⎛⎫+= ⎪⎝⎭，显然只有当240b ac -≥时，方程才有实数根.一元二次方程根与系数的关系 （1）当c a ＜0时，方程的两根必一正一负.若0b a-≥，则次方程的整根不小于负根的绝对值；若b a-＜0，则此方程的正根小于负根的绝对值. （2）当c a ＞0时，方程的两根同正或同负.若b a-＞0，则此方程的两根均为正根；若b a -＜0，则此方程两根均为负根. 一般的结论是：若12,x x 是()200ax bx c a ++=≠的两根（其中12x x ≥），且m 为实数，当0∆≥时，一般地：①()()120x m x m --＜12,x m x m ⇔＞＜②()()120x m x m --＞且()()120x m x m -+-＞12,x m x m ⇔＞＞③()()120x m x m --＞且()()120x m x m -+-＜12,x m x m ⇔＜＜特殊是，当m =0时，上述就转化为()200ax bx c a ++=≠有两异根、两正根、两负根的条件韦达定理的应用：（1）已知方程的一个根，求另一个根以及确定方程参数的值（2）已知方程，求关于方程的两根的代数式的值（3）已知方程的两根，构造方程（4）结合根的判别式，讨论根的符号特征（5）逆用构造一元二次方程辅助解题，当已知等式具有相同的结构时，就可以把两个变元看作某一个一元二次方程的两根，以便利用韦达定理（6）利用韦达定理求出一元二次方程中待定系数后，一定要验证方程的∆是否为非负【例1】（1）关于x 的方程()21-210k x --=，有两个不相等的实数根，求k 的取值范围.（2）已知a ＞0，b ＞a +c ，判断关于x 的方程20ax bx c ++=的根的情况，并给出必要的说明.（3）设a 、b 、c 为互不相等的非零实数，求证：以下三个方程220ax bx c ++=，220bx cx a ++=，220cx ax b ++=，不可能都有2个相等的实数根.（4）若()()()()()()x a x b x b x c x c x a ++++++++是关于x 的完全平方式.证明：a =b =c .【例2】已知关于x 的二次方程2110x p x q ++=与2220x p x q ++=，求证：当()12122p p q q =+时，这两个方程中至少有一个方程有实数根.【例3】设方程24x ax +=只有3个不相等的实数根，求a 的取值和相应的3个根.【例4】（1）已知a 、b 、c 分别是△ABC 的三边长，求证：方程()2222220b x b c a x c ++-+=没有实数根.（2）已知△ABC 的三边a 、b 、c 满足：b +c =8，21252bc a a =-+，试确定△ABC 的形状.【例5】在等腰△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，已知a =3，b 和c 是关于x 的方程21202x mx m ++-=的两个实数根，求△ABC 的周长.。

二次方程与根的关系二次方程是一个数学概念，通常表示成 ax^2 + bx + c = 0 的形式，其中 a、b、c 是已知的实数系数，而 x 是未知数。

二次方程在数学中有着广泛的应用，特别是在物理学、工程学和经济学等领域。

二次方程的一条重要性质是它与根的关系。

根是指使方程成立的解，即满足方程的 x 的值。

二次方程的根可能有两个、一个或没有，具体取决于方程的判别式（b^2 - 4ac）的值。

当判别式大于零时，二次方程有两个不相等的实根。

这意味着方程在坐标平面上表示的是一个开口向上或向下的抛物线与 x 轴相交于两个不同的点。

这两个实根可以通过求解二次方程来得到，公式为：x = (-b ± √(b^2 - 4ac)) / (2a)其中 "±" 表示加号或减号，表示两个不同的解。

当判别式等于零时，二次方程有一个实根。

这意味着方程在坐标平面上表示的是一个与 x 轴相切于一个点的抛物线。

这个实根可以通过求解二次方程来得到，公式为：x = -b / (2a)当判别式小于零时，二次方程没有实根。

这意味着方程在坐标平面上表示的是一个没有与 x 轴相交的抛物线，也就是抛物线在 x 轴上方或下方。

在这种情况下，解是虚数，表示为 a+bi 或 a-bi 的形式，其中a 和b 都是实数，而 i 是虚数单位，满足 i^2 = -1。

二次方程与根的关系在数学和实际应用中都非常重要。

它们帮助我们解决许多问题，例如找出物体在重力影响下的运动轨迹、计算交通工具的加速度以及确定经济模型中的最优解等。

二次方程还与二次函数紧密相连，可以用来研究函数的性质和图像。

除了与根的关系，二次方程还有其他一些重要特性。

例如，二次方程的对称轴是一个垂直于 x 轴的直线，它通过抛物线的顶点。

对称轴的方程可以通过将二次方程转化为顶点的标准形式来获得。

二次方程还有极大值或极小值，这些值对应于抛物线的顶点。

在实际问题中，我们经常需要解决二次方程的一些特定情况。

第1章 代数式与恒等变形四个公式知识衔接在初中，我们学习了实数与代数式，知道代数式中有整式，分式，根式，它们具有类似实数的属性，可以进行运算。

在多项式乘法运算中，我们学习了乘法公式，如：平方差公式22))((b a b a b a -=-+；完全平方公式2222)(b ab a b a +±=±，并且知道乘法公式在整式的乘除，数值计算，代数式的化简求值以及代数等式的证明等方面有着广泛的应用。

而在高中阶段的学习中，将会遇到更复杂的多项式运算为此在本章中我们将拓展乘法公式的内容。

知识延展1 多项式的平方公式：ac bc ab c b a c b a 222)(2222+++++=++2 立方和公式：3322))((b a b ab a b a +=+-+3 立方差公式：3322))((b a b ab a b a -=++-4 完全立方公式：3223333)(b ab b a a b a ±+±=±注意：（1）公式中的字母可以是数，也可以是单项式或多项式；（2）要充分认识公式自身的价值，在多项式乘积中，正确使用乘法公式能提高运算速度，减少运算中的失误；（3）对公式的认识应当从发现，总结出公式的思维过程中学习探索，概括，抽象的科学方法；（4）由于公式的范围在不断扩大，本章及初中所学的仅仅是其中最基本，最常用的几个公式。

一 计算和化简例1 计算：))(()(222b ab a b a b a +++-变式训练：化简 62222))()()((y xy y x xy y x y x y x +-+++-+二 利用乘法公式求值；例2 已知0132=+-x x ，求331x x +的值。

变式训练：已知3=++c b a 且2=++ac bc ab ，求222c b a ++的值。

三 利用乘法公式证明例3 已知0,0333=++=++c b a c b a 求证：0200920092009=++c b a变式训练：已知2222)32()(14c b a c b a ++=++，求证：3:2:1::=c b a习题精练1 化简：322)())((b a b ab a b a +-+-+2 化简 )1)(1)(1)(1)(1)(1(12622+++-+++-a a a a a a a a3 已知10=+y x 且10033=+y x ，求代数式22y x +的值；4 已知21201,19201,20201+=+=+=x c x b x a ，求代数式ac bc ab c b a ---++222的值；5 已知)(3)(2222z y x z y x ++=++，求证：z y x ==6 已知abcd d c b a 44444=+++且d c b a ,,,均为正数，求证：以d c b a ,,,为边的四边形为菱形。

一元二次方程的判别式与根系关系模块一 一元二次方程的判别式1．定义：在一元二次方程()ax bx c a 2++=0≠0中，只有当系数a 、b 、c 满足条件△≥b ac 2=-40时才有实数根．这里b ac 2-4叫做一元二次方程根的判别式，记作△．2．判别式与根的关系：在实数范围内，一元二次方程()ax bx c a 2++=0≠0的根的情况由△b ac 2=-4确定．设一元二次方程为()ax bx c a 2++=0≠0，其根的判别式为：△b ac 2=-4，则①△>0⇔方程()ax bx c a 2++=0≠0有两个不相等的实数根,x 12．②△=0⇔方程()ax bx c a 2++=0≠0有两个相等的实数根bx x a12==-2．③△<0⇔方程()ax bx c a 2++=0≠0没有实数根．特殊的：（1）若a ，b ，c 为有理数，且△为完全平方式，则方程的解为有理根；（2）若△为完全平方式，同时b -2a 的整数倍，则方程的根为整数根． 模块二 一元二次方程的根与系数关系 1．韦达定理：如果()ax bx c a 2++=0≠0的两根是x 1，x 2，则b x x a 12+=-，cx x a12=．（使用前提：△≥0）特别地，当一元二次方程的二次项系数为1时，设x 1，x 2是方程x px q 2++=0的两个根，则x x p 12+=-，x x q 12=． 2．韦达定理的逆定理：如果有两个数x 1，x 2满足b x x a 12+=-，cx x a12=，那么x 1，x 2必定是()ax bx c a 2++=0≠0的两个根．特别地，以两个数x 1、x 2为根的一元二次方程（二次项系数为1）是()x x x x x x 21212-++=0．3．韦达定理与根的符号关系：在△≥b ac 2=-40的条件下，我们有如下结论：（1）当ca <0时，方程的两根必一正一负．①若≥b a -0，则此方程的正根不小于负根的绝对值；②若ba -<0，则此方程的正根小于负根的绝对值．（2）当ca >0时，方程的两根同正或同负．①若b a ->0，则此方程的两根均为正根；②若ba -<0，则此方程的两根均为负根．注意：（1）若ac <0，则方程()ax bx c a 2++=0≠0必有实数根．（2）若ac >0，方程()ax bx c a 2++=0≠0不一定有实数根．模块一 一元二次方程的判别式例1、（1）不解方程，直接判断下列方程的解的情况：①x x 27--1=0 ②()x x 29=43-1③x x 2+7+15=0 ④()mx m x 2-+1+=02（m 为常数）（2）已知a 、b 、c 分别是三角形的三边，则方程()()a b x cx a b 2++2++=0的根的情况是（ ） A ．没有实数根 B ．可能有且只有一个实数根 C ．有两个相等的实数根D ．有两个不相等的实数根【解析】（1）①△>0，有两个不等实根；②△=0，有两个相等实根； ③△<0，无实根；④△m 2=+1>0，方程有两个不等实根．（2）由题()()()()△c a b a b c c a b 22=2-4+=4++--∵a b c ++>0，c a b --<0，故方程没有实根．选A ．【点评】这道题（1）主要考察判别式与根的关系，属于特别基础的题，锻炼孩子们的思维，（2）结合三角形三边关系来考察一元二次方程的判别式和根的个数的关系．例2、（1）若关于x 的一元二次方程()k x x 21-1+-=04有实根，则k 的取值范围为______．（2）关于x的一元二次方程()k x 21-2--1=0有两个不相等的实数根，则k 的取值范围______． （3）当a 、b 为何值时，方程()x a x a ab b 222+21++3+4+4+2=0有实根？ 【解析】（1）≥k 0且≠k 1；（2）≤k -1<2且k 1≠2，由题意，得()()k k k k 4+1+41-2>0⎧⎪+1≥0⎨⎪1-2≠0⎩，解得≤k -1<2且k 1≠2；（3）要使关于x 的一元二次方程()x a x a ab b 222+21++3+4+4+2=0有实根，则必有△≥0，即()()≥a a ab b 22241+-43+4+4+20，得()()a b a 22+2+-1≤0．又因为()()a b a 22+2+-1≥0，所以()()a b a 22+2+-1=0，得a =1，b 1=-2．【点评】这道题（1）（2）主要是结合一元二次方程的定义和判别式与根的关系的考察，（3）把判别式和平方的非负性结合起来考查．例3、已知关于x 的一元二次方程()a x ax 213-1-+=04有两个相等的实数根，求代数式a a a 21-2+1+的值．【解析】由题，一元二次方程()a x ax 213-1-+=04有两个相等的实数根，所以a a 2-3+1=0．所以有a a a 2-2+1=，a a 2+1=3．代入a a a21-2+1+，得a a a a a a a a a 2211+13-2+1+=+===3．【点评】这道题主要是考察判别式与代数式的结合，难度不大．例4、在等腰△ABC 中，A ∠、B ∠、C ∠的对边分别为a 、b 、c ，已知a =3，b 和c 是关于x 的方程x mx m 21++2-=02的两个实数根，求△ABC 的周长．【解析】当b c =时，方程有两个相等的实数根，则=△m m 21⎛⎫-42-=0 ⎪2⎝⎭，∴m 1=-4，m 2=2．若m =-4，原方程化为x x 2-4+4=0， 则x x 12==2，即b c ==2，∴△ABC 的周长为2+2+3=7．若m =2，原方程化为x x 2+2+1=0， 则x x 12==-1，不合题意．当a b =或a c =时，x =3是方程的一个根，则m m 19+3+2-=02，则m 22=-5，原方程化为x x 22221-+=055，解得x 1=3，x 27=5，∴ABC △的周长为7373+3+=55．综上所述，ABC △的周长为7或375．【点评】这道题主要考察学生们的分类讨论能力，应对多种情况是要理清思路．模块二 一元二次方程的根与系数的关系 例5、（1）已知一元二次方程ax ax c 2+2+=0的一根x 1=2，则方程的另一根______x 2=．（2）已知x 1，x 2是方程x x 2-3+1=0的两个实数根，则：①x x 2212+；②()()x x 12-2⋅-2；③x x x x 221122+⋅+；④x x x x 2112+；⑤x x 12-；⑥x x 2212-；⑦x x 1211-． 【解析】（1）-4；（2）()x x x x x x 2222121212+=+-2⋅=3-2⨯1=7，()()()x x x x x x 121212-2⋅-2=⋅-2++4=1-2⨯3+4=-1，()x x x x x x x x 22211221212+⋅+=+-⋅=9-1=8，x x x x x x x x 2221211212+7+===7⋅1，()()x x x x x x 222121212-=+-4⋅=3-4⨯1=5，∴x x 12-=∴()()(x x x x x x 22121212-=+-=3⨯=x x x x x x 21121211--=== 【点评】第三小题，主要是考察韦达定理的灵活运用，包含了各种变形情况．例6、（1）已知关于x 的方程()x k x k 22+2-3+-3=0有两个实数根x 1，x 2，且x x x x 121211+=+，求k 值． （2）已知x 1，x 2是方程ax ax a 24-4++4=0的两实根，是否能适当选取a 的值，使得()()x x x x 1221-2-2的值等于54． 【解析】（1）∵方程()x k x k 22+2-3+-3=0有两个实数根x 1，x 2，∴()()△≥k k k 22=2-3-4-3=21-120得：≤k 74．由韦达定理得，()x x k x x k 12212+=-2-3⎧⎪⎨⋅=-3⎪⎩． ∵x x x x 121211+=+，∴x x x x x x 121212++=，x x 12+=0或x x 12=1，当x x 12+=0时，k 3-2=0，k 3=2，∵k 37=<24，所以k 3=2符合题意．当x x 12=1时，k 2-3=1，k =±2，∵k 7≤4，∴k =2舍去．∴k 的值为32或-2．（2）显然a ≠0由()△a a a 2=16-16+4≥0得a <0，由韦达定理知x x 12+=1，a x x a12+4=4，所以()()()()()a x x x x x x x x x x x x a 2221221121212129+4-2-2=5-2+=9-2+=-24a a+36=4 若有()(),x x x x 12215-2-2=4则a a +365=44，∴a =9，这与0a <矛盾，故不存在a ，使()()x x x x 12215-2⋅-2=4．【点评】这道题主要锻炼孩子们的过程，以及有两个实根，解出来别忘了限制条件，这种类型的题比较常见，一定不要忽视∆的限定条件以及用韦达定理可得到的限定条件．例6、（1）若m ，n 是方程x x 2+-1=0的两个实数根，则m m n 2+2+-1的值为________．（2）已知a ，b 是方程x x 2+2-5=0的两个实数根，则a ab a b 2-+3+的值为__________．（3）已知m 、n 是方程x x 2+2016+7=0的两个根，则()()m m n n 22+2015+6+2017+8= ________． 【解析】（1）∵m ，n 是方程x x 2+-1=0的两个实数根，∴m n +=-1，m m 2+-1=0，则原式()()m m m n 2=+-1++=-1=-1，（2）∵a 是方程x x 2+2-5=0的实数根，∴a a 2+2-5=0，∴a a 2=5-2，∴a ab a b a ab a b a b ab 2-+3+=5-2-+3+=+-+5， ∵a ，b 是方程x x 2+2-5=0的两个实数根，∴a b +=-2，ab =-5，∴a ab a b 2-+3+=-2+5+5=8． 故答案为8．（3）∵m 、n 是方程x x 2+2016+7=0的两个根，∴m n +=-2016，mn =7；∴m m 2+2016+7=0，n n 2+2016+7=0，()()()()m m n n m m m n n n 2222+2015+6+2017+8=+2016+7--1+2016+7++1 ()()()()m n mn m n =-+1+1=-+++1=-7-2016+1=2008故答案是：2008．【点评】这道题主要考查韦达定理根系关系的应用，进一步强化孩子对于韦达定理应用的理解．例7、（1）已知一元二次方程()ax a x a 2+3-2+-1=0的两根都是负数，则k 的取值范围是_________． （2）已知二次方程342x x k 2-+-=0的两根都是非负数，则k 的取值范围是__________．【解析】（1）此方程两实根为,x x 12，由已知得a x x x x 1212≠0⎧⎪∆0⎪⎨+<0⎪⎪>0⎩≥，∴()()a a a a a a a a2≠0⎧⎪3-24-10⎪⎪2-3⎨<0⎪⎪-1⎪>0⎩-≥,即a 91<8≤．（2）此方程两实根为,x x 12，由已知得≥x x x x 1212∆≥0⎧⎪+≥0⎨⎪0⎩，得：∴2()43()k k ⎧⎪-4-⨯-2≥0⎪4⎪>0⎨3⎪-2⎪≥0⎪3⎩即k 102≤≤3．【点评】这道题主要考查韦达定理和判别式结合不等式组的形式去判定根的具体情况，这类题是比较常见一类题，要将这种不等的思想传授给孩子． 课后作业 1．已知关于x 的一元二次方程()()k x k x 22-1+2+1+1=0有两个不相等的实数根，则k 的取值范围为_____________．A ．k 1≥4B ．k 1>4且≠k 1 C ．k 1<4且≠k 1 D ．k 1≥4且≠k 1【解析】B ．2．已知关于x 的一元二次方程x m 2-=0有两个不相等的实数根，则m 的取值范围__________． 3．关于x 的方程()()m x m x 22-4+2+1+1=0有实根，则m 的取值范围__________．【解析】2．由题意可知，原方程的判别式(m m m 21∆=+4=1+3>0⇒>-3．又≥≤m m 1-0⇒1，故≤m 1-<13．3．题设中的方程未指明是一元二次方程，还是一元一次方程，所以应分0m 2-4=和m 2-4≠0，两种情形讨论：当m 2-4=0即m =±2时，()m 2+1≠0，方程为一元一次方程，总有实根； 当m 2-4≠0即m ≠±2时，方程有根的条件是： [()]()≥m m m 22=2+1-4-4=8+20∆0，解得m 5≥-2．∴当m 5≥-2且m ≠±2时，方程有实根．综上所述：当m 5≥-2时，方程有实根．4．已知关于x 的方程()x k x k 2-+1+2-2=0． （1）求证：无论k 为何值，方程总有实根；（2）若等腰ABC △，底边a =3，另两边b 、c 恰好是此方程的两根，求ABC △的周长． 【解析】（1）()()()≥△k k k 22=+1-42-2=-30，∴无论k 为何值，方程总有实根．（2）当a =3为底，b ，c 为腰时，b c =，∴方程有两个相等的实根，∴∆=0，即()k 2-3=0，k =3，此时方程为x x 2-4+4=0，解x x 12==2，∴ABC △的周长为3+2+2=7，当a =3为腰，则方程有一根为3，将x =3代入方程，得k =4，方程为x x 2-5+6=0，解得x 1=2，x 2=3，∴ABC △的周长为2+3+3=8，综上所述，ABC △的周长为7或8．5．关于x 的方程x kx 22+=10的一个根是-2，则方程的另一根是_______；k =________．6．已知a ，b ，c 为正数，若二次方程ax bx c 2++=0有两个实数根，那么方程a x b x c 2222++=0的根的情况是（ ） A ．有两个不相等的正实数根 B ．有两个异号的实数根 C ．有两个不相等的负实数根 D ．不一定有实数根7．设α，β是一元二次方程x x 2+3-7=0的两个根，则ααβ2+4+=________．【解析】5．设另一根为x ，由根与系数的关系可建立关于x 和k 的方程组，解之即得．x 5=2，k =-1． 6．a x b x c 2222++=0的()()D b a c b ac b ac 42222=-4=+2-2， ∵二次方程ax bx c 2++=0有两个实数根， ∴≥b ac 2-40， ∴b ac 2-2>0，∴()()△b a c b ac b ac 42222=-4=+2-2>0∴方程有两个不相等的实数根，而两根之和为负，两根之积为正． 故有两个负根．故选C ．7．∵α，β是一元二次方程x x 2+3-7=0的两个根， ∴αβ+=-3，αα2+3-7=0，∴αα2+3=7，∴ααβαααβ22+4+=+3++=7-3=4，故答案为：4．8．已知关于x 的方程()x m x m 22+2+2+-5=0有两个实数根，并且这两个根的平方和比这两个根的积大16，求m 的值．【解析】有实数根，则∆≥0，且x x x x 221212+-=16，联立解得m 的值．依题意有：()2()3()()x x m x x m x x x x m m 12212121222+=-2+2⎧⎪=-5⎪⎨+-=16⎪⎪∆=4+2-4-5≥0⎩，解得：m =-1或m =-15且m 9≥-4， ∴ m =-1．。

第五讲一元二次方程根的判别式与根系关系第一讲一元二次方程根的判别式与根系关系一、【基础知识精讲】1．一元二次二次方程根的判别式（1）根的判别式：一元二次方程ax 2+bx +c =0(a ≠0) 是否有实根，由b +4ac 决定，因此我们把叫做一元二次方程根的判别式，并用∆表示，即∆=b +4ac 。

（2）一元二次方程根的情况与判别式的关系：∆>0方程有∆=0方程有∆①使用前应先将方程化为一般形式；②使用此性质时要保证方程为一元二次方程，即a ≠0；③性质顺用、逆用均可；④不解方程，可以判断根的情况；⑤根据根的情况，可确定方程中字母系数的值或取值范围；2．根与系数的关系（韦达定理）（1）对于一元二次方程ax +bx +c =0(a ≠0) 的两根x 1, x 2，有222b ｃx 1+x 2=－，x 1∙x 2=a a（2）推论如果方程x +ｐx +ｑ=0的两个根是x 1, x 2，那么x 1+x 2=－ｐ，x 1∙x 2=ｑ（3）常用变形：x x +2x ) -21x 2x (x 1-x 2) =(x 1+x 2) -4x 1x 2 １+x ２=(1注：使用此性质要保证一元二次方程有两根，即a ≠0和∆≥0；（4）应用①不解方程，可求代数式的值；②根据两根之间的关系，可求方程中字母系数的值；③与根的判别式一起使用可确定根的符号问题。

２２2222二、【典型例题】知识点一一元二次二次方程根的判别式题型一根据根的情况求方程中字母系数的值【例1】（1）当m 取什么值时，关于x 的方程x 2+2(2m +1) x +(2m +2) 2=0。

①有两个相等实根；②有两个不相等的实根；③没有实根。

（2）是否存在这样的非负整数m ，使得关于x 的一元二次方程mx 2-2(3m -1) x +9m -1=0有两个不相等的实根，若存在，请求出m 的值，若不存在，请说明理由。

【变式练习】（1）当m 为什么值时，关于x 的方程(m 2-4) x 2+2(m +1) x +1=0有实根。

【第6讲】一元二次方程根与系数的关系【根底知识回忆】知识点1一元二次方程的根的判断式一元二次方程20 (0)ax bx c a ++=≠，用配方法将其变形为：2224()24b b ac x a a-+=(1) 当240b ac ->时，右端是正数，方程有两个不相等的实数根：x =(2) 当240b ac -=时，右端是零．因此，方程有两个相等的实数根：1,22b x a=- (3) 当240b ac -<时，右端是负数．因此，方程没有实数根．由于可以用24b ac -的取值情况来判定一元二次方程的根的情况．因此，把24b ac -叫做一元二次方程20 (0)ax bx c a ++=≠的根的判别式，表示为：24b ac ∆=- 知识点2一元二次方程的根与系数的关系一元二次方程20 (0)ax bx c a ++=≠的两个根为：,22b b x x a a-+--==所以：1222b b b x x a a a-+--+=+=-，12244ac cx x a a⋅====韦达定理：如果一元二次方程20 (0)ax bx c a ++=≠的两个根为12,x x ，那么：1212,b cx x x x a a+=-=【合作探究】探究一 ∆与根个数之间的关系【例1】不解方程，判断以下方程的实数根的个数：(1) 22310x x -+=(2) 24912y y +=(3) 25(3)60x x +-=【解析】：(1)2 (3)42110∆=--⨯⨯=>，∴ 原方程有两个不相等的实数根．(2) 原方程可化为：241290y y -+=2 (12)4490∆=--⨯⨯=，∴ 原方程有两个相等的实数根．(3) 原方程可化为：256150x x -+=2 (6)45152640∆=--⨯⨯=-<，∴ 原方程没有实数根．归纳总结：在求判断式时，务必先把方程变形为一元二次方程的一般形式．【练习1-1】关于x 的一元二次方程2320x x k -+=，根据以下条件，分别求出k 的范围： (1) 方程有两个不相等的实数根； (2) 方程有两个相等的实数根(3)方程有实数根；(4) 方程无实数根．【解析】：2(2)43412k k ∆=--⨯⨯=-(1) 141203k k ->⇒<； (2) 141203k k -=⇒=；(3) 141203k k -≥⇒≥；(4) 141203k k -<⇒<．【练习1-2】实数x 、y 满足22210x y xy x y +-+-+=，试求x 、y 的值．【解析】：可以把所给方程看作为关于x 的方程，整理得：22(2)10x y x y y --+-+= 由于x 是实数，所以上述方程有实数根，因此：222[(2)]4(1)300y y y y y ∆=----+=-≥⇒=，代入原方程得：22101x x x ++=⇒=-．综上知：1,0x y =-=探究二一元二次方程的根与系数的关系【例2-1】假设12,x x 是方程2220070x x +-=的两个根，试求以下各式的值：(1) 2212x x +；(2)1211x x +； (3) 12(5)(5)x x --； (4) 12||x x -．【解析】：由题意，根据根与系数的关系得：12122,2007x x x x +=-=-(1) 2222121212()2(2)2(2007)4018x x x x x x +=+-=---=(2)121212112220072007x x x x x x +-+===- (3) 121212(5)(5)5()2520075(2)251972x x x x x x --=-++=---+=-(4) 12||x x -====归纳总结：利用根与系数的关系求值，要熟练掌握以下等式变形：222121212()2x x x x x x +=+-，12121211x x x x x x ++=，22121212()()4x x x x x x -=+-，12||x x -=2212121212()x x x x x x x x +=+，33312121212()3()x x x x x x x x +=+-+等等．韦达定理表达了整体思想．【练习2】假设x 1和x 2分别是一元二次方程2x 2＋5x －3＝0的两根．〔1〕求| x 1－x 2|的值； 〔2〕求221211x x +的值；〔3〕x 13＋x 23． 【解析】：∵x 1和x 2分别是一元二次方程2x 2＋5x －3＝0的两根，∴1252x x +=-，1232x x =-． 〔1〕∵| x 1－x 2|2＝x 12+ x 22－2 x 1x 2＝(x 1＋x 2)2－4 x 1x 2＝253()4()22--⨯-＝254＋6＝494，∴| x 1－x 2|＝72．〔2〕22221212122222221212125325()2()3()2113722439()9()24x x x x x x x x x x x x --⨯-+++-+=====⋅-．〔3〕x 13＋x 23＝(x 1＋x 2)( x 12－x 1x 2＋x 22)＝(x 1＋x 2)[ ( x 1＋x 2) 2－3x 1x 2] ＝(－52)×[(－52)2－3×(32-)]＝－2158． 【例2-2】两个数的和为4，积为－12，求这两个数．【解析】：法一 设这两个数分别是x ，y ，那么{412x y xy +==-1126x y =-⎧⇒⎨=⎩或2262x y =⎧⎨=-⎩．因此，这两个数是－2和6．法二 由韦达定理知，这两个数是方程x 2－4x －12＝0的两个根．解方程得：x 1＝－2，x 2＝6．所以，这两个数是－2和6．【例2-2】关于x 的方程221(1)104x k x k -+++=，根据以下条件，分别求出k 的值． (1) 方程两实根的积为5； (2) 方程的两实根12,x x 满足12||x x =． 【解析】：(1) ∵方程两实根的积为5∴ 222121[(1)]4(1)034,412154k k k k x x k ⎧∆=-+-+≥⎪⎪⇒≥=±⎨⎪=+=⎪⎩ 所以，当4k =时，方程两实根的积为5． (2) 由12||x x =得知： ①当10x ≥时，12x x =，所以方程有两相等实数根，故302k ∆=⇒=； ②当10x <时，12120101x x x x k k -=⇒+=⇒+=⇒=-，由于302k ∆>⇒>，故1k =-不合题意，舍去．综上可得，32k =时，方程的两实根12,x x 满足12||x x =． 探究三一元二次方程的根的范围【例3-1】假设关于x 的一元二次方程x 2－x ＋a －4＝0的一根大于零、另一根小于零，求实数a 的取值范围．【解析】：设x 1，x 2是方程的两根，那么x 1x 2＝a －4＜0， ①且Δ＝(－1)2－4(a －4)＞0． ② 由①得 a ＜4， 由②得 a ＜174．∴a 的取值范围是a ＜4．【例3-2】一元二次方程有两个实根，一个比3大，一个比3小，求的取值范围。

第2讲 根的判别式与根系关系题型一 用于参数方程根的判定【例1】关于x 的一元二次方程2(3)220x a x a -+++=． （1）求证：方程总有两个实数根；（2）若方程有一根大于3，求a 的取值范围． 【解析】（1）∵22(3)41(22)(1)0a a a ⎡⎤∆=-+-⨯⨯+=-⎣⎦≥，∴方程总有两个实数根；（2）∵[]2(3)22(2)(1)0x a x a x x a -+++=--+=，∴12x =，21x a =+， ∵13a +>，∴2a >．题型二 判别式求参数的取值范围【例2】若关于x 的方程22(1)2(2)10m x m x --++=有实数根，求m 的取值范围．【解析】分两种情况讨论：①210m -≠，此时[]222(2)4(1)0m m ∆=-+--≥，解得54m -≥且1m ≠±；②210m -=，即1m =±，此时方程为一元一次方程，显然有实数根. 综合①②两种情况，得出m 的取值范围为54m -≥．【例3】已知关于x 的一元二次方程2(12)10k x ---=有两个不相等的实数根，求k 的取值范围．【解答】2(4(12)(1)0k ∆=--⨯-⨯->，且120k -≠，且10k +≥． 解得12k -<≤，且12k ≠．∴k 的取值范围是12k -<≤且12k ≠． 【点评】注意例2与例3的区别与联系．【例4】若关于x 的方程24x ax +=只有3个不相等的实数根，求a 的值或取值范围. 【解析】原方程可化为下面两个方程：240x ax +-=①，240x ax ++=②， 方程①21160a ∆=+>，方程②22160a ∆=-≥．因为12∆>∆， 所以只可能20∆=，即4a =±．故4a =±． 题型三 判别式用于整数根问题例5 当m 是什么整数时，关于x 的方程2440mx x -+=与2244450x mx m m -+--=的根都是整数？ 解析：由两个方程都有实数根，得514m -≤≤，∵ m 为整数，∴ m ＝－1,0,1当m ＝0时，代入第二个方程，得250,x x -== 当m ＝1时，方程2440mx x -+=为212440,2x x x x -+===其根为方程2244450x mx m m -+--=为2450x x --=，其根为125,1x x ==- 当m ＝－1时，方程2440mx x -+=为2440x x -+=其根不是整数；综上，当m ＝1时，方程2440mx x -+=与2244450x mx m m -+--=的根都是整数题型四 判别式法求极值例6 若x ，y 是实数，且224644m x xy y x y =-+--,试确定m 的最小值解析：解法一：将原等式改写为2246440x xy y x y m -+---=，即22(44)640x y x y y m -++--=，∵ x 是实数，∴ 判别式△≥0，即22(44)4(64)0y y y m +---≥，配方，得28(3)8840y m --++≥，∴ 当y ＝3时，m 有最小值－22解法二：2222224(1)(22)64(22)(22)2(3)22m x y x y y y y x y y =-++++--+=--+-- ∴ 当x －2y －2＝0且y －3＝0时，即x ＝8且y ＝3时，m 取得最小值－22针对练习11、当k ＝ 时，关于x 的二次三项式22(1)7x k x k -+++是完全平方式 解：－3或22、已知关于x 的方程21(1)(1)04k x k x ---+=有两个相等的实数根，求k 的值 解：∵ 关于x 的方程21(1)(1)04k x k x ---+=有两个相等的实数根，∴△＝0且k －1≠0∴ 221[(1)]4(1)03204k k k k ----⋅=⇒-+=，解得k ＝1(舍去)或k ＝2，∴ k ＝23、m 为何值时，关于x 的方程2(1)230m x mx m -+++= （1）有两个实根？ （2）只有一个实根？ （3）有实根？解：（1）由题意得m ≠1且△≥0，得312m m ≤≠且，∴当312m m ≤≠且时，方程有两个实数根 （2）由题意，方程为一元一次方程，此时m －1＝0, ∴当m ＝1时，方程为2x ＋4＝0，方程只有一个实数根（3）①当m ＝1时，方程2x ＋4＝0，方程有一个实数根；②当m ≠1时，由题意得23=2)4(1)(3)8120.2m m m m m ∆--+=-+≥≤（解得 ∴ 当312m m ≤≠且时，方程有两个实数根。

知识导航经典例题1当2已知关于3若关于1已知2已知知识导航经典例题1已知方程2已知关于1已知2设1已知关于2已知关于三、数学万花筒古代方程趣味题赏析我国古代历史悠久，特别是数学成就更是十分辉煌，在民间流传着许多趣味数学题，一般都是以朗朗上口的诗歌形式表达出来，以下几例供大家欣赏。

（一）周瑜的年龄大江东去浪淘尽，千古风流数人物 。

而立之年督东吴，早逝英年两位数 。

十比个位正小三，个位六倍与寿符 。

哪位学子算得快，多少年华属周瑜 ？解析：依题意得周瑜的年龄是两位数，且个位数字比十位数字大3，若设十位数字为x，则个位数字为（x+3），由“个位6倍与寿符”可列方程得：6(x+3)=10x+(x+3),解得x=3,所以周瑜的年龄为36岁 。

（二）壶中原有多少酒李白街上走 ，提壶去买酒 。

遇店加一倍 ，见花喝一斗 。

三遇店和花 ，喝光壶中酒 。

试问酒壶中 ，原有多少酒？解析：李白的壶中原有x斗酒，第一次遇到店加了x斗酒后变为2x斗酒，第一次赏花喝去1斗酒，此时还剩下（2x-1）斗酒，第二次遇到店时，壶中酒变为2（2x-1）斗酒，第二次赏花又喝去1斗酒，此时壶中还剩下【2（2x-1）-1】斗酒，第三次遇店时，壶中酒变为2【2（2x-1）-1】斗酒，第三次赏花时又喝去1斗酒，这是正好壶中的酒喝完。

因此可得到下面的方程：2【2（2x-1）-1】-1=0，解得x=7/8,所以壶中原有7/8斗酒。

（三）寺内多少僧人巍巍古寺在山林 ，不知寺内几多僧 。

三百六十四只碗 ，看看用尽不差争 。

三人共食一碗菜 ，四人共吃一碗羹 。

一元二次方程专题复习（二）根与系数的关系及其应用如果一元二次方程ax 2＋bx ＋c=0(a ≠0)的两根为x 1，x 2，那么反过来，如果x 1，x 2满足x 1+x 2=p ，x 1x 2=q ，则x 1，x 2是一元二次方程x 2-px+q=0的两个根．一元二次方程的韦达定理，揭示了根与系数的一种必然联系．利用这个关系，我们可以解决诸如已知一根求另一根、求根的代数式的值、构造方程、证明等式和不等式等问题，它是中学数学中的一个有用的工具．【典型例题】应用一：已知一个根，求另一个根；例1 ： 方程(1998x)2-1997·1999x-1=0的大根为a ，方程x 2＋1998x-1999=0的小根为b ，求a-b 的值．解 : 先求出a ，b ．由观察知，1是方程(1998x)2-1997·1999x-1=0的根，于是由韦达定理知，另一根为219981-，于是可得a=1.又从观察知，1也是方程x 2＋1998x-1999=0的根，此方程的另一根为-1999，从而b=-1999．所以a-b=1-(-1999)=2000．应用二：求根的代数式的值不解方程，利用一元二次方程根与系数的关系求两个代数式的值关键是把所给的代数式经过恒等变形，化为含，的形式，然后把，的值代入，即可求出所求代数式的值．常见的代数式变形有：① ②③ ④⑤例2： 已知二次方程x 2-3x ＋1=0的两根为α，β，求：（1）βα11+ （2）22βα+ (3)α3＋β3解： 由韦达定理知 ： α+β=3， α·β=1．（1）31311==+=+αββαβα（2）()72912322222=-=⨯-=-+=+αββαβα (3)α3＋β3=(α+β)(α2-αβ+β2)=(α+β)[(α+β)2-3αβ]=3(9-3)=18；例3： 设方程4x 2-2x -3=0的两个根是α和β，求4α2＋2β的值．解： 因为α是方程4x 2-2x -3=0的根，所以4α2-2α-3＝0，即 4α2=2α＋3．由韦达定理可知，21=+βα.所以4α2+2β=2α+3+2β=2(α+β)+3=4．例4： 已知α，β分别是方程x 2＋x -1=0的两个根，求2α5+5β3的值．解： 由于α，β分别是方程x 2＋x -1=0的根，所以α2+α-1=0，β2+β-1=0，即 α2=1-α，β2=1-β．α5=(α2)2·α=(1-α)2α=(α2-2α+1)α=(1-α-2α+1)α= -3α2+2α = -3(1-α)+2α=5α-3，β3=β2·β=(1-β)β=β-β2=β-(1-β)=2β-1．所以 2α5+5β3=2(5α-3)+5(2β-1)=10(α+β)-11=-21．说明： 此解法的关键在于利用α，β是方程的根，从而可以把它们的幂指数降次，最后都降到一次，这种方法很重要．应用三：与两根之比有关的问题；例5： 已知x 1，x 2是一元二次方程 4x 2-(3m -5)x -6m 2＝0的两实数根，且23x x 21=，求m 的值.解： 首先，△=(3m -5)2＋96m 2＞0，方程有两个实数根．由韦达定理知从上面两式中消去k ，便得即 m 2-6m+5=0， 所以m 1=1，m 2=5．应用四：求作新的二次方程例6： 求一个一元二次方程，使它的两根分别是212313， 。

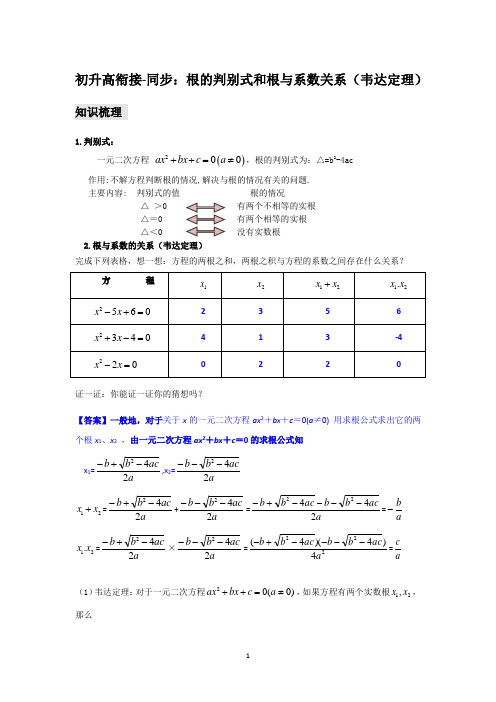
初升高衔接-同步：根的判别式和根与系数关系（韦达定理）知识梳理1.判别式：一元二次方程 ()200ax bx c a ++=≠，根的判别式为：△=b 2-4ac作用:不解方程判断根的情况,解决与根的情况有关的问题. 主要内容: 判别式的值 根的情况△ ＞有两个不相等的实根△＝有两个相等的实根△＜没有实数根 2.根与系数的关系（韦达定理）完成下列表格，想一想：方程的两根之和，两根之积与方程的系数之间存在什么关系？证一证：你能证一证你的猜想吗？【答案】一般地，对于关于x 的一元二次方程ax 2＋bx ＋c ＝0(a ≠0) 用求根公式求出它的两个根x 1、x 2 ，由一元二次方程ax 2＋bx ＋c ＝0的求根公式知x 1=a ac b b 242-+-,x 2=aac b b 242---12x x +=a ac b b 242-+-+aac b b 242---=a acb b ac b b 24422----+-=a b -12.x x =a ac b b 242-+-×aac b b 242---=2224)4)(4(a ac b b ac b b ----+-=a c（1）韦达定理：对于一元二次方程20(0)ax bx c a ++=≠，如果方程有两个实数根12,x x ，那么1212,b cx x x x a a+=-=特殊情况：当a=1时，x 2+px+q=0 ,x 1+ x 2= -p,x 1 x 2=q（2） 以x 1, x 2为根的一元二次方程（二次项系数为1）是x 2–(x 1+ x 2)x+ x 1 x 2=0①定理成立的条件0∆≥ ②注意公式重12bx x a+=-的负号与b 的符号的区别. 3. 222121212()2x x x x x x +=+-，12121211x x x x x x ++=，22121212()()4x x x x x x -=+-，12||x x -=2212121212()x x x x x x x x +=+，33312121212()3()x x x x x x x x +=+-+4. 在24b ac ∆=-≥0的条件下，我们有如下结论：⑴当0c a<时，方程的两根必一正一负．若0ba -≥，则此方程的正根不小于负根的绝对值；若0ba -<，则此方程的正根小于负根的绝对值．⑵当0c a>时，方程的两根同正或同负．若0b a ->，则此方程的两根均为正根；若0b a -<，则此方程的两根均为负根． 更一般的结论是：若1x ，2x 是20(0)ax bx c a ++=≠的两根（其中12x x ≥），且m 为实数，当0∆≥时，一般地：① 121()()0x m x m x m --<⇔>，2x m <② 12()()0x m x m -->且12()()0x m x m -+->1x m ⇔>，2x m > ③ 12()()0x m x m -->且12()()0x m x m -+-<1x m ⇔<，2x m <特殊地：当0m =时，上述就转化为20(0)ax bx c a ++=≠有两异根、两正根、两负根的条件．典例精讲20 min. 类型一：根的判别式例1.（★★★）不解方程，判断下列方程根的情况（1）231270x x -+=； （2）225154x x x x -+=-； （3）223x +=. 【分析】判断方程根的情况也就是判断∆的大小，对于第（2）（3）题都是先把原方程化为一般式，再算∆的值.【答案】（1）∵()212437600∆=--⨯⨯=>，所以原方程有两个不相等的实数根； （2）把原方程化为29610x x -+=，∵()264910∆=--⨯⨯=，所以原方程有两个相等的实数根；（3）把原方程化为2320x -+=.∵()23420∆=--⨯<，所以原方程没有实数根.【一元二次方程的根的情况是由24b ac ∆=-值的符号决定的，因此必须先将方程化成一般形式确定a 、b 、c 的值，代入24b ac ∆=-计算，根据值判断出“△”的符号，根据判别式的符号判定根的情况．】巩固练习 1．（★★★）不解方程，判断下列关于x 的方程的根的情况：（1）()2324x x +=； （2）232x +=； （3）()22410x mx m -+-=； （4）()200ax c a +=≠.【答案】(1)将方程化为一般形式：23460x x -+=，因为()2244436560b ac ∆=-=--⨯⨯=-<．所以，原方程投有实数根；(2)将方程化为一般形式：23620x -+=，因为(2244320b ac ∆=-=--⨯⨯=，所以，原方程有两个相等的实数根；(3)()()()()222242414144442b ac m m m m m ∆=-=--⨯⨯-=-+=-.因为()220m -≥，所以()2420m -≥，即△≥0，所以，原方程有两个实数根； (4)因为0a ≠．所以此方程是缺少一次项的不完全的一元二次方程． 2044ac ac ∆=-=-．需要讨论a 、c 的符号，才能确定△的符号： ①当0c =时，△=0，方程有两个相等的实数根．②当a 与c 异号时．0ac <，则40ac ->，即0∆>．方程有两个不相等的实数根， ③当a 与c 同号时．0ac >．则40ac -<．即0∆<，方程没有实数根．例2.（★★★）已知关于x 的方程()21230k x x +-+=，k 取何值时，此方程（1）有两个实数根； （2）有实数根. 【分析】①中方程“有两个实数根”，意味着方程一定是一元二次方程，并且有两个实数根，此时判别式必大于等于零.②只是说“有实数根”，没有说几个实数根，蕴含的意思是“可能有两个实数根”，“也有可能只有一个实数根”前者意味着方程是一次方程，后者意味着方程可以是二次方程，也可以是一次方程，因为二次项系数含字母，所以都是可能的，因此必须分类讨论.【答案】（1）因为方程有两个实数根，所以0∆≥且10k +≠，即()()224130,10.k k ⎧--+⨯≥⎪⎨+≠⎪⎩解得：23k ≤-且1k ≠-.当23k ≤-且1k ≠-时，方程有两个实数根. （2）①当方程是关于x 的一元一次方程时，即当10k +=，1k =-时，方程为3230,2x x -+==，有一个实根. ②当方程是关于x 的一元二次方程时，k 应当满足()()22413010k k ⎧--+⨯≥⎪⎨+≠⎪⎩解得23k ≤-且1k ≠-.综合①②所述，当23k ≤-时，关于x 的方程()21230k x x +-+=有实根. 【二次项前面系数含有字母时，要注意考虑系数是否可以为0】 巩固练习1.（★★★） 当m 为什么值时，关于x 的方程01)1(2)4(22=+++-x m x m 有实根. 【答案】当42-m ＝0即2±=m 时，)1(2+m ≠0，方程为一元一次方程，总有实根；当42-m ≠0即2±≠m 时，方程有根的条件是：△＝[]208)4(4)1(222+=--+m m m ≥0，解得m ≥25-∴当m ≥25-且2±≠m 时，方程有实根. 综上所述：当m ≥25-时，方程有实根.例3.（★★★）已知∆ABC 的三条边长为,,a b c ，且关于x 的方程()220x bx ab bc ca -++-=有两个相等的实数根，试判断∆ABC 的形状.【分析】已知方程有两个相等的根，可以得到0∆=，即()()0b a b c --=，可以得到,,a b c 的关系a b c ==，即得∆ABC 是等腰三角形.【答案】由已知得()2440b a b b c c a ∆=-+-=，即20b a b b ca c --+=，亦即()()0b a bc --=所以b a =或b c =.所以∆ABC 是等腰三角形.巩固练习1．（★★★）已知a 、b 、c 是三角形的三边, 且方程()()221210b x ax c x +-+-=有两个相等的实数根, 求证：这个三角形是直角三角形.【答案】由已知得()()()()22222440a b c b c a b c∆=--+-=-+=，即2220a b c -+=，所以222a cb +=，由三角形勾股定理可知，这个三角形是直角三角形.类型二：韦达定理例1.（★★★）若12,x x 是方程2220070x x +-=的两个根，试求下列各式的值：(1) 2212x x +； (2)1211x x +； (3) 12(5)(5)x x --；(4) 12||x x -．【答案】由题意，根据根与系数的关系得：12122,2007x x x x +=-=-(1) 2222121212()2(2)2(2007)4018x x x x x x +=+-=---=(2)121212112220072007x x x x x x +-+===- (3) 121212(5)(5)5()2520075(2)251972x x x x x x --=-++=---+=-(4) 12||x x -====例2.（★★★）已知关于x 的方程2x －（m ＋1）x ＋1－m=0的一个根为4，求另一个根。

第1章 代数式与恒等变形 1.1 四个公式知识衔接在初中，我们学习了实数与代数式，知道代数式中有整式，分式，根式，它们具有类似实数的属性，可以进行运算。

在多项式乘法运算中，我们学习了乘法公式，如：平方差公式22))((b a b a b a -=-+；完全平方公式2222)(b ab a b a +±=±，并且知道乘法公式在整式的乘除，数值计算，代数式的化简求值以及代数等式的证明等方面有着广泛的应用。

而在高中阶段的学习中，将会遇到更复杂的多项式运算为此在本章中我们将拓展乘法公式的内容。

知识延展1 多项式的平方公式：ac bc ab c b a c b a 222)(2222+++++=++2 立方和公式：3322))((b a b ab a b a +=+-+3 立方差公式：3322))((b a b ab a b a -=++-4 完全立方公式：3223333)(b ab b a a b a ±+±=±注意：（1）公式中的字母可以是数，也可以是单项式或多项式；（2）要充分认识公式自身的价值，在多项式乘积中，正确使用乘法公式能提高运算速度，减少运算中的失误；（3）对公式的认识应当从发现，总结出公式的思维过程中学习探索，概括，抽象的科学方法；（4）由于公式的范围在不断扩大，本章及初中所学的仅仅是其中最基本，最常用的几个公式。

一 计算和化简例1 计算：))(()(222b ab a b a b a +++-变式训练：化简 62222))()()((y xy y x xy y x y x y x +-+++-+二 利用乘法公式求值；例2 已知0132=+-x x ，求331x x +的值。

变式训练：已知3=++c b a 且2=++ac bc ab ，求222c b a ++的值。

三 利用乘法公式证明例3 已知0,0333=++=++c b a c b a 求证：0200920092009=++c b a变式训练：已知2222)32()(14c b a c b a ++=++，求证：3:2:1::=c b a习题精练1 化简：322)())((b a b ab a b a +-+-+2 化简 )1)(1)(1)(1)(1)(1(12622+++-+++-a a a a a a a a3 已知10=+y x 且10033=+y x ，求代数式22y x +的值；4 已知21201,19201,20201+=+=+=x c x b x a ，求代数式ac bc ab c b a ---++222的值；5 已知)(3)(2222z y x z y x ++=++，求证：z y x ==6 已知abcd d c b a 44444=+++且d c b a ,,,均为正数，求证：以d c b a ,,,为边的四边形为菱形。