高数可分离变量的微分方程教案
- 格式:doc
- 大小:94.50 KB
- 文档页数:4




《可分离变量微分方程》教学设计一、教学背景《高等数学》是我院学生的一门公共基础课,是所有铁路专业学生的必修课。
在高数教学中不仅要使学生熟悉最基本的概念,掌握最基本的运算,而且要始终与专业课程密切结合,培养学生应用数学知识解决专业问题的能力。
在教学设计中,通过专业实例先引出数学知识,接着帮助学生分析相应的数学知识,再引导学生用数学知识一步一步地解决实际问题。
这样既能提高学生的学习兴趣,又能培养学生用数学知识解决问题的能力。
二、学情分析一方面,学生通过对导数概念的学习,对导数已经有了基本了解。
另一方面,学生对数学课程兴趣的培养需要诱因,要先布置任务让学生带着任务探究学习。
应当鼓励学生自主学习、自主探究,进行小组讨论与交流,通过小组比拼等方法与师生共同归纳学习。
三、教学目标1.知识目标(1)了解可变量分离微分方程的特点;(2)掌握可变量分离微分方程的解法。
2.能力目标学会将现实生活中含变化率的问题转化为微分方程模型解决。
3.素质目标(1)培养学生清晰的逻辑思维能力;(2)培养学生解决实际问题的能力。
四、教学重、难点教学重点:可分离变量微分方程的特征及求解方法。
教学难点:将现实生活中含变化率的问题转化为微分方程模型解决。
五、教学方法根据本讲课的教学特点,在教学方法上主要使用案例引入法、启发引导法、讲练结合法和直观演示法。
六、教学过程七、教学反思(总结教学特色)本节课采用案例引入法、启发引导法、PPT演示等多种教学方法和手段,通过演示与专业相关的简单案例,引出相关数学知识,以启发引导的形式进行讨论学习,从而让学生更深刻地掌握变量分离法这种微分方程的求解方法。

可分离变量微分方程教学设计一、课程背景和教学目标1.1 课程背景微分方程作为现代数学的重要分支,在应用数学和自然科学中都有重要的地位,可分离变量微分方程是微分方程中的一种常见形式,解法简单易懂,基础知识掌握后能为学生后续学习提供很好的帮助。
1.2 教学目标1.学生掌握可分离变量微分方程的基本思想和解法;2.学生能够根据题目条件写出能够推导出解法的可分离变量微分方程;3.学生能够熟练运用可分离变量微分方程解决实际问题。
二、教学内容和方法2.1 教学内容1.可分离变量微分方程的定义和基本形式;2.可分离变量微分方程一阶和二阶的解法;3.可分离变量微分方程的应用实例。
2.2 教学方法1.前置知识讲解:向学生介绍微积分和微分方程的基本概念和定义,以及函数的连续性和可导性等概念。
2.讲解主要内容:通过导入一个实际问题,向学生介绍可分离变量微分方程的定义和基本形式,讲解可分离变量微分方程的一阶和二阶解法。
通过具体的例子引导学生掌握解法的技巧,并注重转化思想的重要性;3.贴近实际应用:介绍可分离变量微分方程的应用实例,让学生了解可分离变量微分方程在生活中的实际应用。
同时注重深化学生对方程解法的理解,引导学生在解题过程中及时发现问题和规律。
三、教学重点和难点3.1 教学重点1.可分离变量微分方程的定义、基本形式和一阶、二阶解法;2.可分离变量微分方程应用实例的讲解。
3.2 教学难点1.学生对微积分、连续性和可导性等概念掌握不牢固;2.学生对可分离变量微分方程和其解法的认知较模糊;3.学生解题能力不强。
四、教学过程设计4.1 教学步骤第一步:引入1.导入一个实际问题;2.说明问题中所涉及的关键变量和关系式,并将其转换为可分离变量微分方程。
第二步:讲解1.可分离变量微分方程的定义及基本形式;2.可分离变量微分方程的一阶解法;3.可分离变量微分方程的二阶解法。
第三步:练习1.带着学生做1-2个相关例题,让学生通过实际操作掌握不同类型可分离变量微分方程的解法技巧;2.让学生自行完成1-2个练习题,通过对自己的解法进行总结,加深理解。



创新教育177DOI:10.16660/ki.1674-098X.2007-5640-5232可分离变量微分方程教学再设计①董艳(陕西铁路工程职业技术学院 陕西西安 714000)摘 要:本文是对可分离变量微分方程的第二次教学设计,区别之处在于课堂引入中案例的设计、课堂活动的安排以及课堂评价方式的改变等方面。
本文首先以“蛟龙号”案例作为课堂引入,通过设置一系列前后衔接的问题进行新课讲解,接着在课堂练习中通过“旋转木马”和“大家一起来找茬”等课堂活动使得学生达到掌握知识的目的,最后采用多种评价方式相结合,提高了课堂教学的质量。
本节课内容通过具体实践,荣获陕西省课堂创新大赛一等奖,得到了专家的一致好评。
关键词:教学设计 课堂活动 蛟龙号 旋转木马 课堂创新中图分类号:G64 文献标识码:A 文章编号:1674-098X(2020)11(a)-0177-03Redesign of the Teaching of Separable Variable DifferentialEquationDONG Yan(Shaanxi Railway Institute, Xi'an, Shaanxi Province, 714000 China)Abstract: This paper is the author's second teaching design for the differential equation of separable variables. The difference is that the design in classroom introduction, the arrangement of classroom activities and the change of classroom evaluation method. This paper first took the case of "Jiao Long" as the classroom introduction. The new lesson was explained through a series of back-and-forth issues. Then, we made students achieve the goal of mastering knowledge through the "carousel" and "everyone together to find the dragonf ly" in the classroom practice. Finally, we improve the quality of classroom teaching by a variety of evaluation methods. The design method of this lesson won the first prize of Shaanxi Provincial Classroom Innovation Competition, and was highly praised by experts.Key Words: Teaching design; Classroom activities; Jiao Long; Merry-go-round; Classroom innovation①基金项目:陕西铁路工程职业技术学院课堂思政项目:《高等数学》课程思政教学实践与思考(项目编号:2019SZ-21)。

《可分离变量的微分方程》课堂教学设计——以智慧教室为依托摘要:通过个人设计、集体备课、课堂实践、效果反馈、案例修改等步骤,从教学目标设定、教学对象分析、教学内容选取、教学保障、教学实施等方面,以《可分离变量的微分方程》为例,着重针对学员的常见问题给出相应的对策,重点突出“学为中心、能力为本”的设计理念。
1.教学目标设定知识目标:掌握判断可分离变量微分方程的方法,会求解可分离变量微分方程的通解;能力目标:提升学员观察、分析以及解决实际问题的能力;素质目标:培养理性消费、远离网贷的良好品质,不被表面所迷惑,树立正确的世界观、人生观、价值观。
2.教学对象分析教学对象是本科一年级学员。
知识储备:前期已经学习过不定积分的相关知识,对微分方程的通解和特解有了一定的认识;认知特点:在上大学之前,学员形成了以常量数学为对象的思维定势。
对方程有直观的认识,但对于如何求解微分方程有一定的障碍;学习态度:有进一步探究知识的求知欲,但部分学员有畏难情绪,缺乏学习积极性和主动性。
3.教学内容选取内容取自同济大学第七版教材《高等数学》第七章第二节。
一阶微分方程阶数最低、形式最简单,然而此类微分方程的求解目前尚无一般的解法,即没有一个普遍适用的公式可以表示所有情况下的解析解。
本节课的教学内容为可分离变量的微分方程的定义、解法以及应用。
其中可分离变量的微分方程的定义、解法、应用为教学重点,可分离变量的微分方程的应用为教学难点。
4.教法设计以问题为导向,通过数形结合、合作探究、互动与启发引导相结合多措并举,引导学员找到微分方程的解法,同时鼓励学员运用所学知识解决实际问题,达到学以致用的目的。
5.教学保障智慧教室1间6.常见问题及解决方法具体实施中,着重介绍针对学员出现的常见错误,给出相应的解决办法。
常见问题1:学员学习积极性不高解决方法:(1)开篇以网络平台上充斥的一类借贷广告以及各种因为借网贷被骗、因网贷自杀的悲剧视频引入,思考借款是怎样像滚雪球般变大的呢?假设某人与套路贷公司签了以下合约,贷款金额为,利率为7%。

可分离变量的微分方程课程思政教学设计发布时间:2022-09-21T03:40:32.815Z 来源:《教学与研究》2022年56卷5月10期作者:唐伟明[导读] 可分离变量的微分方程是最简单也是最基础的微分方程类型之一,为后续齐次方程的学习提供解题思路,而且可分离变量的微分方程在生活实际中的应用也非常广泛,唐伟明武警警官学院四川成都 610000摘要:可分离变量的微分方程是最简单也是最基础的微分方程类型之一,为后续齐次方程的学习提供解题思路,而且可分离变量的微分方程在生活实际中的应用也非常广泛,本文主要探讨用可分离变量建立传染病数学模型来预测新冠疫情的传播规律,从而做到精准施策,科学防控。
关键词:可分离变量微分方程传染病模型一、课程导入上节课我们给出了微分方程解、通解以及特解的概念,但是并没有给出微分方程解的具体求法。
所以从这节课开始,我们一起探讨微分方程解的求法,首先从最基础的可分离变量的微分方程讲起。
大家看到的图片是我的家乡--湖北武汉,晴川历历汉阳树,芳草萋萋鹦鹉洲。
武汉,是一座充满活力与浪漫的城市。
然而,2020年初,一场突如其来的新冠疫情席卷这座城市,一时间,整个城市笼罩在一层灰暗之中,当昔日熙熙攘攘的街道变得冷冷清清的时候,我意识到:武汉,我的城市生病了。
面对疫情,当西方国家选择“躺平”的时候,我国却一直坚持人民至上,生命至上的抗疫理念,习主席在多个场合特别强调,我们一定要精准施策,科学防控。
所以,建立传染病的数学模型来描述传染病的传播过程,分析受感染人数的变化规律,预报疫情拐点的到来等等,一直是医学专家关注的问题。
首先我们假设:(1)在较短时间内,地区总人口数保持不变;(2)新冠确诊人数和健康人数比例分别为和;(3)每个新冠确诊人数每天接触人数为,且使接触的健康人致病。
根据以上假设我们可知,在时刻,每个病人每天可使个健康者变成病人,病人数为,故每天共有个健康者被感染,即:我们来看这个方程,大家先思考一下,这个方程有什么特征呢?给1分钟的时间大家思考,可以小组讨论。
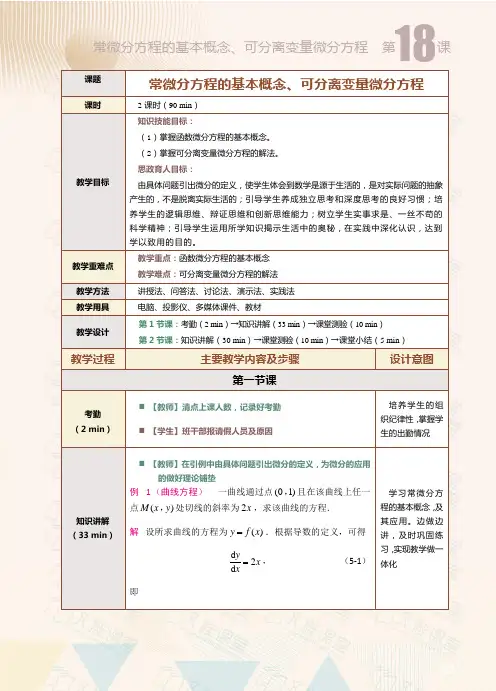
教学目的:熟练掌握可分离变量的微分方程、齐次微分方程的解法.教学重点:可分离变量方程与齐次方程的解法.教学难点:可分离变量方程与齐次方程的解法.教学内容:本节开始,我们讨论一阶微分方程(1)的一些解法.一阶微分方程有时也写成如下的对称形式:(2) 在方程(2)中,变量与对称,它既可以看作是以为自变量、为未知函数的方程,也可看作是以为自变量、为未知函数的方程,在第一节的例1中,我们遇到一阶微分方程,或把上式两端积分就得到这个方程的通解:。
但是并不是所有的一阶微分方程都能这样求解。
例如,对于一阶微分方程(3)就不能像上面那样直接两端用积分的方法求出它的通解。
原因是方程(3)的右端含有未知函数积分求不出来。
为我解决这个困难,在方程(3)的两端同时乘以,使方程(3)变为,这样,变量与已分离在等式的两端,然后两端积分得或(4)其中C是任意常数。
可以验证,函数(4)确实满足一阶微分方程(3),且含有一个任意常数,所以它是方程(3)的通解。
一般地,如果一个一阶微分方程能写成(5)的形式,就是说,能把微分方程写成一端只含的函数和,另一端只含的函数和,那么原方程就称为可分离变量的微分方程。
假定方程(5)中的函数和是连续的,设是方程的解,将它代入(5)中得到恒等式将上式两端积分,并由引进变量,得设及依次为和的原函数,于是有(6)因此,方程(5)满足关系式(6)。
反之,如果是由关系到式(6)所确定的隐函数,那么在的条件下,也是方程(5)的解。
事实上,由隐函数的求导法可知,当时,这就表示函数满足方程(5)。
所以如果已分离变量的方程(5)中和是连续的,且,那么(5)式两端积分后得到的关系式(6),就用隐式给出了方程(5)的解,(6)式就叫做微分方程(5)的隐式解。
又由于关系式(6)中含有任意常数,因此(6)式所确定的隐函数是方程(5)的通解,所以(6)式叫做微分方程(5)的隐式通解。
例1求微分方程(7)的通解。
解方程(7)是可分离变量的,分离变量后得两端积分得从而。
高职数学中可分离变量的微分方程的教学设计作者:逯清玉来源:《课程教育研究·上》2016年第06期【摘要】青海地处欧亚大陆结合部的边缘地区,是一个地震多发区,这就要求建筑物的设计要考虑它的抗震能力,其中微分方程是不可缺少的计算工具之一,本文秉着“教师为主导,学生为主体”的教育理念,设计了可分离变量微分方程的教学设计,旨在努力培养学生提出问题、分析问题、解决问题的能力。
【关键词】可分离变量微分方程通解【Abstract】Qinghai is located in the marginal areas of Eurasia juncture, known as an earthquake?鄄prone area, so that the building designer is required to consider its seismic capacity, in which the differential equation is one of the essential computation tools. This thesis has designed the teaching design for separable differential equation by adhering to the teaching philosophy of “teacher?鄄led and students?鄄centered”,in a great attempt to cultivate students’ ability in raising, analyzing and solving questions.【Keywords】differential equation of separated variables; general solution【中图分类号】G71 【文献标识码】A 【文章编号】2095-3089(2016)06-0113-01一、教学设计的基本信息二、教与学的过程设计三、板书设计四、教学反思本节课采用案例引入法、启发引导法、ppt演示、讲练结合等教学方法和教学手段,通过简单案例引出相关数学知识,一启发引导的形式讨论学习,从而让学生更深刻地掌握变量分离法这种求微分方程的方法。
§7. 2 可分离变量的微分方程观察与分析:1. 求微分方程y '=2x 的通解. 为此把方程两边积分, 得y =x 2+C .一般地, 方程y '=f (x )的通解为C dx x f y +=⎰)((此处积分后不再加任意常数). 2. 求微分方程y '=2xy 2 的通解.因为y 是未知的, 所以积分⎰dx xy 22无法进行, 方程两边直 接积分不能求出通解.为求通解可将方程变为xdx dy y 212=, 两边积分, 得 C x y +=-21, 或Cx y +-=21, 可以验证函数C x y +-=21是原方程的通解. 一般地, 如果一阶微分方程y '=ϕ(x , y )能写成g (y )dy =f (x )dx形式, 则两边积分可得一个不含未知函数的导数的方程G (y )=F (x )+C ,由方程G (y )=F (x )+C 所确定的隐函数就是原方程的通解对称形式的一阶微分方程:一阶微分方程有时也写成如下对称形式:P (x , y )dx +Q (x , y )dy =0在这种方程中, 变量x 与y 是对称的.若把x 看作自变量、y 看作未知函数, 则当Q (x ,y )≠0时, 有),(),(y x Q y x P dx dy -=. 若把y 看作自变量、x 看作未知函数, 则当P (x ,y )≠0时, 有),(),(y x P y x Q dy dx -=.可分离变量的微分方程:如果一个一阶微分方程能写成g (y )dy =f (x )dx (或写成y '=ϕ(x )ψ(y ))的形式, 就是说, 能把微分方程写成一端只含y 的函数和dy , 另一端只含x 的函数和dx , 那么原方程就称为可分离变量的微分方程.讨论: 下列方程中哪些是可分离变量的微分方程?(1) y '=2xy , 是. ⇒y -1dy =2xdx .(2)3x 2+5x -y '=0, 是. ⇒dy =(3x 2+5x )dx .(3)(x 2+y 2)dx -xydy =0, 不是.(4)y '=1+x +y 2+xy 2, 是. ⇒y '=(1+x )(1+y 2).(5)y '=10x +y , 是. ⇒10-y dy =10x dx . (6)xy y x y +='. 不是. 可分离变量的微分方程的解法:第一步 分离变量, 将方程写成g (y )dy =f (x )dx 的形式;第二步 两端积分:⎰⎰=dx x f dy y g )()(, 设积分后得G (y )=F (x )+C ;第三步 求出由G (y )=F (x )+C 所确定的隐函数y =Φ(x )或x =ψ(y )G (y )=F (x )+C , y =Φ (x )或x =ψ(y )都是方程的通解, 其中G (y )=F (x )+C 称为隐式(通)解. 例1 求微分方程xy dxdy 2=的通解. 解 此方程为可分离变量方程, 分离变量后得xdx dy y21=, 两边积分得⎰⎰=xdx dy y 21,即 ln|y |=x 2+C 1, 从而 2112x C C x e e e y ±=±=+. 因为1C e ±仍是任意常数, 把它记作C , 便得所给方程的通解2x Ce y =.例2 铀的衰变速度与当时未衰变的原子的含量M 成正比. 已知t =0时铀的含量为M 0, 求在衰变过程中铀含量M (t )随时间t 变化的规律.解 铀的衰变速度就是M (t )对时间t 的导数dtdM . 由于铀的衰变速度与其含量成正比, 故得微分方程M dtdM λ-=, 其中λ(λ>0)是常数, λ前的曲面号表示当t 增加时M 单调减少. 即0<dt dM . 由题意, 初始条件为 M |t =0=M 0.将方程分离变量得dt M dM λ-=. 两边积分, 得⎰⎰-=dt M dM )(λ, 即 ln M =-λt +ln C , 也即M =Ce -λt .由初始条件, 得M 0=Ce 0=C ,所以铀含量M (t )随时间t 变化的规律M =M 0e -λt .例3 设降落伞从跳伞塔下落后, 所受空气阻力与速度成正比, 并设降落伞离开跳伞塔时速度为零. 求降落伞下落速度与时间的函数关系.解 设降落伞下落速度为v (t ). 降落伞所受外力为F =mg -kv ( k 为比例系数). 根据牛顿第二运动定律F =ma , 得函数v (t )应满足的方程为kv mg dtdv m -=, 初始条件为v |t =0=0.方程分离变量, 得mdt kv mg dv =-, 两边积分, 得⎰⎰=-m dt kv mg dv , 1)ln(1C m t kv mg k +=--, 即 t m k Ce k mg v -+=(ke C kC 1--=), 将初始条件v |t =0=0代入通解得kmg C -=, 于是降落伞下落速度与时间的函数关系为)1(t m k e kmg v --=. 例4 求微分方程221xy y x dxdy +++=的通解. 解 方程可化为)1)(1(2y x dxdy ++=, 分离变量得 dx x dy y )1(112+=+, 两边积分得⎰⎰+=+dx x dy y )1(112, 即C x x y ++=221arctan . 于是原方程的通解为)21tan(2C x x y ++=. 师生互动设计 P304:1(1)(2)(3)(5),2(3) 作业:P304:1(4)(7)(8)(10),2(2),6。
§7. 2 可分离变量的微分方程
观察与分析:
1. 求微分方程y '=2x 的通解. 为此把方程两边积分, 得
y =x 2+C .
一般地, 方程y '=f (x )的通解为C dx x f y +=⎰)((此处积分后不再加任意常数). 2. 求微分方程y '=2xy 2 的通解.
因为y 是未知的, 所以积分⎰
dx xy 22无法进行, 方程两边直 接积分不能求出通解.
为求通解可将方程变为
xdx dy y 212
=, 两边积分, 得 C x y +=-21, 或C
x y +-=21, 可以验证函数C x y +-=21是原方程的通解. 一般地, 如果一阶微分方程y '=ϕ(x , y )能写成
g (y )dy =f (x )dx
形式, 则两边积分可得一个不含未知函数的导数的方程
G (y )=F (x )+C ,
由方程G (y )=F (x )+C 所确定的隐函数就是原方程的通解
对称形式的一阶微分方程:
一阶微分方程有时也写成如下对称形式:
P (x , y )dx +Q (x , y )dy =0
在这种方程中, 变量x 与y 是对称的.
若把x 看作自变量、y 看作未知函数, 则当Q (x ,y )≠0时, 有
)
,(),(y x Q y x P dx dy -=. 若把y 看作自变量、x 看作未知函数, 则当P (x ,y )≠0时, 有
)
,(),(y x P y x Q dy dx -=.
可分离变量的微分方程:
如果一个一阶微分方程能写成
g (y )dy =f (x )dx (或写成y '=ϕ(x )ψ(y ))
的形式, 就是说, 能把微分方程写成一端只含y 的函数和dy , 另一端只含x 的函数和dx , 那么原方程就称为可分离变量的微分方程.
讨论: 下列方程中哪些是可分离变量的微分方程?
(1) y '=2xy , 是. ⇒y -1dy =2xdx .
(2)3x 2+5x -y '=0, 是. ⇒dy =(3x 2+5x )dx .
(3)(x 2+y 2)dx -xydy =0, 不是.
(4)y '=1+x +y 2+xy 2, 是. ⇒y '=(1+x )(1+y 2).
(5)y '=10x +y , 是. ⇒10-y dy =10x dx . (6)x
y y x y +='. 不是. 可分离变量的微分方程的解法:
第一步 分离变量, 将方程写成g (y )dy =f (x )dx 的形式;
第二步 两端积分:⎰⎰=dx x f dy y g )()(, 设积分后得G (y )=F (x )+C ;
第三步 求出由G (y )=F (x )+C 所确定的隐函数y =Φ(x )或x =ψ(y )
G (y )=F (x )+C , y =Φ (x )或x =ψ(y )都是方程的通解, 其中G (y )=F (x )+C 称为隐式(通)解. 例1 求微分方程xy dx
dy 2=的通解. 解 此方程为可分离变量方程, 分离变量后得
xdx dy y
21=, 两边积分得
⎰⎰=xdx dy y 21,
即 ln|y |=x 2+C 1, 从而 2
112x C C x e e e y ±=±=+. 因为1C e ±仍是任意常数, 把它记作C , 便得所给方程的通解
2
x Ce y =.
例2 铀的衰变速度与当时未衰变的原子的含量M 成正比. 已知t =0时铀的含量为M 0, 求在衰变过程中铀含量M (t )随时间t 变化的规律.
解 铀的衰变速度就是M (t )对时间t 的导数dt
dM . 由于铀的衰变速度与其含量成正比, 故得微分方程
M dt
dM λ-=, 其中λ(λ>0)是常数, λ前的曲面号表示当t 增加时M 单调减少. 即0<dt dM . 由题意, 初始条件为 M |t =0=M 0.
将方程分离变量得
dt M dM λ-=. 两边积分, 得⎰
⎰-=dt M dM )(λ, 即 ln M =-λt +ln C , 也即M =Ce -λt .
由初始条件, 得M 0=Ce 0=C ,
所以铀含量M (t )随时间t 变化的规律M =M 0e -λt .
例3 设降落伞从跳伞塔下落后, 所受空气阻力与速度成正比, 并设降落伞离开跳伞塔时速度为零. 求降落伞下落速度与时间的函数关系.
解 设降落伞下落速度为v (t ). 降落伞所受外力为F =mg -kv ( k 为比例系数). 根据牛顿第二运动定律F =ma , 得函数v (t )应满足的方程为
kv mg dt
dv m -=, 初始条件为
v |t =0=0.
方程分离变量, 得
m
dt kv mg dv =-, 两边积分, 得⎰⎰=-m dt kv mg dv , 1
)ln(1
C m t kv mg k +=--, 即 t m k Ce k mg v -+=(k
e C kC 1--=), 将初始条件v |t =0=0代入通解得k
mg C -=, 于是降落伞下落速度与时间的函数关系为)1(t m k e k
mg v --=. 例4 求微分方程
221xy y x dx
dy +++=的通解. 解 方程可化为
)1)(1(2y x dx
dy ++=, 分离变量得 dx x dy y )1(112
+=+, 两边积分得
⎰⎰+=+dx x dy y )1(112, 即C x x y ++=221arctan . 于是原方程的通解为)2
1
tan(2C x x y ++=. 师生互动设计 P304:1(1)(2)(3)(5),2(3) 作业:P304:1(4)(7)(8)(10),2(2),6。