近世代数课件(全)--3-5_环的同态、极大理想

I是R的一个理想，则 R/I是一个域 I是最大理想。
p 是素数. Z /( p ) 定理9： 是域
2015-3-10
练习： 求Z12的全部最大理想.
2015-3-10
( : a ker (a) )
2015-3-10
例5
Z[ x] / ( x 1) Z[i]
2
（ : f ( x) f (i)
Z[ x ] ~ Z[i ]
Ker ( x 2 1)
）
定理7
子环与理想在同态满射之下不变.
2015-3-10
三、最大理想 定义3：一个环 R 的一个不等于 R 的理想 I 叫做 一个最大理想，假如， 除了 R 同 I 自己以外，没有包含 I 的理想. 例6： 求整数环的所有最大理想. 所有理想：
2015-3-10
问：同态环有无零因子传递吗？ 例1 R 为4阶循环环，即 R {0, a, 2a, 3a} ，且 a 2 a .
: n na, (n Z ) Z~R 2 2a 2a 4a 4a 0 R 有零因子， Z 无.
2015-3-10
例2
做成环. : (a, b) a, (a, b Z ) R 的零元是 (0, 0) ，而
又令 S {( a, 0) | a Z }
SZ
Z
((a, 0) a) ( R S)
R Z {(a, b) | 0 b Z }, Z R
RR
2015-3-10
二、环同态基本定理 定理 5 R ~ R / I （ :aa I ） 定义2 设 为环 R到R 的同态,称集合 Ker {a R | (a) 0} 为同态 的核. 定理6（环同态基本定理）设 为环 R到R 的同态满射,则 (1) Ker为R的理想; ( 2) R / Ker R
( d ) dZ , d 0
是素数.
(d )
是最大理想
d
2015-3-10
引理 剩余类环R/I只有平凡理想 I是最大理想. 引理2：如果一个有单位元的交换环R 只有平凡理想， 那么R一定是一个域.
引理1：假定 I≠R 是环 R 的理想，
2015-3-10
定理8：假定R是一个有单位元的交换环，
2015-3-10
x y ( 1 ( x) 1 ( 1 ( y '))
例4 设环
R {(a, b) | a, b Z },
(a1 , b1 ) (a2 , b2 ) (a1 a2 , b1 b2 ), (a1 , b1 )(a2 , b2 ) (a1a2 , b1b2 )
(1) (a b) (a) (b) (2) ( a b) ( a) ( b)
如果 既是单映射又是满映射,则称 为同构，记作 : R R ,并称 R与R 同构.
2015-3-10
定理1 若 R 与 R 是各有两个代数运算的系统， 且 : R ~ R ，则当 R 是环时，R 也是环. 定理2 若 R 与 R 是环，且 : R ~ R ，则 (2) ( a) (a) (1) (0R ) 0R n n (3) (a ) ( (a)) (4)当 R 是交换环时，R 也是交换环； (5)当 R 是有单位元环时，R 也是有 单位元环时，且 1R (1R ).
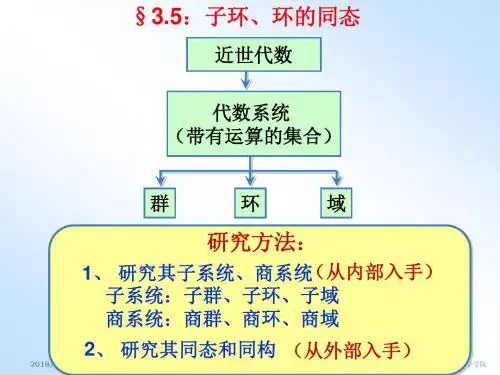
近世代数
第三章 环与域 §5 环的同态、最大理想
2015-3-10
一、环同态的定义与性质 定义1 设 R和R 是两个环, 是集合 R到R 的映射.如果对任意的 a, b R ,有 ，则称 为环 R到R 的一个同态. 如果 为满映射,则称 为满同态, 记作 : R ~ R ,并称 R与R 同态.
R {(a, b) | a, b Z }, (a1 , b1 ) (a2 , b2 ) (a1 a2 , b1 b2 ), (a1 , b1 )(a2 , b2 ) (a1a2 , b1b2 )
R~ Z
( a, 0)(0, b) (0, 0)
，故 R 有零因子, Z 无. 注：同态环有无零因子不具传递性； 同态环性质不完全传递； 但是同构环性质完全相同.
2015-3-10
定理3 若 R 与 R 是环，且 R R ，则
R 是无零因子环（整环、除环、域）
R 是无零因子环（整环、除环、域）
2015-3-10
定理4（环的挖补定理） 设 S 为环 R 的子环，且 S 与环 S 同构， 即 R S S ，又若 S ( R S ) ，即 S 与 S 在 R 里的余集无公共元素，则存在 环 R ,使 R R ， S R. 证明: 令 S {a, b, }, S {a , b , }, x x , R S {u, v, } R S ( R S ) {a, b, } {u, v, } 令 R S ( R S ) {a , b , } {u, v, } 规定 : x x , x S , y y, y R S 运算