当前位置：文档之家 › 波动学基础

波动学基础

  • 格式：doc
  • 大小：157.25 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第5章波动学基础

第5章波动学基础


量纲!
Y
T为绳索或弦线中张力;
为质量线密度
ul
* 细长的棒状媒质中纵波波速为
Y 为媒质的杨氏弹性模量; 为质量密度

G * 各向同性均匀固体媒质横波波速 u t G为媒质的切变弹性模量; 为质量密度
在同一种固体媒质中，横波波速比纵波波速小些。
震中
26
*
5.3 平面波的动力学方程 p172—177(不要求)
质量为 m 的媒质其动能为：
2
x y A cos[ (t )] u x y A sin[ (t )] u
1 x y 1 2 2 2 Wk m VA sin [ (t )] 2 2 u t 以棒内传播纵波为例讨论弹性势能：
2 2 2x y A cos( t ) T 2
0

u
X
21
0 0.2m 0.4m
2 2x y A cos( t ) T 2
0.4 10 cos(100t 5x 2) (m)
2
因为：
y ( x, t ) x v y A sin[ (t ) ] t u 2
10
惠更斯原理 1. 惠更斯原理
• 媒质中波传到的各点,都可看作开始发射子波的 子波源 (点波源)。 • 在以后的任一时刻, 这些子波面的包络面就是 实际的波在该时刻的波前 。 2. 应用 :
t时刻波面 t+t时刻波面波的传播方向
11
t 时刻波面
· · · · ·
t+t时刻波面
波传播方向
y x 1 y A 2 cos[ (t ) 0 ] 2 2 2 x u u u t 2 2 动平 y 1 y 力面 2 学波 2 2 x u t 方动

第二章 波动力学基础

第二章 波动力学基础

第二章波动力学基础§2.1波函数的统计解释按照德布罗意的观念，和每个粒子相联系的，都有一个波。

怎么理解粒子性和波动性之NJ 的联系，这是 量子力学首先碰到的一个根本问题。

能否认为波由粒子所组成?答案是否定的。

因为粒子束的单缝或双缝等实验表明，若减小入射粒子流的强度，让粒子近似地一个一个地从粒子源射出，实验发现，虽则开始时底片上的感光点是无规则的，但只要时间足够长，感光点足够多，底片上仍会出现衍射花样。

这说明，粒子的衍射现象与是否有其他粒子无关。

如果波由粒子组成，波的干涉、衍射等现象必然依赖于粒子间的相互作用。

这和上述实验结果矛盾。

实际上，单个粒子也有波动性。

那么，能否认为粒子由波所组成.比方，是否可以认为粒子就是波包?答案也是否定的。

以自由粒子为例。

对于自由粒子，由于不受外力场的作用，粒子的能量E 和动量P 均为常矢量。

按德布罗意关系(1.4.1)和(1.4. 2)式，和自由粒子相联系的波的频率。

，波矢k 均为常数及常矢量。

因此和自由粒子相联系的波是平面波。

即()()Et r p h i t r k i Ae Ae -∙-∙==ωϕ （2.1.1）其振幅A 与坐标无关。

因此它充满全空间。

若认为自由粒子由波组成，则一个自由粒子将占据整个空间，这当然是不合理的。

而且，自由粒子的德布罗意波的相速度是k 的函数，按§1.4，必然存在色散。

如果把自由粒子看成是个物质波包，即使在真空中，也会因为存在色散而使粒子自动解体。

这当然与实际情况不符。

在历史上，对波粒二象性和波函数的解释，一直是有争议的。

即使到现代，也仍然有不同观点。

而且持不同观点的人有些还是量子力学的奠基人之一。

但被物理学家们普遍接受的波函数的解释是玻恩(M. Barn)提出的统计解释。

他认为，粒子在衍射或干涉实验中所揭示的波动性质，既可以看成是大量粒子在同一个实验中的统计结果，也可以认为是单个粒子在许多次相同实验中显示的统计结果。

大学物理练习册习题及答案6--波动学基础

大学物理练习册习题及答案6--波动学基础

⼤学物理练习册习题及答案6--波动学基础习题及参考答案第五章波动学基础参考答案思考题5-1把⼀根⼗分长的绳⼦拉成⽔平，⽤⼿握其⼀端，维持拉⼒恒定，使绳端在垂直于绳⼦的⽅向上作简谐振动，则（A ）振动频率越⾼，波长越长；（B ）振动频率越低，波长越长；（C ）振动频率越⾼，波速越⼤；（D ）振动频率越低，波速越⼤。

5-2在下⾯⼏种说法中，正确的说法是（A ）波源不动时，波源的振动周期与波动的周期在数值上是不同的；（B ）波源振动的速度与波速相同；（C ）在波传播⽅向上的任⼆质点振动位相总是⽐波源的位相滞后；（D ）在波传播⽅向上的任⼀质点的振动位相总是⽐波源的位相超前 5-3⼀平⾯简谐波沿ox 正⽅向传播，波动⽅程为010cos 2242t x y ππ??=-+ ?. (SI)该波在t =0.5s 时刻的波形图是（）5-4图⽰为⼀沿x 轴正向传播的平⾯简谐波在t =0时刻的波形，若振动以余弦函数表⽰，且此题各点振动初相取-π到π之间的值，则（）（A ）1点的初位相为φ1=0(m)(A )(m)(m)(B )(C )(D )思考题5-3图思考题5-4图（B ）0点的初位相为φ0=-π/2 （C ）2点的初位相为φ2=0 （D ）3点的初位相为φ3=05-5⼀平⾯简谐波沿x 轴负⽅向传播。

已知x=b 处质点的振动⽅程为[]0cos y A t ωφ=+，波速为u ，则振动⽅程为（）(A)()0cos y A t b x ωφ??=+++??(B)(){}0cos y A t b x ωφ??=-++??(C)(){}0cos y A t x b ωφ??=+-+?? (D)(){}0cos y A t b x u ωφ??=+-+?? 5-6⼀平⾯简谐波，波速u =5m?s -1，t =3s 时刻的波形曲线如图所⽰，则0x =处的振动⽅程为（）（A ）211210cos 22y t ππ-??=?- (SI) （B ）()2210cos y t ππ-=?+ (SI) （C ）211210cos 22y t ππ-??=?+ (SI) （D ）23210cos 2y t ππ-?=-(SI) 5-7⼀平⾯简谐波沿x 轴正⽅向传播，t =0的波形曲线如图所⽰，则P 处质点的振动在t =0时刻的旋转⽮量图是（）5-8当⼀平⾯简谐机械波在弹性媒质中传播时，下述各结论⼀哪个是正确的？（A ）媒质质元的振动动能增⼤时，其弹性势能减少，总机械能守恒；（B ）媒质质元的振动动能和弹性势能都作周期变化，但两者的位相不相同；（C ）媒质质元的振动动能和弹性势能的位相在任⼀时刻都相同，但两者的数值不相等；（D ）媒质质元在其平衡位置处弹性势能最⼤。

第十二章 波动学基础

第十二章 波动学基础

形式的形变叫切应变。
S
切应力(tangenntial stress)： F
切应变： Δd
S
D
在弹性限度内，切变的应力和应变成正
F
Δd
F
比。
F G Δd SD
S
D
G 称作切变模量。由材料的性质决定。
F
2021/9/26
3. 体应变
一块物质周围受到的压强改变时，
其体积也会发生改变，称体应变。
p
V
体应变： ΔV V
x
Sdx Sdx v
x
t
Y 2y 2y
x 2
t 2
d
2y 1 2y
x2 Y t 2
2 y 1 2 y
x2 Y t 2
y A cos[ ( t x ) ]
u
表示棒中各点振动的位移满足的 微分方程， 称为细棒中平面波 的波动方程(wave equation)。 是动力学方程。
在弹性限度内，外力和形变具有简单的关系，由于外力 施加的方式不同，形变可以有以下几种基本方式：线应变、 切应变和体应变。
2021/9/26
1. 线应变(strain)
F
l
l
S
F
一段固体棒，当在其两端沿轴的方向加以方向相反大小 相等的外力时，其长度会发生改变，伸长或压缩视二者方 向而定。这种形式的形变叫线应变。
二、波函数的物理意义
表示x0处质元的振动表达式。
平面简谐波的波函数
y(x,t)
A
c o s
t
x u
+、 －分别表示波沿负、 正方向传播。
(2) 当 t = t 0 (常数) 时，
y(x)
A

chapter3波动学基础 (2)

chapter3波动学基础 (2)


光纤传输系统 EDFA
孤子源
调制
探测
隔离器 脉冲源 EDFA EDFA EDFA
光孤子通信系统构成方框图
光孤子源产生一系列脉冲宽度很窄的光脉冲，即光孤子流，
作为信息的载体进入光调制器，使信息对光孤子流进行调制。 被调制的光孤子流经掺铒光纤放大器和光隔离器后，进入光 纤进行传输。 为克服光纤损耗引起的光孤子减弱，在光纤线路上周期地插
光孤子的形成

在讨论光纤传输理论时，假设了光纤折射率n 和入射光强(光功率)无关，始终保持不变。 这种假设在低功率条件下是正确的，获得了 与实验良好一致的结果。 然而，在高功率条件下，折射率n随光强而变 化，这种特性称为非线性效应。


在强光作用下，光纤折射率n可以表示为 2 n n0 |E| n2
环光纤间接实验系统 (参看图7.37(b))，传输速率为2.4Gb/s，传
输距离达12000km；改进实验系统，传输速率为 10Gb/s，传输 距离达106km。
事实上，对于单信道光纤通信系统来说，光孤子通信系统的
性能并不比在零色散波长工作的常规(非光孤子)系统更好。 然而，零色散波长系统只能实现单信道传输，而光孤子系统 则可用于 WDM 系统，使传输速率大幅度增加，因而具有广 阔的应用前景。
包层包层输入光谱光强光发射输出光脉冲光强光输出光接收1213141516pskmnm30201010203011材料色散自由空间波长色度色散波导色散4210051005所有光源都是在一定波长范围内发射的非单色光当各种波长的光进入纤芯后由于波长与折射率有关所以在光纤波导中的光以不同的群速度在纤芯内传输波长短的波速度慢波长长的波速度快所以它们到达光纤末端的时间也不同导致输出脉冲展宽

波动学基础练习及答案

波动学基础练习及答案
（A）波长为 5 m ； （B）波速为10 m ⋅ s−1 ；
（C）周期为 1 秒； （D）波沿 x 正方向传播。 3
（C ）
根据公式ω =6 π ，T = 2π / ω =1/3 秒。其它均不正确， λ = 100 / 3, u = 100 （忽略单位），传
播方向为-x。
3．下列叙述中不正确的是
（A）在波的传播方向上，相位差为 2π 的两个质元间的距离称波长；
t (s)
-A
d
O
Px
计算题 1 图
5
解：（1）
yP
=
A cos( 1 2
πt
+
π)
；
（2）
y
=
Acos[2π( t 4
+
x
− λ
d
)
+
π] ；（3）
y0
=
Acos(
1 2
πt) 。
解：（1）由振动曲线可知，P 处质点振动方程为
yP
=
Acos[( 2π t) 4
+
π] =
A cos( 1 2
πt
+
（D ） 由传播方向可知，时间项为正的 x/u；
设表达式为 y = A cos[ω(t + x / u) + φ] ，依图可知，x=0 处在 t=T/4 时相位为 − π ，代入后相 2
位公式得： φ =- π ，等价于 π 。
5．在同一介质中两列相干的平面简谐波的强度之比是 I1 I 2 = 4 ，则两列波的振幅之比是
2
2
O
（C） π 与 − π ； （D） − π 与 π 。
22
22
u

第7章 波动学基础

第7章 波动学基础

（痛阈）
强到失去听 觉只有痛觉
听觉 强度范围甚宽，实用上需要以更方便的单位来表示。
声强级
人对声强的主观感觉即响度,用声强级数表示。 单位:分贝 (dB)
贝(B)
10
分贝(dB)
常用分贝(dB)为单位 1贝(B) =10分贝(dB), 好比 1米(m) =10分米(dm) 。
闻阈 正常呼吸 悄悄话 室内正常谈话 大声喊叫 重型卡车 电动切草机 摇滚乐 痛阈 伤害人体
平面波（波面为平面的波）
波线（波射线） 球面波（波面为球面的波）
波的传播方向。在各向同性媒质中， 波线恒与波面垂直。
正向波 反向波
正向波 反向波
若给定某点 P 的
，波函数变为 P 点处质点的
P点的
距原点为
处质点振动的初相
若给定 ，波动方程表示所给定的 时刻波线上各振动质 点相对各自平衡点的位置分布，即该时刻的
观察者测得的频率
观察者每秒接收到的整波数，即观察者测得的频率为
观察者测得的频率是波源的振动频率的
如果波源静止观察者背离波源运动，观察者测得的频率为
倍。
3. 观察者静止，波源（相对于媒质）向观察者运动。
先看一个普通现象
一列等间距的小石子，等时先后落入水中，
（点击鼠标） 它们所激起的水波的 波阵面分布是一系列偏心圆。
来自同一波源的入射波传播到带有小孔的屏时，通过小孔时，在 小孔的另一侧都产生以小孔作为点波源的前进波，可将其抽象为从 小孔处发出的一种次波或子波，其频率与入射波频率相同,在叠加区 域有相同的振动方向,且相位差恒定,它们是相干波.可以产生干涉.
A
当
A1
2
A2
2
2 A1 A2 cos (j20 当

波动学基础

波动学基础

上一页
下一页
返回
9. 1机械波的产生和传播
波动的传播既然与介质的弹性有密切的关系，因而波速必然与介 质的弹性模量有关。另外，波速也应该与介质的密度有关，因为密度 是描述介质惯性的物理量，它反映介质中任一部分在力的作用下，运 动改变的难易程度。理论证明横波和纵波在固态介质中的波速u可分 别用下列两式计算
下一页
返回
9. 1机械波的产生和传播
9.1.2横波与纵波
波在传播时，质元的振动方向和波的传播方向不一定相同。如 果质元的振动方向和波的传播方向相互垂直，这种波称为横波，如绳 中传播的波。其外形特征是具有凸起的波峰和凹下的波谷。如果质元 的振动方向和波的传播方向一致，这种波称为纵波，如空气中传播的 声波。纵波的外形特征是具有“稀疏”和“稠密”的区域。横波和纵 波是自然界中存在着的两种最简单的波，其他如水面波、地震波等， 情况就比较复杂。 如图9一1所示，绳的一端固定，另一端握在手中并不停地上下 抖动，使手拉的一端作垂直于绳索的振动，我们可以看到一个接一个 的波形沿着绳索向固定端传播形成绳索上的横波。
第9章波动学基础
9. 1机械波的产生和传播 9. 2平面简谐波 9. 3波的能量 9. 4波的干涉
9. 1机械波的产生和传播
9.1.1机械波的形成
机械振动系统(如音叉)在介质中振动时可以影响周围的介质，使 它们也陆续地发生振动。这就是说，机械振动系统能够把振动向周围 介质传播出去，形成机械波。 机械波的产生，首先，要有作机械振动的物体，它称为机械波 的波源;其次，要有能够传播这种机械振动的介质。例如，音叉在振 动时，音叉就是波源，而空气就是传播声波的介质。 应当注意，波所传播的只是振动状态，而介质中的各质元仅在 它们各自的平衡位置附近振动，并没有随波前进。例如，在漂浮着树 叶的静水里，当投入石子而引起水波时，树叶只在原位置附近上下振 动，并不移动到别处去。振动状态的传播速度称为波速。它与质元的 振动速度是不同的，不要把两者混淆起来。

大学物理_波动学基础

大学物理_波动学基础
绳的微振动横波
a T a Y

T：绳的张力
杆的纵向微振动波
杆的横向微振动波 声音在空气中传播 真空中的电磁波
Y：杨氏弹性模量
a G

G：切变弹性摸量 B：体变模量
a
B
a
0 0 ０真空介电常数，０真空磁导率
1
《大学物理》课件
介质的几种典型模量
(1).杨氏模量 若在截面为S，长为l的细棒两端加上大小相等、方向相反 的轴向拉力F，使棒伸长l，实验证明：在弹性限度内，正应 力F/S与线性应变l/l成正比，即
y Acos( t
l
u
)
《大学物理》课件
例题2-4 波沿x轴正向传播，A=10cm, =7rad/s; 当t=1s时, ya=0, a<0, yb=5cm,b>0 。设>10cm, 求该波 的波动方程。 y x ) o ] (t 解 y Acos[ u u
o
3.波长 — 一个周期内波动传播的距离。
u

T

4.平面简谐波—波面为平面，媒质中各质点 都作同频率的简谐振动形成的波动。本章主要讨 论这种波。
《大学物理》课件
1 1 例题2-1 已知： y 0.5cos ( t x )(SI), 2 2 求：(1)波的传播方向，A、T、、u，原点 的初相； (2) x=2m处质点的振动方程，及t=1s时质点 的速度和加速度。 (3)x1=1m和x2=2m两点的相差。
· ·· · · · · t · · · ·· · ·
u t 平面波
球面波
惠更斯原理的不足：不能求出波的强度分布； 不能解释后退波问题等。
《大学物理》课件
§5.2 平面简谐行波的波动方程 !

大学物理参考答案(白少民)第10章 波动学基础

大学物理参考答案(白少民)第10章 波动学基础
450。已知波速为 15cm/s，试求波的频率和波长。 解：波长可看成是沿波射线相位差 2π 的两点间的距离，则由题知其波长为
3.5 u 15 = 28 cm ， 进而可求得波的频率为 ν = = = 0.54 Hz π /4 λ 28 10.14 证 明 y = A cos( kx −ω t ) 可 写 成 下 列 形 式 ： y = A cos k ( x − u t ) ， x x 1 x y = A cos 2π ( − ν t ) ， y = A cos 2π ( − ) ，以及 y = A cos ω( − t ) 。 λ T u λ ω 2πν t ) = k ( x − ut ) 证明 ： kx − ω t = k ( x − t ) = k ( x − k 2π / λ 所以波函数可写为： y = A cos k ( x − ut ) 2π x x x − 2πν t = 2π ( −νt ) ，则波函数还可写为 y = A cos 2π ( −ν t ) 又 kx − ω t = λ λ λ 1 x t 由ν = 则还可得： y = A cos 2π ( − ) T λ T k x x kx − ω t = ω( x − t ) = ω( − t ) ，则波函数还可写为 y = A cos ω( − t ) ω u u 10.15 波源 做 简谐振动，位移与时间的关系为 y = ( 4.00 ×10 −3 ) cos 240π t m ，它所 激发的波以 30.0m/s 的速率沿一直线传播。求波的周期和波长，并写出波函数。 解：由波源的振动方程 y = ( 4.00 ×10 −3 ) cos 240πt m 知振动角频率 ω = 240π . 而波的频率就等于波源的振动频率，所以波的频率和周期分别为 ω 1 1 ν= = 120 Hz ， T = = = 8.33 ×10 −3 s ν 120 2π u 30.0 = 0.25 m 进一步计算波长为 λ = = ν 120 x x −3 )m 最后可写出波函数为 y = A cos ω(t − ) = ( 4.00 ×10 ) cos 240π (t − u 30 10.16 沿 绳子 行进的 横 波波函数为 y =10 cos(0.01π x − 2π t ) ，式中长度的 单 位是 cm，时间的单位是 s。试求：（1）波的振幅、 频率、传播速率和波长；（2）绳上某质点的最 大横向振动速率。 解：（1）由 y = 10 cos(0.01π x − 2π t ) = 10 cos 2π (t − 5.0 ×10 −3 x ) 知： ω 2π ν= = = 1 Hz ； 波 长 振 幅 A = 10cm = 0.1m ； 频 率 2π 2π

波动学基础.ppt

波动学基础.ppt

（1）体现波动在时间上和空间上都具有周期性
（2）用 x = x1（定值）代入，得 x1 点的振动表达式
y(x1, t)
Acos( 2
T
t
2
x1 )
y(x2 , t)
Acos( 2
T
t
2
x2 )
在波的传播方向上，各质点的振动相位依次
落后。两定点 x1 和 x2 振动的相位差为
x1
x2
T
波的周期和频率就是介质中各质点的 振动周期和频率，等于波源的振动周期和 频率。 周期和频率反映了波动在时间上的周期性
频率与传播介质有没有关系？
波速 u —— 振动相位的传播速度
u
T
波速和波长由介质的性质决定，而波的 频率与介质的性质无关，由波源决定。
二、 平面简谐波的波函数
平面简谐波 —— 波阵面为平面的简谐波
y(x,t) Acos(t 2 x ) 2
(2). t=0时波形曲线方程为:
y A cos( 2 x ) A sin 2 x
2
t=T时的波形与上式给出的应该相同
y
TC T+T/4
u
B
oA
D E F
I H
x
G
附(1): A, B, C, D, E, F, G, H, I在t=T时刻的运动方向? 根据波前进方向, 看t+dt时波形图则清楚!
x) u
A cos
(t
x u
)
沿 x 轴正方向传播的平面简谐波的波函数
y(x,t) Acos (t x )
u
y(x,t) Acos 2 (t x ) Acos 2 ( t x )
Tu

大学物理波动学基础

大学物理波动学基础

单位时间内振动状态(振动相位)的传 播速度，又称相速。
振动状态完全相同的相邻两质点 间的距离。 位相差为 2 ，一个完整波形长度
u

T
f
2、周期 T： 波传播一个波长所需要的时间 该时间内波源正好完成一次全振动，⑵ 波速由弹性介质性质决定，频率 波动周期＝振动周期 (或周期)则由波源的振动特性决定。 T由波源决定，与介质无关。 §12-2 平面简谐波的波函数 或 f 3、频率 ： ——定量地描述前进中的波动（行波） 单位时间内传播完整波的个数 一、波函数的建立 （等于波源的振动频率）
P.6/91
波动学基础
P点的振动表达式：
（3）若波源在 x＝x0处，则
x yP A cos t 0 u
即t=x/u时，P点的振动状态与O点 t=0时的状态相同。 x P点的相位落后O点
x x0 y A cos t u
② “±”反应波传播方向： “－”：波向右传波（x 轴正方向） ③ x0为波源坐标。
2016/7/2
t x x0 y A cos 2π 0 “＋”：波向左传波（x 轴负方向） T
P.8/91
波动学基础
二、波函数的物理意义
讨论： 由波动→振动：
x x0 t t t u
'
x y A cos t 0 u 平面简谐波波函数（波源在原点）：
② “±”反应波传播方向： “－”：波向右传波（x 轴正方向）
“＋”：波向左传波（x 轴负方向）
x y A cos t 0 u
机械波：机械振动在弹性介质中的 传播过程 电磁波：交变电磁场在空间的传播 过程 物质波：微观粒子的运动，其本身 具有的波粒二象性

第10章 波动学基础

第10章 波动学基础

P
x
x
x y P A cos[ (t ) ] u 2 y ( x, t ) A cos(t x ) ④

t时刻位于x处P质元 的振动方程为： 这就是沿 x 轴负方向 传播的平面简谐波的 波动方程(波函数).
小结
若原点O 振动方程为： y(0, t ) A cos(t ) 沿x轴正向传播的平面简谐波波函数标准形式
波形移动速度为u, t时间移动距离 x
u t
波线上各点的简谐振动图
例1 一平面简谐波波函数为 y 0.05cos(10 π t 4 π x) m 试求:(1)波的振幅、频率、波速和波长；(2) x1 0.2m 处质 元在 t1 1.0s 时的运动状态；(3)此振动状态在 t2 1.5s 时传 到波线上哪一点？ 解 1）把波函数化为标准式
点P
t-x/u 时刻点O 的运动 P点的振动方程

t 时刻点 P 的运动
x x yP ( t ) y ( t t ) A cos ( t ) O A cos y ( x, t ) [ ( t u) ]
u
波函数的推导
1.以速度u沿x轴正向 传播的平面简谐波
例2
例1中波沿x负向传播：
ys (t ) A cos( t
求波动方程

u x
P
3
ห้องสมุดไป่ตู้) Ｏ
x0 x
x0 4
Ｓ Ｘ
解：S点状态传播到x处的P点所需时间：
x ( ) tsp u u 4u u x yP (t ) ys (t t ) A cos[ (t ) )] u 4u 3

12波动学基础

12波动学基础

三、驻波方程：
适当选择计时起点和原点，使两振源
1 2 0
分析：1、
为坐标x质点的振
幅，参与波动的每个点振幅恒定; 不同的 点振幅不同。
驻波中各点的相位：两 相邻波节之间的各点振 动相位相同，在一个波 节的两侧(相邻两段)的 各振动点反相位。
波腹： 位移为2A处坐标 波腹间距 波节：位移为0处坐标 波节间距
(1) 此波的波函数
y Acos(t ) 0.02cos(10t )
4
波函数 y(x,t) 0.02cos(10t 2 x ) 4
0.02cos(10t 2 x )
0.07 4
(2) 与原点相距为x1= 3.5×10-2m处质 点的振动表达式及其初相
(2)
y(x,t) 0.02cos(10t 2 0.35 )
如果波沿正方向传播，速度为u， 那么B点处质点振动比O点振动落后x/u 时间，因此可得B点的振动表达式。
B为任意点，所以上式即为波函数。
波动表达式
y
Acost
x u
讨论:
(1)如果波沿x轴的负方向传播，则B点的相位要比O点的相位超 前t=x/u
(2)如果波源振动的初相位为φ (3)若波源在 x＝x0处，则
例12-1: 一平面简谐波在介质中以速度 u = 20 m/s，沿Ｏx轴的负
向传播。已知A点的振动方程为y = 3cos 4t ，(1) 以A点为坐标原 点求波函数；(2) 以距A点5m处的B为坐标原点求波函数。
解： A点为坐标原点，u = 20 m/s，
B点的振动方程为
y
y
u
B B点为原点，波函数为
(2)
是相邻的两个因干涉而静止的点。 求波长和两波源间最小相位差。 (2)-(1)

高一物理章节内容课件 第五章波动学基础

高一物理章节内容课件 第五章波动学基础

线。
四、质点运动速度方向的判断 沿波的传播速度方向看： 波峰 波谷 质点运动速度 波谷 波峰 质点运动速度
本次课重点 1．机械波的产生和传播； 2. 波函数的推导方法、表达式及其物理 意义 3. 质点运动速度方向的判断
例二（3071）一平面简谐波以速度 沿X轴
正向传播，在
时波形曲线如图所
示。求坐标原点 的振动方程
二、机械波的产生和传播
结论：振动是产生波动的原因 波动是某一质点的振动状态由近而远 的传播过程
是质点1的位移值、速度值、加速度值逐渐传 到了质点2、再传到质点3、经过四分之一周 期传到了质点4、经过二分之一周期传到了质 点7这样一个所谓振动状态由近而远的传播过 程。这样，随着时间的推移，作为绳子上的 每一个质点它都会在各自的平衡位置上下来 回往复地运动起来，在同一个时刻，不同的 质点一般会有不同的位移。那么，在任意时 刻 ，平衡位置坐标为 的质点的位移 与所处的时刻、与平衡位置的坐标究竟存在 什么样的相互关系呢？这是波动学中，我们
无半波损失。 设入射波方程（波函数）
波密，反射波
此波在
处引起的振动方程
该振动即为反射波源
无半波损失时 有半波损失时 所以，本题反射波的波动方程为
与已知条件相比，可得
驻波方程
波节位置
例二（ 3311 ）在弦线上有一简谐波，其表达 式为
为了在此弦线上形成驻波，并且在 处为一波腹，此弦线上还应有一简谐 波，其表达式为 （A）
第五章 波动学基础
复习与自学安排（所有均为考试内容） 5月27日至6月2日 2.1 行波 2.2 简谐波 2. 3 物体的弹性形变 2. 4 波动方程与波速 2. 5 波的能量 2. 6 惠更斯原理与波的反射和折射 2. 7 波的叠加 驻波 2. 8 声波

波动学基础-1

波动学基础-1
机械波的传播速度与媒质有关，而与波的频率无关。
2)波长
沿波的传播方向，两个相邻的、相位差为 2π 的振动质点
之间的距离，即一个完整波形的长度。对于横波，波长就 是相邻两个波峰或波谷的距离，对于纵波就是相邻两个疏 部或密部的距离。
Ay
u
O
x
-A
3) 周期T 波传播一个波长的距离所需要的时间.
u
sin i u1 1 n 21 sin r u2 2
u1/u2为第二种介质相对第一种介质的折射率。
惠更斯原理不足之处（未涉及振幅，相位等 的分布规律）。
7.2 平面简谐波的波函数
平面简谐波：若在平面波的传播过程中，振源作简谐振动， 而且波所经历的所有质元都做简谐振动，则此平面波称为平 面简谐波。
.
u
8m 5m 9m
C
B oA
Dx
1）以 A 为坐标原点，写出波动方程
A 310-2 m T 0.5s 0 uT 10m
y Acos[2π ( t - x ) ] T
y 310-2 cos2π( t - x ) 0.5 10
2）以 B 为坐标原点，写出波动方程 yA 310 -2 cos 4 π t
这是一个二阶偏微分方程。对于任一平面波，可以认为是 许多不同频率的平面简谐波的合成，也可得到此结果。它 反映了平面波的共同特征，所以称为平面波的波动方程。
举例
1.已知波函数求各物理量 2.已知各物理量求波函数
例1 已知波动方程如下，求波长、周期和波速.
y 5cosπ[2.50t - 0.01x].
➢ 波动表达式的其它形式
y(x,t) Acos[2 π( t x ) ]
Tλ
y(x,t) Acos[2 (t x ) ]

波动学基本

波动学基本

ππ
π
y1
=
A cos(200π
t
−16 ×
2
−
2
)
=
A cos( 200π
t
−
) 2
同理,
y2
=
A cos( 200π
t
−
20 ×
π 2
−
π 2
)
=
A cos(200π
t
−
π) 2
4
自治区精品课程—大学物理学
黄新民、张晋鲁主编《普通物理学》习题解答
初相位分别为：t=0
时， φ1 0
=
−π 2
,φ20
2π
f
(2)
∵平面简谐波的波动方程为： y
=
Acos ω(t −
x )
c
∴绳子上各质点的振动速度为: ν = ∂y = − Aω sin ω(t − x)
∂t
c
绳子上各质点的振动加速度为: a = ∂ 2 y = − Aω 2 cosω(t − x )
∂t 2
c
∴绳子上各质点振动时的最大速度为 vmax = Aω =0.5π=1.57(m/s)
当取波源为原点并且该波沿+X 方向传播时，波动方程为
y
=
0.1cos(4π
t
π −
x)
5
(2) 沿波传播方向距离波源为λ/2 处的振动方程为：
y = 0.1cos(4π t − π ⋅ λ ) = −0.1cos(4π t) 52
(3) 距离波源分别为 λ , λ , 3λ 和λ的各点的振动方程为： 42 4
B
2π
CC
∵ c = λf ，∴ λ = CT = B ⋅ 2π = 2π ． CB C
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

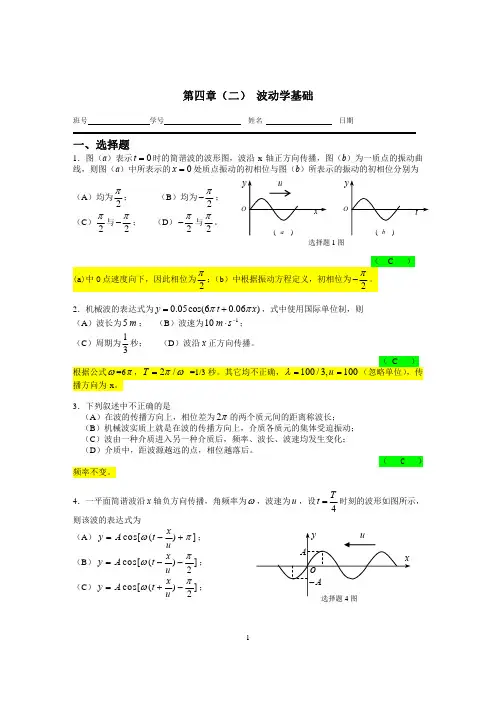
（二） 波动学基础
班号 学号 姓名 日期_________________
一、选择题
1．频率为500Hz 的机械波，波速为1
s m 360-⋅，则同一波线上相位差为3π的两点相距为 （A ）0.24m ； （B ）0.48m ； （C ）0.36m ； （D ）0.12m 。

（ ）
2．下列叙述中不正确的是
（A ）在波的传播方向上，相位差为π2的两个质元间的距离称波长；
（B ）机械波实质上就是在波的传播方向上，介质各质元的集体受迫振动； （C ）波由一种介质进入另一种介质后，频率、波长、波速均发生变化； （D ）介质中，距波源越远的点，相位越落后。

（ ）
3．已知s 5.0=t 时余弦的波形如图所示，波速大小1s m 10-⋅=u ，若此时P 点处介质元的振动动能在
逐渐增大，则波动表达式为
（A ）()[]10cos 10x t y +=πcm ；
（B ）()[]ππ++=10cos 10x t y cm ； （C ）()[]10cos 10x t y -=πcm ；
（D ）()[]ππ+-=10cos 10x t y cm 。

（ ）
4．在同一介质中两列相干的平面简谐波的强度之比是421=I I ，则两列波的振幅之比是
（A ）421=A A ； （B ）221=A A ；
（C ）1621=A A ； （D ）4121=A A 。

（ ）
5．当一平面简谐波在弹性介质中传播时，下列各结论哪一个是正确的？ （A ）介质质元的振动动能增大时，其弹性势能减小，总机械能守恒；
（B ）介质质元的振动动能和弹性势能都作周期性变化，但两者的相位不相同；
（C ）介质质元的振动动能和弹性势能的相位在任一时刻都相同，但两者的数值不相等； （D ）介质质元在其平衡位置处弹性势能最大。

（ ） 6．在弦线上有一平面简谐波，其表达式为()[]3420100cos 100.22
1ππ-+⨯=-x t y （SI ）
，为了在此弦线上形成驻波，并且在0=x 处为一波腹，此弦线上还应有一平面简谐波，其表达
式为
（A ）⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛
-⨯=-320100cos 10
0.22
2ππx t y （SI ）
； （B ）⎥⎦
⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯=-3420100cos 100.22
2ππx t y （SI ）
； （C ）⎥⎦⎤⎢⎣
⎡-⎪⎭⎫ ⎝⎛-⨯=-320100cos 100.22
2ππx t y （SI ）
；
（D ）⎥⎦
⎤
⎢⎣⎡-⎪⎭⎫ ⎝
⎛
-
⨯=-3420100cos 100.222ππx t y （SI ）。

（ ）
二、填空题
1．A 、B 是简谐波波线上的两点。

已知，B 点的相位比A 点落后π，A 、B 两点相距0.5m ，波的频率为100Hz ，则该波的波长=λ_____________m ，波速=u ____________1
s m -⋅。

2．一列平面简谐波沿Ox 轴正向无衰减地传播，波的振幅为3
102-⨯m ，周期为0.01s ，波速为
1s m 400-⋅。

当0=t 时Ox 轴原点处的质元正通过平衡位置向y 轴的正方向运动，则该简谐波
的波动表达式为__________________________。

3．已知某平面简谐波的波源的振动表达式为t y π2
1sin
06.0=（SI ），波速为1s m 2-⋅，则离波源5m 处质点的振动表达式为__________________________。

4．机械波从一种介质进入另一种介质，波长λ，频率ν，周期T 和波速u 诸物理量中发生改变的为_____________，_____________，保持不变的为_____________，_____________。

5．一平面简谐波在两个不同时刻的波形如图所示，且已知周期s 1≥T ，则由波形图可求得：波的振幅A ＝_____________，波长λ＝_____________，波速u ＝_____________，周期T ＝____________，频率ν＝_____________，波动表达式y ＝__________________________。

6．如图所示，1S ，2S 为相干波源，相距1/4波长，1S 的相位较2S 超前2π。

设强度均为0I 的两波源分别发出两列波，沿1S 2S 连线上传播，
强度保持不变。

则2S 外侧各点合成波的强度为__________；1S 外侧各点合成波的强度为__________。

7．正在报警的警钟，每隔0.5s 钟响一声，一声接一声地响着。

有一个人在以1
h km 60-⋅的速度向警钟所在地接近的火车中，则这个人在5分钟内听到_____________响。

空气中的声速为
1s m 340-⋅。

三、计算题
1．如图，一平面简谐波在介质中以速度1
s m 20-⋅=u 沿Ox 轴负方向传播，已知A 点的振动表达式为 t y π4cos 3=(SI )，试求:
（1）以A 点为坐标原点写出波动表达式； （2）以距A 点5m 处的B 点为坐标原点，写出波动表达式。

2．如图所示,一平面简谐波在0=t 时刻的波形图，设此简谐波的频率为250Hz ，且此时质点P 的运动方向向下，求
（1）该波的波动表达式；
（2）在距原点为100m 处质点的振动表达式与振动速度表达式。

3 ．一弦线的驻波的波函数为t x y 750
cos 16.0cos 2=，式中长度以厘米为单位，时间以秒为单位。

试问：
（1
）组成此驻波的两列波的振幅及波速各为多少？ （2）相邻两波节间的距离为多大？
（3）3
102-⨯=t s 时刻、位于cm 0.5=x 处的质点的振动速度为多大？
u 计算题1图。