(完整版)八年级上专题讲义： 旋转模型与方法

中考数学共顶点旋转模型一、题源分析(人教版八年级上册第55页)如图, ,求证(人教版九年级上册第63页)如图,都就是等边三角形,BＥ与DC有什么关系?您能用旋转得性质说明上述关系成立得理由吗?二、共顶点旋转模型简要概述共顶点模型，就是指两个等腰或者等边三角形得顶点重合,两个三角形得两条腰分别构成得两个三角形全等或者相似。

例如上题中得三角形ADC与三角形AＢE。

寻找共顶点旋转模型得步骤如下: (1）寻找公共得顶点(２)列出两组相等得边或者对应成比例得边(３)将两组相等得边分别分散到两个三角形中去,证明全等或相似即可。

典例分析１:（20１4年河南)（1）问题发现如图1,△ACB与△DＣＥ均为等边三角形,点A、Ｄ、E在同一直线上,连接BE填空:(1）∠ＡEＢ得度数为;(2)线段AD、BＥ之间得数量关系就是。

(２)拓展探究如图2,△ACB与△ＤＣE均为等腰三角形,∠ACB＝∠ＤCE=900, 点A、D、E在同一直线上，CＭ为△DCE 中ＤＥ边上得高,连接ＢE。

请判断∠ＡEB得度数及线段CM、ＡE、BE之间得数量关系,并说明理由。

思路点拨:（1)第一问,考虑到两个等边三角形有一个公共顶点Ｃ，在点C处可以找到两组相等得边，列出来即可表示为:,观察边得形式,就可以得到全等得两个三角形就是：、(2)类比第一问,可以得到，故而全等得三角形为,之后再做计算即可。

典例分析２:(2015年安徽)如图1,在四边形ABCD中,点Ｅ、F分别就是AB、CD得中点,过点E作AB得垂线,过点F作CＤ得垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠ＡＧＤ=∠BG C．(１)求证:AＤ=BC; ﻩ(2)求证：△AGD∽△EGF;(3)如图２,若AＤ、ＢＣ所在直线互相垂直,求错误!得值.思路点拨:（1)第一问,结合共顶点旋转全等模型即可（2)类比第一问,全等模型得延伸,相似模型。

根据，类比全等证明相似。

(3)结合前两问得相似即可得到错误!即为相似比,亦即求解得值即可。

A．55° B．60° C．65° D．70°
3、在等腰三角形ABC，∠ABC=90°， AB=a，O为AC中点，∠EOF=45°，求 BE+BF+EF的值。
问题引入：生活中的美丽图案
基础知识回顾
旋转的概念： 在平面内，将一个图形绕一个定点沿某个方向 转动一定的角度，这样的图形变换为旋转，这 个定点叫旋转中心，转动的角度叫旋转角。
图形旋转特点： 旋转变换不改变图形的形状和大小。通过旋转 ，图形上的每一点都绕旋转中心沿相同的方向 转动同样大小的角度。旋转变换前后的图形有 下列性质： （1）对应点到旋转中心的距离相等； （2）对应点与旋转中心的连线所有的角等于旋 转角； （3）对应线段相等，对应线段的夹角等于旋转 角，对应线段的垂直平分线都经过旋转中心。
∴MN=MG
MN=MG
AM=AM （SSS） N AN=AG
∴△ANM △AGM
A
B
∴∠MAN=∠MAG
又∵∠GAN=90°
∴∠MAN=∠MAG=45°
当堂练习：
如图，P为等边三角形ABC内的一点，且P到三个顶点A，B，C的距 离分别为3，4，5，求：△ABC的面积；
A
A
A
A4
3 S1 S2
P 4 S3 5
25 3 18 2
S1+S2+S3=
25 3 9 4
课堂小结:
特殊图形：
旋转题型的关键点：
（1）等腰直角三角形
（1）对应边相等
（2）等边三角形
（2）对应边的夹角等于旋转角
（3）正方形
（3）对应角相等
特征：
（4）对应点与旋转中心的连线相等
（1）有边相等，旋转后能重叠
（2）旋转后能形成特殊的角或图形

回顾本章节学习的重点知识 点，加深对平移和旋转的理 解和掌握。
5.2 个人思考与感想
思考平移和旋转对我们生活 和学习的重要性，并分享个 人的思考和感想。
5.3 下一步学习计划
制定下一步学习计划，明确 未来在几何学习中的重点和 目标。
3. 平移与旋转的组合
3.1 平移与旋转的基本概念
了解平移和旋转相结合的基本概念，如平移中 心、旋转中心等。
3.2 平移与旋转的性质
深入研究平移与旋转的性质，包括它们的可逆 性和运算法则。
3.3 平移与旋转的表示方法
掌握如何同时使用向量和角度等工具来表示和 操作平移和旋转。
3.4 平移与旋转的相互转化
4
探索将多个平移操作合成为一个平移 操作的方法，以便更高效地进行几何
变换。
1.1 平移的概念
了解什么是平移，平移是一个物体在 平面上不改变形状和大小的情况下， 沿着一个方向移动一定距离。
1.3 平移的表示方法
学习如何用向量和坐标表示平移，从 而能够准确地描述平移的过程。
2. 旋转
2.1 旋转的概念
八年级上第十一章平移与 旋转ppt课件
在这个八年级上第十一章平移与旋转的PPT课件中，我们将学习平移和旋转 的基本概念、性质、表示方法以及它们在几何中和生活中的应用。
1. 平移
1
1.2 平移的性质
2
通过平移操作，物体的位置发生改变，
但是其他特征，如长度、角度、形状
等都保持不变。
3
1.4 平移的合成
学习如何在平移和旋转之间进行相互转化，以 及转化的方4.1 平移与旋转在几何中的应用
探索平移和旋转在几何形状的对称性、相似性和变换等方面的应用。
2
4.2 平移与旋转在生活中的应用

02
4. 开始旋转平台，并观察物体在 旋转过程中的变化。
操作步骤及观察记录要点
观察记录要点 1. 记录物体在旋转过程中标记点的位置变化。
2. 观察物体形状、大小在旋转时是否发生变化。
操作步骤及观察记录要点
3. 注意观察物体是否有倾斜、翻滚 等现象发生。
4. 将观察结果详细记录在记录本中， 包括旋转速度、物体名称、形状、大 小等信息。
探讨多种解法
思考是否存在其他方法解决同一问题，比较不同解法的优 劣。
拓展思路
通过一题多解，培养发散思维和灵活运用数学知识的能力。
06 实验操作：观察并描述物 体在旋转时变化
准备实验器材和注意事项
实验器材
旋转平台、各种形状的小物体（如立方体、圆柱体、球体等）、彩色标记笔、测 量尺、记录本等。
注意事项
向量法
引入向量概念，根据向量 旋转的公式判断旋转方向。
02 平面图形在旋转中变化
点、线、面旋转规律
点的旋转
点在旋转时，会绕着旋转 中心作圆周运动，旋转角 度决定了点的新位置。
线的旋转
线段在旋转时，其两个端 点分别绕旋转中心旋转相 同的角度，得到新的线段。
面的旋转
平面图形在旋转时，其上 的每一点都绕旋转中心旋 转相同的角度，得到新的 平面图形。
确保旋转平台平稳且能够匀速旋转；选择的小物体应具有代表性且易于观察；在 物体上做好标记以便于观察其旋转时的变化。
操作步骤及观察记录要点
操作步骤 1. 将旋转平台放置在平稳的桌面上，并调整好旋转速度。
2. 选择一个小物体，将其放置在旋转平台的中心位置。
操作步骤及观察记录要点
01
3. 用彩色标记笔在物体上做好标 记，以便于观察其旋转时的变化 。

B
A
B' C
A'
C'
旋转的性质
• 性质1 对应点到旋转中心的距离相等.
• 性质2 对应点与旋转中心的连线所成的角 彼此相等，且等于旋转角.
• 性质3 旋转不改变图形的形状和大小
练 习
1、你能作出 “将方格中的小旗子绕 O点按顺时针方 向旋转90˚”后的图案吗？

2. 如图 3—17，△ABC绕C 点旋转后，顶点A的对应点为 点 D。试确定顶点 B的对应位置，以及旋转后的三角形。 解:（1）连接CD； （2） 以CB 为一边作∠BCE ， 使得∠BCE=∠ACD； （3）在射线CE上截取CE=CB A
认真把握旋转的概 念.
这个定点叫旋转中心(center of rotation).
角α叫作旋转角(angle of rotation).
原位置的图形F叫原像，新位置的图形F’叫作图 形F在旋转下的像. 图形F上的每一个点P与它在旋转下的像点F’叫 作在旋转下的对应点(corresponding points).
义务教育课程标准实验教科书 SHUXUE 八年级上
3.1 旋
转
观察这四幅图案，你 能总结出他们是怎么样得 来的吗？
观 察
石英钟的指针是怎样走动的呢？
动脑筋
观 察
电扇启动后，它的叶子是怎么样转动的呢？
动脑筋
观 察
动脑筋
大风车迎风而动，它是怎么转动的？
分
析
像前面三个实例那样，将每一个平面图 形F上的每一个点，绕这个平面内一定点旋 转同一个角α（即，把F上每一个点与定点 的连线绕定点璇转角α ），得到图形F’，图 形的这种变换就叫做旋转(rotation).
练 习

常见旋转模型知识点总结一、常见的旋转模型旋转模型是三维图形学中的重要概念，指的是在三维空间中，通过旋转变换对物体进行转动的模型。

常见的旋转模型包括以下几种：1. 旋转矩阵：旋转矩阵是描述旋转变换的数学工具，通常用一个3x3的矩阵表示。

旋转矩阵可以绕任意轴进行旋转，也可以通过欧拉角（Euler angles）或四元数（quaternions）来描述旋转。

2. 旋转向量：旋转向量是描述绕一个固定轴旋转的向量，通常用一个三维向量表示。

旋转向量可以直观地描述物体的旋转方向和角度。

3. 旋转角度：旋转角度是描述物体旋转的角度，通常用弧度（radians）或角度（degrees）表示。

旋转角度可以描述物体绕任意轴的旋转，也可以描述物体在空间中的旋转方向。

4. 旋转轴：旋转轴是物体进行旋转的轴线，可以是任意方向的直线。

通过旋转轴，可以描述物体进行绕轴旋转的动作。

以上这些旋转模型在三维图形学中都是非常重要的概念，对于理解和实现三维旋转变换具有重要意义。

接下来将分别介绍这些旋转模型的具体知识点。

二、旋转矩阵1. 旋转矩阵的表示方法旋转矩阵通常用一个3x3的矩阵表示，一般情况下，可以表示为：R = \begin{bmatrix}cos\theta & -sin\theta & 0\\sin\theta & cos\theta & 0\\0 & 0 & 1\end{bmatrix}其中θ表示旋转角度，cosθ和sinθ表示角度的余弦和正弦值。

这是绕Z轴旋转的旋转矩阵，同样可以表示为绕X轴和Y轴的旋转矩阵。

2. 旋转矩阵的运算旋转矩阵可以进行相乘运算，表示组合多个旋转变换。

比如，先绕X轴旋转再绕Y轴旋转，可以表示为R_y * R_x，其中R_y是绕Y轴旋转的矩阵，R_x是绕X轴旋转的矩阵。

此外，旋转矩阵还可以进行逆矩阵运算，表示将旋转变换的反向操作。

通过逆矩阵运算，可以将物体进行逆时针旋转变换。

初二数学全等三角形旋转模型知识归纳总结及解析一、全等三角形旋转模型1．问题背景如图（1），在四边形ABCD中，∠B+∠D＝180°，AB＝AD，∠BAD＝α，以点A为顶点作一个角，角的两边分别交BC，CD于点E，F，且∠EAF12=α，连接EF，试探究：线段BE，DF，EF之间的数量关系．（1）特殊情景在上述条件下，小明增加条件“当∠BAD＝∠B＝∠D＝90°时”如图（2），小明很快写出了：BE，DF，EF之间的数量关系为______．（2）类比猜想类比特殊情景，小明猜想：在如图（1）的条件下线段BE，DF，EF之间的数量关系是否仍然成立？若成立，请你帮助小明完成证明；若不成立，请说明理由．（3）解决问题如图（3），在△ABC中，∠BAC＝90°，AB＝AC＝4，点D，E均在边BC上，且∠DAE＝45°，若BD2=DE的长．答案：B解析：（1）BE+DF＝EF；（2）成立；（3）DE23 =【分析】（1）将△ABE绕点A逆时针旋转90°，得到△ADG，由旋转的性质可得AE＝AG，BE＝DG，∠BAE＝∠DAG，根据∠EAF=12∠BAD可得∠BAE+∠DAF＝45°，即可得出∠∠EAF＝∠FAG，利用SAS可证明△AFE≌△AFG，可得EF=FG，进而可得EF=BE+FD；（2）将△ABE 绕点A逆时针旋转α得到△ADH，由旋转的性质可得∠ABE＝∠ADH，∠BAE＝∠DAH，AE＝AH，BE＝DH，根据∠BAD＝α，∠EAF12=α可得∠BAE+∠FAD12=α，进而可证明∠FAH＝∠EAF，利用SAS可证明△AEF≌△AHF，可得EF=FH=BE+FD；（3）将△AEC绕点A顺时针旋转90°，得到△AE′B，连接DE′，由旋转的性质可得BE′＝EC，AE′＝AE，∠C＝∠ABE′，∠EAC＝∠E′AB，根据等腰直角三角形的性质可得∠ABC＝∠ACB＝45°，BC＝2，即可求出∠E′BD＝90°，利用SAS可证明△AEF≌△AHF，可得DE＝DE′，利用勾股定理求出DE的长即可的答案.【详解】（1）BE+DF＝EF，如图1，将△ABE绕点A逆时针旋转90°，得到△ADG，∵∠ADC＝∠B＝∠ADG＝90°，∴∠FDG＝180°，即点F，D，G共线．由旋转可得AE＝AG，BE＝DG，∠BAE＝∠DAG．∠BAD=90°-45°＝45°，∵∠BAE+∠DAF＝∠BAD﹣∠EAF＝90°﹣12∴∠DAG+∠DAF＝45°，即∠FAG=45°，∴∠EAF＝∠FAG，∴△AFE≌△AFG（SAS），∴EF＝FG．又∵FG＝DG+DF＝BE+DF，∴BE+DF＝EF，故答案为BE+DF＝EF．（2）成立．如图2，将△ABE绕点A逆时针旋转α得到△ADH，可得∠ABE＝∠ADH，∠BAE＝∠DAH，AE＝AH，BE＝DH．∵∠B+∠ADC＝180°，∴∠ADH+∠ADC＝180°，∴点C，D，H在同一直线上．∵∠BAD＝α，∠EAF1=α，2∴∠BAE+∠FAD1=α，2∴∠DAH+∠FAD1=α，2∴∠FAH＝∠EAF，又∵AF＝AF，∴△AEF≌△AHF（SAS），∴EF＝FH＝DF+DH＝DF+BE；（3）DE 523=， 如图3，将△AEC 绕点A 顺时针旋转90°，得到△AE′B ，连接DE′．可得BE′＝EC ，AE′＝AE ，∠C ＝∠ABE′，∠EAC ＝∠E′AB ，在Rt △ABC 中，∵AB ＝AC ＝4，∠BAC=90°，∴∠ABC ＝∠ACB ＝45°，BC ＝2，∴2，∴∠ABC+∠ABE′＝90°，即∠E′BD ＝90°，∴E′B 2+BD 2＝E′D 2．易证△AE′D ≌△AED ，∴DE ＝DE′，∴DE 2＝BD 2+EC 2，即DE 2222)(32)DE =+，解得23DE =． 【点睛】本题考查旋转的性质、全等三角形的判定与性质、勾股定理，旋转后不改变图形的大小和形状，并且对应点到旋转中心的距离相等，对应点与旋转中心的连线的夹角等于旋转角，熟练掌握旋转的性质及全等三角形的判定定理是解题关键.2．一位同学拿了两块45︒三角尺MNK ∆，ACB ∆做了一个探究活动：将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处，设4AC BC ==.（1）如图1所示，两三角尺的重叠部分为ACM ∆，则重叠部分的面积为______，周长为______.（2）将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒，得到如图2所示，此时重叠部分的面积为______，周长为______.（3）如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形，如图3所示，请你猜想此时重叠部分的面积为______.（4）在如图3所示情况下，若1AD =，求出重叠部分图形的周长.答案：A解析：（1）4，442+；（2）4，8；（3）4；（4）425+【分析】()1根据4AC BC ==，90ACB ∠=，得出AB 的值，再根据M 是AB 的中点，得出AM MC =，求出重叠部分的面积，再根据AM ，MC ，AC 的值即可求出周长；()2易得重叠部分是正方形，边长为12AC ，面积为214AC ，周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、.E 求得Rt MHD ≌Rt MEG ，则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，根据DMH EMH ∠∠=，MH ME =，得出Rt DHM ≌Rt EMG ，从而得出HD GE =，CE AD =，最后根据AD 和DF 的值，算出5DM =.【详解】解：()14AC BC ==，90ACB ∠=，22224442AB AC BC ∴=++= M 是AB 的中点，22AM ∴=45ACM ∠=，AM MC ∴=，∴22224⨯=， ∴周长为：22224442AM MC AC ++==+故答案为4，442+； ()2重叠部分是正方形，∴边长为1422⨯=，面积为14444⨯⨯=， 周长为248⨯=．故答案为4，8．()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、E ，M 是ABC 斜边AB 的中点，4AC BC ==，12MH BC ∴=， 12ME AC =， MH ME ∴=，又90NMK HME ∠∠==，90NMH HMK ∠∠∴+=，90EMG HMK ∠∠+=，HMD EMG ∠∠∴=，在MHD 和MEG 中，HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩， MHD ∴≌()MEG ASA ，∴阴影部分的面积等于正方形CEMH 的面积， 正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=； ∴阴影部分的面积是4；故答案为4．()4如图所示， 过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，∴四边形MECH 是矩形，MH CE ∴=，45A ∠=，45AMH ∠∴=，AH MH ∴=，AH CE ∴=，在Rt DHM 和Rt GEM 中，DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩， Rt DHM ∴≌.Rt GEMGE DH ∴=，AH DH CE GE ∴-=-，CG AD ∴=，1AD =，1.DH ∴= 145DM ∴=+= ．∴四边形DMGC 的周长为：CE CD DM ME +++2AD CD DM =++425=+．【点睛】此题考查了等腰直角三角形，利用等腰直角三角形的性质，等腰直角三角形的面积公式，正方形的面积公式，全等三角形的判定和性质求解．3．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是 ，位置关系是 ；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．解析：（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492． 【分析】 （1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =， 点P ，M 是CD ，DE 的中点，//PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠， 90BAC ∠=︒， 90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大． 方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大． 【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．4．问题提出：（1）如图1，在ABC 中，AB AC BC =≠，点D 和点A 在直线BC 的同侧，BD BC =，90BAC ∠=︒，30DBC ∠=︒，连接AD ，将ABD △绕点A 逆时针旋转90︒得到ACD '，连接BD '（如图2），可求出ADB ∠的度数为______．问题探究：（2）如图3，在（1）的条件下，若BAC α∠=，DBC β∠=，且120αβ+=︒，DBC ABC ∠<∠ ，①求ADB ∠的度数．②过点A 作直线AE BD ⊥，交直线BD 于点E ，7,2BC AD ==．请求出线段BE 的长．答案：A解析：（1）30°；（2）①30︒；②73-【分析】（1）由旋转的性质，得△ABD ≌ACD '∆，则ADB AD C '∠=∠，然后证明BCD '∆是等边三角形，即可得到30ADB AD C '∠=∠=︒；（2）①将ABD △绕点A 逆时针旋转，使点B 与点C 重合，得到'ACD △，连接'BD ．与（1）同理证明D BC '∆为等边三角形，然后利用全等三角形的判定和性质，即可得到答案；②由解直角三角形求出3DE =【详解】解：（1）根据题意，∵AB AC BC =≠，90BAC ∠=︒，∴ABC ∆是等腰直角三角形，∴45ABC ACB ∠=∠=︒，∵30DBC ∠=︒，∴15ABD ∠=︒，由旋转的性质，则△ABD ≌ACD '∆，∴ADB AD C '∠=∠，15ABD ACD '∠=∠=︒，BC CD '=，∴60BCD '∠=︒，∴BCD '∆是等边三角形，∴60BD C '∠=︒，BD CD ''=∵AB AC =，AD AD ''=，∴ABD '∆≌ACD '∆，∴30AD B AD C ''∠=∠=︒，∴30ADB AD C '∠=∠=︒；（2）①DBC ABC ∠<∠，60120α︒︒∴<<．如图1，将ABD △绕点A 逆时针旋转，使点B 与点C 重合，得到'ACD △，连接'BD ．AB AC =，ABC ACB ∴∠=∠，BAC α∠=，()111809022ABC αα︒︒∴∠=-=-， 1902ABD ABC DBC αβ︒∴∠=∠-∠=--， 119090180()22D CB ACD ACB αβααβ''︒︒︒∴∠=∠+∠=--+-=-+． 120,αβ︒+=60D CB '︒∴∠=．,BD BC BD CD '==，,BC CD '∴=D BC '∴为等边三角形，D B D C ''∴=，AD B AD C ''∴≌，AD B AD C ''∴∠=∠，1302AD B BD C ''︒∴∠=∠=， 30ADB ︒∴∠=．②如图2，由①知，30ADB ︒∠=，在Rt ADE △中，30,2ADB AD ︒∠==， 3DE ∴=．BCD '是等边三角形，7BD BC '∴==，7BD BD '∴==，73BE BD DE ∴=-=-．【点睛】本题考查了解直角三角形，旋转的性质，全等三角形的判定和性质，等边三角形的判定和性质，等腰直角三角形的性质，以及三角形的内角和定理，解题的关键是熟练掌握所学的知识，正确利用旋转模型进行解题．5．如图，在ABC 中，,AB AC BAC α=∠=，过A 作AD BC ⊥于点D ，点E 为直线AD 上一动点，把线段CE 绕点E 顺时针旋转α，得到线段EF ，连接FC 、FB ，直线AD 与BF 相交于点G ．（1）（发现）如图1，当60α=︒时，填空：①AE BF的值为___________； ②AGB ∠的度数为___________；（2）（探究）如图2，当120α=︒时，请写出AE BF的值及AGB ∠的度数，并就图2的情形给出证明；（3）（应用）如图3，当90α=︒时，若15AB ACE =∠=︒，请直接写出DFG 的面积．答案：G解析：（1）1；60°；（2）3AE BF =，∠G =30°，理由见解析；（3） 【分析】（1）①根据已知条件可以证明三角形ABC 和三角形EFC 都是等边三角形，然后根据等边三角形的性质证明△AEC ≌△BFC ，即BF =AE 从而得出答案；②根据①中的证明∠ABG =90°，∠BAG =30°，从而计算出∠AGB 的度数；（2）根据题目已知条件可以计算出BC =，同理可以证得CF =，再证ECA FCB ∠=∠即△ACE ∽△BCF ，从而得到比值和角的度数；（3）根据第（2）问的计算结论分E 在AD 上和E 在DA 的延长线上分类讨论求解即可．【详解】解：（1）①∵AB =AC ，CE =EF ，∠BAC =∠FEC =60°∴△ABC 和△EFC 都是等边三角形∴∠ACB =∠ECF =60°，AC =CB ，CE =CF∴∠ACE =∠BCF∴△ACE ≌△BCF∴A E =BF ，即1AE BF= ②∵△ACE ≌△BCF∴∠EAC =∠CBF 由①可知△ABC 是等边三角形∴AD 平分∠BAC ，BD ⊥AD∴∠CAE =∠CBF =30°∴∠AGB =∠180°-∠CBF -∠BDG =60°（2）AE BF = ∵AB =AC ，∠BAC =120°，AD ⊥BC∴∠ABD =30°=∠ACB∴22BD AB AC CD === ∴BC =同理∵∠FEC =120°，EF =EC ∴CF =∴BC CF AC CE=，∠ACB =∠ECF =30° ∴△ACE ∽△BCF∴∠CAE =∠CBF∴AE AC BF BC ==∵AD ⊥BC ，∠BAC =120°，∴∠CAE =∠CBF =60°又∵∠BDG =90°∴∠G =30°（3）第一种情况，如图所示，当E 在AD 上时 ∵AB AC ==∠BAC =90°，AD ⊥BC ∴sin 4562BC AD BD CD AB =====∠DAC =45° ∵∠ACE =15° ∴∠CED =∠CAD +∠ACE =60° ∴2tan 60DC DE ==∴AE AD DE =-=BC CF AC CE==，∠ACB =∠ECF =45° 又∵AD ⊥BC ，∠BAC =90°，∴∠CAE =∠CBF =45°∴△ACE ∽△BCF∴BF BC AE AC==∴2BF == ∵∠ADC =∠BDG∴∠G =∠ACB =45°∴BG ==∴2FG BG BF =-=过点D 作DM ⊥BG 交BG 于M ，∵∠G =∠ACB =45°，∠BDG =90°∴=DG BD CD ==∴DM DG == ∴132DFG S FG DM ==△第二种情况：当E 在DA 的延长线上时过点D 作DM ⊥BG 交BG 于M ， 同上可证2BF BC AE AC ==，6BG BD ==，3DM = ∵∠ACE =15°，∠DAC =45°∴∠DEC =30° ∵AD ⊥CD ，6CD =∴32tan 30DC DE == ∴=6DG BD CD ==326AE DE AD =-=-∴2623FB AE ==-∴6FG BF BG =+=1332DFG S FG DM ==△ 故答案为：3或33．【点睛】本题主要考查了相似三角形的性质与判定，旋转的性质，三角函数等知识点，解题的关键在于能够熟练的掌握相关知识点．6．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB∠＝ °，线段BD 、CE 之间的数量关系是 ；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．答案：C解析：（1）60BD CE ，＝；（2）452CEB BD CE ∠︒＝，＝，理由见解析；（3）CE 的长为2或2【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论； （2）证明ACE ABD ∽，得出AEC ADB ∠=∠，2BD CE =，即可得出结论； （3）先判断出2BD CE =，再求出210AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAEAD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝ ，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝， EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE==∴AEC ADB BD ∠∠＝，，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，BD ∴，在Rt ABC中，AC ＝AB ∴＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝ ，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，226BP AB AP -＝＝，4BD BP AP ∴-＝＝，1222CE BD ∴＝＝； ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6，∴BD ＝BP +DP ＝8，122CE BD ∴＝＝4， 综上CE 的长为22或42．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE 和三角形ABD 相似是关键．7．如图，ABD △和ACE △都是等边三角形．（1）连接CD 、BE 交于点P ，求∠BPD ；（2）连接PA ，判断线段PA 、PB 、PD 之间的数量关系并证明；（3）如图，等腰ABC 中AB ＝AC ，∠BAC ＝α（0＜α＜90），在ABC 内有一点M ，连接MA 、MB 、MC ．当MA ＋MB ＋MC 最小时，∠ABM ＝ （用含α的式子表示）答案：D解析：（1）60BPD ∠=︒（2）PD PB PA =+，证明见详解（3）1602α︒-【分析】（1）证明()DAC BAE SAS ≅，得ADC ABE ∠=∠，就可以证明60BPD DAB ∠=∠=︒；（2）在DP 上截取PF=PB ，连接BF ，证明()DBF ABP SAS ≅，得DF PA =，即可证明PD PB PA =+；（3）分别以AB 和AC 为边，向两边作等边三角形ABD 和等边三角形ACE ，连接BE 和CD ，交于点M ，连接AM ，此时MA MB MC ++最小，然后利用等腰三角形ADC ，求出ADC ∠的度数，即可得到ABM ∠的度数．【详解】解：（1）∵ABD △和ACE △是等边三角形，∴AD AB =，AC AE =，60DAB CAE ∠=∠=︒，∵DAB BAC CAE BAC ∠+∠=∠+∠，∴DAC BAE ∠=∠，在DAC △和BAE △中，AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩，∴()DAC BAE SAS ≅，∴ADC ABE ∠=∠，∵ADC DAB ABE BPD ∠+∠=∠+∠，∴60BPD DAB ∠=∠=︒；（2）如图，在DP 上截取PF=PB ，连接BF ，∵60BPD ∠=︒，PF PB =，∴PFB △是等边三角形，∴BF BP =，60FBP ∠=︒，∴DBA FBP ∠=∠，∵DBA FBA FBP FBA ∠-∠=∠-∠，∴DBF ABP ∠=∠，在DBF 和ABP △中，DB AB DBF ABP BF BP =⎧⎪∠=∠⎨⎪=⎩，∴()DBF ABP SAS ≅，∴DF PA =，∵PD PF FD =+，∴PD PB PA =+；（3）如图，分别以AB 和AC 为边，作等边三角形ABD 和等边三角形ACE ，连接BE 和CD ，交于点M ，连接AM ，此时MA MB MC ++最小，由（2）中的结论可得MD MA MB =+，则当D 、M 、C 三点共线时MA MB MC ++最小，即CD 的长，由（1）得ADC ABM ∠=∠，∵AD AB AC ==，60DAC α∠=︒+，∴()1806016022ADC αα︒-︒+∠==︒-， ∴1602ABM α∠=︒-， 故答案是：1602α︒-．【点睛】本题考查全等三角形的性质和判定，等边三角形的性质，解题的关键是做辅助线构造全等三角形来进行证明求解．8．如图１，在△ABC 和△ADE 中，∠DAE=∠BAC ，AD=AE ，AB=AC ．（1）求证：△ABD ≌△ACE ；（2）如图2，在△ABC 和△ADE 中，∠DAE=∠BAC ，AD=AE ，AB=AC ，∠ADB=90°，点E 在△ABC 内，延长DE 交BC 于点F ，求证：点F 是BC 中点；（3）△ABC 为等腰三角形，∠BAC=120°，AB=AC ，点P 为△ABC 所在平面内一点，∠APB=120°，AP=2，BP=4，请直接写出 CP 的长．答案：D解析：（1）证明见详解；（2）证明见详解；（3）2713【分析】（1）因为∠DAE=∠BAC ，可以得到∠DAB=∠EAC ，因为AD=AE ，AB=AC ，即可得到△ABD ≌△ACE ；（2）连接CE ，延长EF 至点H ，取CF=CH ，连接CH ，由（1）可得△ABD ≌△ACE ，所以∠AEC=90°和CE=BD ，可以推出∠BDF=∠CEF ，再证明△DBF ≌△ECH ，所以BF=CH ，等量代换即可得到BF=FC ，即可解决；（3）点P 在△ABC 内部，将△ABP 逆时针旋转120°，得到ACP ∆'，连接PP '和PC ，可以得到△PP C '是直角三角形，利用勾股定理即可求出PC 的值；当点P 在△ABC 外部，将△APB 绕点A 逆时针旋转120︒得到PDC ∆，连接PP '和PC ，过点P 作PD ⊥'CP 于点D ，连接PD 可以得到△PP D '，△PP D '是直角三角形和，利用勾股定理即可求出'DP 及PC 的值．【详解】解：（1）证明：∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ，AB=AC∴△ABD ≌△ACE（2）证明：连接CE ，延长EF 至点H ，取CF=CH ，连接CH ，如图所示：∵△ADB≌△AEC∴BD=EC，∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF≌△ECH∴BF=CH∴BF=CF∴点F是BC的中点∆'，连接（3）当点P在△ABC内部，如图所示，将△ABP逆时针旋转120°，得到ACPPP'和PC∆'∵将△ABP旋转120°得到ACP∴∠PAP'=120°，AP='AP=2，BP=CP'=4∴PP'3∵∠AP C'=120°，∠AP P'=30°，∴∠PP C'=90°，∴()2223427+=．当点P在△ABC外部，如图所示，将△APB 绕点A 逆时针旋转120︒到△'AP C ，过点P 作PD ⊥'CP 于点D ，连接PD ， ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°，AP='AP =2，BP=CP '=4，∴PP '=23， ∵∠AP C '=120°,∠AP P '=30°，∴∠PP C '=150°，∴∠PP D '=30°，在Rt 'PDP 中，1'32PD PP ==， 22''3DP PP PD ∴=-=，''347DC DP P C ∴=+=+=，()222237213PC PD DC ∴=+=+= ． 综上所述，27213PC =或【点睛】本题主要考查了全等三角形以及旋转，合理的作出辅助线以及熟练旋转的性质是解决本题的关键．9．如图，抛物线y ＝24x 2+2x ﹣62交x 轴于A 、B 两点（点A 在点B 的左侧），交y 轴于C 点，D 点是该抛物线的顶点，连接AC 、AD 、CD ．（1）求△ACD 的面积；（2）如图，点P 是线段AD 下方的抛物线上的一点，过P 作PE ∥y 轴分别交AC 于点E ，交AD 于点F ，过P 作PG ⊥AD 于点G ，求EF+52FG 的最大值，以及此时P 点的坐标； （3）如图，在对称轴左侧抛物线上有一动点M ，在y 轴上有一动点N ，是否存在以BN 为直角边的等腰Rt △BMN ？若存在，求出点M 的横坐标，若不存在，请说明理由．答案：A解析：（1）24；（2）最大值为922，点P （﹣32，﹣1522）；（3）存在，点M 的横坐标为﹣2﹣26或22﹣26．【分析】（1）先求出抛物线与坐标轴的交点坐标和顶点坐标，再用待定系数法求得AC 的解析式，进而求出点N 、D 的坐标，再根据三角形的面积公式求出结果；（2）证明EF+52FG 即为EP 的长度，即可求解； （3）分∠BNM 为直角、∠MBN 为直角，利用三角形全等即可求解．【详解】解：（1）令x ＝0，得202062624y =⨯+⨯-=-， ∴C （0，﹣62），令y ＝0，得2226204y x x =+-=， 解得162x =-，222x =，∴A （62-，0），点B （22，0），设直线AC 的解析式为：y ＝kx+b （k ≠0），则62062k b b ⎧-+=⎪⎨=-⎪⎩， ∴162k b =-⎧⎪⎨=-⎪⎩， ∴直线AC 的解析式为：62y x =--，∵()2222262228244y x x x =+-=+-，∴D （22-，82-），过D 作DM ⊥x 轴于点M ，交AC 于点N ，如图，令22x =-，()226242y =---=-，则N （22-，42-），∴42DN =，∴1142622422ACD S DN AO =⋅=⨯⨯=； （2）如图，过点D 作x 轴的平行线交FP 的延长线于点H ，由点A 、D 的坐标得，直线AD 的表达式为：2122y x =--∴tan ∠FDH ＝2，则sin ∠FDH 2555=， ∵∠HDF+∠HFD ＝90°，∠FPG+∠PFG ＝90°，∴∠FDH ＝∠FPG ，在Rt △PGF 中，PF ＝FG sin G FP ∠＝ FG sin FDH ∠255=5FG ， 则5FG ＝EF+PF ＝EP ， 设点P （x ，22224x x +-E （x ，62x -- 则5FG ＝EF+PF ＝EP ＝222262262344x x x x x ⎛--+-=-- ⎝， ∵2＜0，故EP 有最大值，此时x ＝﹣2b a ＝﹣2，最大值为22； 当x ＝32-2215226242y x x =+-=-， 故点P （32-1522-）； （3）存在，理由： 设点M 的坐标为（m ，n ），则222624n m m =+-，点N （0，s ）， ①当∠MNB 为直角时，如图，过点N 作x 轴的平行线交过点B 与y 轴的平行线于点H ，交过点M 与y 轴的平行线于点G ，∵∠MNG+∠BNH ＝90°，∠MNG+∠GMN ＝90°，∴∠GMN ＝∠BNH ，∵∠NGM ＝∠BHN ＝90°，MN ＝BN ，∴△NGM ≌△BHN （AAS ），∴GN ＝BH ，MG ＝NH ， 即22n s -=且m s -=-，联立并解得：226m =-±（舍去正值），故226m =--，则点M （226--，226-）； ②当∠NBM 为直角时，如图，过点B 作y 轴的平行线交过点N 与x 轴的平行线于点G ，交过点M 与x 轴的平行线于点H ，同理可证：△MHB ≌△BGN （AAS ）， 则BH ＝NG ，即22n =- 当22n =-时，2222224m m +-=-2226m = 故2226m =M （2226，22-）；综上，点M 的横坐标为226-2226．【点睛】本题考查二次函数的综合题，涉及三角形面积的求解，用胡不归原理求最值，等腰直角三角形的存在性问题，解题的关键是需要掌握这些特定题型的特定解法，熟练运用数形结合的思想去解决问题．10．综合与实践实践操作：①如图1，ABC ∆是等边三角形，D 为BC 边上一个动点，将ACD ∆绕点A 逆时针旋转60︒得到AEF ∆，连接CE ．②如图2，在ABC ∆中，AD BC ⊥于点D ，将ABD ∆绕点A 逆时针旋转90︒得到AEF ∆，延长FE 与BC 交于点G ．③如图3，将图2中得到AEF ∆沿AE 再一次折叠得到AME ∆，连接MB ．问题解决：（1）小明在探索图1时发现四边形ABCE 是菱形．小明是这样想的：请根据小明的探索直接写出图1中线段CD ，CF ，AC 之间的数量关系为 ： （2）猜想图2中四边形ADGF 的形状，并说明理由；问题再探：（3）在图3中，若AD=6，BD=2，则MB 的长为 ．答案：C解析：（1）CD+CF=AC ；（2）四边形ADGF 为正方形；理由见解析；（3）13【分析】（1）先证明C 、F 、E 在同一直线上，再证明△BAD ≌△CAF （SAS ），则∠ADB=∠AFC ，BD=CF ，可得AC=CF+CD ；（2）先根据∠ADC=∠DAF=∠F=90°，证明得四边形ADGF 是矩形，由邻边相等可得四边形ADGF 是正方形；（3）证明△BAM ≌△EAD （SAS ），根据BM=DE 及勾股定理可得结论．【详解】解：（1）如图：由旋转得：∠DAF=60°=∠BAC，AD=AF，∴∠BAD=∠CAF，∵△ABC是等边三角形，∴AB=AC，∴△BAD≌△CAF（SAS），∴∠ADB=∠AFC，BD=CF，∵∠ADC+∠ADB=∠AFC+∠AFE=180°，∴C、F、E在同一直线上，∴AC=BC=BD+CD=CF+CD，+=；故答案为：CD CF AC（2）四边形ADGF是正方形，理由如下：如图：∵Rt△ABD绕点A逆时针旋转90°得到△AEF，∴AF=AD，∠DAF=90°，∵AD⊥BC，∴∠ADC=∠DAF=∠F=90°，∴四边形ADGF是矩形，∵AF=AD，∴四边形ADGF是正方形；（3）如图3，连接DE，∵四边形ADGF 是正方形，DG=FG=AD=AF=6，∵△ABD 绕点A 逆时针旋转90°，得到△AEF ，∴∠BAD=∠EAF ，BD=EF=2，∴EG=FG-EF=6-2=4，∵将△AFE 沿AE 折叠得到△AME ，∴∠MAE=∠FAE ，AF=AM ，∴∠BAD=∠EAM ，∴∠BAD+∠DAM=∠EAM+∠DAM ，即∠BAM=∠DAE ，∵AF=AD ，∴AM=AD ，在△BAM 和△EAD 中，∵AM AD BAM DAE AB AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAM ≌△EAD （SAS ），∴BM=DE=22EG DG +=2246213+=．故答案为：213．【点睛】本题属于四边形综合题，主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是熟练掌握等边三角形和全等三角形的性质，依据图形的性质进行计算求解．11．如图1，ABC ∆中，CA CB =，ACB α∠=，D 为ABC ∆内一点，将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆，点,A D 的对应点分别为点,B E ，且,,A D E 三点在同一直线上．（1）填空：CDE ∠=______（用含α的代数式表示）；（2）如图2，若60α=︒，请补全图形，再过点C 作CF AE ⊥于点F ，然后探究线段CF ，AE ，BE 之间的数量关系，并证明你的结论；（3）如图3，若90α=︒，52AC =ABEC 面积的最大值______．解析：（1）1802α-；（2）233AE BE CF =+；证明见解析；（3）25(21)2+． 【分析】 （1）由旋转的性质可得CD CE =，DCE α∠=，即可求解；（2）由旋转的性质可得AD BE =，CD CE =，60DCE ∠=︒，可证CDE ∆是等边三角形，由等边三角形的性质可得33DF EF CF ==，即可求解； （3）如图3中，过点C 作CF BE ⊥交BE 的延长线于F ，设AE 交BC 于J ．证明90ACJBEJ ，推出点E 在以AB 为直径的圆上运动，即图中BC 上运动，当CE EB 时，四边形ABEC 的面积最大，此时EC EB =，分别求出ABC ∆，BCE ∆的面积即可解决问题．【详解】解：（1）如图1中，将CAD ∆绕点C 按逆时针方向旋转角α得到CBE ∆ACD BCE ∴∆≅∆，DCE α∠=CD CE ∴=1802CDE α︒-∴∠=． 故答案为：1802α︒-． （2）233AE BE CF =+ 理由如下：如图2中，将CAD ∆绕点C 按逆时针方向旋转角60︒得到CBE ∆ACD BCE ∴∆≅∆AD BE ∴=，CD CE =，60DCE ∠=︒CDE ∴∆是等边三角形，且CF DE ⊥ 33DF EF CF ∴== AE AD DF EF =++ 233AE BE CF ∴=+． （3）如图3中，过点C 作CWBE 交BE 的延长线于W ，设AE 交BC 于J ．CAD ∆绕点C 按逆时针方向旋转90︒得到CBE ∆， CAD CBE ，CAD CBE ∴∠=∠，AJC BJE ，90ACJ BEJ ，∴点E 在以AB 为直径的圆上运动，即图中BC 上运动，当CEEB 时，四边形ABEC 的面积最大，此时EC EB =， CD CE =，90DCE ∠=︒，45CED ∴∠=︒， 90AEW AEB ， 45CEW ， CF EW ，45WCE CEW ， CW EW ，设CW EWx ，则2EC EB x ==， 在Rt BCW 中，222BC CW BW ， 222(2)(52)x x x ， 225(22)2x ，21225(21)222BCE S BE CW x ，2521252115252222ABC BCE ABEC S S S 四边形．【点睛】本题考查了圆的性质，等腰三角形的性质，全等三角形的判定和性质，解直角三角形等知识，熟悉相关性质，灵活运用所学知识解决问题是解题的关键．12．已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）求证：EG ＝CG ；（2）将图①中BEF 绕B 点逆时针旋转45°，如图②所示，取DF 中点G ，连接EG ，CG ．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由； （3）将图①中BEF 绕B 点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．答案：E解析：（1）见解析；（2）依然成立，见解析；（3）依然成立，EG ⊥CG【分析】（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG ＝EG ；（2）结论仍然成立，连接AG ，过G 点作MN ⊥AD 于M ，与EF 的延长线交于N 点；再证明△DAG ≌△DCG ，得出AG ＝CG ；再证出△DMG ≌△FNG ，得到MG ＝NG ；再证明△AMG ≌△ENG ，得出AG ＝EG ；最后证出CG ＝EG ；（3）结论依然成立，证明方法类似（2）．【详解】（1）证明：∵四边形ABCD 是正方形，∴∠DCF ＝90°，在Rt △FCD 中，∵G 为DF 的中点，∴CG ＝12FD ， 同理，在Rt △DEF 中，EG ＝12FD ， ∴CG ＝EG ． （2）解：（1）中结论仍然成立，即EG ＝CG ．证法：如图，连接AG ，过G 点作MN ⊥AD 于M ，与EF 的延长线交于N 点，在△DAG与△DCG中，∵AD＝CD，∠ADG＝∠CDG，DG＝DG，∴△DAG≌△DCG（SAS），∴AG＝CG；在△DMG与△FNG中，∵∠DGM＝∠FGN，FG＝DG，∠MDG＝∠NFG，∴△DMG≌△FNG（ASA），∴MG＝NG；∵∠EAM＝∠AEN＝∠AMN＝90°，∴四边形AENM是矩形，在矩形AENM中，AM＝EN，在△AMG与△ENG中，∵AM＝EN，∠AMG＝∠ENG，MG＝NG，∴△AMG≌△ENG（SAS），∴AG＝EG，∴EG＝CG．（3）解：（1）中的结论仍然成立．理由如下：如图，过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N，∵G为FD中点，∴FG=GD，∵MF∥CD，∴∠FMG=∠DCG，∠GDC=∠GFM，∴△CDG≌△MFG，∴CD＝FM，∵NF∥BC，∴∠NFH+∠NHF=∠EHB+∠EBH，又∵∠NHF=∠EBH，∴∠NFH=∠EBH，∴∠EFM＝∠EBC，又∵BE=EF，则△EFM≌△EBC，∠FEM＝∠BEC，EM＝EC∵∠FEC+∠BEC＝90°，∴∠FEC+∠FEM＝90°，即∠MEC＝90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG＝CG，EG⊥CG．【点睛】本题考查全等三角形的判定和性质、矩形的判定与性质，正方形的性质，旋转的性质，解题的关键是掌握相关性质．13．如图1，在Rt△ABC中，AB＝AC，∠A＝90°，点D、E分别在边AB、AC上，AD＝AE，连结DC，点M、P、N分别为DE、DC、BC的中点．（1）观察猜想：图1中，线段PM与PN的数量关系是________，位置关系是__________；（2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连结MN，判断△PMN的形状，并说明理由；（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若DE＝2，BC＝4，请直接写出△PMN面积的最大值．答案：C解析：（1）PM=PN，PM⊥PN，理由见详解；（2）△PMN是等腰直角三角形，理由见详解；（3）△PMN面积的最大值是94．【分析】（1）利用三角形的中位线得出PM=12CE，PN=12BD，进而判断出BD=CE，即可得出结论，再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA，最后用互余即可得出结论；（2）先判断出△ABD≌△ACE，得出BD=CE，同（1）的方法得出PM=12BD，PN=12BD，即可得出PM=PN，同（1）的方法即可得出结论；（3）先判断出BD最大时，△PMN的面积最大，而BD最大是AB+AD=14，即可得出结论．【详解】解：（1）∵点P，N是BC，CD的中点，∴PN∥BD，PN=12BD，∵点P，M是CD，DE的中点，∴PM∥CE，PM=12CE，∵AB=AC，AD=AE，∴BD=CE，∴PM=PN，∵PN∥BD，∴∠DPN=∠ADC，∵PM∥CE，∴∠DPM=∠DCA，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN；故答案为：PM=PN，PM⊥PN；（2）△PMN是等腰直角三角形；理由：由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，BD=CE，同（1）的方法，利用三角形的中位线得，PN=12BD，PM=12CE，∴PM=PN，∴△PMN是等腰三角形，同（1）的方法得，PM∥CE，∴∠DPM=∠DCE，同（1）的方法得，PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC =∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC ，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN 是等腰直角三角形；（3）由（2）知，△PMN 是等腰直角三角形，PM=PN=12BD ， ∴PM 最大时，△PMN 面积最大，即：BD 最大时，△PMN 面积最大，∴点D 在BA 的延长线上，∵DE ＝2，BC ＝4，∴2222AD =⨯=，24222AB =⨯= ∴BD=AB+AD=32，∴PM=322， ∴S △PMN 最大=12PM 2=21329()224⨯=； 【点睛】此题是几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质，解（1）的关键是判断出PM=12CE ，PN=12BD ，解（2）的关键是判断出△ABD ≌△ACE ，解（3）的关键是判断出BD 最大时，△PMN 的面积最大，是一道中考常考题．14．如图，△ABC 是边长为4的等边三角形，点D 是线段BC 的中点，∠EDF=120°，把∠EDF 绕点D 旋转，使∠EDF 的两边分别与线段AB 、AC 交于点E 、F ．（1）当DF ⊥AC 时，求证：BE=CF ；（2）在旋转过程中，BE+CF 是否为定值？若是，求出这个定值；若不是，请说明理由答案：D解析：（1）证明见解析；（2）是，2.【解析】【分析】（1）根据四边形内角和为360°，可求∠DEA=90°，根据“AAS”可判定△BDE ≌△CDF ，即可证BE=CF ；（2）过点D 作DM ⊥AB 于M ，作DN ⊥AC 于N ，如图2，易证△MBD ≌△NCD ，则有BM=CN ，DM=DN ，进而可证到△EMD ≌△FND ，则有EM=FN ，就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=12BC=2. 【详解】（1）∵△ABC 是边长为4的等边三角形，点D 是线段BC 的中点，∴∠B=∠C=60°，BD=CD ，∵DF ⊥AC ，∴∠DFA=90°，∵∠A+∠EDF+∠AFD+∠AED=180°，∴∠AED=90°，∴∠DEB=∠DFC ，且∠B=∠C=60°，BD=DC ，∴△BDE ≌△CDF （AAS ）（2）过点D 作DM ⊥AB 于M ，作DN ⊥AC 于N ，则有∠AMD=∠BMD=∠AND=∠CND=90°．∵∠A=60°，∴∠MDN=360°-60°-90°-90°=120°．∵∠EDF=120°，∴∠MDE=∠NDF ．在△MBD 和△NCD 中，BMD CND B CBD CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△MBD ≌△NCD （AAS ）BM=CN ，DM=DN ．在△EMD 和△FND 中，EMD FND DM DNMDE NDF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△EMD ≌△FND （ASA ）∴EM=FN ，∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=12BC=2. 【点睛】 本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、特殊角的三角函数值等知识，通过证明三角形全等得到BM=CN ，DM=DN ，EM=FN 是解决本题的关键． 15．问题背景：如图1，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，120ABC ∠=︒，60MBN ∠=︒，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．探究图中线段AE ，CF ，EF 之间的数量关系．小李同学探究此问题的方法是：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，再证明BFC BFE △≌△，可得出结论，他的结论就是_______________；探究延伸1：如图2，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由． 探究延伸2：如图3，在四边形ABCD 中，BA BC =，180BAD BCD ∠+∠=︒，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？并说明理由．实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O 处）北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E 、F 处，且指挥中心观测两舰艇视线之间的夹角为70︒，试求此时两舰艇之间的距离．答案：E解析：EF=AE+CF ．探究延伸1：结论EF=AE+CF 成立．探究延伸2：结论EF=AE+CF 仍然成立．实际应用：210海里．【分析】延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸1：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；探究延伸2：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，可得BG=BE ，∠CBG=∠ABE ，再证明BGF BEF ≌，可得GF=EF ，即可解题；。

旋转专题（一） 一、基础知识1.，把一个图形绕着某一点O 转动一个角度的图形变换叫做旋转，点O 叫做旋转中心，转动的角叫做旋转角．2.旋转的性质（1）对应点到旋转中心的距离相等；（2）对应点与旋转中心所连线段的夹角等于旋转角； （3）旋转前、后的图形全等．3.把一个图形绕某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称；这个点叫做对称中心；这两个图形中的对应点叫做关于对称中心的对称点．4.中心对称图形的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合．那么这个图形叫做中心对称图形，这个点就是它的对称中心． 二．基础练习1．（1）下列物体的运动不是旋转的是( )A ．坐在摩天轮里的小朋友B ．正在走动的时针C ．骑自行车的人D ．正在转动的风车叶片（2）下列现象中属于旋转的有____个．①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头的转动；⑤钟摆的运动；⑥荡秋千运动．3．A 点(2，－3)关于原点对称的点的坐标为（ ） A ．(2，3) B ．(－2，－3) C ．(－2，3)D ．(3，－2)4．下列图形中，为中心对称图形的是（ ）5．正三角形绕其中心旋转一定角度后，能与自身重合，旋转角至少为（ ） A ．30°B ．60°C ．120°D ．180°5．Rt △ABC 中，∠ACB ＝90°，∠A ＝35°，将Rt △ABC 绕C 点顺时针旋转至Rt △A ′B ′C ′的位置时，B ′点恰好在AB 上，则旋转角度为（ ） A ．50° B ．70° C ．60° D ．45°6.（2014桂林市）如图，在△ABC 中，∠CAB=70°，将△ABC 绕点A 逆时针旋转到△AB`C`的位置，使得CC`∥AB ，则∠BAB`的度数是（ ）CC`AB`A ．70°B ．35°C ．40°D ．50°7.如图，△ABC 中，AB ＝BC ，点O 是△ABC 内一点，将△ABO 旋转后能与△BCD 重合 (1) 旋转中心是点__________ (2) 若∠ACB ＝70°，旋转角是__________度 (3) 若∠ACB ＝60°，请判断△BOD 的形状并说明理由(1) B ；(2) 40°；(3) 等边三角形 三、典型例题 例1．（1）如图，如果把钟表的指针看做三角形OAB ，它绕O 点按顺时针方向旋转得到△OEF ，在这个旋转过程中：（1）旋转中心是什么？旋转角是什么？（2）经过旋转，点A 、B 分别移动到什么位置？（2）.将△ABC 绕O 点按顺时针方向旋转得到△OEF1．线段OA 与OA ′，OB 与OB ′，OC 与OC ′有什么关系？ 2．∠AOA ′，∠BOB ′，∠COC ′有什么关系？ 3．△ABC 与△A ′B ′C ′形状和大小有什么关系？ 归纳1．OA=OA ′，OB=OB ′，OC=OC ′，也就是对应点到旋转中心相等．2．∠AOA ′=∠BOB ′=∠COC ′，我们把这三个相等的角，•即对应点与旋转中心所连线段的夹角称为旋转角．3．△ABC 和△A ′B ′C ′形状相同和大小相等，即全等．例2、（华一9月）如图，点O 是等边△ABC 内一点，∠AOB=110°，∠BOC=a ，将△BOC 绕点C 按顺时针方向旋转60°，得△ADC ，连接OD 。

1.旋转不改变图形的大小和形状． 2.经过旋转，图形上的每一点都绕旋 转中心沿相同方向转动了相同的角度． 任意一对对应点与旋转中心的连线 所成的角度都是旋转角． 对应点到旋转中心的距离相等．
例题解析
例１：钟表的分针匀速旋转一周需要60 分． （１）指出它的旋转中心； （２）经过20分，分针旋 转了多少度？
3.3 生活中的旋转
想一想
上面情景中的转动现象，有 什么共同的特征？ 钟表的指针、秋千在转动过 程中，其形状、大小、位置是 否发生变化呢？
引入新知
在平面内，将一个图形绕一个顶点沿 某个方向转动一个角度，这样的图形运动 称为旋转，这个定点称为旋转中心，转动 的角称为旋转角. 注意：“将一个图形绕着某个方向旋 转一个角度”意味着图形上的每个点都同 时都按相同的方向转动相同的角度，因此， 旋转具有如下特征： 旋转不改变图形的大小和形状.
．
．
O
例题解析

本图案可以看做是一个菱形通过几次旋 转得到的？每次旋转了多少度？
旋转5次得到，旋 转角度分别等于 60°120°180°
240°300°
本课作业
3.4
共同进步！
欢迎批评指导！！
2019
ppt资料
14
议一议：
如图所示，如果把钟表的指针看作四边形AOBC， 它绕O点按顺时针方向旋转得到四边形 DOEF．在这个旋转过程中： 1.旋转中心是什么？旋转角是什么？ 2.经过旋转，点A，B分别移动 到什么位置？ 3.AO与DO的长有什么关系？ BO与EO呢？ 4.∠AOD与∠BOE有什么大 小关系？
旋转的基本性质
例题解析
解：（１）它的旋转中心是钟表的轴心；
（２）分针匀速旋转一周需要60分，因 此旋转20分，分针旋转的角度为:

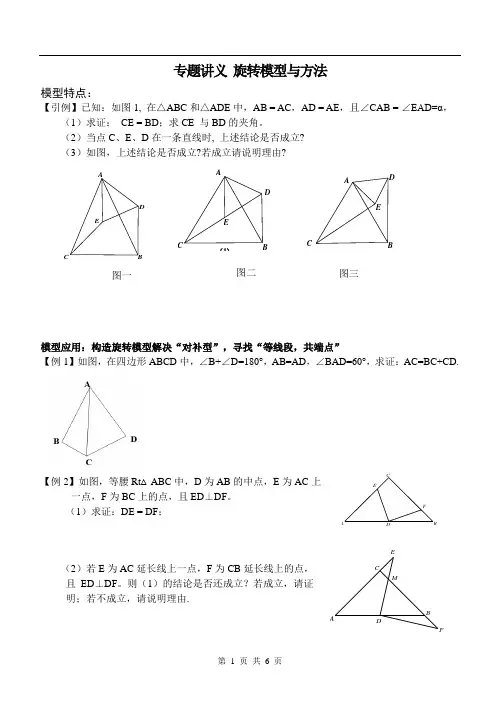
专题讲义 旋转模型与方法模型特点：【引例】已知：如图1, 在△ABC 和△ADE 中，AB = AC ，AD = AE ，且∠CAB = ∠EAD=α，（1）求证： CE = BD ；求CE 与BD 的夹角。

（2）当点C 、E 、D 在一条直线时, 上述结论是否成立? （3）如图，上述结论是否成立?若成立请说明理由?模型应用：构造旋转模型解决“对补型”，寻找“等线段，共端点” 【例1】如图，在四边形ABCD 中，∠B+∠D=180°，AB=AD ，∠BAD=60°，求证：AC=BC+CD.【例2】如图，等腰Rt △ABC 中，D 为AB 的中点，E 为AC 上一点，F 为BC 上的点，且ED ⊥DF 。

（1）求证：DE = DF ；（2）若E 为AC 延长线上一点，F 为CB 延长线上的点，且ED ⊥DF 。

则（1）的结论是否还成立？若成立，请证明；若不成立，请说明理由.E C D B A 1()EC DBA ED C B A 图二 图一 图三 FEDCB A MF E DC B A【例3】如图， 已知△ABC 中，∠B=300，现将△ABC 绕点A 顺时针旋转角度α至△ADE ，直 线BC 与直线DE 交于点F ，连结AF1）若α=600（如图1），则∠AFB= ；若α=900（如图2），则∠AFB= ， 2）若00＜α＜1200（如图3），则∠AFB= （用α表示）3）若1200＜α＜1800（如图4），则∠AFB 与α的数量关系是 ，并给予证明.〖练〗如图，任意△ABC ，分别以AB 、AC 为腰，以A 为顶角的顶点向△ABC 的两侧作等腰△ABM ，等腰△ACN ，且∠ANC=∠ABM ，MC 与NB 的延长线交于点O. （1）如图1，若∠ANC=∠ABM=30°，则∠O= ； （2）如图2，若∠ANC=∠ABM=45°，则∠O= ；（3）如图3，若∠ANC=∠ABM=α)900(︒<α<︒，猜想∠O 的度数（用含α的式子表示），并证明你的结论.图1 图2 图3图1F E D C B A 图2F E DC B A图3F ED CBA图4FEDCBANM O A C B NM OA CB N【例4】如图，已知在Rt △ABC 中，AB ＝BC ，∠ABC ＝90°，BD 为斜边AC 上的中线，E 为DC 上的一点，AG ⊥BE 于G ，BD 交AG 于点F.（1）求证：△ABF ≌△BCE ；（2）若点E 在DC 的延长线上，其他条件不变，则（1）中的结论还成立吗？若成立，请画出图形，并给予证明；若不成立，请说明理由.手牵手模型【例5】（1）如图1，△ABC 和△ECD 都是等边三角形；写出你认为正确的结论，并证明。

初中数学旋转的六大模型初中数学中，旋转是一个重要的几何变换。

通过旋转操作，可以改变图形的方向和位置，使得解题更加灵活、直观。

以下介绍了初中数学中与旋转相关的六大模型：1. 点的旋转点的旋转是最基本的模型。

通过指定旋转中心和旋转角度，可以将一个点绕着旋转中心进行旋转。

旋转角度可以为正数表示顺时针旋转，也可以为负数表示逆时针旋转。

点的旋转常用于解决图形对称、位置移动等问题。

2. 直线的旋转直线的旋转是指将一条直线绕着某个旋转中心进行旋转。

旋转后，直线上的点保持在同一直线上，但相对于旋转中心的位置发生变化。

直线的旋转常用于解决图形对称、位置移动等问题，也可以通过与其他图形的交点来求解交角等问题。

3. 多边形的旋转多边形的旋转是指将一个多边形绕着某个旋转中心进行旋转。

旋转后，多边形的所有边和角度都保持不变，只是位置发生变化。

多边形的旋转常用于解决图形对称、位置移动等问题，也可以通过旋转后的多边形与其他图形的关系来求解各种几何性质。

4. 圆的旋转圆的旋转是指将一个圆绕着某个旋转中心进行旋转。

旋转后，圆的半径和内外切直线都保持不变，只是位置发生变化。

圆的旋转常用于解决图形对称、位置移动等问题，也可以通过旋转后的圆与其他图形的关系来求解各种几何性质。

5. 坐标轴的旋转坐标轴的旋转是指将整个坐标系绕着某个旋转中心进行旋转。

旋转后，坐标轴的方向和位置都发生变化，但坐标系中的点的坐标值保持不变。

坐标轴的旋转常用于解决图形对称、位置移动等问题，也可以通过旋转后的坐标系来求解各种几何性质。

6. 空间立体图形的旋转空间立体图形的旋转是指将一个立体图形绕着某个旋转轴进行旋转。

旋转后，立体图形的形状和大小都保持不变，只是位置发生变化。

空间立体图形的旋转常用于解决立体几何中的对称、位置移动等问题，也可以通过旋转后的立体图形来求解各种几何性质。

知识图谱错题回顾旋转知识精讲一．半角模型“半角”旋转模型，经常会出现在等腰直角三角形、正方形中，在一般的等腰三角形中也会有涉及．二．等腰三角形旋转模型等腰三角形的旋转模型比较多，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化，证明的基本思想“SAS”．1．一般等腰三角形的旋转共顶点等腰三角形的旋转2．等边三角形的旋转3．等腰直角三角形的旋转三．对角互补模型四边形对角互补模型多数题目给出的条件会以四边形或三角形等旋转为载体．四．旋转相似模型共顶点相似的一般三角形模型：如图，图中 ABD ACE ∆∆∽，得到AB AD BDAC AE CE==，ABD ACE ∠=∠，ADB AEC ∠=∠，BAD CAE ∠=∠，则有 ABC ADE ∆∆∽．一．考点：1．旋转全等模型； 2．旋转相似模型；共顶点等边三角形的旋转共顶点等腰直角三角形的旋转三点剖析3．旋转中的轨迹与最值问题；二．重难点：1．这类题的关键是找到题目中所给的特殊条件，结合问题所要证明或者求解的边长角度问题，再去选择是要构造旋转全等还是通过已经得到的旋转全等的性质进一步证明．2．观察图形发现旋转得到的相似；3．通过添加辅助线构造旋转相似或者去挖掘隐含的相似图形．三．易错点：1．在利用旋转构造全等的时候注意辅助线的做法问题；2．构造旋转全等时候一定要有相等边长的条件．3．全等是相似的一个特例，旋转有时候也会出现全等，注意和旋转全等的区别和联系．题模一：旋转与全等例1.1.1已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．例1.1.2（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD．求证：EF=BE+FD；（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？题模精讲（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．例1.1.3如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．例1.1.4如图，△AEF中，∠EAF=45°，AG⊥EF于点G，现将△AEG沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE和DF相交于点C．（1）求证：四边形ABCD是正方形；（2）连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．（3）若EG=4，GF=6，BM=32，求AG、MN的长．题模二：旋转与相似例1.2.1如图1，点P在正方形ABCD的对角线AC上，正方形的边长是a，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N．（1）操作发现：如图2，固定点P，使△PEF绕点P旋转，当PM⊥BC时，四边形PMCN是正方形．填空：①当AP=2PC时，四边形PMCN的边长是________；②当AP=nPC时（n是正实数），四边形PMCN的面积是___________．（2）猜想论证如图3，改变四边形ABCD的形状为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则PMPN=__________．（3）拓展探究如图4，当四边形ABCD满足条件：∠B+∠D=180°，∠EPF=∠BAD时，点P在AC上，PE、PF分别交BC，CD于M、N点，固定P点，使△PEF绕点P旋转，请探究PMPN的值，并说明理由．例1.2.2数学活动课上，小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动．操作：使点D落在线段AB的中点处并使DF过点C（如图1），然后将其绕点D顺时针旋转，直至点E落在AC的延长线上时结束操作，在此过程中，线段DE与AC或其延长线交于点K，线段BC与DF相交于点G（如图2，3）．探究1：在图2中，求证：△ADK∽△BGD．探究2：在图2中，求证：KD平分∠AKG．探究3：①在图3中，KD仍平分∠AKG吗？若平分，请加以证明；若不平分，请说明理由．②在以上操作过程中，若设AC=BC=8，KG=x，△DKG的面积为y，请求出y与x的函数关系式，并直接写出x的取值范围．题模三：旋转中的轨迹与最值问题例1.3.1如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为．例1.3.2如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为______；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为______．（结果都保留π）例1.3.3如图1，点O为正方形ABCD的中心．（1）将线段OE绕点O逆时针方向旋转90︒，点E的对应点为点F，连结EF，AE，BF，请依题意补全图1；（2）根据图1中补全的图形，猜想并证明AE与BF的关系；（3）如图2，点G是OA中点，△EGF是等腰直角三角形，H是EF的中点，90∠=︒，EGF 22AB=，2GE=，△EGF绕G点逆时针方向旋转α角度，请直接写出旋转过程中BH的最大值．随练1.1在ABC ∆中，2AB BC ==，90ABC ∠=︒，BD 为斜边AC 上的中线，将ABD ∆绕点D 顺时针旋转α(0180α︒<<︒)得到EFD ∆，其中点A 的对应点为点E ，点B 的对应点为点F ，BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________;（2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN =__________;（3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系：____________________________.随练1.2在菱形ABCD 中，120BAD ∠=︒，4AB =，把一个含60°角的三角板与这个菱形叠合，使三角板的60°角的顶点与点A 重合，两边分别落在AB 、AC 上．将三角板绕点A 按逆时针旋转，设旋转角为α．（1）如图①，当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你通过观察或测量写出图中现有的两组相等线段(菱形的边和对角线除外)．（2）如图②，当60120α︒<<︒时，三角板的两边分别与BC 、CD 的延长线相交于点E 、F ，你在(1)中得到的结论还成立吗?若成立，请你选择一组加以证明；若不成立，请你说明理由． （3）当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你求出这个三角板与这个菱形重合部分的面积．OBDCAE 图1 CBH EFGODA图2随堂练习图1aH FEDA BC图2a H FE MNDA BCa HFEDAB C图3随练1.3如图1所示，在正方形ABCD 和正方形CGEF 中，点B 、C 、G 在同一条直线上，M 是线段AE 的中点，DM 的延长线交EF 于点N ，连接FM ，易证：DM=FM ，DM ⊥FM （无需写证明过程）（1）如图2，当点B 、C 、F 在同一条直线上，DM 的延长线交EG 于点N ，其余条件不变，试探究线段DM 与FM 有怎样的关系？请写出猜想，并给予证明；（2）如图3，当点E 、B 、C 在同一条直线上，DM 的延长线交CE 的延长线于点N ，其余条件不变，探究线段DM 与FM 有怎样的关系？请直接写出猜想．随练1.4已知：在ABC △中，AB AC =，点D 为BC 边的中点，点F 在AB 上，连结DF 并延长到点E ,使BAE BDF ∠=∠，点M 在线段DF 上，且ABE DBM ∠=∠． （1）如图，当45ABC ∠=°时， 求证：2AE MD =；（2）如图，当60ABC ∠=°时，则线段AE MD 、之间的数量关系为____________；（3）在（2）的条件下，延长BM 到P ，使MP BM =，连接CP ，若727AB AE ==，，求tan EAB ∠的值．CBD AEF MC BDAF EM随练1.5在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别在直线AB AC ，上移动时，BM NC MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系． （1）如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时QL=__________（2）如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明； （3）如图③，当点M N ，分别在边AB CA ，的延长线上时，若AN x =，则Q =_________（用x L ，表示）随练1.6（1）正方形ABCD 中，对角线AC 与BD 相交于点O ，如图1，请直接猜想并写出AO 与CD 之间的数量关系：；（2）如图2，将（1）中的△BOC 绕点B 逆时针旋转得到△BO 1C 1，连接AO 1，DC 1，请猜想线段AO 1与DC 1的数量关系，并证明你的猜想；（3）如图3，矩形ABCD 和Rt △BEF 有公共顶点，且∠BEF=90°，∠EBF=∠ABD=30°，则AEDF =______．随练1.7如图，正方形OABC 的边长为2，以O 为圆心，EF 为直径的半圆经过点A ，连接AE ，CF 相交于点P ，将正方形OABC 从OA 与OF 重合的位置开始，绕着点O 逆时针旋转90°，交点P 运动的路径长是______．图①M NDCBA图②MND CBAN图③MD CBA随练1.8已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．随练1.9如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．（1）求证：DE⊥AG；（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．①在旋转过程中，当∠OAG′是直角时，求α的度数；②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．自我总结课后作业作业1如图1，在△ABC中，∠BAC=90°，AB=AC．（1）若点M为AC上的任意一点，过M作MN⊥BC于点N，取BM的中点D，连接AD、DM，求证：AD=DN．（2）如图2，若M为BC上的任意一点，以线段CM为底边作等腰Rt△MCN，此时，取BM的中点D，连接AD、DN，则AD与DN有怎样的数量关系？说明理由．（3）如图3，在（2）的条件下将Rt△MNC绕C点旋转任意角度，连接BM，取BM的中点D，再连接AD、DN，则（2）中的结论仍然成立吗，它们之间又有怎样的位置关系？请说明理由．作业2已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．作业3在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？答：____（填“成立”或“不成立”）作业4在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．请直接写出AC1与BD1的数量关系和位置关系．（2）如图2，若四边形ABCD是菱形，AC=6，BD=8，判断AC1与BD1的数量关系和位置关系，并给出证明；（3）如图3，若四边形ABCD是平行四边形，AC=6，BD=12，连接DD1，设AC1=kBD1，请直接写出k的值和AC12+（kDD1）2的值．作业5在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．（一）尝试探究如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=________度，线段BE、EF、FD之间的数量关系为________．（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．（二）拓展延伸如图4，在等边△ABC 中，E 、F 是边BC 上的两点，∠EAF=30°，BE=1，将△ABE 绕点A 逆时针旋转60°得到△A ′B ′E ′（A ′B ′与AC 重合），连接EE ′，AF 与EE ′交于点N ，过点A 作AM ⊥BC 于点M ，连接MN ，求线段MN 的长度．作业6探索绕公用顶点的相似多边形的旋转：（1）如图1，已知：等边ABC ∆和ADE ∆，根据__________（指出三角形的全等或相似），可得到CE 与BD 的大小关系为：__________．（2）如图2，正方形ABCD 和正方形AEFG ，求：FCEB 的值；（3）如图3，矩形ABCD 和矩形AEFG ，AB kBC =，AE kEF =，求：FCEB 的值．作业7如图，边长为6的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针转60°得到FC ，连接DF ．则在点E 运动过程中，DF 的最小值是（ ）A ．6B ．3C ．2D ．1.5作业8已知等边△ABC 边长为2，放置在如图的水平桌面上，将△ABC 水平向右作无滑动翻滚，使△ABC 首次落回开始的位置，则等边△ABC 的中心O 经过的路径长为_________．作业9已知，点O 是等边△ABC 内的任一点，连接OA ，OB ，OC ．（1）如图1，已知∠AOB=150°，∠BOC=120°，将△BOC 绕点C 按顺时针方向旋转60°得△ADC ．①∠DAO 的度数是 ；②用等式表示线段OA ，OB ，OC 之间的数量关系，并证明； （2）设∠AOB=α，∠BOC=β．①当α，β满足什么关系时，OA+OB+OC 有最小值？请在图2中画出符合条件的图形，并说明理由；②若等边△ABC 的边长为1，直接写出OA+OB+OC 的最小值．作业10如图1，已知线段2BC =，点B 关于直线AC 的对称点是点D ，点E 为射线CA 上一点，且ED BD =，连接DE ，BE ．（1）依题意补全图1，并证明：△BDE 为等边三角形；（2）若45ACB ∠=︒，点C 关于直线BD 的对称点为点F ，连接FD 、FB ．将△CDE 绕点D 顺时针旋转α度（0360α︒<<︒）得到△''C DE ，点E 的对应点为'E ，点C 的对应点为点'C ．①如图2，当30α=︒时，连接'BC ．证明：'EF BC =； ②如图3，点M 为DC 中点，点P 为线段''C E 上的任意一点，试探究：在此旋转过程中，线段PM 长度的取值范围？作业11在矩形ABCD 中，点P 在AD 上，2AB =，1AP =，将三角板的直角顶点放在点P 处，三角板的两直角边分别能与AB 、BC 边相交于点E 、F ，连接EF ．（1）如图，当点E 与点B 重合时，点F 恰好与点C 重合，求此时PC 的长；（2）将三角板从（1）中的位置开始，绕点P 顺时针旋转，当点E 与点A 重合时停止，在这个过程中，请你观察、探究并解答：①PEF ∠的大小是否发生变化？请说明理由；②直接写出从开始到停止，线段EF 的中点所经过的路线长．ED M C'E'BCF AP答案解析 旋转题模一：旋转与全等 例 1.1.1【答案】图2成立，证明见解析，图3不成立，图3中AE 、CF 、EF 的关系是AE ﹣CF=EF 【解析】∵AB ⊥AD ，BC ⊥CD ，AB=BC ，AE=CF ， 在△ABE 和△CBF 中，90AB BC A C AE CF =⎧⎪∠=∠=⎨⎪=⎩， ∴△ABE ≌△CBF （SAS ）； ∴∠ABE=∠CBF ，BE=BF ； ∵∠ABC=120°，∠MBN=60°， ∴∠ABE=∠CBF=30°， ∴AE=12BE ，CF=12BF ； ∵∠MBN=60°，BE=BF ，∴△BEF 为等边三角形； ∴AE+CF=12BE+12BF=BE=EF ； 图2成立，图3不成立．证明图2．延长DC 至点K ，使CK=AE ，连接BK ， 在△BAE 和△BCK 中，90AB CB A BCK AE CK =⎧⎪∠=∠=⎨⎪=⎩则△BAE ≌△BCK ，∴BE=BK ，∠ABE=∠KBC ， ∵∠FBE=60°，∠ABC=120°， ∴∠FBC+∠ABE=60°，题模精讲∴∠FBC+∠KBC=60°， ∴∠KBF=∠FBE=60°， 在△KBF 和△EBF 中， BK BE KBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴△KBF ≌△EBF ， ∴KF=EF ， ∴KC+CF=EF ， 即AE+CF=EF ． 图3不成立，AE 、CF 、EF 的关系是AE ﹣CF=EF ．例1.1.2 【答案】（1）证明见解析（2）成立（3）EF=BE ﹣FD 【解析】（1）延长EB 到G ，使BG=DF ，连接AG ．∵∠ABG=∠ABC=∠D=90°，AB=AD ， ∴△ABG ≌△ADF ． ∴AG=AF ，∠1=∠2． ∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD ． ∴∠GAE=∠EAF ．又AE=AE，∴△AEG≌△AEF．∴EG=EF．∵EG=BE+BG．∴EF=BE+FD（2）（1）中的结论EF=BE+FD仍然成立．（3）结论EF=BE+FD不成立，应当是EF=BE﹣FD．证明：在BE上截取BG，使BG=DF，连接AG．∵∠B+∠ADC=180°，∠ADF+∠ADC=180°，∴∠B=∠ADF．∵AB=AD，∴△ABG≌△ADF．∴∠BAG=∠DAF，AG=AF．∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD．∴∠GAE=∠EAF．∵AE=AE，∴△AEG≌△AEF．∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD．例1.1.3【答案】（1）见解析（2）见解析（3）△ACN仍为等腰直角三角形【解析】（1）证明：如图1，∵EN∥AD，∴∠MAD=∠MNE，∠ADM=∠NEM．∵点M为DE的中点，∴DM=EM．在△ADM和△NEM中，∴MAD MNEADM NEM DM EM∠=∠⎧⎪∠=∠⎨⎪=⎩．∴△ADM ≌△NEM ． ∴AM=MN ．∴M 为AN 的中点． （2）证明：如图2，∵△BAD 和△BCE 均为等腰直角三角形， ∴AB=AD ，CB=CE ，∠CBE=∠CEB=45°． ∵AD ∥NE ，∴∠DAE+∠NEA=180°． ∵∠DAE=90°， ∴∠NEA=90°． ∴∠NEC=135°．∵A ，B ，E 三点在同一直线上， ∴∠ABC=180°﹣∠CBE=135°． ∴∠ABC=∠NEC ．∵△ADM ≌△NEM （已证）， ∴AD=NE ． ∵AD=AB ， ∴AB=NE ．在△ABC 和△NEC 中， AB NE ABC NEC BC EC =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△NEC ．∴AC=NC ，∠ACB=∠NCE ． ∴∠ACN=∠BCE=90°．∴△ACN 为等腰直角三角形．（3）△ACN 仍为等腰直角三角形． 证明：如图3，延长AB 交NE 于点F ， ∵AD ∥NE ，M 为中点， ∴易得△ADM ≌△NEM ， ∴AD=NE ． ∵AD=AB ， ∴AB=NE ． ∵AD ∥NE ， ∴AF ⊥NE ，在四边形BCEF 中， ∵∠BCE=∠BFE=90°∴∠FBC+∠FEC=360°﹣180°=180° ∵∠FBC+∠ABC=180° ∴∠ABC=∠FEC在△ABC 和△NEC 中，AB NE ABC NEC BC EC =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△NEC ．∴AC=NC ，∠ACB=∠NCE ． ∴∠ACN=∠BCE=90°．∴△ACN 为等腰直角三角形．例1.1.4 【答案】（1）见解析（2）MN 2=ND 2+DH 2；理由见解析 （3）AG=12；MN=52【解析】（1）证明：∵△AEB 由△AED 翻折而成， ∴∠ABE=∠AGE=90°，∠BAE=∠EAG ，AB=AG ， ∵△AFD 由△AFG 翻折而成，∴∠ADF=∠AGF=90°，∠DAF=∠FAG ，AD=AG ， ∵∠EAG +∠FAG=∠EAF=45°，∴∠ABE=∠AGE=∠BAD=∠ADC=90°， ∴四边形ABCD 是矩形， ∵AB=AD ，∴四边形ABCD 是正方形； （2）MN 2=ND 2+DH 2， 理由：连接NH ，∵△ADH 由△ABM 旋转而成， ∴△ABM ≌△ADH ， ∴AM=AH ，BM=DH ，∵由（1）∠BAD=90°，AB=AD ， ∴∠ADH=∠ABD=45°， ∴∠NDH=90°，∵AM AH EAF NAH AN AN =⎧⎪∠=∠⎨⎪=⎩， ∴△AMN ≌△AHN ， ∴MN=NH ，∴MN 2=ND 2+DH 2；（3）设AG=BC=x ，则EC=x ﹣4，CF=x ﹣6， 在Rt △ECF 中，∵CE 2+CF 2=EF 2，即（x ﹣4）2+（x ﹣6）2=100，x 1=12，x 2=﹣2（舍去） ∴AG=12，∵AG=AB=AD=12，∠BAD=90°， ∴BD=22AB AD +=221212+=122，∵BM=32，∴MD=BD ﹣BM=122﹣32=92， 设NH=y ，在Rt △NHD 中，∵NH 2=ND 2+DH 2，即y 2=（92﹣y ）2+（32）2，解得y=52，即MN=52．题模二：旋转与相似例1.2.1【答案】（1）①13a②()221an+（2）ab（3）见解析【解析】（1）①如图2，∵PM⊥BC，AB⊥BC ∴△PMC∽△ABC∴CP PM CA AB=又∵AP=2PC∴PMAB=13，即PMa=13∴PM=13a，即正方形PMCN的边长是13a②当AP=nPC时（n是正实数），PMAB=11n+∴PM=11n+a∴四边形PMCN的面积=（11n+a）2=()221an+（2）如图3，过P作PG⊥BC于G，作PH⊥CD于H，则∠PGM=∠PHN=90°，∠GPH=90°∵Rt△PEF中，∠FPE=90°∴∠GPM=∠HPN∴△PGM∽△PHN∴PMPN=PGPH由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==∵AB=a，BC=b∴PG PHa b=，即PGPH=ab∴PM PN=ab（3）如图4，过P作PG∥AB，交BC于G，作PH∥AD，交CD于H，则∠HPG=∠DAB ∵∠EPF=∠BAD∴∠EPF=∠GPH，即∠EPH+∠HPN=∠EPH+∠GPM∴∠HPN=∠GPM∵∠B+∠D=180°∴∠PGC+∠PHC=180°又∵∠PHN+∠PHC=180°∴∠PGC=∠PHN∴△PGM ∽△PHN ∴PM PN =PGPH① 由PG ∥AB ，PH ∥AD 可得， PG CP PHAB CA AD==即PG ABPH AD=② ∴由①②可得，PM PN =ABAD例1.2.2【答案】探究1：见解析；探究2：见解析；探究3：①KD 仍平分∠AKG ②y=2x ，其中4838x ≤≤- 【解析】探究1，∵∠KAD=∠KDG=∠DBG=45°， ∴∠KDA+∠BDG=135°． ∵∠BDG+∠BGD=135°， ∴∠KDA=∠BGD ， ∴△ADK ∽△BGD ；探究2，∵△ADK ∽△BGD ， ∴AK KD =BD DG， ∵点D 是线段AB 的中点， ∴BD=AD ，∴AK KD=AD DG，∴AK AD=KD DG，∵∠KAD=∠KDG=45°，∴△ADK∽△DCK，∴∠AKD=∠DKC，∴KD平分∠AKG．探究3，①KD仍平分∠AKG．理由如下：∵同探究1可得△ADK∽△BGD，同探究2可得，△ADK∽△DGK，∴∠AKD=∠DKG，∴KD仍平分∠AKG；②如图，过点D作DM⊥AC于点M，DN⊥KG于点N，由①知线段KD平分∠AKG，∴DM=DN．∵AC=BC=8，点D是线段AB的中点，∠KAD=45°，∴DM=DN=4．∵KG=x，∴S△DKG=y=12×4x=2x，对于图3的情况同理可得y=2x，综上所示，y=2x，其中4≤x≤83﹣8．题模三：旋转中的轨迹与最值问题例1.3.1【答案】18﹣52【解析】如图，作AP1⊥BD垂足为P1，∵∠DBA=45°，AB=10，∴∠P1AB=∠DBA=45°，AP1=P1B=52，∵AM=MD=12AD=4，当AP1旋转到与射线AD的重合时（点P1与点E重合），ME就是MQ最小值=52﹣4，当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值=AM+AF=14，∴MQ的最大值与最小值的差=14﹣（52﹣4）=18﹣52．故答案为18﹣52．例1.3.2【答案】33π，2313+nπ【解析】∵菱形ABCD中，AB=2，∠C=60°，∴△ABD是等边三角形，BO=DO=1，AO=223AD DO-=，第一次旋转的弧长=6033 1803ππ⨯=，∵第一、二次旋转的弧长和=60360323 1801803ππ⨯⨯+=π，第三次旋转的弧长为：601 1803ππ⨯=∵3n÷3=n，故经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为：n×（233π+3π）=2313+nπ．例1.3.3【答案】（1）见解析（2）AE ⊥BF （3）25+ 【解析】（1）正确画出图形；………………1分（2）延长EA 交OF 于点H ，交BF 于点G …2分∵O 为正方形ABCD 的中心， ∴OB OA =，∠AOB ＝90°……3分∵OE 绕点O 逆时针旋转90°角得到OF ∴OF OE =∴∠AOB ＝∠EOF ＝90° ∴∠EOA ＝∠FOB ……4分 在△EOA 和△FOB 中，OF OE =，OB OA =，∠EOA ＝∠FOB ， ∴△EOA ≌△FOB ∴BF AE =.……5分 ∴∠OEA ＝∠OFB ∵∠OEA +∠OHA ∴∠OFB +∠FHG =90° ∴AE ⊥BF ……6分（3）BH 的最大值为25+……8分随练1.1【答案】（1）BE FC =；（2）22FC ；（3）222BF CE AC +=. 【解析】（1）BE FC =； （2）证明：如图，随堂练习∵AB BC =，90ABC ∠=︒，BD 为斜边中线，∴12BD AD CD AC ===，BD AC ⊥ ∵EFD ∆是由ABD ∆旋转得到的，∴DE DF DB DC ===，90EDF ADB BDC ∠=∠=∠=︒ ∴EDF BDF BDC BDF ∠+∠=∠+∠，即BDE FDC ∠=∠，∴BDE FDC ∆∆≌，∴BE FC =且12∠=∠又∵34∠=∠，∴90FHE FDE ∠=∠=︒ ,即BE CF ⊥连接BF ，取BF 中点G ，连接MG 、NG .∵M 为EF 中点，G 为BF 中点，N 为BC 中点 ∴MG BE ∥，12MG BE =；NG FC ∥，12NG FC = 又∵EB FC =，BE FC ⊥∴MG NG =，90MGN ∠=︒，∴MGN ∆为等腰直角三角形，∴MN =. （3）222BF CE AC +=. 随练1.2【答案】见解析【解析】（1）BE CF =，AE AF =，CE DF =．写出两组即可． （2）（1）中的结论仍然成立．如图，BE CF =的结论仍然成立． 证明如下：∵在菱形ABCD 中，120BAD ∠=︒，∴60BAC ABC ACD CAD ∠=∠=∠=∠=︒，∴AB AC =． 又由题意可知，60EAF ∠=︒，∴BAE CAF ∠=∠． 在△BAE 和△CAF 中，ABE ACF AB ACBAE CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAE ≌△CAF ．∴BE CF =．（3）当060α︒<<︒时，三角板与这个菱形重合部分的面积就是四边形AECF 的面积． 由题意可证△BAE ≌△CAF ．∴四边形AECF 的面积就是△ABC 的面积． ∵4AB =，∴所求图形的面积为43平方单位．随练1.3 【答案】（1）DM=FM ，DM ⊥FM （2）DM ⊥FM ，DM=FM 【解析】（1）如图2，DM=FM ，DM ⊥FM ， 证明：连接DF ，NF ，∵四边形ABCD 和CGEF 是正方形， ∴AD ∥BC ，BC ∥GE ， ∴AD ∥GE ，∴∠DAM=∠NEM ， ∵M 是AE 的中点， ∴AM=EM ，在△MAD 与△MEN 中， AMD=EMN AM=EM DAM=NEM ∠∠⎧⎪⎨⎪∠∠⎩， ∴△MAD ≌△MEN ， ∴DM=MN ，AD=EN ， ∵AD=CD ， ∴CD=NE ，∵CF=EF ，∠DCF=∠DCB=90°， 在△DCF 与△NEF 中， CD=NE DCF=NEF=90CF=EF ⎧⎪∠∠︒⎨⎪⎩， ∴△DCF ≌△NEF ，∴DF=NF ，∠CFD=∠EFN ， ∵∠EFN+∠NFC=90°， ∴∠DFC+∠CFN=90°， ∴∠DFN=90°，∴DM ⊥FM ，DM=FM（2）猜想：DM ⊥FM ，DM=FM ， 证明如下：如图3，连接DF ，NF ， 连接DF ，NF ，∵四边形ABCD 是正方形， ∴AD ∥BC ，∵点E 、B 、C 在同一条直线上， ∴AD ∥CN ，∴∠ADN=∠MNE ，在△MAD 与△MEN 中， AMD=EMN AM=EM DAM=NEM ∠∠⎧⎪⎨⎪∠∠⎩， ∴△MAD ≌△MEN ， ∴DM=MN ，AD=EN ， ∵AD=CD ， ∴CD=NE ， ∵CF=EF ，∵∠DCF=90°+45°=135°，∠NEF=180°﹣45°=135°， ∴∠DCF=∠NEF ， 在△DCF 与△NEF 中， CD=NE DCF=NEF=135CF=EF ⎧⎪∠∠︒⎨⎪⎩， ∴△MAD ≌△MEN ，∴DF=NF ，∠CFD=∠EFN ， ∵∠CFD+∠EFD=90°， ∴∠NFE+∠EFD=90°， ∴∠DFN=90°，∴DM ⊥FM ，DM=FM ．随练1.4【答案】（1）见解析（2）2AE MD =（3）32【解析】该题考查的是四边形综合． （1）如图，连结AD ∵AB AC =，BD CD = ∴AD BC ⊥又∵45ABC ∠=°∴cos BD AB ABC =∠即2AB BD = ∵BAE BDM ∠=∠，ABE DBM ∠=∠ ∴△ABE ∽△DBM ∴2AE ABDM DB== ∴2AE MD =（2）与（1）类似可知△DBM ∽△ABE ， 又60ABC ∠=︒，∴12MD BD AE AB ==， ∴2AE MD = （3）如图2连结AD 、EP ， ∵△ABE ∽△DBM∴AEB BM D ∠=∠，2BE ABBM DB== ∴2EB BM = 又∵BM MP = ∴EB BP =∵ABE DBM ∠=∠ ∴60EBP ABC ∠=∠=︒ ∴△BEP 等边三角形∴EM BP ⊥即90BMD ∠=︒ ∴90AEB BMD ∠=∠=︒在Rt △AEB中，AE =7AB =， tan EAB ∠的值为随练1.5【答案】见解析【解析】(Ⅰ)BM 、NC 、MN 之间的数量关系BM NC MN +=．此时23Q L =． (Ⅱ)猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE BM =，连结DE ． ∵BD CD =，且120BDC ∠=︒． ∴30DBC DCB ∠=∠=︒．又△ABC 是等边三角形，∴90MBD NCD ∠=∠=︒．在△MBD 与△ECD 中，BM CE MBD ECD BD DC =⎧⎪∠=∠⎨⎪=⎩∴△MBD ≌△ECD (SAS)．∴DM DE =，BDM CDE ∠=∠． ∴60EDN BDC MDN ∠=∠-∠=︒．在△MDN 与△EDN 中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩∴△MDN ≌△EDN (SAS)． ∴MN NE NC BM ==+． △AMN 的周长Q AM AN MN =++()AM AN NC BM =+++()()AM BM AN NC =+++AB AC =+2AB =．而等边△ABC 的周长3L AB = ∴2233Q AB L AB ==． (Ⅲ)如图③，当M 、N 分别在AB 、CA 的延长线上时，若AN x =，则223Q x L =+（用x 、L 表示）．随练1.6【答案】（1）AO=22CD ．理由如下：∵四边形ABCD 为正方形，∴AO=OC=OD ，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=22CD ，故答案为AO=22CD ；（2）∵四边形ABCD 为正方形，∴AB=BC ，AC=BD ，OB=OC ，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC 和△OBC 都是等腰直角三角形，∴2,2AC AB BC BD ==，∴2BD AB =，∵△BOC 绕点B 逆时针方向旋转得到△BO 1C 1，∴∠O 1BC 1=∠OBC=45°，OB=O 1B ，BC 1=BC ，∴BC 1=2BO 1，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC 1∽△BAO 1，∴11DC AO BD BA ==，∴11AO =； （3）在R t △EBF 中，cos ∠EBF=EBFB在R t △ABD 中，cos ∠ABD=ADBD ，∵∠EBF=∠ABD=30°，∴BE AD BF BD ==，∵∠EBF+∠FBA=∠ABD+∠FBA ，即∠EBA=∠FBD ，∴△AEB ∽△FBD ，∴AEDF =，故答案为【解析】（1）根据正方形的性质得AO=OC=OD ，∠ODC=∠OCD=45°，∠DOC=90°，由勾股定理得到AO 与CD 之间的数量关系；（2）如图2根据正方形的性质得AB=BC ，AC=BD ，OB=OC ，∠OBC=∠ABO=45°，∠BOC=90°，得到△ABC 和△OBC 都是等腰直角三角形，求出 BO ，得到，因为△BOC 绕点B 逆时针方向旋转得到△BO 1C 1，所以∠O 1BC 1=∠OBC=45°，OB=O 1B ，BC 1=BC ，BC 1BO 1，由∠1+∠3=45°，∠2+∠3=45°，得到∠1=∠2，于是得到△BDC 1∽△BAO 1，求出结论；（3）如图3在R t △ABD 中，cos ∠ABD=AB BD ，在R t △EBF 中，cos ∠EBF=EBFB 因为∠EBF=∠ABD=30°得到BE AD BF BD ==，再由∠EBF+∠FBA=∠ABD+∠FBA ，得到∠EBA=∠FBD ，△AEB ∽△FBD ，由相似的性质得到解．解：（1）AO=CD ．理由如下：如图1，∵四边形ABCD 为正方形，∴AO=OC=OD ，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=CD ，故答案为AO=CD ；（2）如图2，∵四边形ABCD 为正方形，∴AB=BC ，AC=BD ，OB=OC ，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC 和△OBC 都是等腰直角三角形，∴,AC BC ，∴BD ，∵△BOC 绕点B 逆时针方向旋转得到△BO 1C 1，∴∠O 1BC 1=∠OBC=45°，OB=O 1B ，BC 1=BC ，∴BC 1BO 1，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC 1∽△BAO 1，∴11DC AO BD BA ==，∴11AO =； （3）如图3 在R t △EBF 中，cos ∠EBF=EBFB在R t △ABD 中，cos ∠ABD=ADBD ，∵∠EBF=∠ABD=30°，∴BE AD BF BD ==，∵∠EBF+∠FBA=∠ABD+∠FBA ，即∠EBA=∠FBD ，∴△AEB ∽△FBD ，∴AEDF =，故答案为．随练1.7【答案】2π【解析】如图点P运动的路径是以G为圆心的弧EF，在⊙G上取一点H，连接EH、FH．∵四边形AOCB是正方形，∴∠AOC=90°，∴∠AFP=12∠AOC=45°，∵EF是⊙O直径，∴∠EAF=90°，∴∠APF=∠AFP=45°，∴∠H=∠APF=45°，∴∠EGF=2∠H=90°，∵EF=4，GE=GF，∴EG=GF=22，∴EF的长=9022180π•=2π．随练1.8【答案】（1）见解析；（2）①∠CMD=135° ②2【解析】（1）如图1中，∵CA=CB，∠ACB=90°，∴∠A=∠ABC=45°，∵△CEF是由△CAD旋转逆时针α得到，α=90°，∴CB与CE重合，∴∠CBE=∠A=45°，∴∠ABF=∠ABC+∠CBF=90°，∵BG=AD=BF，∴∠BGF=∠BFG=45°，∴∠A=∠BGF=45°，∴GF∥AC．（2）①如图2中，∵CA=CE，CD=CF，∴∠CAE=∠CEA，∠CDF=∠CFD，∵∠ACD=∠ECF，∴∠ACE=∠CDF，∵2∠CAE+∠ACE=180°，2∠CDF+∠DCF=180°，∴∠CAE=∠CDF，∴A、D、M、C四点共圆，∴∠CMF=∠CAD=45°，∴∠CMD=180°﹣∠CMF=135°．②如图3中，O是AC中点，连接OD、CM．∵AD=DB，CA=CB，∴CD⊥AB，∴∠ADC=90°，由①可知A、D、M、C四点共圆，∴当α从90°变化到180°时，点M在以AC为直径的⊙O上，运动路径是弧CD，∵OA=OC，CD=DA，∴DO⊥AC，∴∠DOC=90°，∴CD ∧的长=901180π=2π． ∴当α从90°变化到180°时，点M 运动的路径长为2π． 随练1.9【答案】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，090OA OD AOG DOE OG OE =⎧⎪∠=∠=⎨⎪=⎩，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①α=30°；②α=315°．【解析】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，090OA OD AOG DOE OG OE =⎧⎪∠=∠=⎨⎪=⎩，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①在旋转过程中，∠OAG′成为直角有两种情况：（Ⅰ）α由0°增大到90°过程中，当∠OAG′=90°时，∵OA=OD=12OG=12OG′， ∴在Rt △OAG′中，sin ∠AG′O='OA OG =12， ∴∠AG′O=30°，∵OA⊥OD，OA⊥AG′，∴OD∥AG′，∴∠DOG′=∠AG′O=30°，即α=30°；（Ⅱ）α由90°增大到180°过程中，当∠OAG′=90°时，同理可求∠BOG′=30°，∴α=180°﹣30°=150°．综上所述，当∠OAG′=90°时，α=30°或150°．②如图3，当旋转到A、O、F′在一条直线上时，AF′的长最大，∵正方形ABCD 的边长为1，∴OA=OD=OC=OB=22，∵OG=2OD，∴OG′=OG=2，∴OF′=2，∴AF′=AO+OF′=22+2，∵∠COE′=45°，∴此时α=315°．作业1【答案】（1）见解析；（2）AD=DN；（3）AD=DN，AD⊥DN【解析】（1）证明：解法一：如图1中，延长AD到K，使得DK=AD，连接AN、KN、KM．课后作业在△ADB 和△KDM 中，AD DK ADB KDM BD DM =⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△KDM ，∴AB=KM=AC ，∠BAD=∠MKD ，∴AB ∥KM ，∴∠KMC=∠BAC=90°，∵AB=AC ，∠BAC=90°，∴∠C=45°，∵MN ⊥BC ，∴∠MNC=90°，∠NMC=45°=∠KMC=∠C ，∴MN=NC ，在△ANC 和△KNM 中，CN MN ACN KMN AC KM =⎧⎪∠=∠⎨⎪=⎩，∴△ANC ≌△KNM ，∴AN=KN ，∠ANC=∠KNM ，∴∠KNA=∠MNC=90°∵AD=DK ，∴DN=AD=DK ，即AD=DN ．解法二：根据直角三角形斜边中线性质，可知AD=12BM ，DN=12BM ，由此即可证明． （2）如图2中，结论：AD=DN ．理由：延长AD 到K ，使得DK=AD ，连接AN 、KN 、KM ．在△ADB 和△KDM 中，AD DK ADB KDM BD DM=⎧⎪∠=∠⎨⎪=⎩，∴△ADB ≌△KDM ，∴AB=KM=AC ，∠BAD=∠MKD ，∴AB ∥KM ，∴∠KMN=∠B=45°，∵∠NMC=∠NCM=∠ACB=45°∴MN=NC ，∠KMN=∠ACN=90°在△ANC 和△KNM 中，CN MN ACN KMN AC KM =⎧⎪∠=∠⎨⎪=⎩，∴△ANC ≌△KNM ，∴AN=KN ，∠ANC=∠KNM ，∴∠KNA=∠MNC=90°∵AD=DK ，∴DN=AD=DK ，即AD=DN ．（3）如图3中，结论：AD=DN ，AD ⊥DN ．理由：延长AD 到K ，使得DK=AD ，连接AN 、KN 、KM ，延长KN 交AC 于G ．在△ADB 和△KDM 中，AD DK ADB KDM BD DM =⎧⎪∠=∠⎨⎪=⎩， ∴△ADB ≌△KDM ，∴AB=KM=AC ，∠BAD=∠MKD ，∴AB ∥KM ，∴∠KGC=∠BAC=90°，∴∠ACN+∠NMG=180°，∵∠KMN+∠NMG=180°，∴∠ACN=∠NMK ，在△ANC 和△KNM 中，CN MN ACN KMN AC KM =⎧⎪∠=∠⎨⎪=⎩， ∴△ANC ≌△KNM ，∴AN=KN ，∠ANC=∠KNM ，∴∠KNA=∠MNC=90°∵AD=DK ，∴DN=AD=DK ，DN ⊥AK ，即AD=DN ．AD ⊥DN ．作业2【答案】（1）见解析（2）成立（3）见解析【解析】本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质．（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG ．（2）结论仍然成立，连接AG ，过G 点作MN⊥AD 于M ，与EF 的延长线交于N 点；再证明⊥DAG⊥⊥DCG ，得出AG=CG ；再证出⊥DMG⊥⊥FNG ，得到MG=NG ；再证明⊥AMG⊥⊥ENG ，得出AG=EG ；最后证出CG=EG ．（3）结论依然成立．还知道EG⊥CG ．（1）证明：⊥四边形ABCD 是正方形，⊥⊥DCF=90°，在Rt⊥FCD 中，⊥G 为DF 的中点， ⊥CG=12FD ， 同理，在Rt⊥DEF 中， EG=12FD ， ⊥CG=EG ．（1） （1）中结论仍然成立，即EG=CG ．。